CFD Modeling of Chamber Filling in a Micro-Biosensor for Protein Detection
Abstract
1. Introduction
2. Materials and Methods
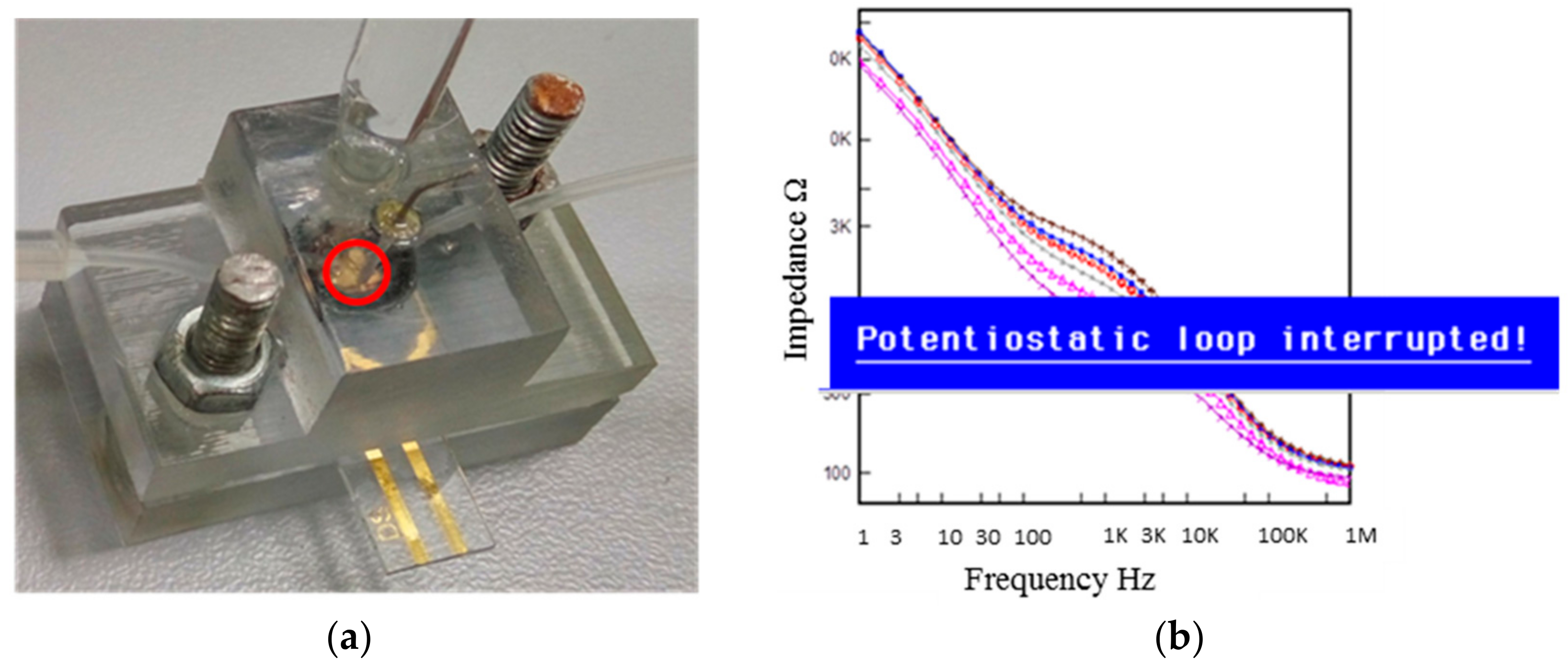
2.1. Fabrication of the Microfluidic Flow Cell
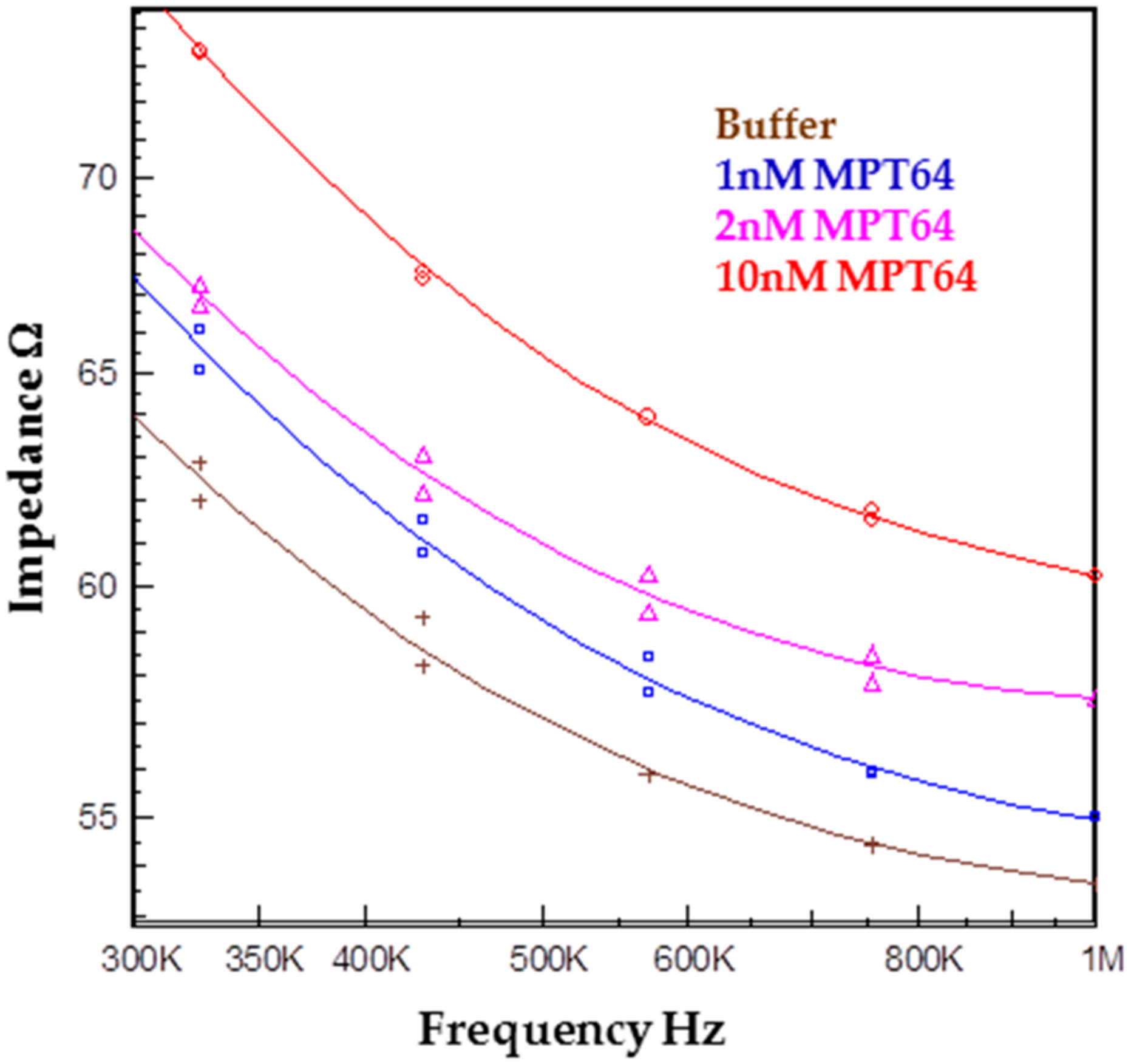
2.2. Preliminary Testing of a Biological Sample
3. CFD Analysis
3.1. Governing Equations and Physical Models
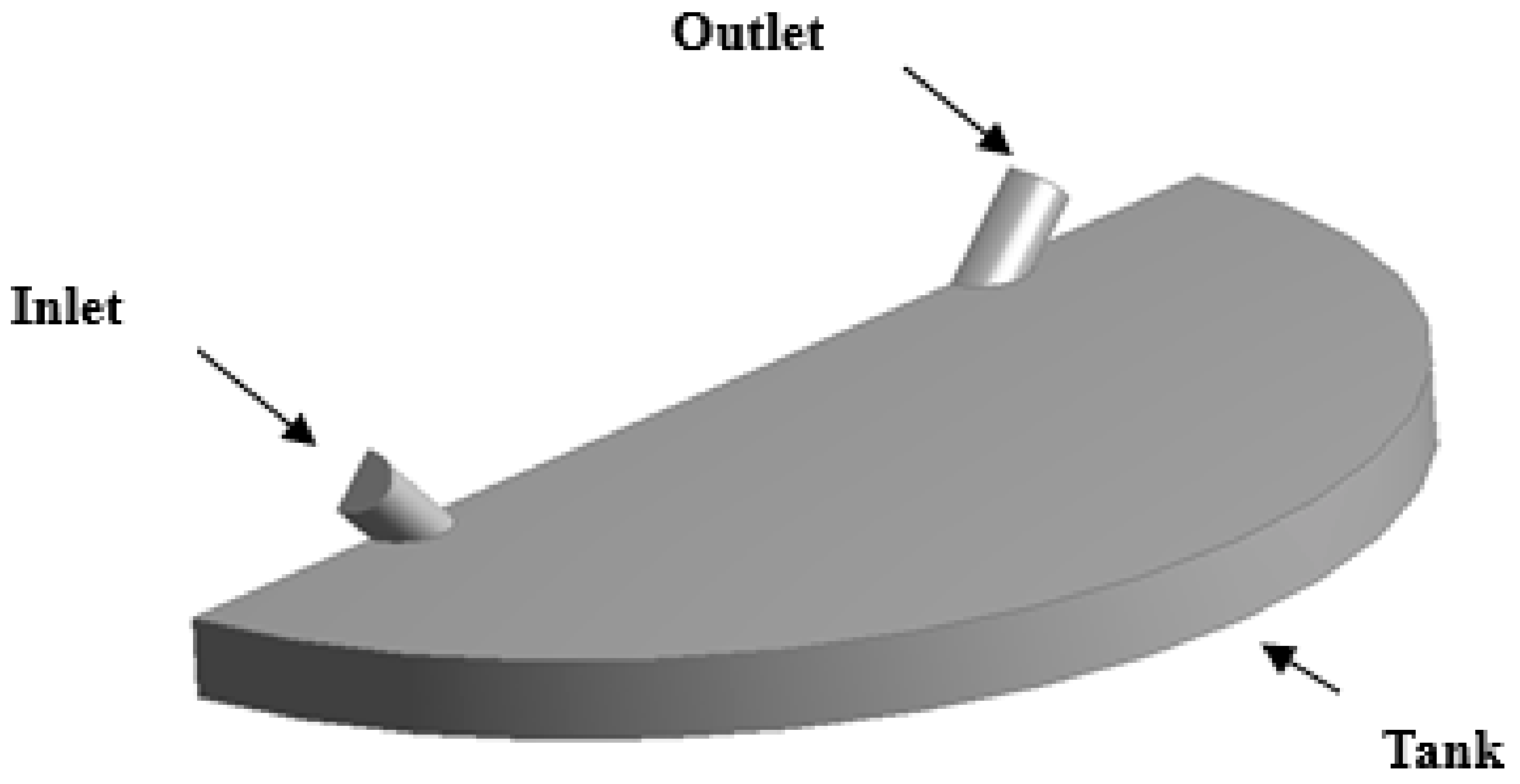
3.2. Computational Domain and Boundary Conditions
3.3. Mesh Verification and Boundary Conditions
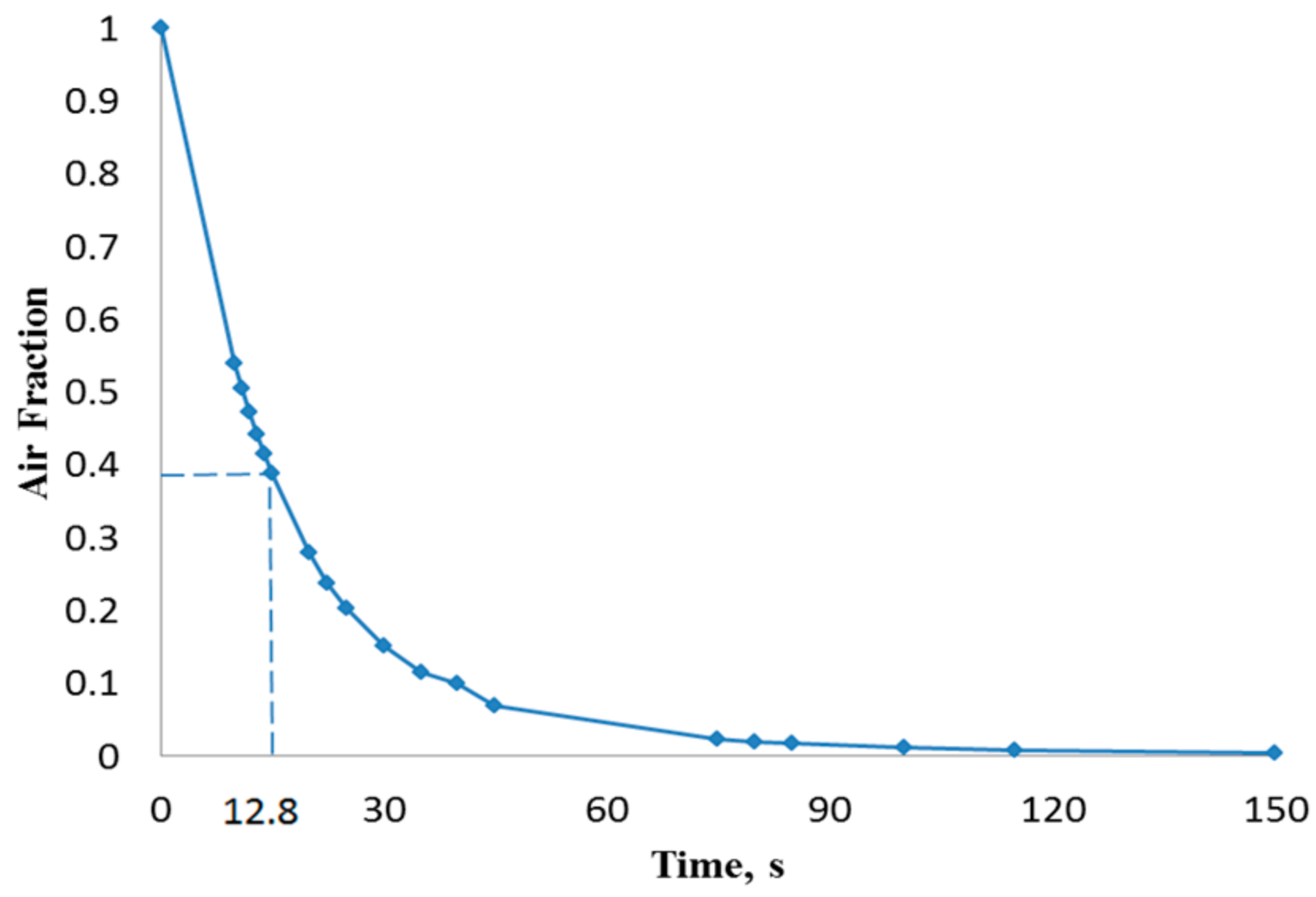
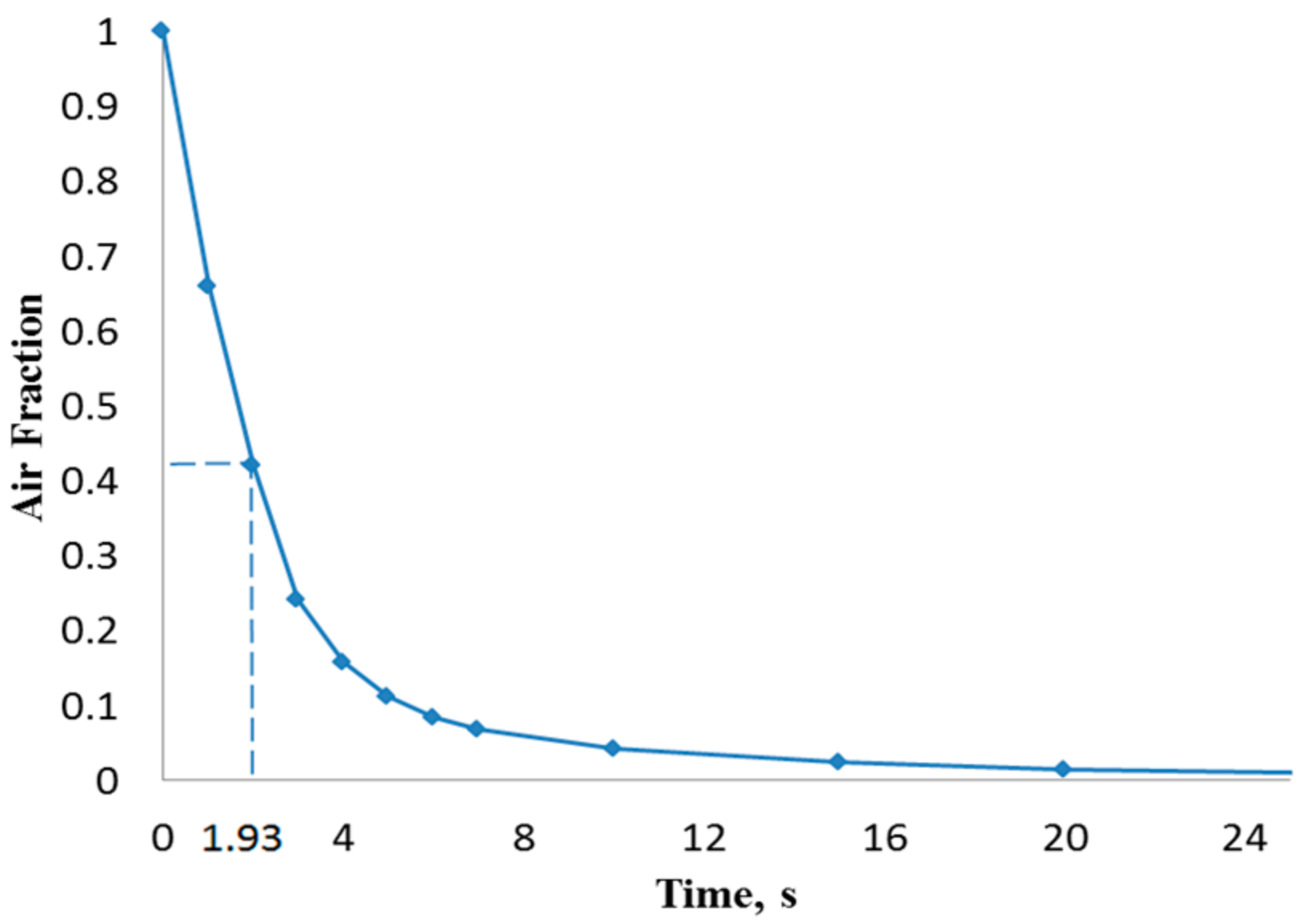
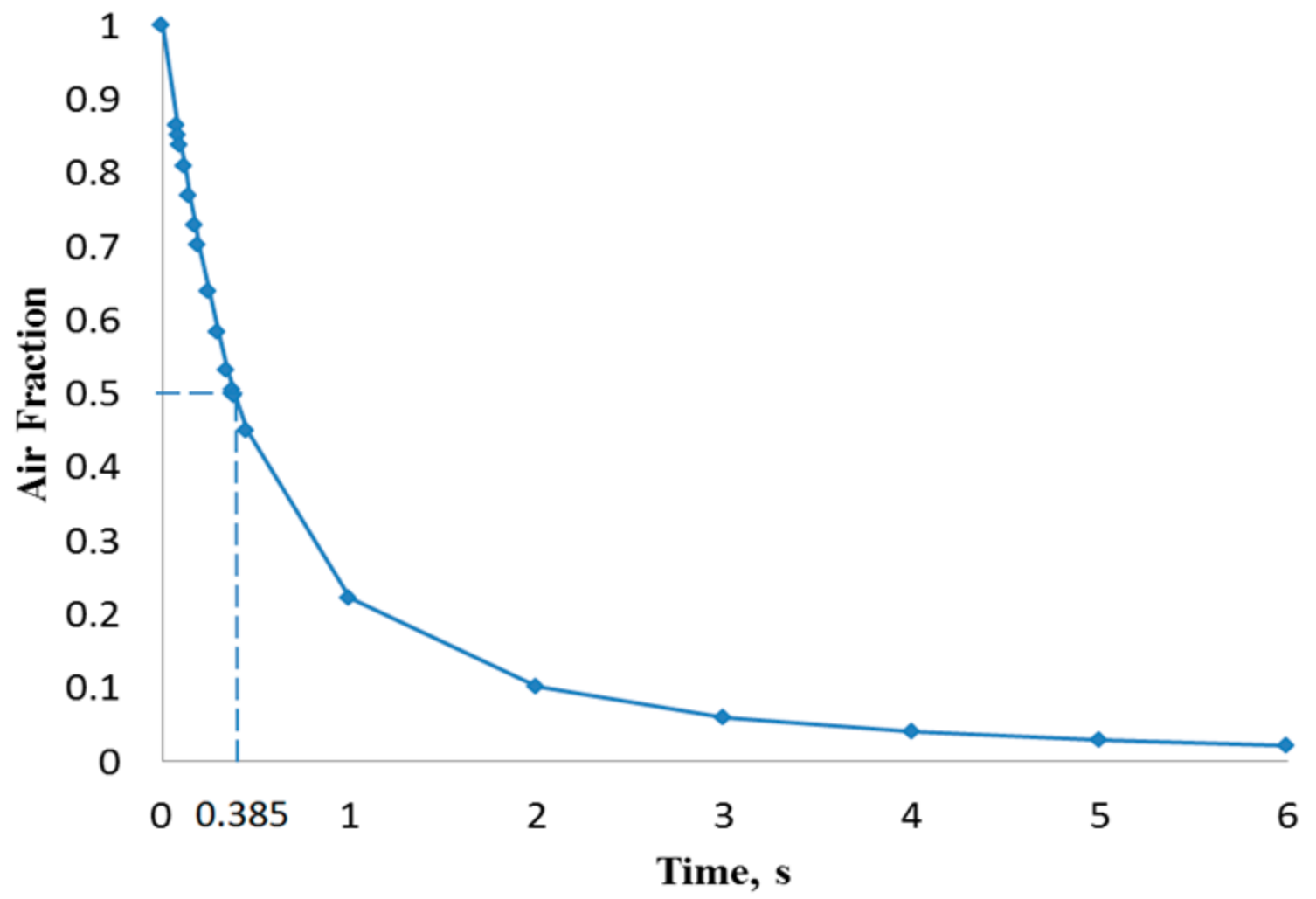
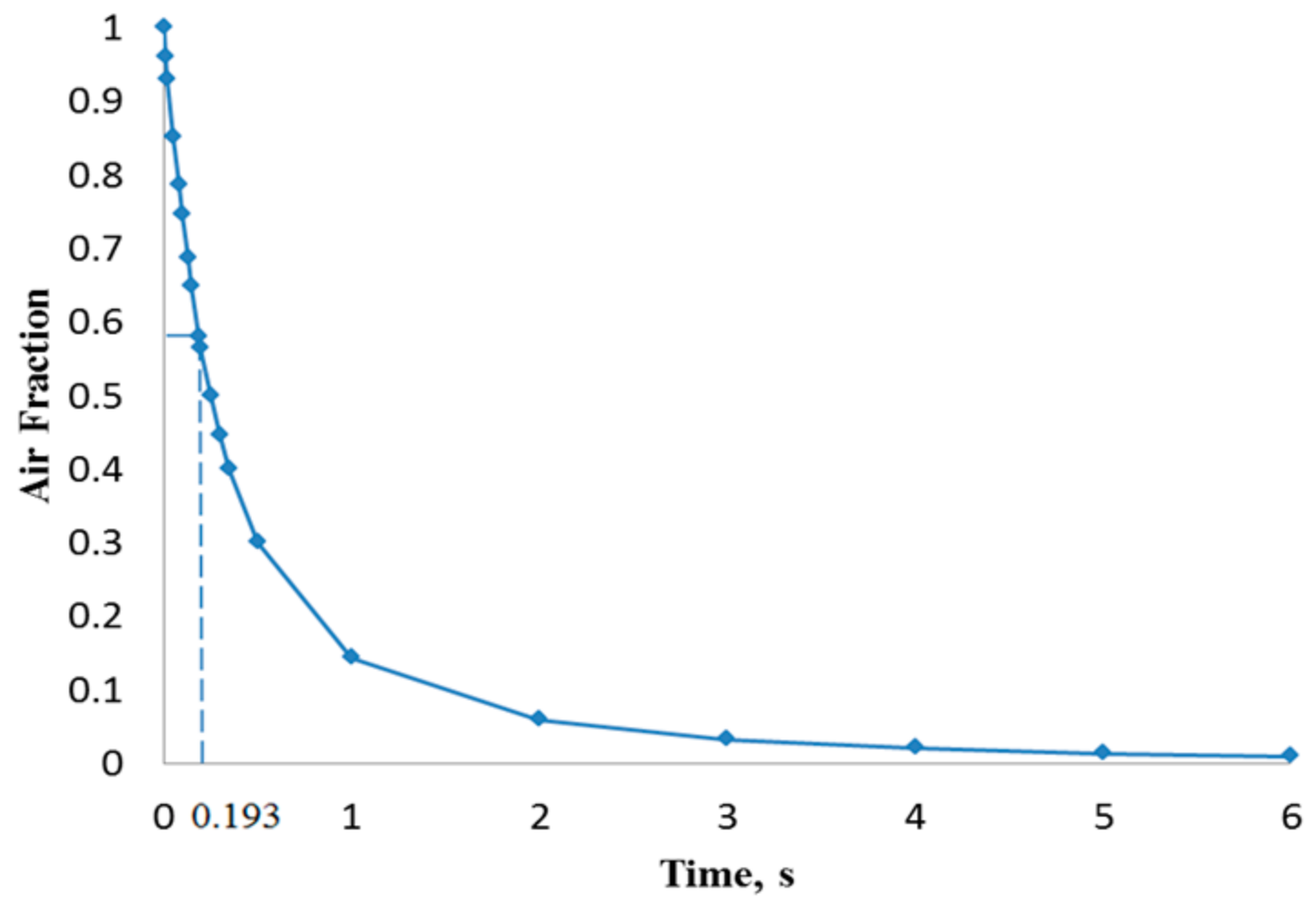
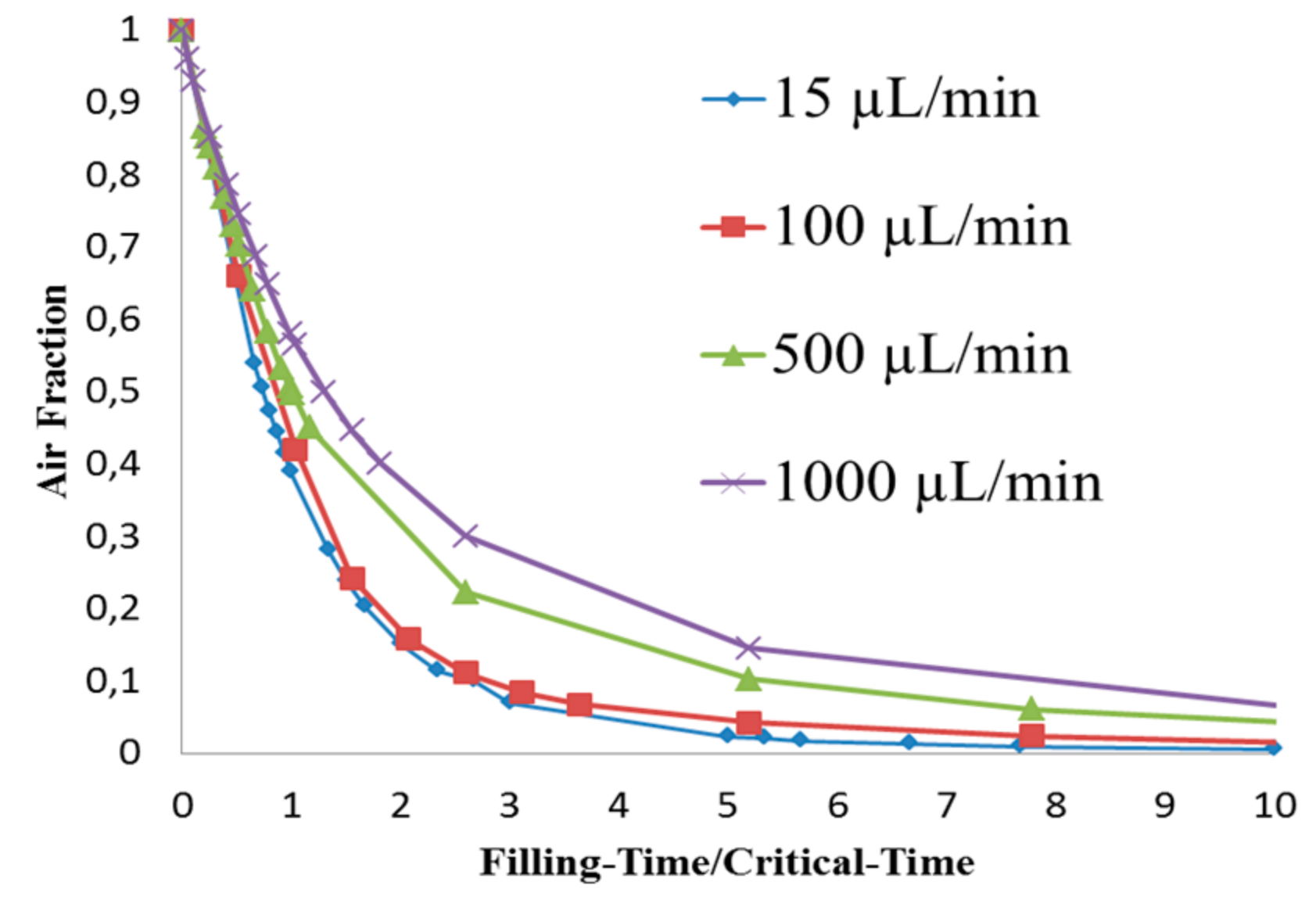
4. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- World Health Organization. Global Tuberculosis Report; WHO Press: Geneva, Switzerland, 2015. [Google Scholar]
- American Lung Association. Trends in Tuberculosis Morbidity and Mortality (ALA Research and Health Education Epidemiology and Statistics Unit 2013). Available online: http://www.lung.org/assets/documents/research/tb-trend-report.pdf (accessed on 1 June 2017).
- Steingart, K.R.; Ng, V.; Henry, M.; Hopewell, P.C.; Ramsay, A.; Cunningham, J.; Urbanczik, R.; Perkins, M.D.; Aziz, M.A.; Pai, M. Sputum processing methods to improve the sensitivity of smear microscopy for tuberculosis: A systematic review. Lancet Infect. Dis. 2006, 6, 664–674. [Google Scholar] [CrossRef]
- Kanayeva, D.; Bekniyazov, I.; Ashikbayeva, Z. Detection of tuberculosis using biosensors: Recent progress and future trends. Sens. Transducers 2013, 149, 166–173. [Google Scholar]
- Bekmurzayeva, A.; Sypabekova, M.; Kanayeva, D. Tuberculosis diagnosis using immunodominant, secreted antigens of mycobacterium tuberculosis. Tuberculosis 2013, 93, 381–388. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Inci, F.; De Libero, G.; Singhal, A.; Demirci, U. Point-of-care assays for tuberculosis: Role of nanotechnology/microfluidics. Biotechnol. Adv. 2013, 31, 438–449. [Google Scholar] [CrossRef]
- Noh, J.; Kim, H.C.; Chung, T.D. Biosensors in microfluidic chips. Microfluid. Technol. Appl. 2011, 304, 117–152. [Google Scholar]
- Ahmet Koyun, E.A.; İpek, Y.K. Biosensors and their principles. In A Roadmap of Biomedical Engineers and Milestones; Kara, S., Ed.; Intech: Rijeka, Croatia, 2012. [Google Scholar] [CrossRef]
- Fan, L.; Zhao, G.; Shi, H.; Liu, M.; Li, Z. A highly selective electrochemical impedance spectroscopy-based aptasensor for sensitive detection of acetamiprid. Biosens. Bioelectron. 2013, 43, 12–18. [Google Scholar] [CrossRef] [PubMed]
- Hiatt, L.A.; Cliffel, D.E. Real-time recognition of mycobacterium tuberculosis and lipoarabinomannan using the quartz crystal microbalance. Sens. Actuators B Chem. 2012, 174, 245–252. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.; He, F.; Yi, S.; Cui, X. A new mspqc for rapid growth and detection of mycobacterium tuberculosis. Biosens. Bioelectron. 2008, 24, 403–409. [Google Scholar] [CrossRef] [PubMed]
- Hong, S.C.; Chen, H.; Lee, J.; Park, H.-K.; Kim, Y.S.; Shin, H.-C.; Kim, C.-M.; Park, T.J.; Lee, S.J.; Koh, K.; et al. Ultrasensitive immunosensing of tuberculosis cfp-10 based on spr spectroscopy. Sens. Actuators B Chem. 2011, 156, 271–275. [Google Scholar] [CrossRef]
- Hong, S.C.; Lee, J.; Shin, H.-C.; Kim, C.-M.; Park, J.Y.; Koh, K.; Kim, H.-J.; Chang, C.L.; Lee, J. Clinical immunosensing of tuberculosis cfp-10 in patient urine by surface plasmon resonance spectroscopy. Sens. Actuators B Chem. 2011, 160, 1434–1438. [Google Scholar] [CrossRef]
- Jolly, P.; Formisano, N.; Tkac, J.; Kasak, P.; Frost, C.G.; Estrela, P. Label-free impedimetric aptasensor with antifouling surface chemistry: A prostate specific antigen case study. Sens. Actuators B Chem. 2015, 209, 306–312. [Google Scholar] [CrossRef]
- Sypabekova, M.; Bekmurzayeva, A.; Wang, R.H.; Li, Y.B.; Nogues, C.; Kanayeva, D. Selection, characterization, and application of dna aptamers for detection of mycobacterium tuberculosis secreted protein mpt64. Tuberculosis 2017, 104, 70–78. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Potter, B.M.; Gray, A.M.; Sacksteder, K.A.; Geisbrecht, B.V.; Laity, J.H. The solution structure of antigen mpt64 from mycobacterium tuberculosis defines a new family of beta-grasp proteins. J. Mol. Biol. 2007, 366, 375–381. [Google Scholar] [CrossRef]
- Kruh-Garcia, N.A.; Wolfe, L.M.; Chaisson, L.H.; Worodria, W.O.; Nahid, P.; Schorey, J.S.; Davis, J.L.; Dobos, K.M. Detection of mycobacterium tuberculosis peptides in the exosomes of patients with active and latent M. Tuberculosis infection using MRM-MS. PLoS ONE 2014, 9, e103811. [Google Scholar] [CrossRef]
- Arora, J.; Kumar, G.; Verma, A.K.; Bhalla, M.; Sarin, R.; Myneedu, V.P. Utility of mpt64 antigen detection for rapid confirmation of mycobacterium tuberculosis complex. J. Glob. Infect. Dis. 2015, 7, 66–69. [Google Scholar] [PubMed]
- Tadele, A.; Beyene, D.; Hussein, J.; Gemechu, T.; Birhanu, A.; Mustafa, T.; Tsegaye, A.; Aseffa, A.; Sviland, L. Immunocytochemical detection of mycobacterium tuberculosis complex specific antigen, MPT64, improves diagnosis of tuberculous lymphadenitis and tuberculous pleuritis. BMC Infect. Dis. 2014, 14, 585. [Google Scholar] [CrossRef] [PubMed]
- Kohli, R.; Punia, R.S.; Kaushik, R.; Kundu, R.; Mohan, H. Relative value of immunohistochemistry in detection of mycobacterial antigen in suspected cases of tuberculosis in tissue sections. Indian J. Pathol. Microbiol. 2014, 57, 574–578. [Google Scholar] [PubMed]
- Avci-Adali, M.; Paul, A.; Wilhelm, N.; Ziemer, G.; Wendel, H.P. Upgrading selex technology by using lambda exonuclease digestion for single-stranded dna generation. Molecules 2010, 15, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Keighley, S.D.; Li, P.; Estrela, P.; Mighorato, P. Optimization of dna immobilization on gold electrodes for label-free detection by electrochemical impedance spectroscopy. Biosens. Bioelectron. 2008, 23, 1291–1297. [Google Scholar] [CrossRef] [PubMed]
- Formisano, N.; Jolly, P.; Bhalla, N.; Cromhout, M.; Flanagan, S.P.; Fogel, R.; Limson, J.L.; Estrela, P. Optimisation of an electrochemical impedance spectroscopy aptasensor by exploiting quartz crystal microbalance with dissipation signals. Sens. Actuators B Chem. 2015, 220, 369–375. [Google Scholar] [CrossRef]
- Qin, L.H.; Liu, Z.H.; Yang, H.; Cai, J.L.; Bai, W.J.; Wang, J.; Liu, J.M.; Hu, Z.Y. Dynamic evolution and immunoreactivity of aptamers binding to polyclonal antibodies against mpt64 antigen of mycobacterium tuberculosis. Eur. J. Clin. Microbiol. Infect. Dis. 2014, 33, 1199–1209. [Google Scholar] [CrossRef] [PubMed]
- Hirt, C.; Nichols, B. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P.; Osher, S. A Level Set Approach for Computing Solutions to Incompressible Two-Phase Flow. J. Comput. Phys. 1994, 114, 146–159. [Google Scholar] [CrossRef]
- Sussman, M.; Fatemi, E.; Smereka, P.; Osher, S. An improved level set method for incompressible two-phase flows. Comput. Fluids 1998, 27, 663–680. [Google Scholar] [CrossRef]
- Sussman, M.; Almgren, A.; Bell, J.; Colella, P.; Howell, L.; Welcome, M. An Adaptive Level Set Approach for Incompressible Two-Phase Flows. J. Comput. Phys. 1999, 148, 81–124. [Google Scholar] [CrossRef]
- Sussman, M.; Puckett, E. A Coupled Level Set and Volume-of-Fluid Method for Computing 3D and Axisymmetric Incompressible Two-Phase Flows. J. Comput. Phys. 2000, 162, 301–337. [Google Scholar] [CrossRef]
- Tryggvason, G.; Bunner, B.; Esmaeeli, A.; Juric, D.; Al-Rawahi, N.; Tauber, W.; Han, J.; Nas, S.; Jan, Y. A Front-Tracking Method for the Computations of Multiphase Flow. J. Comput. Phys. 2001, 169, 708–759. [Google Scholar] [CrossRef]
- Unverdi, S.; Tryggvason, G. A front-tracking method for viscous, incompressible, multi-fluid flows. J. Comput. Phys. 1992, 99, 180. [Google Scholar] [CrossRef]
- Zheng, X.; Karniadakis, G. A phase-field/ALE method for simulating fluid–structure interactions in two-phase flow. Comput. Methods Appl. Mech. Eng. 2016, 309, 19–40. [Google Scholar] [CrossRef]
- Sun, D.; Tao, W. A coupled volume-of-fluid and level set (VOSET) method for computing incompressible two-phase flows. Int. J. Heat Mass Transf. 2010, 53, 645–655. [Google Scholar] [CrossRef]
- Nourgaliev, R.; Wiri, S.; Dinh, N.; Theofanous, T. On improving mass conservation of level set by reducing spatial discretization errors. Int. J. Multiph. Flow 2005, 31, 1329–1336. [Google Scholar] [CrossRef]
- Sethian, J. Fast Marching Methods. SIAM Rev. 1999, 41, 199–235. [Google Scholar] [CrossRef]
- Rojas-Solórzano, L.R.; Anna, B.; Bradeddine, S.L.; Amon, C.H. Modeling and Simulation of a Rollerball Microfluidic Device, ICNMM2009-82010. In Proceedings of the 7th International Conference on Nanochannels, Microchannels and Minichannels, Pohang, Korea, 22–24 June 2009. [Google Scholar]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A Continuum Method for Modelling Surface Tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Kalová, J.; Mareš, R. Reference Values of Surface Tension of Water. Int. J. Thermophys. 2015, 36, 1396–1404. [Google Scholar] [CrossRef]
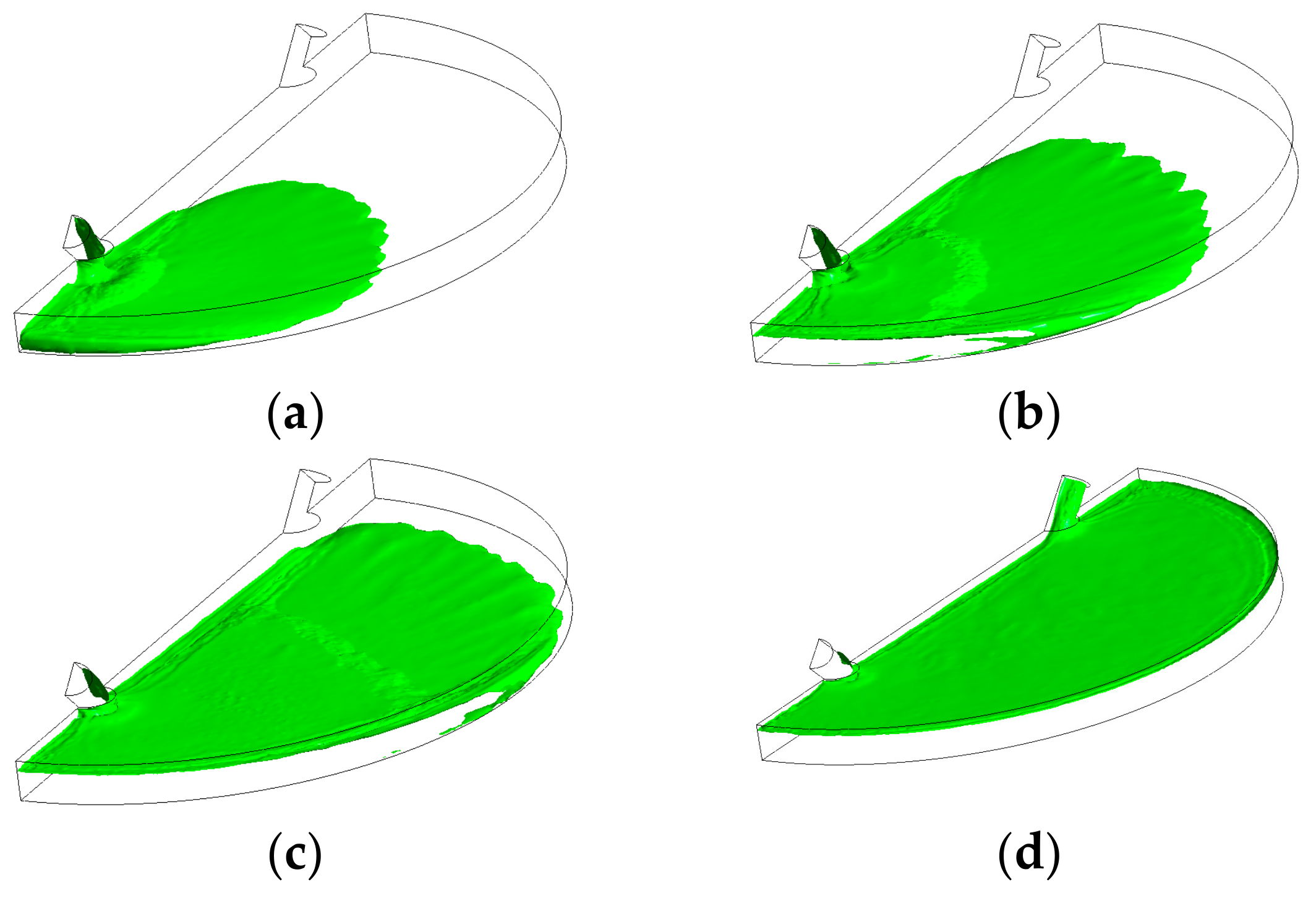
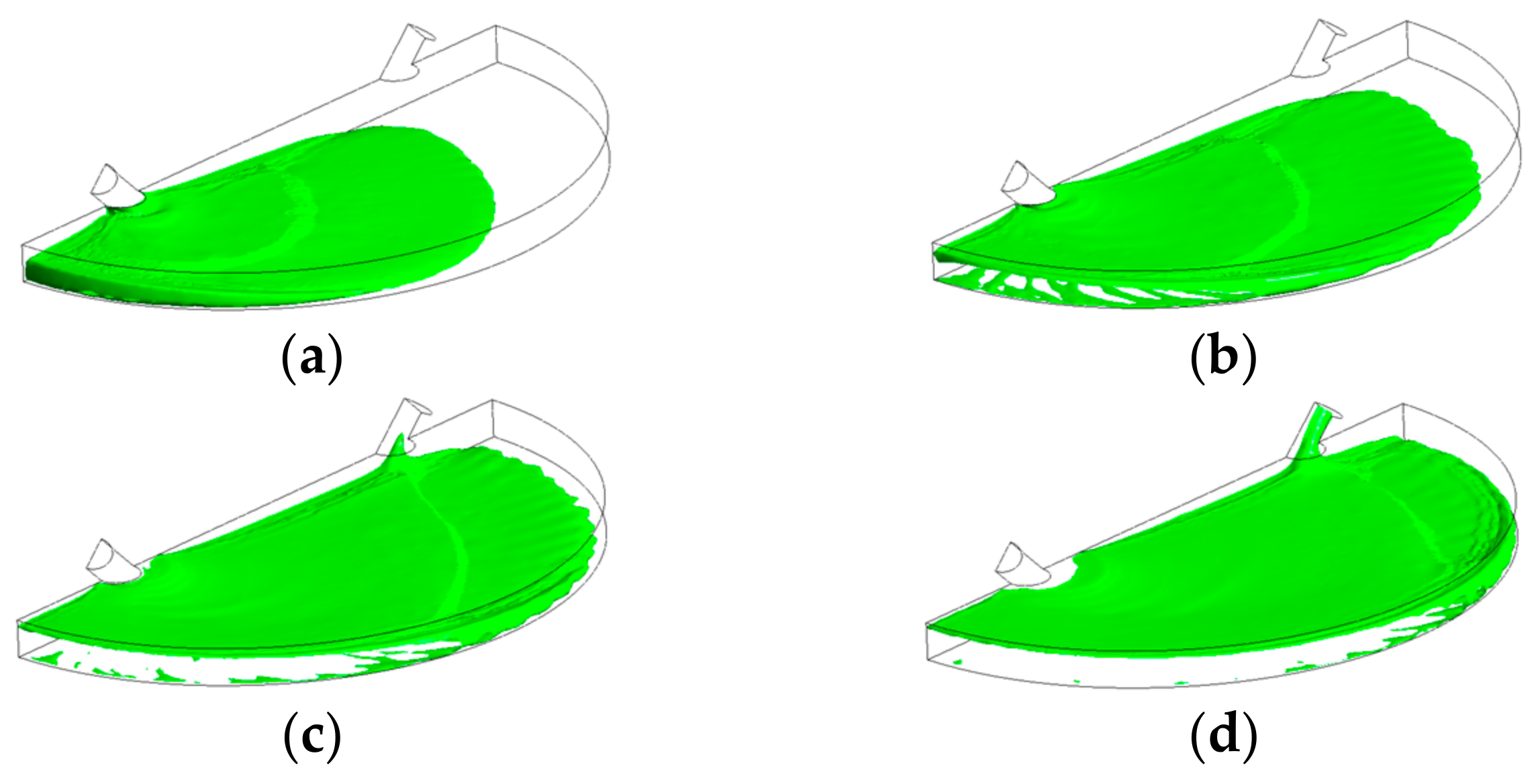
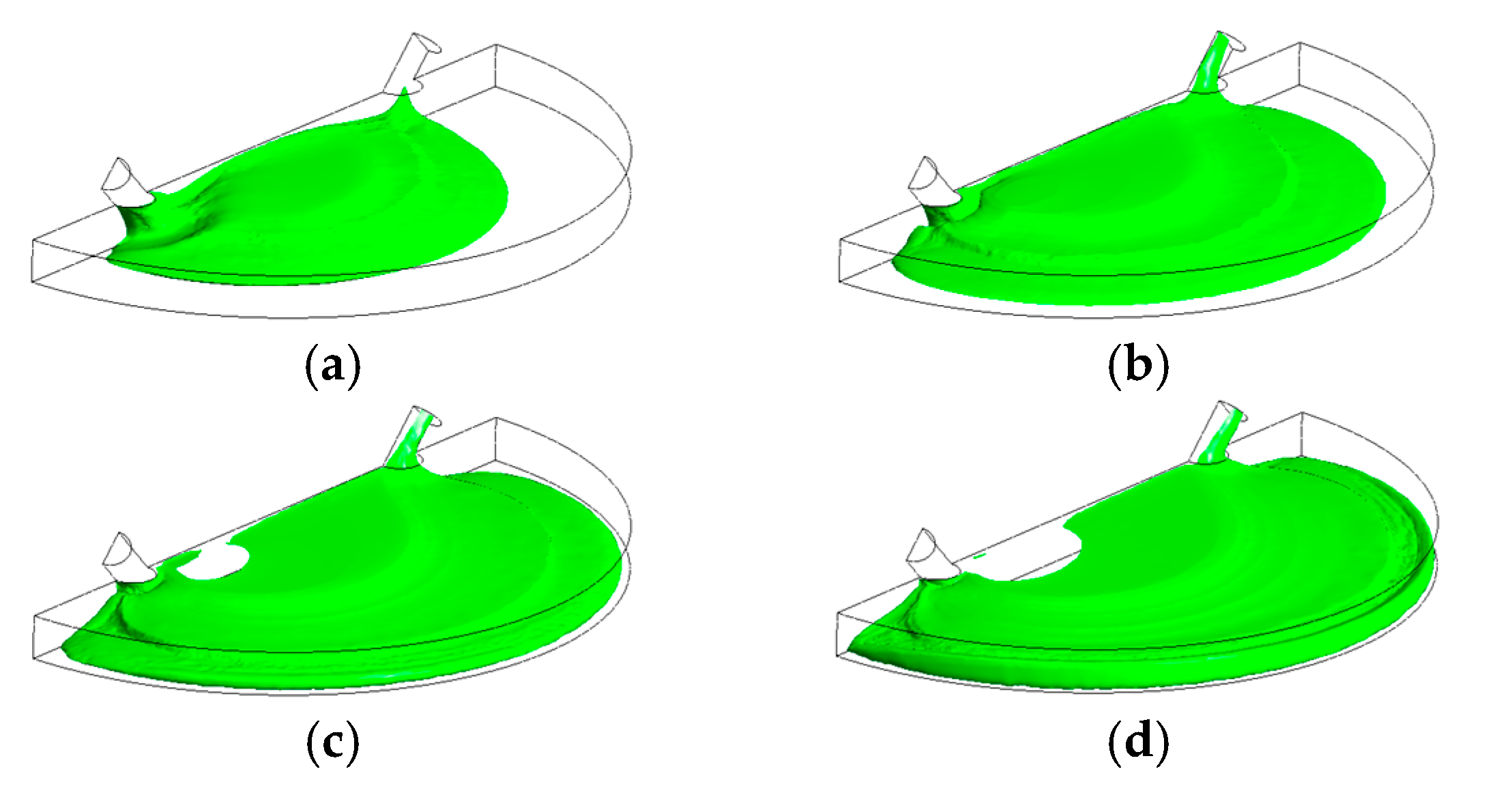
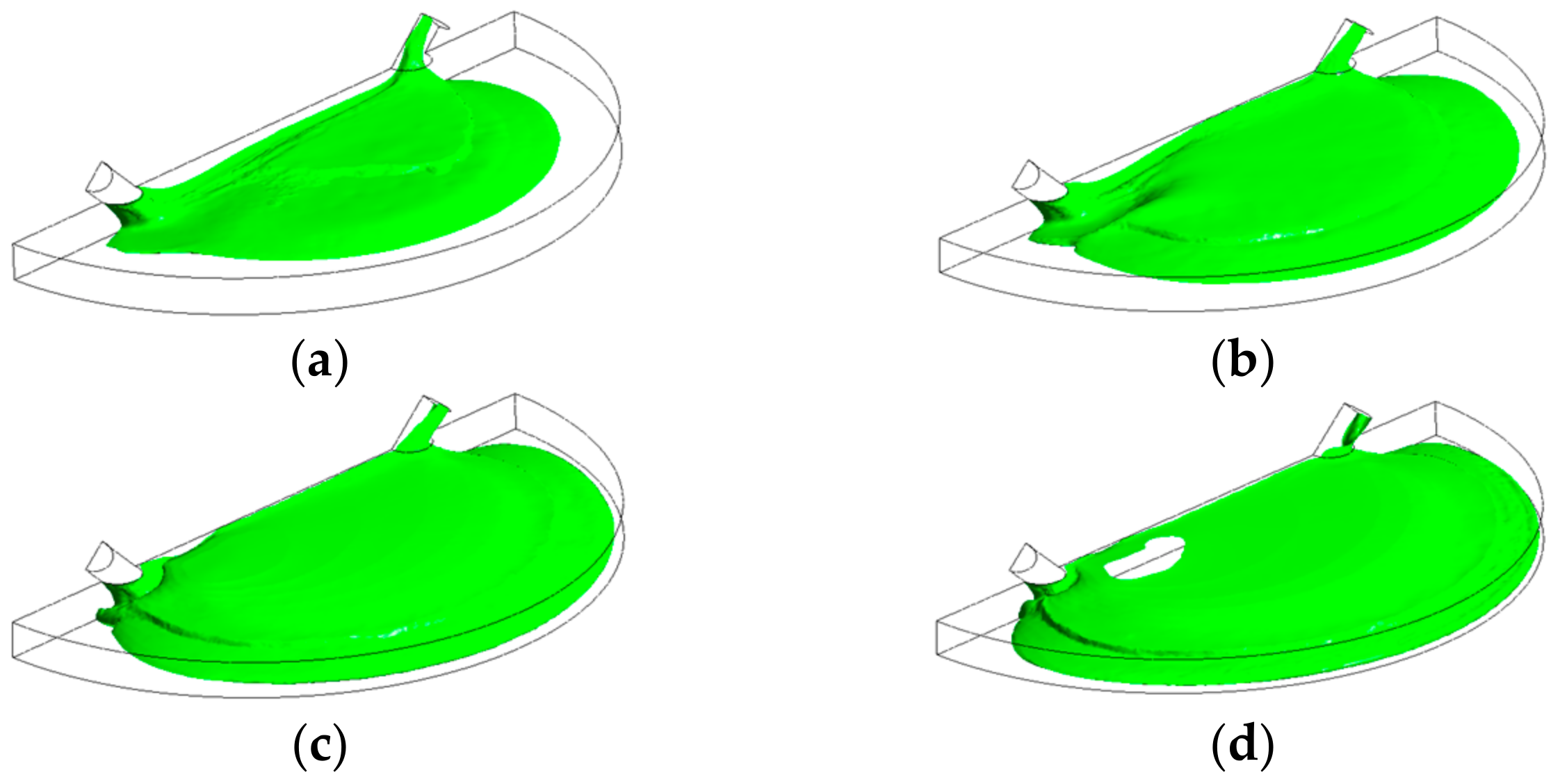


| Mesh (Feature) | Air Fraction | Deviation, % | |
|---|---|---|---|
| 1 | 54,000 (XX-course) | 0.240 | |
| 2 | 110,000 (Coarse) | 0.299 | 24.35 |
| 3 | 230,000 (Medium) | 0.329 | 9.94 |
| 4 | 494,115 (Fine) | 0.332 | 0.91 |
| Flow Rate, (µL/min) | Inlet Velocity (m/s) | Critical Time, τc (s) |
|---|---|---|
| 15 | 0.0052 | 12.8 |
| 100 | 0.0347 | 1.93 |
| 500 | 0.173 | 0.385 |
| 1000 | 0.346 | 0.193 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Islamov, M.; Sypabekova, M.; Kanayeva, D.; Rojas-Solórzano, L. CFD Modeling of Chamber Filling in a Micro-Biosensor for Protein Detection. Biosensors 2017, 7, 45. https://doi.org/10.3390/bios7040045
Islamov M, Sypabekova M, Kanayeva D, Rojas-Solórzano L. CFD Modeling of Chamber Filling in a Micro-Biosensor for Protein Detection. Biosensors. 2017; 7(4):45. https://doi.org/10.3390/bios7040045
Chicago/Turabian StyleIslamov, Meiirbek, Marzhan Sypabekova, Damira Kanayeva, and Luis Rojas-Solórzano. 2017. "CFD Modeling of Chamber Filling in a Micro-Biosensor for Protein Detection" Biosensors 7, no. 4: 45. https://doi.org/10.3390/bios7040045
APA StyleIslamov, M., Sypabekova, M., Kanayeva, D., & Rojas-Solórzano, L. (2017). CFD Modeling of Chamber Filling in a Micro-Biosensor for Protein Detection. Biosensors, 7(4), 45. https://doi.org/10.3390/bios7040045






