Experimental Validation of the Sensitivity of Waveguide Grating Based Refractometric (Bio)sensors
Abstract
:1. Introduction

2. Material and Methods
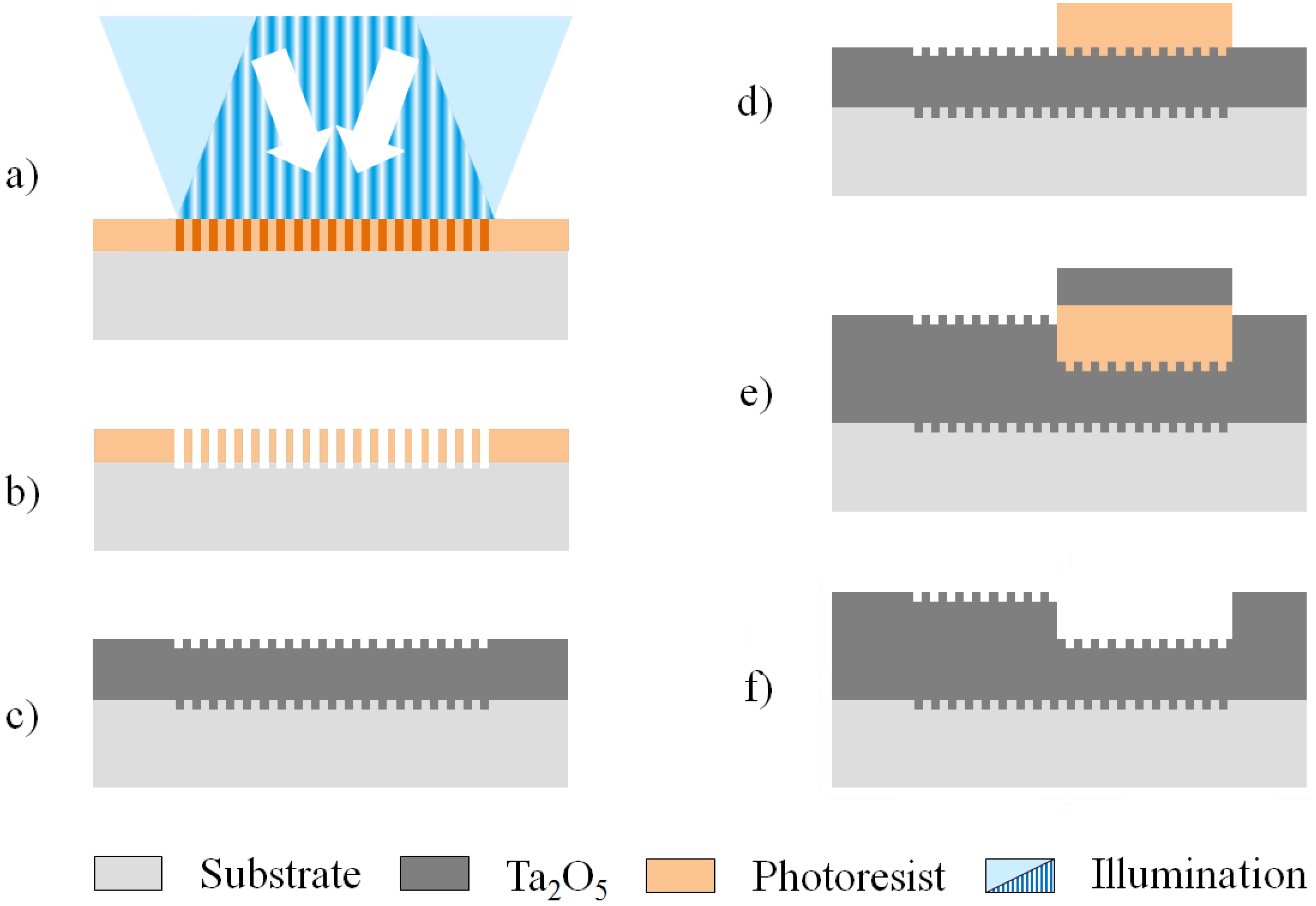
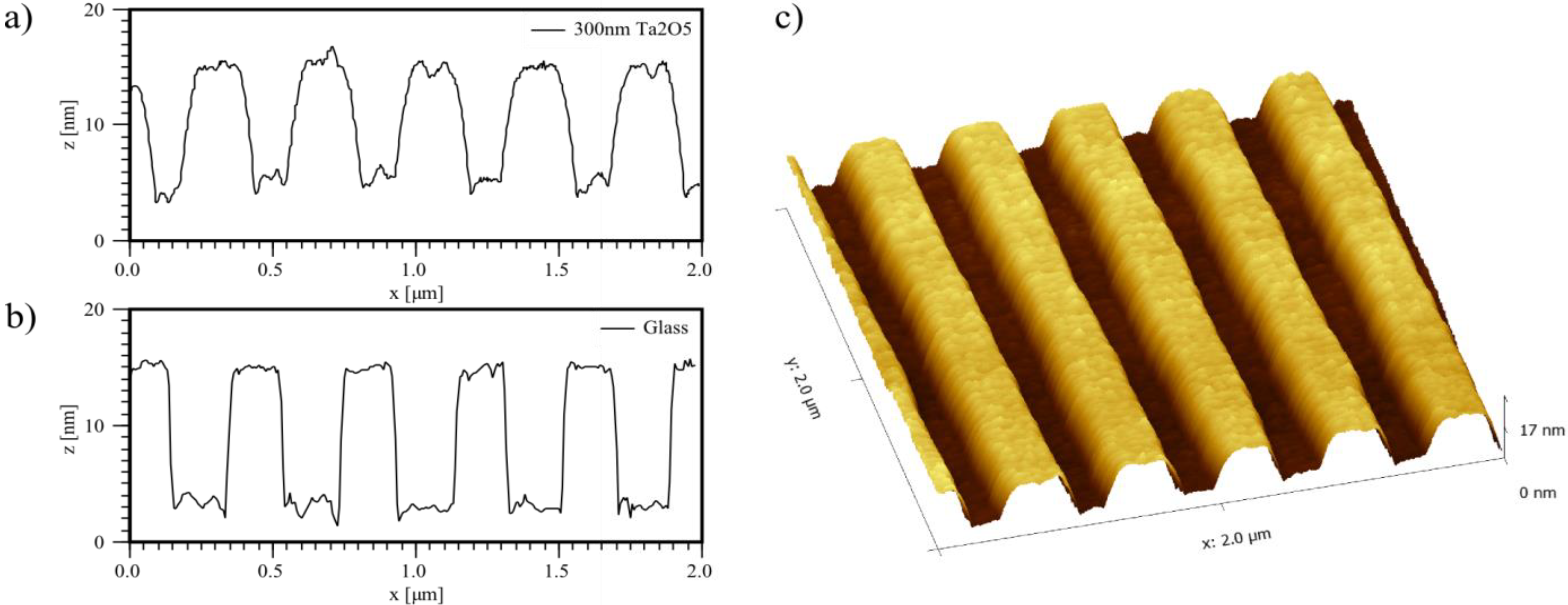
2.1. Sample Preparation and Measurement of the Refractometric Sensitivity
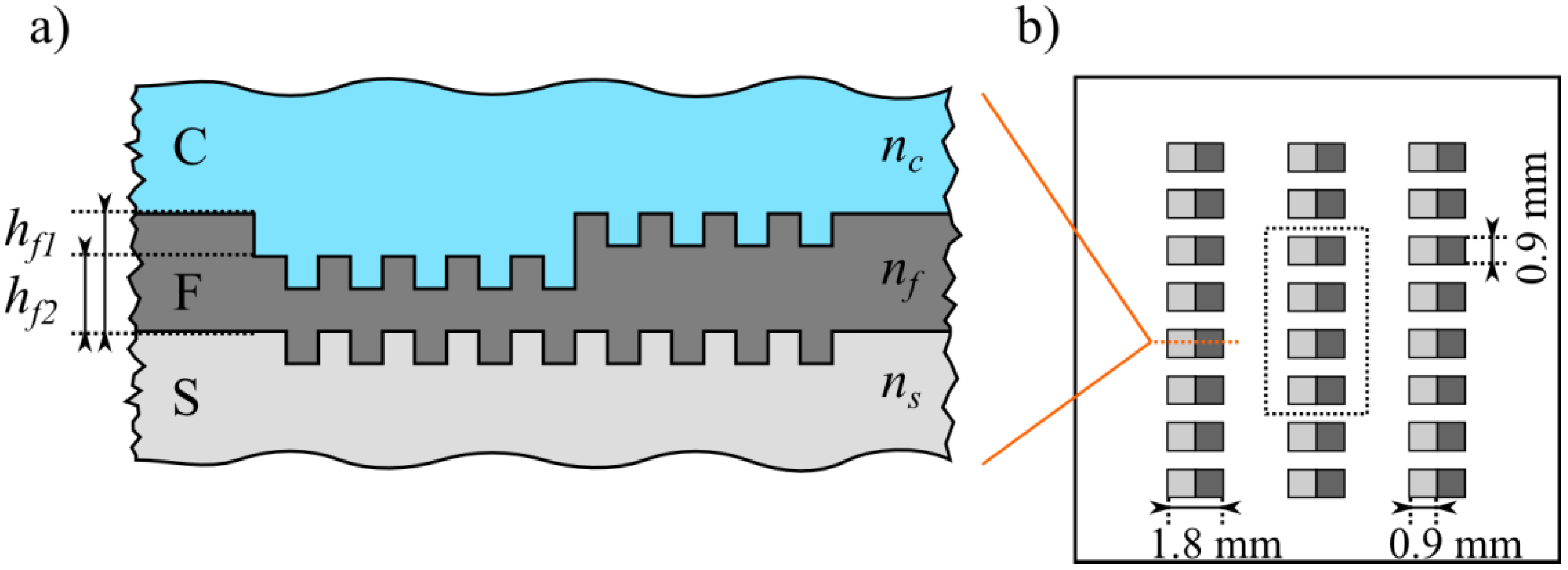
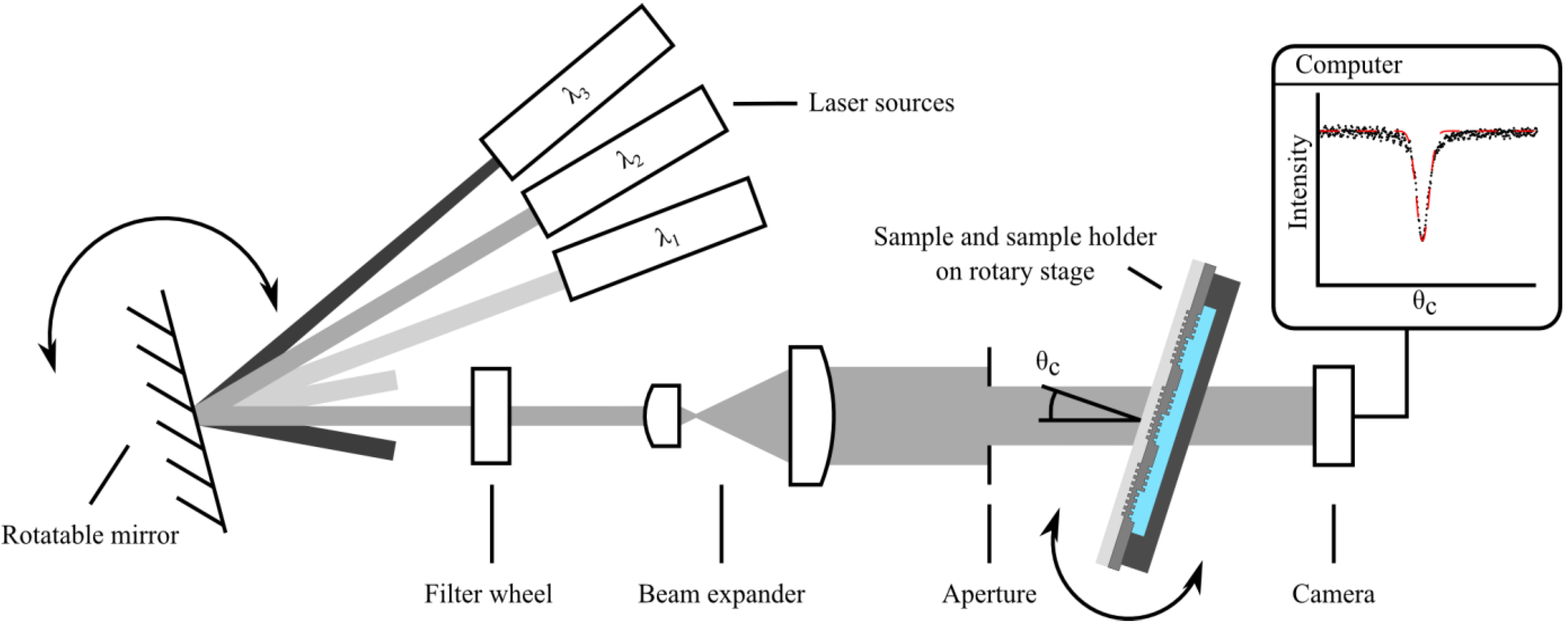

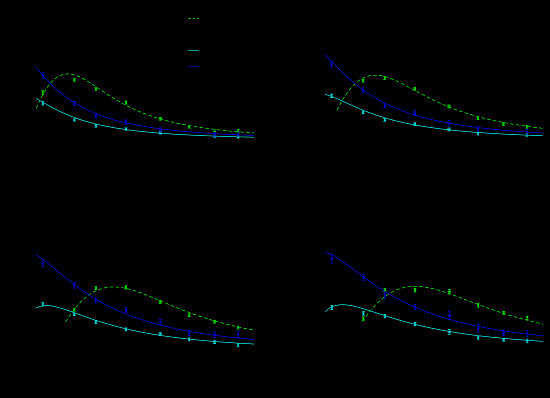
2.2. Calculation of the Theoretical Sensitivity
| λ [nm] | nf | ns | nwater | nindex·matching·liquid |
|---|---|---|---|---|
| 532.3 | 2.1511 | 1.5264 | 1.3354 | 1.5247 |
| 632.8 | 2.1229 | 1.5213 | 1.3321 | 1.5173 |
| 779.7 | 2.1024 | 1.5168 | 1.3290 | 1.5115 |
| 845.1 | 2.0918 | 1.5157 | 1.3279 | 1.5099 |
3. Results and Discussion
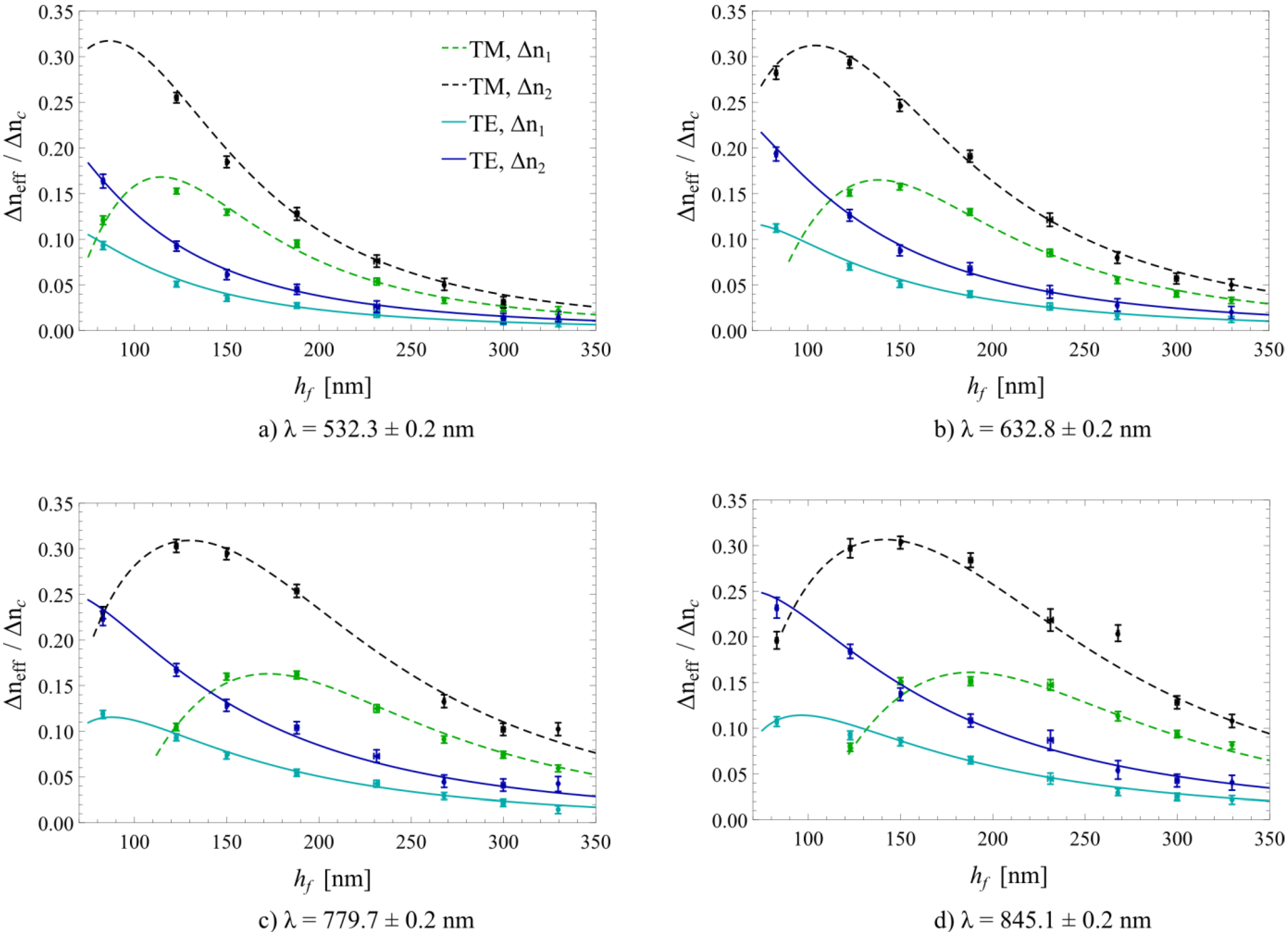
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tiefenthaler, K.; Lukosz, W. Sensitivity of grating couplers as integrated-optical chemical sensors. J. Opt. Soc. Am. B 1989, 6, 209–220. [Google Scholar] [CrossRef]
- Nellen, P.M.; Tiefenthaler, K.; Lukosz, W. Integrated optical input grating couplers as biochemical sensors. Sens. Act. 1988, 15, 285–295. [Google Scholar] [CrossRef]
- Cooper, M.A. Optical biosensors in drug discovery. Nat. Rev. Drug Discov. 2002, 1, 515–528. [Google Scholar] [CrossRef] [PubMed]
- Pasche, S.; Wenger, B.; Ischer, R.; Giazzon, M.; Angeloni, S.; Voirin, G. Integrated optical biosensor for in-line monitoring of cell cultures. Biosens. Bioelectron. 2010, 26, 1478–1485. [Google Scholar] [CrossRef] [PubMed]
- Adrian, J.; Pasche, S.; Diserens, J.M.; Sánchez-Baeza, F.; Gao, H.; Marco, M.P.; Voirin, G. Waveguide interrogated optical immunosensor (WIOS) for detection of sulfonamide antibiotics in milk. Biosens. Bioelectron. 2009, 24, 3340–3346. [Google Scholar] [CrossRef] [PubMed]
- Bier, F.F.; Schmid, R.D. Real time analysis of competitive binding using grating coupler immunosensors for pesticide detection. Biosens. Bioelectron. 1994, 9, 125–130. [Google Scholar] [CrossRef]
- Vörös, J.; Graf, R.; Kenausis, G.L.; Bruinink, A.; Mayer, J.; Textor, M.; Wintermantel, E.; Spencer, N.D. Feasibility study of an online toxicological sensor based on the optical waveguide technique. Biosens. Bioelectron. 2000, 15, 423–429. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, K.; Oehse, K.; Sulz, G.; Hoffmann, C. Evanescent field sensors based on tantalum pentoxide waveguides—A review. Sensors 2008, 8, 711–738. [Google Scholar] [CrossRef]
- Kozma, P.; Kehl, F.; Ehrentreich-Förster, E.; Stamm, C.; Bier, F.F. Integrated planar optical waveguide interferometer biosensors: A comparative review. Biosens. Bioelectron. 2014, 58, 287–307. [Google Scholar] [CrossRef] [PubMed]
- Lukosz, W. Integrated optical chemical and direct biochemical sensors. Sens. Actuators B Chem. 1995, 29, 37–50. [Google Scholar] [CrossRef]
- Kunz, R.E.; Cottier, K. Optimizing integrated optical chips for label-free (bio-) chemical sensing. Anal. Bioanal. Chem. 2006, 384, 180–190. [Google Scholar] [CrossRef] [PubMed]
- Guillod, T.; Kehl, F.; Hafner, C. FEM-Based method for the simulation of dielectric waveguide grating biosensors. PIER 2013, 137, 565–583. [Google Scholar] [CrossRef]
- Kunz, R.E.; Dübendorfer, J.; Morf, R.H. Finite grating depth effects for integrated optical sensors with high sensitivity. Biosens. Bioelectron. 1996, 11, 653–667. [Google Scholar] [CrossRef]
- Parriaux, O.; Veldhuis, G.J. Normalized analysis for the sensitivity optimization of integrated optical evanescent-wave sensors. J. Lightwave Technol. 1998, 16, 573–582. [Google Scholar] [CrossRef]
- Tiefenthaler, K.; Lukosz, W. Grating couplers as integrated optical humidity and gas sensors. Thin Solid Films 1985, 126, 205–211. [Google Scholar] [CrossRef]
- Lukosz, W.; Nellen, Ph.M.; Stamm, Ch.; Weiss, P. Output grating couplers on planar waveguides as integrated optical chemical sensors. Sens. Actuators B Chem. 1990, 1, 585–588. [Google Scholar] [CrossRef]
- Tamir, T.; Peng, S.T. Analysis and design of grating couplers. Appl. Phys. 1977, 14, 235–254. [Google Scholar] [CrossRef]
- Löfås, S.; Johnsson, B. A novel hydrogel matrix on gold surfaces in surface plasmon resonance sensors for fast and efficient covalent immobilization of ligands. J. Chem. Soc. Chem. Commun. 1990, 21, 1526–1528. [Google Scholar] [CrossRef]
- Wiki, M.; Kunz, R.E. Wavelength-interrogated optical sensor for biochemical applications. Opt. Lett. 2000, 25, 463–465. [Google Scholar] [CrossRef] [PubMed]
- Cottier, K.; Wiki, M.; Voirin, G.; Gao, H.; Kunz, R.E. Label-free highly sensitive detection of (small) molecules by wavelength interrogation of integrated optical chips. Sens. Actuators B Chem. 2003, 91, 241–251. [Google Scholar] [CrossRef]
- Brazas, J.C.; Li, L. Analysis of input-grating couplers having finite lengths. Appl. Opt. 1995, 34, 3786–3792. [Google Scholar]
- MATLAB Release R2010b; The MathWorks, Inc.: Natick, MA, USA, 2010.
- Daimon, M.; Masamura, A. Measurement of the refractive index of distilled water from the near-infrared region to the ultraviolet region. Appl. Opt. 2007, 46, 3811–3820. [Google Scholar] [CrossRef] [PubMed]
- Ciddor, P.E. Refractive index of air: new equations for the visible and near infrared. Appl. Opt. 1996, 35, 1566–1573. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, K.; Hoffmann, C. High-Refractive Index Waveguide Platforms for Chemical and Biosensing. In Optical Guided-wave Chemical and Biosensors I, Springer Series on Chemical Sensors and Biosensors, 1st ed.; Zourob, M., Lakhtakia, A., Eds.; Springer Verlag: Berlin, Heidelberg, Germany, 2010; Volume 7, pp. 21–54. [Google Scholar]
- Ramsden, J.J.; Lvov, Y.M.; Decher, G. Determination of optical constants of molecular films assembled via alternate polyion adsorption. Thin Solid Films 1995, 254, 246–251. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gartmann, T.E.; Kehl, F. Experimental Validation of the Sensitivity of Waveguide Grating Based Refractometric (Bio)sensors. Biosensors 2015, 5, 187-198. https://doi.org/10.3390/bios5020187
Gartmann TE, Kehl F. Experimental Validation of the Sensitivity of Waveguide Grating Based Refractometric (Bio)sensors. Biosensors. 2015; 5(2):187-198. https://doi.org/10.3390/bios5020187
Chicago/Turabian StyleGartmann, Thomas E., and Florian Kehl. 2015. "Experimental Validation of the Sensitivity of Waveguide Grating Based Refractometric (Bio)sensors" Biosensors 5, no. 2: 187-198. https://doi.org/10.3390/bios5020187
APA StyleGartmann, T. E., & Kehl, F. (2015). Experimental Validation of the Sensitivity of Waveguide Grating Based Refractometric (Bio)sensors. Biosensors, 5(2), 187-198. https://doi.org/10.3390/bios5020187