Fiber-Based Ultra-High-Speed Diffuse Speckle Contrast Analysis System for Deep Blood Flow Sensing Using a Large SPAD Camera
Abstract
1. Introduction
2. Materials and Methods
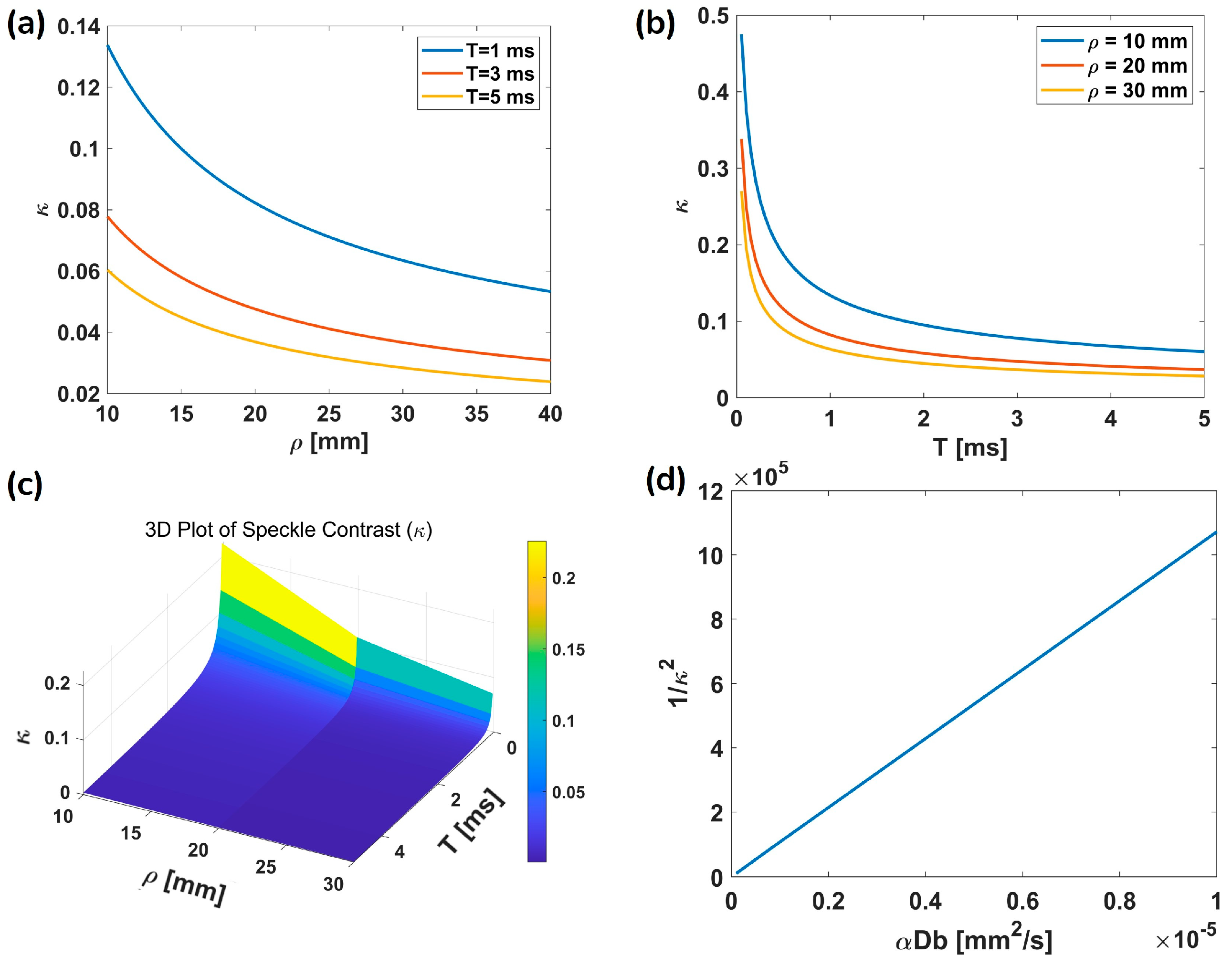
2.1. Theoretical Background
2.2. Noise Correction
- : the measured contrast computed from camera images (after any dark offset subtraction);
- : the contrast arising from photon shot noise (Poisson statistics of photon arrival);
- : the contrast contribution from camera read-out noise;
- : dark current and other system noise induced contrast;
- : the quantization-induced contrast.
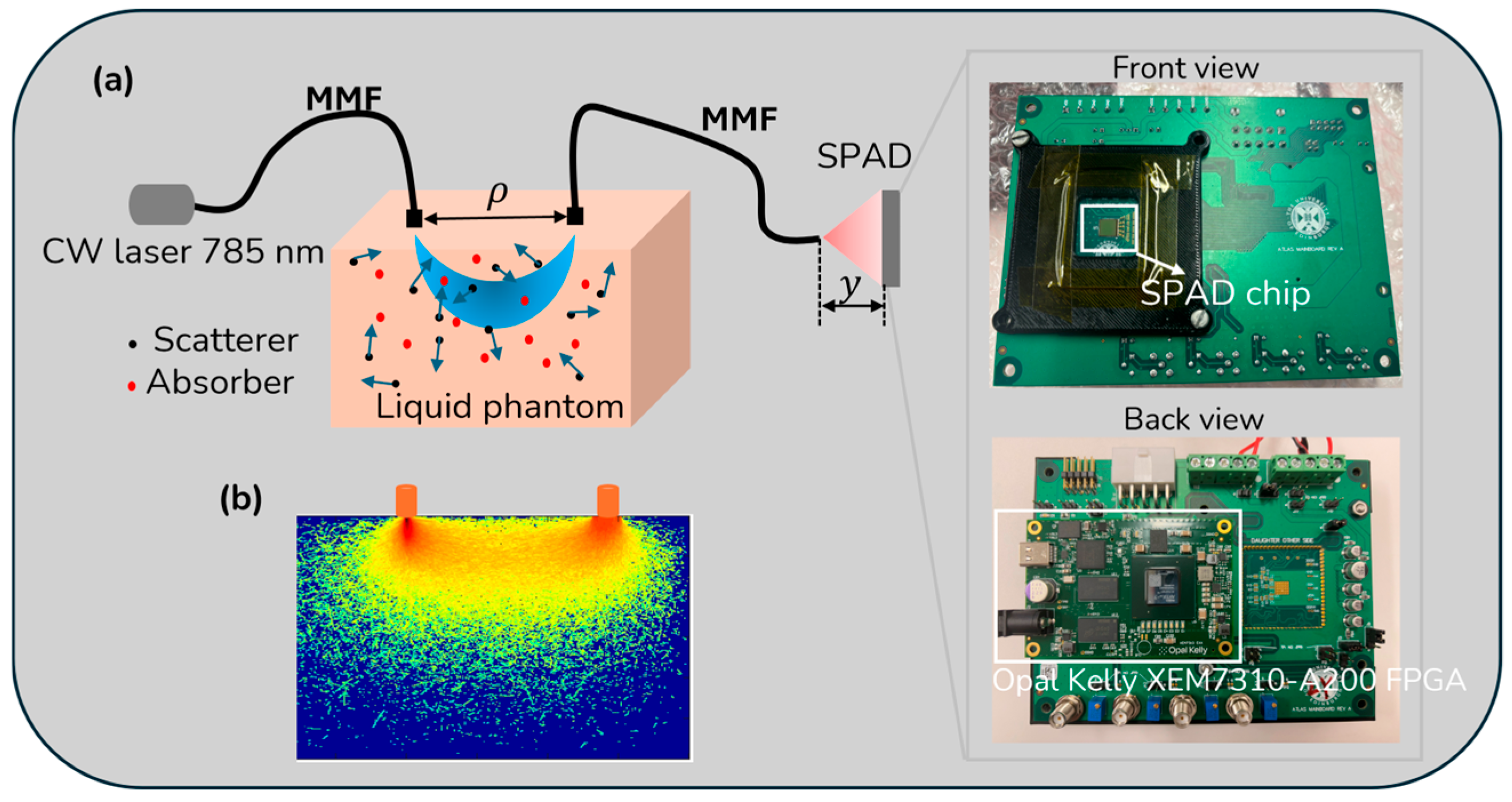
2.3. SPAD (ATLAS) Architecture
2.4. Implementation (Experimental Setup)
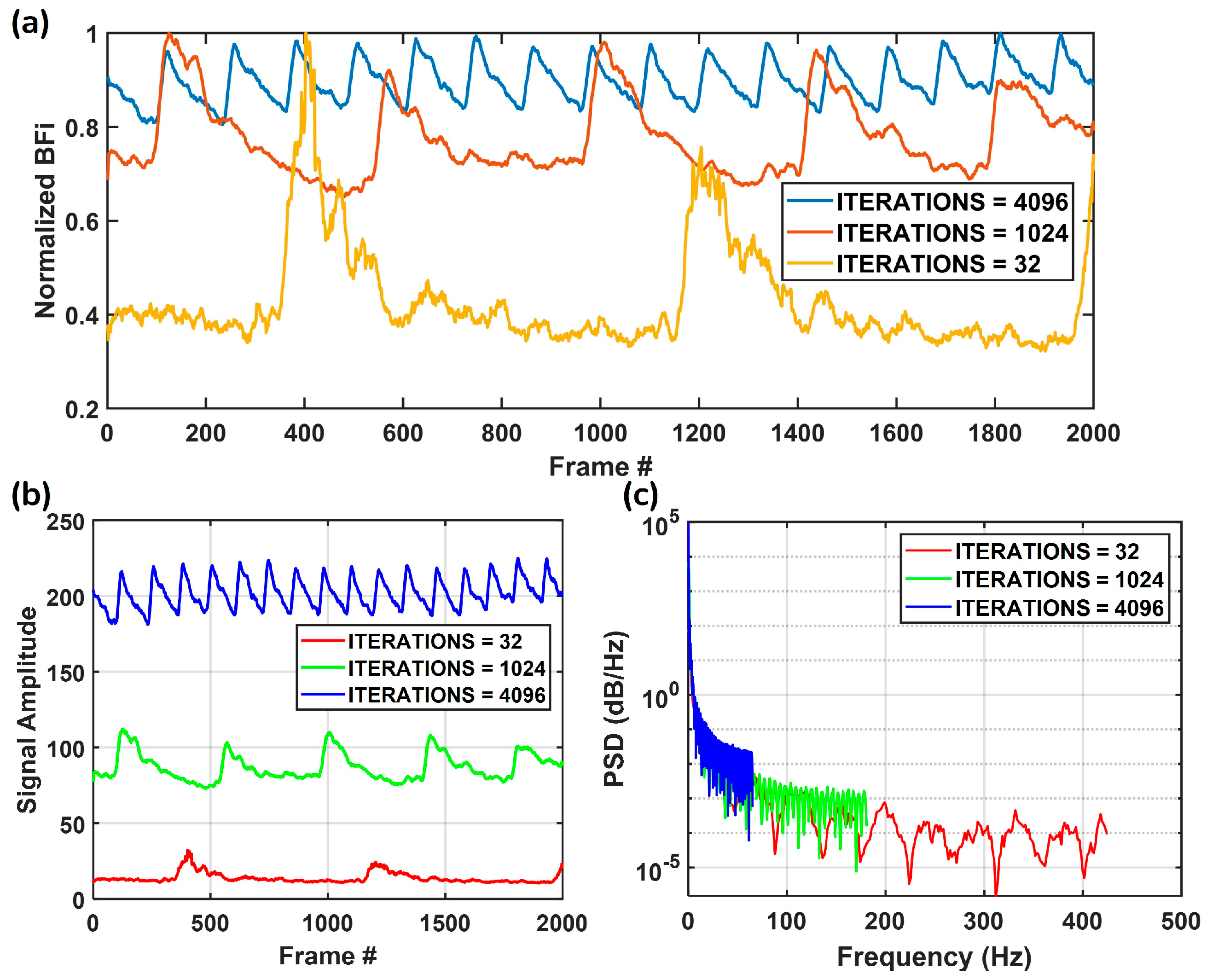
2.5. Data Processing
3. Results
3.1. Simulation Results
3.2. Measurement Flexibility
3.3. Phantom and In Vivo Measurements
3.3.1. Phantom Measurements
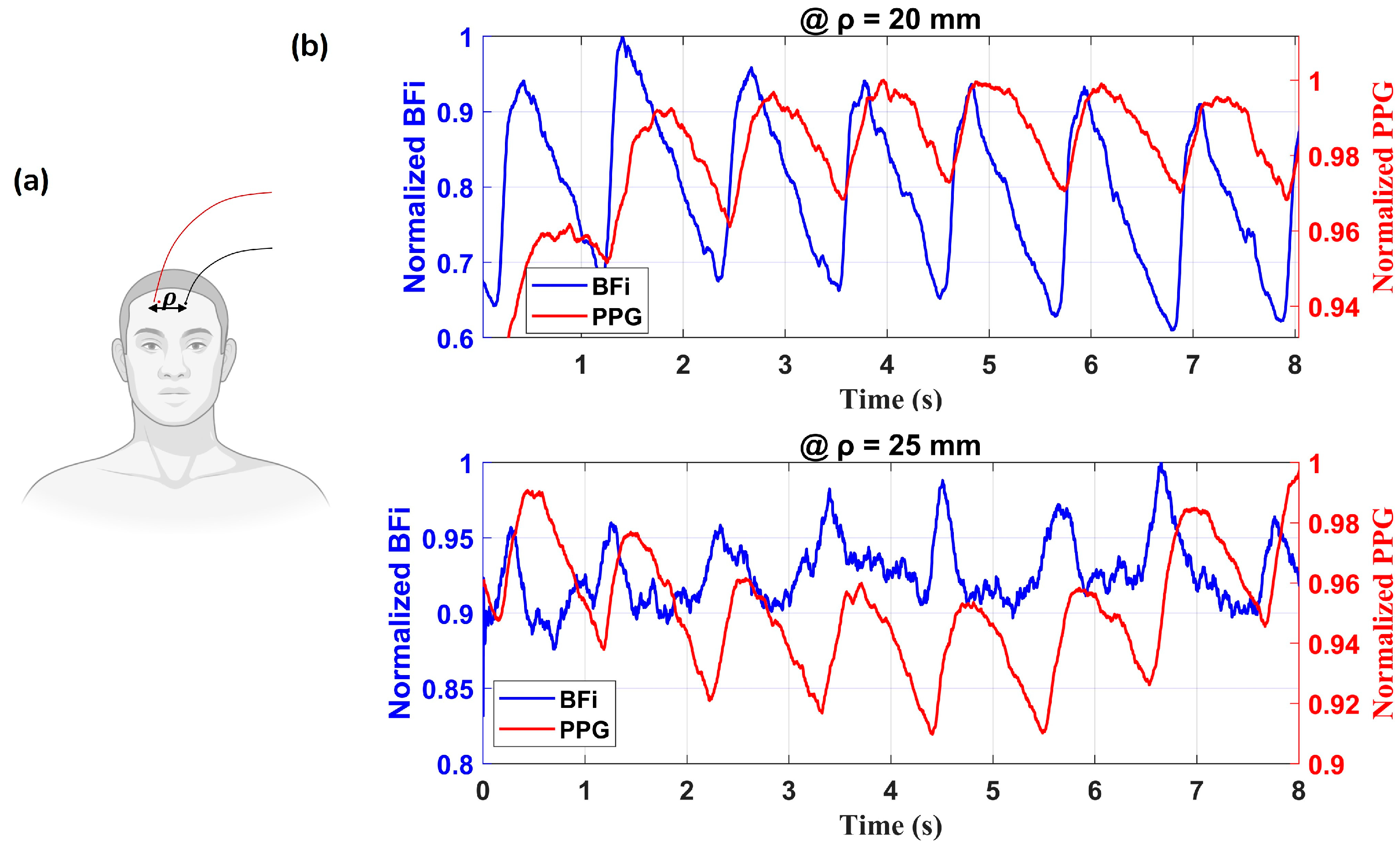
3.3.2. Arm Cuff Occlusion
3.3.3. In Vivo Forehead Measurements
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Zauner, A.; Daugherty, W.P.; Bullock, M.R.; Warner, D.S. Brain Oxygenation and Energy Metabolism: Part I-Biological Function and Pathophysiology. Neurosurgery 2002, 51, 289–301. [Google Scholar]
- Durduran, T.; Yodh, A.G. Diffuse Correlation Spectroscopy for Non-Invasive, Micro-Vascular Cerebral Blood Flow Measurement. NeuroImage 2014, 85, 51–63. [Google Scholar] [CrossRef]
- Devor, A.; Sakadžić, S.; Srinivasan, V.J.; Yaseen, M.A.; Nizar, K.; Saisan, P.A.; Tian, P.; Dale, A.M.; Vinogradov, S.A.; Franceschini, M.A.; et al. Frontiers in Optical Imaging of Cerebral Blood Flow and Metabolism. J. Cereb. Blood Flow. Metab. 2012, 32, 1259–1276. [Google Scholar] [CrossRef]
- Cheung, C.; Culver, J.P.; Takahashi, K.; Greenberg, J.H.; Yodh, A.G. In Vivo Cerebrovascular Measurement Combining Diffuse near-Infrared Absorption and Correlation Spectroscopies. Phys. Med. Biol. 2001, 46, 2053–2065. [Google Scholar] [CrossRef] [PubMed]
- Fantini, S.; Sassaroli, A.; Tgavalekos, K.T.; Kornbluth, J. Cerebral Blood Flow and Autoregulation: Current Measurement Techniques and Prospects for Noninvasive Optical Methods. Neurophoton 2016, 3, 031411. [Google Scholar] [CrossRef] [PubMed]
- Rhee, C.J.; Da Costa, C.S.; Austin, T.; Brady, K.M.; Czosnyka, M.; Lee, J.K. Neonatal Cerebrovascular Autoregulation. Pediatr. Res. 2018, 84, 602–610. [Google Scholar] [CrossRef]
- Durduran, T.; Zhou, C.; Edlow, B.L.; Yu, G.; Choe, R.; Kim, M.N.; Cucchiara, B.L.; Putt, M.E.; Shah, Q.; Kasner, S.E.; et al. Transcranial Optical Monitoring of Cerebrovascular Hemodynamics in Acute Stroke Patients. Opt. Express 2009, 17, 3884–3902. [Google Scholar] [CrossRef] [PubMed]
- Weigl, W.; Milej, D.; Janusek, D.; Wojtkiewicz, S.; Sawosz, P.; Kacprzak, M.; Gerega, A.; Maniewski, R.; Liebert, A. Application of Optical Methods in the Monitoring of Traumatic Brain Injury: A Review. J. Cereb. Blood Flow. Metab. 2016, 36, 1825–1843. [Google Scholar] [CrossRef]
- Ma, K.F.; Kleiss, S.F.; Schuurmann, R.C.L.; Bokkers, R.P.H.; Ünlü, Ç.; De Vries, J.-P.P.M. A Systematic Review of Diagnostic Techniques to Determine Tissue Perfusion in Patients with Peripheral Arterial Disease. Expert Rev. Med. Devices 2019, 16, 697–710. [Google Scholar] [CrossRef]
- Duncan, A.; Meek, J.H.; Clemence, M.; Elwell, C.E.; Fallon, P.; Tyszczuk, L.; Cope, M.; Delpy, D.T. Measurement of Cranial Optical Path Length as a Function of Age Using Phase Resolved near Infrared Spectroscopy. Pediatr. Res. 1996, 39, 889–894. [Google Scholar] [CrossRef]
- Becker, W. Advanced Time-Correlated Single Photon Counting Techniques; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Gurley, K.; Shang, Y.; Yu, G. Noninvasive Optical Quantification of Absolute Blood Flow, Blood Oxygenation, and Oxygen Consumption Rate in Exercising Skeletal Muscle. J. Biomed. Opt. 2012, 17, 0750101. [Google Scholar]
- Senarathna, J.; Rege, A.; Li, N.; Thakor, N.V. Laser Speckle Contrast Imaging: Theory, Instrumentation and Applications. IEEE Rev. Biomed. Eng. 2013, 6, 99–110. [Google Scholar] [CrossRef]
- Bonner, R.F.; Nossal, R. Principles of laser-Doppler flowmetry. In Laser-Doppler Blood Flowmetry; Springer: Boston, MA, USA, 1990; pp. 17–45. [Google Scholar]
- Boas, D.A.; Sakadžic, S.; Selb, J.; Farzam, P.; Franceschini, M.A.; Carp, S.A. Establishing the Diffuse Correlation Spectroscopy Signal Relationship with Blood Flow. Neurophoton 2016, 3, 031412. [Google Scholar] [CrossRef] [PubMed]
- Bi, R.; Dong, J.; Lee, K. Deep Tissue Flowmetry Based on Diffuse Speckle Contrast Analysis. Opt. Lett. 2013, 38, 1401–1403. [Google Scholar] [CrossRef] [PubMed]
- Bandyopadhyay, R.; Gittings, A.S.; Suh, S.S.; Dixon, P.K.; Durian, D.J. Speckle-visibility spectroscopy: A tool to study time-varying dynamics. Rev. Sci. Instrum. 2005, 76, 093110. [Google Scholar] [CrossRef]
- Dragojević, T.; Hollmann, J.L.; Tamborini, D.; Portaluppi, D.; Buttafava, M.; Culver, J.P.; Villa, F.; Durduran, T. Compact, Multi-Exposure Speckle Contrast Optical Spectroscopy (SCOS) Device for Measuring Deep Tissue Blood Flow. Biomed. Opt. Express 2017, 9, 322–333. [Google Scholar] [CrossRef] [PubMed]
- Valdes, C.P.; Varma, H.M.; Kristoffersen, A.K.; Dragojevic, T.; Culver, J.P.; Durduran, T. Speckle Contrast Optical Spectroscopy, a Non-Invasive, Diffuse Optical Method for Measuring Microvascular Blood Flow in Tissue. Biomed. Opt. Express 2014, 5, 2769. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, H.; Lu, J.; Ni, X.; Shen, Z. Simultaneously Extracting Multiple Parameters via Multi-Distance and Multi-Exposure Diffuse Speckle Contrast Analysis. Biomed. Opt. Express 2017, 8, 4537–4550. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, H.; Shen, Z.; Lu, J.; Ni, X. Quantitatively Assessing Flow Velocity by the Slope of the Inverse Square of the Contrast Values versus Camera Exposure Time. Opt. Express 2014, 22, 19327–19336. [Google Scholar] [CrossRef]
- Yeo, C.; Park, H.; Lee, K.; Song, C. Avian Embryo Monitoring during Incubation Using Multi-Channel Diffuse Speckle Contrast Analysis. Biomed. Opt. Express 2016, 7, 93–98. [Google Scholar] [CrossRef]
- Choo, T.W.J.; Zhang, R.; Bi, R.; Olivo, M. Experimental Characterization of Diffuse Speckle Pulsatile Flowmetry System. Front. Phys. 2022, 10, 1006484. [Google Scholar] [CrossRef]
- Kim, B.; Zilpelwar, S.; Sie, E.J.; Marsili, F.; Zimmermann, B.; Boas, D.A.; Cheng, X. Measuring Human Cerebral Blood Flow and Brain Function with Fiber-Based Speckle Contrast Optical Spectroscopy System. Commun. Biol. 2023, 6, 844. [Google Scholar] [CrossRef] [PubMed]
- Bi, R.; Dong, J.; Lee, K. Multi-Channel Deep Tissue Flowmetry Based on Temporal Diffuse Speckle Contrast Analysis. Opt. Express 2013, 21, 22854–22861. [Google Scholar] [CrossRef]
- Huang, C.; Irwin, D.; Lin, Y.; Shang, Y.; He, L.; Kong, W.; Luo, J.; Yu, G. Speckle Contrast Diffuse Correlation Tomography of Complex Turbid Medium Flow. Med. Phys. 2015, 42, 4000–4006. [Google Scholar] [CrossRef]
- Huang, C.; Seong, M.; Morgan, J.P.; Mazdeyasna, S.; Kim, J.G.; Hastings, J.T.; Yu, G. Low-Cost Compact Diffuse Speckle Contrast Flowmeter Using Small Laser Diode and Bare Charge-Coupled-Device. J. Biomed. Opt. 2016, 21, 080501. [Google Scholar] [CrossRef]
- Fathi, F.; Mazdeyasna, S.; Singh, D.; Huang, C.; Mohtasebi, M.; Liu, X.; Rabienia Haratbar, S.; Zhao, M.; Chen, L.; Can Ulku, A.; et al. Time-Resolved Laser Speckle Contrast Imaging (TR-LSCI) of Cerebral Blood Flow. IEEE Trans. Med. Imaging 2025, 44, 1206–1217. [Google Scholar] [CrossRef]
- Della Rocca, F.M.; Rocca, F.M.D.; Sie, E.J.; Erdogan, A.T.; Fisher, L.; Finlayson, N.; Gorman, A.; Gyongy, I.; Mai, H.; Lachaud, T.; et al. A 512 × 512 SPAD laser speckle autocorrelation imager in stacked 65/40nm CMOS. In Proceedings of the 2024 IEEE Symposium on VLSI Technology and Circuits (VLSI Technology and Circuits), Honolulu, HI, USA, 16–20 June 2024; pp. 1–2. [Google Scholar]
- Gorman, A.; Finlayson, N.; Erdogan, A.T.; Fisher, L.; Wang, Y.; Mattioli Della Rocca, F.; Mai, H.; Sie, E.J.; Marsili, F.; Henderson, R.K. ATLAS: A Large Array, on-Chip Compute SPAD Camera for Multispeckle Diffuse Correlation Spectroscopy. Biomed. Opt. Express 2024, 15, 6499–6515. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, H.; Lu, J.; Ni, X.; Shen, Z. Quantitative Model of Diffuse Speckle Contrast Analysis for Flow Measurement. J. Biomed. Opt. 2017, 22, 076016. [Google Scholar] [CrossRef]
- Bi, R.; Du, Y.; Singh, G.; Ho, J.-H.; Zhang, S.; Ebrahim Attia, A.B.; Li, X.; Olivo, M.C. Fast Pulsatile Blood Flow Measurement in Deep Tissue through a Multimode Detection Fiber. J. Biomed. Opt. 2020, 25, 055003. [Google Scholar] [CrossRef]
- Lin, C.-H.P.; Orukari, I.; Tracy, C.; Frisk, L.K.; Verma, M.; Chetia, S.; Durduran, T.; Trobaugh, J.W.; Culver, J.P. Multi-Mode Fiber-Based Speckle Contrast Optical Spectroscopy: Analysis of Speckle Statistics. Opt. Lett. 2023, 48, 1427–1430. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.X.; Mahler, S.; Dickson, M.; Abedi, A.; Tyszka, J.M.; Lo, Y.T.; Russin, J.; Liu, C.; Yang, C. Compact and Cost-Effective Laser-Powered Speckle Contrast Optical Spectroscopy Fiber-Free Device for Measuring Cerebral Blood Flow. J. Biomed. Opt. 2024, 29, 067001. [Google Scholar] [CrossRef]
- Bi, R.; Zhang, R.; Meng, L.; Du, Y.; Low, J.; Qi, Y.; Rajarahm, P.; Lai, A.Y.F.; Tan, V.S.Y.; Ho, P.; et al. A Portable Optical Pulsatile Flowmetry Demonstrates Strong Clinical Relevance for Diabetic Foot Perfusion Assessment. APL Bioeng. 2024, 8, 016109. [Google Scholar] [CrossRef]
- Biswas, A.; Mohammad, P.P.S.; Moka, S.; Takshi, A.; Parthasarathy, A.B. Non-Invasive Low-Cost Deep Tissue Blood Flow Measurement with Integrated Diffuse Speckle Contrast Spectroscopy. Front. Neuroergon. 2024, 4, 1288922. [Google Scholar] [CrossRef]
- Garrett, A.; Kim, B.; Gurel, N.Z.; Sie, E.J.; Wilson, B.K.; Marsili, F.; Forman, J.P.; Hamburg, N.M.; Boas, D.A. Speckle contrast optical spectroscopy improves cuffless blood pressure estimation compared to photoplethysmography. bioRxiv 2024. [Google Scholar] [CrossRef]
- Briers, J.D. Laser Doppler, Speckle and Related Techniques for Blood Perfusion Mapping and Imaging. Physiol. Meas. 2001, 22, R35–R66. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Pan, M.; Kreiss, L.; Samaei, S.; Carp, S.A.; Johansson, J.D.; Zhang, Y.; Wu, M.; Horstmeyer, R.; Diop, M.; et al. A Comprehensive Overview of Diffuse Correlation Spectroscopy: Theoretical Framework, Recent Advances in Hardware, Analysis, and Applications. NeuroImage 2024, 298, 120793. [Google Scholar] [CrossRef] [PubMed]
- Cheng, T.Y.; Kim, B.; Zimmermann, B.B.; Robinson, M.B.; Renna, M.; Carp, S.A.; Franceschini, M.A.; Boas, D.A.; Cheng, X. Choosing a Camera and Optimizing System Parameters for Speckle Contrast Optical Spectroscopy. Sci. Rep. 2024, 14, 11915. [Google Scholar] [CrossRef] [PubMed]
- Veerappan, C.; Richardson, J.; Walker, R.; Li, D.-U.; Fishburn, M.W.; Maruyama, Y.; Stoppa, D.; Borghetti, F.; Gersbach, M.; Henderson, R.K.; et al. A 160× 128 single-photon image sensor with on-pixel 55ps 10b time-to-digital converter. In Proceedings of the 2011 IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 20–24 February 2011; pp. 312–314. [Google Scholar]
- Mamdy, B.; Bianchi, R.A.; Golanski, D.; Rae, B.; Bah, T.M.; Rideau, D.; Twaddle, F.; Helleboid, R.; Buj, C.; Moussy, N.; et al. A high PDE and high maximum count rate and low power consumption 3D-stacked SPAD device for Lidar applications. In Proceedings of the International Image Sensor Workshop, Scotland, UK, 21–25 May 2023. [Google Scholar]
- Marti, D.; Aasbjerg, R.N.N.; Andersen, P.E.E.; Hansen, A.K.K. MCmatlab: An Open-Source, User-Friendly, MATLAB-Integrated Three-Dimensional Monte Carlo Light Transport Solver with Heat Diffusion and Tissue Damage. JBO 2018, 23, 121622. [Google Scholar] [CrossRef]
- Mcxyz.c. Available online: https://omlc.org/software/mc/mcxyz/index.html (accessed on 17 July 2025).
- Losch, M.S.; Kardux, F.; Dankelman, J.; Hendriks, B.H.W. Diffuse Reflectance Spectroscopy of the Spine: Improved Breach Detection with Angulated Fibers. Biomed. Opt. Express 2023, 14, 739. [Google Scholar] [CrossRef]
- Boas, D.A.; Dunn, A.K. Laser Speckle Contrast Imaging in Biomedical Optics. J. Biomed. Opt. 2010, 15, 011109. [Google Scholar] [CrossRef] [PubMed]
- Reisner, A.; Shaltis, P.A.; McCombie, D.; Asada, H.H.; Warner, D.S.; Warner, M.A. Utility of the Photoplethysmogram in Circulatory Monitoring. Anesthesiology 2008, 108, 950–958. [Google Scholar] [CrossRef]
- Kholiqov, O.; Zhou, W.; Zhang, T.; Du Le, V.N.; Srinivasan, V.J. Time-of-Flight Resolved Light Field Fluctuations Reveal Deep Human Tissue Physiology. Nat. Commun. 2020, 11, 391. [Google Scholar] [CrossRef]
- Siddiqui, S.V.; Chatterjee, U.; Kumar, D.; Siddiqui, A.; Goyal, N. Neuropsychology of Prefrontal Cortex. Indian J. Psychiatry 2008, 50, 202–208. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Qian, R.; Xu, S.; Chandra Konda, P.; Jönsson, J.; Harfouche, M.; Borycki, D.; Cooke, C.; Berrocal, E.; Dai, Q.; et al. Fast and Sensitive Diffuse Correlation Spectroscopy with Highly Parallelized Single Photon Detection. APL Photonics 2021, 6, 2. [Google Scholar] [CrossRef]
- Available online: https://www.msdvetmanual.com/multimedia/table/normal-vital-parameter-reference-ranges-for-nonhuman-primates (accessed on 17 July 2025).
- Xu, J.; Jahromi, A.K.; Yang, C. Diffusing Wave Spectroscopy: A Unified Treatment on Temporal Sampling and Speckle Ensemble Methods. APL Photonics 2021, 6, 1. [Google Scholar] [PubMed]
- Robinson, M.B.; Cheng, T.Y.; Renna, M.; Wu, M.M.; Kim, B.; Cheng, X.; Boas, D.A.; Franceschini, M.A.; Carp, S.A. Comparing the Performance Potential of Speckle Contrast Optical Spectroscopy and Diffuse Correlation Spectroscopy for Cerebral Blood Flow Monitoring Using Monte Carlo Simulations in Realistic Head Geometries. Neurophotonics 2024, 11, 015004. [Google Scholar] [CrossRef] [PubMed]





| Laser | Wavelength (nm) | Applications | Sampling Rate (Hz) | Fiber-Based/Fiberless | Source-Detector Separation (mm) | System Name | Year | Sensor | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| CW | 785 | Forearm | 30 | Fiber-based | 24 | DSCA | 2013 | EMCCD | [16] |
| CW | 785 | Forearm and palm | 1 | Fiber-based | 15 | tDSCA | 2013 | CCD | [25] |
| CW | 785 | Forearm | N.A. | Fiberless | 30 | SCOS | 2014 | CCD | [19] |
| CW | 671 | Phantom | N.A. | Fiberless | 18 | DSCA | 2017 | CCD | [31] |
| CW | 785 | Forearm and forehead | N.A. | Fibreless | 20 | SCOS | 2018 | SPAD (32 × 2) | [18] |
| CW | 785 | Forearm, and forehead | 300 | Fiber-based | 25 | DSCA | 2020 | CCD | [32] |
| CW | 785 | Forehead | N.A. | Fiber-based | 26 | SCOS | 2023 | sCMOS | [33] |
| VHG holographic | 852 | Forearm, forehead and arithmetic tests | N.A. | Fiber-based | 45 | SCOS | 2023 | sCMOS | [24] |
| CW | 785 | Forehead | 80 | Compact and fiberless | 50 | SCOS | 2024 | Sony IMX392 | [34] |
| CW | 785 | Diabetic | 330 | Fiber-based | 12 | DSCA | 2024 | CCD | [35] |
| CW | 785 | Forearm | N.A. | Fiber-based | 25 | DSCA | 2024 | Generic photodiode | [36] |
| CW | 808 | Wrist, exercise | 390 | Fiber-based | 4.5 | SCOS | 2024 | Basler boost | [37] |
| CW | 785 | Forearm, forehead and arithmetic tests | 800 | Fiber-based | 25 | DSCA | 2025 | SPAD (512 × 512) | ours |
| TINT_TBIN_ITERATIONS | Exposure Time (s) | Frame Readout Time (s) | Frame Time (s) | Frame Rate (fps) |
|---|---|---|---|---|
| 32 | 5.1200 × 10−5 | 1.1264 × 10−3 | 1.1776 × 10−3 | 849.2 |
| 64 | 1.0240 × 10−4 | 1.1264 × 10−3 | 1.2288 × 10−3 | 813.8 |
| 128 | 2.0480 × 10−4 | 1.1264 × 10−3 | 1.3312 × 10−3 | 751.2 |
| 256 | 4.0960 × 10−4 | 1.1264 × 10−3 | 1.5360 × 10−3 | 651.0 |
| 512 | 8.1920 × 10−4 | 1.1264 × 10−3 | 1.9456 × 10−3 | 514.0 |
| 1024 | 1.6384 × 10−3 | 1.1264 × 10−3 | 2.7648 × 10−3 | 361.7 |
| 2048 | 3.2768 × 10−3 | 1.1264 × 10−3 | 4.4032 × 10−3 | 227.1 |
| 4096 | 6.5536 × 10−3 | 1.1264 × 10−3 | 7.6800 × 10−3 | 130.2 |
| TINT_TBIN_ITERATIONS | SNR | Dark Count Rate (kcps) | (mm) | |
|---|---|---|---|---|
| 4096 | 61.88 | 3829.70 ± 513.76 | 10 | |
| 20.35 | 0.28 | 414.15 ± 22.60 | 20 | |
| 6.8 | 46.19 ± 4.71 | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Bi, R.; Zheng, S.; Erdogan, A.T.; Qi, Y.; Li, C.; Hua, Y.; Pan, M.; Wang, Y.; Finlayson, N.; et al. Fiber-Based Ultra-High-Speed Diffuse Speckle Contrast Analysis System for Deep Blood Flow Sensing Using a Large SPAD Camera. Biosensors 2025, 15, 514. https://doi.org/10.3390/bios15080514
Wang Q, Bi R, Zheng S, Erdogan AT, Qi Y, Li C, Hua Y, Pan M, Wang Y, Finlayson N, et al. Fiber-Based Ultra-High-Speed Diffuse Speckle Contrast Analysis System for Deep Blood Flow Sensing Using a Large SPAD Camera. Biosensors. 2025; 15(8):514. https://doi.org/10.3390/bios15080514
Chicago/Turabian StyleWang, Quan, Renzhe Bi, Songhua Zheng, Ahmet T. Erdogan, Yi Qi, Chenxu Li, Yuanyuan Hua, Mingliang Pan, Yining Wang, Neil Finlayson, and et al. 2025. "Fiber-Based Ultra-High-Speed Diffuse Speckle Contrast Analysis System for Deep Blood Flow Sensing Using a Large SPAD Camera" Biosensors 15, no. 8: 514. https://doi.org/10.3390/bios15080514
APA StyleWang, Q., Bi, R., Zheng, S., Erdogan, A. T., Qi, Y., Li, C., Hua, Y., Pan, M., Wang, Y., Finlayson, N., Olivo, M., Henderson, R. K., & Li, D. D.-U. (2025). Fiber-Based Ultra-High-Speed Diffuse Speckle Contrast Analysis System for Deep Blood Flow Sensing Using a Large SPAD Camera. Biosensors, 15(8), 514. https://doi.org/10.3390/bios15080514






