Multi-Mode Coupling Enabled Broadband Coverage for Terahertz Biosensing Applications
Abstract
1. Introduction
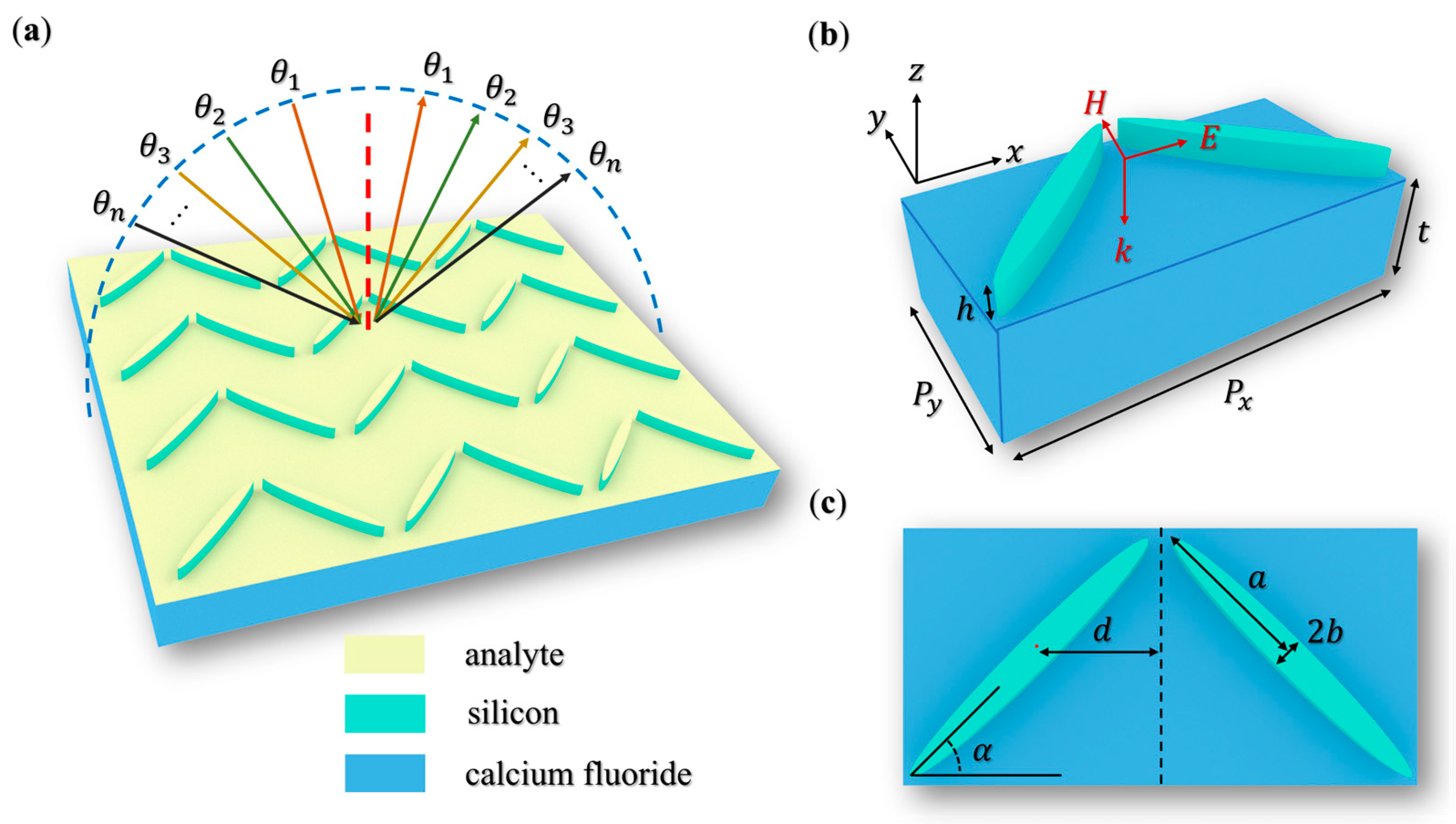
2. Materials and Methods
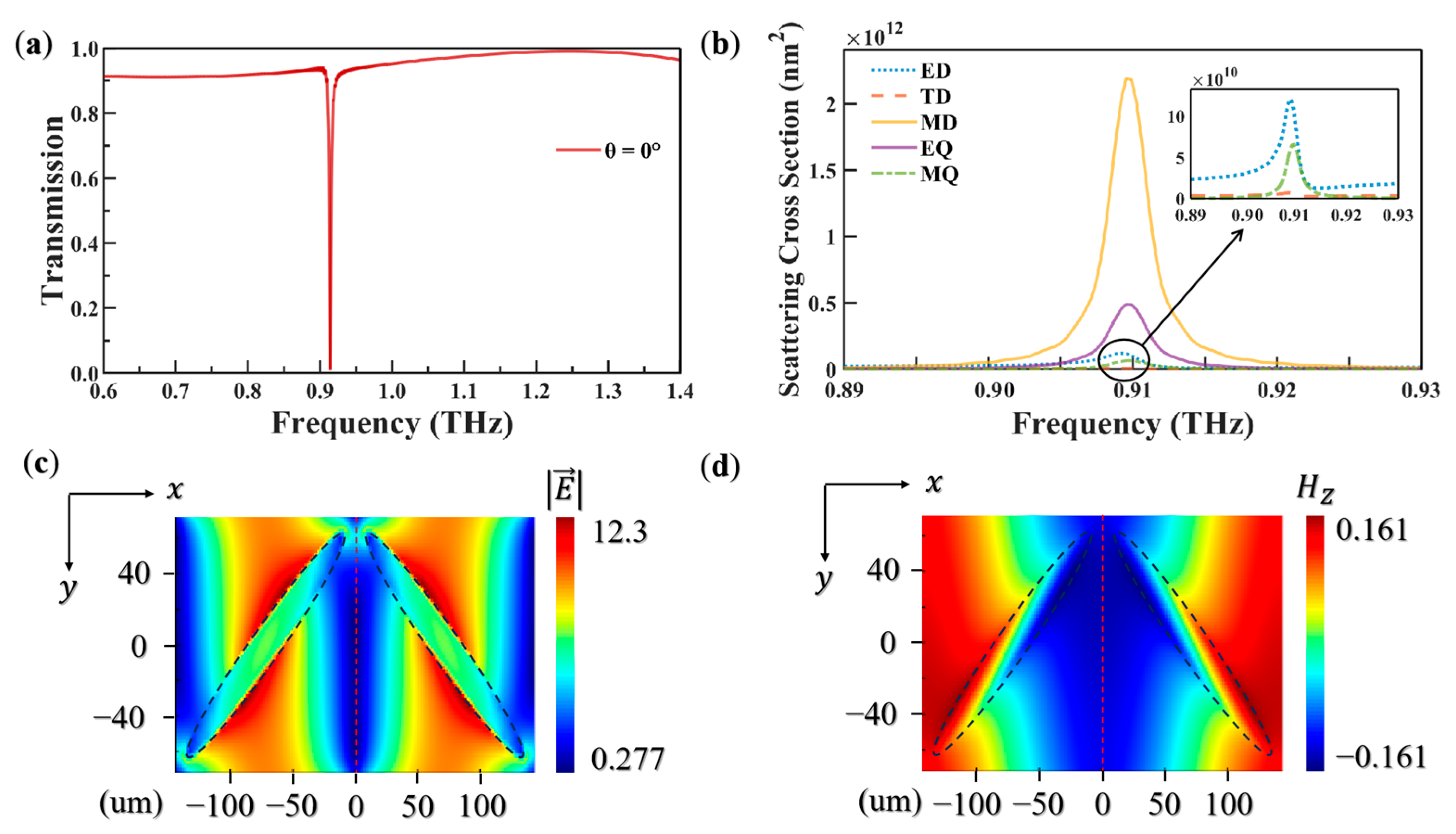
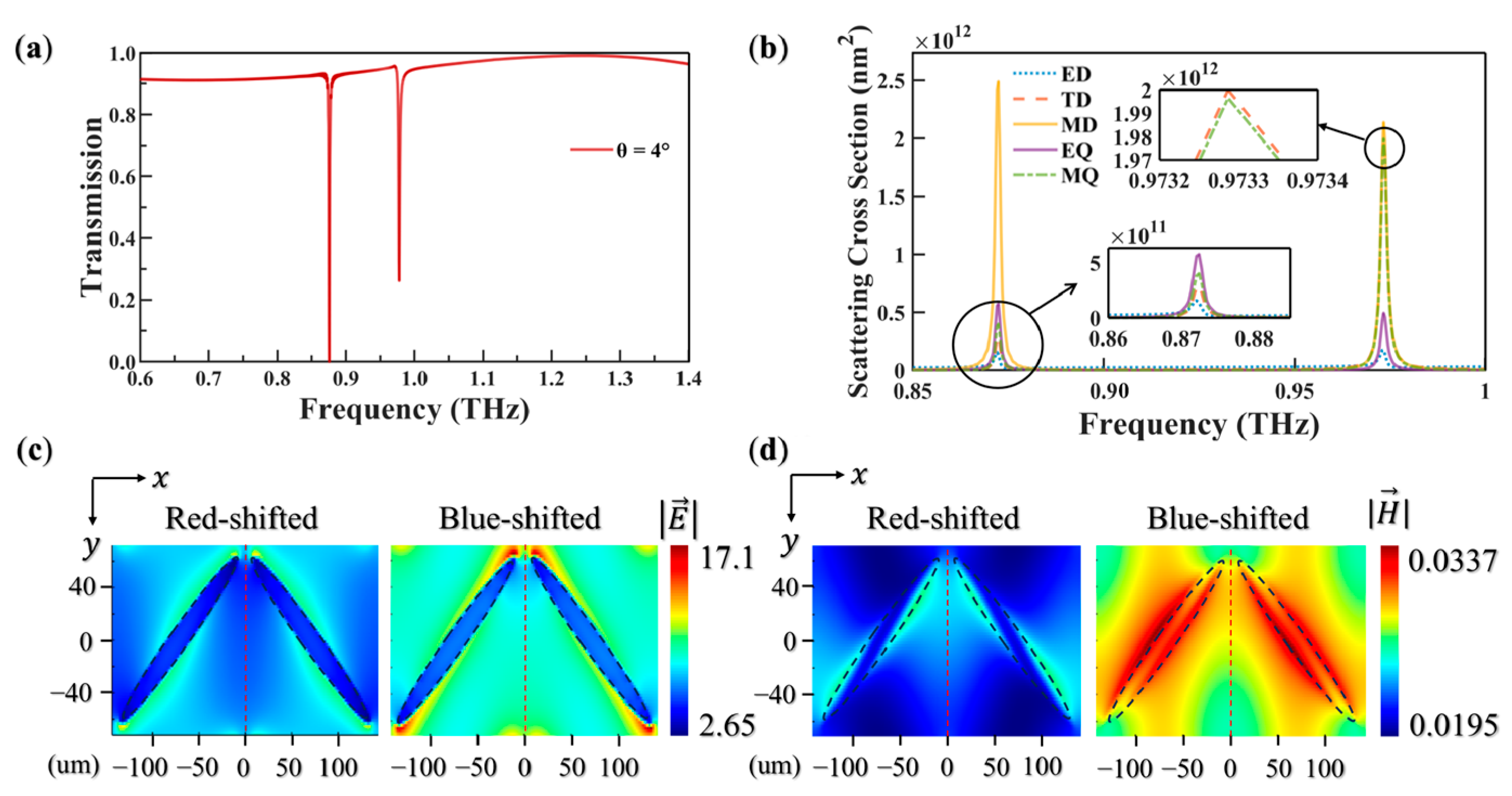
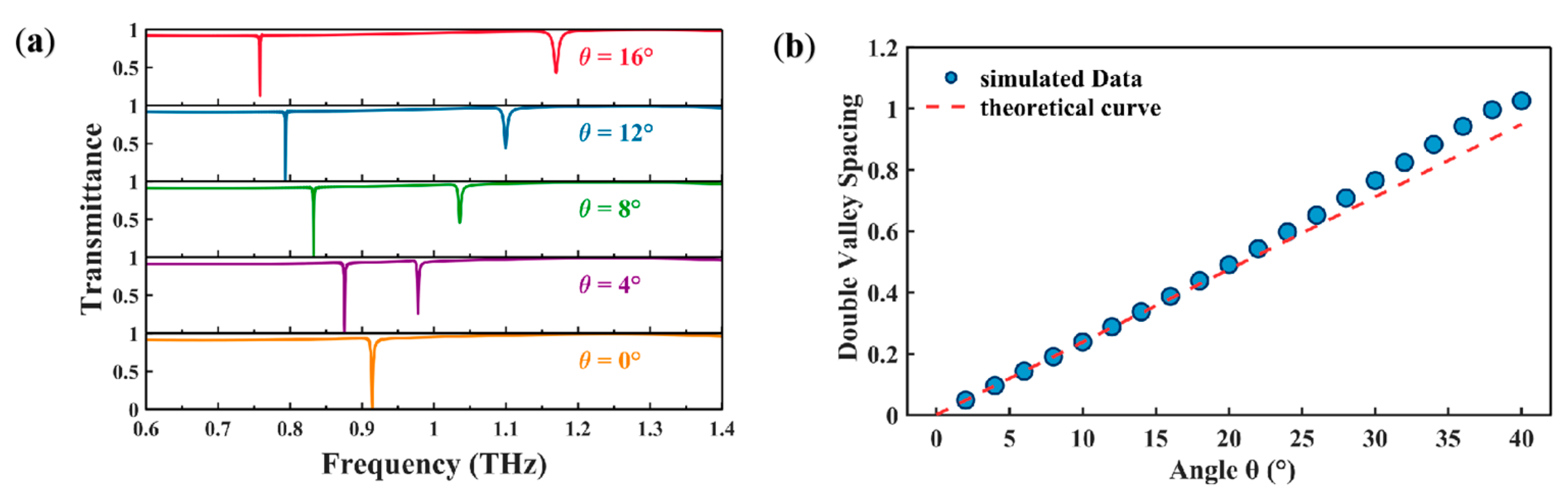
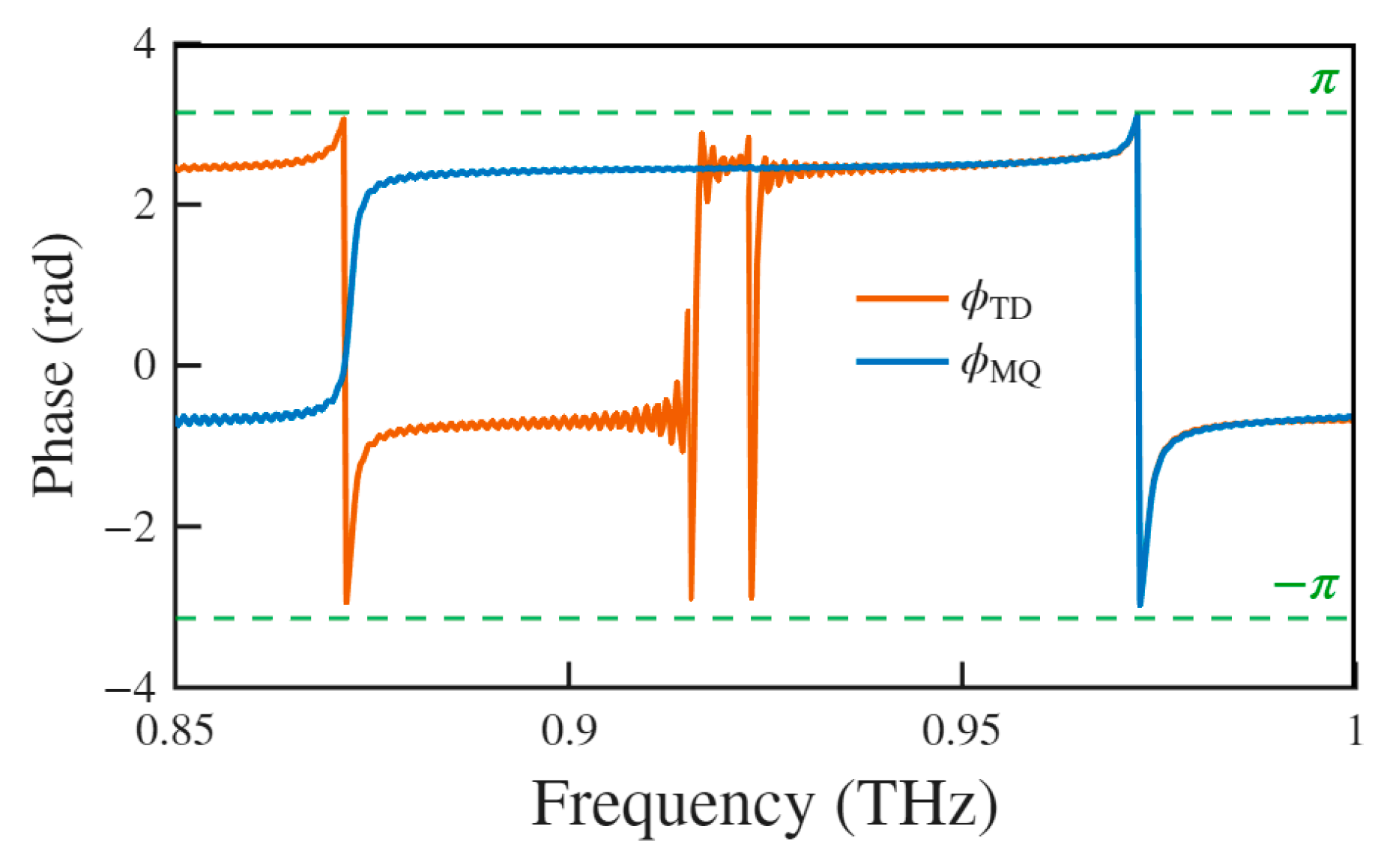
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qin, J.; Ying, Y.; Xie, L. The Detection of Agricultural Products and Food Using Terahertz Spectroscopy: A Review. Appl. Spectrosc. Rev. 2013, 48, 439–457. [Google Scholar] [CrossRef]
- Wang, R.; Xu, L.; Huang, L.; Zhang, X.; Ruan, H.; Yang, X.; Lou, J.; Chang, C.; Du, X. Ultrasensitive Terahertz Biodetection Enabled by Quasi-BIC-Based Metasensors. Small 2023, 19, 2301165. [Google Scholar] [CrossRef] [PubMed]
- Zhou, R.; Wang, C.; Huang, Y.; Huang, K.; Wang, Y.; Xu, W.; Xie, L.; Ying, Y. Label-free terahertz microfluidic biosensor for sensitive DNA detection using graphene-metasurface hybrid structures. Biosens. Bioelectron. 2021, 188, 113336. [Google Scholar] [CrossRef] [PubMed]
- Markelz, A.G.; Mittleman, D.M. Perspective on Terahertz Applications in Bioscience and Biotechnology. ACS Photonics 2022, 9, 1117–1123. [Google Scholar] [CrossRef]
- Fan, S.; He, Y.; Ung, B.S.; Pickwell-MacPherson, E. The Growth of Biomedical Terahertz Research. J. Phys. D Appl. Phys. 2014, 47, 374009. [Google Scholar] [CrossRef]
- Chen, L.; Ren, G.; Liu, L.; Guo, P.; Wang, E.; Zhou, L.; Zhu, Z.; Zhang, J.; Yang, B.; Zhang, W.; et al. Terahertz Signatures of Hydrate Formation in Alkali Halide Solutions. J. Phys. Chem. Lett. 2020, 11, 7146–7152. [Google Scholar] [CrossRef]
- Ho, L.; Pepper, M.; Taday, P. Terahertz Spectroscopy: Signatures and Fingerprints. Nat. Photonics 2008, 2, 541–543. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, Y.; Mao, J.; Yang, F.; Wang, N. Metasurface-Assisted Terahertz Sensing. Sensors 2023, 23, 5902. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Shen, Y.; Xu, Y.; Luo, L.; Gu, J.; Yang, S.; Xu, J.; Deng, X. Experiment on Terahertz Metasurfaces of Metal Split Ring Resonators with Bound State in the Continuum. APL Mater. 2023, 11, 051102. [Google Scholar] [CrossRef]
- Gao, J.; Liu, H.; Zhang, M.; Liu, M.; Zhang, H.; Zhang, Y. Dynamic Switching Between Bound States in the Continuum (BIC) and Quasi-BIC Based on a Dirac Semimetal Terahertz Metasurface. Phys. Chem. Chem. Phys. 2022, 24, 25571–25579. [Google Scholar] [CrossRef]
- Qi, T.; Song, F.; Xiao, B.; Du, Y.; Qin, J. Excitation and Sensing Application of Dual-Bound States in the Continuum in Metallic Terahertz Metasurfaces. Opt. Lasers Eng. 2024, 180, 108287. [Google Scholar] [CrossRef]
- Li, S.Y.; Zhou, C.B.; Liu, T.T.; Xiao, S.Y. Symmetry-Protected Bound States in the Continuum Supported by All-Dielectric Metasurfaces. Phys. Rev. A 2019, 100, 063803. [Google Scholar] [CrossRef]
- Yan, H.; Fan, W.-H.; Jiang, X.-Q.; Chen, X.; Qin, C.; Wu, Q. Dielectric Terahertz Metasurface Governed by Symmetry-Protected BIC for Ultrasensitive Sensing. Phys. Scr. 2024, 99, 085503. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound States in the Continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef]
- Li, J.; Yue, Z.; Li, J.; Zheng, C.; Zhang, Y.; Yao, J. Ultra-narrowband terahertz circular dichroism driven by planar metasurface supporting chiral quasi bound states in continuum. Opt. Laser Technol. 2023, 161, 109173. [Google Scholar] [CrossRef]
- Joseph, S.; Pandey, S.; Sarkar, S.; Joseph, J. Bound States in the Continuum in Resonant Nanostructures: An Overview of Engineered Materials for Tailored Applications. Nanophotonics 2021, 10, 4175–4207. [Google Scholar] [CrossRef]
- Qiu, C.-W.; Zhang, T.; Hu, G.; Kivshar, Y. Quo Vadis, Metasurfaces? Nano Lett. 2021, 21, 5461–5474. [Google Scholar] [CrossRef]
- Wang, L.L.; Cao, J.; Li, X.W.; Zhao, Y.L.; Shi, H.; Fu, L.P.; Liu, D.J.; Liu, F. Quasi-BICs Enabled Proximity Sensing Based on Metal Complementary H-Shaped Arrays at Terahertz Frequencies. IEEE Photon. J. 2022, 14, 4653608. [Google Scholar] [CrossRef]
- Yang, S.; Hong, C.; Jiang, Y.; Ndukaife, J.C. Nanoparticle Trapping in a Quasi-BIC System. ACS Photonics 2021, 8, 1961–1971. [Google Scholar] [CrossRef]
- Han, S.; Pitchappa, P.; Wang, W.; Srivastava, Y.K.; Rybin, M.V.; Singh, R. Extended Bound States in the Continuum with Symmetry-Broken Terahertz Dielectric Metasurfaces. Adv. Opt. Mater. 2021, 9, 2002001. [Google Scholar] [CrossRef]
- Koshelev, K.; Lepeshov, S.; Liu, M.K.; Bogdanov, A.; Kivshar, Y. Asymmetric Metasurfaces with High-Q Resonances Governed by Bound States in the Continuum. Phys. Rev. Lett. 2018, 123, 193903. [Google Scholar] [CrossRef]
- Cong, L.; Singh, R. Symmetry-Protected Dual Bound States in the Continuum in Metamaterials. Adv. Opt. Mater. 2019, 7, 1900383. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Lee, J.; Chua, S.-L.; Johnson, S.G.; Joannopoulos, J.D.; Soljačić, M. Observation of Trapped Light Within the Radiation Continuum. Nature 2013, 499, 188–191. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, Y.K.; Ako, R.T.; Gupta, M.; Bhaskaran, M.; Sriram, S.; Singh, R. Terahertz Sensing of 7 nm Dielectric Film with Bound States in the Continuum Metasurfaces. Appl. Phys. Lett. 2019, 115, 151105. [Google Scholar] [CrossRef]
- Tan, T.C.W.; Plum, E.; Singh, R. Lattice-Enhanced Fano Resonances from Bound States in the Continuum Metasurfaces. Adv. Opt. Mater. 2020, 8, 1901572. [Google Scholar] [CrossRef]
- Dong, B.; Wei, B.; Wei, D.; Ke, Z.; Ling, D. Detection of Low-Concentration Biological Samples Based on a QBIC Terahertz Metamaterial Sensor. Sensors 2024, 24, 3649. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Peng, Y.; Jin, Z.; Wu, X.; Gu, H.; Wei, D.; Zhu, Y.; Zhuang, S. Terahertz Ultrasensitive Biosensor Based on Wide-Area and Intense Light-Matter Interaction Supported by QBIC. Chem. Eng. J. 2023, 462, 142347. [Google Scholar] [CrossRef]
- Xu, W.; Xie, L.; Ying, Y. Mechanisms and Applications of Terahertz Metamaterial Sensing: A Review. Nanoscale 2017, 9, 13864–13878. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.; Du, L.; Liu, Q.; Zhu, L.; Meng, K.; Zou, Y.; Zhang, B. Ultrasensitive Specific Sensor Based on All-Dielectric Metasurfaces in the Terahertz Range. RSC Adv. 2020, 10, 33018–33025. [Google Scholar] [CrossRef]
- Sun, M.; Lin, J.; Xue, Y.; Wang, W.; Shi, S.; Zhang, S.; Shi, Y. A Terahertz Metasurface Sensor Based on Quasi-BIC for Detection of Additives in Infant Formula. Nanomaterials 2024, 14, 883. [Google Scholar] [CrossRef]
- Bi, K.; Wang, Q.; Xu, J.; Chen, L.; Lan, C.; Lei, M. All-Dielectric Metamaterial Fabrication Techniques. Adv. Opt. Mater. 2021, 9, 2001474. [Google Scholar] [CrossRef]
- Wu, T.; EvIyukhin, A.B.; Tuz, V. Separation of a Toroidal Mode in Clusters of Dielectric Particles. Prog. Electromagn. Res. 2024, 180, 103–113. [Google Scholar] [CrossRef]
- Hasebe, H.; Sugimoto, H.; Hinamoto, T.; Fujii, M. Coupled Toroidal Dipole Modes in Silicon Nanodisk Metasurface: Polarization Independent Narrow Band Absorption and Directional Emission. Adv. Opt. Mater. 2020, 8, 2001148. [Google Scholar] [CrossRef]
- Yu, Y.; Li, Y.-Q.; Salas-Montiel, R.; Qiao, D.-Y. Perfect Magnetic Mirror Based on Magnetic Dipole Scattering in All-Dielectric Resonators. J. Appl. Phys. 2022, 131, 153101. [Google Scholar] [CrossRef]
- Wang, W.; Tan, Y.; Liang, B.; Ma, G.; Wang, S.; Cheng, J. Generalized Momentum Conservation and Fedorov-Imbert Linear Shift of Acoustic Vortex Beams at a Metasurface. Phys. Rev. B 2021, 104, 174301. [Google Scholar] [CrossRef]
- Vázquez-Lozano, J.E. Near-Field Directionality Beyond the Dipole Approximation: Electric Quadrupole and Higher-Order Multipole Angular Spectra. Phys. Rev. Appl. 2019, 12, 024065. [Google Scholar] [CrossRef]
- Suh, W.; Wang, Z.; Fan, S. Temporal Coupled-Mode Theory and the Presence of Non-Orthogonal Modes in Lossless Multimode Cavities. IEEE J. Quantum Electron. 2004, 40, 1511–1518. [Google Scholar] [CrossRef]
- Cho, S.-Y.; Sun, J.; Overvig, A.C.; Alù, A.; Zhou, W. Control of Quasibound Waves in Spiral Metasurfaces. ACS Photonics 2022, 9, 3592–3600. [Google Scholar] [CrossRef]
- Cui, Z.; Wang, Y.; Sun, G.; Chen, W.; Zhang, K.; Wang, X. Observation of the Bound States in the Continuum Supported by Mode Coupling in a Terahertz Metasurface. Opt. Lett. 2023, 48, 4809–4812. [Google Scholar] [CrossRef]
- Chen, X.; Yang, Y.; Cai, X.; Auger, D.A.; Meyer, C.H.; Salerno, M.; Epstein, F.H. Accelerated Two-Dimensional Cine DENSE Cardiovascular Magnetic Resonance Using Compressed Sensing and Parallel Imaging. J. Cardiovasc. Magn. Reson. 2016, 18, 38. [Google Scholar] [CrossRef]
- Zhang, D. Coefficients of Determination for Mixed-Effects Models. J. Agric. Biol. Environ. Stat. 2022, 27, 674–689. [Google Scholar] [CrossRef]
- Wang, C.; Tan, S.; Lin, X.; Chen, H.; Gao, F. Terahertz Plasmonic Metagrating Design Simultaneously Enabling Broadband Extraordinary Transmission and Field Enhancement. Prog. Electromagn. Res. 2023, 177, 85–94. [Google Scholar] [CrossRef]
- Lin, J.; Xue, Y.; Wang, W.; Sun, M.; Shi, S.; Zhang, S.; Shi, Y. Enhancing Multi-Spectral Fingerprint Sensing for Trace Explosive Molecules with All-Silicon Metasurfaces. Nanomaterials 2024, 14, 738. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Zhang, L.; Zhang, H.; Li, Y.; Liu, L.; Chen, Y.; Qiu, X.; Yu, D. Development of a Portable SPR Sensor for Nucleic Acid Detection. Micromachines 2020, 11, 526. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, D.; Pan, M.; Shi, Y.; Zhang, Y. Multi-Mode Coupling Enabled Broadband Coverage for Terahertz Biosensing Applications. Biosensors 2025, 15, 368. https://doi.org/10.3390/bios15060368
Hu D, Pan M, Shi Y, Zhang Y. Multi-Mode Coupling Enabled Broadband Coverage for Terahertz Biosensing Applications. Biosensors. 2025; 15(6):368. https://doi.org/10.3390/bios15060368
Chicago/Turabian StyleHu, Dongyu, Mengya Pan, Yanpeng Shi, and Yifei Zhang. 2025. "Multi-Mode Coupling Enabled Broadband Coverage for Terahertz Biosensing Applications" Biosensors 15, no. 6: 368. https://doi.org/10.3390/bios15060368
APA StyleHu, D., Pan, M., Shi, Y., & Zhang, Y. (2025). Multi-Mode Coupling Enabled Broadband Coverage for Terahertz Biosensing Applications. Biosensors, 15(6), 368. https://doi.org/10.3390/bios15060368






