Gait Phase Recognition in Multi-Task Scenarios Based on sEMG Signals
Abstract
1. Introduction
- Based on the theoretical foundation of fuzzy approximate entropy, multi-scale analysis and RMS are introduced for feature extraction, constructing multi-channel electromyographic features. It can effectively capture the dynamic features across multiple scales and significantly distinguish between resting and active states of the sEMG signals.
- Construct the EMACNN model and integrate sEMG entropy features to achieve gait phase recognition.
- Identify gait phases solely from sEMG signals and provide experimental evaluation to demonstrate the effectiveness and generalization of the proposed model.
2. Motion Data Acquisition and Preprocessing
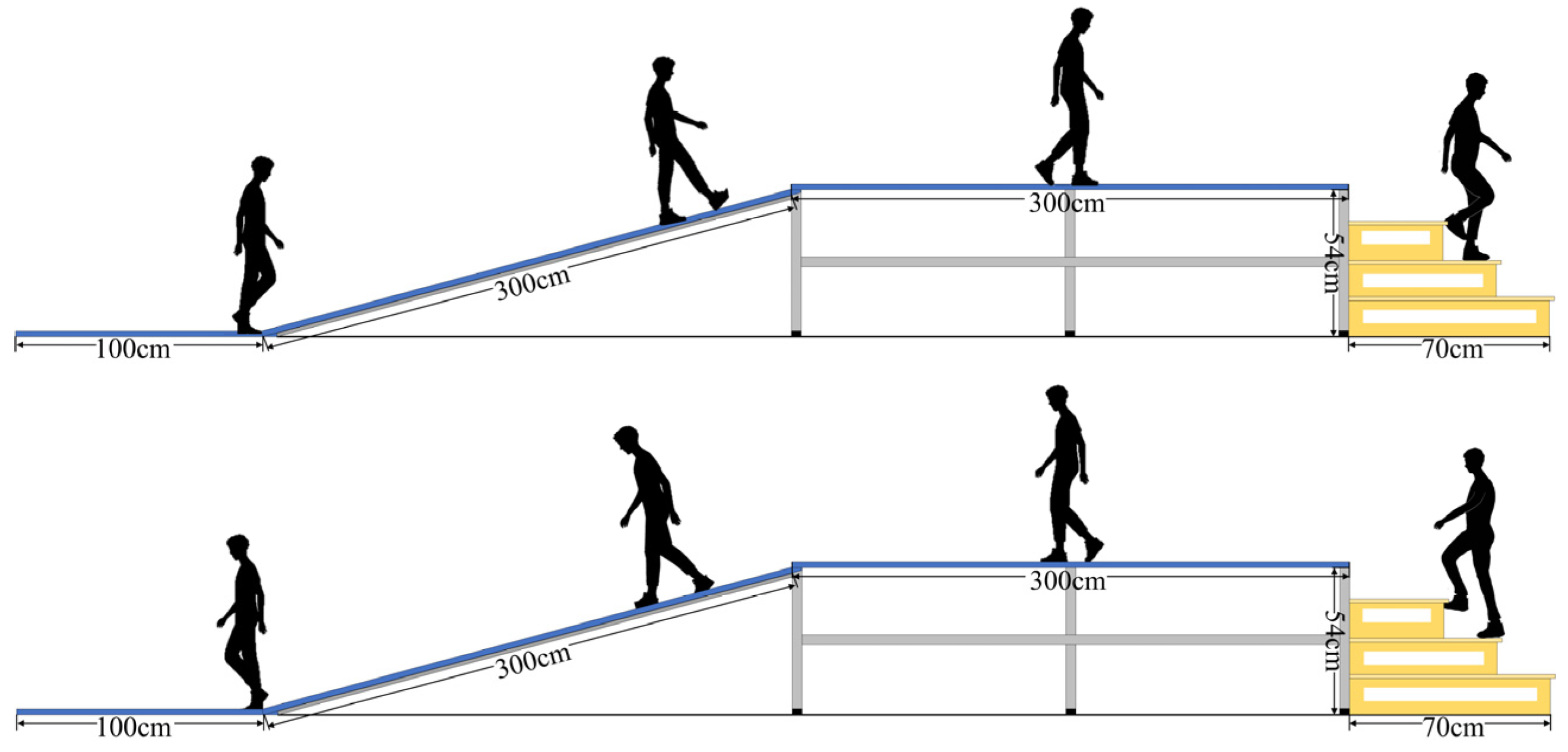
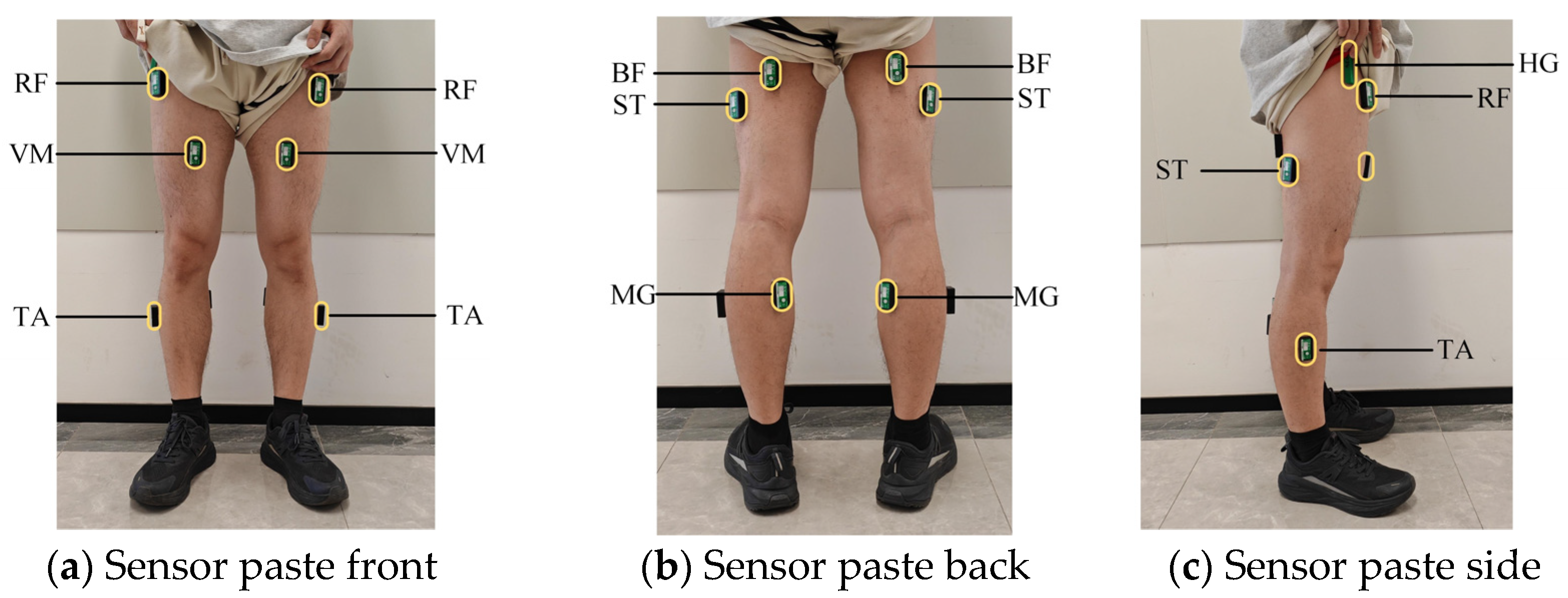
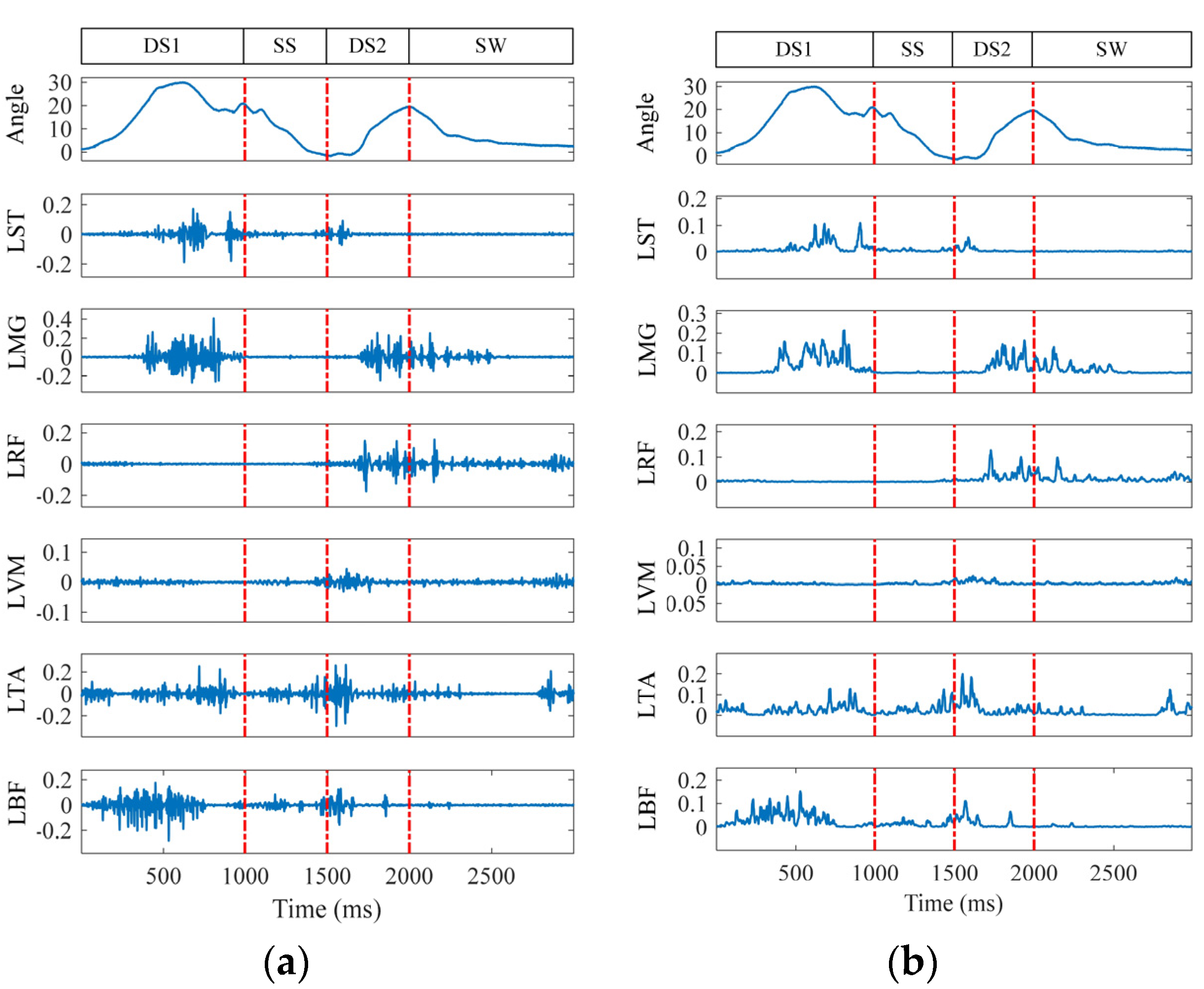
2.1. Data Acquisition
2.2. Data Preprocessing
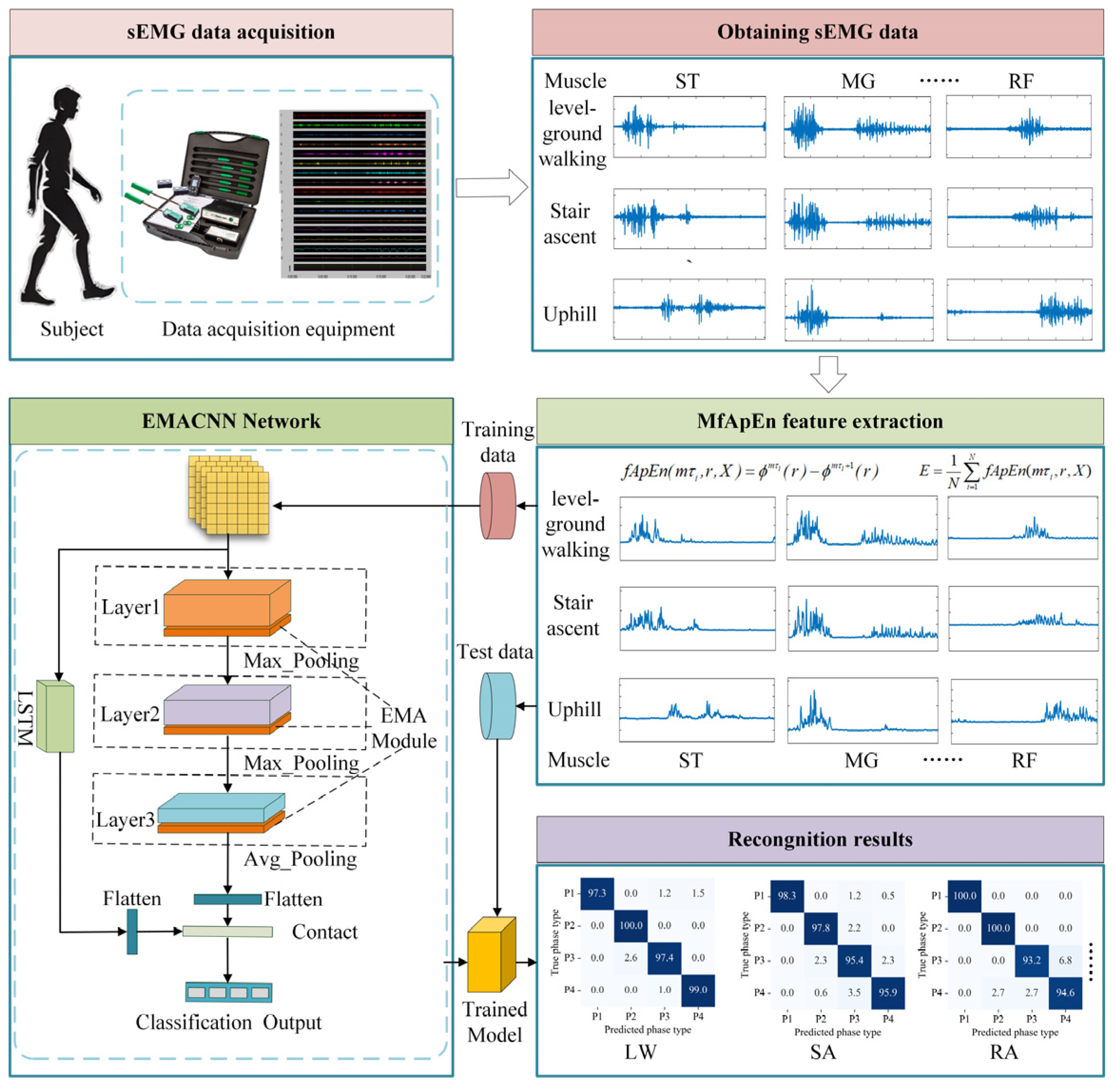
3. Multi-Task Scene Gait Phase Recognition Model Based on sEMG
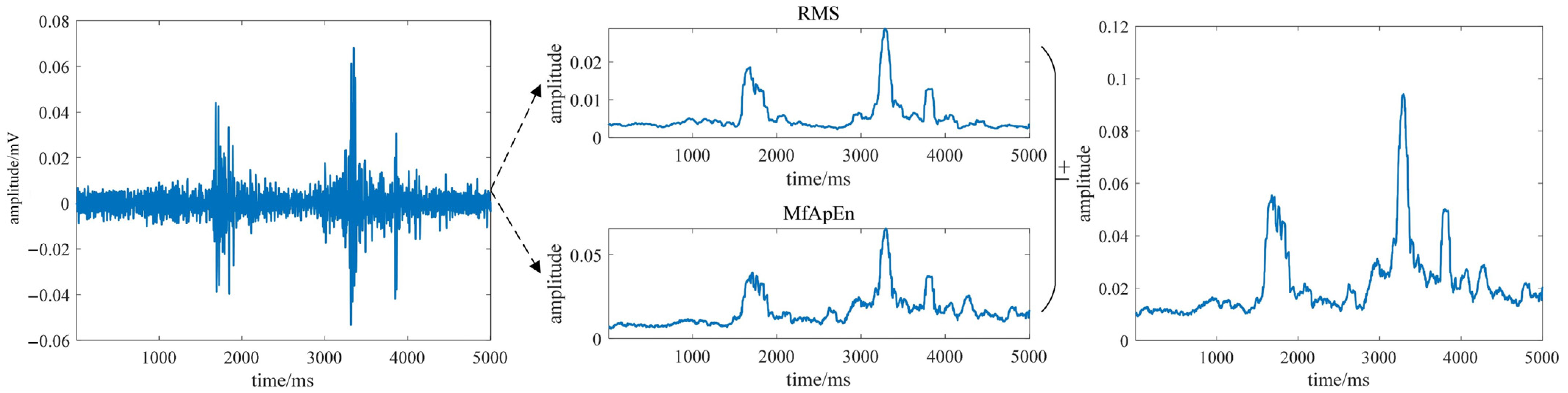
3.1. Gait Phase Feature Extraction Based on MFAREn
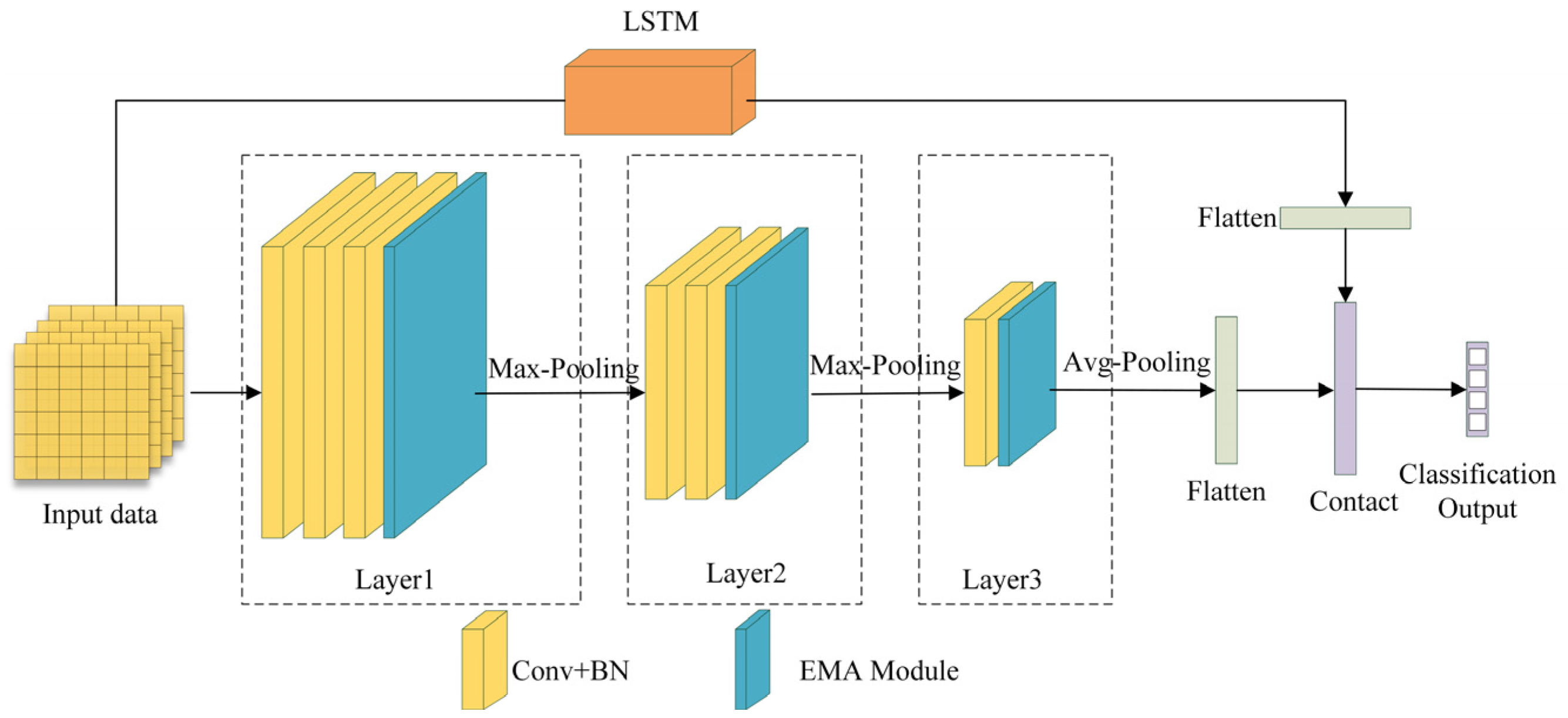
3.2. Efficient Multi-Scale Attention Convolutional Neural Network
3.3. Evaluation Metrics
- (1)
- Accuracy
- (2)
- Precision
- (3)
- Recall rate
- (4)
- F1-score
- (5)
- Average time cost
4. Experimental Validation
4.1. MFAREn Feature Extraction Effect
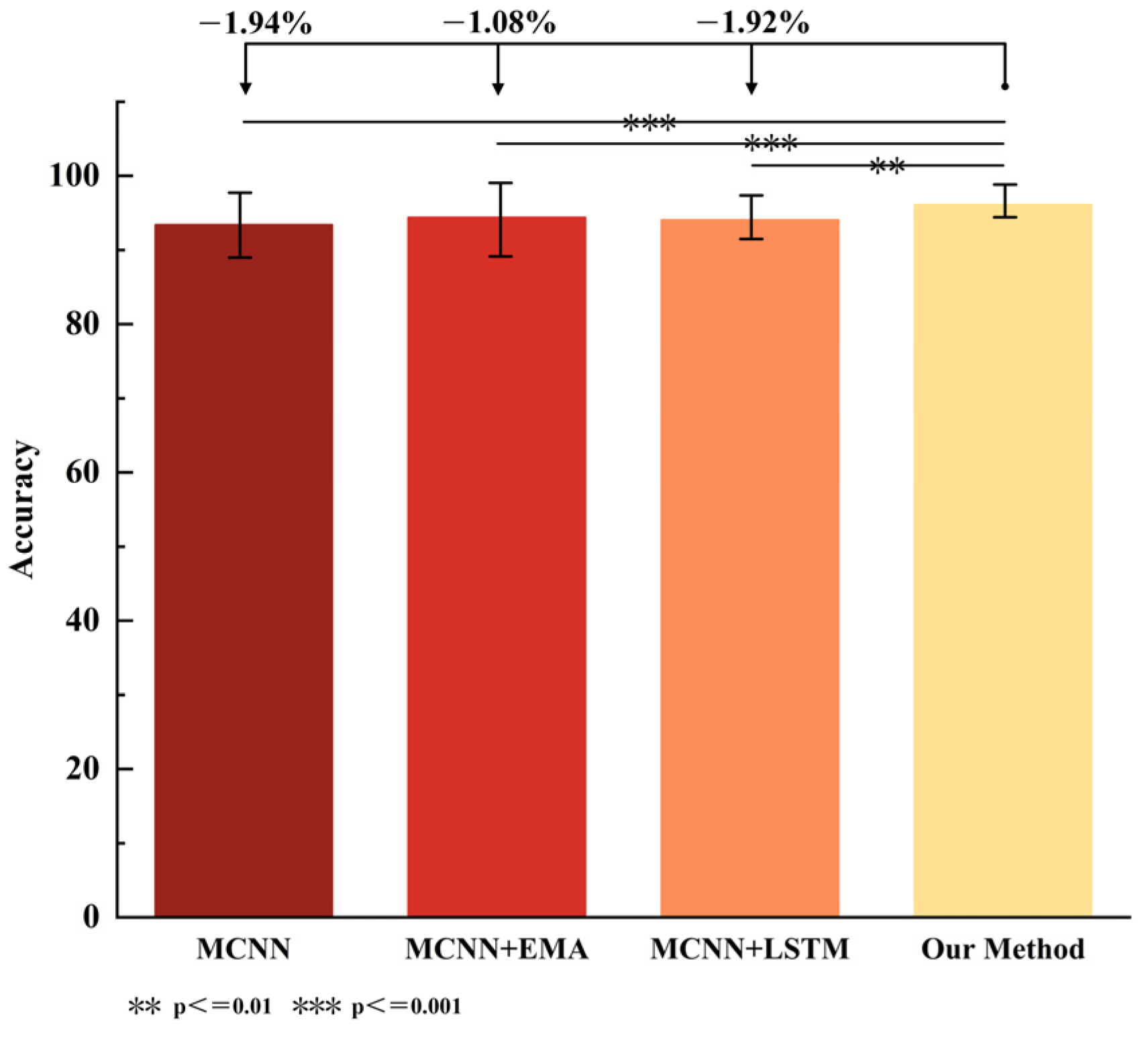
4.2. EMACNN Ablation Experiments
4.3. MFAREn-EMACNN Classification Performance Evaluation
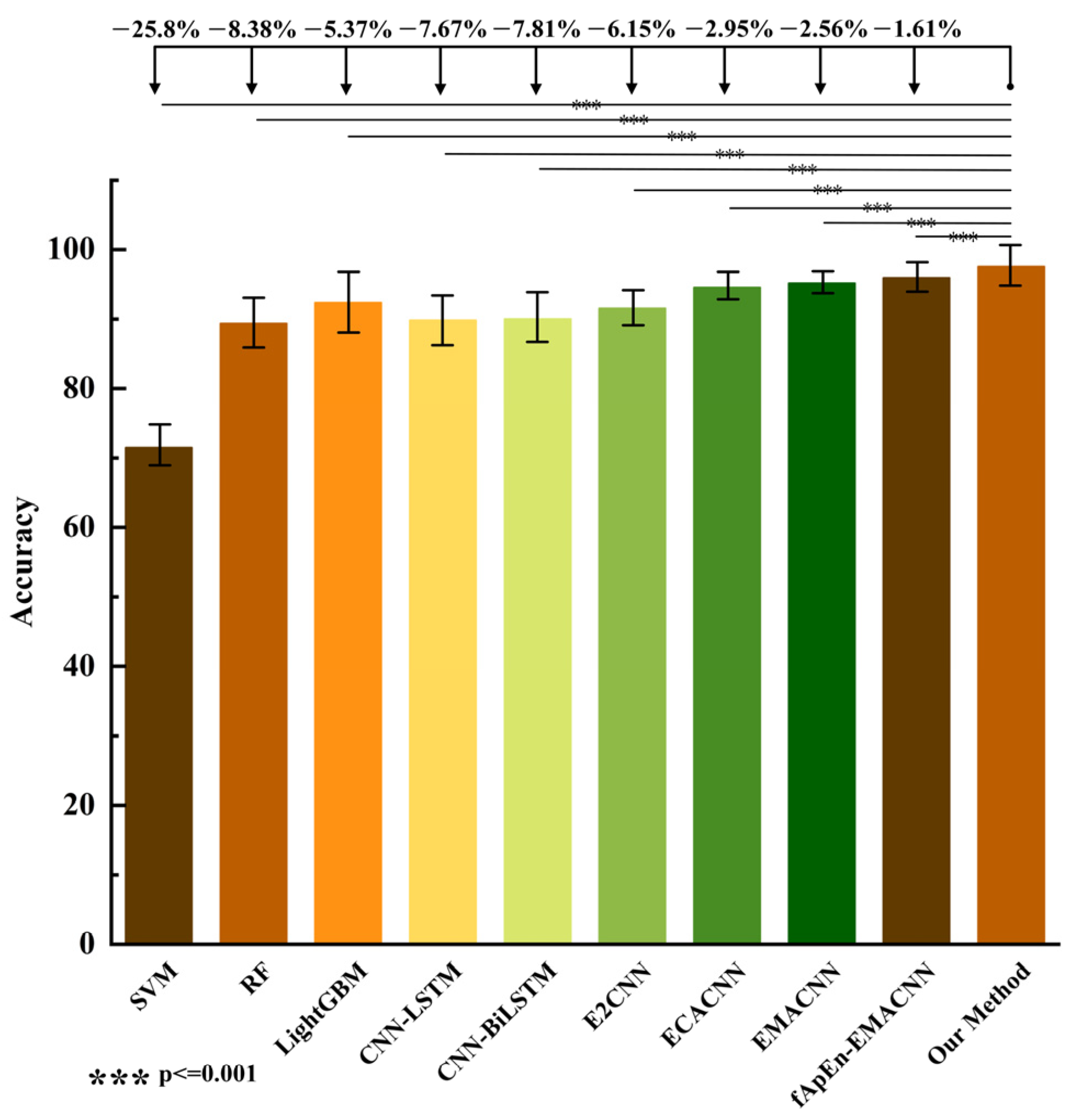
4.4. Comparison with the State-of-the-Art Methods
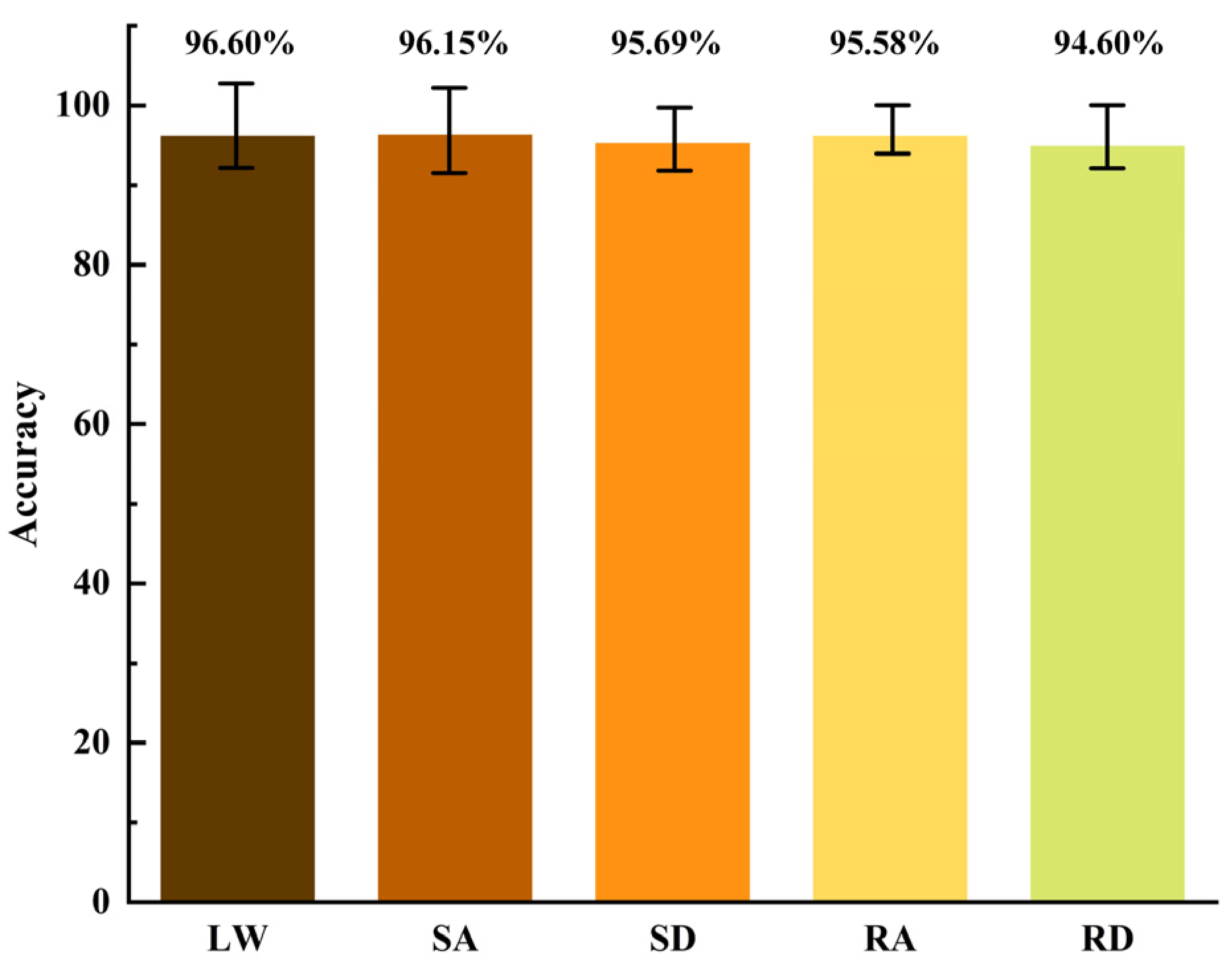
4.5. Experimental Validation of Multi-Scene Gait Phase Recognition
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Al-Ayyad, M.; Abu Owida, H.; De Fazio, R.; Al-Naami, B.; Visconti, P. Electromyography Monitoring Systems in Rehabilitation: A Review of Clinical Applications, Wearable Devices and Signal Acquisition Methodologies. Electronics 2023, 12, 1520. [Google Scholar] [CrossRef]
- Tanzarella, S.; Muceli, S.; Del Vecchio, A.; Casolo, A.; Farina, D. Non-invasive analysis of motor neurons controlling the intrinsic and extrinsic muscles of the hand. J. Neural Eng. 2020, 17, 046033. [Google Scholar] [CrossRef]
- Baud, R.; Manzoori, A.R.; Ijspeert, A. Review of control strategies for lower-limb exoskeletons to assist gait. J. Neuroeng. Rehabil. 2021, 18, 119. [Google Scholar] [CrossRef]
- Shakeel, M.S.; Liu, K.; Liao, X.; Kang, W. TAG: A temporal attentive gait network for cross-view gait recognition. IEEE Trans. Instrum. Meas. 2025, 74, 1–14. [Google Scholar] [CrossRef]
- Guo, X.D.; Zhong, F.Q.; Xiao, J.R.; Zhou, Z.H.; Xu, W. Adaptive random forest for gait prediction in lower limb exoskeleton. J. Biomim. Biomater. Biomed. Eng. 2024, 64, 55–67. [Google Scholar] [CrossRef]
- Xiang, Q.; Wang, J.; Liu, Y.; Guo, S.; Liu, L. Gait recognition and assistance parameter prediction determination based on kinematic information measured by inertial measurement units. Bioengineering 2024, 11, 275. [Google Scholar] [CrossRef]
- Wang, H.; Wang, M.; Li, D.; Deng, F.; Pan, Z.; Song, Y. Gait phase recognition of hip exoskeleton system based on CNN and HHO-SVM model. Electronics 2025, 14, 107. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, J.; Elsabbagh, A. Lower limb motion intention recognition based on sEMG fusion features. IEEE Sens. J. 2022, 22, 7005–7014. [Google Scholar] [CrossRef]
- Zhan, H.; Kou, J.; Cao, Y.; Guo, Q.; Zhang, J.; Shi, Y. Human gait phases recognition based on multi-source data fusion and BILSTM attention neural network. Measurement 2024, 238, 115396. [Google Scholar] [CrossRef]
- Liu, Q.; Sun, W.; Peng, N.; Meng, W.; Xie, S.Q. DCNN-SVM-based gait phase recognition with inertia, EMG, and insole plantar pressure sensing. IEEE Sens. J. 2024, 24, 28869–28878. [Google Scholar] [CrossRef]
- Zhang, C.; Yu, Z.; Wang, X.; Chen, Z.J.; Deng, C. Temporal-constrained parallel graph neural networks for recognizing motion patterns and gait phases in class-imbalanced scenarios. Eng. Appl. Artif. Intell. 2025, 143, 110106. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Z.; Lei, H.; Gu, W. Gait phase recognition of lower limb exoskeleton system based on the integrated network model. Biomed. Signal Process. Control. 2022, 76, 103693. [Google Scholar] [CrossRef]
- Cao, W.; Li, C.; Yang, L.; Yin, M.; Chen, C.; Kobsiriphat, W.; Utakapan, T.; Yang, Y.; Yu, H.; Wu, X. A fusion network with stacked denoise autoencoder and meta learning for lateral walking gait phase recognition and multi-step-ahead prediction. IEEE J. Biomed. Health Inform. 2025, 29, 68–80. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H.; Hu, J.; Zheng, J.; Wang, X.; Deng, J.; Wan, Z.; Wang, H.; Wang, Y. Gait pattern identification and phase estimation in continuous multilocomotion mode based on inertial measurement units. IEEE Sens. J. 2022, 22, 16952–16962. [Google Scholar] [CrossRef]
- Guo, Y.; Hutabarat, Y.; Owaki, D.; Hayashibe, M. Speed-variable gait phase estimation during ambulation via temporal convolutional network. IEEE Sens. J. 2024, 24, 5224–5236. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Song, Q.; Wu, D.; Jin, D. Gait event detection based on fuzzy logic model by using IMU signals of lower limbs. IEEE Sens. J. 2024, 24, 22685–22697. [Google Scholar] [CrossRef]
- Yang, L.; Xiang, K.; Pang, M.; Yin, M.; Wu, X.; Cao, W. Inertial sensing for lateral walking gait detection and application in lateral resistance exoskeleton. IEEE Trans. Instrum. Meas. 2023, 72, 1–14. [Google Scholar] [CrossRef]
- Oh, H.; Hong, Y. Divergent component of motion-based gait intention detection method using motion information from single leg. J. Intell. Robot. Syst. 2023, 107, 51. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, S.; Dai, Y.; Wu, X.; Guo, S.; Su, W. Two-dimensional identification of lower limb gait features based on the variational modal decomposition of sEMG signal and convolutional neural network. Gait Posture 2025, 117, 191–203. [Google Scholar] [CrossRef]
- Ling, Z.Q.; Chen, J.C.; Cao, G.Z.; Zhang, Y.P.; Li, L.L.; Xu, W.X.; Cao, S.B. A Domain Adaptive Convolutional neural network for sEMG-based gait phase recognition against to speed changes. IEEE Sens. J. 2023, 23, 2565–2576. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Y.; Hou, J.; Li, G.; Sun, B.; Lu, P. Deep learning for electromyographic lower-limb motion signal classification using residual learning. IEEE Trans. Neural Syst. Rehabil. Eng. 2024, 32, 2078–2086. [Google Scholar] [CrossRef]
- Dianbiao, D.; Chi, M.; Miao, W.; Huong, T.V.; Vanderborght, B.; Sun, Y. A low-cost framework for the recognition of human motion gait phases and patterns based on multi-source perception fusion. Eng. Appl. Artif. Intell. 2023, 120, 105886. [Google Scholar]
- Wang, Y.; Song, Q.; Ma, T.; Yao, N.; Liu, R.; Wang, B. Research on human gait phase recognition algorithm based on multi-source information fusion. Electronics 2023, 12, 193. [Google Scholar] [CrossRef]
- Liu, J.; Tan, X.; Jia, X.; Li, T.; Li, W. A gait phase recognition method for obstacle crossing based on multi-sensor fusion. Sens. Actuators A Phys. 2024, 376, 115645. [Google Scholar] [CrossRef]
- Wang, E.; Chen, X.; Li, Y.; Fu, Z.; Huang, J. Lower limb motion intent recognition based on sensor fusion and fuzzy multitask learning. IEEE Trans. Fuzzy Syst. 2024, 32, 2903–2914. [Google Scholar] [CrossRef]
- Quin, P.; Shi, X.; Han, K.; Fan, Z. Lower limb motion classification using energy density features of surface electromyography signals’ activation region and dynamic ensemble model. IEEE Trans. Instrum. Meas. 2023, 72, 1–16. [Google Scholar] [CrossRef]
- Quin, P.; Shi, X. Evaluation of feature extraction and classification for lower limb motion based on sEMG signal. Entropy 2020, 22, 852. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, H.; Zhou, B.; Wei, C.; Xu, S. Continuous and simultaneous estimation of lower limb multi-joint angles from sEMG signals based on stacked convolutional and LSTM models. Expert Syst. Appl. 2022, 203, 117340. [Google Scholar] [CrossRef]
- Qin, P.; Shi, X.; Zhang, C.; Han, K. Continuous estimation of the lower-limb multi-joint angles based on muscle synergy theory and state-space model. IEEE Sens. J. 2023, 23, 8491–8503. [Google Scholar] [CrossRef]
- Aviles, M.; Alvarez-Alvarado, J.M.; Robles-Ocampo, J.-B.; Sevilla-Camacho, P.Y.; Rodríguez-Reséndiz, J. Optimizing RNNs for EMG signal classification: A novel strategy using grey wolf optimization. Bioengineering 2024, 11, 77. [Google Scholar] [CrossRef]
- Yifan, L.; Yueling, L.; Rong, S. Phase-dependent modulation of muscle activity and intermuscular coupling during walking in patients after stroke. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 1119–1127. [Google Scholar]
- Qin, P.; Shi, X. A novel method for lower limb joint angle estimation based on sEMG signal. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Xie, H.B.; Guo, J.Y.; Zheng, Y.P. Fuzzy approximate entropy analysis of chaotic and natural complex systems: Detecting muscle fatigue using electromyography signals. Ann. Biomed. Eng. 2010, 38, 1483–1496. [Google Scholar] [CrossRef]
- Shi, X.; Qin, P.; Zhu, J.; Zhai, M.; Shi, W. Feature extraction and classification of lower limb motion based on sEMG signals. IEEE Access 2020, 8, 132882–132892. [Google Scholar] [CrossRef]
- Ouyang, D.; He, S.; Zhang, G.; Luo, M.; Guo, H.; Zhan, J.; Huang, Z. Efficient multi-scale attention module with cross-spatial learning. In Proceedings of the ICASSP 2023-2023 IEEE International Conference on Acoustics, Speech and Signal Processing, Rhodes Island, Greece, 4–10 June 2023. [Google Scholar]
- Zhang, C.; Li, Y.; Yu, Z.; Huang, X.; Xu, J.; Deng, C. An end-to-end lower limb activity recognition framework based on sEMG data augmentation and enhanced CapsNet. Expert Syst. Appl. 2023, 227, 120257. [Google Scholar] [CrossRef]
- Xia, Y.; Li, J.; Yang, D.; Wei, W. Gait phase classification of lower limb exoskeleton based on a compound network model. Symmetry 2023, 15, 163. [Google Scholar] [CrossRef]
- Muhammad-Farrukh, Q.; Zohaib, M.; Muhammad-Zia-Ur, R.; Ernest-Nlandu, K. E2CNN: An efficient concatenated CNN for classification of surface EMG extracted from upper limb. IEEE Sens. J. 2023, 23, 8989–8996. [Google Scholar]



| Experimental Group | Modeling Approach | Acc/% | Pre/% | Re/% | F1/% | T/ms | Param/M | |
|---|---|---|---|---|---|---|---|---|
| EMA | LSTM | |||||||
| 1 | MCNN (baseline) | 94.83 | 94.84 | 94.82 | 94.84 | 3.42 | 0.47 | |
| 2 | √ | 95.69 | 95.70 | 95.69 | 95.71 | 3.58 | 0.50 | |
| 3 | √ | 94.85 | 94.86 | 94.84 | 94.85 | 4.02 | 0.52 | |
| 4 | √ | √ | 96.77 | 96.72 | 96.75 | 96.76 | 4.22 | 0.62 |
| Methods | Acc/% | Pre/% | Re/% | F1/% | T/ms | Para/M |
|---|---|---|---|---|---|---|
| SVM | 72.04 ± 0.43 | 70.45 ± 0.42 | 72.04 ± 0.42 | 70.48 ± 0.42 | 0.86 | 0.24 |
| RF | 89.46 ± 0.48 | 89.42 ± 0.47 | 89.46 ± 0.47 | 89.40 ± 0.48 | 2.52 | 0.25 |
| LightGBM | 92.47 ± 0.72 | 92.67 ± 0.72 | 92.47 ± 0.73 | 92.52 ± 0.72 | 0.06 | 0.02 |
| CNN-LSTM | 90.17 ± 0.46 | 90.22 ± 0.46 | 90.20 ± 0.45 | 90.51 ± 0.46 | 3.20 | 2.18 |
| CNN-BiLSTM | 90.03 ± 0.45 | 90.21 ± 0.45 | 90.02 ± 0.44 | 90.30 ± 0.45 | 3.40 | 4.30 |
| E2CNN | 91.69 ± 0.24 | 91.76 ± 0.23 | 91.69 ± 0.25 | 91.70 ± 0.24 | 1.29 | 0.29 |
| ECACNN | 94.89 ± 0.18 | 94.76 ± 0.18 | 94.89 ± 0.17 | 94.82 ± 0.18 | 11.37 | 0.48 |
| EMACNN | 95.28 ± 0.14 | 95.35 ± 0.14 | 95.28 ± 0.14 | 95.27 ± 0.15 | 4.22 | 0.50 |
| fApEn-EMACNN | 96.23 ± 0.32 | 96.22 ± 0.35 | 96.23 ± 0.35 | 96.21 ± 0.31 | 11.78 | 0.62 |
| Our method | 97.84 ± 0.42 | 97.80 ± 0.42 | 97.81 ± 0.41 | 97.84 ± 0.42 | 11.26 | 0.62 |
| Motion Mode | Subject | Age | Acc/% | Pre/% | Re/% | F1/% | T/ms |
|---|---|---|---|---|---|---|---|
| LW | No.1 | 20 | 97.19 ± 0.16 | 97.13 ± 0.18 | 97.19 ± 0.16 | 97.11 ± 0.17 | 10.27 |
| No.2 | 22 | 97.33 ± 0.28 | 97.37 ± 0.27 | 97.38 ± 0.27 | 97.37 ± 0.28 | 13.72 | |
| No.3 | 25 | 97.53 ± 0.43 | 97.56 ± 0.43 | 97.53 ± 0.42 | 97.54 ± 0.42 | 14.58 | |
| No.4 | 27 | 94.37 ± 0.56 | 94.43 ± 0.55 | 94.37 ± 0.56 | 94.35 ± 0.55 | 13.89 | |
| No.5 | 28 | 96.60 ± 0.66 | 96.74 ± 0.66 | 96.60 ± 0.66 | 96.59 ± 0.65 | 12.63 | |
| SA | No.1 | 20 | 97.07 ± 0.19 | 97.09 ± 0.19 | 97.07 ± 0.18 | 97.07 ± 0.19 | 11.52 |
| No.2 | 22 | 97.45 ± 0.23 | 97.46 ± 0.25 | 97.42 ± 0.23 | 97.44 ± 0.25 | 10.23 | |
| No.3 | 25 | 96.80 ± 0.52 | 96.80 ± 0.53 | 96.77 ± 0.53 | 96.78 ± 0.52 | 12.38 | |
| No.4 | 27 | 94.10 ± 0.46 | 94.16 ± 0.52 | 94.10 ± 0.46 | 94.09 ± 0.48 | 13.52 | |
| No.5 | 28 | 95.32 ± 1.11 | 95.59 ± 0.94 | 95.32 ± 1.11 | 95.25 ± 1.15 | 13.66 | |
| SD | No.1 | 20 | 96.09 ± 0.22 | 96.08 ± 0.22 | 96.09 ± 0.22 | 96.07 ± 0.23 | 12.27 |
| No.2 | 22 | 96.80 ± 0.25 | 96.87 ± 0.25 | 96.80 ± 0.27 | 96.81 ± 0.25 | 12.57 | |
| No.3 | 25 | 96.21 ± 0.58 | 96.21 ± 0.54 | 96.24 ± 0.58 | 96.22 ± 0.58 | 13.83 | |
| No.4 | 27 | 93.89 ± 0.80 | 93.92 ± 0.86 | 93.89 ± 0.80 | 93.86 ± 0.85 | 13.05 | |
| No.5 | 28 | 95.44 ± 0.39 | 95.48 ± 0.38 | 95.44 ± 0.39 | 94.45 ± 0.40 | 13.82 | |
| RA | No.1 | 20 | 97.57 ± 0.23 | 97.64 ± 0.24 | 97.57 ± 0.23 | 97.58 ± 0.24 | 11.92 |
| No.2 | 22 | 97.11 ± 0.33 | 97.15 ± 0.31 | 97.11 ± 0.33 | 97.09 ± 0.33 | 12.03 | |
| No.3 | 25 | 96.38 ± 0.50 | 96.39 ± 0.49 | 96.38 ± 0.50 | 96.40 ± 0.51 | 12.38 | |
| No.4 | 27 | 91.47 ± 1.43 | 91.65 ± 1.37 | 91.47 ± 1.43 | 91.44 ± 1.38 | 12.08 | |
| No.5 | 28 | 95.87 ± 0.53 | 95.96 ± 0.45 | 95.87 ± 0.53 | 95.89 ± 0.51 | 12.67 | |
| RD | No.1 | 20 | 95.11 ± 0.36 | 95.14 ± 0.37 | 95.10 ± 0.36 | 95.11 ± 0.37 | 11.21 |
| No.2 | 22 | 95.38 ± 0.59 | 95.36 ± 0.61 | 95.37 ± 0.59 | 95.41 ± 0.61 | 12.14 | |
| No.3 | 25 | 96.31 ± 0.83 | 96.32 ± 0.87 | 96.31 ± 0.83 | 96.33 ± 0.84 | 11.67 | |
| No.4 | 27 | 92.11 ± 0.94 | 92.39 ± 0.87 | 92.11 ± 0.94 | 92.10 ± 0.90 | 12.57 | |
| No.5 | 28 | 94.11 ± 1.46 | 94.61 ± 1.28 | 94.11 ± 1.46 | 94.03 ± 1.64 | 12.56 |
| Ref. | Number of Tasks | Number of Phase | Sensors | Method | Performance |
|---|---|---|---|---|---|
| [12] | 1 | 4 | IMU | SBLSTM | Acc: 94% |
| [10] | 1 | 5 | EMG + IMU | DCNN-SVM | Acc: 96.00% |
| [23] | 1 | 4 | IMU + pressure sensor | NHMM | Acc: 94.7% |
| [24] | 1 | 5 | IMU + pressure sensor | CNN-PCA-LSTM | Acc: 97.91% |
| This work | 5 | 4 | sEMG | MFAREn-EMACNN | Acc: 95.72%T: 12.59 ms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, X.; Zhang, X.; Qin, P.; Huang, L.; Zhu, Y.; Yang, Z. Gait Phase Recognition in Multi-Task Scenarios Based on sEMG Signals. Biosensors 2025, 15, 305. https://doi.org/10.3390/bios15050305
Shi X, Zhang X, Qin P, Huang L, Zhu Y, Yang Z. Gait Phase Recognition in Multi-Task Scenarios Based on sEMG Signals. Biosensors. 2025; 15(5):305. https://doi.org/10.3390/bios15050305
Chicago/Turabian StyleShi, Xin, Xiaheng Zhang, Pengjie Qin, Liangwen Huang, Yaqin Zhu, and Zixiang Yang. 2025. "Gait Phase Recognition in Multi-Task Scenarios Based on sEMG Signals" Biosensors 15, no. 5: 305. https://doi.org/10.3390/bios15050305
APA StyleShi, X., Zhang, X., Qin, P., Huang, L., Zhu, Y., & Yang, Z. (2025). Gait Phase Recognition in Multi-Task Scenarios Based on sEMG Signals. Biosensors, 15(5), 305. https://doi.org/10.3390/bios15050305





