A Novel Adaptive Independent Component Analysis Method for Multi-Channel Optically Pumped Magnetometers’ Magnetocardiography Signals
Abstract
1. Introduction
2. Materials and Methods
2.1. ICA Dimensionality Reduction
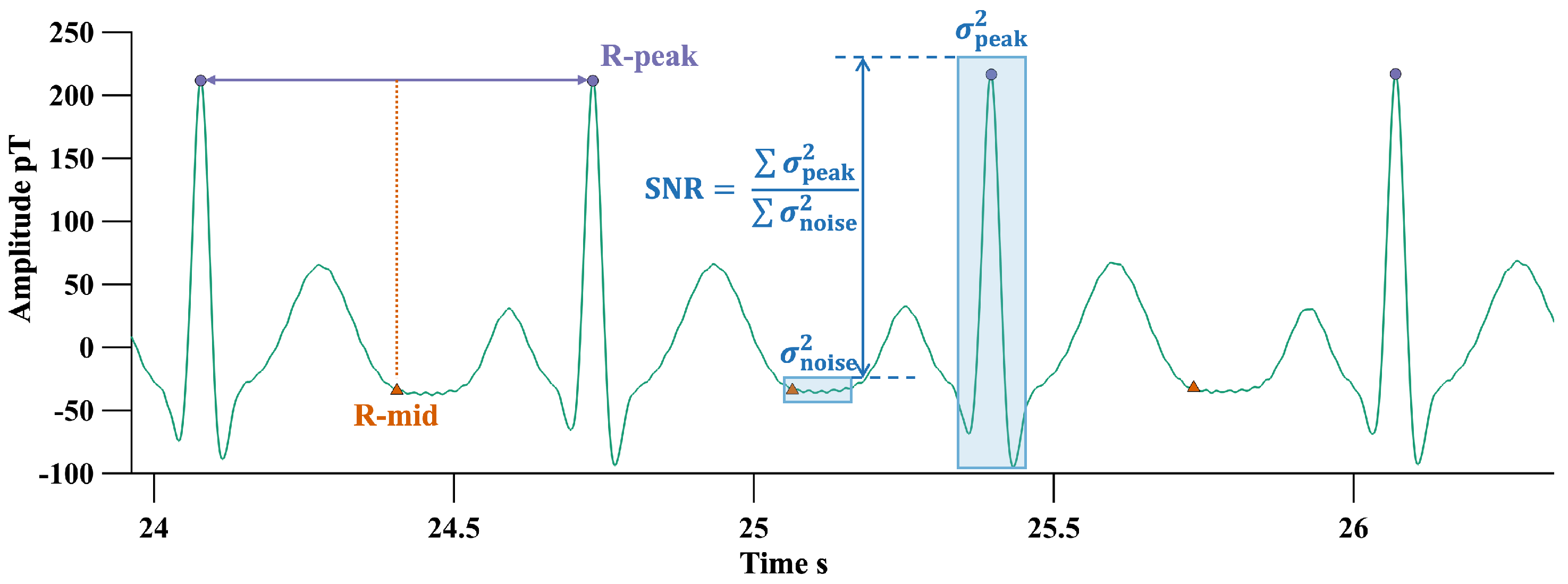
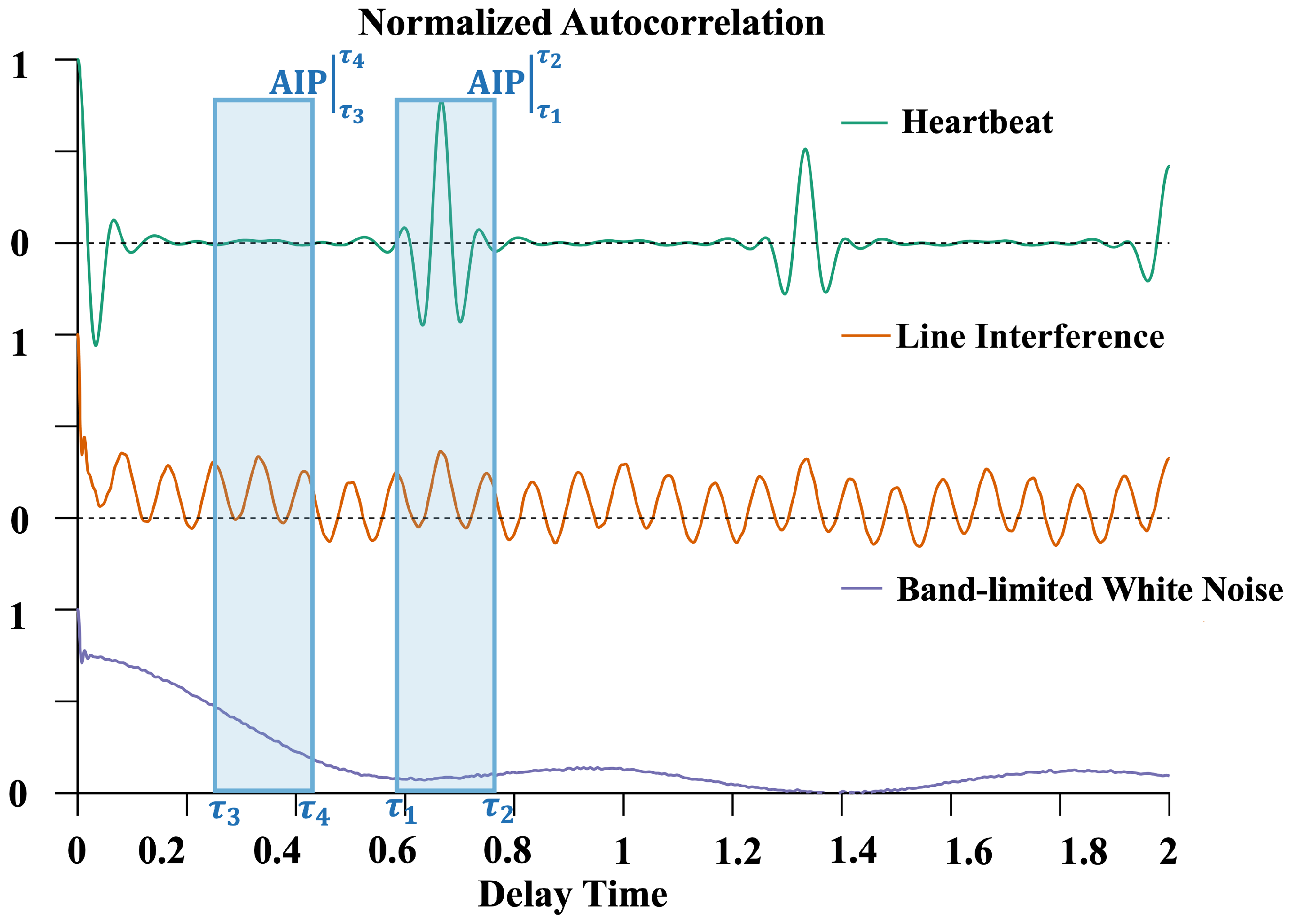
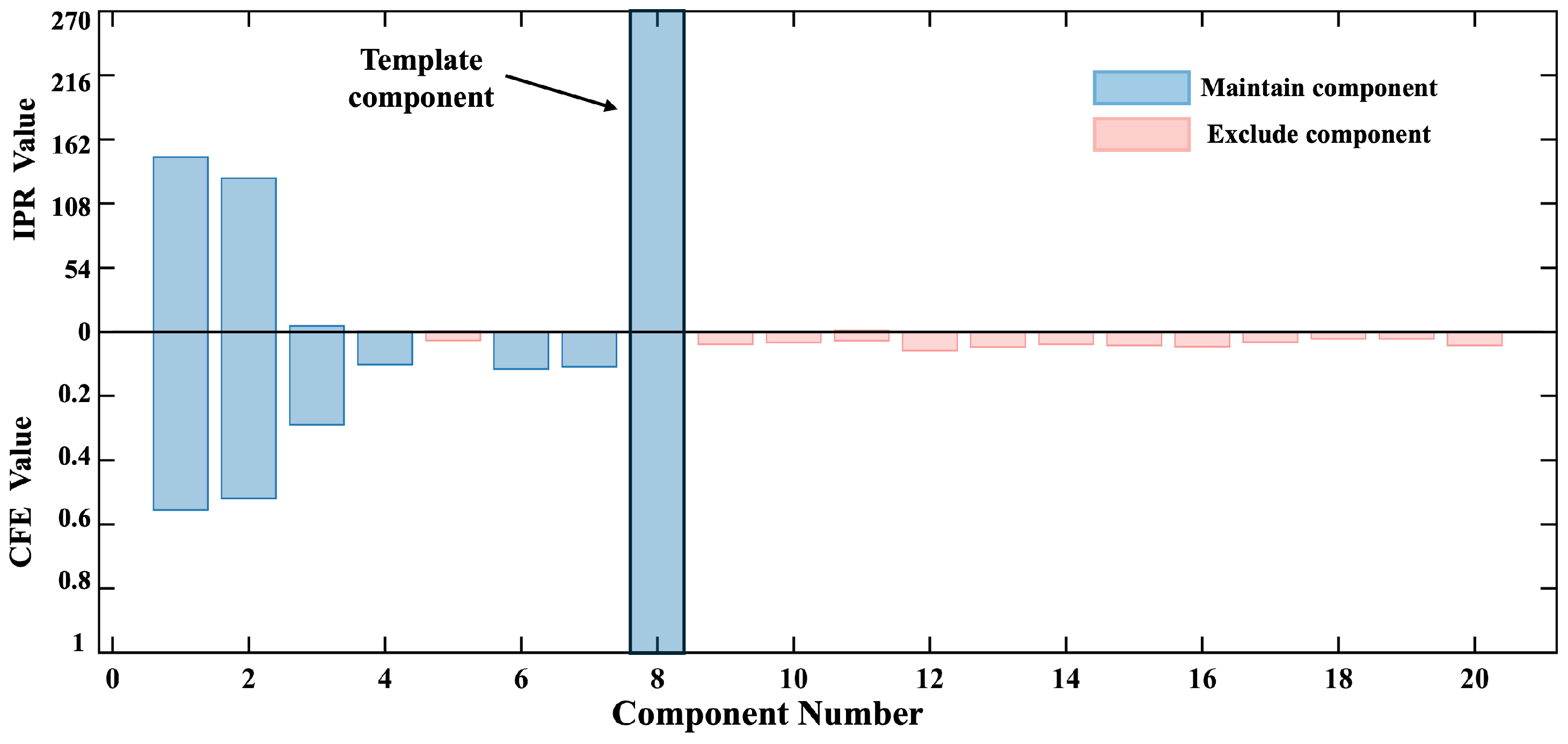
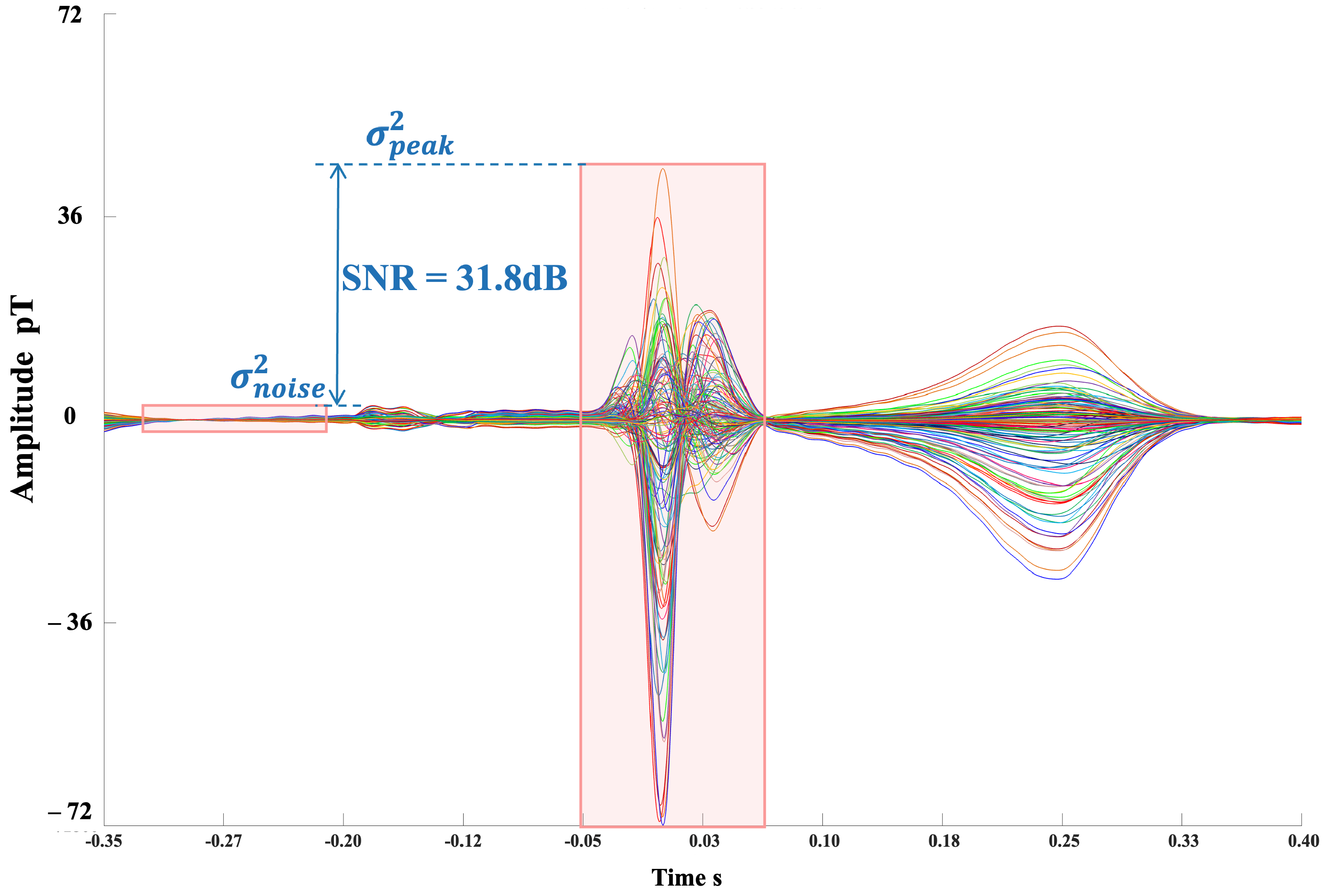
2.2. Autocorrelation Integral Power Ratio (IPR)
- Bandwidth-limited Gaussian white noise (BWN): White noise generally exists in the system’s background noise. The bandwidth limitation of an OPM results in an autocorrelation function with sinc function characteristics, reflecting the time correlation introduced by the limited bandwidth.
- Power line interference (PLI): these signals exhibit periodic characteristics in their autocorrelation functions.
- Typical cardiac cycle: these signals have quasi-periodicity; the components should only have significant values when , where is the shortest heartbeat period within the finite measurement time.
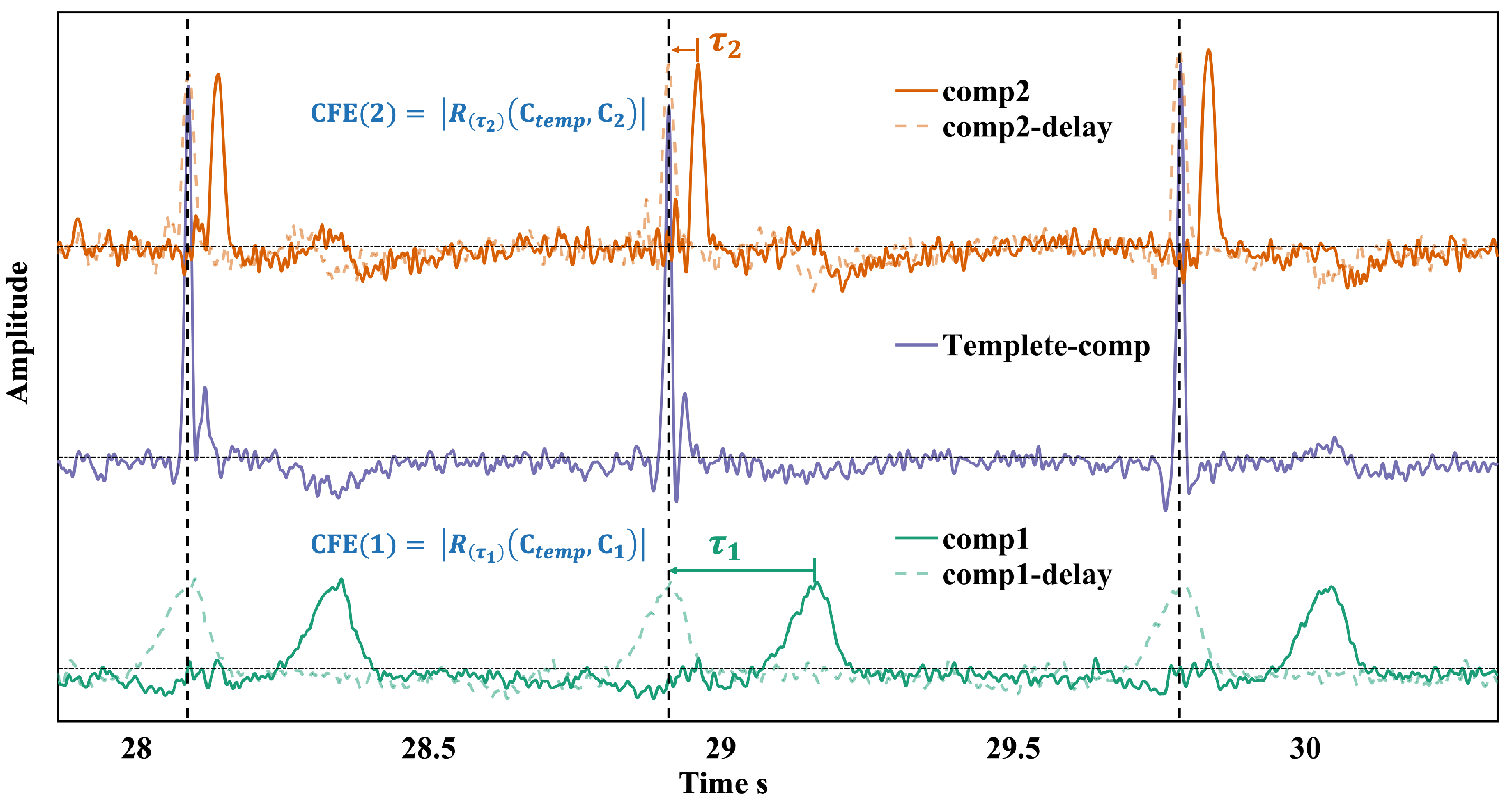
2.3. Cross-Correlation Function Interval Extremum
2.4. Methodology Flow
3. Experiment
3.1. Phantom Experiment
3.2. MCG Data Acquisition
4. Results
4.1. Phantom Experiment
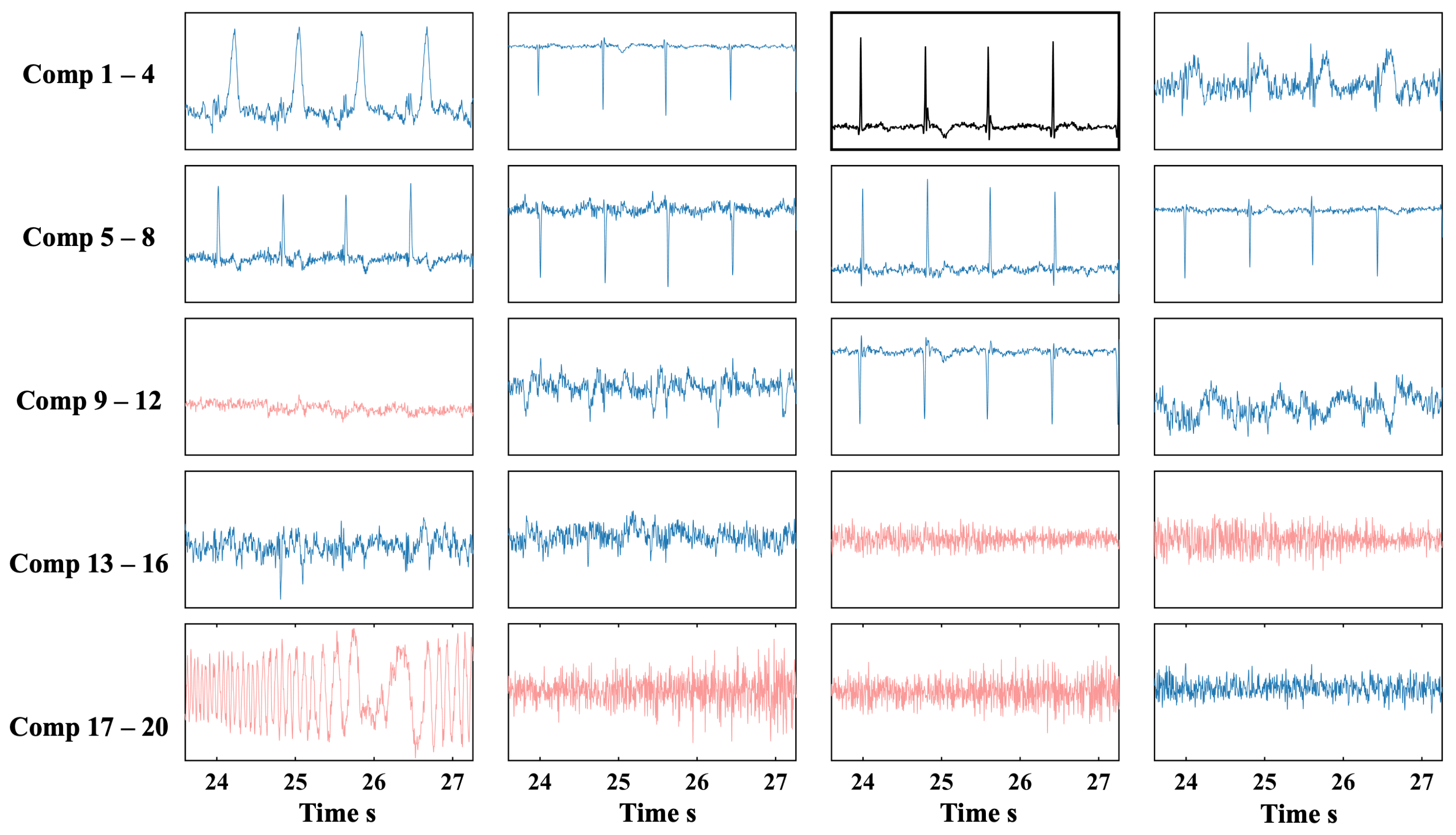
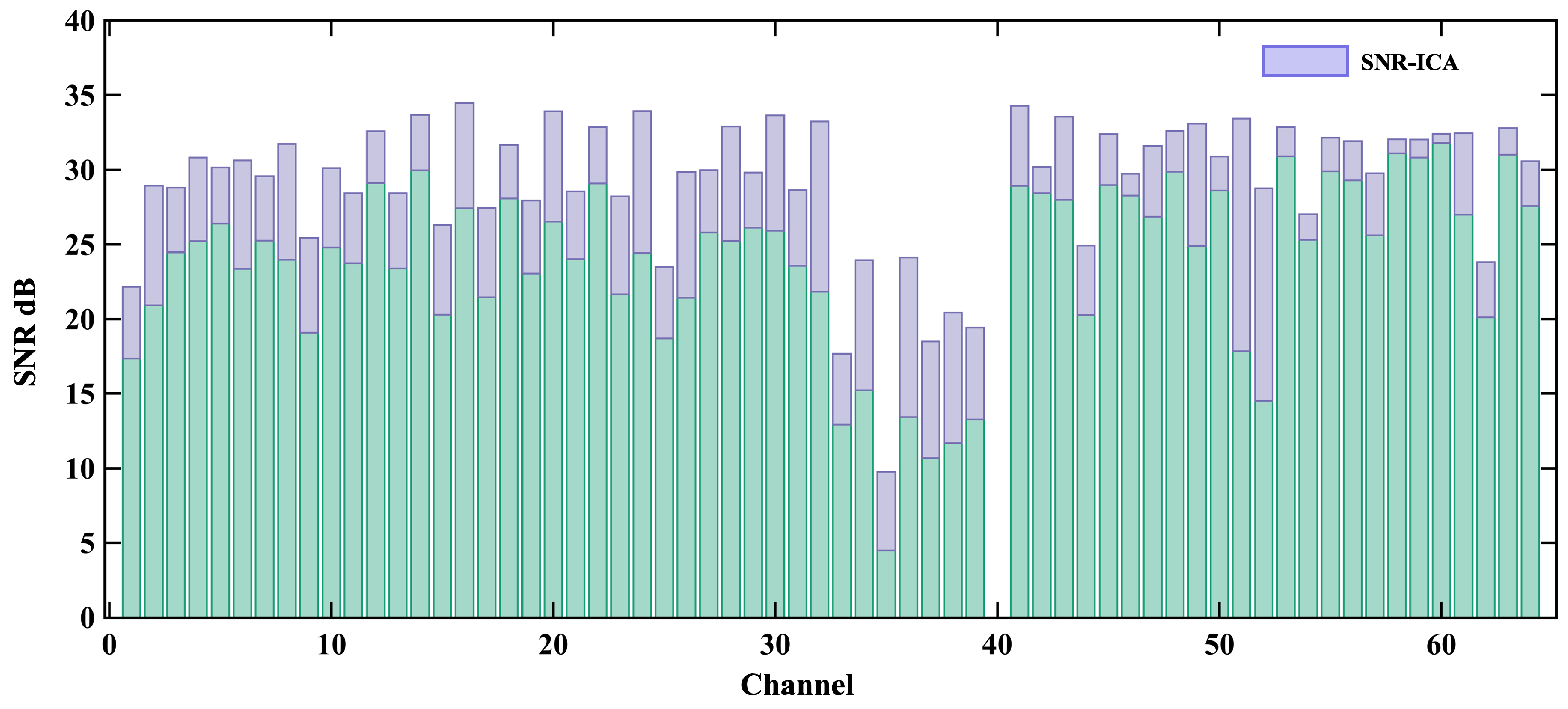
4.2. Real MCG Data
5. Discussion
5.1. Comparison with Previous Work
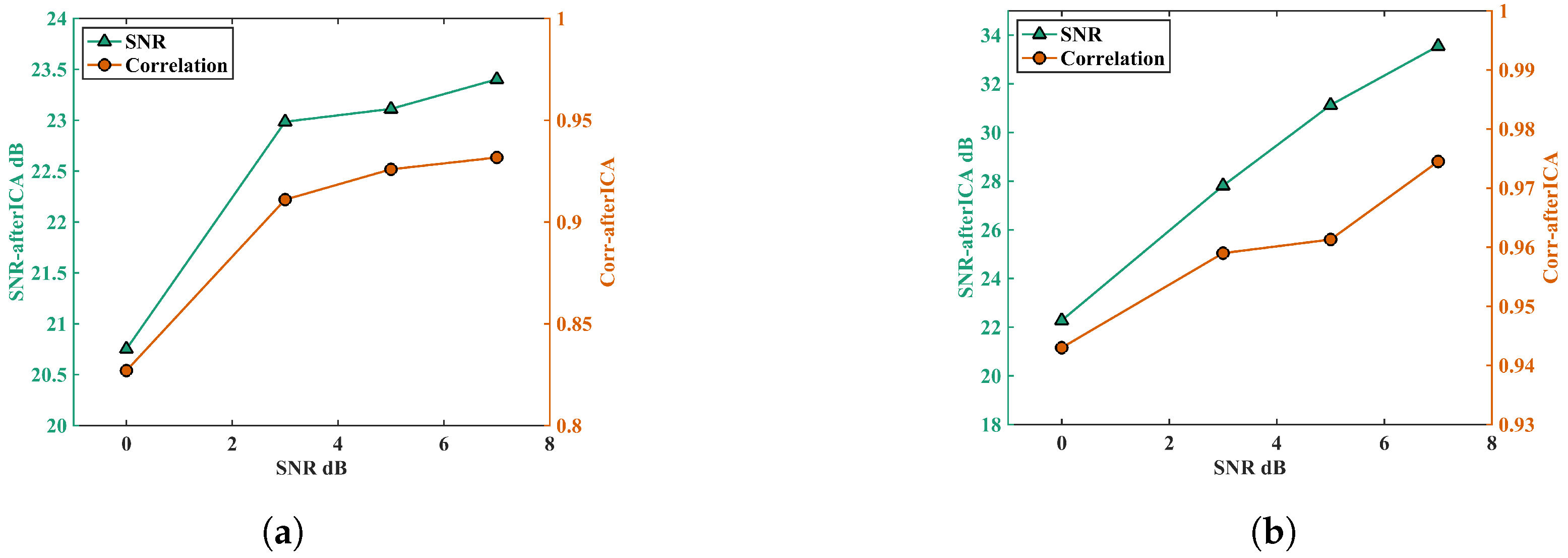
5.2. Performance on Different Input Signals
5.3. Parametric Analysis
5.4. Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Cohen, D. Magnetoencephalography: Detection of the Brain’s Electrical Activity with a Superconducting Magnetometer. Science 1972, 175, 664–666. [Google Scholar] [CrossRef] [PubMed]
- Xiao, W.; Sun, C.; Shen, L.; Feng, Y.; Liu, M.; Wu, Y.; Liu, X.; Wu, T.; Peng, X.; Guo, H. A Movable Unshielded Magnetocardiography System. Sci. Adv. 2023, 9, eadg1746. [Google Scholar] [CrossRef] [PubMed]
- Kwong, J.S.; Leithäuser, B.; Park, J.W.; Yu, C.M. Diagnostic Value of Magnetocardiography in Coronary Artery Disease and Cardiac Arrhythmias: A Review of Clinical Data. Int. J. Cardiol. 2013, 167, 1835–1842. [Google Scholar] [CrossRef]
- Agren, P.; Goranson, H.; Hindmarsh, T.; Knutsson, E.; Mohlkert, D.; Rosenqvist, M.; Bergfeldt, L. Magnetocardiographic Localization of Arrhythmia Substrates: A Methodology Study with Accessory Pathway Ablation as Reference. IEEE Trans. Med. Imaging 1998, 17, 479–484. [Google Scholar] [CrossRef] [PubMed]
- Duchateau, J.; Sacher, F.; Pambrun, T.; Derval, N.; Chamorro-Servent, J.; Denis, A.; Ploux, S.; Hocini, M.; Jaïs, P.; Bernus, O.; et al. Performance and Limitations of Noninvasive Cardiac Activation Mapping. Heart Rhythm 2019, 16, 435–442. [Google Scholar] [CrossRef]
- Zhao, C.; Jiang, S.; Wu, Y.; Zhu, J.; Zhou, D.; Hailer, B.; Gronemeyer, D.; Van Leeuwen, P. An Integrated Maximum Current Density Approach for Noninvasive Detection of Myocardial Infarction. IEEE J. Biomed. Health Inform. 2018, 22, 495–502. [Google Scholar] [CrossRef]
- Kwon, H.; Kim, K.; Lee, Y.H.; Kim, J.M.; Yu, K.K.; Chung, N.; Ko, Y.G. Non-Invasive Magnetocardiography for the Early Diagnosis of Coronary Artery Disease in Patients Presenting With Acute Chest Pain. Circ. J. 2010, 74, 1424–1430. [Google Scholar] [CrossRef]
- Strand, S.; Lutter, W.; Strasburger, J.F.; Shah, V.; Baffa, O.; Wakai, R.T. Low-Cost Fetal Magnetocardiography: A Comparison of Superconducting Quantum Interference Device and Optically Pumped Magnetometers. J. Am. Heart Assoc. 2019, 8, e013436. [Google Scholar] [CrossRef]
- Rea, M.; Boto, E.; Holmes, N.; Hill, R.; Osborne, J.; Rhodes, N.; Leggett, J.; Rier, L.; Bowtell, R.; Shah, V.; et al. A 90-channel Triaxial Magnetoencephalography System Using Optically Pumped Magnetometers. Ann. N. Y. Acad. Sci. 2022, 1517, 107–124. [Google Scholar] [CrossRef]
- Boto, E.; Holmes, N.; Leggett, J.; Roberts, G.; Shah, V.; Meyer, S.S.; Muñoz, L.D.; Mullinger, K.J.; Tierney, T.M.; Bestmann, S.; et al. Moving Magnetoencephalography towards Real-World Applications with a Wearable System. Nature 2018, 555, 657–661. [Google Scholar] [CrossRef]
- Brookes, M.J.; Leggett, J.; Rea, M.; Hill, R.M.; Holmes, N.; Boto, E.; Bowtell, R. Magnetoencephalography with Optically Pumped Magnetometers (OPM-MEG): The next Generation of Functional Neuroimaging. Trends Neurosci. 2022, 45, 621–634. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, M.; Liang, A.; Yin, Y.; Ma, X.; Gao, Y.; Ning, X. A New Wearable Multichannel Magnetocardiogram System with a SERF Atomic Magnetometer Array. Sci. Rep. 2021, 11, 5564. [Google Scholar] [CrossRef] [PubMed]
- Jia, L.; Li, J.; Song, X.; Ning, X.; Yang, J.; Qi, S.; Long, T.; Wu, Z.; Wang, R. Hardware-Based Interference Suppression Techniques for OPM-MEG: A Review. IEEE Sens. J. 2024, 99, 1. [Google Scholar] [CrossRef]
- Seymour, R.A.; Alexander, N.; Mellor, S.; O’Neill, G.C.; Tierney, T.M.; Barnes, G.R.; Maguire, E.A. Interference Suppression Techniques for OPM-based MEG: Opportunities and Challenges. NeuroImage 2022, 247, 118834. [Google Scholar] [CrossRef] [PubMed]
- Iwai, M.; Kobayashi, K. Dimensional Contraction by Principal Component Analysis as Preprocessing for Independent Component Analysis at MCG. Biomed. Eng. Lett. 2017, 7, 221–227. [Google Scholar] [CrossRef]
- DiPietroPaolo, D.; Müller, H.P.; Nolte, G.; Erné, S.N. Noise Reduction in Magnetocardiography by Singular Value Decomposition and Independent Component Analysis. Med. Biol. Eng. Comput. 2006, 44, 489–499. [Google Scholar] [CrossRef]
- Yu, S.; Wakai, R.T. Maternal MCG Interference Cancellation Using Splined Independent Component Subtraction. IEEE Trans. Biomed. Eng. 2011, 58, 2835–2843. [Google Scholar] [CrossRef][Green Version]
- Mariyappa, N.; Sengottuvel, S.; Rajesh, P.; Parasakthi, C.; Gireesan, K.; Janawadkar, M.; Radhakrishnan, T.; Sundar, C. Denoising of Multichannel MCG Data by the Combination of EEMD and ICA and Its Effect on the Pseudo Current Density Maps. Biomed. Signal Process. Control 2015, 18, 204–213. [Google Scholar] [CrossRef]
- Treacher, A.H.; Garg, P.; Davenport, E.; Godwin, R.; Proskovec, A.; Bezerra, L.G.; Murugesan, G.; Wagner, B.; Whitlow, C.T.; Stitzel, J.D.; et al. MEGnet: Automatic ICA-based Artifact Removal for MEG Using Spatiotemporal Convolutional Neural. NeuroImage 2021, 241, 118402. [Google Scholar] [CrossRef]
- Kesavaraja, C.; Sengottuvel, S.; Patel, R.; Mani, A. Machine Learning-Based Automated Method for Effective De-noising of Magnetocardiography Signals Using Independent Component Analysis. Circuits Syst. Signal Process. 2024, 43, 4968–4990. [Google Scholar] [CrossRef]
- Iwai, M.; Kobayashi, K.; Yoshizawa, M.; Uchikawa, Y.; Bui, F.M. Automatic Component Selection for Noise Reduction in Magnetocardiograph Based on Independent Component Analysis. J. Magn. Soc. Jpn. 2017, 41, 41–45. [Google Scholar] [CrossRef]
- Vigário, R.; Sarela, J.; Jousmiki, V.; Hamalainen, M.; Oja, E. Independent component approach to the analysis of EEG and MEG recordings. IEEE Trans. Biomed. Eng. 2000, 47, 589–593. [Google Scholar] [CrossRef] [PubMed]
- Hämäläinen, M.; Hari, R.; Ilmoniemi, R.J.; Knuutila, J.; Lounasmaa, O.V. Magnetoencephalography—Theory, instrumentation, and applications to noninvasive studies of the working human brain. Rev. Mod. Phys. 1993, 65, 413. [Google Scholar] [CrossRef]
- Mariyappa, N.; Sengottuvel, S.; Parasakthi, C.; Gireesan, K.; Janawadkar, M.; Radhakrishnan, T.; Sundar, C. Baseline Drift Removal and Denoising of MCG Data Using EEMD: Role of Noise Amplitude and the Thresholding Effect. Med. Eng. Phys. 2014, 36, 1266–1276. [Google Scholar] [CrossRef]
- Yang, K.; Xu, T.; Pan, D.; Zhang, Z.; Wang, H.; Kong, X. Multi-Channel MCG Signals Filtering Method Based on Multivariate Variational Mode Decomposition. Biomed. Signal Process. Control 2025, 99, 106806. [Google Scholar] [CrossRef]
- Liao, Y.; He, C.; Guo, Q. Denoising of Magnetocardiography Based on Improved Variational Mode Decomposition and Interval Thresholding Method. Symmetry 2018, 10, 269. [Google Scholar] [CrossRef]
- Bing, L.; Si, W.; Tan, R.; Han, X.; Liu, F.; Yu, J. Hybrid Fourier-Wavelet Heart Magnetic Field Signal Denoising Based on Sparse Representation. In Proceedings of the 2019 3rd International Conference on Data Science and Business Analytics (ICDSBA), Istanbul, Turkey, 11–12 October 2019; pp. 266–268. [Google Scholar] [CrossRef]
- Yang, S.; Feng, L.; Zhang, M.; Zhang, M.; Ma, Z.; Zhang, H.; Zhang, Y.; Liu, L.; Zhou, S.; Zhao, X.; et al. Development and Validation of a Clinical Diagnostic Model for Myocardial Ischaemia in Borderline Coronary Lesions Based on Optical Pumped Magnetometer Magnetocardiography: A Prospective Observational Cohort Study. BMJ Open 2024, 14, e086433. [Google Scholar] [CrossRef]
- Tao, R.; Zhang, S.; Huang, X.; Tao, M.; Ma, J.; Ma, S.; Zhang, C.; Zhang, T.; Tang, F.; Lu, J.; et al. Magnetocardiography-Based Ischemic Heart Disease Detection and Localization Using Machine Learning Methods. IEEE Trans. Biomed. Eng. 2019, 66, 1658–1667. [Google Scholar] [CrossRef]






| Excluded Components | Time Cost (s) | SNR_IMP (dB) | |
|---|---|---|---|
| 1 | 9, 10, 13, 14, 15, 16 | 58 | 2.72 |
| 2 | 9, 10, 11, 13, 14, 15, 16 | 48 | 3.27 |
| 3 | 9, 10, 11, 13, 15, 16 | 121 | 3.24 |
| 4 | 9, 10, 11, 13, 14, 15, 16 | 33 | 3.27 |
| 5 | 9, 10, 11, 14, 15, 16 | 89 | 2.92 |
| 6 | 9, 10, 14, 15, 16 | 28 | 2.70 |
| 7 | 6, 9, 10, 11, 13, 14, 15, 16 | 107 | 3.07 |
| Adaptive ICA | 9, 10, 11, 13, 14, 15, 16 | 1.8 | 3.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, S.; Qi, J.; He, J.; Jia, Y.; Wang, A.; Zhao, T.; Wei, C.; Jiao, H.; Feng, L.; Cheng, H. A Novel Adaptive Independent Component Analysis Method for Multi-Channel Optically Pumped Magnetometers’ Magnetocardiography Signals. Biosensors 2025, 15, 243. https://doi.org/10.3390/bios15040243
Liang S, Qi J, He J, Jia Y, Wang A, Zhao T, Wei C, Jiao H, Feng L, Cheng H. A Novel Adaptive Independent Component Analysis Method for Multi-Channel Optically Pumped Magnetometers’ Magnetocardiography Signals. Biosensors. 2025; 15(4):243. https://doi.org/10.3390/bios15040243
Chicago/Turabian StyleLiang, Shuang, Jiahe Qi, Junhuai He, Yikang Jia, Aimin Wang, Ting Zhao, Chaoliang Wei, Hongchen Jiao, Lishuang Feng, and Heping Cheng. 2025. "A Novel Adaptive Independent Component Analysis Method for Multi-Channel Optically Pumped Magnetometers’ Magnetocardiography Signals" Biosensors 15, no. 4: 243. https://doi.org/10.3390/bios15040243
APA StyleLiang, S., Qi, J., He, J., Jia, Y., Wang, A., Zhao, T., Wei, C., Jiao, H., Feng, L., & Cheng, H. (2025). A Novel Adaptive Independent Component Analysis Method for Multi-Channel Optically Pumped Magnetometers’ Magnetocardiography Signals. Biosensors, 15(4), 243. https://doi.org/10.3390/bios15040243





