A Device-on-Chip Solution for Real-Time Diffuse Correlation Spectroscopy Using FPGA
Abstract
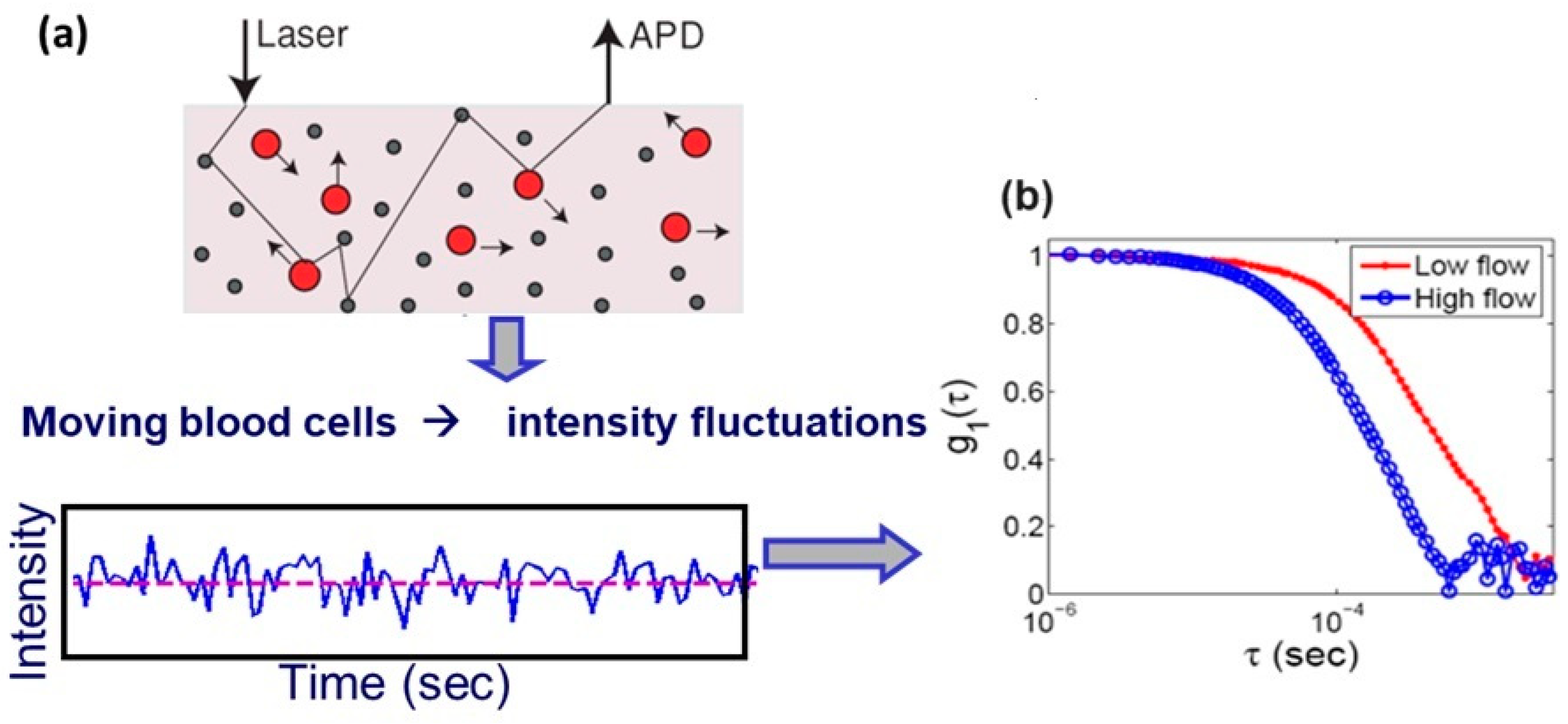
1. Introduction
2. Materials and Methods
2.1. DCS Analyzer Module
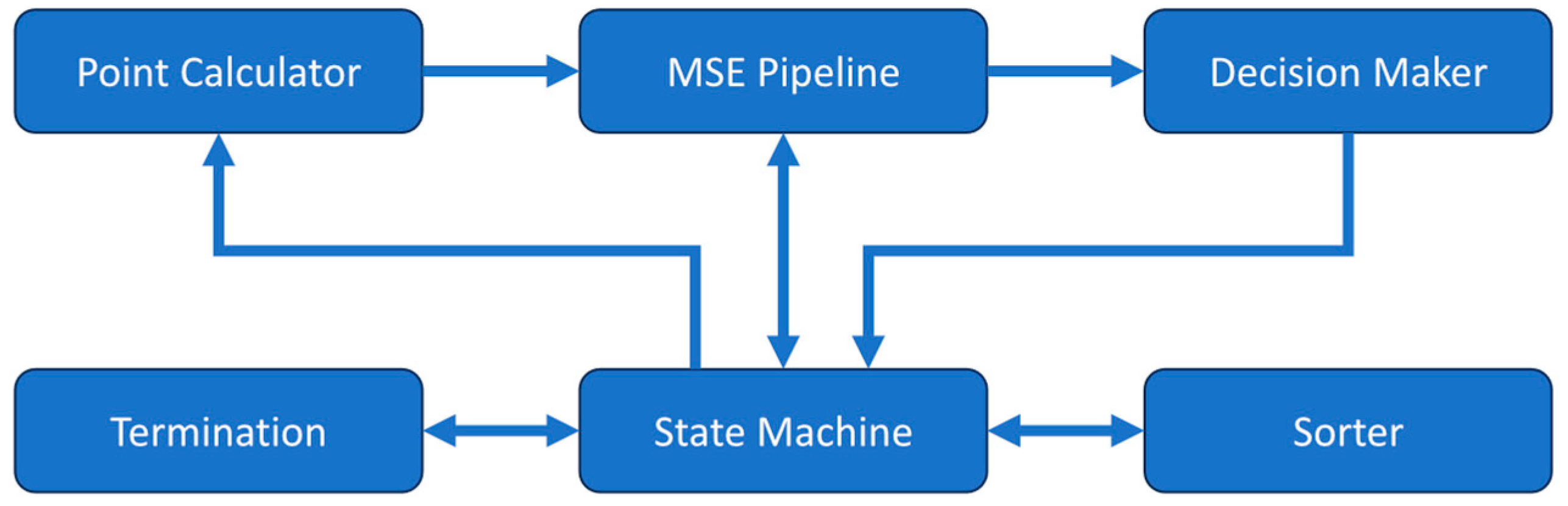
2.2. Autocorrelator Module
2.3. Full DCS System Integration
2.4. System Evaluation and Comparison
3. Results
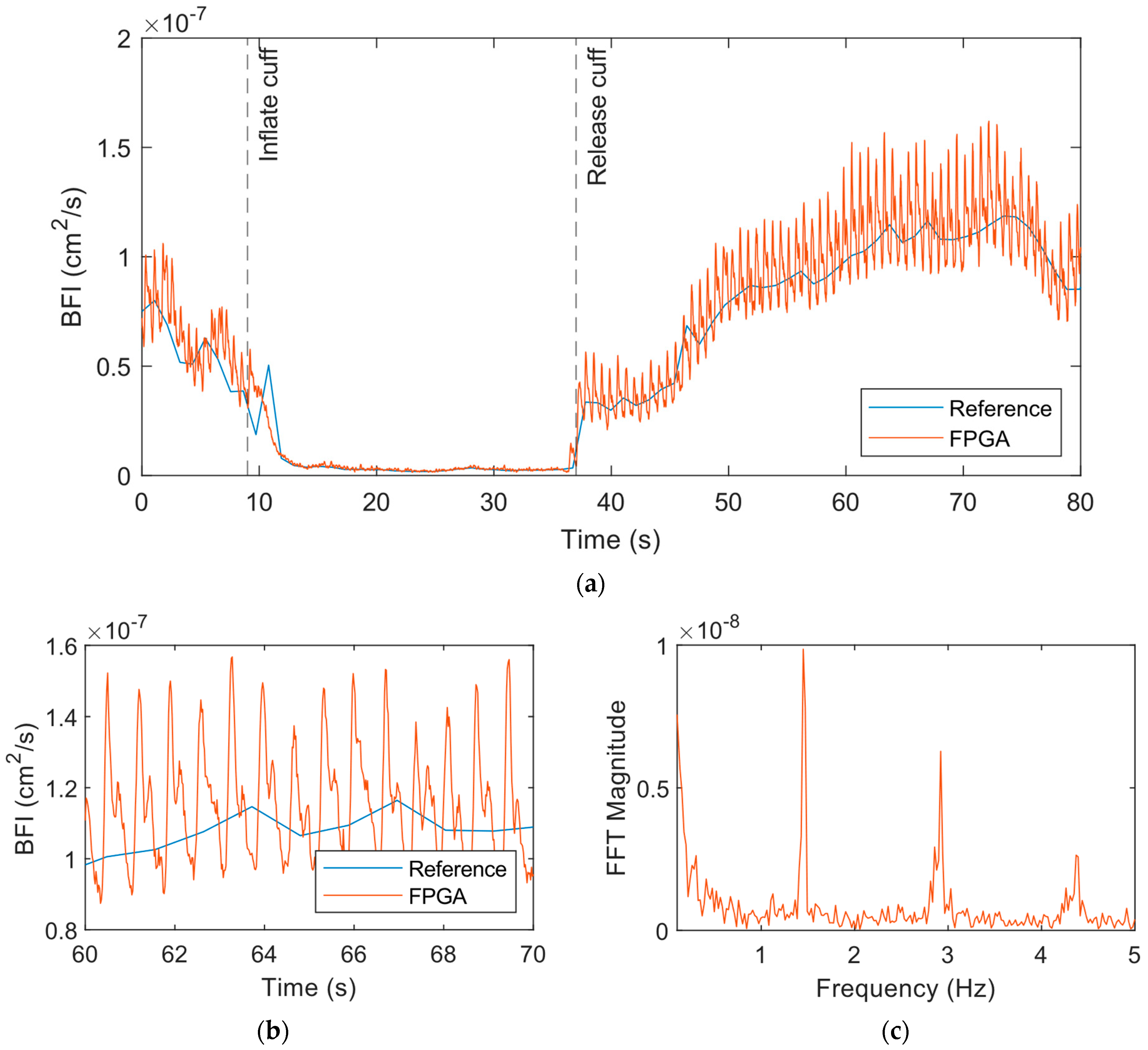
3.1. Optical Phantom Tests
3.2. Cuff Ischemia Tests
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Buckley, E.M.; Parthasarathy, A.B.; Grant, P.E.; Yodh, A.G.; Franceschini, M.A. Diffuse correlation spectroscopy for measurement of cerebral blood flow: Future prospects. Neurophotonics 2014, 1, 011009. [Google Scholar] [CrossRef]
- Durduran, T.; Choe, R.; Baker, W.B.; Yodh, A.G. Diffuse optics for tissue monitoring and tomography. Rep. Prog. Phys. 2010, 73, 076701. [Google Scholar] [CrossRef]
- Durduran, T.; Yodh, A.G. Diffuse correlation spectroscopy for non-invasive, micro-vascular cerebral blood flow measurement. Neuroimage 2014, 85, 51–63. [Google Scholar] [CrossRef]
- Mesquita, R.C.; Durduran, T.; Yu, G.Q.; Buckley, E.M.; Kim, M.N.; Zhou, C.; Choe, R.; Sunar, U.; Yodh, A.G. Direct measurement of tissue blood flow and metabolism with diffuse optics. Philos. Trans. R. Soc. A-Math. Phys. Eng. Sci. 2011, 369, 4390–4406. [Google Scholar] [CrossRef]
- Yu, G.Q.; Durduran, T.; Zhou, C.; Cheng, R.; Yodh, A.G. Near-infrared diffuse correlation spectroscopy for assessment of tissue blood flow. In Handbook of Biomedical Optics; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Carp, S.A.; Dai, G.P.; Boas, D.A.; Franceschini, M.A.; Kim, Y.R. Validation of diffuse correlation spectroscopy measurements of rodent cerebral blood flow with simultaneous arterial spin labeling MRI; towards MRI-optical continuous cerebral metabolic monitoring. Biomed. Opt. Express 2010, 1, 553–565. [Google Scholar] [CrossRef]
- Durduran, T.; Zhou, C.A.; Buckley, E.M.; Kim, M.N.; Yu, G.Q.; Choe, R.; Gaynor, J.W.; Spray, T.L.; Durning, S.M.; Mason, S.E.; et al. Optical measurement of cerebral hemodynamics and oxygen metabolism in neonates with congenital heart defects. J. Biomed. Opt. 2010, 15, 037004. [Google Scholar] [CrossRef]
- Yu, G.Q.; Floyd, T.F.; Durduran, T.; Zhou, C.; Wang, J.J.; Detre, J.A.; Yodh, A.G. Validation of diffuse correlation spectroscopy for muscle blood flow with concurrent arterial spin labeled perfusion MRI. Opt. Express 2007, 15, 1064–1075. [Google Scholar] [CrossRef]
- Favilla, C.G.; Mesquita, R.; Kim, M.; Greenberg, J.H.; Detre, J.A.; Yodh, A.G.; Mullen, M.T.; Shafi, N.; Kasner, S.E. Optical Measurements of Cerebral Hemodynamics in Acute Cortical Stroke. Stroke 2011, 42, E283–E284. [Google Scholar]
- Mesquita, R.C.; Schenkel, S.S.; Minkoff, D.L.; Lu, X.P.; Favilla, C.G.; Vora, P.M.; Busch, D.R.; Chandra, M.; Greenberg, J.H.; Detre, J.A.; et al. Influence of probe pressure on the diffuse correlation spectroscopy blood flow signal: Extra-cerebral contributions. Biomed. Opt. Express 2013, 4, 978–994. [Google Scholar] [CrossRef]
- Parthasarathy, A.B.; Baker, W.B.; Gannon, K.; Mullen, M.T.; Detre, J.A.; Yodh, A.G. Clinical applications of high-speed blood flow measurements with Diffuse Correlation Spectroscopy. In Proceedings of the Conference on Optical Tomography and Spectroscopy of Tissue XII, San Francisco, CA, USA, 30 January–1 February 2017. [Google Scholar]
- Parthasarathy, A.B.; Gannon, K.P.; Baker, W.B.; Favilla, C.G.; Balu, R.; Kasner, S.E.; Yodh, A.G.; Detre, J.A.; Mullen, M.T. Dynamic autoregulation of cerebral blood flow measured non-invasively with fast diffuse correlation spectroscopy. J. Cereb. Blood Flow Metab. 2018, 38, 230–240. [Google Scholar] [CrossRef]
- Yu, G.Q. Near-infrared diffuse correlation spectroscopy in cancer diagnosis and therapy monitoring. J. Biomed. Opt. 2012, 17, 010901. [Google Scholar] [CrossRef]
- Baker, W.B.; Balu, R.; He, L.; Kavuri, V.C.; Busch, D.R.; Amendolia, O.; Quattrone, F.; Frangos, S.; Maloney-Wilensky, E.; Abramson, K.; et al. Continuous non-invasive optical monitoring of cerebral blood flow and oxidative metabolism after acute brain injury. J. Cereb. Blood Flow Metab. 2019, 39, 1469–1485. [Google Scholar] [CrossRef]
- Busch, D.R.; Balu, R.; Baker, W.B.; Guo, W.S.; He, L.; Diop, M.; Milej, D.; Kavuri, V.; Amendolia, O.; St Lawrence, K.; et al. Detection of Brain Hypoxia Based on Noninvasive Optical Monitoring of Cerebral Blood Flow with Diffuse Correlation Spectroscopy. Neurocrit. Care 2019, 30, 72–80. [Google Scholar] [CrossRef]
- Carp, S.A.; Tamborini, D.; Mazumder, D.; Wu, K.C.; Robinson, M.R.; Stephens, K.A.; Shatrovoy, O.; Lue, N.; Ozana, N.; Blackwell, M.H.; et al. Diffuse correlation spectroscopy measurements of blood flow using 1064 nm light. J. Biomed. Opt. 2020, 25, 097003. [Google Scholar] [CrossRef]
- Colombo, L.; Pagliazzi, M.; Sekar, S.K.V.; Contini, D.; Durduran, T.; Pifferi, A. In vivo time-domain diffuse correlation spectroscopy above the water absorption peak. Opt. Lett. 2020, 45, 3377–3380. [Google Scholar] [CrossRef]
- Forti, R.M.; Favilla, C.G.; Cochran, J.M.; Baker, W.B.; Detre, J.A.; Kasner, S.E.; Mullen, M.T.; Messé, S.R.; Kofke, W.A.; Balu, R.; et al. Transcranial Optical Monitoring of Cerebral Hemodynamics in Acute Stroke Patients during Mechanical Thrombectomy. J. Stroke Cerebrovasc. Dis. 2019, 28, 1483–1494. [Google Scholar] [CrossRef]
- Forti, R.M.; Katsurayama, M.; Menko, J.; Valler, L.; Quiroga, A.; Falcao, A.L.E.; Li, L.; Mesquita, R.C. Real-Time Non-invasive Assessment of Cerebral Hemodynamics With Diffuse Optical Spectroscopies in a Neuro Intensive Care Unit: An Observational Case Study. Front. Med. 2020, 7, 147. [Google Scholar] [CrossRef]
- Kim, M.N.; Edlow, B.L.; Durduran, T.; Frangos, S.; Mesquita, R.C.; Levine, J.M.; Greenberg, J.H.; Yodh, A.G.; Detre, J.A. Continuous Optical Monitoring of Cerebral Hemodynamics During Head-of-Bed Manipulation in Brain-Injured Adults. Neurocrit. Care 2014, 20, 443–453. [Google Scholar] [CrossRef]
- Mullen, M.T.; Parthasarathy, A.B.; Zandieh, A.; Baker, W.B.; Mesquita, R.C.; Loomis, C.; Torres, J.; Guo, W.S.; Favilla, C.G.; Messé, S.R.; et al. Cerebral Blood Flow Response During Bolus Normal Saline Infusion after Ischemic Stroke. J. Stroke Cerebrovasc. Dis. 2019, 28, 104294. [Google Scholar] [CrossRef] [PubMed]
- Poon, C.S.; Rinehart, B.; Langri, D.S.; Rambo, T.M.; Miller, A.J.; Foreman, B.; Sunar, U. Noninvasive Optical Monitoring of Cerebral Blood Flow and EEG Spectral Responses after Severe Traumatic Brain Injury: A Case Report. Brain Sci. 2021, 11, 1093. [Google Scholar] [CrossRef]
- Selb, J.; Wu, K.C.; Sutin, J.; Lin, P.Y.; Farzam, P.; Bechek, S.; Shenoy, A.; Patel, A.B.; Boas, D.A.; Franceschini, M.A.; et al. Prolonged monitoring of cerebral blood flow and autoregulation with diffuse correlation spectroscopy in neurocritical care patients. Neurophotonics 2018, 5, 045005. [Google Scholar] [CrossRef] [PubMed]
- Topjian, A.A.; Fry, M.; Jawad, A.F.; Herman, S.T.; Nadkarni, V.M.; Ichord, R.; Berg, R.A.; Dlugos, D.J.; Abend, N.S. Detection of Electrographic Seizures by Critical Care Providers Using Color Density Spectral Array After Cardiac Arrest Is Feasible. Pediatr. Crit. Care Med. 2015, 16, 461–467. [Google Scholar] [CrossRef] [PubMed]
- Busch, D.R.C.R.; Durduran, T.; Baker, W.B.; Foster, E.K.; Averna, T.A.; Friedman, D.; Rosen, M.A.; Schnall, M.D.; Yodh, G.Y. Measurement of micro-vascular blood flow in the human breast during compression with diffuse correlation spectroscopy. In Proceedings of the Biomedical Optics, Miami, FL, USA, 28 April–2 May 2012. [Google Scholar]
- Choe, R.; Putt, M.E.; Carlile, P.M.; Durduran, T.; Giammarco, J.M.; Busch, D.R.; Jung, K.W.; Czerniecki, B.J.; Tchou, J.; Feldman, M.D.; et al. Optically Measured Microvascular Blood Flow Contrast of Malignant Breast Tumors. PLoS ONE 2014, 9, e99683. [Google Scholar] [CrossRef] [PubMed]
- Chung, S.H.; Feldman, M.D.; Martinez, D.; Kim, H.; Putt, M.E.; Busch, D.R.; Tchou, J.; Czerniecki, B.J.; Schnall, M.D.; Rosen, M.A.; et al. Macroscopic optical physiological parameters correlate with microscopic proliferation and vessel area breast cancer signatures. Breast Cancer Res. 2015, 17, 72. [Google Scholar] [CrossRef] [PubMed]
- Cochran, J.M.; Chung, S.H.; Leproux, A.; Baker, W.B.; Busch, D.R.; DeMichele, A.M.; Tchou, J.; Tromberg, B.J.; Yodh, A.G. Longitudinal optical monitoring of blood flow in breast tumors during neoadjuvant chemotherapy. Phys. Med. Biol. 2017, 62, 4637–4653. [Google Scholar] [CrossRef] [PubMed]
- Sunar, U. Monitoring photodynamic therapy of head and neck malignancies with optical spectroscopies. World J. Clin. Cases 2013, 1, 96–105. [Google Scholar] [CrossRef] [PubMed]
- Sunar, U.; Makonnen, S.; Zhou, C.; Durduran, T.; Yu, G.Q.; Wang, H.W.; Lee, W.M.F.; Yodh, A.G. Hemodynamic responses to antivascular therapy and ionizing radiation assessed by diffuse optical spectroscopies. Opt. Express 2007, 15, 15507–15516. [Google Scholar] [CrossRef] [PubMed]
- Sunar, U.; Rohrbach, D.; Rigual, N.; Tracy, E.; Keymel, K.; Cooper, M.T.; Baumann, H.; Henderson, B.H. Monitoring photobleaching and hemodynamic responses to HPPH-mediated photodynamic therapy of head and neck cancer: A case report. Opt. Express 2010, 18, 14969–14978. [Google Scholar] [CrossRef] [PubMed]
- Sunar, U.; Makonnent, S.; Wang, H.W.; Durduran, T.; Zhou, C.; Yu, G.; Lee, W.M.F.; Yodh, A.G. Non-invasive, continuous monitoring of a vascular targeting drug by diffuse optical blood flow and blood oxygenation measurements. In Proceedings of the InfoBase Conference Papers, Fort Lauderdale, FL, USA, 19–22 March 2006. [Google Scholar]
- Yazdi, H.S.; O‘Sullivan, T.D.; Leproux, A.; Hill, B.; Durkin, A.; Telep, S.; Lam, J.; Yazdi, S.S.; Police, A.M.; Carroll, R.M.; et al. Mapping breast cancer blood flow index, composition, and metabolism in a human subject using combined diffuse optical spectroscopic imaging and diffuse correlation spectroscopy. J. Biomed. Opt. 2017, 22, 045003. [Google Scholar] [CrossRef]
- Zhou, C.; Choe, R.; Shah, N.; Durduran, T.; Yu, G.Q.; Durkin, A.; Hsiang, D.; Mehta, R.; Butler, J.; Cerussi, A.; et al. Diffuse optical monitoring of blood flow and oxygenation in human breast cancer during early stages of neoadjuvant chemotherapy. J. Biomed. Opt. 2007, 12, 051903. [Google Scholar] [CrossRef]
- Boas, D.A.; Campbell, L.E.; Yodh, A.G. Scattering and imaging with diffusing temporal field correlations. Phys. Rev. Lett. 1995, 75, 1855–1858. [Google Scholar] [CrossRef] [PubMed]
- Boas, D.A.; Yodh, A.G. Spatially varying dynamical properties of turbid media probed with diffusing temporal light correlation. J. Opt. Soc. Am. A-Opt. Image Sci. Vis. 1997, 14, 192–215. [Google Scholar] [CrossRef]
- Dong, J.; Bi, R.Z.; Ho, J.H.; Thong, P.S.P.; Soo, K.C.; Lee, K. Diffuse correlation spectroscopy with a fast Fourier transform-based software autocorrelator. J. Biomed. Opt. 2012, 17, 097004. [Google Scholar] [CrossRef] [PubMed]
- Urner, T.M.; Cowdrick, K.R.; Brothers, R.O.; Boodooram, T.; Zhao, H.T.; Goyal, V.; Sathialingam, E.; Quadri, A.; Turrentine, K.; Akbar, M.M.; et al. Normative cerebral microvascular blood flow waveform morphology assessed with diffuse correlation spectroscopy. Biomed. Opt. Express 2023, 14, 3635–3653. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.T.; Parthasarathy, A.B.; Baker, W.B.; Gannon, K.; Kavuri, V.; Ko, T.; Schenkel, S.; Li, Z.; Li, Z.R.; Mullen, M.T.; et al. Fast blood flow monitoring in deep tissues with real-time software correlators. Biomed. Opt. Express 2016, 7, 776–797. [Google Scholar] [CrossRef] [PubMed]
- Asif, M.; Guo, X.Z.; Hu, A.Y.; Miao, J.G. An FPGA-Based 1-GHz, 128 × 128 Cross-Correlator for Aperture Synthesis Imaging. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2020, 28, 129–141. [Google Scholar] [CrossRef]
- Asif, M.; Guo, X.Z.; Zhang, J.; Miao, J.G. An FPGA Based 1.6 GHz Cross-correlator for Synthetic Aperture Interferometric Radiometer. In Proceedings of the Progress in Electromagnetics Research Symposium-Fall (PIERS-FALL), Singapore, 19–22 November 2017; pp. 1078–1085. [Google Scholar]
- Buchholz, J.; Krieger, J.W.; Mocsár, G.; Kreith, B.; Charbon, E.; Vámosi, G.; Kebschull, U.; Langowski, J. FPGA implementation of a 32 × 32 autocorrelator array for analysis of fast image series. Opt. Express 2012, 20, 17767–17782. [Google Scholar] [CrossRef] [PubMed]
- Islambek, A.; Yang, K.C.; Li, W.; Li, K. FPGA-based real-time autocorrelator and its application in dynamic light scattering. Optik 2019, 194, 163047. [Google Scholar] [CrossRef]
- Lin, W.; Busch, D.R.; Goh, C.C.; Barsi, J.; Floyd, T.F. Diffuse Correlation Spectroscopy Analysis Implemented on a Field Programmable Gate Array. IEEE Access 2019, 7, 122503–122512. [Google Scholar] [CrossRef]
- Moore, C.H.; Lin, W. FPGA Correlator for Applications in Embedded Smart Devices. Biosensors 2022, 12, 236. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex-method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Lindfield, G.; Penny, J. Numerical Methods Using MATLAB; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Cabal, J. Simple UART for FPGA. Github. 2021. Available online: https://github.com/jakubcabal/uart-for-fpga (accessed on 2 August 2024).
- Li, J.; Poon, C.S.; Kress, J.; Rohrbach, D.J.; Sunar, U. Resting-state functional connectivity measured by diffuse correlation spectroscopy. J. Biophotonics 2018, 11, e201700165. [Google Scholar] [CrossRef] [PubMed]
- Rinehart, B.; Poon, C.S.; Sunar, U. Quantification of perfusion and metabolism in an autism mouse model assessed by diffuse correlation spectroscopy and near-infrared spectroscopy. J. Biophotonics 2021, 14, e202000454. [Google Scholar] [CrossRef] [PubMed]
- Cortese, L.; Lo Presti, G.; Pagliazzi, M.; Contini, D.; Dalla Mora, A.; Pifferi, A.; Konugolu Venkata Sekar, S.; Spinelli, L.; Taroni, P.; Zanoletti, M.; et al. A recipe for near infrared spectroscopy and diffuse correlation spectroscopy phantoms with tunable optical and dynamic properties. In Proceedings of the Optical Tomography and Spectroscopy, Hollywood, FL, USA, 3–6 April 2018. [Google Scholar]
- Della Rocca, F.M.; Sie, E.J.; Catoen, R.; Marsili, F.; Henderson, R.K. Field programmable gate array compression for large array multispeckle diffuse correlation spectroscopy. J. Biomed. Opt. 2023, 28, 057001. [Google Scholar] [CrossRef] [PubMed]
- Wayne, M.A.; Sie, E.J.; Ulku, A.C.; Mos, P.; Ardelean, A.; Marsili, F.; Bruschini, C.; Charbon, E. Massively parallel, real-time multispeckle diffuse correlation spectroscopy using a 500 × 500 SPAD camera. Biomed. Opt. Express 2023, 14, 703–713. [Google Scholar] [CrossRef]
- Xie, J.B.; He, X.D.; Qin, Z.P.; Gao, F. A multi-channel diffuse correlation spectroscopy system for dynamic topography of blood flow index in deep tissues. In Proceedings of the Conference on Optical Biopsy XVIII-Toward Real-Time Spectroscopic Imaging and Diagnosis, San Francisco, CA, USA, 2–5 February 2020. [Google Scholar]
- Robinson, M.B.; Renna, M.; Ozana, N.; Martin, A.N.; Otic, N.; Carp, S.A.; Franceschini, M.A. Portable, high speed blood flow measurements enabled by long wavelength, interferometric diffuse correlation spectroscopy (LW-iDCS). Sci. Rep. 2023, 13, 8803. [Google Scholar] [CrossRef] [PubMed]
- Tamborini, D.; Stephens, K.A.; Wu, M.M.; Farzam, P.; Siegel, A.M.; Shatrovoy, O.; Blackwell, M.; Boas, D.A.; Carp, S.A.; Franceschini, M.A. Portable System for Time-Domain Diffuse Correlation Spectroscopy. IEEE Trans. Biomed. Eng. 2019, 66, 3014–3025. [Google Scholar] [CrossRef] [PubMed]
- Kamaleldin, A.; Ahmed, I.; Obeid, A.M.; Shalash, A.; Ismail, Y.; Mostafa, H. A Cost-Effective Dynamic Partial Reconfiguration Implementation Flow for Xilinx FPGA. In Proceedings of the 1st New Generation of CAS Conference (NGCAS), Genova, Italy, 6–9 September 2017; pp. 281–284. [Google Scholar]
- Forti, R.M.; Martins, G.G.; Baker, W.B.; Mesquita, R.C. Optimizing a two-layer method for hybrid diffuse correlation spectroscopy and frequency-domain diffuse optical spectroscopy cerebral measurements in adults. Neurophotonics 2023, 10, 025008. [Google Scholar] [CrossRef]
- Zhao, H.; Buckley, E.M. Influence of source-detector separation on diffuse correlation spectroscopy measurements of cerebral blood flow with a multilayered analytical model. Neurophotonics 2022, 9, 035002. [Google Scholar] [CrossRef]
- Zhao, H.T.; Sathialingam, E.; Buckley, E.M. Accuracy of diffuse correlation spectroscopy measurements of cerebral blood flow when using a three-layer analytical model. Biomed. Opt. Express 2021, 12, 7149–7161. [Google Scholar] [CrossRef]
- Nakabayashi, M.; Ono, Y. Detection of Blood Flow Speed in Shallow and Deep Tissues Using Diffuse Correlation Spectroscopy. Adv. Biomed. Eng. 2017, 6, 53–58. [Google Scholar] [CrossRef]
- Li, J.; Qiu, L.A.; Poon, C.S.; Sunar, U. Analytical models for time-domain diffuse correlation spectroscopy for multi-layer and heterogeneous turbid media. Biomed. Opt. Express 2017, 8, 5518–5532. [Google Scholar] [CrossRef]
- Wang, Q.; Pan, M.L.; Zang, Z.Y.; Li, D.D.U. Quantification of blood flow index in diffuse correlation spectroscopy using a robust deep learning method. J. Biomed. Opt. 2024, 29, 015004. [Google Scholar] [CrossRef]
- Li, Z.; Bai, J.T.; Jiang, M.N.; Chen, X.; Wei, R.; Jia, K.B. Continuous monitoring of tissue oxygen metabolism based on multi-wavelength diffuse correlation spectroscopy using LSTM-based RNN model. Opt. Laser Technol. 2024, 171, 110384. [Google Scholar] [CrossRef]
- Nakabayashi, M.; Liu, S.W.; Broti, N.M.; Ichinose, M.; Ono, Y. Deep-learning-based separation of shallow and deep layer blood flow rates in diffuse correlation spectroscopy. Biomed. Opt. Express 2023, 14, 5358–5375. [Google Scholar] [CrossRef]
- Feng, J.C.; Jiang, M.N.; Bai, J.T.; Jia, K.B.; Li, Z. Cerebral blood flow monitoring using a ConvGRU model based on diffuse correlation spectroscopy. Infrared Phys. Technol. 2023, 129, 104541. [Google Scholar] [CrossRef]
- Seong, M.; Oh, Y.; Lee, K.; Kim, J.G. Blood flow estimation via numerical integration of temporal autocorrelation function in diffuse correlation spectroscopy. Comput. Meth. Programs Biomed. 2022, 222, 106933. [Google Scholar] [CrossRef]
- Paolella, M.S.; Polak, P.; Walker, P.S. A non-elliptical orthogonal GARCH model for portfolio selection under transaction costs. J. Bank. Financ. 2021, 125, 106046. [Google Scholar] [CrossRef]
- Poon, C.S.; Long, F.X.; Sunar, U. Deep learning model for ultrafast quantification of blood flow in diffuse correlation spectroscopy. Biomed. Opt. Express 2020, 11, 5557–5564. [Google Scholar] [CrossRef]







| Data Source | Mean ± Standard Deviation (×10−11 cm2/s) |
|---|---|
| Reference | 9.869 ± 2.762 |
| FPGA | 10.961 ± 2.956 |
| Methyl Cellulose Concentration (%) | Data Source | Mean ± Standard Deviation (×10−11 cm2/s) |
|---|---|---|
| 0.0625 | Reference | 12.548 ± 2.1360 |
| FPGA | 12.009 ± 2.6367 | |
| 0.5 | Reference | 8.2673 ± 1.7543 |
| FPGA | 7.6094 ± 1.5856 | |
| 1 | Reference | 4.1740 ± 0.59629 |
| FPGA | 3.8712 ± 0.43825 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moore, C.H.; Sunar, U.; Lin, W. A Device-on-Chip Solution for Real-Time Diffuse Correlation Spectroscopy Using FPGA. Biosensors 2024, 14, 384. https://doi.org/10.3390/bios14080384
Moore CH, Sunar U, Lin W. A Device-on-Chip Solution for Real-Time Diffuse Correlation Spectroscopy Using FPGA. Biosensors. 2024; 14(8):384. https://doi.org/10.3390/bios14080384
Chicago/Turabian StyleMoore, Christopher H., Ulas Sunar, and Wei Lin. 2024. "A Device-on-Chip Solution for Real-Time Diffuse Correlation Spectroscopy Using FPGA" Biosensors 14, no. 8: 384. https://doi.org/10.3390/bios14080384
APA StyleMoore, C. H., Sunar, U., & Lin, W. (2024). A Device-on-Chip Solution for Real-Time Diffuse Correlation Spectroscopy Using FPGA. Biosensors, 14(8), 384. https://doi.org/10.3390/bios14080384







