Optimization of Microfluidics for Point-of-Care Blood Sensing
Abstract
1. Introduction
2. Materials and Methods
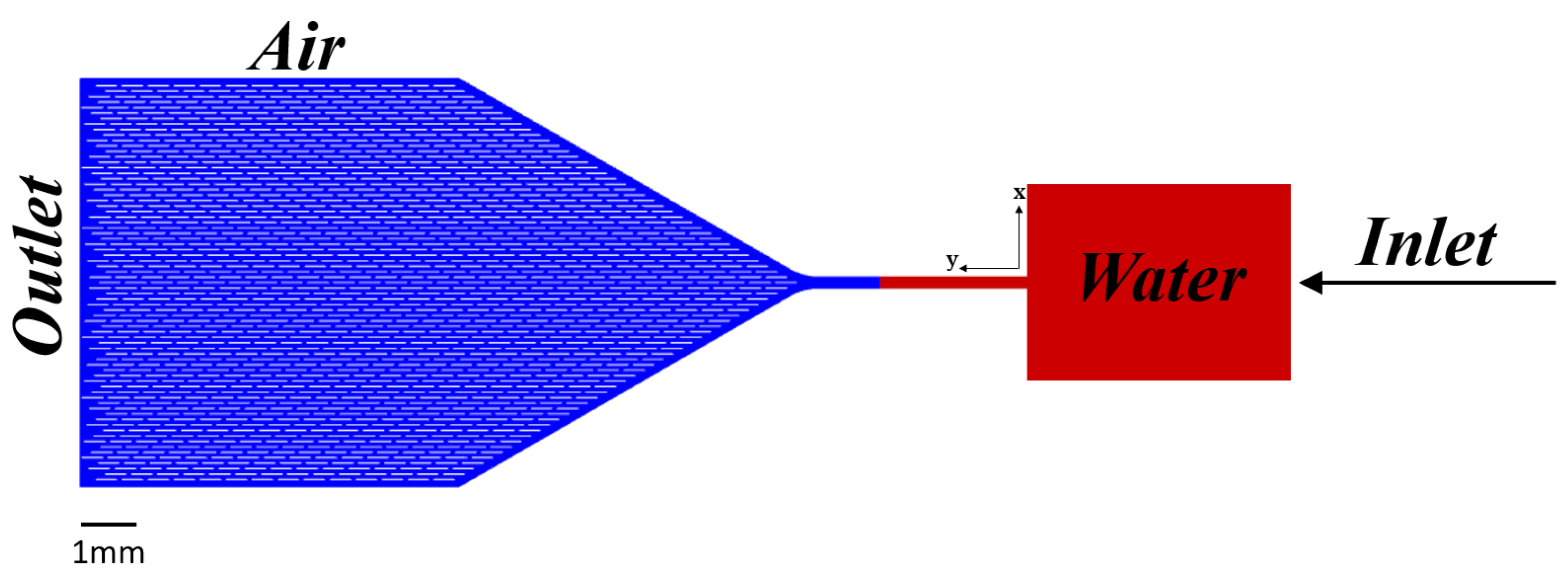
2.1. Microchannel Geometry
2.2. Governing Equations
Initial Boundary Conditions
2.3. Microchannel Fabrication
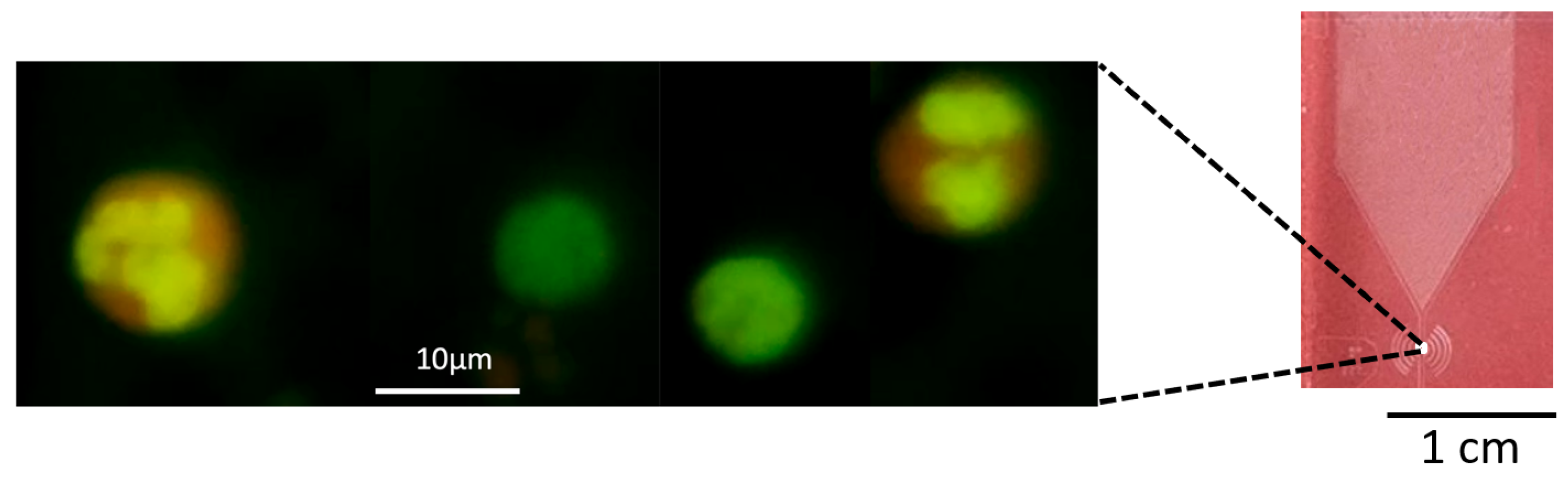
2.4. Experimental Analysis of Hematological Diagnostics Using Microfluidic Chips
3. Results and Discussion
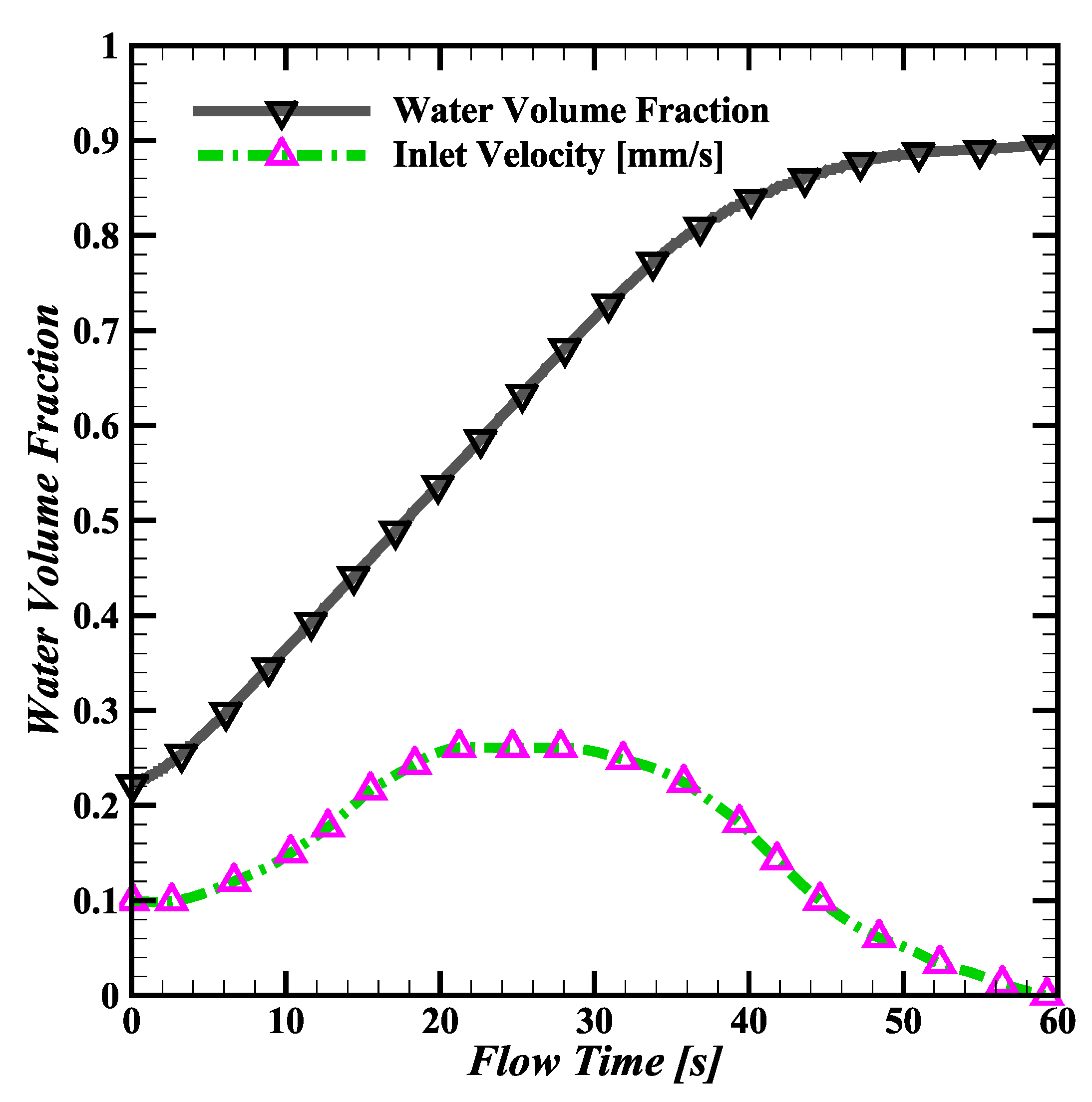
3.1. Water Simulation
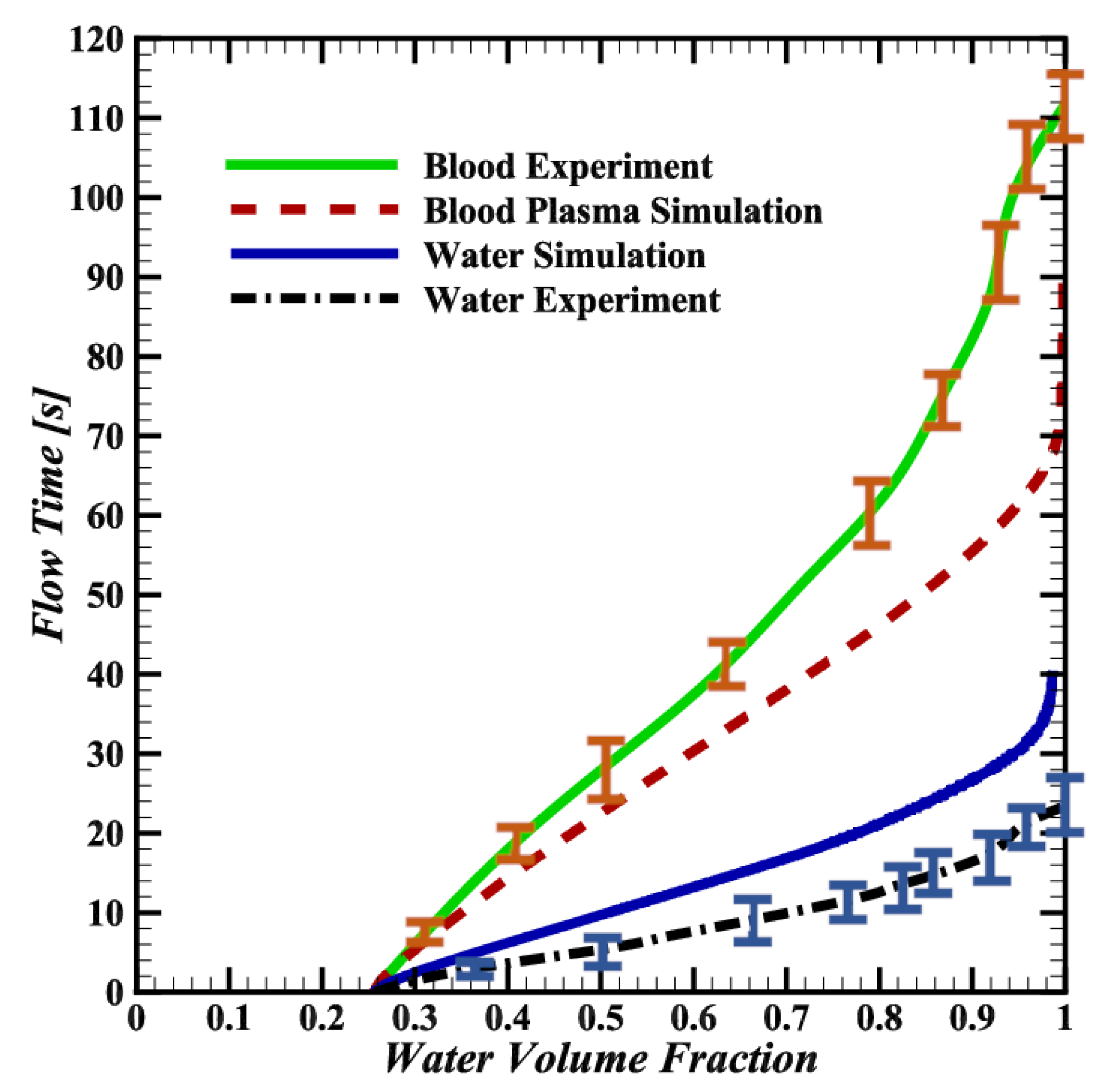
3.2. Comparison of Water and Blood Plasma Simulations
3.3. Discrepancies between Simulations and Experiments
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| AO | Acridine Orange |
| CSF | Continuum Surface Force |
| PDMS | Polydimethylsiloxane |
| PEO | Polyethylene Oxide |
| PoC | Point-of-Care |
| RBC | Red Blood Cell (Erythrocyte) |
| VOF | Volume of Fluid |
| WBC | White Blood Cell (Leukocyte) |
| WHO | World Health Organization |
References
- Duffy, M.J. Tumor markers in clinical practice: A review focusing on common solid cancers. Med Princ. Pract. 2012, 22, 4–11. [Google Scholar] [CrossRef] [PubMed]
- Huckle, D. Point-of-care diagnostics: An advancing sector with nontechnical issues. Expert Rev. Mol. Diagn. 2008, 8, 679–688. [Google Scholar] [CrossRef]
- Drain, P.K.; Hyle, E.P.; Noubary, F.; Freedberg, K.A.; Wilson, D.; Bishai, W.R.; Rodriguez, W.; Bassett, I.V. Diagnostic point-of-care tests in resource-limited settings. Lancet Infect. Dis. 2014, 14, 239–249. [Google Scholar] [CrossRef] [PubMed]
- Hirooka, H.; Renvert, S. Diagnosis of periimplant disease. Implant Dent. 2019, 28, 144–149. [Google Scholar] [CrossRef] [PubMed]
- Lambert, M.J.; Hansen, N.B.; Finch, A.E. Patient-focused research: Using patient outcome data to enhance treatment effects. J. Consult. Clin. Psychol. 2001, 69, 159. [Google Scholar] [CrossRef]
- Yeh, E.C.; Fu, C.C.; Hu, L.; Thakur, R.; Feng, J.; Lee, L.P. Self-powered integrated microfluidic point-of-care low-cost enabling (SIMPLE) chip. Sci. Adv. 2017, 3, e1501645. [Google Scholar] [CrossRef]
- Land, K.J.; Boeras, D.I.; Chen, X.S.; Ramsay, A.R.; Peeling, R.W. REASSURED diagnostics to inform disease control strategies, strengthen health systems and improve patient outcomes. Nat. Microbiol. 2019, 4, 46–54. [Google Scholar] [CrossRef] [PubMed]
- Jiang, N.; Tansukawat, N.D.; Gonzalez-Macia, L.; Ates, H.C.; Dincer, C.; Guder, F.; Tasoglu, S.; Yetisen, A.K. Low-cost optical assays for point-of-care diagnosis in resource-limited settings. ACS Sens. 2021, 6, 2108–2124. [Google Scholar] [CrossRef] [PubMed]
- Narayanamurthy, V.; Jeroish, Z.; Bhuvaneshwari, K.; Bayat, P.; Premkumar, R.; Samsuri, F.; Yusoff, M.M. Advances in passively driven microfluidics and lab-on-chip devices: A comprehensive literature review and patent analysis. RSC Adv. 2020, 10, 11652–11680. [Google Scholar] [CrossRef]
- Hemmig, E.; Temiz, Y.; Gökçe, O.; Lovchik, R.D.; Delamarche, E. Transposing lateral flow immunoassays to capillary-driven microfluidics using self-coalescence modules and capillary-assembled receptor carriers. Anal. Chem. 2019, 92, 940–946. [Google Scholar] [CrossRef]
- Huang, W.H.; Ai, F.; Wang, Z.L.; Cheng, J.K. Recent advances in single-cell analysis using capillary electrophoresis and microfluidic devices. J. Chromatogr. B 2008, 866, 104–122. [Google Scholar] [CrossRef] [PubMed]
- Akceoglu, G.A.; Saylan, Y.; Inci, F. A snapshot of microfluidics in point-of-care diagnostics: Multifaceted integrity with materials and sensors. Adv. Mater. Technol. 2021, 6, 2100049. [Google Scholar] [CrossRef]
- Demirci, U.; Khademhosseini, A.; Langer, R.; Toner, M. Microfluidic Technologies for Human Health; World Scientific: Singapore, 2013. [Google Scholar]
- Zhang, Y.; Liu, Y.; Wang, S. Nitrocellulose Membrane-based Lateral Flow Assay for Rapid and Sensitive Detection of Infectious Agents. J. Clin. Microbiol. 2022, 60, e00445-21. [Google Scholar]
- Chen, X.; et al. Enhanced Capillary-driven Blood Separation and Detection on Paper-based Analytical Devices. Lab Chip 2021, 21, 2735–2743. [Google Scholar]
- Gupta, R.; Chaudhury, K. Recent Advances in Nitrocellulose Membranes and Their Impact on Lateral Flow Immunoassay Performance. Anal. Chem. 2020, 92, 2333–2349. [Google Scholar]
- Smith, J.; Anderson, R. External pump systems in point-of-care testing: Opportunities and challenges. J. Biomed. Eng. 2021, 45, 115–122. [Google Scholar]
- Lee, W.; Kim, H.; Choi, S. Development and evaluation of a pump-driven microfluidic assay for rapid disease diagnostics. Lab Chip 2020, 20, 2231–2240. [Google Scholar]
- Patel, R.; Kumar, A.; Singh, M. Innovations in external pump technologies for point-of-care applications. J. Microfluid. Nanofluid. 2022, 22, 77–85. [Google Scholar]
- Azizian, P.; Casals-Terré, J.; Ricart, J.; Cabot, J.M. Capillary-driven microfluidics: Impacts of 3D manufacturing on bioanalytical devices. Analyst 2023, 148, 2657–2675. [Google Scholar] [CrossRef]
- Sotoudegan, M.S.; Mohd, O.; Ligler, F.S.; Walker, G.M. Based passive pumps to generate controllable whole blood flow through microfluidic devices. Lab Chip 2019, 19, 3787–3795. [Google Scholar] [CrossRef]
- Hassan, S.U.; Tariq, A.; Noreen, Z.; Donia, A.; Zaidi, S.Z.; Bokhari, H.; Zhang, X. Capillary-driven flow microfluidics combined with smartphone detection: An emerging tool for point-of-care diagnostics. Diagnostics 2020, 10, 509. [Google Scholar] [CrossRef] [PubMed]
- Hua, W.; Zhou, W.; Wang, W.; Wang, Z.; Wu, R.; Zhu, L. Maximization of the capillary pump efficiency in microfluidics. SN Appl. Sci. 2021, 3, 315. [Google Scholar] [CrossRef]
- Brakewood, W.; Lee, K.; Schneider, L.; Lawandy, N.; Tripathi, A. A capillary flow-driven microfluidic device for point-of-care blood plasma separation. Front. Lab Chip Technol. 2022, 1, 1051552. [Google Scholar] [CrossRef]
- Shinde, S.K.; Shaligram, A.D. An Experimental Study using Smart Phone for Transient Fluid Testing Based on Image Analysis and Modelling for Capillary Driven Microfluidics Towards Lab-on-Chip Applications in Nutrient Detection. Int. J. Electron. Eng. 2024, 16, 1–6. [Google Scholar]
- Choudhary, B.K.J.; Durai, S.A.; Ahmad, N. Smart Microfluidic Devices for Point-of-Care Applications. J. Adv. Res. Fluid Mech. Therm. Sci. 2024, 114, 119–133. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, J.; Lu, X.; Liu, Q. Isothermal nucleic acid amplification based microfluidic “lab-on-a-chip” for the detection of pathogenic bacteria and viruses in agri-foods. Trends Food Sci. Technol. 2024, 148, 104482. [Google Scholar] [CrossRef]
- Lai, B.J.; Zhu, L.T.; Chen, Z.; Ouyang, B.; Luo, Z.H. Review on Blood Flow Dynamics in Lab-on-a-Chip Systems: An Engineering Perspective. Chem Bio Eng. 2024, 1, 26–43. [Google Scholar] [CrossRef]
- Khodadadi, R.; Eghbal, M.; Ofoghi, H.; Balaei, A.; Tamayol, A.; Abrinia, K.; Sanati-Nezhad, A.; Samandari, M. An integrated centrifugal microfluidic strategy for point-of-care complete blood counting. Biosens. Bioelectron. 2024, 245, 115789. [Google Scholar] [CrossRef] [PubMed]
- Vloemans, D.; Pieters, A.; Dal Dosso, F.; Lammertyn, J. Revolutionizing Sample Preparation: A Novel Autonomous Microfluidic Platform for Serial Dilution. Lab Chip 2024, 24, 2791–2801. [Google Scholar] [CrossRef]
- Drozd, M.; Ivanova, P.; Żukowski, K.; Tokarska, K.; Pietrzak, M.; Brzózka, Z.; Malinowska, E. Printer toner-assisted immobilization of antibodies on PET for genuinely-2D, flexible ELISA spot arrays. Sens. Actuators B Chem. 2024, 403, 135173. [Google Scholar] [CrossRef]
- Zimmermann, M.; Schmid, H.; Hunziker, P.; Delamarche, E. Capillary pumps for autonomous capillary systems. Lab Chip 2007, 7, 119–125. [Google Scholar] [CrossRef] [PubMed]
- Stark, M.; Hoerr, J.; Vaerst, C.; Bessire, C. Three-Differential White Blood Cell Count in Capillary Driven Image Flow Cytometry. In Proceedings of the 12th International Conference on Biomedical Engineering and Technology, Tokyo, Japan, 20–23 April 2022; pp. 57–60. [Google Scholar]
- Bartlett, J.G.; Gerding, D.N. Clinical recognition and diagnosis of Clostridium difficile infection. Clin. Infect. Dis. 2008, 46, S12–S18. [Google Scholar] [CrossRef]
- Raya, Á.; Rodríguez-Pizà, I.; Guenechea, G.; Vassena, R.; Navarro, S.; Barrero, M.J.; Consiglio, A.; Castella, M.; Río, P.; Sleep, E.; et al. Disease-corrected haematopoietic progenitors from Fanconi anaemia induced pluripotent stem cells. Nature 2009, 460, 53–59. [Google Scholar] [CrossRef]
- van Neel, T.L.; Theberge, A.B. Programmable capillary action controls fluid flows. Nature 2021, 595, 31–32. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Y.; Li, X.; Li, M.; Wu, Q.; Song, Y.; Zhu, Z.; Yang, C. Integrated microfluidic devices for in vitro diagnostics at point of care. Aggregate 2022, 3, e184. [Google Scholar] [CrossRef]
- Martinez, A.W.; Phillips, S.T.; Whitesides, G.M. Three-dimensional microfluidic devices fabricated in layered paper and tape. Proc. Natl. Acad. Sci. USA 2008, 105, 19606–19611. [Google Scholar] [CrossRef]
- Wang, H.; Chen, L.; Sun, L. Digital microfluidics: A promising technique for biochemical applications. Front. Mech. Eng. 2017, 12, 510–525. [Google Scholar] [CrossRef]
- Chan, H.N.; Tan, M.J.A.; Wu, H. Point-of-care testing: Applications of 3D printing. Lab Chip 2017, 17, 2713–2739. [Google Scholar] [CrossRef] [PubMed]
- Tian, W.C.; Finehout, E. Microfluidics for Biological Applications; Springer Science & Business Media: New York, NY, USA, 2009; Volume 16. [Google Scholar]
- Gebreyesus, S.T.; Muneer, G.; Huang, C.C.; Siyal, A.A.; Anand, M.; Chen, Y.J.; Tu, H.L. Recent advances in microfluidics for single-cell functional proteomics. Lab Chip 2023, 23, 1726–1751. [Google Scholar] [CrossRef] [PubMed]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Shui, L.; Eijkel, J.C.; Van den Berg, A. Multiphase flow in microfluidic systems–Control and applications of droplets and interfaces. Adv. Colloid Interface Sci. 2007, 133, 35–49. [Google Scholar] [CrossRef] [PubMed]
- Kirby, B.J. Micro- and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Daugherty, R.L. Some Physical Properties of Water and Other Fluids. Trans. Am. Soc. Mech. Eng. 1935, 57, 193–196. [Google Scholar] [CrossRef]
- Colin, S.P. Rarefaction and compressibility effects on steady or transient gas flows in microchannels. In Proceedings of the International Conference on Nanochannels, Microchannels, and Minichannels, Rochester, NY, USA, 17–19 June 2004; Volume 41642, pp. 13–24. [Google Scholar]
- Kumar, V.; Paraschivoiu, M.; Nigam, K. Single-phase fluid flow and mixing in microchannels. Chem. Eng. Sci. 2011, 66, 1329–1373. [Google Scholar] [CrossRef]
- Cohan, A.C.; Arastoopour, H. Numerical simulation and analysis of the effect of rain and surface property on wind-turbine airfoil performance. Int. J. Multiph. Flow 2016, 81, 46–53. [Google Scholar] [CrossRef]
- Brust, M.; Schaefer, C.; Doerr, R.; Pan, L.; Garcia, M.; Arratia, P.; Wagner, C. Rheology of human blood plasma: Viscoelastic versus Newtonian behavior. Phys. Rev. Lett. 2013, 110, 078305. [Google Scholar] [CrossRef] [PubMed]
- Barnes, H. Shear-thickening (“Dilatancy”) in suspensions of nonaggregating solid particles dispersed in Newtonian liquids. J. Rheol. 1989, 33, 329–366. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Croce, R.; Griebel, M.; Schweitzer, M.A. Numerical simulation of bubble and droplet deformation by a level set approach with surface tension in three dimensions. Int. J. Numer. Methods Fluids 2010, 62, 963–993. [Google Scholar] [CrossRef]
- Lauga, E.; Brenner, M.P.; Stone, H.A. Microfluidics: The no-slip boundary condition. arXiv 2005, arXiv:cond-mat/0501557. [Google Scholar]
- Šikalo, Š.; Wilhelm, H.D.; Roisman, I.; Jakirlić, S.; Tropea, C. Dynamic contact angle of spreading droplets: Experiments and simulations. Phys. Fluids 2005, 17, 062103. [Google Scholar] [CrossRef]
- Qin, D.; Xia, Y.; Whitesides, G.M. Soft lithography for micro-and nanoscale patterning. Nat. Protoc. 2010, 5, 491. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Gu, M. Microfluidic sensing: State of the art fabrication and detection techniques. J. Biomed. Opt. 2011, 16, 080901. [Google Scholar] [CrossRef] [PubMed]
- Chebbi, R. Dynamics of blood flow: Modeling of the Fåhræus–Lindqvist effect. J. Biol. Phys. 2015, 41, 313–326. [Google Scholar] [CrossRef] [PubMed]



| Physical Property | Water (H2O) | Blood Plasma | Air |
|---|---|---|---|
| Density (kg/m3) | 1080 | ||
| Dynamic Viscosity (mPa·s) | |||
| Surface Tension (N/m) | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tavakolidakhrabadi, A.; Stark, M.; Bacher, U.; Legros, M.; Bessire, C. Optimization of Microfluidics for Point-of-Care Blood Sensing. Biosensors 2024, 14, 266. https://doi.org/10.3390/bios14060266
Tavakolidakhrabadi A, Stark M, Bacher U, Legros M, Bessire C. Optimization of Microfluidics for Point-of-Care Blood Sensing. Biosensors. 2024; 14(6):266. https://doi.org/10.3390/bios14060266
Chicago/Turabian StyleTavakolidakhrabadi, Amirmahdi, Matt Stark, Ulrike Bacher, Myriam Legros, and Cedric Bessire. 2024. "Optimization of Microfluidics for Point-of-Care Blood Sensing" Biosensors 14, no. 6: 266. https://doi.org/10.3390/bios14060266
APA StyleTavakolidakhrabadi, A., Stark, M., Bacher, U., Legros, M., & Bessire, C. (2024). Optimization of Microfluidics for Point-of-Care Blood Sensing. Biosensors, 14(6), 266. https://doi.org/10.3390/bios14060266






