Noninvasive Estimation of Tumor Interstitial Fluid Pressure from Subharmonic Scattering of Ultrasound Contrast Microbubbles
Abstract
1. Introduction
2. Materials and Methods
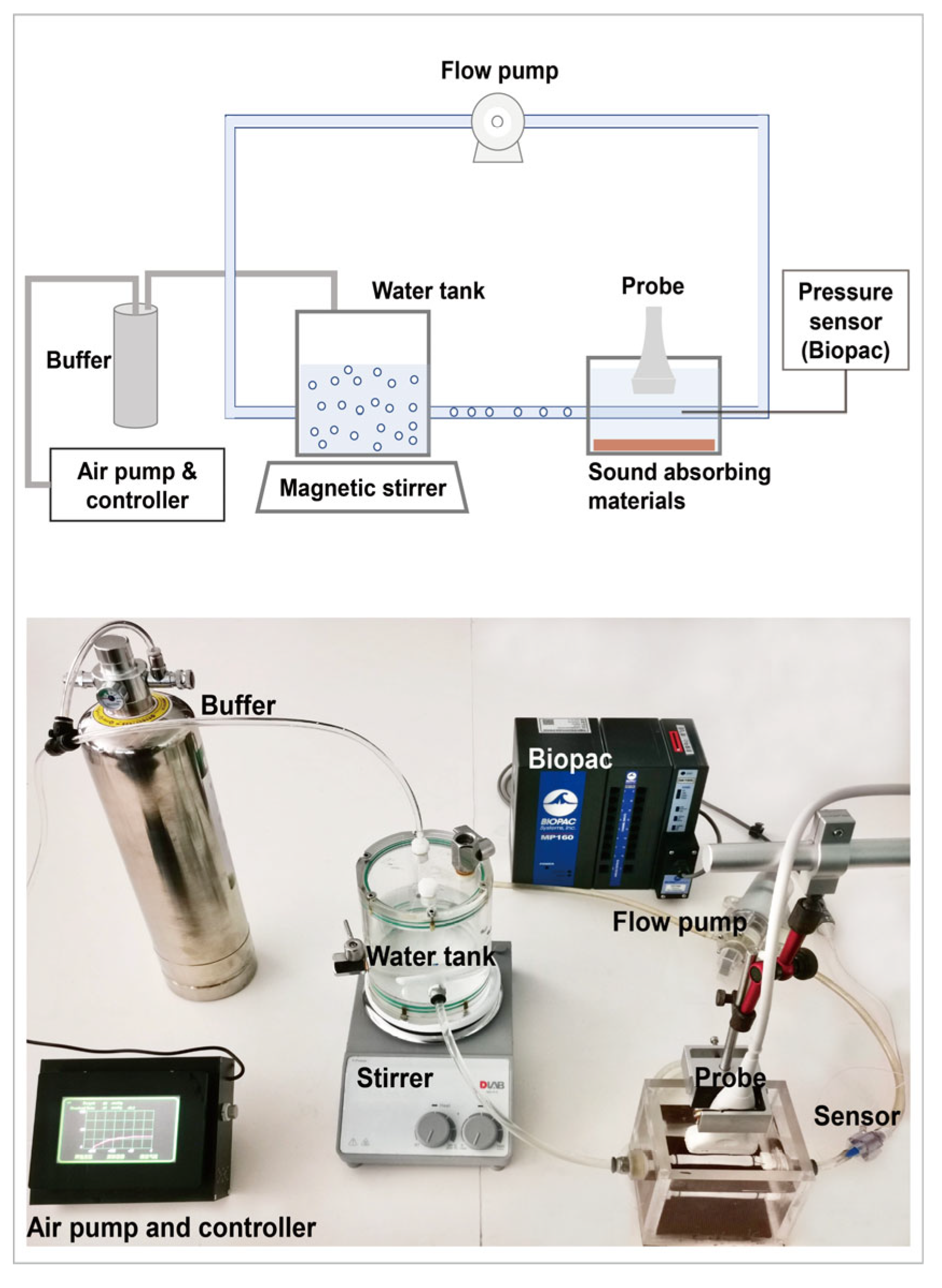
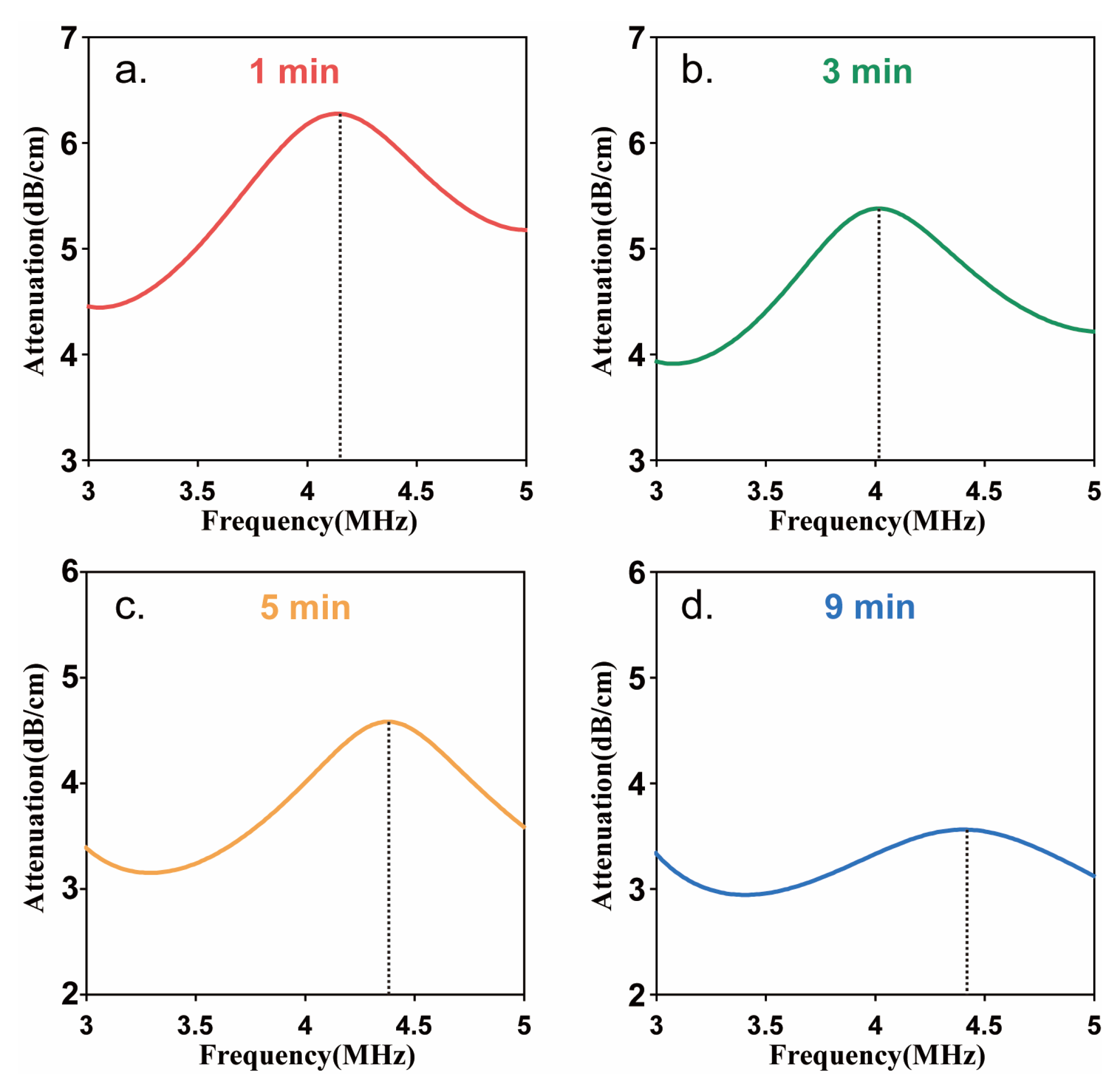
2.1. Acoustic Attenuation Measurement
2.2. Subharmonic Scattering Acquisition under Different Acoustic Pressure Conditions
2.3. Tumor Models
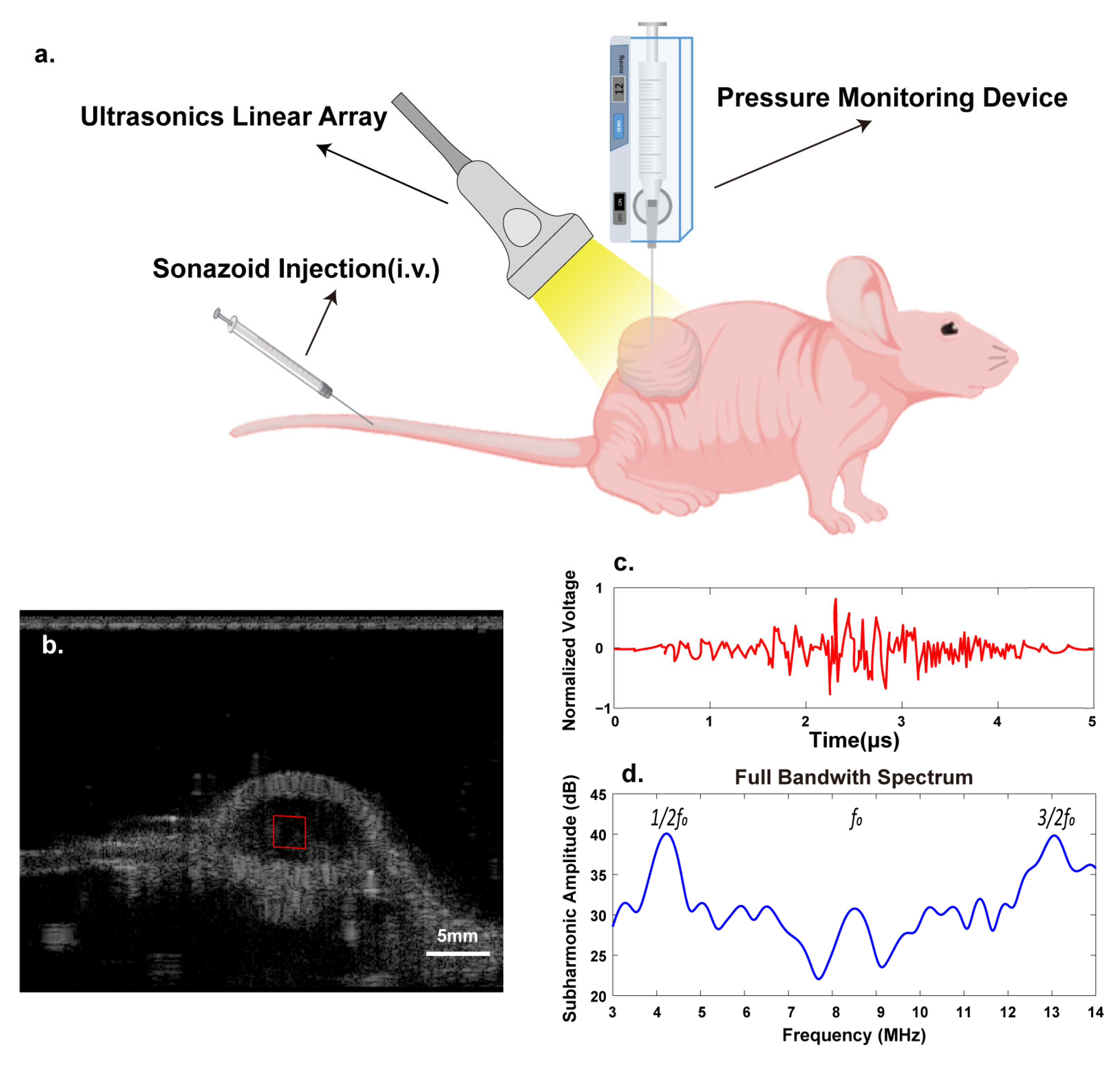
2.4. Tumors’ Subharmonic Scattering Acquisition
2.5. IFP Measurement
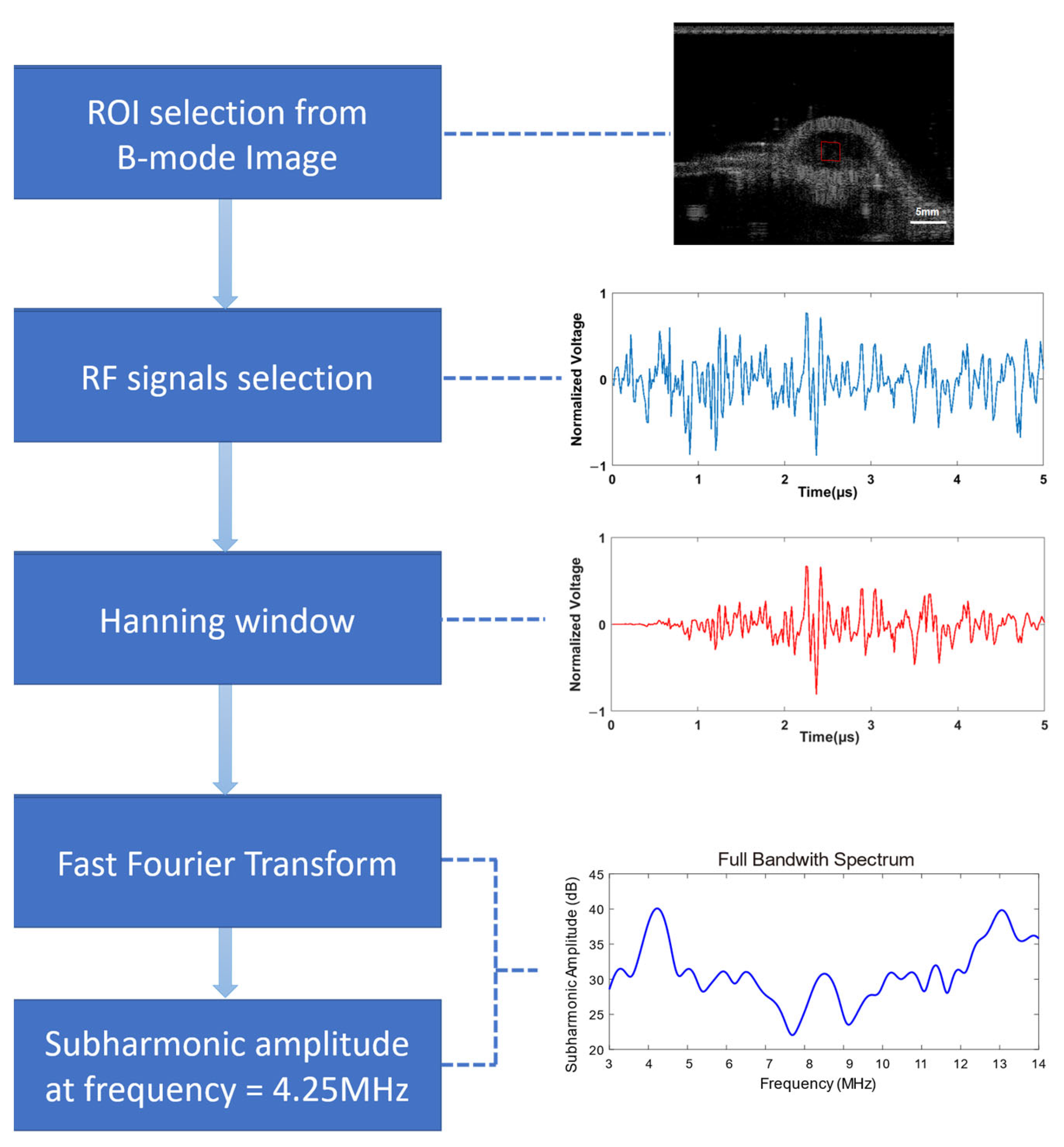
2.6. Data Processing
2.7. Statistical Analysis
3. Results
3.1. Resonance Frequency of Sonazoid
3.2. Relationship between Subharmonic Amplitude and Ambient Pressure
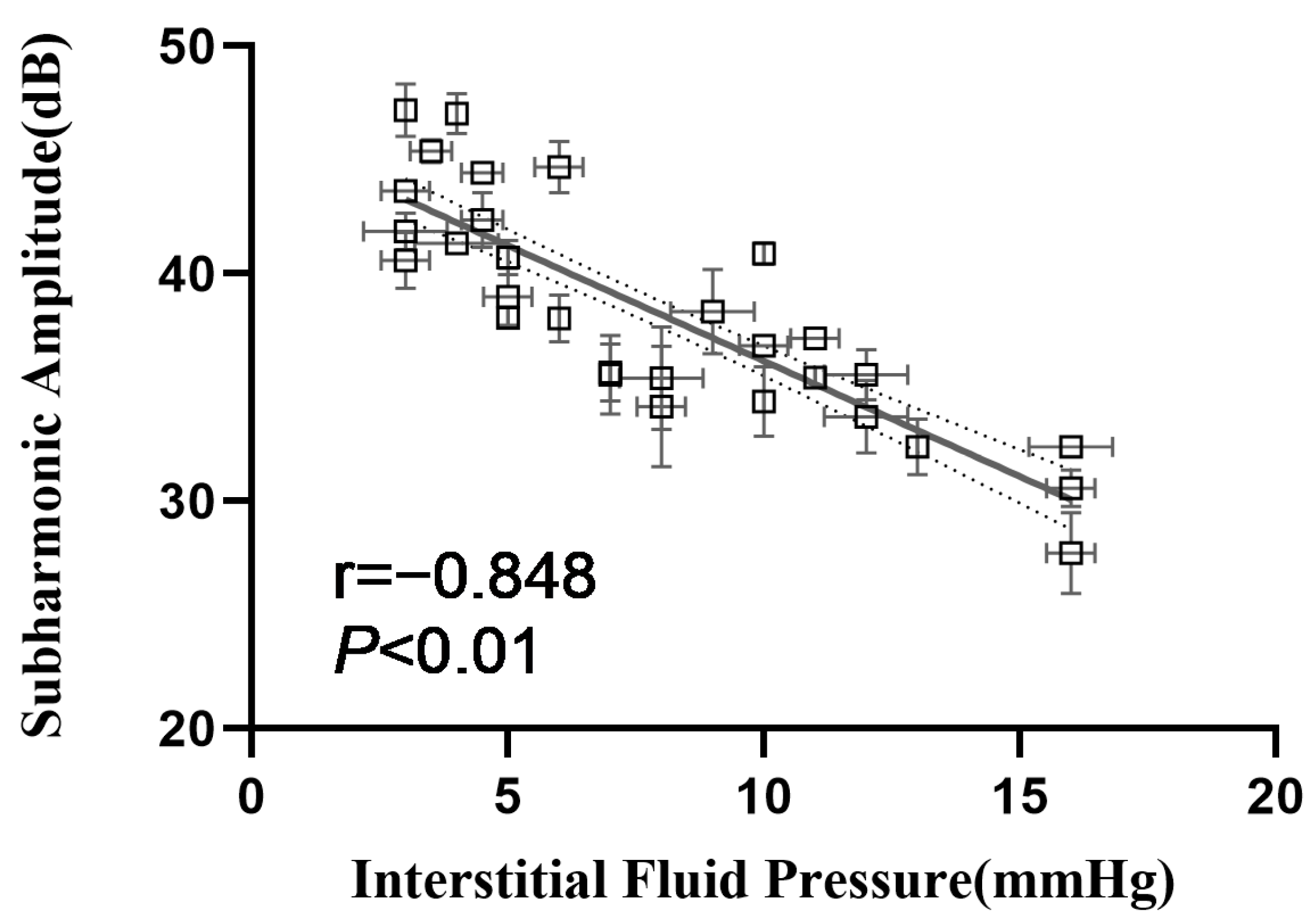
3.3. Correlation between Subharmonic Amplitudes and IFPs
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Salavati, H.; Debbaut, C.; Pullens, P.; Ceelen, W. Interstitial fluid pressure as an emerging biomarker in solid tumors. Biochim. Biophys. Acta. Rev. Cancer 2022, 1877, 188792. [Google Scholar] [CrossRef] [PubMed]
- Boucher, Y.; Jain, R.K. Microvascular pressure is the principal driving force for interstitial hypertension in solid tumors: Implications for vascular collapse. Cancer Res. 1992, 52, 5110–5114. [Google Scholar] [PubMed]
- Haider, T.; Sandha, K.K.; Soni, V.; Gupta, P.N. Recent advances in tumor microenvironment associated therapeutic strategies and evaluation models. Mater. Sci. Eng. C Mater. Biol. Appl. 2020, 116, 111229. [Google Scholar] [CrossRef]
- Heldin, C.H.; Rubin, K.; Pietras, K.; Ostman, A. High interstitial fluid pressure—An obstacle in cancer therapy. Nat. Rev. Cancer 2004, 4, 806–813. [Google Scholar] [CrossRef] [PubMed]
- Böckelmann, L.C.; Schumacher, U. Targeting tumor interstitial fluid pressure: Will it yield novel successful therapies for solid tumors? Expert Opin. Ther. Targets 2019, 23, 1005–1014. [Google Scholar] [CrossRef]
- Ozerdem, U.; Hargens, A.R. A simple method for measuring interstitial fluid pressure in cancer tissues. Microvasc. Res. 2005, 70, 116–120. [Google Scholar] [CrossRef]
- Khalifa, F.; Soliman, A.; El-Baz, A.; Abou El-Ghar, M.; El-Diasty, T.; Gimel’farb, G.; Ouseph, R.; Dwyer, A.C. Models and methods for analyzing DCE-MRI: A review. Med. Phys. 2014, 41, 124301. [Google Scholar] [CrossRef]
- Chong, W.K.; Papadopoulou, V.; Dayton, P.A. Imaging with ultrasound contrast agents: Current status and future. Abdom. Radiol. 2018, 43, 762–772. [Google Scholar] [CrossRef]
- Forsberg, F.; Shi, W.T.; Goldberg, B.J.U. Subharmonic imaging of contrast agents. Ultrasonics 2000, 38, 93–98. [Google Scholar] [CrossRef]
- Versluis, M.; Stride, E.; Lajoinie, G.; Dollet, B.; Segers, T. Ultrasound Contrast Agent Modeling: A Review. Ultrasound Med. Biol. 2020, 46, 2117–2144. [Google Scholar] [CrossRef]
- Helfield, B. A Review of Phospholipid Encapsulated Ultrasound Contrast Agent Microbubble Physics. Ultrasound Med. Biol. 2019, 45, 282–300. [Google Scholar] [CrossRef] [PubMed]
- Eisenbrey, J.R.; Sridharan, A.; Liu, J.B.; Forsberg, F. Recent Experiences and Advances in Contrast-Enhanced Subharmonic Ultrasound. BioMed. Res. Int. 2015, 2015, 640397. [Google Scholar] [CrossRef] [PubMed]
- Dahibawkar, M.; Forsberg, M.A.; Gupta, A.; Jaffe, S.; Dulin, K.; Eisenbrey, J.R.; Halldorsdottir, V.G.; Forsberg, A.I.; Dave, J.K.; Marshall, A.; et al. High and low frequency subharmonic imaging of angiogenesis in a murine breast cancer model. Ultrasonics 2015, 62, 50–55. [Google Scholar] [CrossRef] [PubMed]
- Jones, R.M.; Deng, L.; Leung, K.; McMahon, D.; O’Reilly, M.A.; Hynynen, K. Three-dimensional transcranial microbubble imaging for guiding volumetric ultrasound-mediated blood-brain barrier opening. Theranostics 2018, 8, 2909–2926. [Google Scholar] [CrossRef] [PubMed]
- Sridharan, A.; Eisenbrey, J.R.; Stanczak, M.; Machado, P.; Merton, D.A.; Wilkes, A.; Sevrukov, A.; Ojeda-Fournier, H.; Mattrey, R.F.; Wallace, K.; et al. Characterizing Breast Lesions Using Quantitative Parametric 3D Subharmonic Imaging: A Multicenter Study. Acad. Radiol. 2020, 27, 1065–1074. [Google Scholar] [CrossRef]
- Shi, W.; Forsberg, F.; Raichlen, J.; Needleman, L.; Goldberg, B.B. Pressure dependence of subharmonic signals from contrast microbubbles. Ultrasound Med. Biol. 1999, 25, 275–283. [Google Scholar] [CrossRef] [PubMed]
- Halldorsdottir, V.G.; Dave, J.K.; Leodore, L.M.; Eisenbrey, J.R.; Park, S.; Hall, A.L.; Thomenius, K.; Forsberg, F. Subharmonic contrast microbubble signals for noninvasive pressure estimation under static and dynamic flow conditions. Ultrason. Imaging 2011, 33, 153–164. [Google Scholar] [CrossRef]
- Andersen, K.S.; Jensen, J.A. Impact of acoustic pressure on ambient pressure estimation using ultrasound contrast agent. Ultrasonics 2010, 50, 294–299. [Google Scholar] [CrossRef]
- Li, F.; Wang, L.; Fan, Y.; Li, D. Simulation of noninvasive blood pressure estimation using ultrasound contrast agent microbubbles. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2012, 59, 715–726. [Google Scholar] [CrossRef]
- Nio, A.Q.X.; Faraci, A.; Christensen-Jeffries, K.; Raymond, J.L.; Monaghan, M.J.; Fuster, D.; Forsberg, F.; Eckersley, R.J.; Lamata, P. Optimal Control of SonoVue Microbubbles to Estimate Hydrostatic Pressure. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 67, 557–567. [Google Scholar] [CrossRef]
- Li, F.; Li, D.; Yan, F. Improvement of Detection Sensitivity of Microbubbles as Sensors to Detect Ambient Pressure. Sensors 2018, 18, 4083. [Google Scholar] [CrossRef]
- Xu, G.; Lu, H.; Yang, H.; Li, D.; Liu, R.; Su, M.; Jin, B.; Li, C.; Lv, T.; Du, S.; et al. Subharmonic Scattering of SonoVue Microbubbles Within 10–40-mmHg Overpressures In Vitro. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 3583–3591. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, Y.; Cheng, L.; Wang, H.; Li, R.; Chen, Z.; Zhang, Y.; He, W.; Zhang, W. Noninvasive Assessment of Intracranial Pressure Using Subharmonic-Aided Pressure Estimation: An Experimental Study in Canines. J. Trauma Acute Care Surg. 2022, 93, 882–888. [Google Scholar] [CrossRef] [PubMed]
- Dave, J.K.; Halldorsdottir, V.G.; Eisenbrey, J.R.; Raichlen, J.S.; Liu, J.B.; McDonald, M.E.; Dickie, K.; Wang, S.; Leung, C.; Forsberg, F. Noninvasive LV pressure estimation using subharmonic emissions from microbubbles. JACC Cardiovasc. Imaging 2012, 5, 87–92. [Google Scholar] [CrossRef] [PubMed]
- Dave, J.K.; Halldorsdottir, V.G.; Eisenbrey, J.R.; Merton, D.A.; Liu, J.B.; Zhou, J.H.; Wang, H.K.; Park, S.; Dianis, S.; Chalek, C.L.; et al. Investigating the efficacy of subharmonic aided pressure estimation for portal vein pressures and portal hypertension monitoring. Ultrasound Med. Biol. 2012, 38, 1784–1798. [Google Scholar] [CrossRef]
- Dave, J.K.; Halldorsdottir, V.G.; Eisenbrey, J.R.; Merton, D.A.; Liu, J.B.; Machado, P.; Zhao, H.; Park, S.; Dianis, S.; Chalek, C.L.; et al. On the implementation of an automated acoustic output optimization algorithm for subharmonic aided pressure estimation. Ultrasonics 2013, 53, 880–888. [Google Scholar] [CrossRef]
- Eisenbrey, J.R.; Dave, J.K.; Halldorsdottir, V.G.; Merton, D.A.; Miller, C.; Gonzalez, J.M.; Machado, P.; Park, S.; Dianis, S.; Chalek, C.L.; et al. Chronic liver disease: Noninvasive subharmonic aided pressure estimation of hepatic venous pressure gradient. Radiology 2013, 268, 581–588. [Google Scholar] [CrossRef]
- Gupta, I.; Eisenbrey, J.R.; Machado, P.; Stanczak, M.; Wessner, C.E.; Shaw, C.M.; Gummadi, S.; Fenkel, J.M.; Tan, A.; Miller, C.; et al. Diagnosing Portal Hypertension with Noninvasive Subharmonic Pressure Estimates from a US Contrast Agent. Radiology 2021, 298, 104–111. [Google Scholar] [CrossRef]
- Dave, J.K.; Kulkarni, S.V.; Pangaonkar, P.P.; Stanczak, M.; McDonald, M.E.; Cohen, I.S.; Mehrotra, P.; Savage, M.P.; Walinsky, P.; Ruggiero, N.J., 2nd; et al. Non-Invasive Intra-cardiac Pressure Measurements Using Subharmonic-Aided Pressure Estimation: Proof of Concept in Humans. Ultrasound Med. Biol. 2017, 43, 2718–2724. [Google Scholar] [CrossRef]
- Esposito, C.; Machado, P.; McDonald, M.E.; Savage, M.P.; Fischman, D.; Mehrotra, P.; Cohen, I.S.; Ruggiero, N., 2nd; Walinsky, P.; Vishnevsky, A.; et al. Noninvasive Evaluation of Cardiac Chamber Pressures Using Subharmonic-Aided Pressure Estimation With Definity Microbubbles. JACC Cardiovasc. Imaging 2023, 16, 224–235. [Google Scholar] [CrossRef]
- Halldorsdottir, V.G.; Dave, J.K.; Eisenbrey, J.R.; Machado, P.; Zhao, H.; Liu, J.B.; Merton, D.A.; Forsberg, F. Subharmonic aided pressure estimation for monitoring interstitial fluid pressure in tumours--in vitro and in vivo proof of concept. Ultrasonics 2014, 54, 1938–1944. [Google Scholar] [CrossRef] [PubMed]
- Halldorsdottir, V.G.; Dave, J.K.; Marshall, A.; Forsberg, A.I.; Fox, T.B.; Eisenbrey, J.R.; Machado, P.; Liu, J.B.; Merton, D.A.; Forsberg, F. Subharmonic-Aided Pressure Estimation for Monitoring Interstitial Fluid Pressure in Tumors: Calibration and Treatment with Paclitaxel in Breast Cancer Xenografts. Ultrasound Med. Biol. 2017, 43, 1401–1410. [Google Scholar] [CrossRef] [PubMed]
- Hansem, L.M.K.; Huang, R.; Wegner, C.S.; Simonsen, T.G.; Gaustad, J.V.; Hauge, A.; Rofstad, E.K. Intratumor Heterogeneity in Interstitial Fluid Pressure in Cervical and Pancreatic Carcinoma Xenografts. Transl. Oncol. 2019, 12, 1079–1085. [Google Scholar] [CrossRef]
- Lu, H.; Xu, G.; Wang, Y.; Yang, H.; Li, D.; Huang, L.; Su, M.; Li, C.; Qiu, W.; Mao, Y.; et al. Correlation Between Portal Vein Pressure and Subharmonic Scattering Signals From SonoVue Microbubbles in Canines. Ultrasound Med. Biol. 2023, 49, 203–211. [Google Scholar] [CrossRef]
- Mulvana, H.; Stride, E.; Tang, M.; Hajnal, J.V.; Eckersley, R. Temperature-dependent differences in the nonlinear acoustic behavior of ultrasound contrast agents revealed by high-speed imaging and bulk acoustics. Ultrasound Med. Biol. 2011, 37, 1509–1517. [Google Scholar] [CrossRef]
- Chen, P.; Pollet, A.; Panfilova, A.; Zhou, M.; Turco, S.; den Toonder, J.M.J.; Mischi, M. Acoustic characterization of tissue-mimicking materials for ultrasound perfusion imaging research. Ultrasound Med. Biol. 2022, 48, 124–142. [Google Scholar] [CrossRef]

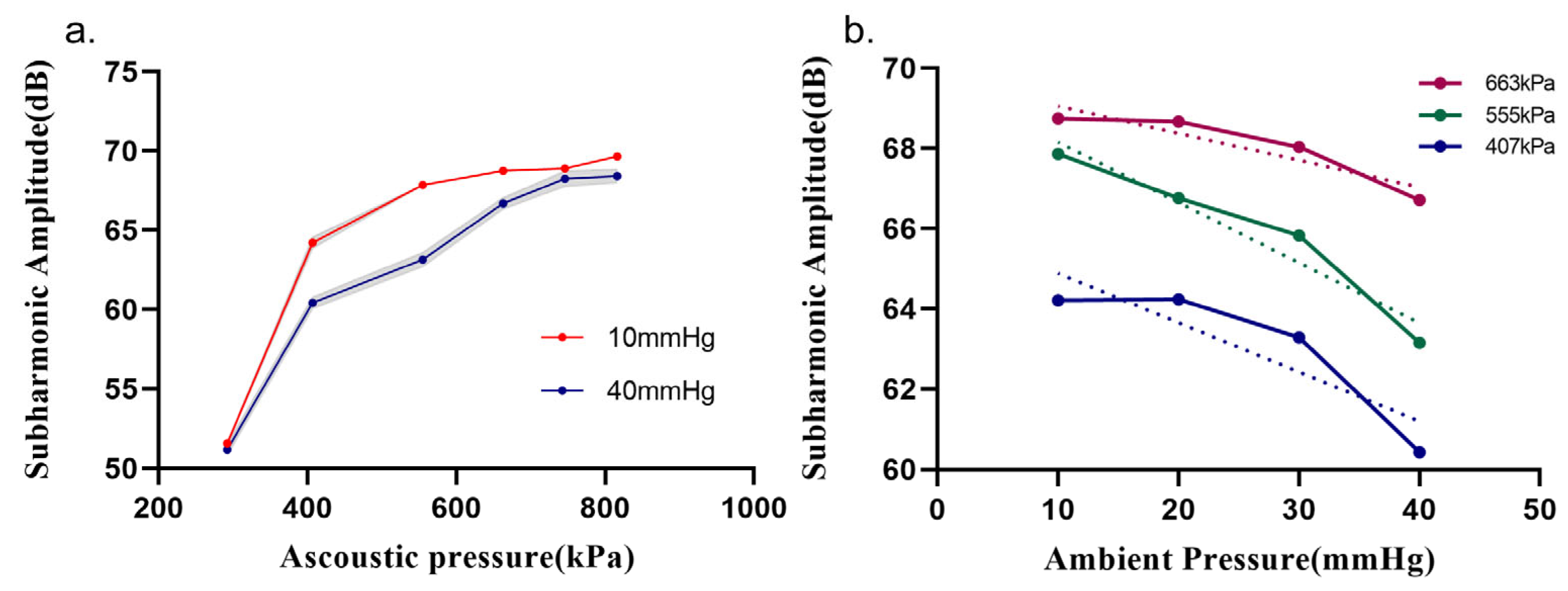
| Acoustic Pressure (kPa) | MI 1 | Sensitivity (dB/mmHg) | Pearson’s r | p Value |
|---|---|---|---|---|
| 292 | 0.100 | 0.012 | −0.862 | 0.138 |
| 407 | 0.140 | 0.123 | −0.883 | 0.117 |
| 555 | 0.190 | 0.150 | −0.966 | 0.034 |
| 663 | 0.227 | 0.068 | −0.924 | 0.076 |
| 746 | 0.256 | 0.029 | −0.999 | 0.001 |
| 816 | 0.280 | 0.028 | −0.569 | 0.431 |
| Random Grouping | Mean Absolute Error (mmHg) | SD (mmHg) | Range (mmHg) | RMSE 1 (mmHg) | p Value |
|---|---|---|---|---|---|
| 1 | 2.09 | 1.56 | [0.06, 4.93] | 2.52 | 0.193 |
| 2 | 2.26 | 1.24 | [0.19, 4.06] | 2.54 | 0.098 |
| 3 | 1.83 | 1.46 | [0.30, 4.16] | 2.25 | 0.192 |
| 4 | 2.95 | 2.28 | [0.16, 6.25] | 3.60 | 0.458 |
| 5 | 2.11 | 1.46 | [0.04, 4.02] | 2.59 | 0.400 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Lu, H.; Huang, L.; Li, D.; Qiu, W.; Li, L.; Xu, G.; Su, M.; Zhou, J.; Li, F. Noninvasive Estimation of Tumor Interstitial Fluid Pressure from Subharmonic Scattering of Ultrasound Contrast Microbubbles. Biosensors 2023, 13, 528. https://doi.org/10.3390/bios13050528
Wang Y, Lu H, Huang L, Li D, Qiu W, Li L, Xu G, Su M, Zhou J, Li F. Noninvasive Estimation of Tumor Interstitial Fluid Pressure from Subharmonic Scattering of Ultrasound Contrast Microbubbles. Biosensors. 2023; 13(5):528. https://doi.org/10.3390/bios13050528
Chicago/Turabian StyleWang, Yun, Huimin Lu, Laixin Huang, Deyu Li, Weibao Qiu, Lingling Li, Gang Xu, Min Su, Jianhua Zhou, and Fei Li. 2023. "Noninvasive Estimation of Tumor Interstitial Fluid Pressure from Subharmonic Scattering of Ultrasound Contrast Microbubbles" Biosensors 13, no. 5: 528. https://doi.org/10.3390/bios13050528
APA StyleWang, Y., Lu, H., Huang, L., Li, D., Qiu, W., Li, L., Xu, G., Su, M., Zhou, J., & Li, F. (2023). Noninvasive Estimation of Tumor Interstitial Fluid Pressure from Subharmonic Scattering of Ultrasound Contrast Microbubbles. Biosensors, 13(5), 528. https://doi.org/10.3390/bios13050528





