Strain Sensor-Inserted Microchannel for Gas Viscosity Measurement
Abstract
1. Introduction
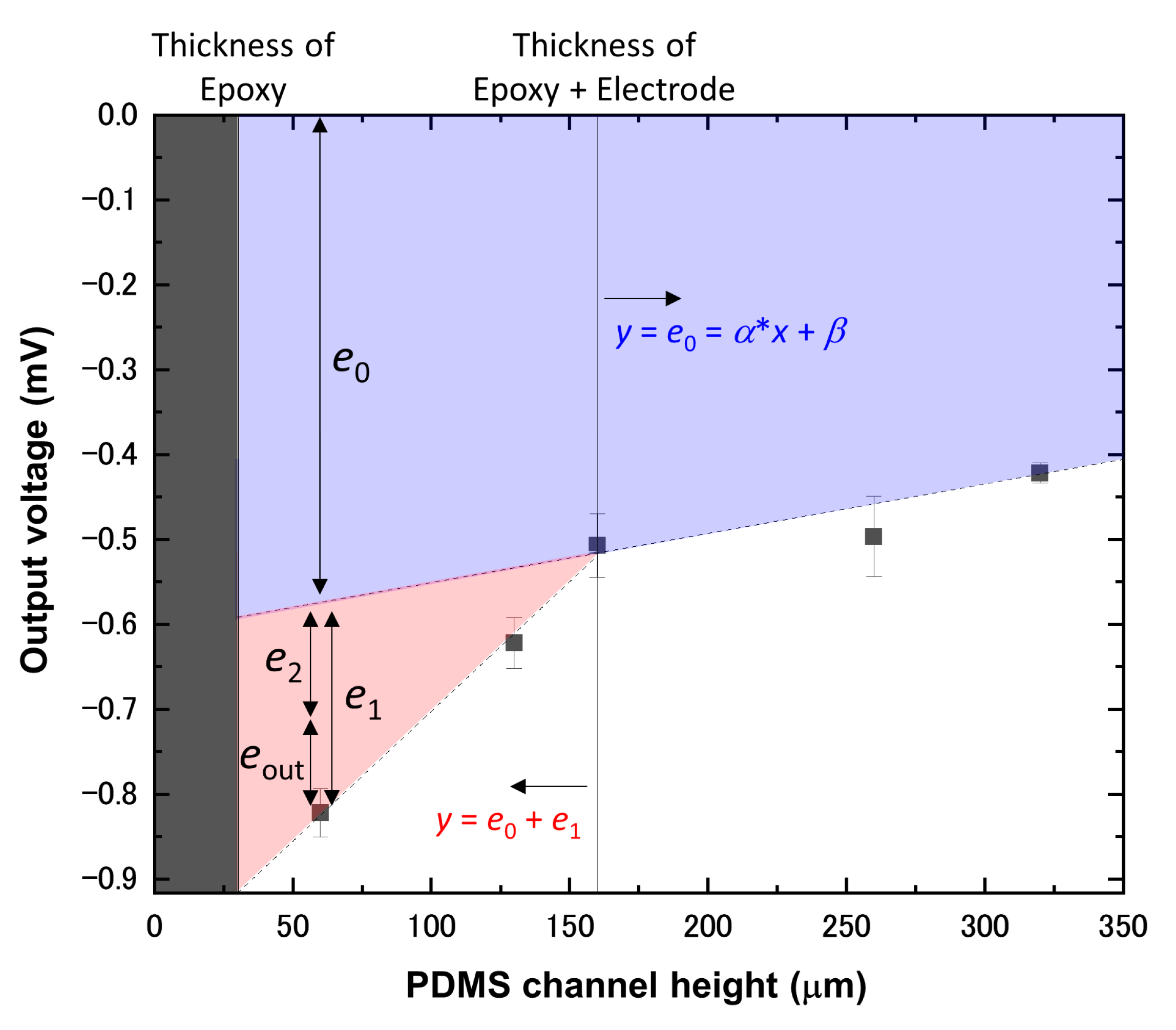
2. Concept
3. Materials and Methods
3.1. Device Fabrication
3.2. Gas Flow Measurement with the PDMS Device
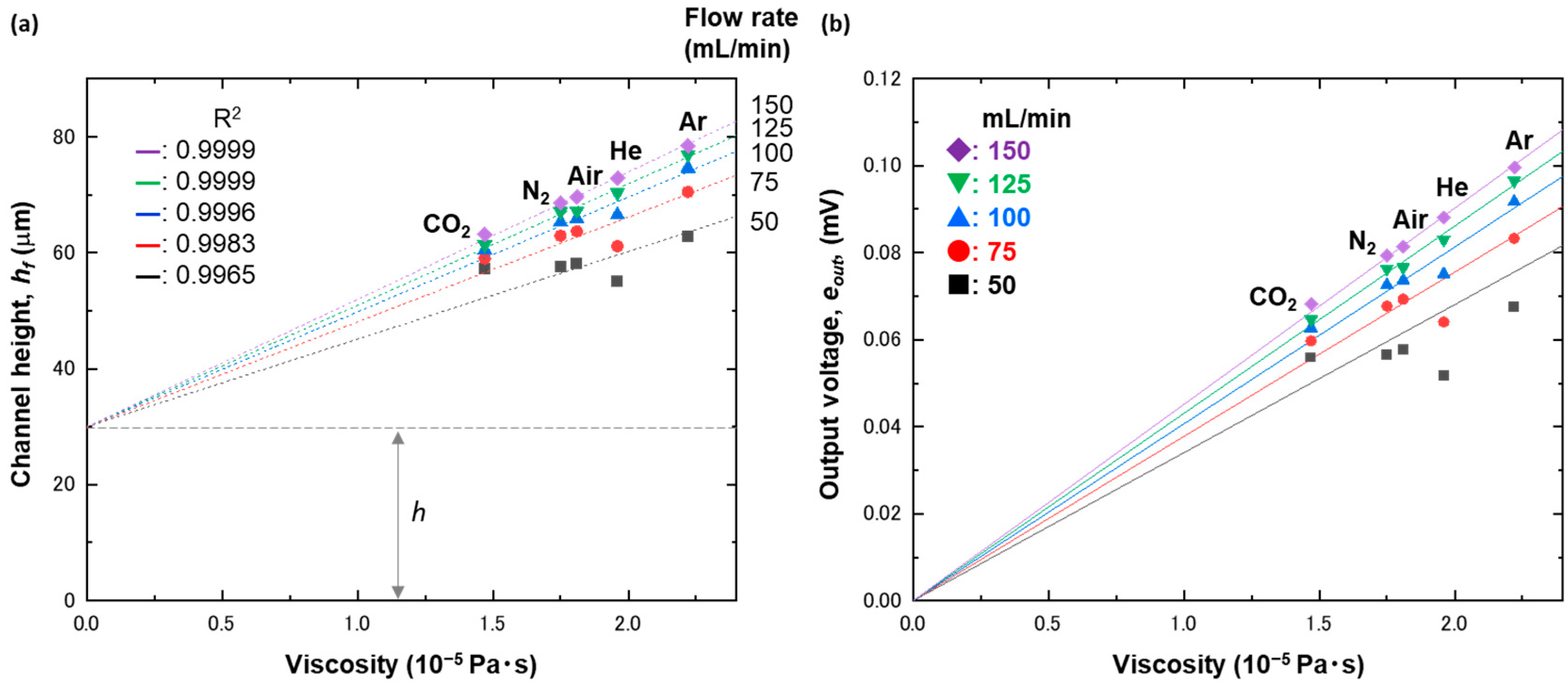
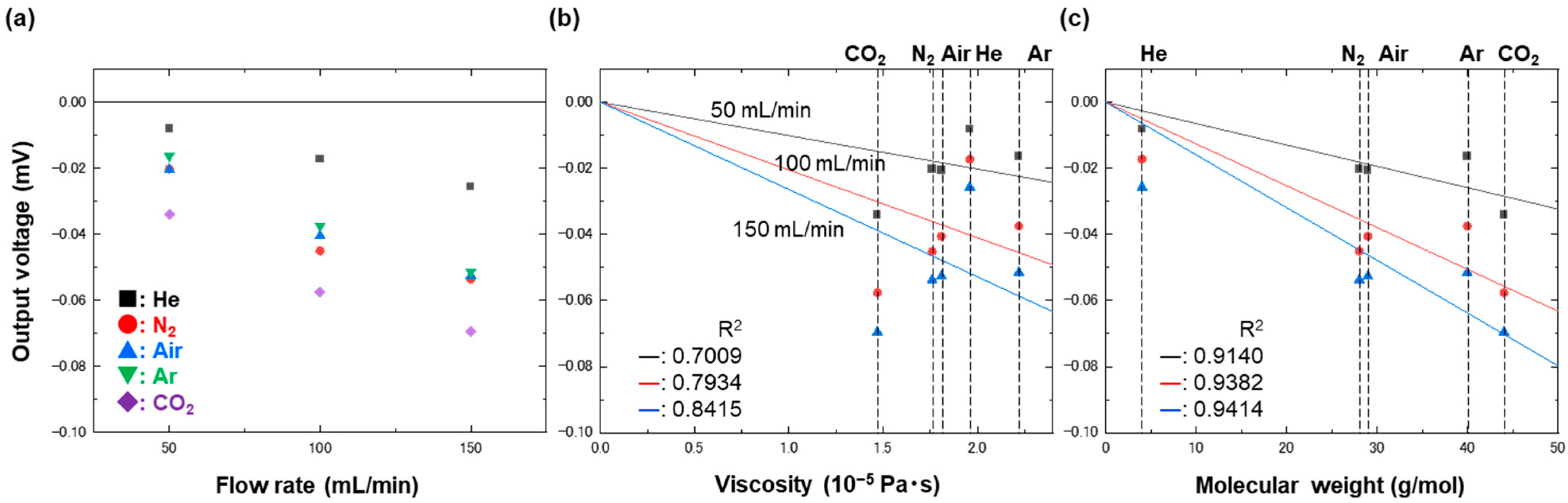
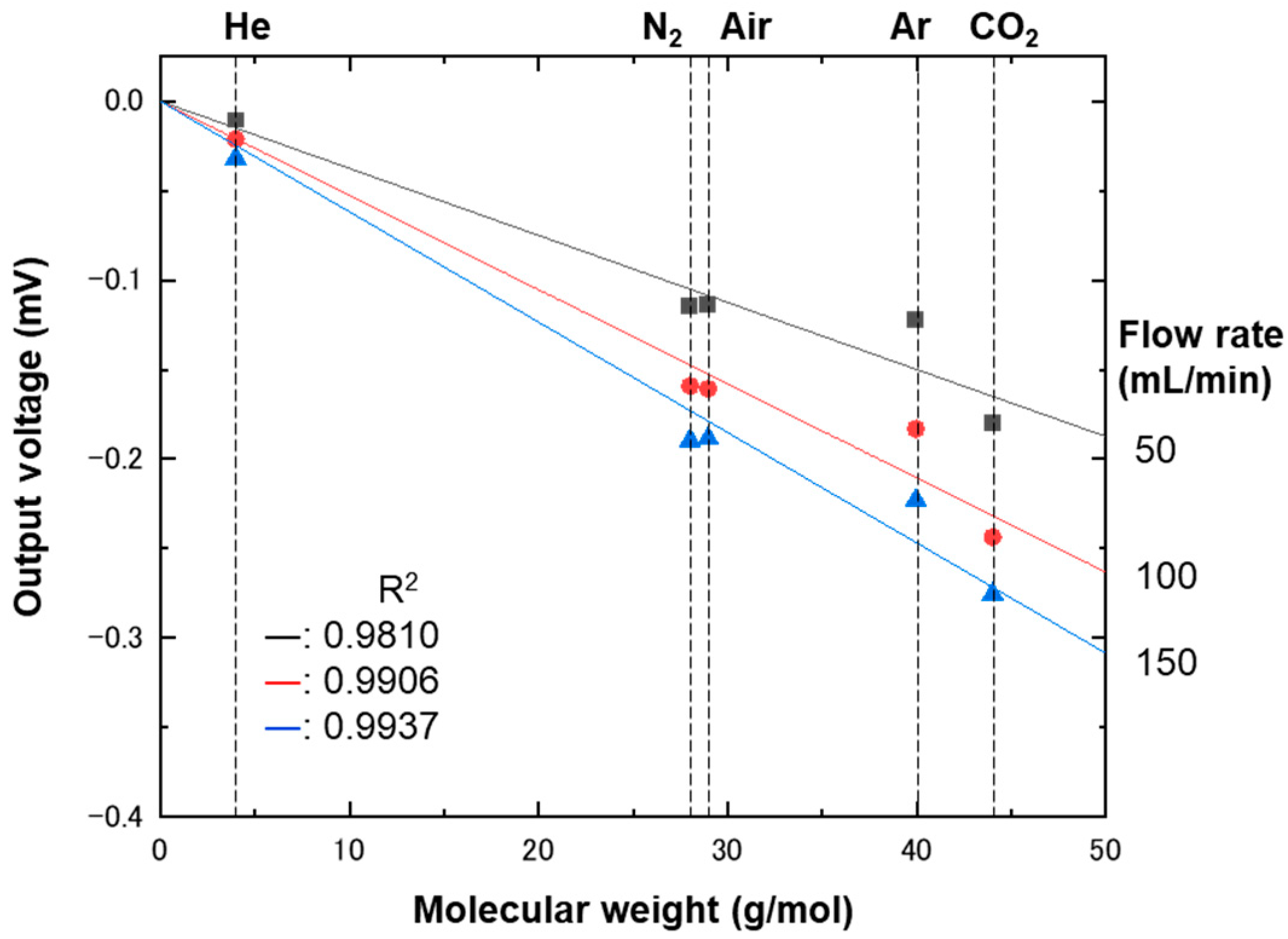
4. Results and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2014.
- Edgeworth, R.; Dalton, B.J.; Parnell, T. The pitch drop experiment. Eur. J. Phys. 1984, 5, 198. [Google Scholar] [CrossRef]
- Mena, S.E.; Li, Y.Z.; McCormick, J.; McCracken, B.; Colmenero, C.; Ward, K.; Burns, M.A. A droplet-based microfluidic viscometer for the measurement of blood coagulation. Biomicrofluidics 2020, 14, 9. [Google Scholar] [CrossRef] [PubMed]
- Kim, G.; Jeong, S.; Kang, Y.J. Ultrasound Standing Wave-Based Cell-to-liquid Separation for Measuring Viscosity and Aggregation of Blood Sample. Sensors 2020, 20, 2284. [Google Scholar] [CrossRef] [PubMed]
- Hermann, M.; Bachus, K.; Gibson, G.T.T.; Oleschuk, R.D. Open sessile droplet viscometer with low sample consumption. Lab Chip 2020, 20, 1869. [Google Scholar] [CrossRef]
- Chen, W.; Wu, B.; Yin, Y.; Zhu, C.; Fu, T.; Zhang, X.; Ma, Y. Gas-liquid hydrodynamics with different liquid viscosities in a split-and-recombine microchannel. Chem. Eng. Process. Process Intensif. 2022, 177, 108988. [Google Scholar] [CrossRef]
- Chakrabarti, S. A novel experimental setup to study the Hagen-Poiseuille and Bernoulli equations for a gas and determination of the viscosity of air. Eur. J. Phys. 2015, 36, 065046. [Google Scholar] [CrossRef]
- Hellgardt, K.; Al-Musa, A.; Cumming, I.W.; Mason, G.; Buffham, B.A. In situ determination of the viscosity of gas mixtures containing trace quantities of oxygen. AIChE J. 2000, 46, 1449. [Google Scholar] [CrossRef]
- Johns, D.P.; Pretto, J.J.; Streeton, J.A. Measurement of gas viscosity with a fleisch pneumotachograph. J. Appl. Physiol. 1982, 53, 290. [Google Scholar] [CrossRef]
- Benton, A.F. The end correction in the determination of gas viscosity by the capillary tube method. Phys. Rev. 1919, 14, 403. [Google Scholar] [CrossRef]
- Igarashi, K.; Kawashima, K.; Kagawa, T. Development of simultaneous measurement system for instantaneous density, viscosity and flow rate of gases. Sens. Actuator A-Phys. 2007, 140, 1. [Google Scholar] [CrossRef]
- Zhang, J.T.; Lin, H.; Che, J. Effects of connecting tubing on a two-capillary viscometer. Metrologia 2013, 50, 377. [Google Scholar] [CrossRef]
- Lassalle, L.J. On the motion of a sphere of oil through carbon dioxide and a determination of the coefficient of viscosity of that gas by the oil drop method. Phys. Rev. 1921, 17, 354. [Google Scholar] [CrossRef]
- Kestin, J.; Whitelaw, J.H. A Relative determination of viscosity of several gases by oscillating disk method. Physica 1963, 29, 335. [Google Scholar] [CrossRef]
- Kestin, J.; Leidenfrost, W. An absolute determination of the viscosity of 11 gases over a range of pressures. Physica 1959, 25, 1033. [Google Scholar] [CrossRef]
- Vanitterbeek, A.; Vanpaemel, O.; Vanlierde, J. Measurements on the viscosity of gas mixtures. Physica 1947, 13, 88. [Google Scholar] [CrossRef]
- van Itterbeek, A.; van Paemel, O. Measurements on the viscosity of gases for low pressures at room temperature and at low temperatures. Physica 1940, 7, 273. [Google Scholar] [CrossRef]
- van Itterbeek, A.; van Paemel, O. Measurements on the viscosity of argon gas at room temperature and between 90 degrees and 55 degrees K. Physica 1938, 5, 1009. [Google Scholar] [CrossRef]
- Meijer, A.S.; de Wijn, A.S.; Peters, M.F.E.; Dam, N.J.; van de Water, W. Coherent Rayleigh-Brillouin scattering measurements of bulk viscosity of polar and nonpolar gases, and kinetic theory. J. Chem. Phys. 2010, 133, 164315. [Google Scholar] [CrossRef]
- Shimokawa, Y.; Matsuura, Y.; Hirano, T.; Sakai, K. Gas viscosity measurement with diamagnetic-levitation viscometer based on electromagnetically spinning system. Rev. Sci. Instrum. 2016, 87, 125105. [Google Scholar] [CrossRef]
- Gao, R.K.; O’Byrne, S.; Sheehe, S.L.; Kurtz, J.; Liow, J.L. Transient gas viscosity measurement using tunable diode laser absorption spectroscopy. Exp Fluids 2017, 58, 156. [Google Scholar] [CrossRef]
- Kurokawa, A.; Hojo, H.; Kobayashi, T. Viscosity Measurement Using Impedance and Frequency of a Quartz Resonator Vibrating in a Viscous Flowing Gas. Appl. Phys. Express 2011, 4, 037201. [Google Scholar] [CrossRef]
- Iglesias, L.; Boudjiet, M.T.; Dufour, I. Discrimination and concentration measurement of different binary gas mixtures with a simple resonator through viscosity and mass density measurements. Sens. Actuator B-Chem. 2019, 285, 487. [Google Scholar] [CrossRef]
- Badarlis, A.; Pfau, A.; Kalfas, A. Measurement and Evaluation of the Gas Density and Viscosity of Pure Gases and Mixtures Using a Micro-Cantilever Beam. Sensors 2015, 15, 24318–24342. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, M.; Seren, H.R.; Ham, G.; Buzi, E.; Bernero, G.; Deffenbaugh, M. Viscosity and Density Measurements Using Mechanical Oscillators in Oil and Gas Applications. IEEE Trans. Instrum. Meas. 2018, 67, 804. [Google Scholar] [CrossRef]
- Shiba, K.; Li, G.; Virot, E.; Yoshikawa, G.; Weitz, D.A. Microchannel measurements of viscosity for both gases and liquids. Lab Chip 2021, 21, 2805. [Google Scholar] [CrossRef]
- Stone, H.A. CMOS Biotechnology; Lee, H., Ham, D., Westervelt, R.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Raj, M.K.; DasGupta, S.; Chakraborty, S. Hydrodynamics in deformable microchannels. Microfluid. Nanofluidics 2017, 21, 70. [Google Scholar] [CrossRef]
- Raj, A.; Sen, A.K. Flow-induced deformation of compliant microchannels and its effect on pressure–flow characteristics. Microfluid. Nanofluidics 2016, 20, 31. [Google Scholar] [CrossRef]
- Cheung, P.; Toda-Peters, K.; Shen, A.Q. In situ pressure measurement within deformable rectangular polydimethylsiloxane microfluidic devices. Biomicrofluidics 2012, 6, 26501. [Google Scholar] [CrossRef]
- Hardy, B.S.; Uechi, K.; Zhen, J.; Kavehpour, H.P. The deformation of flexible PDMS microchannels under a pressure driven flow. Lab Chip 2009, 9, 935. [Google Scholar] [CrossRef]
- Gervais, T.; El-Ali, J.; Günther, A.; Jensen, K.F. Flow-induced deformation of shallow microfluidic channels. Lab Chip 2006, 6, 500. [Google Scholar] [CrossRef]
- Koh, K.L.; Ji, X.; Dasari, A.; Lu, X.; Lau, S.K.; Chen, Z. Fracture Toughness and Elastic Modulus of Epoxy-Based Nanocomposites with Dopamine-Modified Nano-Fillers. Materials 2017, 10, 776. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.; Moon, B.-U.; Hidrovo, C.H. Enhancement of the thermo-mechanical properties of PDMS molds for the hot embossing of PMMA microfluidic devices. J. Micromech. Microeng. 2013, 23, 095024. [Google Scholar] [CrossRef]
- Ledbetter, H.M.; Naimon, E.R. Elastic Properties of Metals and Alloys. II. Copper. J. Phys. Chem. Ref. Data 1974, 3, 897. [Google Scholar] [CrossRef]
- Ding, Y.; Niu, X.-R.; Wang, G.-F.; Feng, X.-Q.; Yu, S.-W. Surface effects on nanoindentation of soft solids by different indenters. Mater. Res. Exp. 2016, 3, 115021. [Google Scholar] [CrossRef]
- Cease, H.; Derwent, P.F.; Diehl, H.T.; Fast, J.; Finley, D. Measurement of Mechanical Properties of Three Epoxy Adhesives at Cryogenic Temperatures for CCD Construction; Fermi Lab Report; Fermi National Accelerator Laboratory: Batavia, IL, USA, 2006; p. 19. [Google Scholar]
- Graham, L. Introduction to Mechanical Measurements. OpenStax CNX. 2006. Available online: https://cnx.org/contents/df8f0907 (accessed on 23 August 2020).
- Johnston, I.D.; McCluskey, D.K.; Tan, C.K.L.; Tracey, M.C. Mechanical characterization of bulk Sylgard 184 for microfluidics and microengineering. J. Micromech. Microeng. 2014, 24, 035017. [Google Scholar] [CrossRef]
- Shiba, K.; Yoshikawa, G. Aero-Thermo-Dynamic Mass Analysis. Sci. Rep. 2016, 6, 28849. [Google Scholar] [CrossRef] [PubMed]




| Symbol or Abbreviation | Detail |
|---|---|
| Load applied to PDMS due to insertion | |
| Cross-sectional radius of a circular punch | |
| Young’s modulus of PDMS | |
| Poisson’s ratio of PDMS | |
| Channel height after insertion of the epoxy film | |
| Cross-sectional length of a rectangle | |
| Cross-sectional width of a rectangle | |
| Strain normal to the epoxy surface | |
| Stress applied to the epoxy surface | |
| Young’s modulus of the epoxy | |
| Strain in the lateral direction | |
| Poisson’s ratio of the epoxy | |
| Gauge factor | |
| Bridge voltage | |
| Channel height under gas flow | |
| Load under gas flow | |
| Viscosity of a gas | |
| Flow rate | |
| Flow-rate-dependent function | |
| Induced pressure change via gas flow |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shiba, K.; Liu, L.; Li, G. Strain Sensor-Inserted Microchannel for Gas Viscosity Measurement. Biosensors 2023, 13, 76. https://doi.org/10.3390/bios13010076
Shiba K, Liu L, Li G. Strain Sensor-Inserted Microchannel for Gas Viscosity Measurement. Biosensors. 2023; 13(1):76. https://doi.org/10.3390/bios13010076
Chicago/Turabian StyleShiba, Kota, Linbo Liu, and Guangming Li. 2023. "Strain Sensor-Inserted Microchannel for Gas Viscosity Measurement" Biosensors 13, no. 1: 76. https://doi.org/10.3390/bios13010076
APA StyleShiba, K., Liu, L., & Li, G. (2023). Strain Sensor-Inserted Microchannel for Gas Viscosity Measurement. Biosensors, 13(1), 76. https://doi.org/10.3390/bios13010076







