Multifrequency Investigation of Single- and Double-Stranded DNA with Scalable Metamaterial-Based THz Biosensors
Abstract
:1. Introduction
2. Materials and Methods
2.1. Structure
2.2. Fabrication
2.3. Dimensioning
2.4. Simulation and Material Model
2.5. Measurement Setup and Data Processing
2.6. Sample Preparation
2.6.1. Materials
2.6.2. Procedures
3. Results
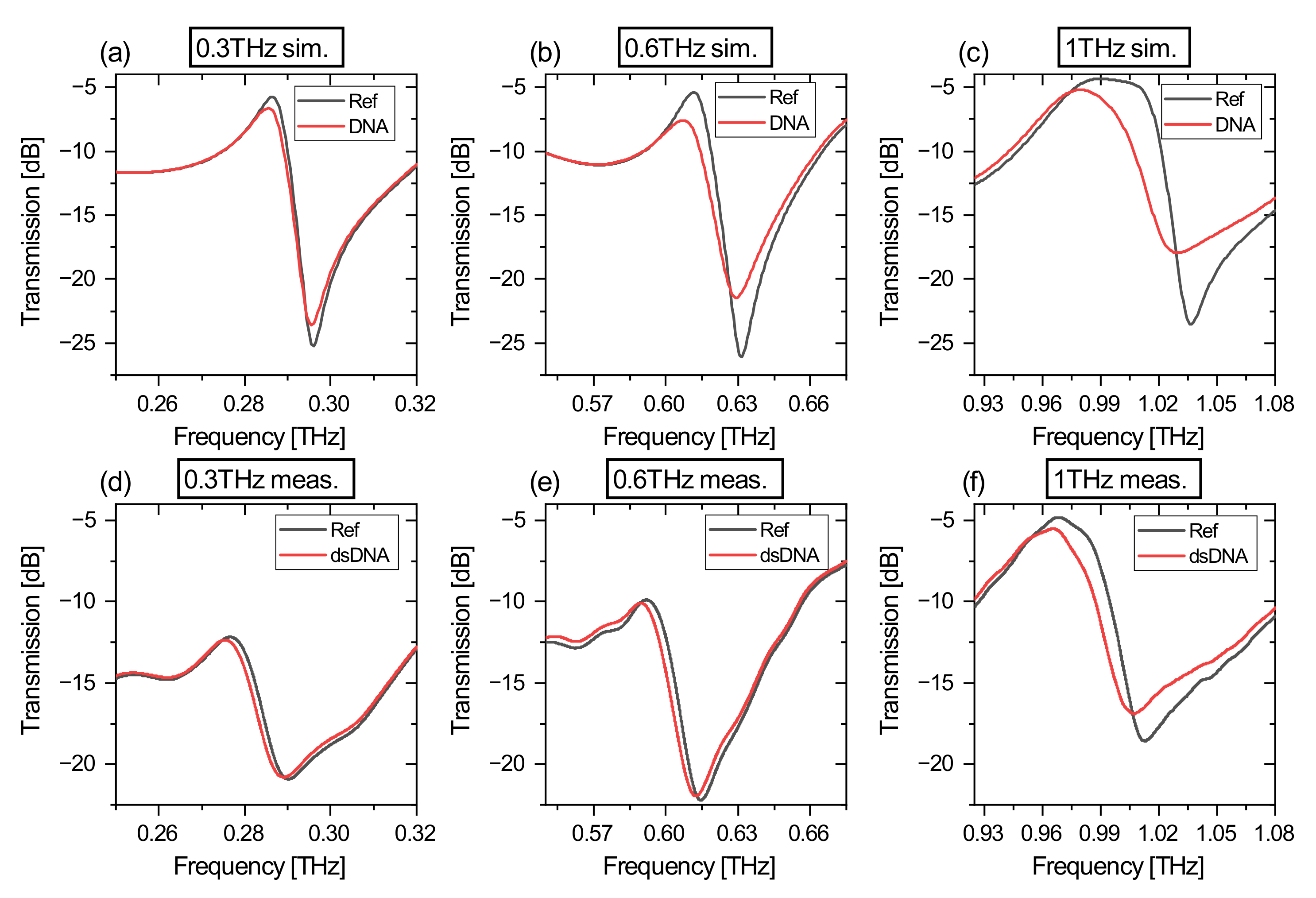
3.1. Simulation and Measurement Comparison
3.2. Parameter Analysis
3.3. Frequency-Dependent Frequency Shift of ss- and dsDNA
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DNA | Deoxyribonucleic acid |
| ssDNA | Single stranded DNA |
| dsDNA | Double stranded DNA |
| aDSRR | Asymmetric double split ring resonator |
| UV | Ultraviolet |
| EIT | Electromagnetically induced transparency |
| HFSS | High-frequency structure simulator |
| DFB | Distributed feedback |
| CW | Continuous wave |
| FFT | Fast Fourier transform |
| IFFT | Inverse FFT |
| SD | Standard deviation of the mean |
| SEM | Standard error of the mean |
| DI | Deionized |
| TCEP | Tris(2-carboxyethyl)phosphine hydrochloride |
| DRF | Double resonance feature |
| PPTD | Peak-to-peak transmission difference |
| LOD | Limit of detection |
Appendix A. Error Calculation
Appendix B. Biosensor Occupation Scheme
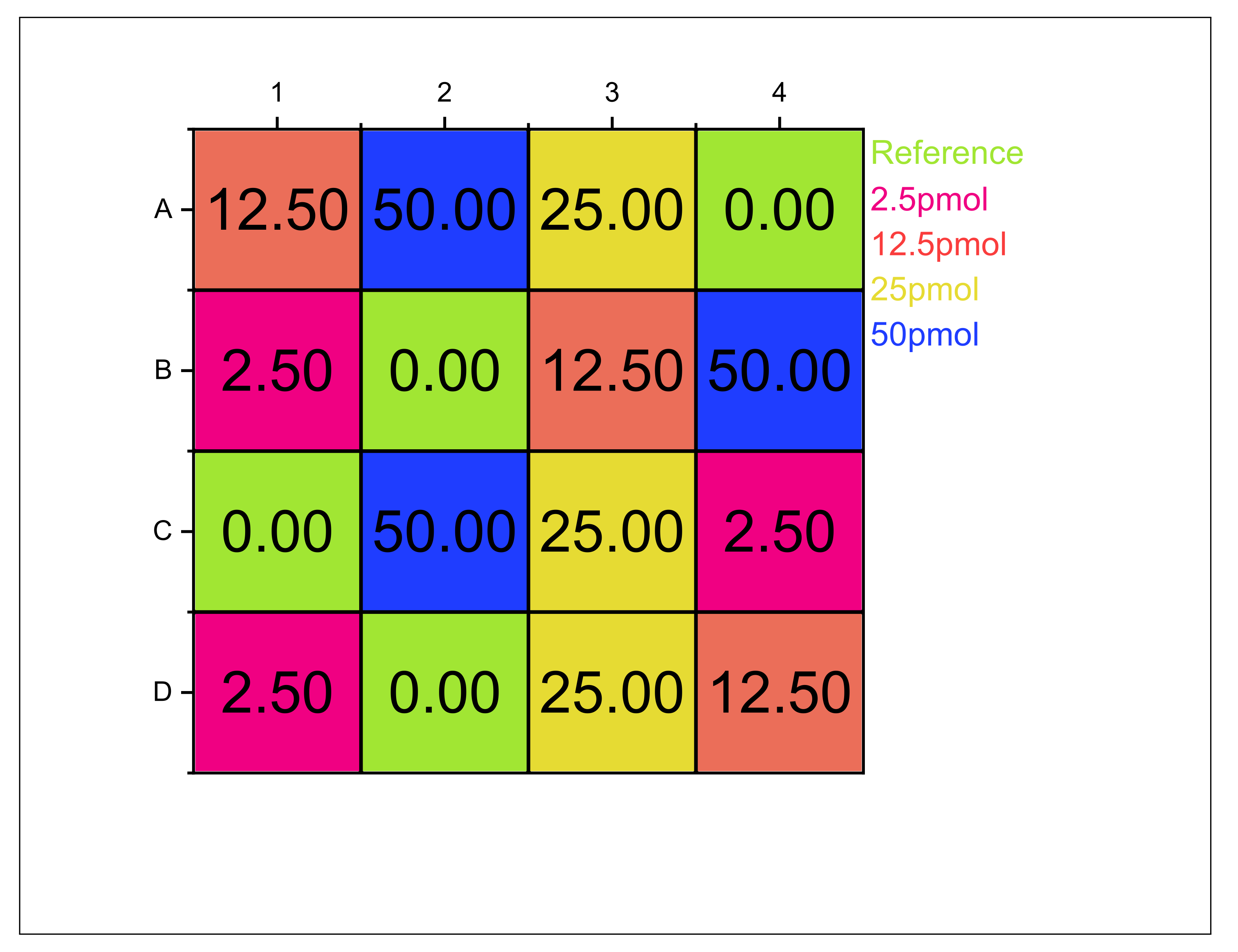
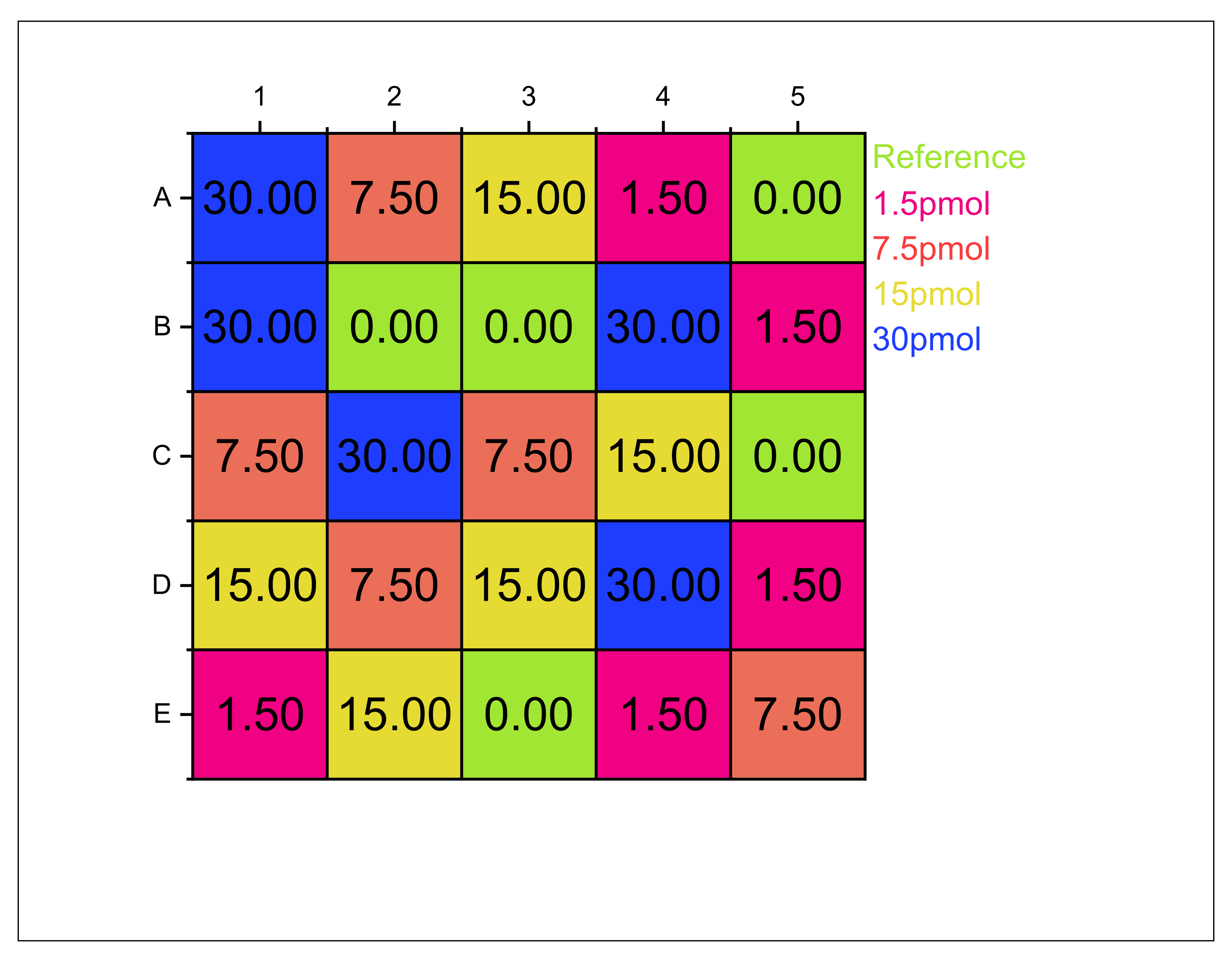
Appendix C. DNA Sample Composition
| Sample | mol L | pmol | pmol | pmol | L |
|---|---|---|---|---|---|
| 20 | 500 | 1000 | 500 | 25 | |
| 10 | 250 | 500 | 250 | 25 | |
| 5 | 125 | 250 | 125 | 25 | |
| 1 | 25 | 50 | 25 | 25 | |
| 20 | 500 | 1000 | 0 | 25 | |
| 10 | 250 | 500 | 0 | 25 | |
| 5 | 125 | 250 | 0 | 25 | |
| 1 | 25 | 50 | 0 | 25 |
References
- Froehlich, H. Long-range coherence and energy storage in biological systems. Int. J. Quantum Chem. 1968, 2, 641–649. [Google Scholar] [CrossRef]
- Zhuang, W.; Feng, Y.; Prohofsky, E.W. Self-consistent calculation of localized DNA vibrational properties at a double-helix-single-strand junction with anharmonic potential. Phys. Rev. A 1990, 41, 7033–7042. [Google Scholar] [CrossRef] [PubMed]
- Brucherseifer, M.; Nagel, M.; Bolívar, P.H.; Kurz, H.; Bosserhoff, A.; Büttner, R.M. Label-free probing of the binding state of DNA by time-domain terahertz sensing. Appl. Phys. Lett. 2000, 77, 4049–4051. [Google Scholar] [CrossRef] [Green Version]
- Markelz, A.G.; Roitberg, A.; Heilweil, E.J. Pulsed terahertz spectroscopy of DNA, bovine serum albumin and collagen between 0.1 and 2.0 THz. Chem. Phys. Lett. 2000, 320, 42–48. [Google Scholar] [CrossRef]
- Fischer, B.M.; Walther, M.; Jepsen, P.U. Far-infrared vibrational modes of DNA components studied by terahertz time-domain spectroscopy. Phys. Med. Biol. 2002, 47, 3807. [Google Scholar] [CrossRef]
- Mickan, S.P.; Menikh, A.; Liu, H.; Mannella, C.A.; MacColl, R.; Abbott, D.; Munch, J.; Zhang, X.C. Label-free bioaffinity detection using terahertz technology. Phys. Med. Biol. 2002, 47, 3789. [Google Scholar] [CrossRef] [Green Version]
- Debus, C.; Bolívar, P.H. Frequency selective surfaces for high sensitivity terahertz sensing. Appl. Phys. Lett. 2007, 91, 184102. [Google Scholar] [CrossRef]
- O’Hara, J.F.; Withayachumnankul, W.; Al-Naib, I. A review on thin-film sensing with terahertz waves. J. Infrared Millim. Terahertz Waves 2012, 33, 245–291. [Google Scholar] [CrossRef]
- Herne, T.M.; Tarlov, M.J. Characterization of DNA probes immobilized on gold surfaces. J. Am. Chem. Soc. 1997, 119, 8916–8920. [Google Scholar] [CrossRef]
- Weisenstein, C.; Schaar, D.; Katharina Wigger, A.; Schäfer-Eberwein, H.; Bosserhoff, A.K.; Haring Bolívar, P. Ultrasensitive THz biosensor for PCR-free cDNA detection based on frequency selective surfaces. Biomed. Opt. Express 2020, 11, 448–460. [Google Scholar] [CrossRef]
- Plusquellic, D.F.; Siegrist, K.; Heilweil, E.J.; Esenturk, O. Applications of Terahertz Spectroscopy in Biosystems. Chem. Phys. Chem. 2007, 8, 2412–2431. [Google Scholar] [CrossRef] [PubMed]
- Arora, A.; Luong, T.Q.; Krüger, M.; Kim, Y.J.; Nam, C.H.; Manz, A.; Havenith, M. Terahertz-time domain spectroscopy for the detection of PCR amplified DNA in aqueous solution. Analyst 2012, 137, 575–579. [Google Scholar] [CrossRef] [PubMed]
- Jeong, S.Y.; Cheon, H.; Lee, D.; Son, J.H. Determining terahertz resonant peaks of biomolecules in aqueous environment. Opt. Express 2020, 28, 3854–3863. [Google Scholar] [CrossRef] [PubMed]
- Globus, T.; Woolard, D.; Crowe, T.W.; Khromova, T.; Gelmont, B.; Hesler, J. Terahertz Fourier transform characterization of biological materials in a liquid phase. J. Phys. Appl. Phys. 2006, 39, 3405–3413. [Google Scholar] [CrossRef]
- Lvovska, M.I.; Seeman, N.C.; Sha, R.; Globus, T.R.; Khromova, T.B.; Dorofeeva, T.S. THz Characterization of DNA Four-Way Junction and Its Components. IEEE Trans. Nanotechnol. 2010, 9, 610–617. [Google Scholar] [CrossRef]
- Yang, K.; Yu, W.; Huang, G.; Zhou, J.; Yang, X.; Fu, W. Highly sensitive detection of Staphylococcus aureus by a THz metamaterial biosensor based on gold nanoparticles and rolling circle amplification. RSC Adv. 2020, 10, 26824–26833. [Google Scholar] [CrossRef]
- Lee, S.H.; Choe, J.H.; Kim, C.; Bae, S.; Kim, J.S.; Park, Q.H.; Seo, M. Graphene assisted terahertz metamaterials for sensitive bio-sensing. Sens. Actuators Chem. 2020, 310, 127841. [Google Scholar] [CrossRef]
- Tang, M.; Zhang, M.; Yan, S.; Xia, L.; Yang, Z.; Du, C.; Cui, H.L.; Wei, D. Detection of DNA oligonucleotides with base mutations by terahertz spectroscopy and microstructures. PLoS ONE 2018, 13, e0191515. [Google Scholar] [CrossRef] [Green Version]
- Tang, M.; Zhang, M.; Xia, L.; Yang, Z.; Yan, S.; Wang, H.; Wei, D.; Du, C.; Cui, H.L. Detection of single-base mutation of DNA oligonucleotides with different lengths by terahertz attenuated total reflection microfluidic cell. Biomed. Opt. Express 2020, 11, 5362. [Google Scholar] [CrossRef]
- Shih, K.; Pitchappa, P.; Jin, L.; Chen, C.H.; Singh, R.; Lee, C. Nanofluidic terahertz metasensor for sensing in aqueous environment. Appl. Phys. Lett. 2018, 113, 071105. [Google Scholar] [CrossRef] [Green Version]
- Naftaly, M.; Miles, R.E. Terahertz time-domain spectroscopy for material characterization. Proc. IEEE 2007, 95, 1658–1665. [Google Scholar] [CrossRef]
- Singh, R.; Al-Naib, I.A.I.; Koch, M.; Zhang, W. Sharp Fano resonances in THz metamaterials. Opt. Express 2011, 19, 6312–6319. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fedotov, V.A.; Rose, M.; Prosvirnin, S.L.; Papasimakis, N.; Zheludev, N.I. Sharp Trapped-Mode Resonances in Planar Metamaterials with a Broken Structural Symmetry. Phys. Rev. Lett. 2007, 99, 147401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Papasimakis, N.; Fedotov, V.A.; Zheludev, N.I.; Prosvirnin, S.L. Metamaterial analog of electromagnetically induced transparency. Phys. Rev. Lett. 2008, 101, 253903. [Google Scholar] [CrossRef] [Green Version]
- Lahiri, B.; McMeekin, S.G.; de La Rue, R.M.; Johnson, N.P. Resonance hybridization in nanoantenna arrays based on asymmetric split-ring resonators. Appl. Phys. Lett. 2011, 98, 153116. [Google Scholar] [CrossRef]
- Falcone, F.; Lopetegi, T.; Laso, M.A.; Baena, J.D.; Bonache, J.; Beruete, M.; Marqués, R.; Martín, F.; Sorolla, M. Babinet principle applied to the design of metasurfaces and metamaterials. Phys. Rev. Lett. 2004, 93, 197401. [Google Scholar] [CrossRef] [Green Version]
- Booker, H.G. Slot aerials and their relation to complementary wire aerials (Babinet’s principle). J. Inst. Electr. Eng.-Part Iiia Radiolocation 1946, 93, 620–626. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Grischkowsky, D.; Keiding, S.; van Exter, M.; Fattinger, C. Far-infrared time-domain spectroscopy with terahertz beams of dielectrics and semiconductors. JOSA B 1990, 7, 2006–2015. [Google Scholar] [CrossRef]
- Debus, C. A high-Sensitivity THz-Sensing Technology for DNA Detection with Split-Ring Resonator Based Biochips. Ph.D. Thesis, Universität Siegen, Siegen, Germany, 2013. [Google Scholar]
- Deninger, A.J.; Roggenbuck, A.; Schindler, S.; Preu, S. 2.75 THz tuning with a triple-DFB laser system at 1550 nm and InGaAs photomixers. J. Infrared Millim. Terahertz Waves 2015, 36, 269–277. [Google Scholar] [CrossRef] [Green Version]
- Guo, S.J.; Ruan, C.J.; Kong, D.Y.; Dai, J.; Zhang, Y.; He, W.L. Research on terahertz transmission characteristics of nonpolar liquid based on frequency-domain spectroscopy. JOSA B 2020, 37, 1942. [Google Scholar] [CrossRef]
- Inutsuka, M.; Horinouchi, A.; Tanaka, K. Aggregation States of Polymers at Hydrophobic and Hydrophilic Solid Interfaces. ACS Macro Lett. 2015, 4, 1174–1178. [Google Scholar] [CrossRef] [PubMed]
- Serita, K.; Murakami, H.; Kawayama, I.; Tonouchi, M. A Terahertz-Microfluidic Chip with a Few Arrays of Asymmetric Meta-Atoms for the Ultra-Trace Sensing of Solutions. Photonics 2019, 6, 12. [Google Scholar] [CrossRef] [Green Version]
- Akoglu, H. User’s guide to correlation coefficients. Turk. J. Emerg. Med. 2018, 18, 91–93. [Google Scholar] [CrossRef]
- Arcella, A.; Portella, G.; Collepardo-Guevara, R.; Chakraborty, D.; Wales, D.J.; Orozco, M. Structure and properties of DNA in apolar solvents. J. Phys. Chem. 2014, 118, 8540–8548. [Google Scholar] [CrossRef]
- Domínguez, C.M.; Ramos, D.; Mendieta-Moreno, J.I.; Fierro, J.L.G.; Mendieta, J.; Tamayo, J.; Calleja, M. Effect of water-DNA interactions on elastic properties of DNA self-assembled monolayers. Sci. Rep. 2017, 7, 536. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, N.H.; Chen, J.Z. Mechanical properties of double-stranded DNA biolayers immobilized on microcantilever under axial compression. J. Biomech. 2009, 42, 1483–1487. [Google Scholar] [CrossRef]
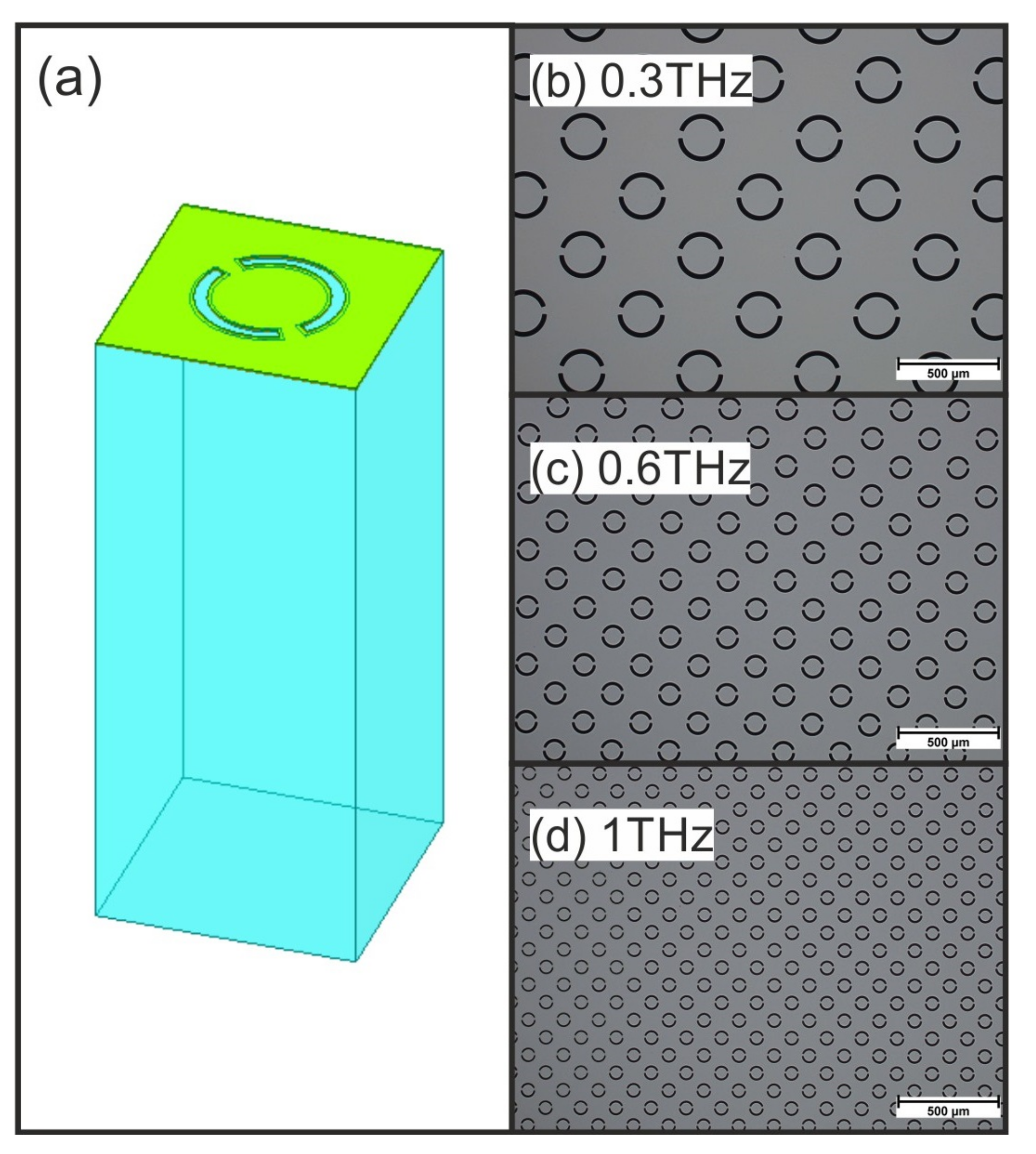

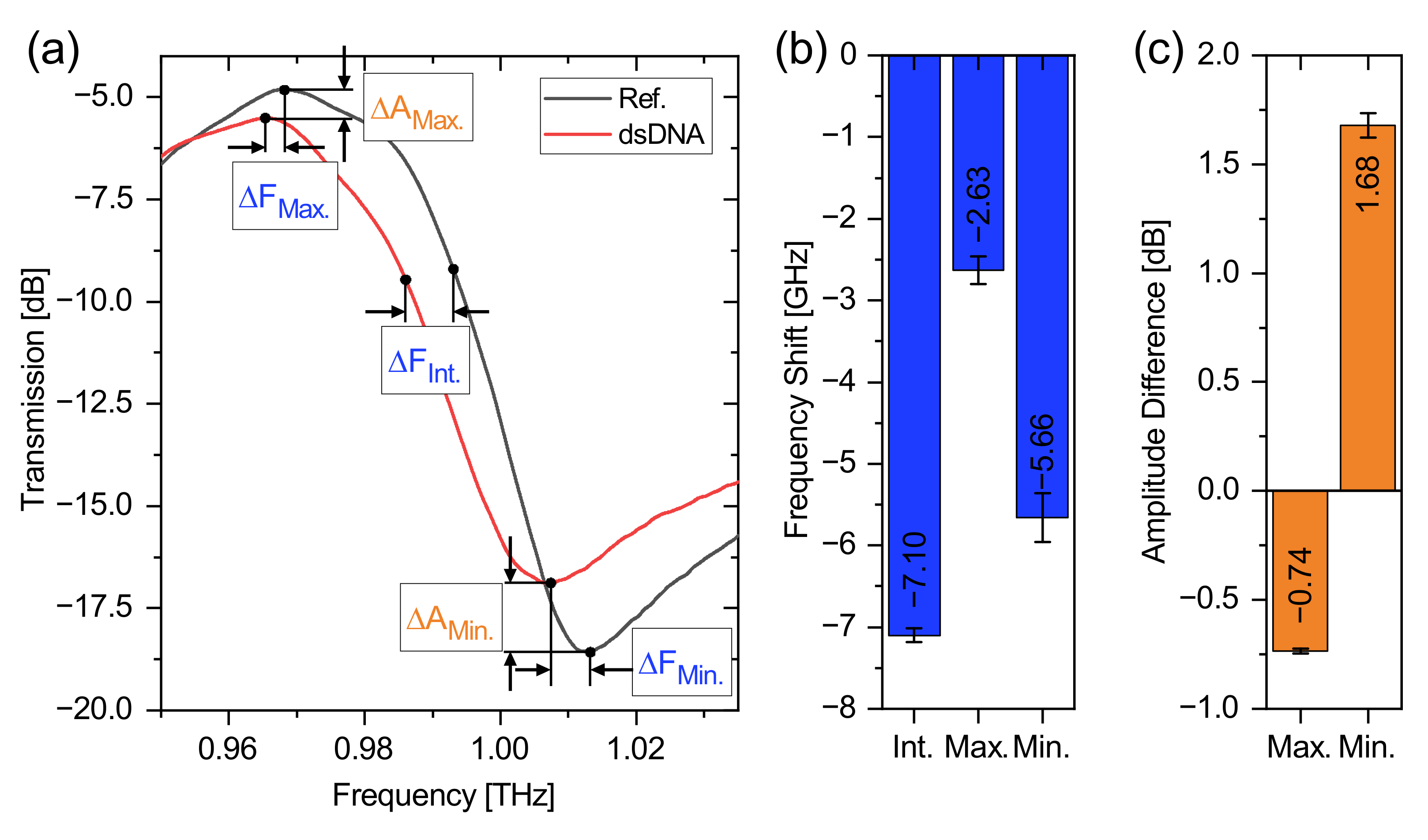
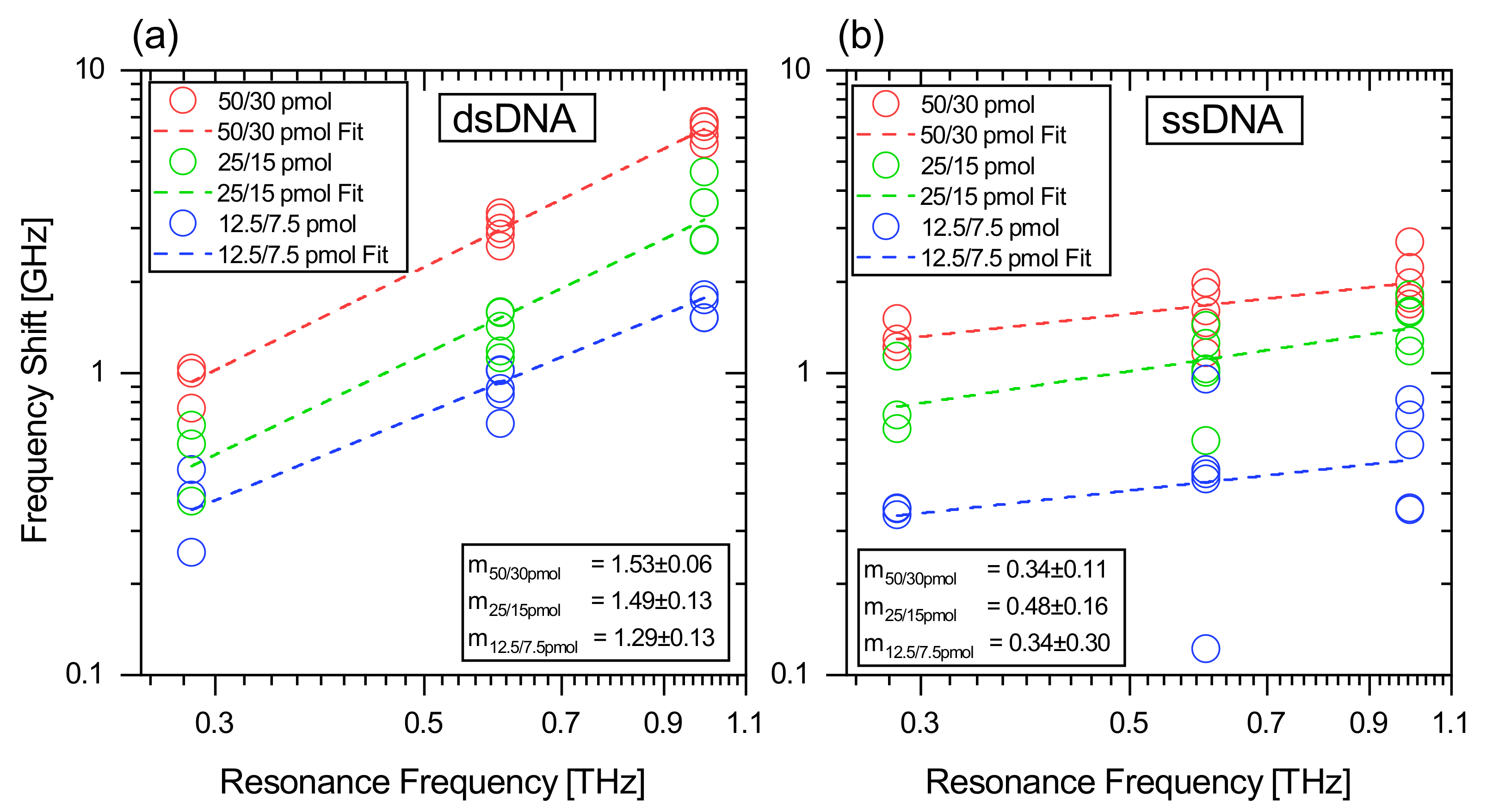
| Frequency | 0.3 THz | 0.6 THz | 1 THz |
| Cell size p | 416 m | 202 m | 124 m |
| Ring radius r | 96 m | 46 m | 29 m |
| Slot width w | 20 m | 10 m | 6 m |
| Offset angle | 42° | 42° | 42° |
| Gap angle | 22° | 22° | 22° |
| Array size A | 61 | 145 | 421 |
| Simulation | Measurement | |||
|---|---|---|---|---|
| Freq. / THz | Ref. / dB/GHz | DNA / dB/GHz | Ref. / dB/GHz | dsDNA / dB/GHz |
| 0.3 | −3.18 | −2.69 | −0.90 | −0.87 |
| 0.6 | −1.57 | −1.00 | −0.86 | −0.78 |
| 1 | −1.15 | −0.52 | −0.61 | −0.48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weisenstein, C.; Richter, M.; Wigger, A.K.; Bosserhoff, A.K.; Haring Bolívar, P. Multifrequency Investigation of Single- and Double-Stranded DNA with Scalable Metamaterial-Based THz Biosensors. Biosensors 2022, 12, 483. https://doi.org/10.3390/bios12070483
Weisenstein C, Richter M, Wigger AK, Bosserhoff AK, Haring Bolívar P. Multifrequency Investigation of Single- and Double-Stranded DNA with Scalable Metamaterial-Based THz Biosensors. Biosensors. 2022; 12(7):483. https://doi.org/10.3390/bios12070483
Chicago/Turabian StyleWeisenstein, Christian, Merle Richter, Anna Katharina Wigger, Anja K. Bosserhoff, and Peter Haring Bolívar. 2022. "Multifrequency Investigation of Single- and Double-Stranded DNA with Scalable Metamaterial-Based THz Biosensors" Biosensors 12, no. 7: 483. https://doi.org/10.3390/bios12070483
APA StyleWeisenstein, C., Richter, M., Wigger, A. K., Bosserhoff, A. K., & Haring Bolívar, P. (2022). Multifrequency Investigation of Single- and Double-Stranded DNA with Scalable Metamaterial-Based THz Biosensors. Biosensors, 12(7), 483. https://doi.org/10.3390/bios12070483





