A Fiber-Optic Sensor-Embedded and Machine Learning Assisted Smart Helmet for Multi-Variable Blunt Force Impact Sensing in Real Time
Abstract
1. Introduction
2. Experimental
2.1. The Working Principle and Fabrication of Fiberoptic FBG Sensors
2.2. Fabrication of the FBG-Embedded Smart Football Helmet
2.3. Signal Interrogation Using Wired and Wireless Methods
2.4. Establishment of a Pendulum Impact System
2.5. Training and Performing of ML Models Using the Collected FBG Datasets
3. Results and Discussion
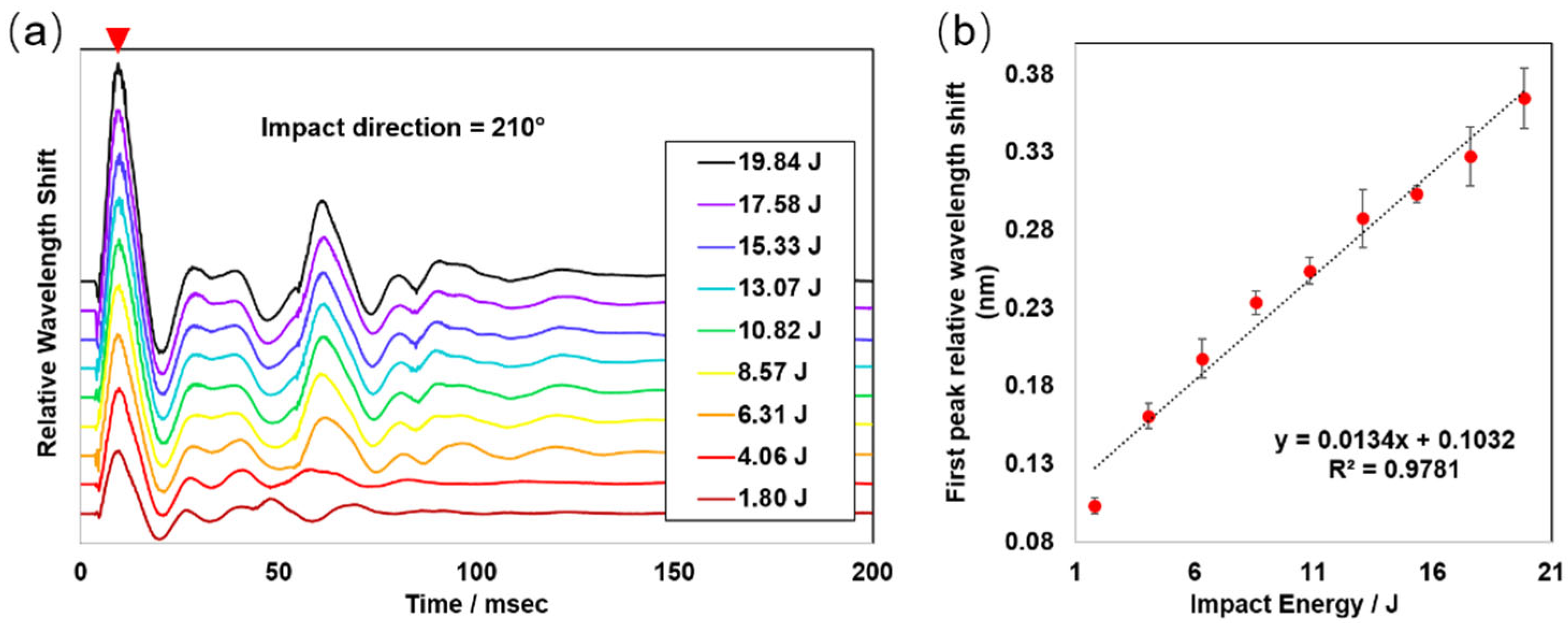
3.1. Linear Correlation of the Kinetic Energy of the Blunt Force Impact with FBG Signal Wavelength Shift
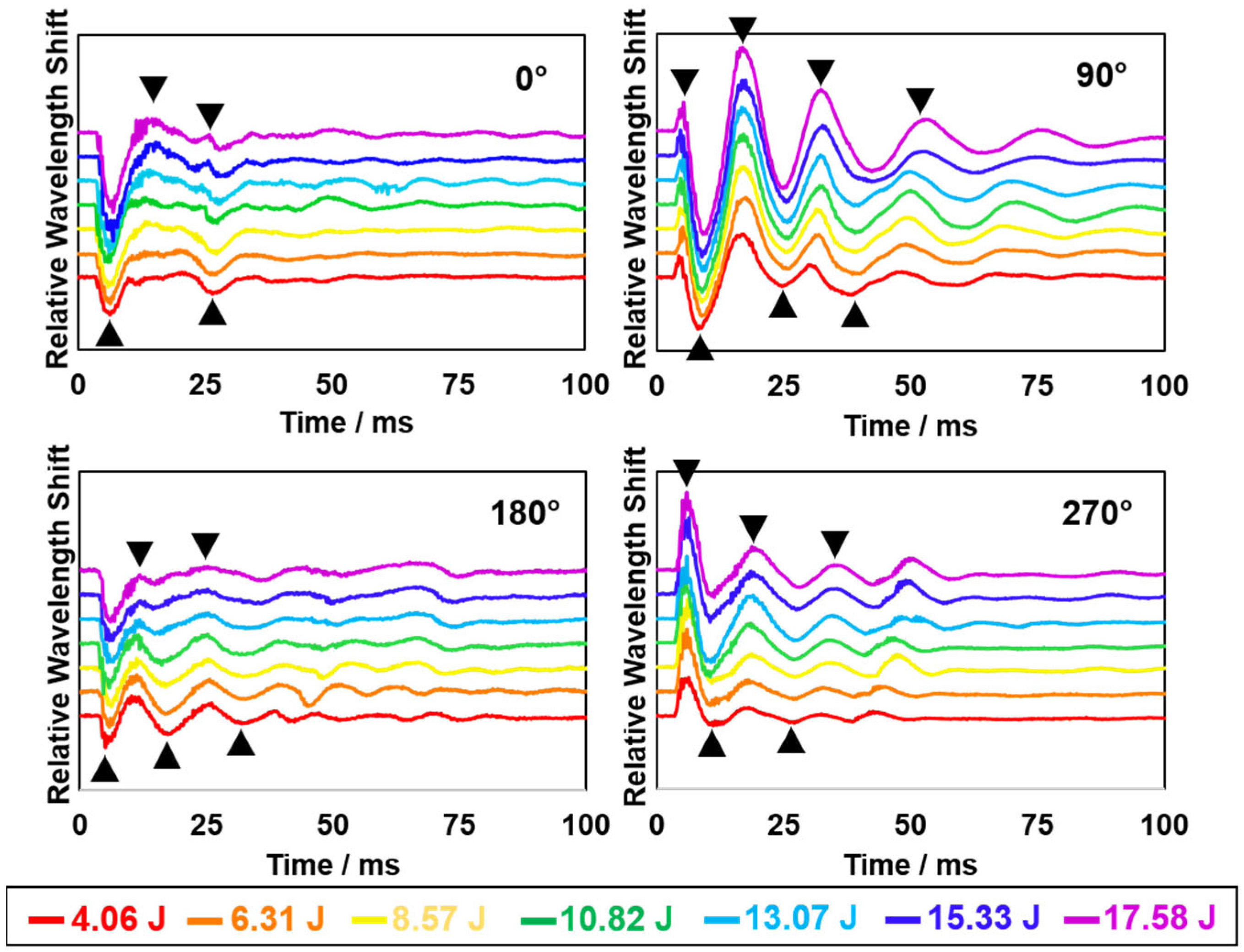
3.2. Recognition of Typical “Fingerprint” Features in Raw Transient Oscillatory FBG Signals
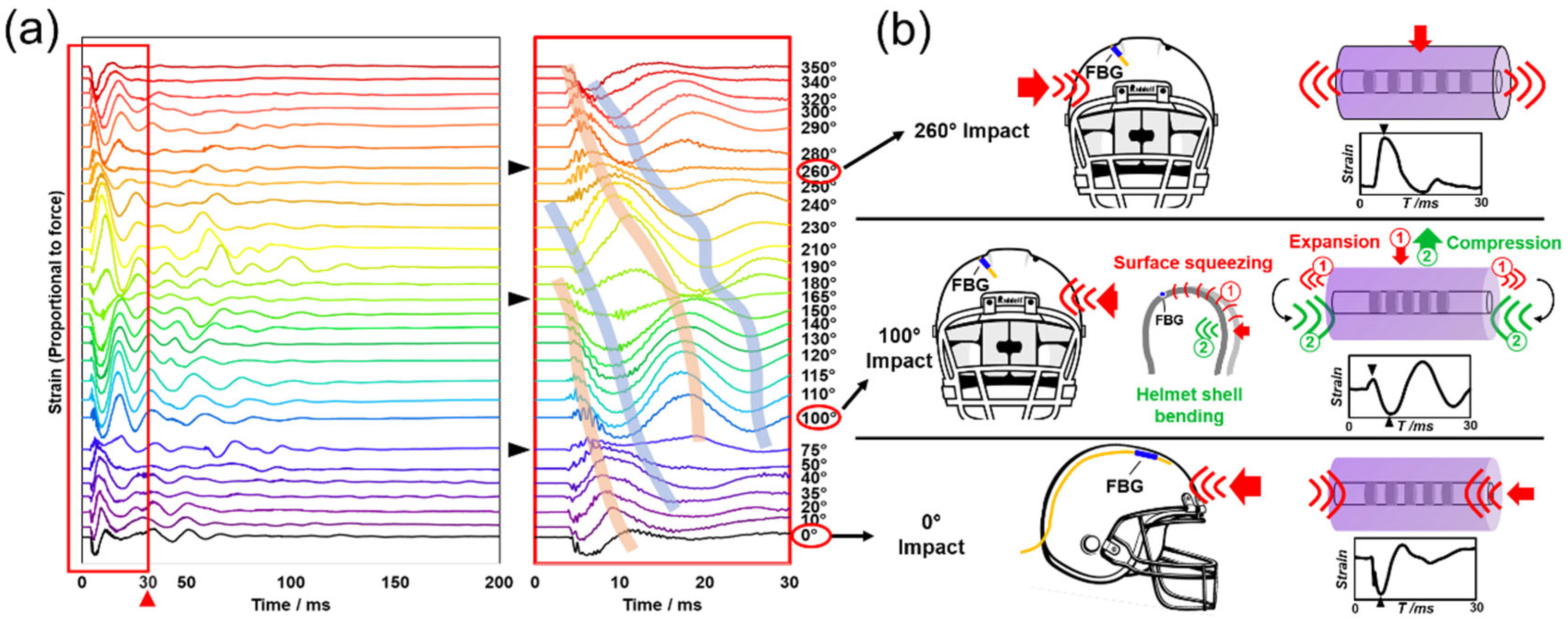
3.3. Physical Interpretation Based on the Comprehensive Impact Signals
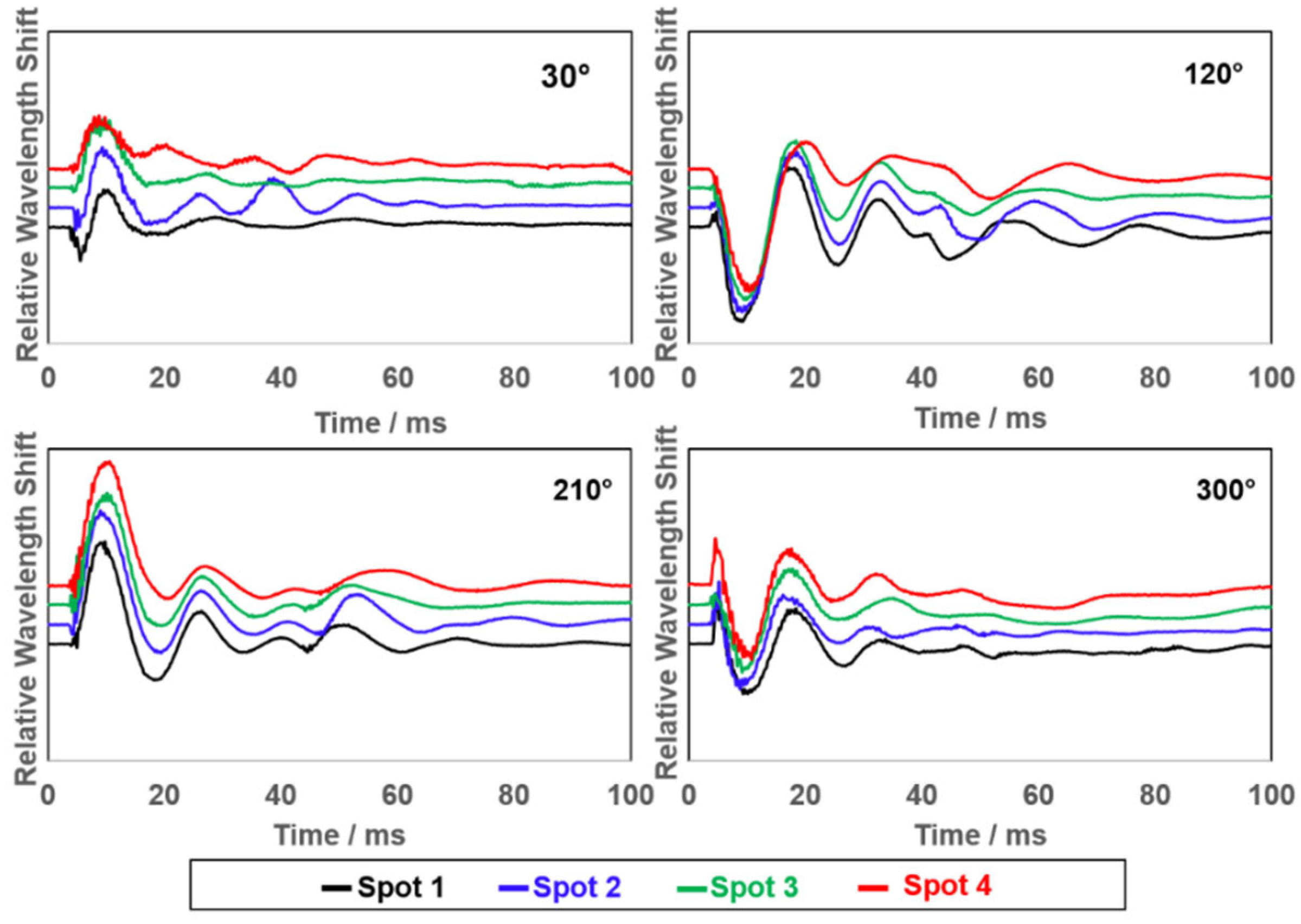
3.4. Realization of True Three-Dimensional Impact Sensing
3.5. Training and Performance of Selected ML Models Using the Collected FBG Datasets
3.6. Increase the Prediction Performance by Using Boosted ML Models and Modified Training Dataset
3.7. Preliminary Evaluation of the Wireless Mode Smart Helmet Sensing
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ghajar, J. Traumatic brain injury. Lancet 2000, 356, 923–929. [Google Scholar] [CrossRef]
- Okie, S. Traumatic brain injury in the war zone. N. Engl. J. Med. 2005, 352, 2043–2047. [Google Scholar] [CrossRef]
- Newgard, C.D.; Meier, E.N.; Bulger, E.M.; Buick, J.; Sheehan, K.; Lin, S.; Minei, J.P.; Barnes-Mackey, R.A.; Brasel, K.; Investigators, R. Revisiting the “golden hour”: An evaluation of out-of-hospital time in shock and traumatic brain injury. Ann. Emerg. Med. 2015, 66, 30–41.e3. [Google Scholar] [CrossRef] [PubMed]
- Dinh, M.M.; Bein, K.; Roncal, S.; Byrne, C.M.; Petchell, J.; Brennan, J. Redefining the golden hour for severe head injury in an urban setting: The effect of prehospital arrival times on patient outcomes. Injury 2013, 44, 606–610. [Google Scholar] [CrossRef] [PubMed]
- Anvari, K. Helmet with Patch Antennas to Detect, Prevent, and Minimize Head Concussion. U.S. Patent 9,007,217, 14 April 2015. [Google Scholar]
- Rowson, S.; Duma, S.M. Brain injury prediction: Assessing the combined probability of concussion using linear and rotational head acceleration. Ann. Biomed. Eng. 2013, 41, 873–882. [Google Scholar] [CrossRef] [PubMed]
- Kimpara, H.; Iwamoto, M. Mild Traumatic Brain Injury Predictors Based on Angular Accelerations During Impacts. Ann. Biomed. Eng. 2012, 40, 114–126. [Google Scholar] [CrossRef] [PubMed]
- Oeur, R.A.; Karton, C.; Hoshizaki, T.B. Impact frequency validation of head impact sensor technology for use in sport. In Proceedings of the ISBS-Conference Proceedings Archive, Tsukuba, Japan, 18–22 July 2016. [Google Scholar]
- Thomas, B.; Bauer, T. Portable Wireless Personal Head Impact Reporting System. U.S. Patent 8,860,570, 14 October 2014. [Google Scholar]
- Bao, X.; Chen, L. Recent progress in distributed fiber optic sensors. Sensors 2012, 12, 8601–8639. [Google Scholar] [CrossRef] [PubMed]
- Rao, Y.-J. Recent progress in fiber-optic extrinsic Fabry–Perot interferometric sensors. Opt. Fiber Technol. 2006, 12, 227–237. [Google Scholar] [CrossRef]
- Guan, B.-O.; Tam, H.-Y.; Tao, X.-M.; Dong, X.-Y. Simultaneous strain and temperature measurement using a superstructure fiber Bragg grating. IEEE Photonic. Technol. L 2000, 12, 675–677. [Google Scholar] [CrossRef]
- Ho, Y.-T.; Huang, A.-B.; Lee, J.-T. Development of a fibre Bragg grating sensored ground movement monitoring system. Meas. Sci. Technol. 2006, 17, 1733. [Google Scholar] [CrossRef]
- Chang, J.; Wang, Q.; Zhang, X.; Ma, L.; Wang, H.; Zhang, S.; Wang, Q.; Ni, J.; Wu, Y. Fiber-optic vibration sensor system. Laser Phys. 2008, 18, 911–913. [Google Scholar] [CrossRef]
- Tsuda, H. Fiber Bragg grating vibration-sensing system, insensitive to Bragg wavelength and employing fiber ring laser. Opt. Lett. 2010, 35, 2349–2351. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.-R.; Tsuda, H.; Toyama, N. Impact wave and damage detections using a strain-free fiber Bragg grating ultrasonic receiver. Ndt E Int. 2007, 40, 85–93. [Google Scholar] [CrossRef]
- Kirikera, G.R.; Balogun, O.; Krishnaswamy, S. Adaptive fiber Bragg grating sensor network for structural health monitoring: Applications to impact monitoring. Struct. Health Monit. 2011, 10, 5–16. [Google Scholar] [CrossRef]
- Butz, R.C.; Dennison, C.R. In-fiber Bragg grating impact force transducer for studying head–helmet mechanical interaction in head impact. J. Light. Technol. 2015, 33, 2831–2838. [Google Scholar] [CrossRef]
- Du, Y.; Chen, Y.; Zhuang, Y.; Zhu, C.; Tang, F.; Huang, J. Probing nanostrain via a mechanically designed optical fiber interferometer. IEEE Photonics Technol. Lett. 2017, 29, 1348–1351. [Google Scholar] [CrossRef]
- Zhu, C.; Zhuang, Y.; Zhang, B.; Muhammad, R.; Wang, P.P.; Huang, J. A miniaturized optical fiber tip high-temperature sensor based on concave-shaped Fabry–Perot cavity. IEEE Photonics Technol. Lett. 2018, 31, 35–38. [Google Scholar] [CrossRef]
- Li, L.; Xia, L.; Xie, Z.; Liu, D. All-fiber Mach-Zehnder interferometers for sensing applications. Opt. Express 2012, 20, 11109–11120. [Google Scholar] [CrossRef]
- Shin, W.; Lee, Y.L.; Yu, B.-A.; Noh, Y.-C.; Ahn, T.J. Highly sensitive strain and bending sensor based on in-line fiber Mach–Zehnder interferometer in solid core large mode area photonic crystal fiber. Opt. Commun. 2010, 283, 2097–2101. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, S.; Luo, J.; Chen, Y.; Fu, C.; Xiong, C.; Wang, Y.; Jing, S.; Bai, Z.; Liao, C. Torsion, refractive index, and temperature sensors based on an improved helical long period fiber grating. J. Light. Technol. 2020, 38, 2504–2510. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Zou, F.; Jiang, C.; Mou, C.; Wang, T. Humidity sensor based on a long-period fiber grating coated with polymer composite film. Sensors 2019, 19, 2263. [Google Scholar] [CrossRef] [PubMed]
- Liehr, S.; Jäger, L.A.; Karapanagiotis, C.; Münzenberger, S.; Kowarik, S. Real-time dynamic strain sensing in optical fibers using artificial neural networks. Opt. Express 2019, 27, 7405–7425. [Google Scholar] [CrossRef] [PubMed]
- Thompson, A.J.; Power, M.; Yang, G.-Z. Micro-scale fiber-optic force sensor fabricated using direct laser writing and calibrated using machine learning. Opt. Express 2018, 26, 14186–14200. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Wang, L.; Guo, N.; Shu, C.; Lu, C. Brillouin optical time-domain analyzer assisted by support vector machine for ultrafast temperature extraction. J. Light. Technol. 2017, 35, 4159–4167. [Google Scholar] [CrossRef]
- Makarenko, A.V. Deep learning algorithms for signal recognition in long perimeter monitoring distributed fiber optic sensors. In Proceedings of the 2016 IEEE 26th International Workshop on Machine Learning for Signal Processing (MLSP), Vietri sul Mare, Italy, 13–16 September 2016; pp. 1–6. [Google Scholar]
- Campanella, C.E.; Cuccovillo, A.; Campanella, C.; Yurt, A.; Passaro, V. Fibre Bragg grating based strain sensors: Review of technology and applications. Sensors 2018, 18, 3115. [Google Scholar] [CrossRef]
- Drissi-Habti, M.; Raman, V.; Khadour, A.; Timorian, S. Fiber optic sensor embedment study for multi-parameter strain sensing. Sensors 2017, 17, 667. [Google Scholar] [CrossRef]
- Raman, V.; Drissi-Habti, M.; Limje, P.; Khadour, A. Finer SHM-coverage of inter-plies and bondings in smart composite by dual sinusoidal placed distributed optical fiber sensors. Sensors 2019, 19, 742. [Google Scholar] [CrossRef]
- White, I.M.; Oveys, H.; Fan, X. Liquid-core optical ring-resonator sensors. Opt. Lett. 2006, 31, 1319–1321. [Google Scholar] [CrossRef]
- Madani, A.; Harazim, S.M.; Quiñones, V.A.B.; Kleinert, M.; Finn, A.; Naz, E.S.G.; Ma, L.; Schmidt, O.G. Optical microtube cavities monolithically integrated on photonic chips for optofluidic sensing. Opt. Lett. 2017, 42, 486–489. [Google Scholar] [CrossRef]
- Miao, S.; Chen, D.; Madani, A.; Jorgensen, M.R.; Bolaños Quiñones, V.A.; Ma, L.; Hickey, S.G.; Eychmüller, A.; Schmidt, O.G. Optofluidic sensor: Evaporation kinetics detection of solvents dissolved with Cd3P2 colloidal quantum dots in a Rolled-Up microtube. Adv. Opt. Mater. 2015, 3, 187–193. [Google Scholar] [CrossRef]

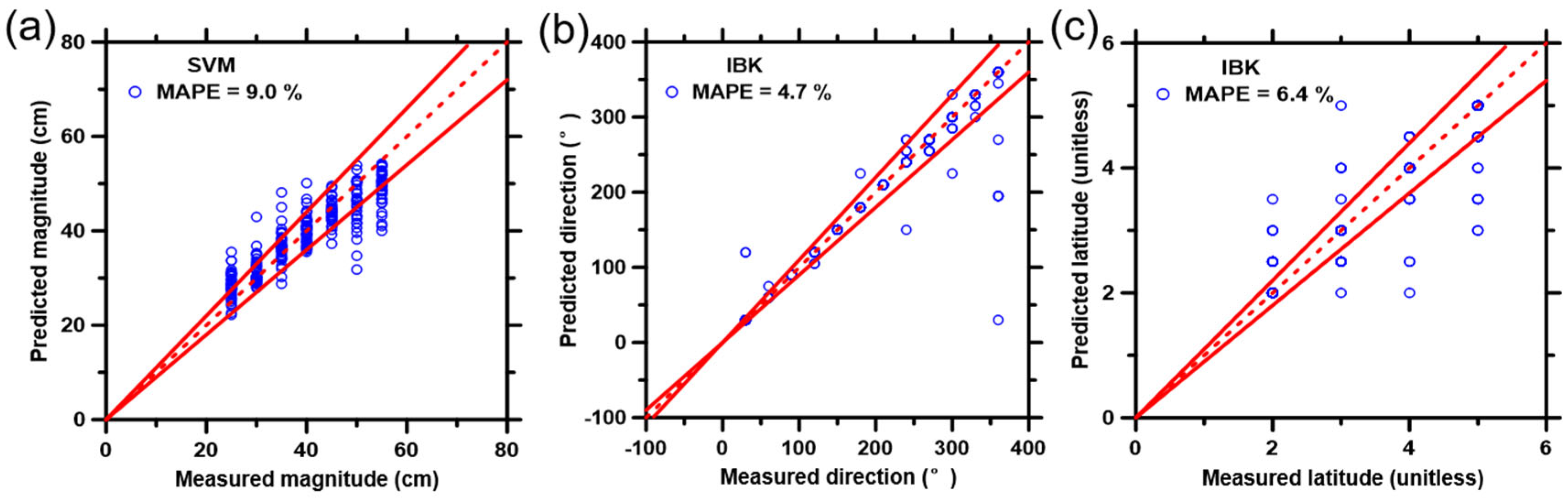
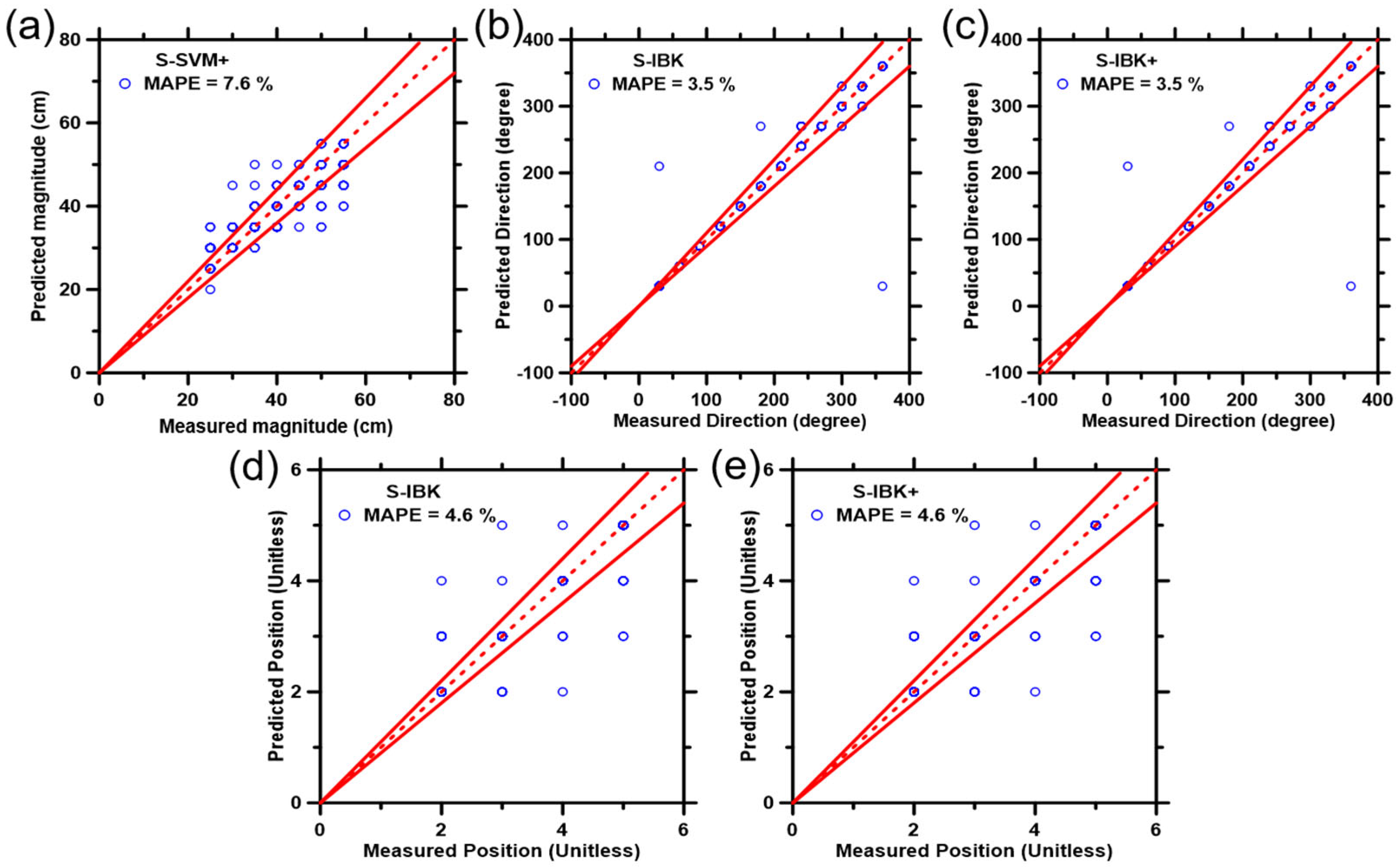

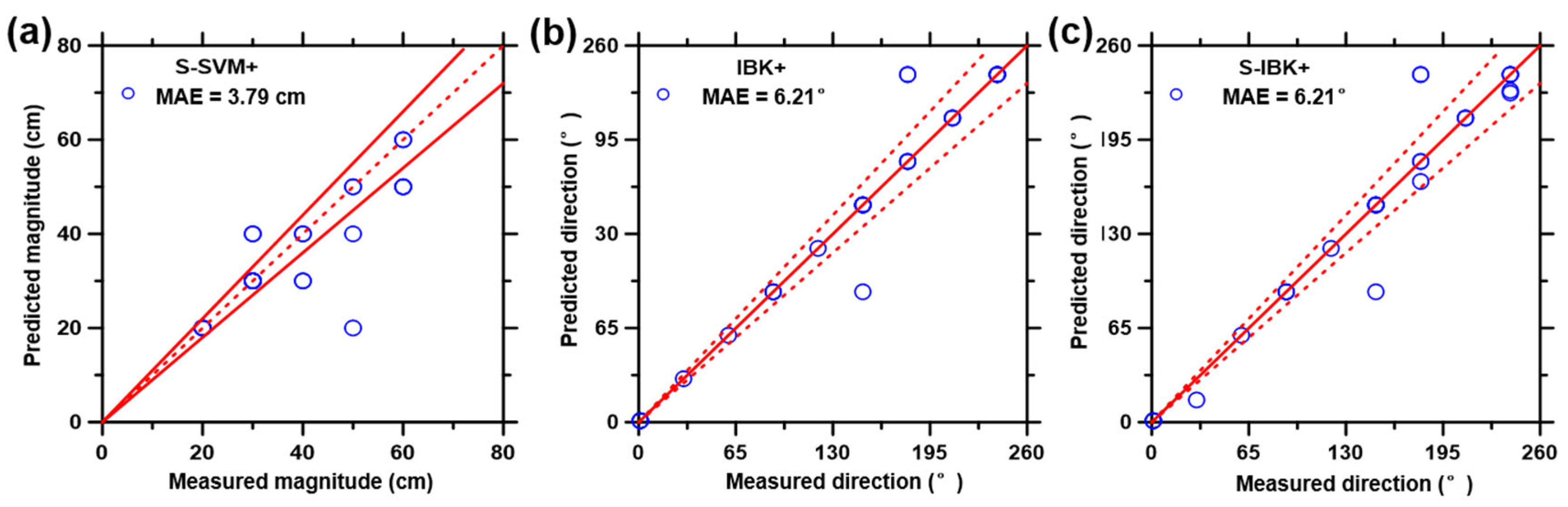
| ML Model | R | R2 | MAE | MAPE | RMSE | CPI |
|---|---|---|---|---|---|---|
| Unitless | Unitless | cm | % | cm | Unitless | |
| SVM-Magnitude | 0.891 | 0.793 | 3.492 | 8.991 | 4.73 | 0 |
| IBK-Direction | 0.952 | 0.905 | 7.492 | 4.67 | 32.586 | 0.108 |
| IBK-Latitude | 0.915 | 0.837 | 0.204 | 6.373 | 0.454 | 0.061 |
| ML Model | R | R2 | MAE | MAPE | RMSE | CPI |
|---|---|---|---|---|---|---|
| Unitless | Unitless | cm | % | cm | Unitless | |
| S-SVM+-Magnitude | 0.889 | 0.790 | 2.980 | 7.635 | 4.680 | 0.042 |
| S-IBK-Direction | 0.971 | 0.942 | 3.960 | 3.536 | 25.385 | 0.000 |
| S-IBK+-Direction | 0.971 | 0.942 | 3.960 | 3.536 | 25.385 | 0.000 |
| S-IBK-Latitude | 0.927 | 0.859 | 0.140 | 4.600 | 0.424 | 0.270 |
| S-IBK+-Latitude | 0.927 | 0.859 | 0.140 | 4.600 | 0.424 | 0.270 |
| ML Model | R | R2 | MAE | MAPE | RMSE | CPI |
|---|---|---|---|---|---|---|
| Unitless | Unitless | cm | % | cm | Unitless | |
| S-SVM+-Magnitude | 0.852 | 0.726 | 3.793 | 8.506 | 7.656 | 0.071 |
| IBK+-Direction | 0.973 | 0.946 | 6.207 | 3.678 | 19.298 | 0.340 |
| S-IBK+-Direction | 0.973 | 0.946 | 6.207 | 3.678 | 19.298 | 0.340 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, Y.; Han, T.; Yang, Q.; O’Malley, R.; Kumar, A.; Gerald, R.E., II; Huang, J. A Fiber-Optic Sensor-Embedded and Machine Learning Assisted Smart Helmet for Multi-Variable Blunt Force Impact Sensing in Real Time. Biosensors 2022, 12, 1159. https://doi.org/10.3390/bios12121159
Zhuang Y, Han T, Yang Q, O’Malley R, Kumar A, Gerald RE II, Huang J. A Fiber-Optic Sensor-Embedded and Machine Learning Assisted Smart Helmet for Multi-Variable Blunt Force Impact Sensing in Real Time. Biosensors. 2022; 12(12):1159. https://doi.org/10.3390/bios12121159
Chicago/Turabian StyleZhuang, Yiyang, Taihao Han, Qingbo Yang, Ryan O’Malley, Aditya Kumar, Rex E. Gerald, II, and Jie Huang. 2022. "A Fiber-Optic Sensor-Embedded and Machine Learning Assisted Smart Helmet for Multi-Variable Blunt Force Impact Sensing in Real Time" Biosensors 12, no. 12: 1159. https://doi.org/10.3390/bios12121159
APA StyleZhuang, Y., Han, T., Yang, Q., O’Malley, R., Kumar, A., Gerald, R. E., II, & Huang, J. (2022). A Fiber-Optic Sensor-Embedded and Machine Learning Assisted Smart Helmet for Multi-Variable Blunt Force Impact Sensing in Real Time. Biosensors, 12(12), 1159. https://doi.org/10.3390/bios12121159




_Yang.png)


