On the Classification of ECG and EEG Signals with Various Degrees of Dimensionality Reduction
Abstract
1. Introduction
- (a)
- Techniques that preserve the local arrangement: locally linear embedding (LLE), Laplacian eigenmaps (LE), manifold charting (MC), Hessian locally linear embedding (HLLE), and
- (b)
- Techniques that conserve global structure: isometric mapping (ISOMAP), diffusion map.
- a nearest-neighbor search,
- defining of distances or affinities between elements,
- resolving a generalized eigenproblem to obtain the embedding of the initial space into a lower dimensional one.
2. Materials and Methods
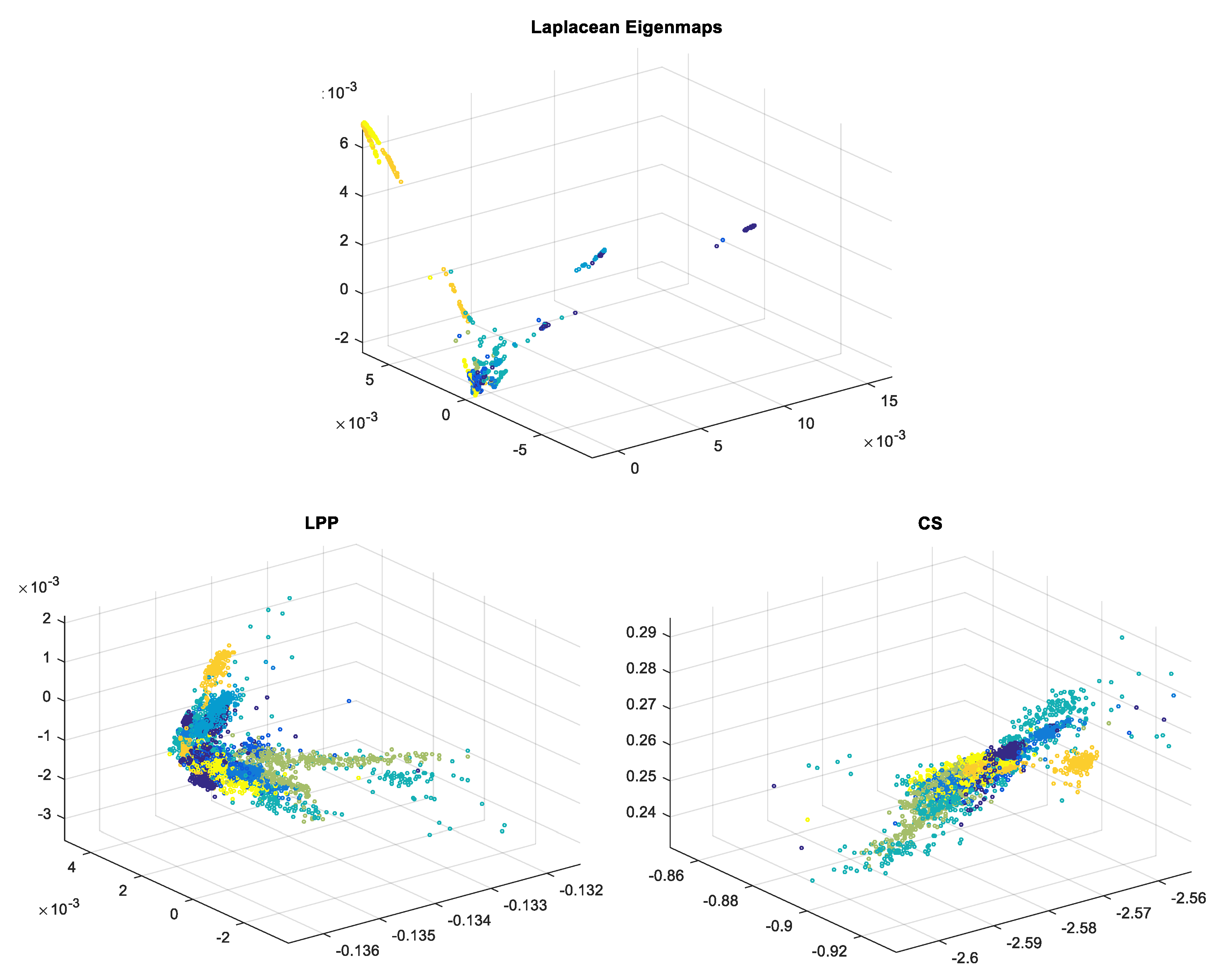
2.1. Laplacian Eigenmaps—LE
- (i.)
- Nearest-neighbor search and adjacency graph construction
- (ii.)
- Weighted adjacency matrix (Choosing the weights)
- (iii.)
- Eigenmaps
2.2. Locality Preserving Projections—LPP
2.3. Compressed Sensing—CS
2.4. Classifier Types
2.4.1. Decision Trees
2.4.2. Discriminant Analysis
2.4.3. Naive Bayes
2.4.4. Support Vector Machine—SVM
2.4.5. Nearest Neighbor
2.4.6. Ensembles of Classifiers
3. Experimental Results and Discussions
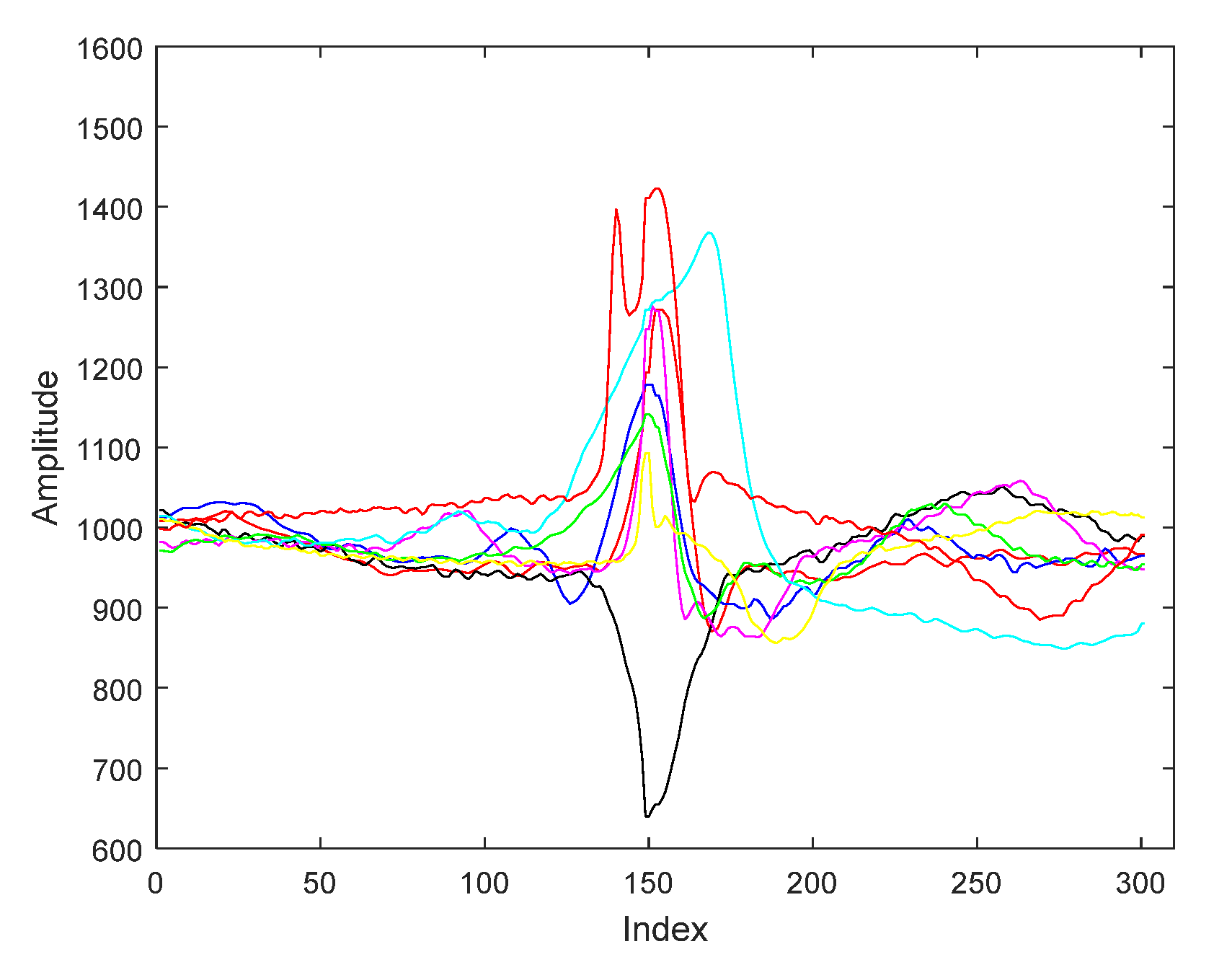
3.1. ECG Signals
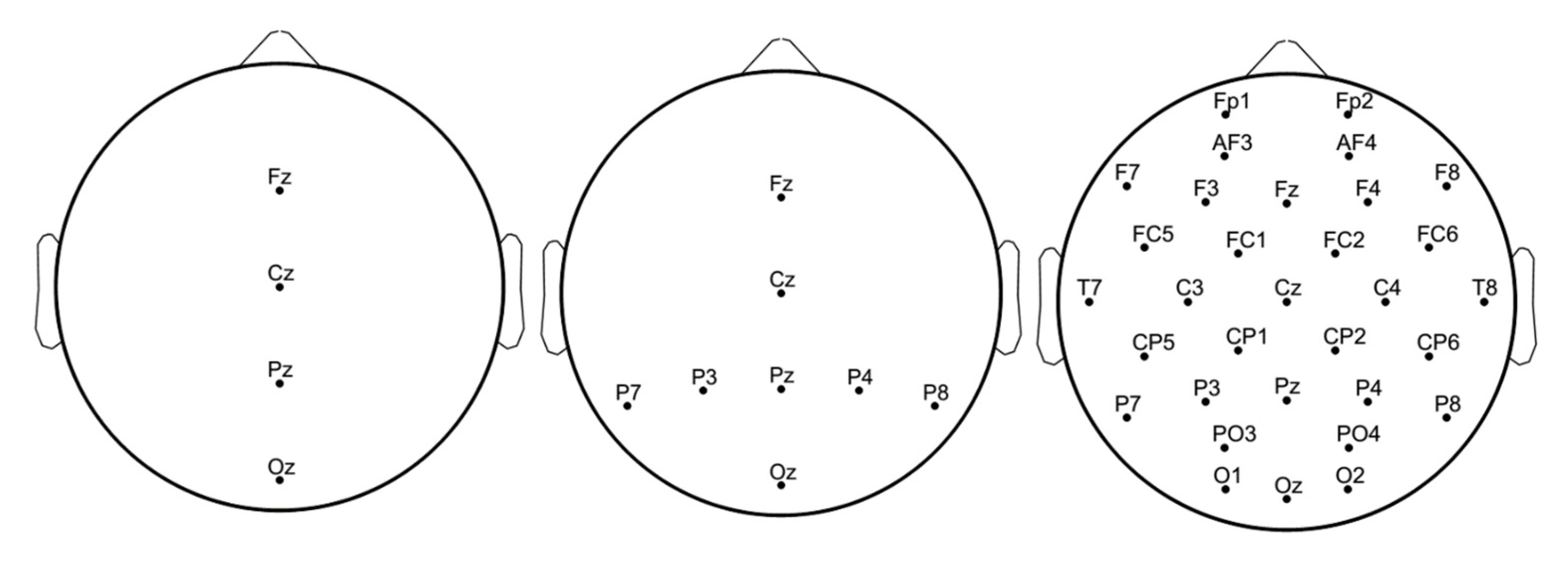
3.2. EEG Signals
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mordohai, P.; Medioni, G. Dimensionality Estimation, Manifold Learning and Function Approximation using Tensor Voting. J. Mach. Learn. Res. 2010, 11, 411–450. [Google Scholar]
- Boehmke, B.; Greenwell, B.M. Dimension Reduction. In Hands-On Machine Learning with R; Chapman & Hall, CRC Press: Boca Raton, FL, USA, 2019; pp. 343–396. [Google Scholar]
- Bingham, E.; Mannila, H. Random projection in dimensionality reduction: Applications to image and text data. In Proceedings of the 7-th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 26–29 August 2001; pp. 245–250. [Google Scholar]
- Lee, J.A.; Verleysen, M. Nonlinear Dimensionality Reduction; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Bengio, Y.; Paiement, J.; Vincent, P.; Delalleau, O.; Le Roux, N.; Ouimet, M. Out-of-sample extensions for LLE, Isomap, MDS, eigenmaps, and spectral clustering. Adv. Neural Inf. Process. Syst. 2004, 16, 177–186. [Google Scholar]
- Fodor, I. A Survey of Dimension Reduction Techniques; Technical Report; Center for Applied Scientific Computing, Lawrence Livermore National: Livermore, CA, USA, 2002.
- Belkin, M.; Niyogi, P. Laplacian Eigenmaps and Spectral Techniques for Embedding and Clustering. Adv. Neural Inf. Process. Syst. 2001, 14, 586–691. [Google Scholar]
- Belkin, M. Problems of Learning on Manifolds. Ph.D. Thesis, Department of Mathematics, The University of Chicago, Chicago, IL, USA, August 2003. [Google Scholar]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef]
- He, X.; Niyogi, P. Locality preserving projections. In Proceedings of the Conference on Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–13 December 2003. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candès, E.J.; Wakin, M.B. An Introduction to Compressive Sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Duda, R.; Hart, P. Pattern Recognition and Scene Analysis; Wiley Interscience: Hoboken, NJ, USA, 1973. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Alpaydin, E. Introduction to Machine Learning, 4th ed.; MIT Press: Cambridge, MA, USA, 2020. [Google Scholar]
- MIT-BIH. Arrhythmia Database. Available online: http://www.physionet.org/physiobank/database/mitdb/ (accessed on 8 January 2021).
- Fira, M.; Goraș, L.; Cleju, N.; Barabașa, C. On the classification of compressed sensed signals. In Proceedings of the International Symposium on Signals, Circuits and Systems (ISSCS) 2011, Iasi, Romania, 30 June 2011. [Google Scholar]
- Fira, M.; Goraș, L. On Some Methods for Dimensionality Reduction of ECG Signals. Int. J. Adv. Comput. Sci. Appl. 2019, 10, 326–607. [Google Scholar] [CrossRef]
- EPFL. Available online: http://mmspg.epfl.ch/cms/page-58322.html (accessed on 22 May 2017).
- Hoffmann, U.; Vesin, J.M.; Ebrahimi, T.; Diserens, K. An efficient P300-based brain-computer interface for disabled subjects. J. Neurosci. Methods 2008, 167, 115–125. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, U.; Garcia, G.; Vesin, J.-M.; Diserens, K.; Ebrahimi, T. A Boosting Approach to P300 Detection with Application to Brain-Computer Interfaces. In Proceedings of the IEEE EMBS Conference on Neural Engineering, Arlington, VA, USA, 16–20 March 2005. [Google Scholar]
- Farwell, L.A.; Donchin, E. Talking off the top of your head: A mental prosthesis utilizing event-related brain potentials. Electroencephalogr. Clin. Neurophysiol. 1988, 70, 510–523. [Google Scholar] [CrossRef]
- Martišius, I.; Šidlauskas, K.; Damaševičius, R. Real-Time Training of Voted Perceptron for Classification of EEG Data. Int. J. Artif. Intell. 2013, 10, 207–217. [Google Scholar]




| ECG Original Centered | Compressed Sensed (CS) | Laplacian Eigenmaps (LE) | Locality Preserving Projections (LPP) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ECG Original | CS 2 | CS 3 | CS 25 | LE 2 | LE 3 | LE 25 | LPP 2 | LPP 3 | LPP 25 | |
| Fine Trees | 83.44 | 49.41 | 55.34 | 79.81 | 76.25 | 77.32 | 86.73 | 54.00 | 66.65 | 81.15 |
| Medium Trees | 71.32 | 45.35 | 48.00 | 69.23 | 71.53 | 68.85 | 79.62 | 52.34 | 60.43 | 67.91 |
| Coarse Trees | 42.83 | 32.21 | 34.41 | 40.32 | 45.64 | 45.64 | 50.67 | 40.85 | 41.54 | 49.75 |
| Linear Discriminant | 76.32 | 24.23 | 33.72 | 73.94 | 34.77 | 38.81 | 77.44 | 30.42 | 35.41 | 73.64 |
| Quadratic Discriminant | 70.00 | 34.00 | 47.53 | 89.77 | 47.34 | 54.54 | 84.22 | 44.41 | 56.24 | 91.51 |
| Naive Bayes | 47.63 | 33.43 | 38.93 | 52.22 | 37.64 | 38.34 | 74.36 | 42.51 | 49.37 | 77.21 |
| Kernel Naive Bayes | 62.53 | 45.94 | 48.8 | 71.85 | 70.34 | 69.95 | 81.74 | 52.54 | 62.26 | 82.64 |
| Linear SVM | 87.34 | 29.52 | 38.9 | 85.14 | 49.08 | 61.37 | 85.62 | 37.52 | 47.72 | 85.92 |
| Quadratic SVM | 95.11 | 44.54 | 54.3 | 94.54 | 43.95 | 59.92 | 90.54 | 44.52 | 64.64 | 94.24 |
| Cubic SVM | 95.24 | 42.72 | 53.00 | 94.50 | 26.10 | 33.00 | 91.20 | 27.10 | 47.92 | 94.24 |
| Fine Gaussian SVM | 87.47 | 51.80 | 62.90 | 87.91 | 75.36 | 78.75 | 90.69 | 54.40 | 70.10 | 61.14 |
| Medium Gaussian SVM | 92.91 | 49.84 | 58.74 | 93.00 | 67.92 | 69.88 | 87.12 | 53.44 | 67.84 | 94.14 |
| Coarse Gaussian SVM | 79.47 | 32.85 | 43.65 | 80.97 | 54.36 | 55.41 | 80.92 | 44.45 | 57.82 | 83.82 |
| Fine KNN | 93.42 | 39.14 | 55.14 | 93.71 | 79.92 | 83.36 | 89.84 | 45.11 | 63.90 | 93.74 |
| Medium KNN | 90.27 | 48.72 | 60.82 | 90.82 | 80.76 | 83.92 | 89.65 | 52.42 | 68.00 | 91.32 |
| Coarse KNN | 77.62 | 50.47 | 57.71 | 77.44 | 74.00 | 75.35 | 80.12 | 53.63 | 65.74 | 78.34 |
| Cosine KNN | 90.54 | 29.64 | 47.15 | 90.74 | 61.25 | 81.42 | 89.55 | 32.80 | 54.62 | 92.76 |
| Cubic KNN | 90.22 | 48.81 | 60.81 | 90.81 | 80.88 | 83.95 | 89.72 | 52.38 | 68.34 | 90.77 |
| Weighted KNN | 91.47 | 43.60 | 59.44 | 92.34 | 81.52 | 84.82 | 90.32 | 48.51 | 67.42 | 92.35 |
| Ensemble Boosted Trees | 78.34 | 45.97 | 49.45 | 76.81 | 72.65 | 70.19 | 82.49 | 53.55 | 61.36 | 77.67 |
| Ensemble Bagged Trees | 91.81 | 43.94 | 59.45 | 90.4 | 80.00 | 83.91 | 90.91 | 48.86 | 68.31 | 91.84 |
| Ensemble Subspace Discriminant | 76.24 | 24.31 | 29.14 | 70.3 | 35 | 38.95 | 76.93 | 30.22 | 34.32 | 73.05 |
| Ensemble Subspace KNN | 94.71 | 23.34 | 44.00 | 94.04 | 51.24 | 80.82 | 89.98 | 24.14 | 56.10 | 95.34 |
| Ensemble RUS Boosted Trees | 71.54 | 45.34 | 47.94 | 69.31 | 71.54 | 68.84 | 79.64 | 52.84 | 60.67 | 67.97 |
| ECG Original Centered | CS 2 | CS 3 | CS 4 | CS 5 | CS 7 | CS 9 | CS 10 | CS 15 | CS 20 | CS 25 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fine Tree | 83.4 | 49.4 | 55.3 | 58.1 | 68.6 | 72.3 | 71.5 | 72.4 | 75.7 | 77.3 | 79.8 |
| Medium Tree | 71.3 | 45.3 | 48.0 | 49.3 | 54 | 52.8 | 51.6 | 52.3 | 52.7 | 60.6 | 69.2 |
| Coarse Tree | 42.8 | 32.2 | 34.4 | 34.2 | 36.5 | 35.2 | 36.2 | 36.7 | 35.9 | 38.0 | 40.3 |
| Linear Discriminant | 76.3 | 24.2 | 33.7 | 35.2 | 41.4 | 47.3 | 55.3 | 60.0 | 69.2 | 71.6 | 73.9 |
| Quadratic Discriminant | 70.0 | 34.0 | 47.5 | 50.3 | 63.2 | 74.1 | 77.8 | 82.0 | 87.6 | 89.1 | 89.7 |
| Naive Bayes | 47.6 | 33.4 | 38.9 | 40.8 | 47.2 | 48.6 | 47.8 | 49.1 | 50.3 | 50.9 | 52.2 |
| Kernel Naive Bayes | 62.5 | 45.9 | 48.8 | 51.7 | 62.4 | 66.1 | 68.0 | 68.1 | 70.5 | 70.5 | 71.8 |
| Linear SVM | 87.3 | 29.5 | 38.9 | 41.6 | 54.2 | 63.2 | 71.3 | 75.9 | 82.8 | 84.4 | 85.1 |
| Quadratic SVM | 95.1 | 44.5 | 54.3 | 61.7 | 74.7 | 85.2 | 88.9 | 90.8 | 93.3 | 94.2 | 94.5 |
| Cubic SVM | 95.2 | 42.7 | 53.0 | 62.2 | 75.9 | 86.6 | 90.1 | 91.7 | 93.4 | 94.7 | 94.5 |
| Fine Gaussian SVM | 87.4 | 51.8 | 62.9 | 69.5 | 82.0 | 86.4 | 87.8 | 88.5 | 88.0 | 87.6 | 87.9 |
| Medium Gaussian SVM | 92.9 | 49.8 | 58.7 | 65.4 | 78.0 | 85.4 | 87.3 | 88.6 | 91.2 | 92.0 | 93.0 |
| Coarse Gaussian SVM | 79.4 | 32.8 | 43.6 | 45.2 | 62.1 | 67.2 | 69.5 | 71.8 | 77.5 | 79.5 | 80.9 |
| Fine KNN | 93.4 | 39.1 | 55.1 | 64.4 | 80.7 | 87.6 | 89.4 | 91.0 | 92.4 | 93.5 | 93.7 |
| Medium KNN | 90.2 | 48.7 | 60.8 | 67.5 | 80.6 | 86.5 | 87.8 | 88.4 | 89.6 | 90.3 | 90.8 |
| Coarse KNN | 77.6 | 50.4 | 57.7 | 61.5 | 69.2 | 73.8 | 74.9 | 75.5 | 76.3 | 76.6 | 77.4 |
| Cosine KNN | 90.5 | 29.6 | 47.1 | 58.2 | 73.8 | 83.2 | 85.9 | 86.7 | 88.3 | 89.7 | 90.7 |
| Cubic KNN | 90.2 | 48.8 | 60.8 | 67.7 | 80.3 | 86.4 | 87.7 | 88.5 | 89.8 | 90.5 | 90.8 |
| Weighted KNN | 91.4 | 43.6 | 59.4 | 68.2 | 81.9 | 88.1 | 89.3 | 90.1 | 91.5 | 92.1 | 92.3 |
| Ensemble Boosted Trees | 78.3 | 45.9 | 49.4 | 52.2 | 61.8 | 66.1 | 67.5 | 70.6 | 69.5 | 73.8 | 76.8 |
| Ensemble Bagged Trees | 91.8 | 43.9 | 59.4 | 65.6 | 80.3 | 85.2 | 87.1 | 88.2 | 89.7 | 90.2 | 90.4 |
| Ensemble Subspace Discriminant | 76.2 | 24.3 | 29.1 | 31.5 | 40.0 | 43.9 | 45.6 | 47.0 | 61.1 | 64.4 | 70.3 |
| Ensemble Subspace KNN | 94.7 | 23.3 | 44.0 | 49.5 | 74.2 | 86.0 | 89.0 | 90.3 | 92.4 | 93.6 | 94.0 |
| Ensemble RUSBoosted Trees | 71.5 | 45.3 | 47.9 | 49.4 | 53.9 | 53.8 | 52.0 | 52.5 | 52.8 | 60.6 | 69.3 |
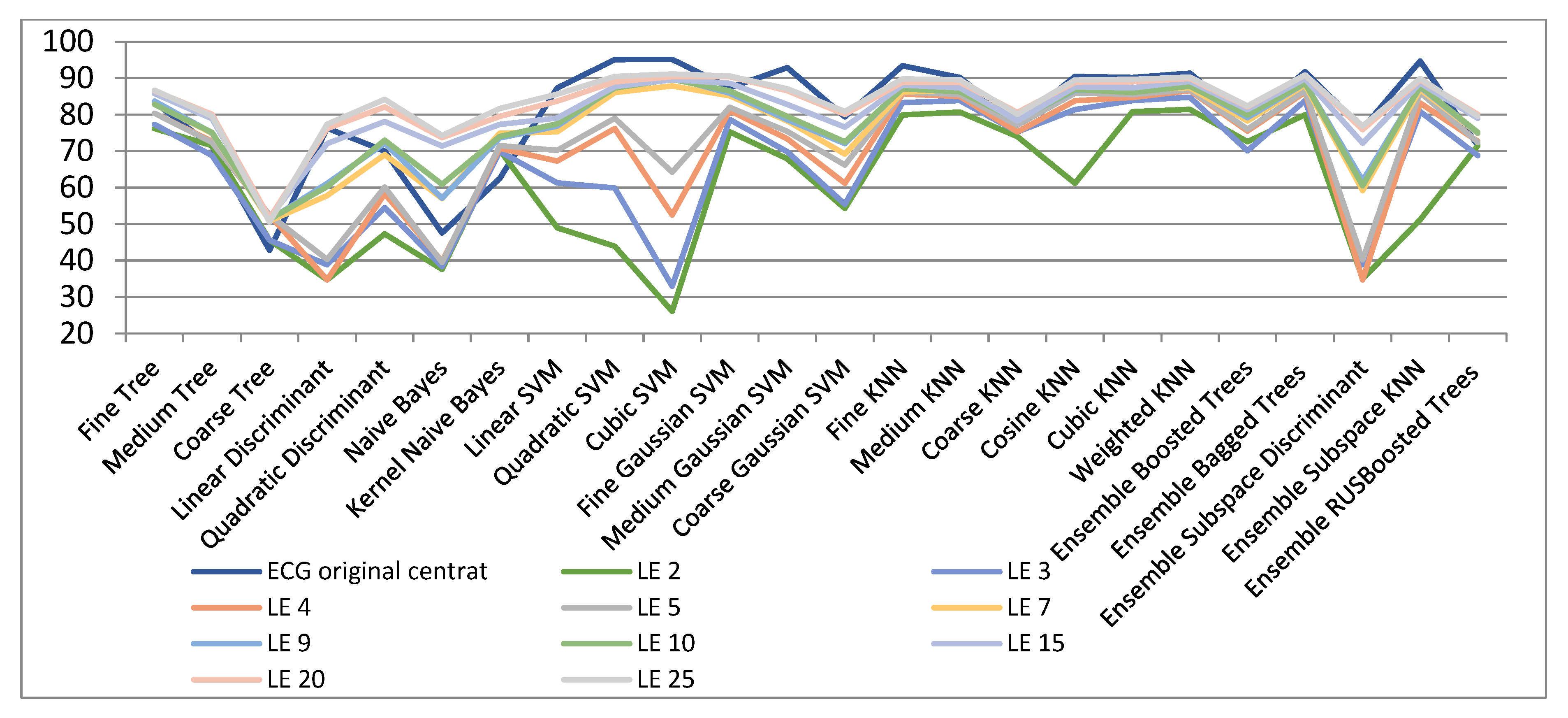
| ECG Original Centred | LE 2 | LE 3 | LE 4 | LE 5 | LE 7 | LE 9 | LE 10 | LE 15 | LE 20 | LE 25 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fine Tree | 83.4 | 76.2 | 77.3 | 80.4 | 80.4 | 82.9 | 83.7 | 82.8 | 85.8 | 86.5 | 86.7 |
| Medium Tree | 71.3 | 71.5 | 68.8 | 72.7 | 72.4 | 74.9 | 75 | 75.1 | 78.9 | 80.1 | 79.6 |
| Coarse Tree | 42.8 | 45.6 | 45.6 | 52.5 | 52.5 | 50.9 | 51.2 | 51.3 | 51.8 | 51.6 | 50.6 |
| Linear Discriminant | 76.3 | 34.7 | 38.8 | 34.7 | 40.3 | 57.8 | 61.1 | 60.3 | 72.1 | 76.2 | 77.4 |
| Quadratic Discriminant | 70 | 47.3 | 54.5 | 58.3 | 60.1 | 69 | 72.2 | 73 | 78.1 | 82.1 | 84.2 |
| Naive Bayes | 47.6 | 37.6 | 38.3 | 39.8 | 39.5 | 57 | 57.1 | 60.9 | 71.4 | 73.7 | 74.3 |
| Kernel Naive Bayes | 62.5 | 70.3 | 69.9 | 70.8 | 71.5 | 74.9 | 73.6 | 74 | 77.3 | 79.5 | 81.7 |
| Linear SVM | 87.3 | 49 | 61.3 | 67.3 | 70.2 | 75.3 | 76.9 | 77.5 | 79.1 | 83.7 | 85.6 |
| Quadratic SVM | 95.1 | 43.9 | 59.9 | 76.2 | 79 | 86.1 | 87.6 | 87.3 | 87.7 | 89 | 90.5 |
| Cubic SVM | 95.2 | 26.1 | 33 | 52.5 | 64.2 | 87.9 | 90.1 | 89.7 | 89.6 | 90.4 | 91.2 |
| Fine Gaussian SVM | 87.4 | 75.3 | 78.7 | 81.1 | 82 | 85.2 | 85.9 | 86.5 | 88.6 | 90.4 | 90.6 |
| Medium Gaussian SVM | 92.9 | 67.9 | 69.8 | 73.4 | 75.4 | 78.3 | 78.6 | 79.5 | 82.8 | 86.6 | 87.1 |
| Coarse Gaussian SVM | 79.4 | 54.3 | 55.4 | 61.2 | 66.2 | 69.2 | 72.1 | 72.5 | 76.6 | 80.1 | 80.9 |
| Fine KNN | 93.4 | 79.9 | 83.3 | 85.7 | 86.2 | 86.2 | 87.2 | 87.1 | 88.1 | 88.9 | 89.8 |
| Medium KNN | 90.2 | 80.7 | 83.9 | 85 | 85.5 | 86.8 | 87 | 86.3 | 87.4 | 88.9 | 89.6 |
| Coarse KNN | 77.6 | 74 | 75.3 | 75.3 | 77.1 | 79 | 78.6 | 78.5 | 78.3 | 80.6 | 80.1 |
| Cosine KNN | 90.5 | 61.2 | 81.4 | 83.8 | 85.9 | 86.9 | 86.7 | 86.9 | 87.6 | 88.9 | 89.5 |
| Cubic KNN | 90.2 | 80.8 | 83.9 | 84.7 | 85.5 | 86.8 | 86.8 | 86.1 | 87.4 | 89 | 89.7 |
| Weighted KNN | 91.4 | 81.5 | 84.8 | 86.6 | 86.9 | 87.4 | 88.1 | 87.8 | 89.1 | 89.9 | 90.3 |
| Ensemble Boosted Trees | 78.3 | 72.6 | 70.1 | 75.5 | 76 | 78.3 | 79.2 | 79.9 | 81.4 | 82.2 | 82.4 |
| Ensemble Bagged Trees | 91.8 | 80 | 83.9 | 86.2 | 86.6 | 88.2 | 88.6 | 88.7 | 89.9 | 90.9 | 90.9 |
| Ensemble Subspace Discriminant | 76.2 | 35 | 38.9 | 34.7 | 40.2 | 59.2 | 61.9 | 60.5 | 72.2 | 75.9 | 76.9 |
| Ensemble Subspace KNN | 94.7 | 51.2 | 80.8 | 83.2 | 86.1 | 86.9 | 87.6 | 87.8 | 88.7 | 89.6 | 89.9 |
| Ensemble RUSBoosted Trees | 71.5 | 71.5 | 68.8 | 72.7 | 72.4 | 74.9 | 75 | 75.1 | 79 | 80.1 | 79.6 |
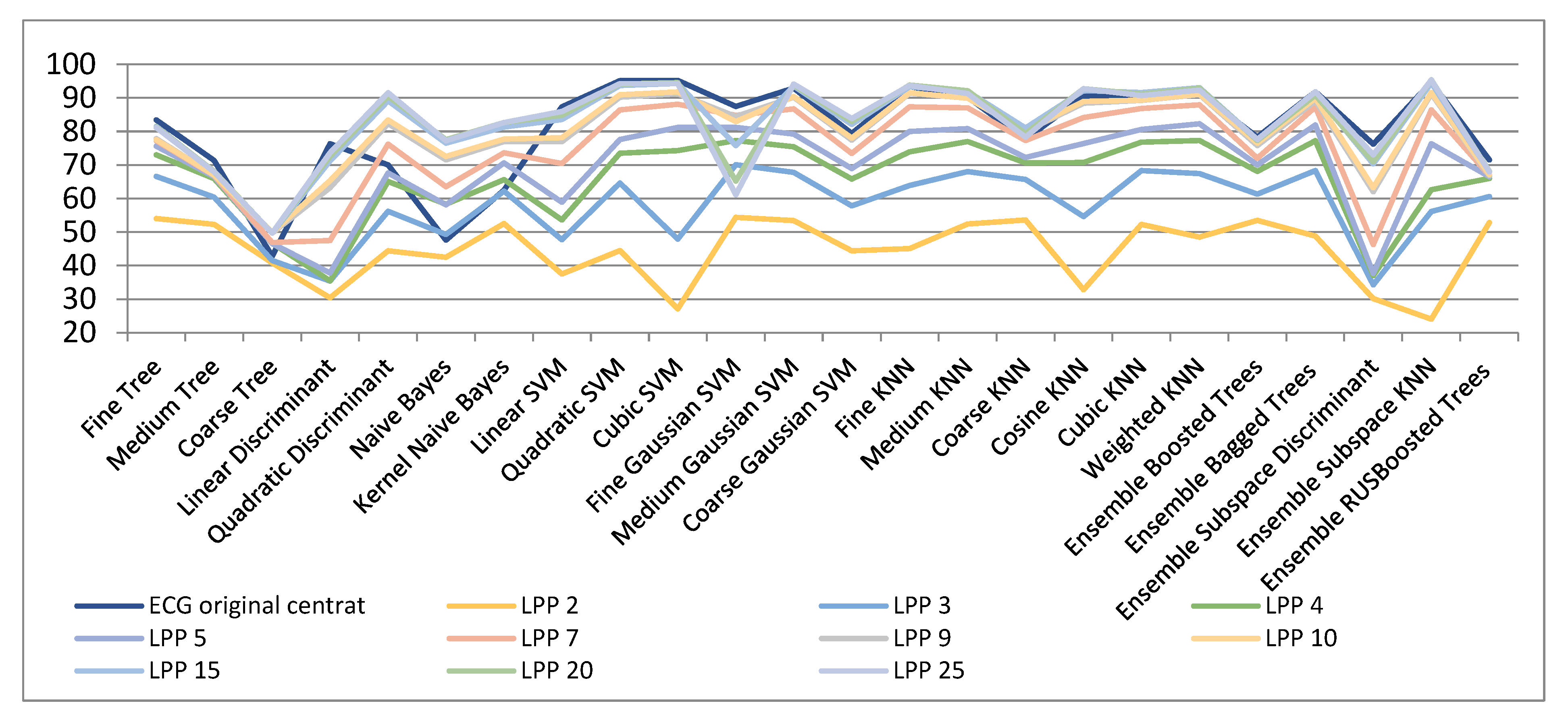
| ECG Original Centered | LPP 2 | LPP 3 | LPP 4 | LPP 5 | LPP 7 | LPP 9 | LPP 10 | LPP 15 | LPP 20 | LPP 25 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fine Tree | 83.4 | 54 | 66.6 | 73 | 75.6 | 77.2 | 77.8 | 77.5 | 81.5 | 81.3 | 81.1 |
| Medium Tree | 71.3 | 52.3 | 60.4 | 65.9 | 66.5 | 66.8 | 66.9 | 67 | 68 | 68.1 | 67.9 |
| Coarse Tree | 42.8 | 40.8 | 41.5 | 46.7 | 46.6 | 46.9 | 49.7 | 49.9 | 49.7 | 49.7 | 49.7 |
| Linear Discriminant | 76.3 | 30.4 | 35.4 | 35.5 | 37.8 | 47.5 | 63.2 | 65.3 | 71.2 | 72.6 | 73.6 |
| Quadratic Discriminant | 70 | 44.4 | 56.2 | 65.1 | 67.6 | 76.2 | 82.3 | 83.4 | 89.1 | 90.5 | 91.5 |
| Naive Bayes | 47.6 | 42.5 | 49.3 | 58.3 | 58.1 | 63.5 | 71.5 | 72.5 | 76.5 | 77.5 | 77.2 |
| Kernel Naive Bayes | 62.5 | 52.5 | 62.2 | 65.6 | 70.6 | 73.6 | 77 | 77.7 | 81.3 | 82.6 | 82.6 |
| Linear SVM | 87.3 | 37.5 | 47.7 | 53.6 | 58.9 | 70.4 | 76.9 | 78.1 | 83.5 | 84.8 | 85.9 |
| Quadratic SVM | 95.1 | 44.5 | 64.6 | 73.5 | 77.6 | 86.4 | 90.2 | 90.9 | 93.7 | 94.1 | 94.2 |
| Cubic SVM | 95.2 | 27.1 | 47.9 | 74.3 | 81.2 | 88.1 | 91.2 | 91.8 | 94.3 | 94.5 | 94.2 |
| Fine Gaussian SVM | 87.4 | 54.4 | 70.1 | 77.3 | 81.2 | 84.8 | 84.4 | 82.9 | 75.8 | 65.2 | 61.1 |
| Medium Gaussian SVM | 92.9 | 53.4 | 67.8 | 75.4 | 79.2 | 86.7 | 90.2 | 90.4 | 93.5 | 93.8 | 94.1 |
| Coarse Gaussian SVM | 79.4 | 44.4 | 57.8 | 65.8 | 68.9 | 73.4 | 77.4 | 78 | 82.1 | 83 | 83.8 |
| Fine KNN | 93.4 | 45.1 | 63.9 | 73.9 | 80 | 87.3 | 91.4 | 91.5 | 93.3 | 93.8 | 93.7 |
| Medium KNN | 90.2 | 52.4 | 68 | 77 | 80.8 | 87 | 89.9 | 89.9 | 91.9 | 92.1 | 91.3 |
| Coarse KNN | 77.6 | 53.6 | 65.7 | 70.6 | 72.2 | 77.3 | 80 | 80.3 | 81 | 79.3 | 78.3 |
| Cosine KNN | 90.5 | 32.8 | 54.6 | 70.7 | 76.4 | 84.1 | 88.4 | 88.9 | 92.2 | 92.7 | 92.7 |
| Cubic KNN | 90.2 | 52.3 | 68.3 | 76.8 | 80.6 | 86.8 | 89.2 | 89.3 | 91.6 | 91.1 | 90.7 |
| Weighted KNN | 91.4 | 48.5 | 67.4 | 77.3 | 82.3 | 87.9 | 91 | 91.1 | 93 | 92.9 | 92.3 |
| Ensemble Boosted Trees | 78.3 | 53.5 | 61.3 | 68.1 | 70 | 72 | 75.8 | 76.5 | 77.6 | 77.3 | 77.6 |
| Ensemble Bagged Trees | 91.8 | 48.8 | 68.3 | 77.2 | 81.9 | 87.3 | 89.1 | 89.9 | 91.2 | 90.8 | 91.8 |
| Ensemble Subspace Discriminant | 76.2 | 30.2 | 34.3 | 37 | 37.7 | 46.3 | 62 | 63.2 | 70.3 | 70.9 | 73 |
| Ensemble Subspace KNN | 94.7 | 24.1 | 56.1 | 62.6 | 76.3 | 86.4 | 91.2 | 91.6 | 94.5 | 95.4 | 95.3 |
| Ensemble RUSBoosted Trees | 71.5 | 52.8 | 60.6 | 66 | 66.5 | 66.8 | 66.8 | 67.1 | 68 | 68.1 | 67.9 |
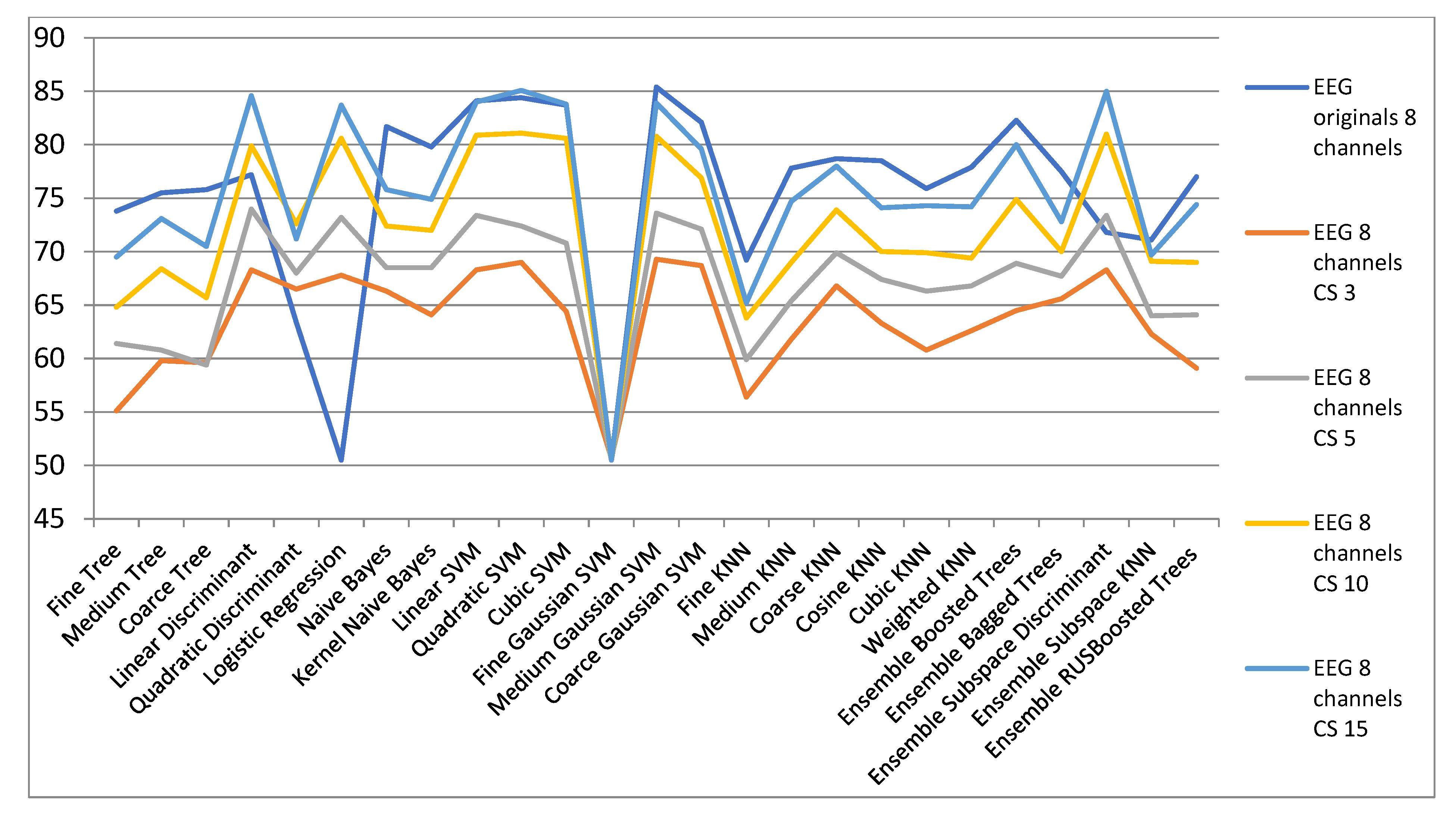
| ECG Orig. | EEG 8 Channels CS | ||||
|---|---|---|---|---|---|
| 8 Channels | CS 3 | CS 5 | CS 10 | CS 15 | |
| Fine Tree | 73.8 | 55.1 | 61.4 | 64.8 | 69.5 |
| Medium Tree | 75.5 | 59.8 | 60.8 | 68.4 | 73.1 |
| Coarse Tree | 75.8 | 59.6 | 59.4 | 65.7 | 70.5 |
| Linear Discriminant | 77.2 | 68.3 | 74 | 79.9 | 84.6 |
| Quadratic Discriminant | 63.4 | 66.5 | 68 | 72.6 | 71.2 |
| Logistic Regression | 50.5 | 67.8 | 73.2 | 80.6 | 83.7 |
| Naive Bayes | 81.7 | 66.3 | 68.5 | 72.4 | 75.8 |
| Kernel Naive Bayes | 79.8 | 64.1 | 68.5 | 72 | 74.9 |
| Linear SVM | 84.1 | 68.3 | 73.4 | 80.9 | 84 |
| Quadratic SVM | 84.4 | 69 | 72.4 | 81.1 | 85.1 |
| Cubic SVM | 83.7 | 64.4 | 70.8 | 80.6 | 83.8 |
| Fine Gaussian SVM | 50.5 | 50.7 | 50.5 | 50.5 | 50.5 |
| Medium Gaussian SVM | 85.4 | 69.3 | 73.6 | 80.8 | 83.9 |
| Coarse Gaussian SVM | 82.1 | 68.7 | 72.1 | 76.9 | 79.6 |
| Fine KNN | 69.2 | 56.4 | 59.9 | 63.8 | 65.2 |
| Medium KNN | 77.8 | 61.8 | 65.4 | 69 | 74.7 |
| Coarse KNN | 78.7 | 66.8 | 69.9 | 73.9 | 78 |
| Cosine KNN | 78.5 | 63.3 | 67.4 | 70 | 74.1 |
| Cubic KNN | 75.9 | 60.8 | 66.3 | 69.9 | 74.3 |
| Weighted KNN | 77.9 | 62.6 | 66.8 | 69.4 | 74.2 |
| Ensemble Boosted Trees | 82.3 | 64.5 | 68.9 | 74.9 | 80 |
| Ensemble Bagged Trees | 77.5 | 65.6 | 67.7 | 70 | 72.8 |
| Ensemble Subspace Discriminant | 71.8 | 68.3 | 73.4 | 81 | 85 |
| Ensemble Subspace KNN | 71.1 | 62.3 | 64 | 69.1 | 69.7 |
| Ensemble RUSBoosted Trees | 77 | 59.1 | 64.1 | 69 | 74.4 |
| ECG Originals | EEG 8 Channels LE | ||||
|---|---|---|---|---|---|
| 8 Channels | LE 3 | LE 5 | LE 10 | LE 15 | |
| Fine Tree | 73.8 | 71.1 | 72 | 70.3 | 69.6 |
| Medium Tree | 75.5 | 75.1 | 75.3 | 71.8 | 72.3 |
| Coarse Tree | 75.8 | 75.1 | 74.3 | 74.1 | 75.2 |
| Linear Discriminant | 77.2 | 79.1 | 81.6 | 83.2 | 81.1 |
| Quadratic Discriminant | 63.4 | 77.8 | 76.9 | 77.9 | 77.2 |
| Logistic Regression | 50.5 | 78.7 | 81.4 | 81.6 | 78.8 |
| Naive Bayes | 81.7 | 76.5 | 76.6 | 77 | 77.1 |
| Kernel Naive Bayes | 79.8 | 75.5 | 77.1 | 76.1 | 76.3 |
| Linear SVM | 84.1 | 79.2 | 80.8 | 82.8 | 80.8 |
| Quadratic SVM | 84.4 | 78.2 | 79.1 | 81.7 | 81.1 |
| Cubic SVM | 83.7 | 72.9 | 77.7 | 79.5 | 80.4 |
| Fine Gaussian SVM | 50.5 | 50.7 | 50.5 | 50.5 | 50.5 |
| Medium Gaussian SVM | 85.4 | 79.2 | 80.3 | 81.1 | 81 |
| Coarse Gaussian SVM | 82.1 | 79.2 | 80 | 81.4 | 79 |
| Fine KNN | 69.2 | 66.1 | 69.1 | 67.6 | 68.2 |
| Medium KNN | 77.8 | 73.1 | 74.4 | 75.6 | 76.1 |
| Coarse KNN | 78.7 | 77.7 | 77.8 | 79.1 | 78.8 |
| Cosine KNN | 78.5 | 74.4 | 74.8 | 75.5 | 76.4 |
| Cubic KNN | 75.9 | 72.7 | 73.5 | 74.5 | 73.8 |
| Weighted KNN | 77.9 | 73.5 | 74.3 | 76.5 | 76.8 |
| Ensemble Boosted Trees | 82.3 | 77.7 | 78.3 | 78.3 | 78 |
| Ensemble Bagged Trees | 77.5 | 76.8 | 74.4 | 72.9 | 76 |
| Ensemble Subspace Discriminant | 71.8 | 79 | 80 | 82.5 | 81.7 |
| Ensemble Subspace KNN | 71.1 | 73 | 75.2 | 74.8 | 73 |
| Ensemble RUSBoosted Trees | 77 | 75.4 | 74.9 | 72.6 | 73.6 |
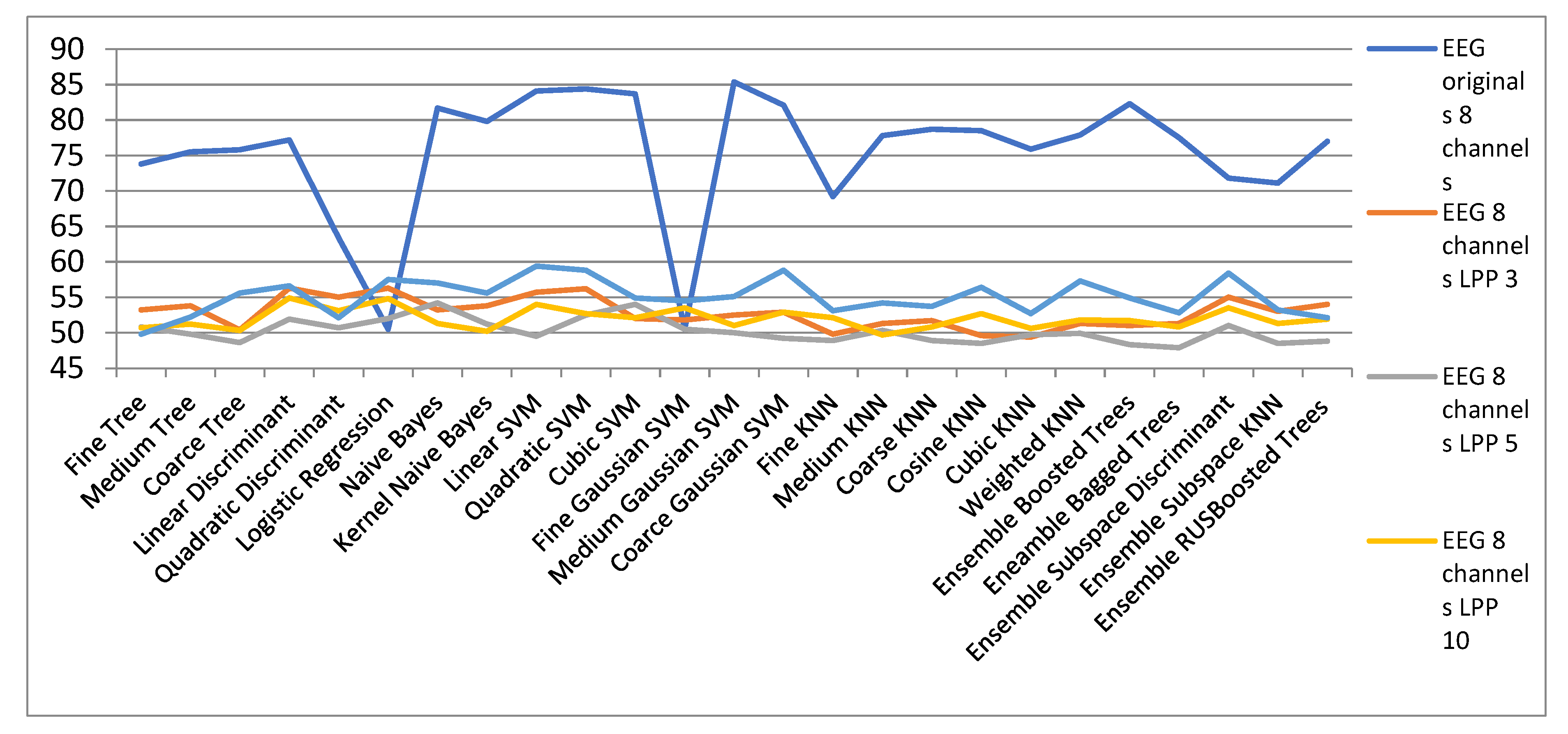
| EEG Orig. | EEG 8 Channels | ||||
|---|---|---|---|---|---|
| 8 Channels | LPP 3 | LPP 5 | LPP 10 | LPP 15 | |
| Fine Tree | 73.8 | 53.2 | 50.8 | 50.7 | 49.8 |
| Medium Tree | 75.5 | 53.8 | 49.8 | 51.2 | 52.2 |
| Coarse Tree | 75.8 | 50.4 | 48.6 | 50.3 | 55.6 |
| Linear Discriminant | 77.2 | 56.3 | 51.9 | 54.9 | 56.6 |
| Quadratic Discriminant | 63.4 | 55 | 50.7 | 53.1 | 52.1 |
| Logistic Regression | 50.5 | 56.3 | 52 | 54.8 | 57.5 |
| Naïve Bayes | 81.7 | 53.2 | 54.2 | 51.3 | 57 |
| Kernel Naïve Bayes | 79.8 | 53.8 | 51.2 | 50.2 | 55.6 |
| Linear SVM | 84.1 | 55.7 | 49.5 | 54 | 59.4 |
| Quadratic SVM | 84.4 | 56.2 | 52.5 | 52.7 | 58.8 |
| Cubic SVM | 83.7 | 52 | 54 | 52.1 | 54.9 |
| Fine Gaussian SVM | 50.5 | 51.8 | 50.5 | 53.5 | 54.5 |
| Medium Gaussian SVM | 85.4 | 52.5 | 50 | 51 | 55.1 |
| Coarce Gaussian SVM | 82.1 | 52.9 | 49.2 | 52.9 | 58.8 |
| Fine KNN | 69.2 | 49.8 | 48.9 | 52.1 | 53.1 |
| Medium KNN | 77.8 | 51.3 | 50.3 | 49.7 | 54.2 |
| Coarse KNN | 78.7 | 51.7 | 48.9 | 50.8 | 53.7 |
| Cosine KNN | 78.5 | 49.6 | 48.5 | 52.7 | 56.4 |
| Cubic KNN | 75.9 | 49.4 | 49.7 | 50.6 | 52.7 |
| Weighted KNN | 77.9 | 51.3 | 49.9 | 51.8 | 57.3 |
| Ensemble Boosted Trees | 82.3 | 51 | 48.3 | 51.7 | 54.9 |
| Ensemble Bagged Trees | 77.5 | 51.3 | 47.9 | 50.8 | 52.8 |
| Ensemble Subspace Discriminant | 71.8 | 55 | 51 | 53.5 | 58.4 |
| Ensemble Subspace KNN | 71.1 | 53 | 48.5 | 51.3 | 53.2 |
| Ensemble RUSBoosted Trees | 77 | 54 | 48.8 | 51.9 | 52.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fira, M.; Costin, H.-N.; Goraș, L. On the Classification of ECG and EEG Signals with Various Degrees of Dimensionality Reduction. Biosensors 2021, 11, 161. https://doi.org/10.3390/bios11050161
Fira M, Costin H-N, Goraș L. On the Classification of ECG and EEG Signals with Various Degrees of Dimensionality Reduction. Biosensors. 2021; 11(5):161. https://doi.org/10.3390/bios11050161
Chicago/Turabian StyleFira, Monica, Hariton-Nicolae Costin, and Liviu Goraș. 2021. "On the Classification of ECG and EEG Signals with Various Degrees of Dimensionality Reduction" Biosensors 11, no. 5: 161. https://doi.org/10.3390/bios11050161
APA StyleFira, M., Costin, H.-N., & Goraș, L. (2021). On the Classification of ECG and EEG Signals with Various Degrees of Dimensionality Reduction. Biosensors, 11(5), 161. https://doi.org/10.3390/bios11050161





