Neurophysiological Factors Affecting Muscle Innervation Zone Estimation Using Surface EMG: A Simulation Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Motor Unit Pool Simulation
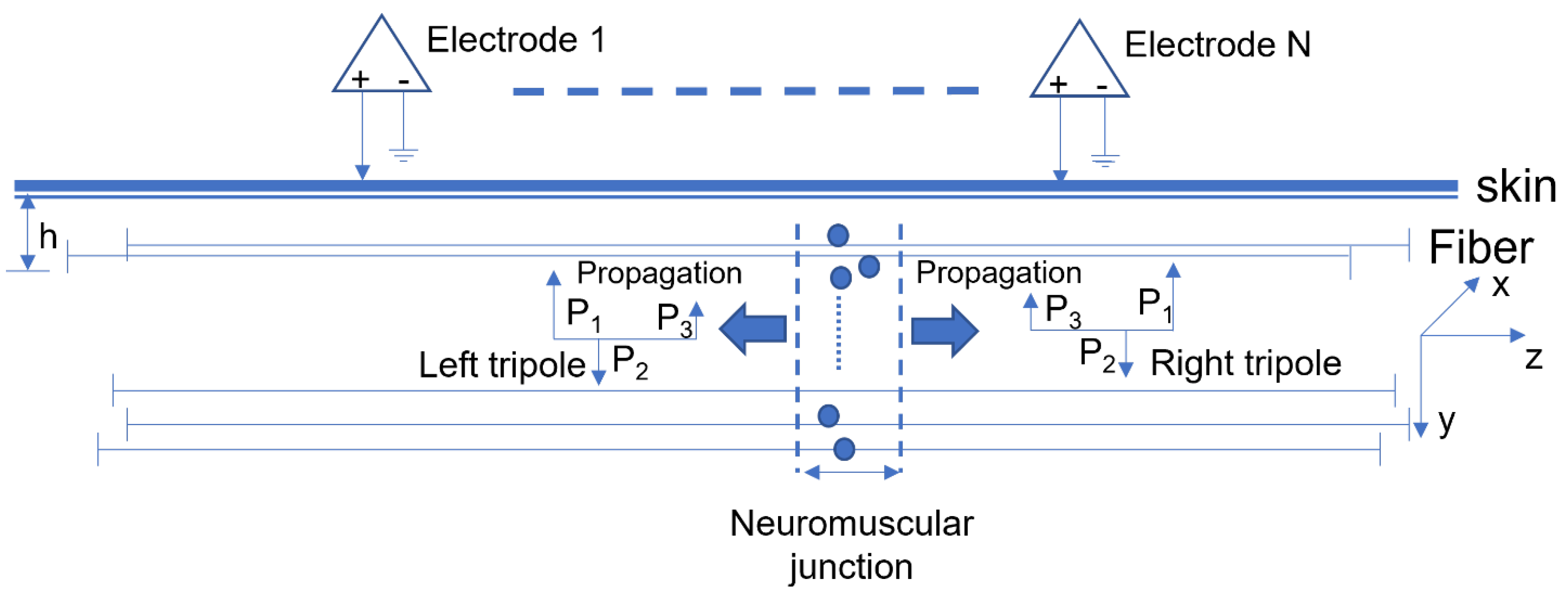
2.2. Surface EMG Simulation
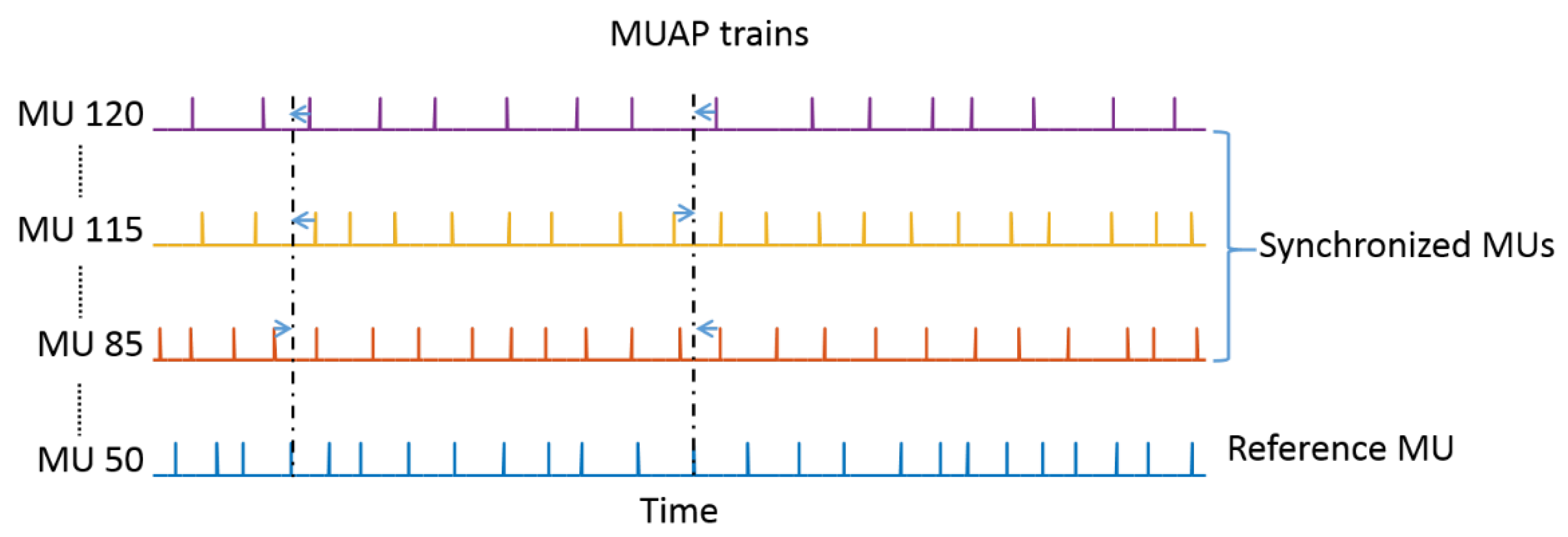
2.3. Motor Unit Synchronization
2.4. IZ Location Estimation
2.5. Simulation Procedures
3. Results
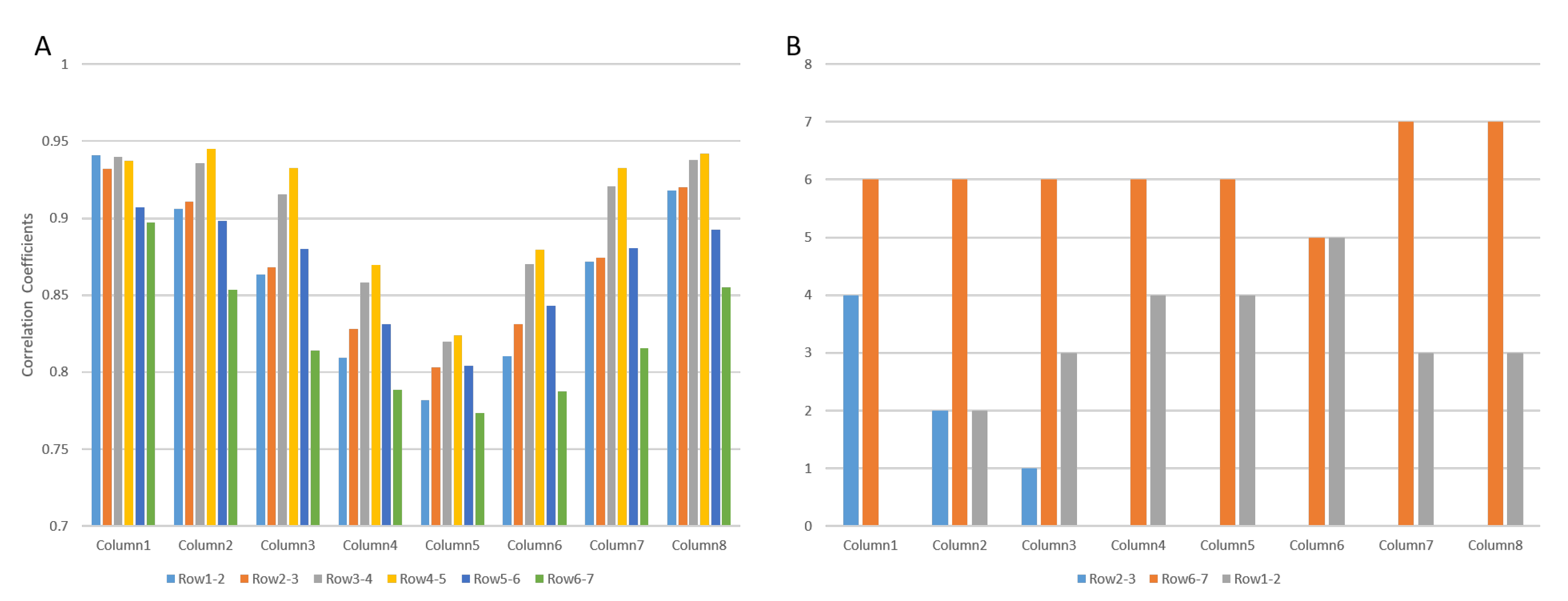
3.1. Muscle with Single IZ
3.2. Muscle with Double IZs
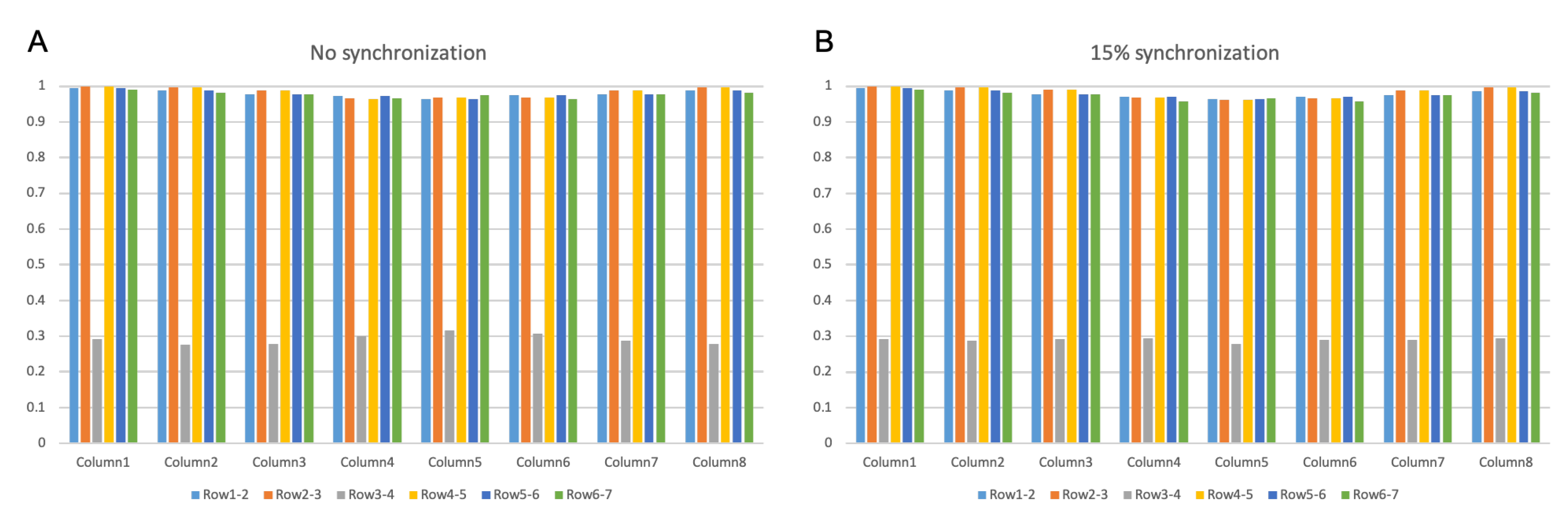
3.2.1. IZ Estimation at No MU Synchronization
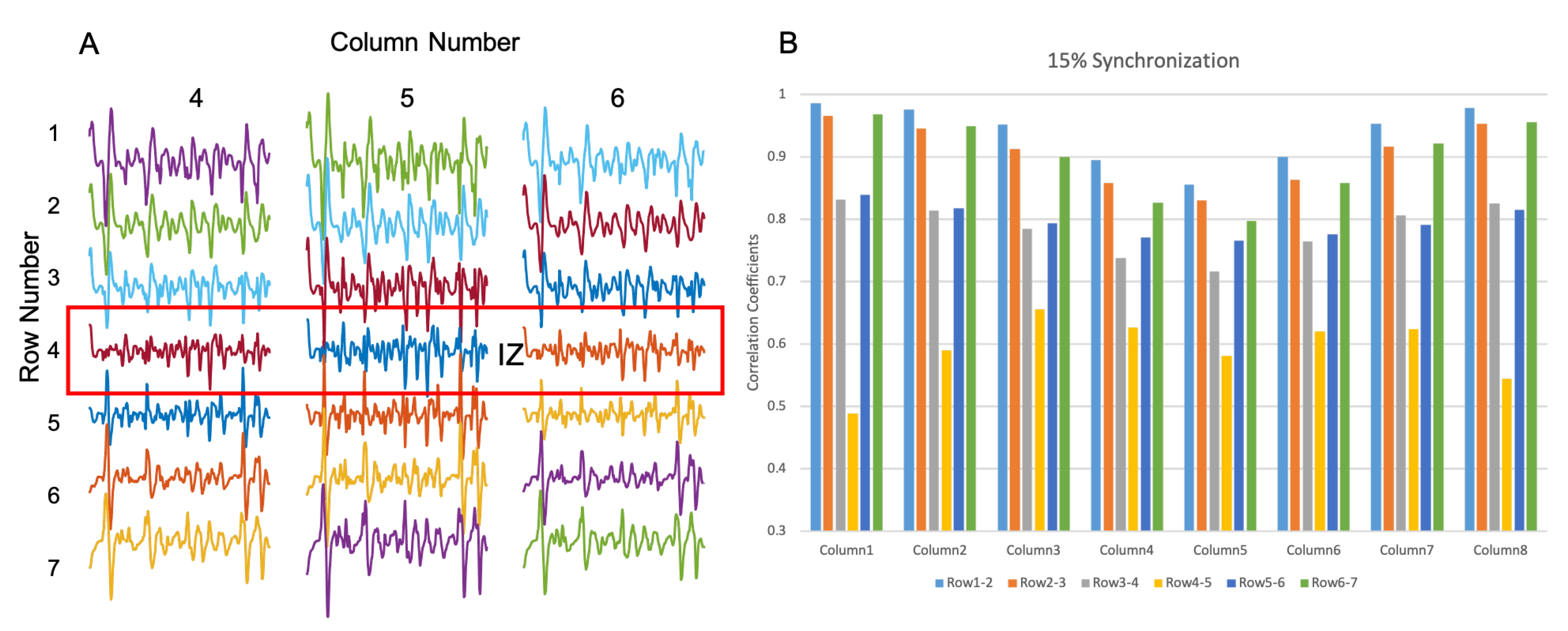
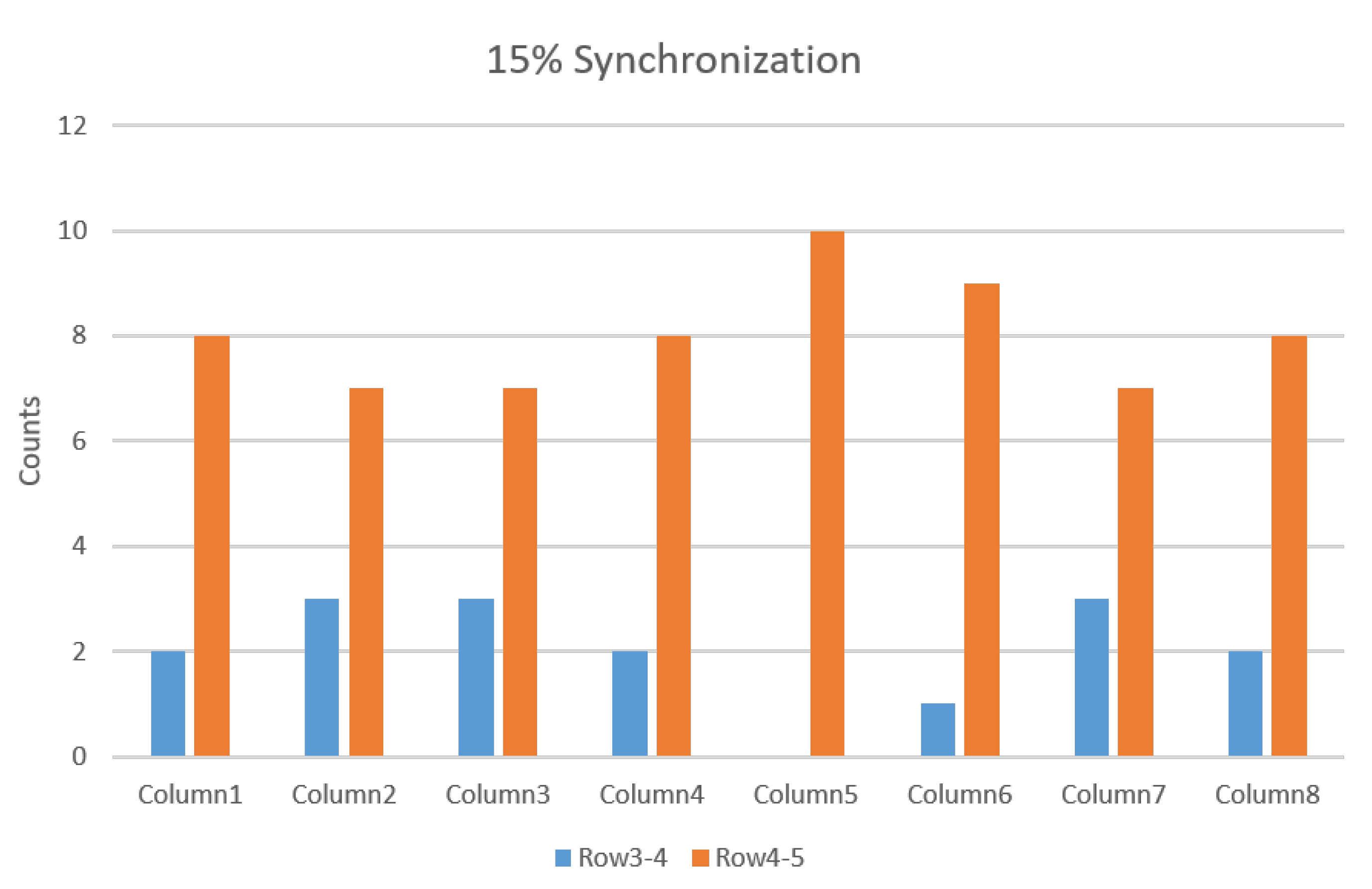
3.2.2. IZ Estimation with 15% MU Synchronization
3.2.3. IZ Estimation with M Waves
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barbero, M.; Merletti, R.; Rainoldi, A. Atlas of Muscle Innervation Zones: Understanding Surface Electromyography and Its Applications; Springer Science & Business Media; Springer Mailand: Milan, Italy, 2012. [Google Scholar]
- Rasool, G.; Afsharipour, B.; Suresh, N.L.; Rymer, W.Z. Spatial Analysis of Multichannel Surface EMG in Hemiplegic Stroke. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 1802–1811. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Y.-T.; Liu, Y.; Zhou, P.; Li, S.; Zhang, Y. Three dimensional innervation zone imaging in spastic muscles of stroke survivors. J. Neural Eng. 2019, 16, 034001. [Google Scholar] [CrossRef]
- Jahanmiri-Nezhad, F.; Barkhaus, P.E.; Rymer, W.Z.; Zhou, P. Innervation zones of fasciculating motor units: Observations by a linear electrode array. Front. Hum. Neurosci. 2015, 9, 239. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, X.; Lu, Z.; Wang, I.; Li, L.; Stampas, A.; Zhou, P. Assessing redistribution of muscle innervation zones after spinal cord injuries. J. Electromyogr. Kinesiol. 2021, 59, 102550. [Google Scholar] [CrossRef]
- Kaymak, B.; Kara, M.; On, A.Y.; Soylu, A.R.; Özçakar, L. Innervation zone targeted botulinum toxin injections. Eur. J. Phys. Rehabil. Med. 2018, 54, 100–109. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Chen, Y.-T.; Liu, Y.; Magat, E.; Gutierrez-Verduzco, M.; Francisco, G.E.; Zhou, P.; Li, S.; Zhang, Y. Improving Botulinum Toxin Efficiency in Treating Post-Stroke Spasticity Using 3D Innervation Zone Imaging. Int. J. Neural Syst. 2021, 31, 2150007. [Google Scholar] [CrossRef] [PubMed]
- Lapatki, B.G.; Van Dijk, J.P.; Van De Warrenburg, B.P.C.; Zwarts, M.J. Botulinum toxin has an increased effect when targeted toward the muscle’s endplate zone: A high-density surface EMG guided study. Clin. Neurophysiol. 2011, 122, 1611–1616. [Google Scholar] [CrossRef]
- Chen, Y.-T.; Zhang, C.; Liu, Y.; Magat, E.; Verduzco-Gutierrez, M.; Francisco, G.E.; Zhou, P.; Zhang, Y.; Li, S. The Effects of Botulinum Toxin Injections on Spasticity and Motor Performance in Chronic Stroke with Spastic Hemiplegia. Toxins 2020, 12, 492. [Google Scholar] [CrossRef]
- Začesta, V.; Rezeberga, D.; Plaudis, H.; Drusany-Staric, K.; Cescon, C. Could the correct side of mediolateral episiotomy be determined according to anal sphincter EMG? Int. Urogynecol. J. 2018, 29, 1501–1507. [Google Scholar] [CrossRef]
- Piccoli, M.B.; Rainoldi, A.; Heitz, C.; Wüthrich, M.; Boccia, G.; Tomasoni, E.; Spirolazzi, C.; Egloff, M.; Barbero, M. Innervation zone locations in 43 superficial muscles: Toward a standardization of electrode positioning. Muscle Nerve 2014, 49, 413–421. [Google Scholar] [CrossRef]
- Mesin, L.; Merletti, R.; Rainoldi, A. Surface EMG: The issue of electrode location. J. Electromyogr. Kinesiol. 2009, 19, 719–726. [Google Scholar] [CrossRef] [Green Version]
- Nishihara, K.; Chiba, Y.; Suzuki, Y.; Moriyama, H.; Kanemura, N.; Ito, T.; Takayanagi, K.; Gomi, T. Effect of position of electrodes relative to the innervation zone onsurface EMG. J. Med. Eng. Technol. 2010, 34, 141–147. [Google Scholar] [CrossRef] [PubMed]
- Rainoldi, A.; Melchiorri, G.; Caruso, I. A method for positioning electrodes during surface EMG recordings in lower limb muscles. J. Neurosci. Methods 2004, 134, 37–43. [Google Scholar] [CrossRef] [PubMed]
- Beck, T.W.; Housh, T.J.; Cramer, J.T.; Weir, J.P. The effect of the estimated innervation zone on EMG amplitude and center frequency. Med. Sci. Sport. Exerc. 2007, 39, 1282–1290. [Google Scholar] [CrossRef] [PubMed]
- Gallina, A.; Merletti, R.; Gazzoni, M. Innervation zone of the vastus medialis muscle: Position and effect on surface EMG variables. Physiol. Meas. 2013, 34, 1411. [Google Scholar] [CrossRef] [PubMed]
- Bhadane, M.; Liu, J.; Rymer, W.Z.; Zhou, P.; Li, S. Re-evaluation of EMG-torque relation in chronic stroke using linear electrode array EMG recordings. Sci. Rep. 2016, 6, 28957. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beck, T.W.; DeFreitas, J.M.; Stock, M.S. Accuracy of three different techniques for automatically estimating innervation zone location. Comput. Methods Programs Biomed. 2012, 105, 13–21. [Google Scholar] [CrossRef] [PubMed]
- Mesin, L.; Gazzoni, M.; Merletti, R. Automatic localisation of innervation zones: A simulation study of the external anal sphincter. J. Electromyogr. Kinesiol. 2009, 19, e413–e421. [Google Scholar] [CrossRef] [Green Version]
- Barbero, M.; Gatti, R.; Conte LLo Macmillan, F.; Coutts, F.; Merletti, R. Reliability of surface EMG matrix in locating the innervation zone of upper trapezius muscle. J. Electromyogr. Kinesiol. 2011, 21, 827–833. [Google Scholar] [CrossRef]
- Cescon, C. Automatic Location of Muscle Innervation Zones From Multi-Channel Surface EMG Signals. In Proceedings of the IEEE International Workshop on Medical Measurement and Applications; MeMea: Benevento, Italy, 2006; pp. 87–90. [Google Scholar]
- Ullah, K.; Cescon, C.; Afsharipour, B.; Merletti, R. Automatic detection of motor unit innervation zones of the external anal sphincter by multichannel surface EMG. J. Electromyogr. Kinesiol. 2014, 24, 860–867. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Falces, J. A new method for the localization of the innervation zone based on monopolar surface-detected potentials. J. Electromyogr. Kinesiol. 2017, 35, 47–60. [Google Scholar] [CrossRef]
- Ostlund, N.; Gerdle, B.; Stefan Karlsson, J. Location of innervation zone determined with multichannel surface electromyography using an optical flow technique. J. Electromyogr. Kinesiol. 2007, 17, 549–555. [Google Scholar] [CrossRef]
- Marateb, H.R.; Farahi, M.; Rojas, M.; Mañanas, M.A.; Farina, D. Detection of multiple innervation zones from multi-channel surface EMG recordings with low signal-to-noise ratio using graph-cut segmentation. PLoS ONE 2016, 11, e0167954. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Ning, Y.; Li, S.; Zhou, P.; Rymer, W.Z.; Zhang, Y. Three-Dimensional Innervation Zone Imaging from Multi-Channel Surface EMG Recordings. Int. J. Neural Syst. 2015, 25, 1550024. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, J.; Li, S.; Jahanmiri-Nezhad, F.; Rymer, W.Z.; Zhou, P. Motor unit innervation zone localization based on robust linear regression analysis. Comput. Biol. Med. 2019, 106, 65–70. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Dias, N.; He, J.; Zhou, P.; Li, S.; Zhang, Y. Global Innervation Zone Identification With High-Density Surface Electromyography. IEEE Trans. Biomed. Eng. 2020, 67, 718–725. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, C.; Dias, N.; Chen, Y.T.; Li, S.; Zhou, P.; Zhang, Y. Transcutaneous innervation zone imaging from high-density surface electromyography recordings. J. Neural Eng. 2020, 17, 016070. [Google Scholar] [CrossRef]
- Zhang, C.; Peng, Y.; Liu, Y.; Li, S.; Zhou, P.; Rymer, W.Z.; Zhang, Y. Imaging three-dimensional innervation zone distribution in muscles from M-wave recordings. J. Neural Eng. 2017, 14, 36011. [Google Scholar] [CrossRef]
- Lateva, Z.C.; McGill, K.C.; Johanson, M.E. The innervation and organization of motor units in a series-fibered human muscle: The brachioradialis. J. Appl. Physiol. 2010, 108, 1530–1541. [Google Scholar] [CrossRef] [Green Version]
- Masuda, T.; Miyano, H.; Sadoyama, T. The position of innervation zones in the biceps brachii investigated by surface electromyography. IEEE Trans. Biomed. Eng. 1985, 32, 36–42. [Google Scholar] [CrossRef]
- Semmler, J.G. Motor unit synchronization and neuromuscular performance. Exerc. Sport Sci. Rev. 2002, 30, 8–14. [Google Scholar] [CrossRef]
- De Luca, C.J. Control properties of motor units. J. Exp. Biol. 1985, 115, 125–136. [Google Scholar] [CrossRef]
- De Luca, C.J.; Erim, Z. Common drive in motor units of a synergistic muscle pair. J. Neurophysiol. 2002, 87, 2200–2204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mori, S. Entrainment of motor-unit discharges as a neuronal mechanism of synchronization. J. Neurophysiol. 1975, 38, 859–870. [Google Scholar] [CrossRef] [PubMed]
- De Luca, C.J.; Roy, A.M.; Erim, Z. Synchronization of motor-unit firings in several human muscles. J. Neurophysiol. 1993, 70, 2010–2023. [Google Scholar] [CrossRef] [Green Version]
- Kline, J.C.; De Luca, C.J. Synchronization of motor unit firings: An epiphenomenon of firing rate characteristics not common inputs. J. Neurophysiol. 2016, 115, 178–192. [Google Scholar] [CrossRef] [Green Version]
- Yao, W.; Fuglevand, R.J.; Enoka, R.M. Motor-Unit Synchronization Increases EMG Amplitude and Decreases Force Steadiness of Simulated Contractions. J. Neurophysiol. 2000, 83, 441–452. [Google Scholar] [CrossRef] [PubMed]
- Fuglevand, A.J.; Winter, D.A.; Patla, A.E. Models of recruitment and rate coding organization in motor-unit pools. J. Neurophysiol. 1993, 70, 2470–2488. [Google Scholar] [CrossRef]
- Merletti, R.; Conte, L.L.; Avignone, E.; Guglielminotti, P. Modeling of surface myoelectric signals. I. Model implementation. IEEE Trans. Biomed. Eng. 1999, 46, 810–820. [Google Scholar] [CrossRef] [PubMed]
- Zhou, P.; Rymer, W.Z. Factors Governing the Form of the Relation Between Muscle Force and the EMG: A Simulation Study. J. Neurophysiol. 2004, 92, 2878–2886. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Potvin, J.R.; Fuglevand, A.J. A motor unit-based model of muscle fatigue. PLoS Comput. Biol. 2017, 13, e1005581. [Google Scholar] [CrossRef] [Green Version]
- Shin, H.; Suresh, N.L.; Rymer, W.Z.; Hu, X. Relative contribution of different altered motor unit control to muscle weakness in stroke: A simulation study. J. Neural Eng. 2017, 15, 016014. [Google Scholar] [CrossRef] [Green Version]
- Zhou, P.; Suresh, N.L.; Rymer, W.Z. Model based sensitivity analysis of EMG–force relation with respect to motor unit properties: Applications to muscle paresis in stroke. Ann. Biomed. Eng. 2007, 35, 1521–1531. [Google Scholar] [CrossRef]
- Keenan, K.G.; Valero-Cuevas, F.J. Experimentally valid predictions of muscle force and EMG in models of motor-unit function are most sensitive to neural properties. J. Neurophysiol. 2007, 98, 1581–1590. [Google Scholar] [CrossRef] [Green Version]
- De Luca, C.J.; Contessa, P. Hierarchical control of motor units in voluntary contractions. J. Neurophysiol. 2012, 107, 178–195. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Inglis, J.G.; Gabriel, D.A. Is the ‘reverse onion skin’phenomenon more prevalent than we thought during intramuscular myoelectric recordings from low to maximal force outputs? Neurosci. Lett. 2021, 743, 135583. [Google Scholar] [CrossRef] [PubMed]
- Piotrkiewicz, M.; Türker, K.S. Onion skin or common drive? Front. Cell. Neurosci. 2017, 11, 2. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guzmán-Venegas, R.; Bralic, M.; Cordero, J.; Cavada, G.; Araneda, O.; Guzmán-Venegas, R. Concordance of the location of the innervation zone of the tibialis anterior muscle using voluntary and imposed contractions by electrostimulation. J. Electromyogr. Kinesiol. 2016, 27, 18–23. [Google Scholar] [CrossRef]
- Huang, C.; Klein, C.S.; Meng, Z.; Zhang, Y.; Li, S.; Zhou, P. Innervation zone distribution of the biceps brachii muscle examined using voluntary and electrically-evoked high-density surface EMG. J. Neuroeng. Rehabil. 2019, 16, 73. [Google Scholar] [CrossRef]
- Mottram, C.J.; Wallace, C.L.; Chikando, C.N.; Rymer, W.Z. Origins of spontaneous firing of motor units in the spastic—paretic biceps brachii muscle of stroke survivors. J. Neurophysiol. 2010, 104, 3168–3179. [Google Scholar] [CrossRef] [Green Version]
- Schmied, A.; Pouget, J.; Vedel, J.-P. Electromechanical coupling and synchronous firing of single wrist extensor motor units in sporadic amyotrophic lateral sclerosis. Clin. Neurophysiol. 1999, 110, 960–974. [Google Scholar] [CrossRef]
- Dartnall, T.J.; Nordstrom, M.A.; Semmler, J.G. Adaptations in biceps brachii motor unit activity after repeated bouts of eccentric exercise in elbow flexor muscles. J. Neurophysiol. 2011, 105, 1225–1235. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Griffin, L.; Painter, P.E.; Wadhwa, A.; Spirduso, W.W. Motor unit firing variability and synchronization during short-term light-load training in older adults. Exp. Brain Res. 2009, 197, 337–345. [Google Scholar] [CrossRef]
- Mochizuki, G.; Ivanova, T.D.; Garland, S.J. Synchronization of Motor Units in Human Soleus Muscle During Standing Postural Tasks. J. Neurophysiol. 2005, 94, 62–69. [Google Scholar] [CrossRef] [PubMed]
- Kilner, J.M.; Alonso-Alonso, M.; Fisher, R.; Lemon, R.N. Modulation of synchrony between single motor units during precision grip tasks in humans. J. Physiol. 2002, 541, 937–948. [Google Scholar] [CrossRef] [Green Version]
- Holtermann, A.; Gronlund, C.; Karlsson, J.S.; Roeleveld, K. Motor unit synchronization during fatigue: Described with a novel sEMG method based on large motor unit samples. J. Electromyogr. Kinesiol. 2009, 19, 232–241. [Google Scholar] [CrossRef]
- Boonstra, T.W.; Daffertshofer, A.; Van Ditshuizen, J.C.; Van den Heuvel MR, C.; Hofman, C.; Willigenburg, N.W.; Beek, P.J. Fatigue-related changes in motor-unit synchronization of quadriceps muscles within and across legs. J. Electromyogr. Kinesiol. 2008, 18, 717–731. [Google Scholar] [CrossRef]
- Holobar, A.; Farina, D.; Gazzoni, M.; Merletti, R.; Zazula, D. Estimating motor unit discharge patterns from high-density surface electromyogram. Clin. Neurophysiol. 2009, 120, 551–562. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Zhou, P. A Novel Framework Based on FastICA for High Density Surface EMG Decomposition. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 117–127. [Google Scholar] [CrossRef] [Green Version]
- Glaser, V.; Holobar, A.; Zazula, D. Real-Time Motor Unit Identification From High-Density Surface EMG. IEEE Trans. Neural Syst. Rehabil. Eng. 2013, 21, 949–958. [Google Scholar] [CrossRef]
- Defreitas, J.M.; Beck, T.W.; Ye, X.; Stock, M.S. Synchronization of low- and high-threshold motor units. Muscle Nerve 2014, 49, 575–583. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, M.; Graven-Nielsen, T.; Farina, D. Effect of innervation-zone distribution on estimates of average muscle-fiber conduction velocity. Muscle Nerve 2008, 37, 68–78. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.; Chen, M.; Li, X.; Zhang, Y.; Li, S.; Zhou, P. Neurophysiological Factors Affecting Muscle Innervation Zone Estimation Using Surface EMG: A Simulation Study. Biosensors 2021, 11, 356. https://doi.org/10.3390/bios11100356
Huang C, Chen M, Li X, Zhang Y, Li S, Zhou P. Neurophysiological Factors Affecting Muscle Innervation Zone Estimation Using Surface EMG: A Simulation Study. Biosensors. 2021; 11(10):356. https://doi.org/10.3390/bios11100356
Chicago/Turabian StyleHuang, Chengjun, Maoqi Chen, Xiaoyan Li, Yingchun Zhang, Sheng Li, and Ping Zhou. 2021. "Neurophysiological Factors Affecting Muscle Innervation Zone Estimation Using Surface EMG: A Simulation Study" Biosensors 11, no. 10: 356. https://doi.org/10.3390/bios11100356
APA StyleHuang, C., Chen, M., Li, X., Zhang, Y., Li, S., & Zhou, P. (2021). Neurophysiological Factors Affecting Muscle Innervation Zone Estimation Using Surface EMG: A Simulation Study. Biosensors, 11(10), 356. https://doi.org/10.3390/bios11100356





