Effect of the Order-Disorder Transition on the Seebeck Coefficient of Nanostructured Thermoelectric Cu2ZnSnS4
Abstract
:1. Introduction
2. Materials and Methods
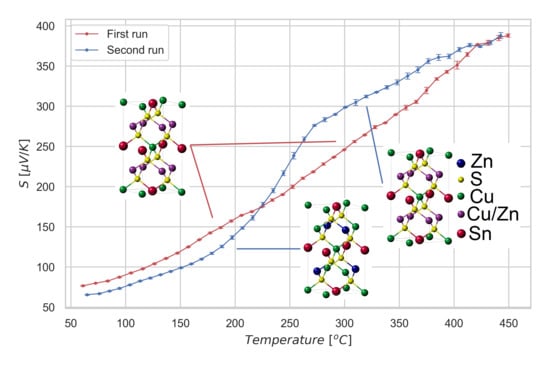
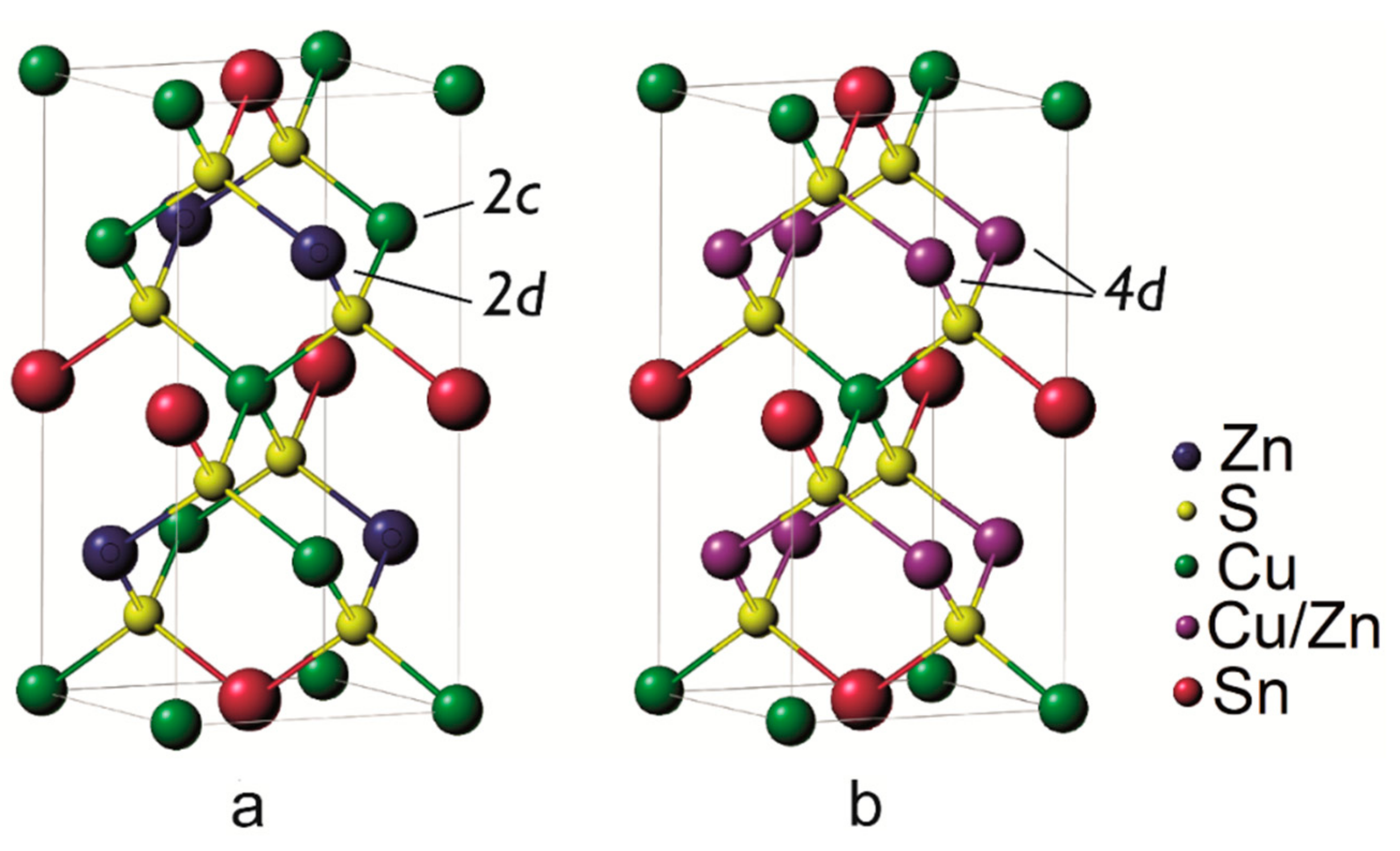
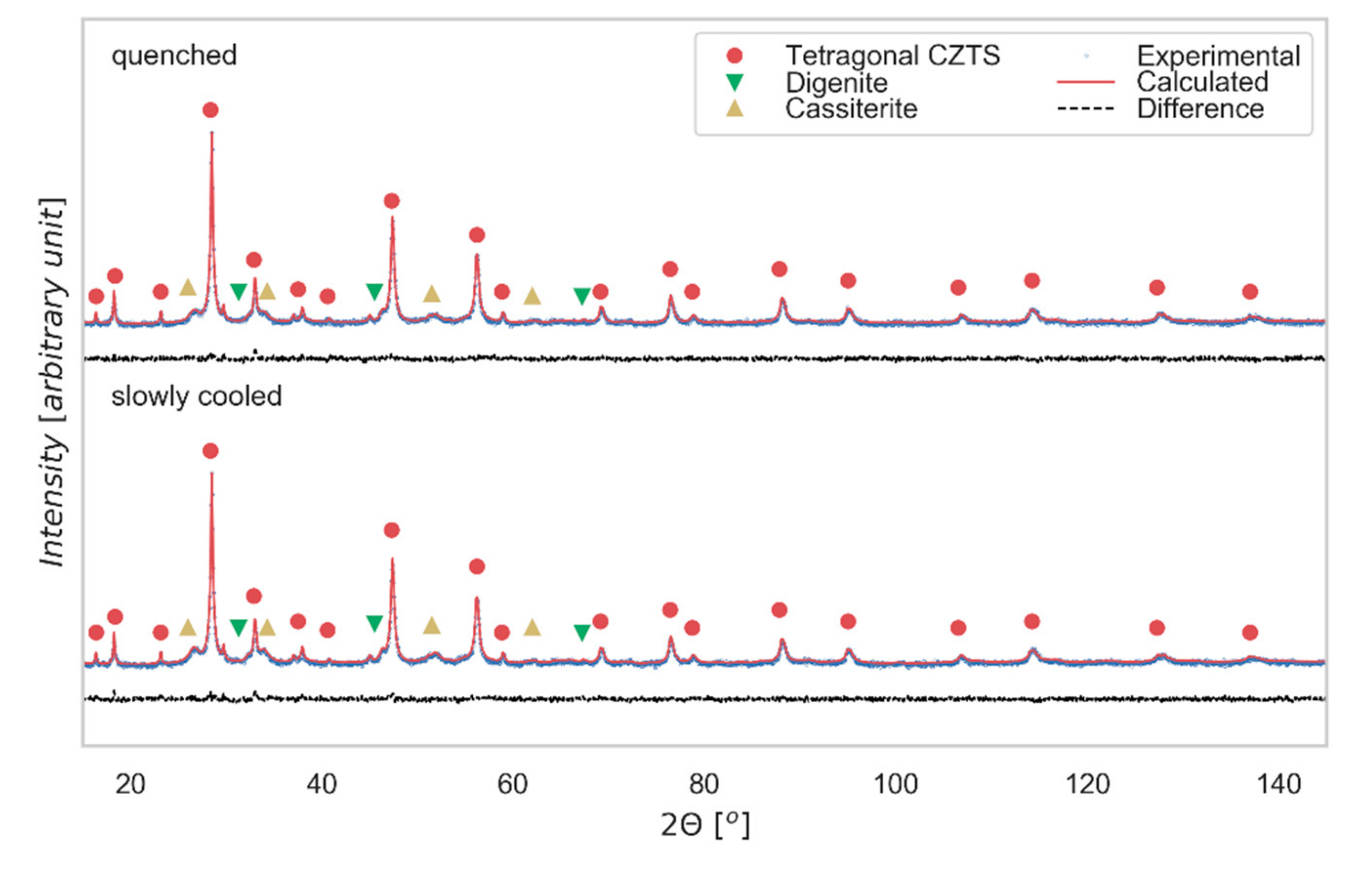
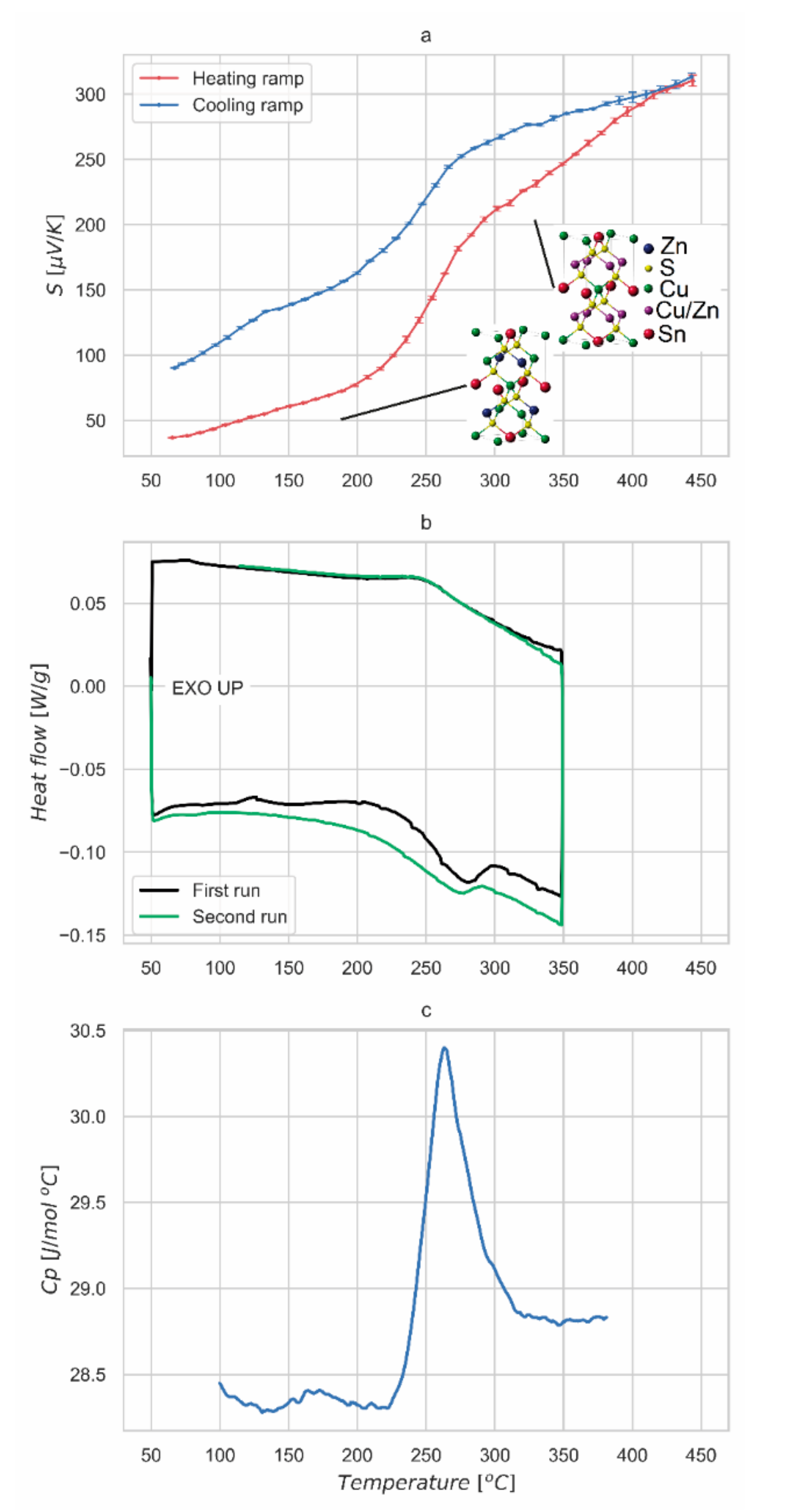
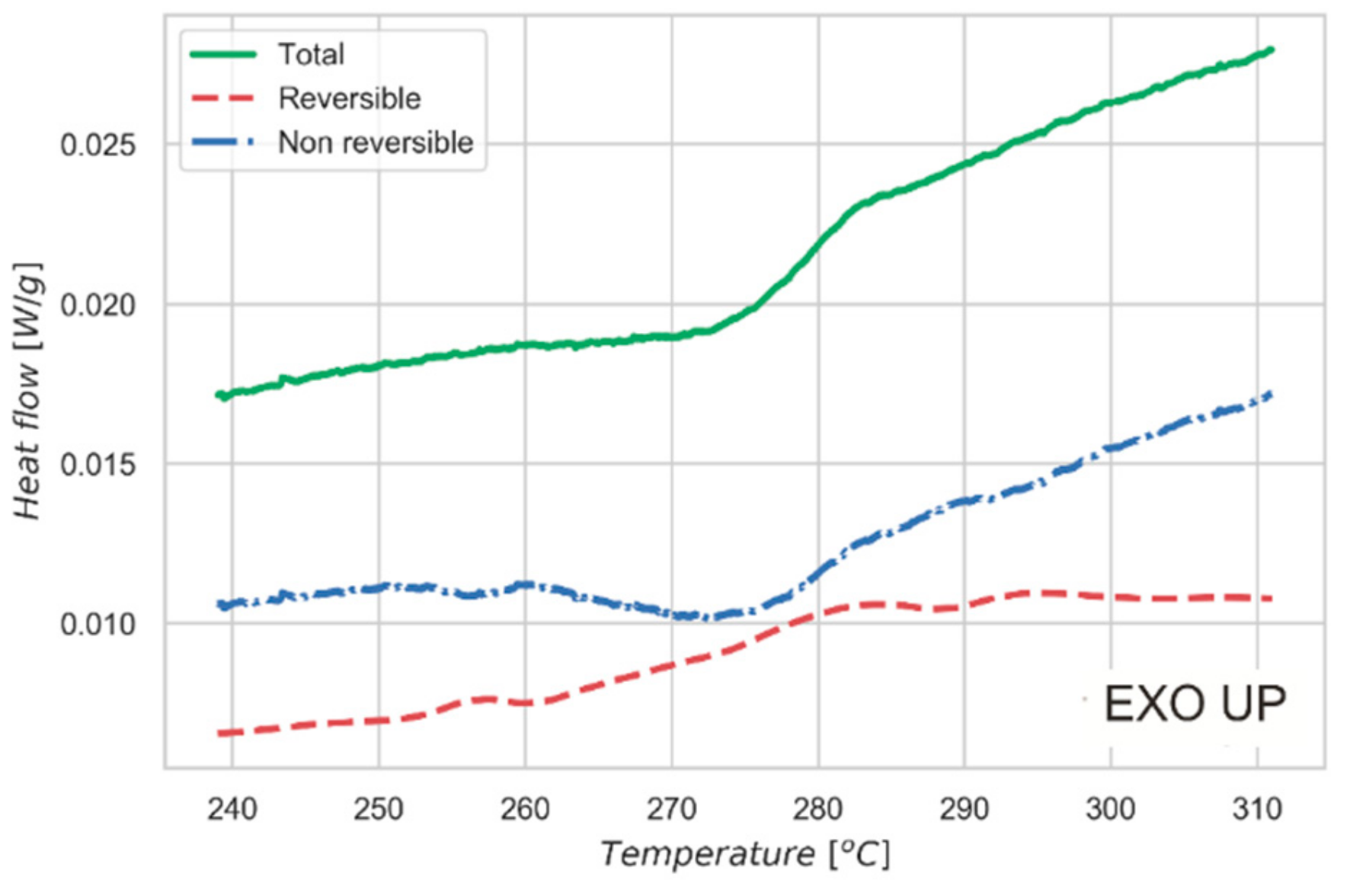
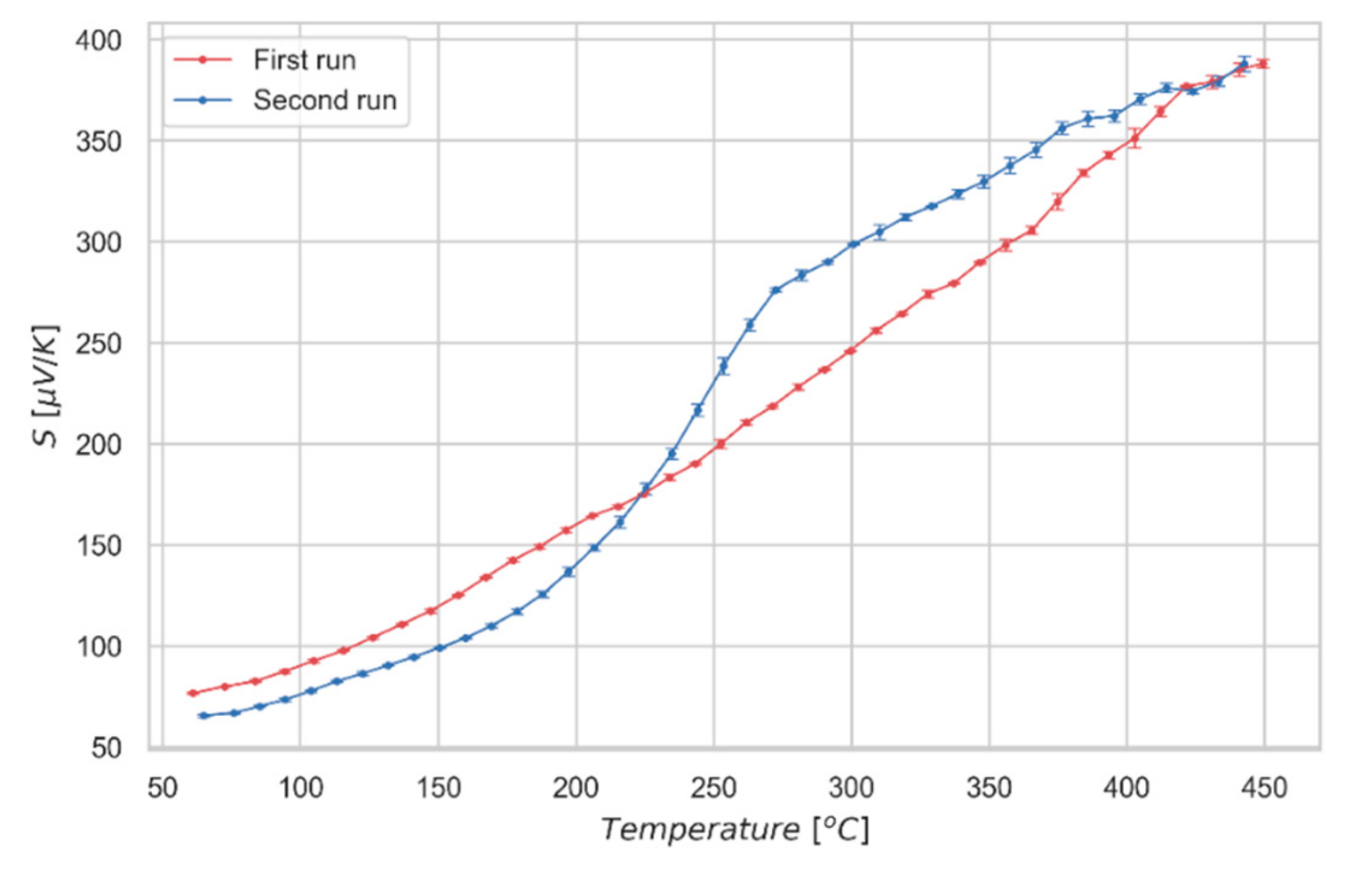
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Seebeck, T.J. Ueber die magnetische Polarisation der Metalle und Erze durch Temperaturdifferenz. [Magnetic polarization of metals and ores by temperature differences]. Abhandlungen der K. Akad. der Wissenschaften zu Berlin 1826, 82, 265–373. (In German) [Google Scholar]
- Peltier, J.C.H. Nouvelles expériences sur la caloricité des courants électrique. [New experiments on the heat effects of electric currents]. Ann. Chim. Phys. 1834, 56, 371–386. (In French) [Google Scholar]
- Rowe, D.M. Thermoelectrics and Its Energy Harvesting; CRC PRESS: Boca Raton, FL, USA, 2012; ISBN 9781439874707 (hardback v.1) 9781439874721 (hardback v.2). [Google Scholar]
- Zeier, W.G.; Snyder, G.J.; Zevalkink, A.; Gibbs, Z.M.; Hautier, G.; Kanatzidis, M.G. Thinking Like a Chemist: Intuition in Thermoelectric Materials. Angew. Chem. Int. Ed. 2016, 55, 6826–6841. [Google Scholar] [CrossRef]
- Zeier, W.G. New tricks for optimizing thermoelectric materials. Curr. Opin. Green Sustain. Chem. 2017, 4, 23–28. [Google Scholar] [CrossRef]
- Liu, M.L.; Huang, F.Q.; Chen, L.D.; Chen, I.W. A wide-band-gap p -type thermoelectric material based on quaternary chalcogenides of Cu2ZnSnQ4(Q=S,Se). Appl. Phys. Lett. 2009, 94. [Google Scholar] [CrossRef]
- Yang, H.; Jauregui, L.A.; Zhang, G.; Chen, Y.P.; Wu, Y. Nontoxic and abundant copper zinc tin sulfide nanocrystals for potential high-temperature thermoelectric energy harvesting. Nano Lett. 2012, 12, 540–545. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Ansari, M.Z.; Khare, N. Influence of compactness and formation of metallic secondary phase on the thermoelectric properties of Cu2ZnSnS4 thin films. Thin Solid Films 2018, 645, 300–304. [Google Scholar] [CrossRef]
- Sharma, S.D.; Neeleshwar, S. Thermoelectric Properties of hot pressed CZTS micro spheres synthetized by microwave method. MRS Adv. 2018, 3, 1373–1378. [Google Scholar] [CrossRef]
- Sharma, S.D.; Khasimsaheb, B.; Chen, Y.Y.; Neeleshwar, S. Enhanced thermoelectric performance of Cu 2 ZnSnS 4 (CZTS) by incorporating Ag nanoparticles. Ceram. Int. 2019, 45, 2060–2068. [Google Scholar] [CrossRef]
- Katagiri, H.; Jimbo, K.; Yamada, S.; Kamimura, T.; Maw, W.S.; Fukano, T.; Ito, T.; Motohiro, T. Enhanced conversion efficiencies of Cu2ZnSnS4-based thin film solar cells by using preferential etching technique. Appl. Phys. Express 2008, 1. [Google Scholar] [CrossRef]
- Mitzi, D.B.; Gunawan, O.; Todorov, T.K.; Barkhouse, D.A.R. Prospects and performance limitations for Cu–Zn–Sn–S–Se photovoltaic technology. Philos. Trans. R. Soc. A 2013, 371, 20110432. [Google Scholar] [CrossRef] [PubMed]
- Adachi, S. Introduction, 1st ed.; John Wiley and Sons, Ltd.: Chichester West Sussex, UK, 2015; ISBN 9781119052814. [Google Scholar]
- Scragg, J.J.S.; Choubrac, L.; Lafond, A.; Ericson, T.; Platzer-Björkman, C. A low-temperature order-disorder transition in Cu2ZnSnS4 thin films. Appl. Phys. Lett. 2014, 104, 041911. [Google Scholar] [CrossRef]
- Scragg, J.J.S.; Larsen, J.K.; Kumar, M.; Persson, C.; Sendler, J.; Siebentritt, S. Cu–Zn disorder and band gap fluctuations in Cu2ZnSn(S,Se)4: Theoretical and experimental investigations. Phys. Satus Solidi B 2016, 253, 247–254. [Google Scholar] [CrossRef]
- Chen, S.; Gong, X.G.; Walsh, A.; Wei, S. Defect physics of the kesterite thin-film solar cell absorber. Appl. Phys. Lett. 2010, 96, 021902. [Google Scholar] [CrossRef]
- Rudisch, K.; Davydova, A.; Platzer-björkman, C. The effect of stoichiometry on Cu-Zn ordering kinetics in Cu2ZnSnS4 thin films. J. Appl. Phys. 2018, 123, 161558. [Google Scholar] [CrossRef]
- Valentini, M.; Malerba, C.; Menchini, F.; Tedeschi, D.; Polimeni, A.; Capizzi, M.; Mittiga, A. Effect of the order-disorder transition on the optical properties of Cu2ZnSnS4. Appl. Phys. Lett. 2016, 108, 211909. [Google Scholar] [CrossRef]
- Malerba, C.; Valentini, M.; Mittiga, A. Cation Disorder in Cu2ZnSnS4 Thin Films: Effect on Solar Cell Performances. Sol. RRL 2017, 1, 1700101. [Google Scholar] [CrossRef]
- Schorr, S.; Gonzalez-Aviles, G. In-situ investigation of the structural phase transition in kesterite. Phys. Status Solidi Appl. Mater. Sci. 2009, 206, 1054–1058. [Google Scholar] [CrossRef]
- Ritscher, A.; Hoelzel, M.; Lerch, M. The Order-Disorder Transition in Cu2ZnSnS4—A Neutron Scattering Investigation. J. Solid State Chem. 2016, 238, 68–73. [Google Scholar] [CrossRef]
- Paris, M.; Lafond, A.; Guillot-deudon, C. Solid-State NMR and Raman Spectroscopy To Address the Local Structure of Defects and the Tricky Issue of the Cu/Zn Disorder in Cu-Poor, Zn-Rich CZTS Materials. Inorg. Chem. 2014, 53, 8646–8653. [Google Scholar] [CrossRef] [PubMed]
- Rey, G.; Redinger, A.; Weiss, T.P.; Guennou, M. The band gap of Cu2ZnSnSe4: Effect of order-disorder. Appl. Phys. Lett. 2014, 105, 112106. [Google Scholar] [CrossRef]
- Dimitrievska, M.; Saucedo, E.; Jawhari, T.; Pérez-Rodríguez, A.; Fontané, X. Multiwavelength excitation Raman scattering study of polycrystalline kesterite Cu2ZnSnS4 thin films. Appl. Phys. Lett. 2014, 104, 021901. [Google Scholar] [CrossRef]
- Stone, K.H.; Christensen, S.T.; Harvey, S.P.; Teeter, G.; Repins, I.L.; Repins, I.L.; Toney, M.F. Quantifying point defects in Cu2ZnSn(S,Se)4 thin films using resonant x-ray diffraction. Appl. Phys. Lett. 2016, 109, 161901. [Google Scholar] [CrossRef]
- Chen, S.; Walsh, A.; Gong, X.; Wei, S. Classification of Lattice Defects in the Kesterite Cu2ZnSnS4 and Cu2ZnSnSe4 Earth-Abundant Solar Cell Absorbers. Adv. Mater. 2013, 25, 1522–1539. [Google Scholar] [CrossRef] [PubMed]
- Gabka, G.; Bujak, P.; Gryszel, M.; Ostrowski, A.; Malinowska, K.; Zukowska, G.Z.; Agnese, F.; Pron, A.; Reiss, P. Synthesis and surface chemistry of high quality wurtzite and kesterite Cu2ZnSnS4 nanocrystals using tin(II) 2-ethylhexanoate as a new tin source. Chem. Commun. 2015, 51, 12985–12988. [Google Scholar] [CrossRef]
- Ataollahi, N.; Malerba, C.; Ciancio, R.; Edla, R.; Scardi, P.; Cappelletto, E.; Di Maggio, R. Control of composition and grain growth in Cu2ZnSnS4 thin films from nanoparticle inks. Thin Solid Films 2019, 674, 12–21. [Google Scholar] [CrossRef]
- Ricardo, C.L.A.; Su, M.S.; Müller, M.; Scardi, P. Production of Cu2(Zn,Fe)SnS4 powders for thin film solar cell by high energy ball milling. J. Power Sources 2013, 230, 70–75. [Google Scholar] [CrossRef]
- Broseghini, M.; Gelisio, L.; D’Incau, M.; Azanza Ricardo, C.L.; Pugno, N.M.; Scardi, P. Modeling of the planetary ball-milling process: The case study of ceramic powders. J. Eur. Ceram. Soc. 2016, 36, 2205–2212. [Google Scholar] [CrossRef]
- Isotta, E.; Pugno, N.M.; Scardi, P. Nanostructured kesterite (Cu2ZnSnS4) for applications in thermoelectric devices. Powder Diffr. 2019, 1–6. [Google Scholar] [CrossRef]
- Coelho, A.A. TOPAS and TOPAS-Academic: An optimization program integrating computer algebra and crystallographic objects written in C++. J. Appl. Crystallogr. 2018, 51, 210–218. [Google Scholar] [CrossRef]
- [Database] ICDD. PDF-4+ 2019 (Database); Kabekkodu, S., Ed.; International Centre for Diffraction Data: Newtown Square, PA, USA, 2019. [Google Scholar]
- Matsushita, H.; Ichikawa, T.; Katsui, A. Structural, thermodynamical and optical properties of Cu 2-II-IV-VI4 quaternary compounds. J. Mater. Sci. 2005, 40, 2003–2005. [Google Scholar] [CrossRef]
- Guen, L.; Glaunsinger, W.S. Electrical, magnetic, and EPR studies of the quaternary chalcogenides Cu2AIIBIVX4 prepared by iodine transport. J. Solid State Chem. 1980, 35, 10–21. [Google Scholar] [CrossRef]
- Scardi, P.; Leoni, M. Whole powder pattern modeling. Acta Crystallogr. Sect. A Found. Crystallogr. 2002, 58, 190–200. [Google Scholar] [CrossRef]
- Scardi, P.; Azanza Ricardo, C.L.; Perez-Demydenko, C.; Coelho, A.A. Whole powder pattern modeling macros for TOPAS. J. Appl. Crystallogr. 2018, 51, 1752–1765. [Google Scholar] [CrossRef]
- Scardi, P. Microstructural Properties: Lattice Defects and Domain Size Effects. In Powder Diffraction: Theory and Practice; Royal Society of Chemistry: Cambridge, UK, 2008; pp. 378–417. [Google Scholar]
- Mott, N.F.; Jones, H. The Theory of the Properties of Metals and Alloys. J. Chem. Educ. 1936, 14, 99. [Google Scholar]
- Zeier, W.G.; Zhu, H.; Gibbs, Z.M.; Ceder, G.; Tremel, W.; Snyder, G.J. Band convergence in the non-cubic chalcopyrite compounds Cu2MGeSe4. J. Mater. Chem. C 2014, 2, 10189–10194. [Google Scholar] [CrossRef]
- Zhang, Q.; Song, Q.; Wang, X.; Sun, J.; Zhu, Q.; Dahal, K.; Lin, X.; Cao, F.; Zhou, J.; Chen, S.; et al. Deep defect level engineering: A strategy of optimizing the carrier concentration for high thermoelectric performance. Energy Environ. Sci. 2018, 11, 933–940. [Google Scholar] [CrossRef]
- Wang, H.; Pei, Y.; Lalonde, A.D.; Snyder, G.J. Thermoelectric Nanomaterials; Springer: Berlin, Germany, 2013; Volume 182, ISBN 978-3-642-37536-1. [Google Scholar]
- Botti, S.; Kammerlander, D.; Marques, M.A.L. Band structures of Cu2 ZnSnS4 and Cu2 ZnSnSe4 from many-body methods. Appl. Phys. Lett. 2011, 98, 241915. [Google Scholar] [CrossRef]
- Wang, B.; Xiang, H.; Nakayama, T.; Zhou, J.; Li, B. Theoretical investigation on thermoelectric properties of Cu-based chalcopyrite compounds. Phys. Rev. B 2017, 95, 035201. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isotta, E.; Fanciulli, C.; Pugno, N.M.; Scardi, P. Effect of the Order-Disorder Transition on the Seebeck Coefficient of Nanostructured Thermoelectric Cu2ZnSnS4. Nanomaterials 2019, 9, 762. https://doi.org/10.3390/nano9050762
Isotta E, Fanciulli C, Pugno NM, Scardi P. Effect of the Order-Disorder Transition on the Seebeck Coefficient of Nanostructured Thermoelectric Cu2ZnSnS4. Nanomaterials. 2019; 9(5):762. https://doi.org/10.3390/nano9050762
Chicago/Turabian StyleIsotta, Eleonora, Carlo Fanciulli, Nicola M. Pugno, and Paolo Scardi. 2019. "Effect of the Order-Disorder Transition on the Seebeck Coefficient of Nanostructured Thermoelectric Cu2ZnSnS4" Nanomaterials 9, no. 5: 762. https://doi.org/10.3390/nano9050762
APA StyleIsotta, E., Fanciulli, C., Pugno, N. M., & Scardi, P. (2019). Effect of the Order-Disorder Transition on the Seebeck Coefficient of Nanostructured Thermoelectric Cu2ZnSnS4. Nanomaterials, 9(5), 762. https://doi.org/10.3390/nano9050762