The Effect of Thermal Contact Number on the Tube–Tube Contact Conductance of Single-Walled Carbon Nanotubes
Abstract
:1. Introduction
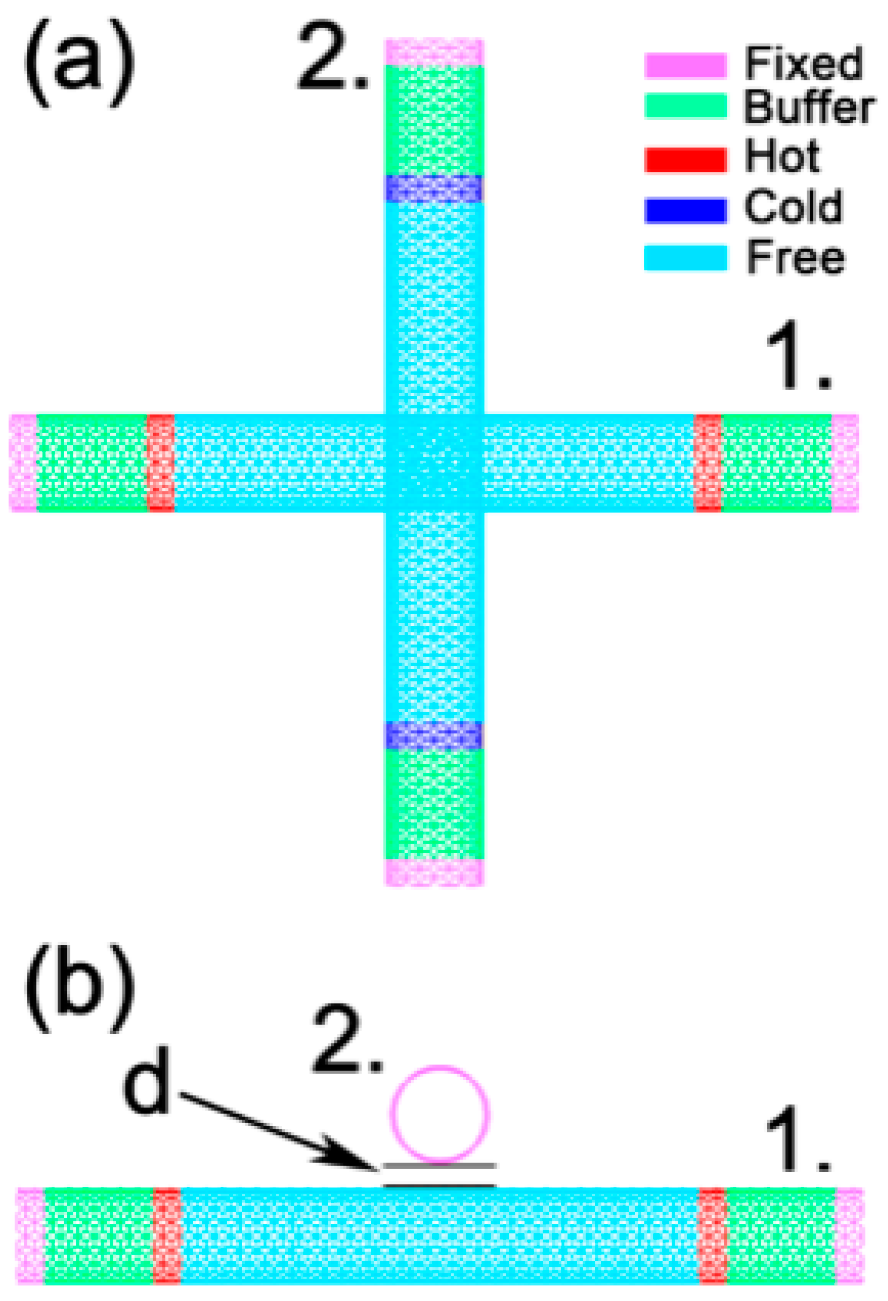
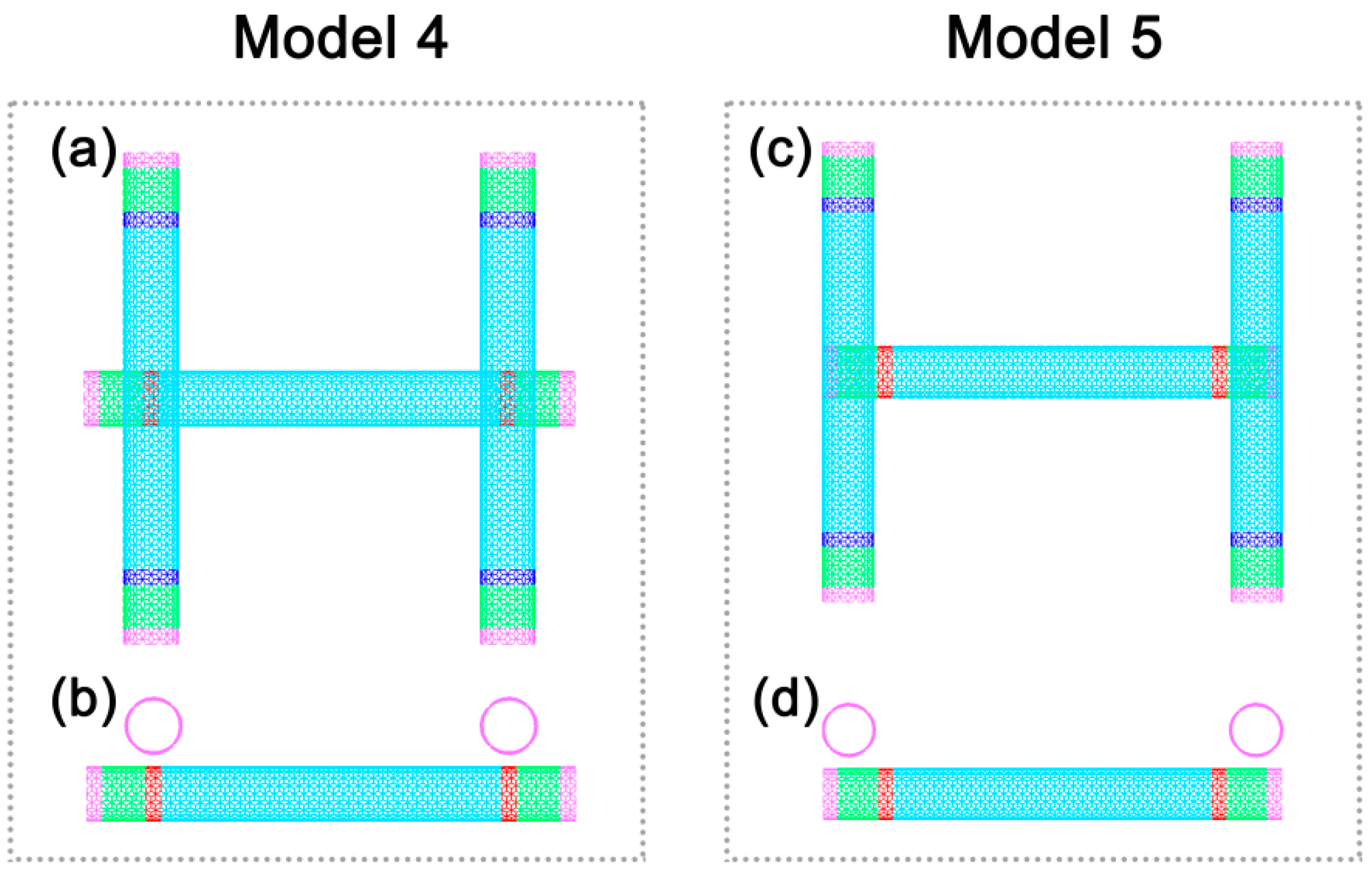
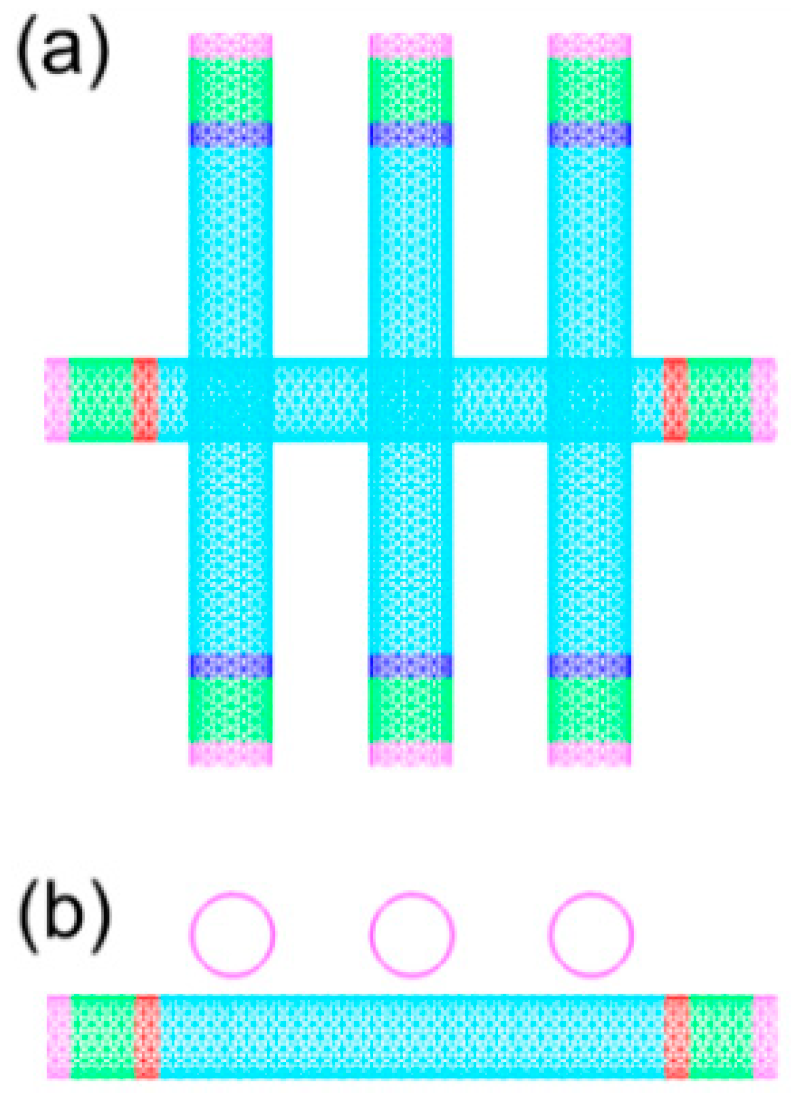
2. Materials and Methods
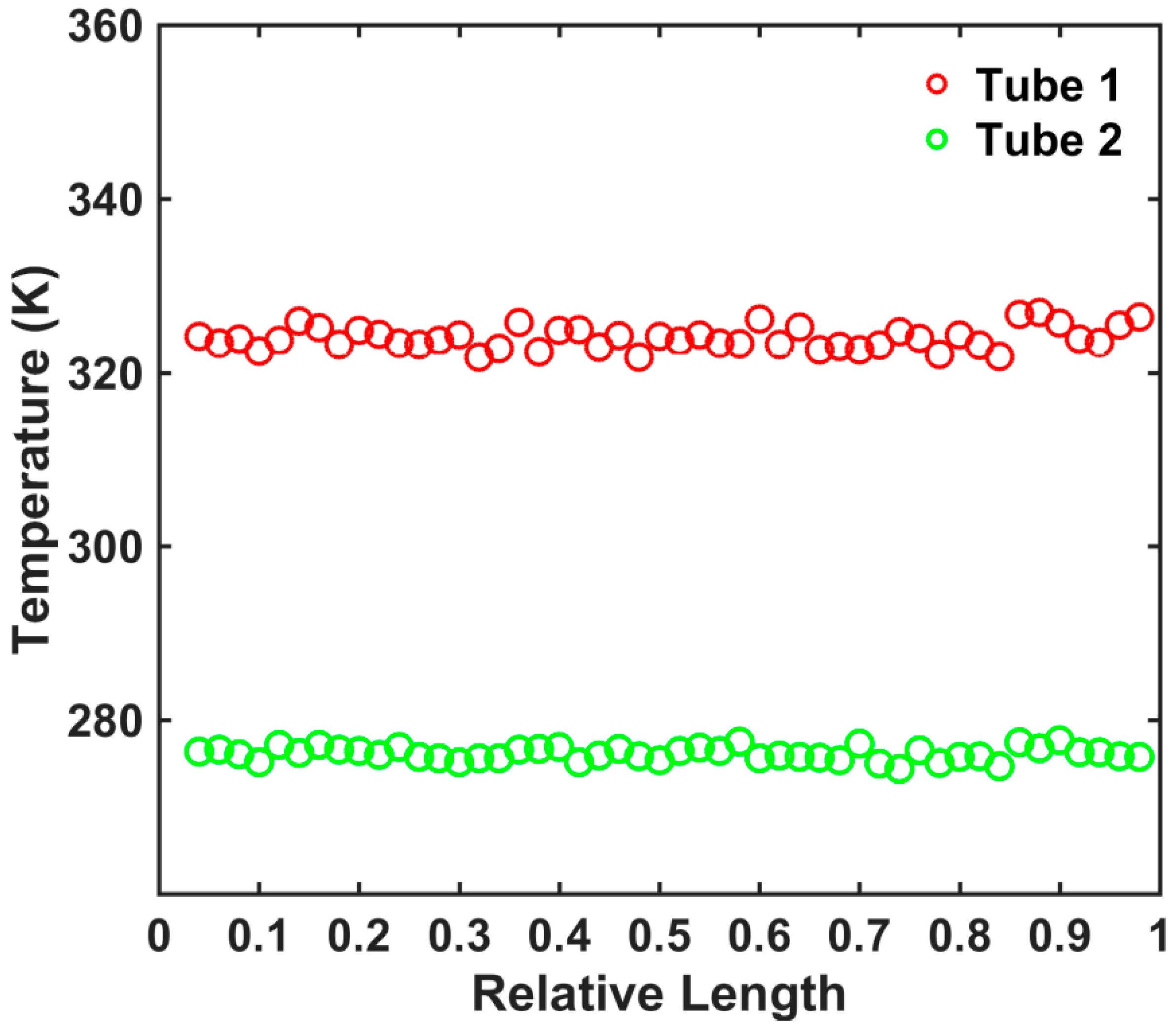
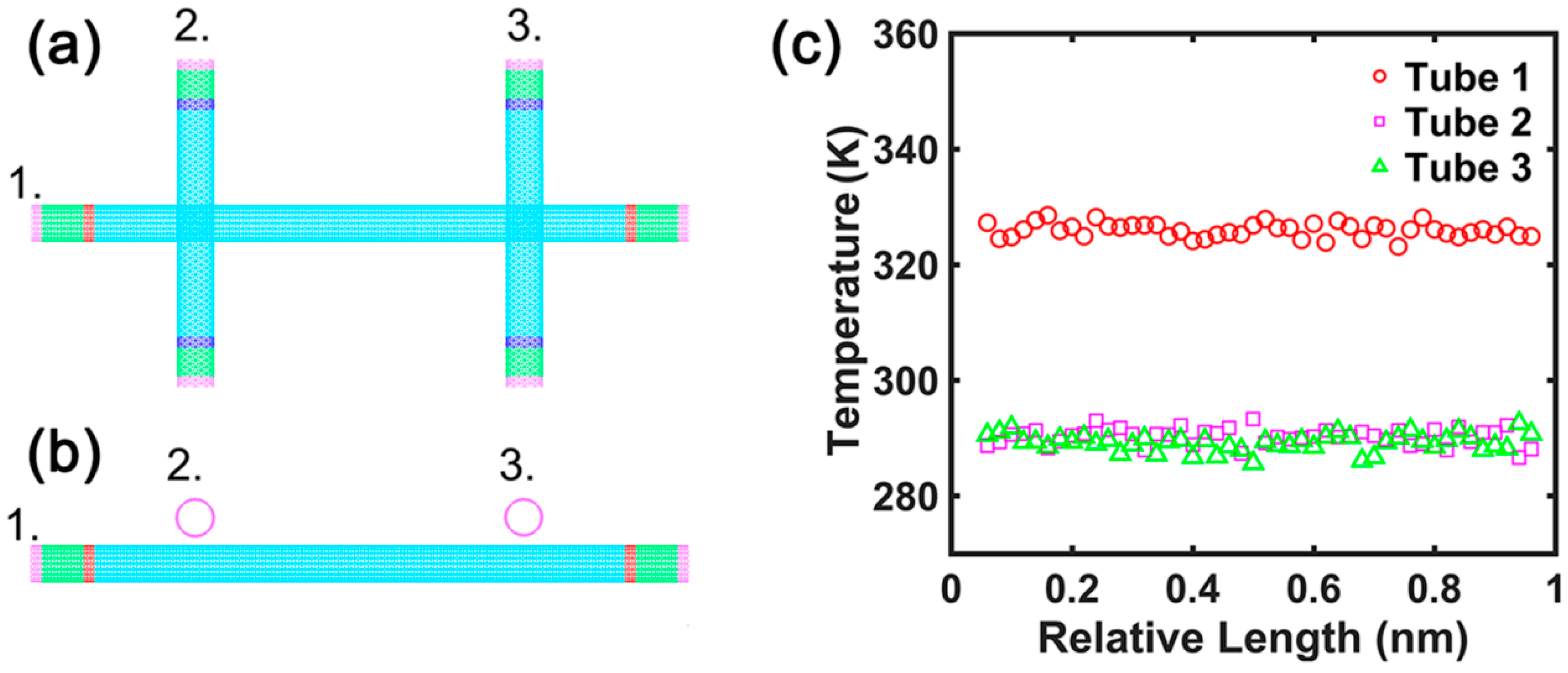
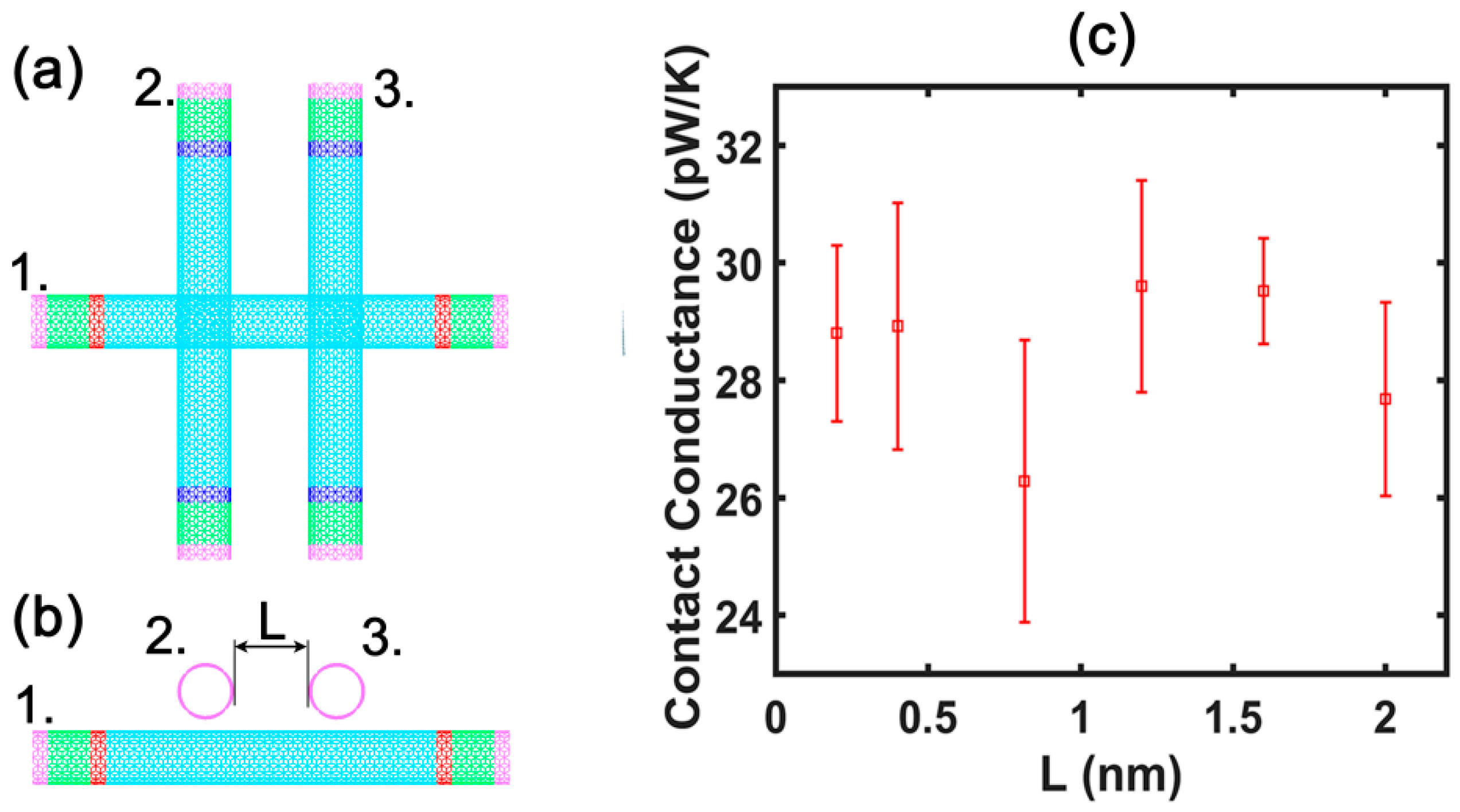
3. Results and Discussion
Contact Conductance
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56. [Google Scholar] [CrossRef]
- Berber, S.; Kwon, Y.K.; Tomanek, D. Unusually high thermal conductivity of carbon nanotubes. Phys. Rev. Lett. 2000, 84, 4613. [Google Scholar] [CrossRef] [PubMed]
- Pop, E.; Mann, D.; Wang, Q.; Goodson, K.; Dai, H. Thermal conductance of an individual single-wall carbon nanotube above room temperature. Nano Lett. 2006, 6, 96–100. [Google Scholar] [CrossRef] [PubMed]
- Marconnet, A.M.; Panzer, M.A.; Goodson, K.E. Thermal conduction phenomena in carbon nanotubes and related nanostructured materials. Rev. Mod. Phys. 2013, 85, 1295. [Google Scholar] [CrossRef]
- Zhou, Q.L.; Meng, F.Y.; Liu, Z.H.; Shi, S.Q. The thermal conductivity of carbon nanotubes with defects and intramolecular junctions. J. Nanomater. 2013, 2013, 842819. [Google Scholar] [CrossRef]
- Feng, D.L.; Feng, Y.H.; Chen, Y.; Li, W.; Zhang, X.X. Effects of doping, Stone-Wales and vacancy defects on thermal conductivity of single-wall carbon nanotubes. Chin. Phys. B 2013, 22, 016501. [Google Scholar] [CrossRef]
- Park, J.; Bifano, M.F.P.; Prakash, V. Sensitivity of thermal conductivity of carbon nanotubes to defect concentrations and heat-treatment. J. Appl. Phys. 2013, 113, 034312. [Google Scholar] [CrossRef]
- Ventura, I.A.; Rahaman, A.; Lubineau, G. The thermal properties of a carbon nanotube-enriched epoxy: Thermal conductivity, curing, and degradation kinetics. J. Appl. Polym. Sci. 2013, 130, 2722–2733. [Google Scholar] [CrossRef]
- Prasher, R.S.; Hu, X.J.; Chalopin, Y.; Mingo, N.; Lofgreen, K.; Volz, S.; Cleri, F.; Keblinski, P. Turning carbon nanotubes from exceptional heat conductors into insulators. Phys. Rev. Lett. 2009, 102, 105901. [Google Scholar] [CrossRef] [PubMed]
- Zhong, H.L.; Lukes, J.R. Interfacial thermal resistance between carbon nanotubes: Molecular dynamics simulations and analytical thermal modeling. Phys. Rev. B 2006, 74, 125403. [Google Scholar] [CrossRef]
- Maruyama, S.; Igarashi, Y.; Taniguchi, Y.; Shiomi, J. Anisotropic heat transfer of single-walled carbon nanotubes. J. Therm. Sci. Technol. 2006, 1, 138–148. [Google Scholar] [CrossRef]
- Xu, Z.; Buehler, M.J. Nanoengineering heat transfer performance at carbon nanotube interfaces. ACS Nano 2009, 3, 2767–2775. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Waltermire, S.; Chen, Y.; Zinn, A.A.; Xu, T.T.; Li, D. Contact thermal resistance between individual multiwall carbon nanotubes. Appl. Phys. Lett. 2010, 96, 023109. [Google Scholar] [CrossRef]
- Chalopin, Y.; Volz, S.; Mingo, N. Upper bound to the thermal conductivity of carbon nanotube pellets. J. Appl. Phys. 2009, 105, 084301. [Google Scholar] [CrossRef]
- Chalopin, Y.; Volz, S.; Mingo, N. Thermoelectric properties of nanostructured Si1-xGex and potential for further improvement. J. Appl. Phys. 2010, 108, 124306. [Google Scholar] [CrossRef]
- Volkov, A.N.; Zhigilei, L.V. Scaling laws and mesoscopic modeling of thermal conductivity in carbon nanotube materials. Phys. Rev. Lett. 2010, 104, 215902. [Google Scholar] [CrossRef]
- Volkov, A.N.; Zhigilei, L.V. Heat conduction in carbon nanotube materials: Strong effect of intrinsic thermal conductivity of carbon nanotubes. Appl. Phys. Lett. 2012, 101, 043113. [Google Scholar] [CrossRef]
- Yang, X.M.; Chen, D.C.; Han, Z.H.; Ma, X.S.; To, A.C. Effects of welding on thermal conductivity of randomly oriented carbon nanotube networks. Int. J. Heat Mass Transf. 2014, 70, 803–810. [Google Scholar] [CrossRef]
- Zhang, K.J.; Yadav, A.; Kim, K.H.; Oh, Y.; Islam, M.F.; Uher, C.; Pipe, K.P. Thermal and electrical transport in ultralow density single-walled carbon nanotube networks. Adv. Mater. 2013, 25, 2926–2931. [Google Scholar] [CrossRef]
- Itkis, M.E.; Borondics, F.; Yu, A.; Haddon, R.C. Thermal conductivity measurements of semitransparent single-walled carbon nanotube films by a bolometric technique. Nano Lett. 2007, 7, 900–904. [Google Scholar] [CrossRef]
- Cummings, A.; Osman, M.; Srivastava, D.; Menon, M. Thermal conductivity of Y-junction carbon nanotubes. Phys. Rev. B 2004, 70, 115405. [Google Scholar] [CrossRef]
- Ren, C.; Xu, Z.; Zhang, W.; Li, Y.; Zhu, Z.; Huai, P. Theoretical study of heat conduction in carbon nanotube hetero-junctions. Phys. Lett. A 2010, 374, 1860–1865. [Google Scholar] [CrossRef]
- Yang, X.M.; Chen, D.C.; Du, Y.R.; To, A.C. Heat conduction in extended X-junctions of single-walled carbon nanotubes. J. Phys. Chem. Solids 2014, 75, 123–129. [Google Scholar] [CrossRef]
- Plimpton, S.J. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, M.; Poulikakos, D. A low-frequency wave motion mechanism enables efficient energy transport in carbon nanotubes at high heat fluxes. Nano Lett. 2012, 12, 3410–3416. [Google Scholar] [CrossRef]
- Salaway, R.N.; Zhigilei, L.V. Molecular dynamics simulations of thermal conductivity of carbon nanotubes: Resolving the effects of computational parameters. Int. J. Heat Mass Tranf. 2014, 70, 954–964. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, Y.; Chen, Y.; Hu, M. Robustly engineering thermal conductivity of bilayer graphene by interlayer bonding. Sci. Rep. 2016, 6, 22011. [Google Scholar] [CrossRef] [PubMed]
- Ikeshoji, T.; Hafskjold, B. Non-equilibrium molecular dynamics calculation of heat conduction in liquid and through liquid-gas interface. Mol. Phys. 1994, 81, 251–261. [Google Scholar] [CrossRef]
- Yang, X.M.; To, A.C.; Tian, R. Anomalous heat conduction behavior in thin finite-size silicon nanowires. Nanotechnology 2010, 21, 155704. [Google Scholar] [CrossRef] [PubMed]
- Evans, W.J.; Shen, M.; Keblinski, P. Inter-tube thermal conductance in carbon nanotubes arrays and bundles: Effects of contact area and pressure. Appl. Phys. Lett. 2012, 100, 261908. [Google Scholar] [CrossRef]
- Hu, G.J.; Cao, B.Y. Thermal resistance between crossed carbon nanotubes: Molecular dynamics simulations and analytical modeling. J. Appl. Phys. 2013, 114, 224308. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Zhang, X.; Cao, B. The Effect of Thermal Contact Number on the Tube–Tube Contact Conductance of Single-Walled Carbon Nanotubes. Nanomaterials 2019, 9, 477. https://doi.org/10.3390/nano9030477
Yang X, Zhang X, Cao B. The Effect of Thermal Contact Number on the Tube–Tube Contact Conductance of Single-Walled Carbon Nanotubes. Nanomaterials. 2019; 9(3):477. https://doi.org/10.3390/nano9030477
Chicago/Turabian StyleYang, Xueming, Xinyao Zhang, and Bingyang Cao. 2019. "The Effect of Thermal Contact Number on the Tube–Tube Contact Conductance of Single-Walled Carbon Nanotubes" Nanomaterials 9, no. 3: 477. https://doi.org/10.3390/nano9030477
APA StyleYang, X., Zhang, X., & Cao, B. (2019). The Effect of Thermal Contact Number on the Tube–Tube Contact Conductance of Single-Walled Carbon Nanotubes. Nanomaterials, 9(3), 477. https://doi.org/10.3390/nano9030477




