Computational Screening of Metal–Organic Framework Membranes for the Separation of 15 Gas Mixtures
Abstract
:1. Introduction
2. Model and Methods
2.1. Model
2.2. Methods
3. Results
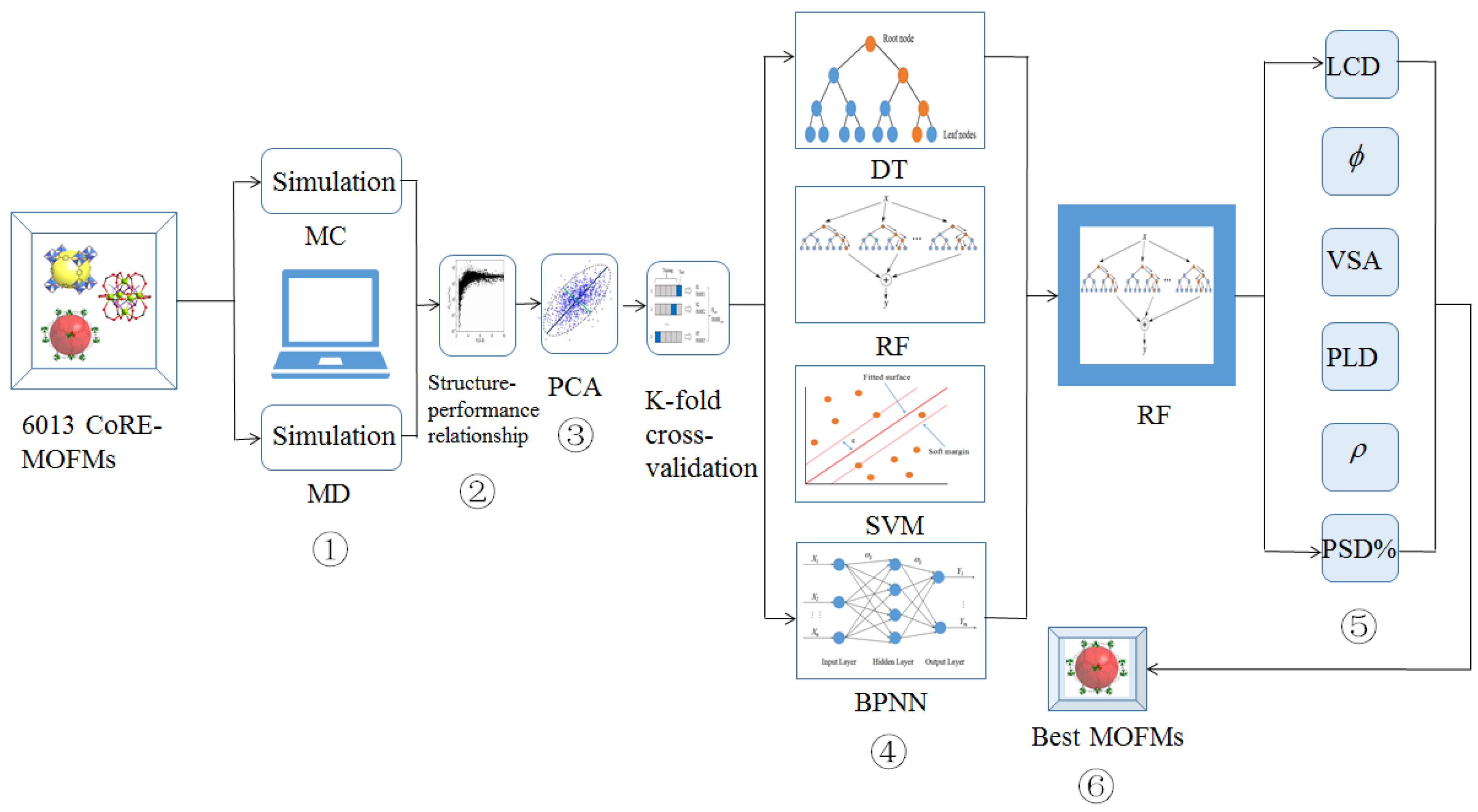
3.1. Map for Project Structure
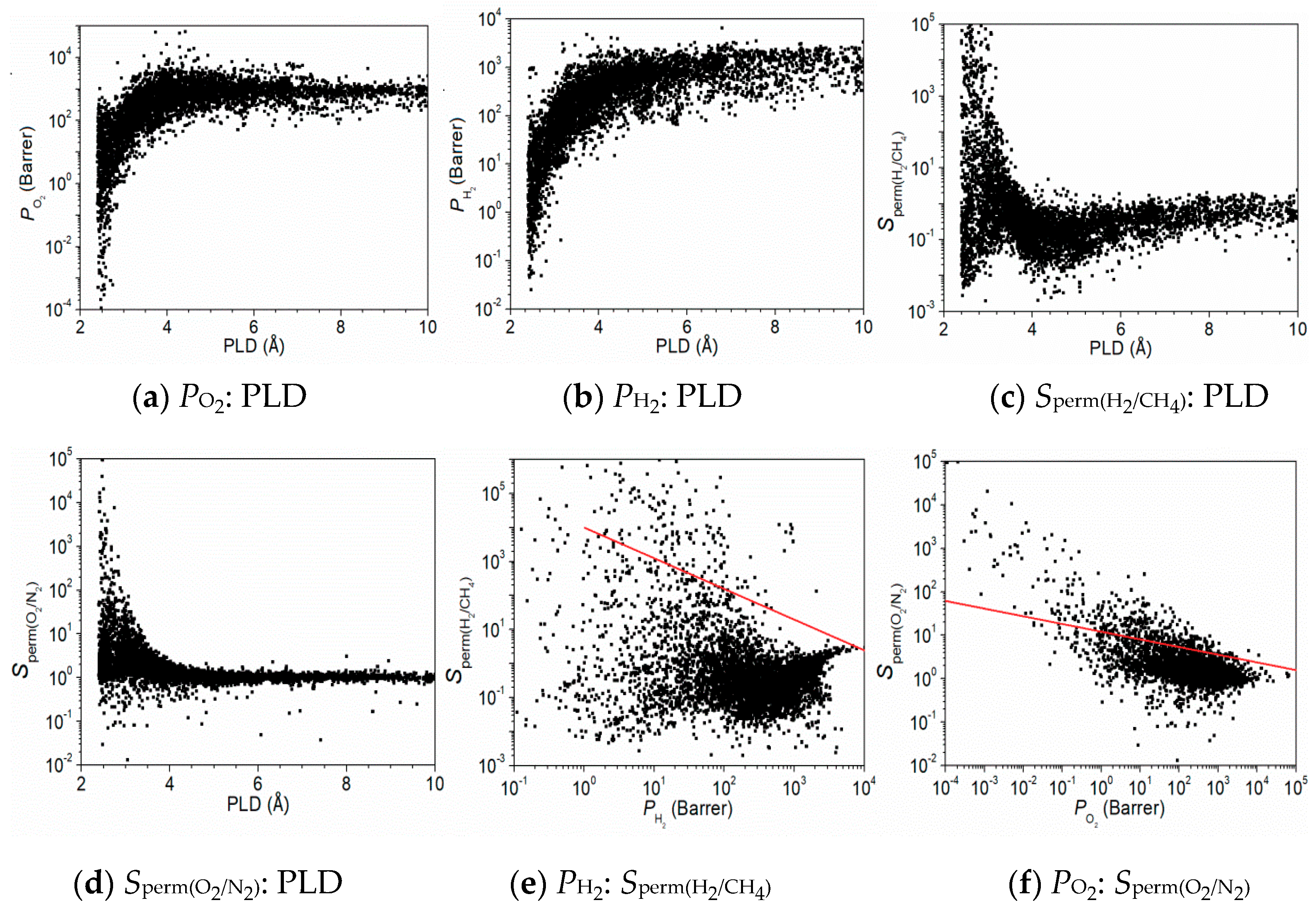
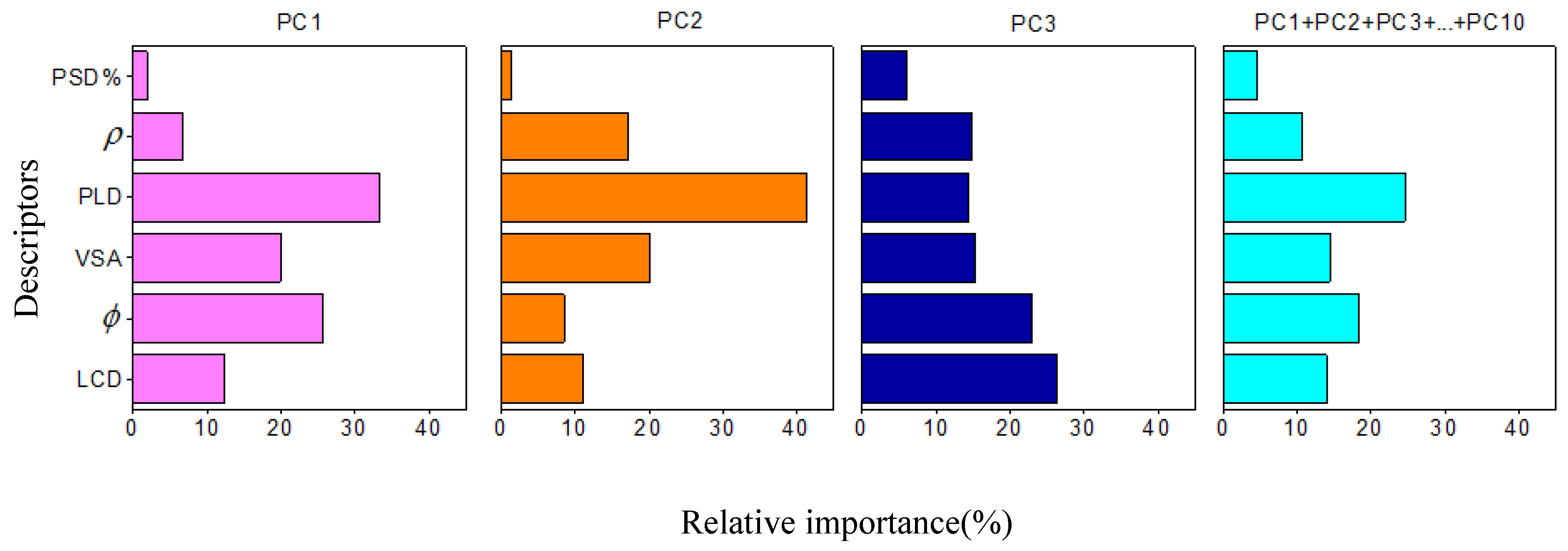
3.2. Feature Descriptors and Performance Metrics
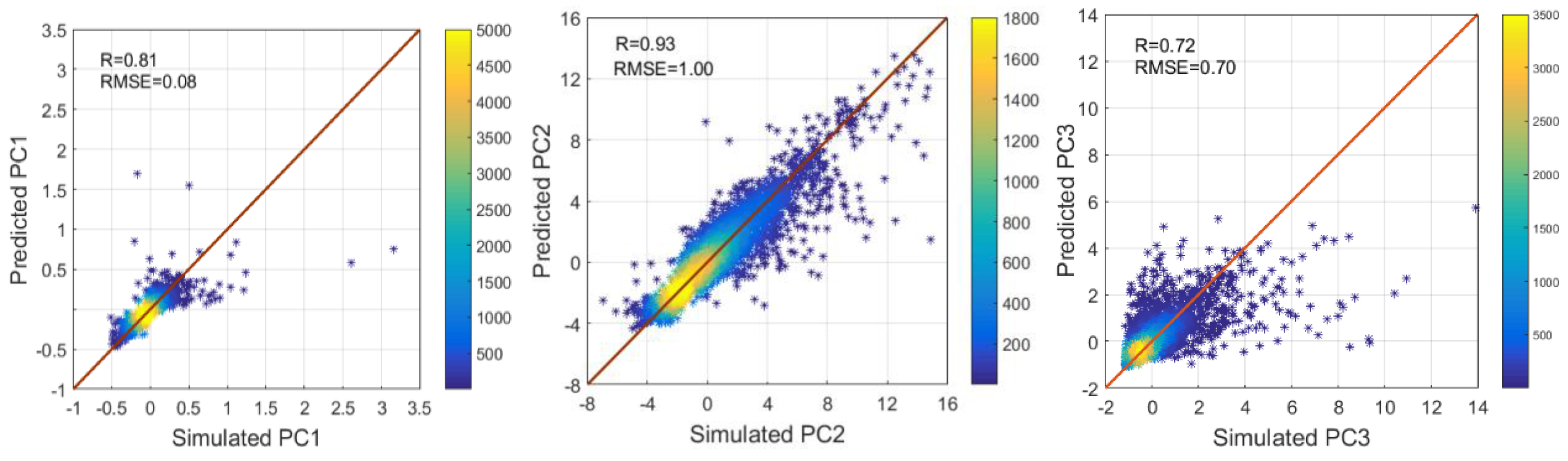
3.3. Machine Learning
3.4. Best CoRE-MOFMs
4. Conclusion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, S.H.; Ding, J.; Zhong, X.S.; Cheng, D.Y.; Hu, X.Y.; Li, X.L. A feasible energy-saving analysis of a new system for CO2 cryogenic capture. Int. J. Low-Carbon Technol. 2016, 11, 235–239. [Google Scholar] [CrossRef]
- Chiappe, C.; Pomelli, C.S. Hydrogen Sulfide and Ionic Liquids: Absorption, Separation, and Oxidation. Top. Curr. Chem. 2017, 52, 375–400. [Google Scholar] [CrossRef]
- Li, H.F.; Su, S.; Hu, S.; Xu, K.; Jiang, L.; Wang, Y.; Xu, J.; Xiang, J. Effect of preparation conditions on MnxOy /Al2O3 sorbent for H2S removal from high-temperature synthesis gas. Fuel 2018, 223, 115–124. [Google Scholar] [CrossRef]
- Linga, P.; Kumar, R.; Englezos, P. Gas hydrate formation from hydrogen/carbon dioxide and nitrogen/carbon dioxide gas mixtures. Chem. Eng. Sci. 2007, 62, 4268–4276. [Google Scholar] [CrossRef]
- Linga, P.; Kumar, R.; Englezos, P. The clathrate hydrate process for post and pre-combustion capture of carbon dioxide. J. Hazard. Mater. 2007, 149, 625–629. [Google Scholar] [CrossRef] [PubMed]
- Kertik, A.; Wee, L.H.; Pfannmoller, M.; Bals, S.; Martens, J.A.; Vankelecom, L.F.J. Highly selective gas separation membrane using in situ amorphised metal–organic frameworks. Energy. Environ. Sci. 2017, 10, 2342–2351. [Google Scholar] [CrossRef]
- Liu, G.P.; Chernikova, V.; Liu, Y.; Zhang, K.; Belmabkhout, Y.; Shekhah, O.; Zhang, C.; Yi, S.L.; Eddaoudi, M.; Koros, W.J. Mixed matrix formulations with MOF molecular sieving for key energy-intensive separations. Nat. Mater. 2018, 17, 283–289. [Google Scholar] [CrossRef]
- Yang, Y.Q.; Chuah, C.Y.; Nie, L.; Bae, T.H. Enhancing the mechanical strength and CO2/CH4 separation performance of polymeric membranes by incorporating amine-appended porous polymers. J. Membr. Sci. 2019, 569, 149–156. [Google Scholar] [CrossRef]
- Jusoh, N.; Yeong, Y.F.; Lau, K.K.; Shariff, A.M. Enhanced gas separation performance using mixed matrix membranes containing zeolite T and 6FDA-durene polyimide. J. Membr. Sci. 2017, 525, 175–186. [Google Scholar] [CrossRef]
- Freeman, B.D. Basis of Permeability/Selectivity Tradeoff Relations in Polymeric Gas Separation Membranes. Macromolecules 1999, 32, 375–380. [Google Scholar] [CrossRef]
- Kosinov, N.; Gascon, J.; Kapteijn, F.; Hensen, E.J.M. Recent developments in zeolite membranes for gas separation. J. Mem. Sci. 2015, 499, 65–79. [Google Scholar] [CrossRef]
- Yaghi, O.M.; O’keeffe, M.; Ockwig, N.W.; Chae, H.K.; Eddaoudi, M.; Kim, J. Reticular synthesis and the design of new materials. Nature 2003, 423, 705–714. [Google Scholar] [CrossRef]
- Rezaei, F.; Lawson, S.; Hosseini, H.; Thakkar, H.; Hajari, A.; Monjezi, S.; Rownaghi, A.A. MOF-74 and UTSA-16 Film Growth on Monolithic Structures and their CO2 Adsorption Performance. Chem. Eng. J. 2017, 313, 1346–1353. [Google Scholar] [CrossRef]
- Yu, J.; Xie, L.H.; Li, J.R.; Ma, Y.; Seminario, J.M.; Balbuena, P.B. CO2 Capture and Separations Using MOFs: Computational and Experimental Studies. Chem. Rev. 2017, 117, 9674–9754. [Google Scholar] [CrossRef]
- Li, H.; Wang, K.C.; Sun, Y.J.; Lollar, C.T.; Li, J.L.; Zhou, H.C. Recent advances in gas storage and separation using metal–organic frameworks. Mat. Today. 2018, 21, 108–121. [Google Scholar] [CrossRef]
- Smit, B. Screening Materials Relevant for Energy Technologies. Chimia. Int. J. Chem. 2015, 69, 248–252. [Google Scholar] [CrossRef]
- Huang, Y.B.; Liang, J.; Wang, X.S.; Cao, R. Multifunctional metal-organic framework catalysts: synergistic catalysis and tandem reactions. Chem. Soc. Rev. 2017, 46, 126–157. [Google Scholar] [CrossRef]
- Altintas, C.; Avci, G.; Daglar, H.; Gulcay, E.; Erucar, I.; Keskin, S. Computer simulations of 4240 MOF membranes for H2/CH4 separations: insights into structure-performance relations. J. Mater. Chem. A 2018, 6, 5836–5847. [Google Scholar] [CrossRef]
- Hou, J.M.; Wei, Y.Y.; Zhou, S.; Wang, Y.J.; Wang, H.H. Highly efficient H2/CO2 separation via an ultrathin metal-organic framework membrane. Chem. Eng. Sci. 2018, 182, 180–188. [Google Scholar] [CrossRef]
- Wang, X.R.; Chi, C.L.; Zhang, K.; Qian, Y.H.; Gupta, K.M.; Kang, Z.X.; Jiang, J.W.; Zhao, D. Reversed thermo-switchable molecular sieving membranes composed of two-dimensional metal-organic nanosheets for gas separation. Nat. Commun. 2017, 8, 14460–14470. [Google Scholar] [CrossRef]
- Borboudakis, G.; Stergiannakos, T.; Frysali, M.; Klontzas, E.; Tsamardinos, L.; Froudakis, G.E. Chemically intuited, large-scale screening of MOFs by machine learning techniques. Comput. Mat. 2017, 3, 1–40. [Google Scholar] [CrossRef]
- Anderson, R.; Rodgers, J.; Argueta, E.; Biong, A.; Gomez-Gualdron, D.A. Role of pore chemistry and topology in the CO2 capture capabilities of MOFs: from molecular simulation to machine learning. Chem. Mater. 2018, 30, 6325–6337. [Google Scholar] [CrossRef]
- Avci, G.; Velioglu, S.; Keskin, S. High-Throughput Screening of MOF Adsorbents and Membranes for H2 Purification and CO2 Capture. Appl. Mater. Interfaces 2018, 10, 33693–33706. [Google Scholar] [CrossRef] [PubMed]
- Daglar, H.; Keskin, S. Computational Screening of Metal–Organic Frameworks for Membrane-Based CO2/N2/H2O Separations: Best Materials for Flue Gas Separation. J. Phys. Chem. C 2018, 122, 17347–17357. [Google Scholar] [CrossRef]
- Qiao, Z.W.; Xu, Q.S.; Jiang, J.W. High-throughput computational screening of metal-organic framework membranes for upgrading of natural gas. J. Membr. Sci. 2018, 551, 47–54. [Google Scholar] [CrossRef]
- Watanabe, T.; Sholl, D.S. Accelerating applications of metal-organic frameworks for gas adsorption and separation by computational screening of materials. Langmuir 2012, 28, 14114–14128. [Google Scholar] [CrossRef]
- Rowe, B.W.; Robeson, L.M.; Freeman, B.D.; Paul, D.R. Influence of temperature on the upper bound: Theoretical considerations and comparison with experimental results. J. Mem. Sci. 2010, 360, 58–69. [Google Scholar] [CrossRef]
- Robeson, L.M. Polymer membranes for gas separation. Curr. Opin. Solid State Mat. Sci. 1999, 4, 549–552. [Google Scholar] [CrossRef]
- Baker, R. Future Directions of Membrane Gas Separation Technology. Ind. Eng. Chem. Res. 2002, 41, 5–10. [Google Scholar] [CrossRef]
- Smith, Z.P.; Tiwari, R.R.; Dose, M.E.; Gleason, K.L.; Murphy, T.M.; Sanders, D.F.; Gunawan, G.; Robeson, L.M.; Paul, D.R.; Freeman, B.D. Influence of Diffusivity and Sorption on Helium and Hydrogen Separations in Hydrocarbon, Silicon, and Fluorocarbon-Based Polymers. Macromolecules 2014, 47, 3170–3184. [Google Scholar] [CrossRef]
- Chung, Y.G.; Camp, J.; Haranczyr, M.; Sikora, B.J.; Bury, W.; Krungleviciute, V.; Yildirim, T.; Farha, O.K.; Sholl, D.S.; Snurr, R.Q. Computation-Ready, Experimental Metal–Organic Frameworks: A Tool To Enable High-Throughput Screening of Nanoporous Crystals. Chem. Mat. 2014, 26, 6185–6192. [Google Scholar] [CrossRef]
- Available online: https://github.com/gregchung/gregchung.github.io/blob/master/CoRE-MOFs/structure-doi-CoRE-MOFsV2.0.csv (accessed on 6 July 2017).
- Rappe, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A.; Skiff, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Kadantsev, E.S.; Boyd, P.G.; Daff, T.D.; Woo, T.K. Fast and Accurate Electrostatics in Metal Organic Frameworks with a Robust Charge Equilibration Parameterization for High-Throughput Virtual Screening of Gas Adsorption. J. Phys. Chem. Lett. 2013, 4, 3056–3061. [Google Scholar] [CrossRef]
- Willems, T.F.; Rycroft, C.H.; Kazi, M.; Meza, J.C.; Haranczyk, M. Algorithms and tools for high-throughput geometry-based analysis of crystalline porous materials. Microporous Mesoporous Mater. 2012, 149, 134–141. [Google Scholar] [CrossRef]
- Dubbeldam, D.; Calero, S.; Ellis, D.E.; Snurr, R.Q. RASPA: molecular simulation software for adsorption and diffusion in flexible nanoporous materials. Mol. Simul. 2016, 42, 81–101. [Google Scholar] [CrossRef]
- Potoff, J.J.; Siepmann, J.I. Vapor–liquid equilibria of mixtures containing alkanes, carbon dioxide, and nitrogen. AIChE. J. 2001, 47, 1676–1682. [Google Scholar] [CrossRef]
- Shah, M.S.; Tsapatsis, M.; Siepmann, J.I. Development of the Transferable Potentials for Phase Equilibria Model for Hydrogen Sulfide. J. Phys. Chem. B 2015, 119, 7041–7052. [Google Scholar] [CrossRef]
- Robeson, L.M. The upper bound revisited. J. Membr. Sci. 2008, 320, 390–400. [Google Scholar] [CrossRef]
| ML | R Values | RMSE | ||||
|---|---|---|---|---|---|---|
| PC1 | PC2 | PC3 | PC1 | PC2 | PC3 | |
| DT | 0.80 | 0.89 | 0.62 | 0.081 | 1.190 | 0.601 |
| RF | 0.81 | 0.93 | 0.72 | 0.080 | 1.000 | 0.700 |
| SVM | 0.79 | 0.89 | 0.63 | 0.080 | 1.210 | 0.790 |
| BPNN | 0.74 | 0.87 | 0.60 | 0.090 | 1.230 | 0.820 |
| No. | i/j | CSD code | LCD (Å) | φ | VSA (m2/cm3) | PLD (Å) | ρ (g/m3) | PSD% | Pi (Barrer) | Pj (Barrer) | Sperm(i/j) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | CO2/CH4 | XUZDUS c | 4.25 | 0.16 | 15.50 | 2.99 | 1.82 | 3.31 | 1.26 × 109 | 1.75 × 103 | 7.16 × 105 |
| XEJXER | 4.12 | 0.19 | 4.33 | 3.58 | 1.60 | 0 | 1.33 × 108 | 9.26 × 102 | 1.44 × 105 | ||
| 2 | CO2/N2 | ELUQIM06 | 2.89 | 0.04 | 0 | 2.41 | 1.80 | 100 | 7.20 × 106 | 7.72 × 102 | 9.32 × 103 |
| NHBZZN10 | 3.41 | 0.08 | 0 | 2.94 | 1.54 | 68.84 | 1.57 × 104 | 2.32 × 102 | 67.63 | ||
| 3 | H2/CO2 | TUMGOX a | 3.47 | 0.27 | 0 | 2.61 | 1.87 | 54.55 | 7.75 × 103 | 1.76 × 103 | 4.39 |
| HEDCEA | 4.76 | 0.27 | 226.10 | 2.93 | 1.28 | 2.15 | 2.35 × 103 | 5.95 × 102 | 3.95 | ||
| 4 | H2S/CH4 | SEYFAE | 4.14 | 0.28 | 87.08 | 3.31 | 2.03 | 0.43 | 5.57 × 104 | 7.32 × 102 | 76.12 |
| GUXPUL | 2.79 | 0.02 | 0 | 2.58 | 1.60 | 100 | 4.11 × 104 | 3.15 × 103 | 13.07 | ||
| 5 | H2/CH4 | TESGUU | 4.82 | 0.26 | 338.16 | 3.58 | 1.92 | 0 | 8.90 × 102 | 0.07 | 1.20 × 104 |
| ZIJVOF | 5.29 | 0.43 | 622.86 | 3.32 | 1.23 | 0.10 | 9.35 × 102 | 0.10 | 9.37 × 103 | ||
| 6 | H2/O2 | TOWPAY b | 3.47 | 0.27 | 0 | 2.61 | 1.87 | 54.55 | 7.75 × 103 | 1.89 × 103 | 4.10 |
| POWBIO | 4.34 | 0.19 | 142.64 | 2.60 | 3.66 | 1.54 | 4.56 × 103 | 1.18 × 103 | 3.87 | ||
| 7 | CO2/H2S | FAPYEA | 2.53 | 0.00 | 0 | 2.46 | 1.58 | 100 | 1.93 × 109 | 5.11 × 105 | 3.78 × 103 |
| XUZDUS c | 4.25 | 0.16 | 15.50 | 2.99 | 1.82 | 3.31 | 1.26 × 109 | 6.80 × 106 | 1.85 × 102 | ||
| 8 | H2/N2 | TUMGOX a | 3.47 | 0.27 | 0 | 2.61 | 1.87 | 54.55 | 7.75 × 103 | 2.01 × 103 | 3.85 |
| DIMQOH | 4.69 | 0.42 | 626.81 | 3.15 | 1.40 | 2.97 | 3.80 × 103 | 1.12 × 103 | 3.39 | ||
| 9 | He/N2 | TUMGOX a | 3.47 | 0.27 | 0 | 2.61 | 1.87 | 54.55 | 7.11 × 103 | 2.01 × 103 | 3.53 |
| COWXOC d | 5.83 | 0.30 | 517.90 | 2.91 | 1.28 | 0.57 | 7.79 × 103 | 2.43 × 103 | 3.21 | ||
| 10 | He/H2 | BUYNAL | 4.62 | 0.47 | 617.88 | 3.97 | 0.92 | 0 | 20.34 | 5.12 | 3.97 |
| VULKOD | 5.02 | 0.33 | 489.24 | 3.96 | 1.40 | 0.95 | 25.60 | 6.52 | 3.93 | ||
| 11 | He/CH4 | YEKWOC e | 8.21 | 0.50 | 1099.57 | 3.05 | 1.28 | 0 | 1.21 × 102 | 0.11 | 1.15 × 103 |
| COXFOL | 5.01 | 0.33 | 403.58 | 3.19 | 1.43 | 1.70 | 3.24 × 102 | 7.48 | 43.32 | ||
| 12 | N2/CH4 | YEKWOC e | 8.21 | 0.50 | 1099.57 | 3.05 | 1.28 | 0 | 6.82 × 103 | 0.11 | 6.44 × 104 |
| BAHGUN04 | 4.27 | 0.26 | 108.86 | 3.29 | 1.49 | 0 | 6.24 × 105 | 11.11 | 5.62 × 104 | ||
| 13 | He/CO2 | PUPNAQ | 3.59 | 0.15 | 0 | 2.70 | 1.44 | 32.37 | 38.34 | 4.11 | 9.33 |
| TUMGOX a | 3.47 | 0.27 | 0 | 2.61 | 1.87 | 54.55 | 7.11 × 103 | 1.76 × 103 | 4.03 | ||
| 14 | O2/N2 | GETXAG | 3.33 | 0.10 | 0 | 2.61 | 1.54 | 99.99 | 1.11 × 104 | 3.17 × 103 | 3.48 |
| GOLQII | 3.73 | 0.14 | 9.74 | 3.37 | 2.17 | 0 | 8.32 × 102 | 2.48 × 102 | 3.35 | ||
| 15 | He/O2 | COWXOC d | 5.83 | 0.30 | 517.90 | 2.91 | 1.28 | 0.57 | 7.79 × 103 | 2.07 × 103 | 3.76 |
| TOWPAY b | 3.47 | 0.27 | 0 | 2.61 | 1.87 | 54.55 | 7.11 × 103 | 1.89 × 103 | 3.76 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Liang, H.; Peng, F.; Liu, Z.; Liu, J.; Qiao, Z. Computational Screening of Metal–Organic Framework Membranes for the Separation of 15 Gas Mixtures. Nanomaterials 2019, 9, 467. https://doi.org/10.3390/nano9030467
Yang W, Liang H, Peng F, Liu Z, Liu J, Qiao Z. Computational Screening of Metal–Organic Framework Membranes for the Separation of 15 Gas Mixtures. Nanomaterials. 2019; 9(3):467. https://doi.org/10.3390/nano9030467
Chicago/Turabian StyleYang, Wenyuan, Hong Liang, Feng Peng, Zili Liu, Jie Liu, and Zhiwei Qiao. 2019. "Computational Screening of Metal–Organic Framework Membranes for the Separation of 15 Gas Mixtures" Nanomaterials 9, no. 3: 467. https://doi.org/10.3390/nano9030467
APA StyleYang, W., Liang, H., Peng, F., Liu, Z., Liu, J., & Qiao, Z. (2019). Computational Screening of Metal–Organic Framework Membranes for the Separation of 15 Gas Mixtures. Nanomaterials, 9(3), 467. https://doi.org/10.3390/nano9030467






