Tunable Graphene-Based Plasmon-Induced Transparency Based on Edge Mode in the Mid-Infrared Region
Abstract
1. Introduction
2. Structures and Methods
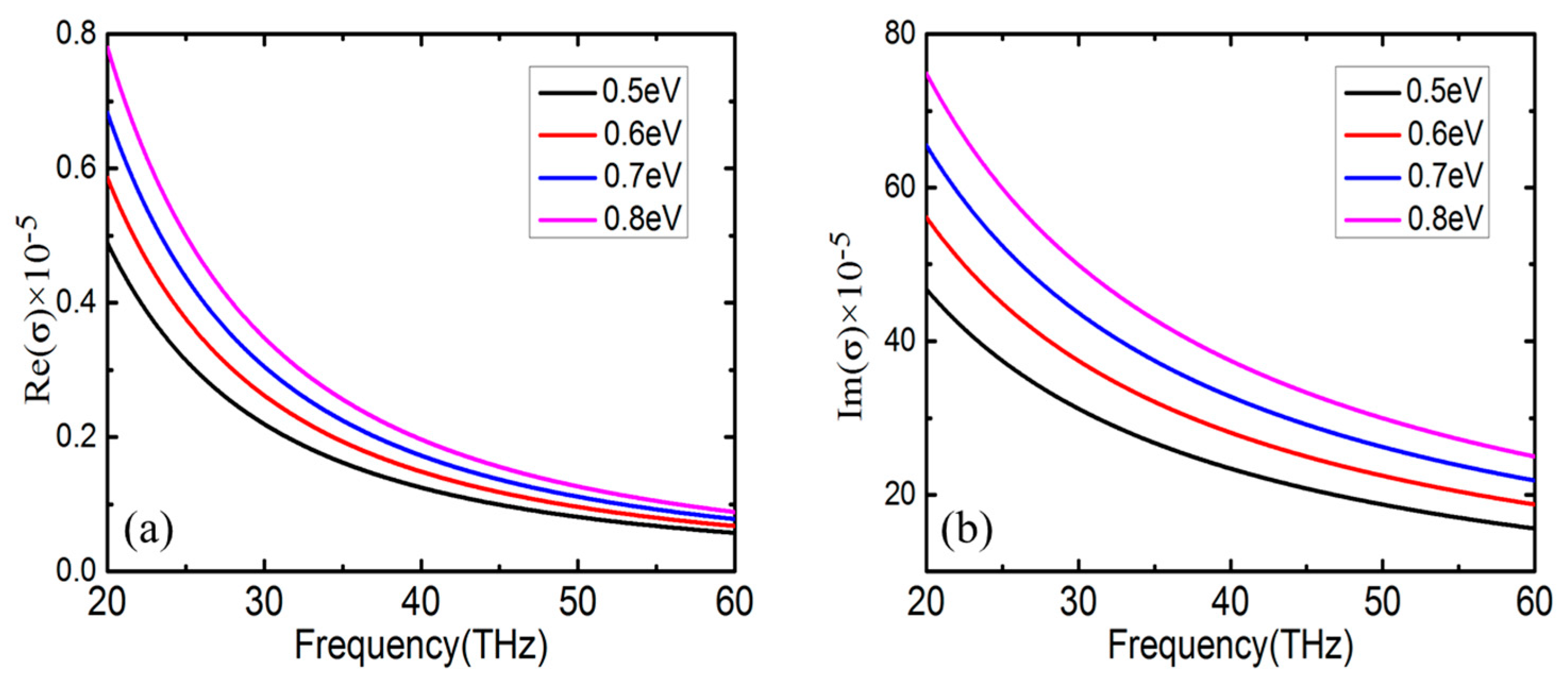
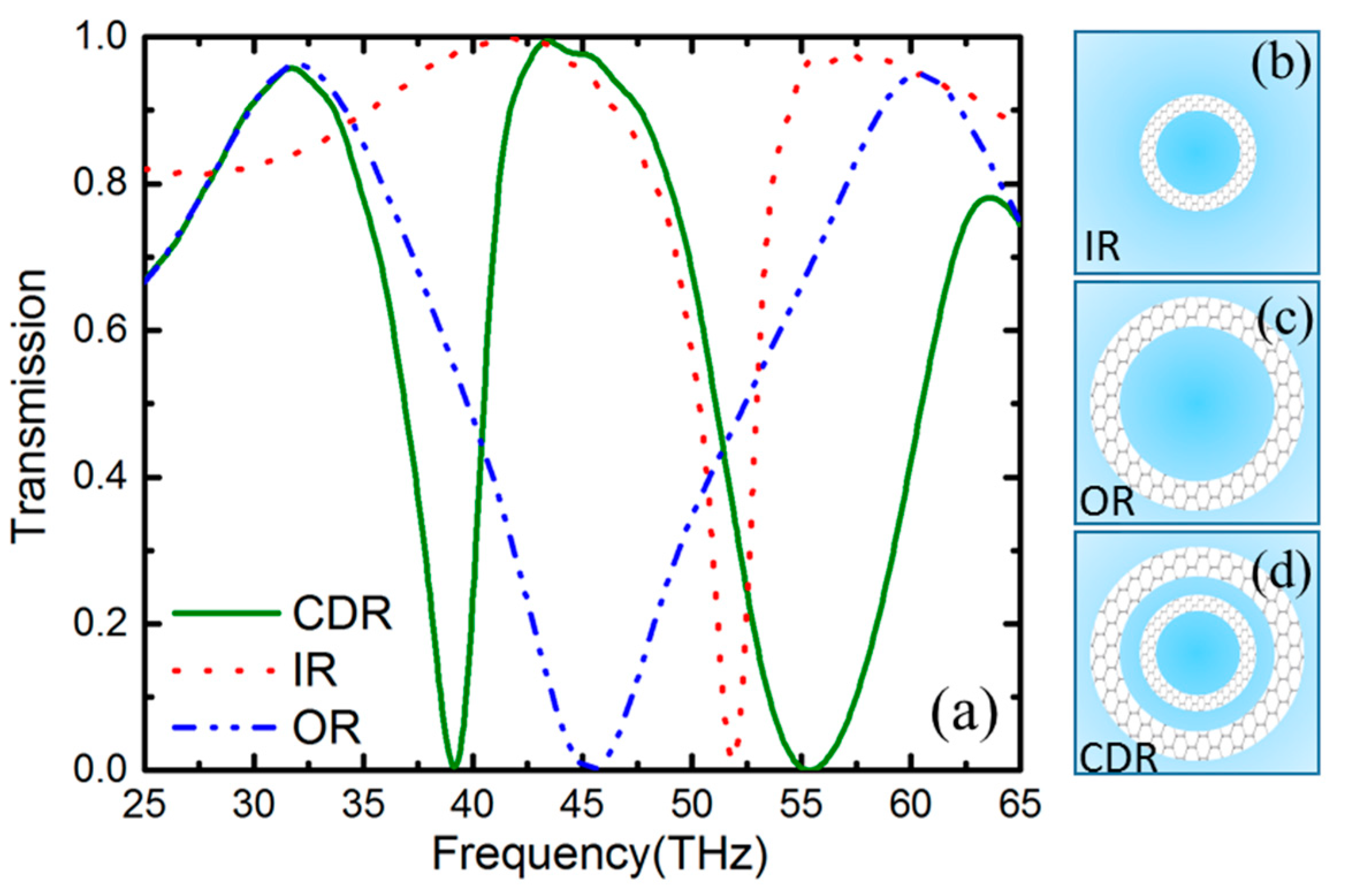
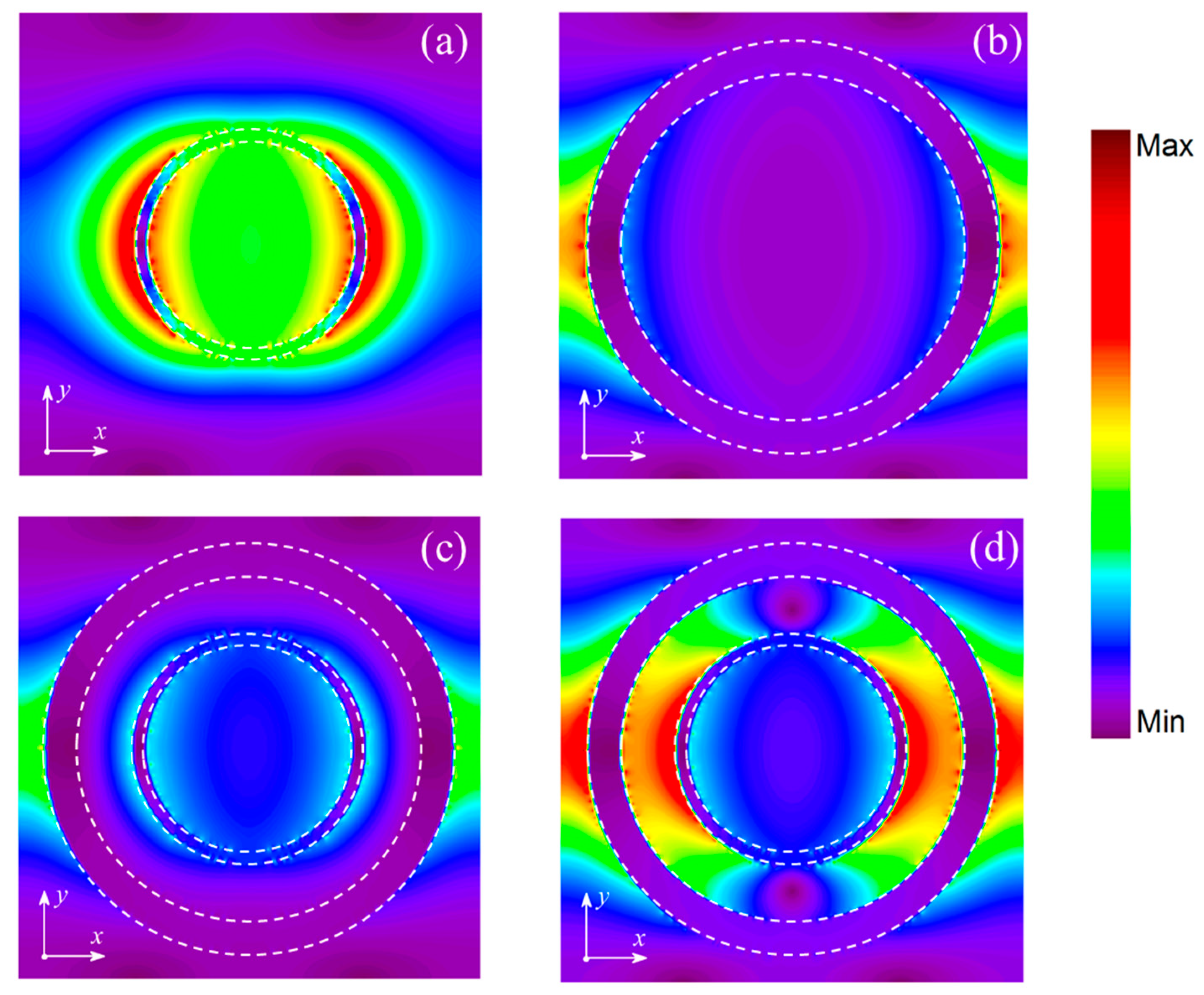
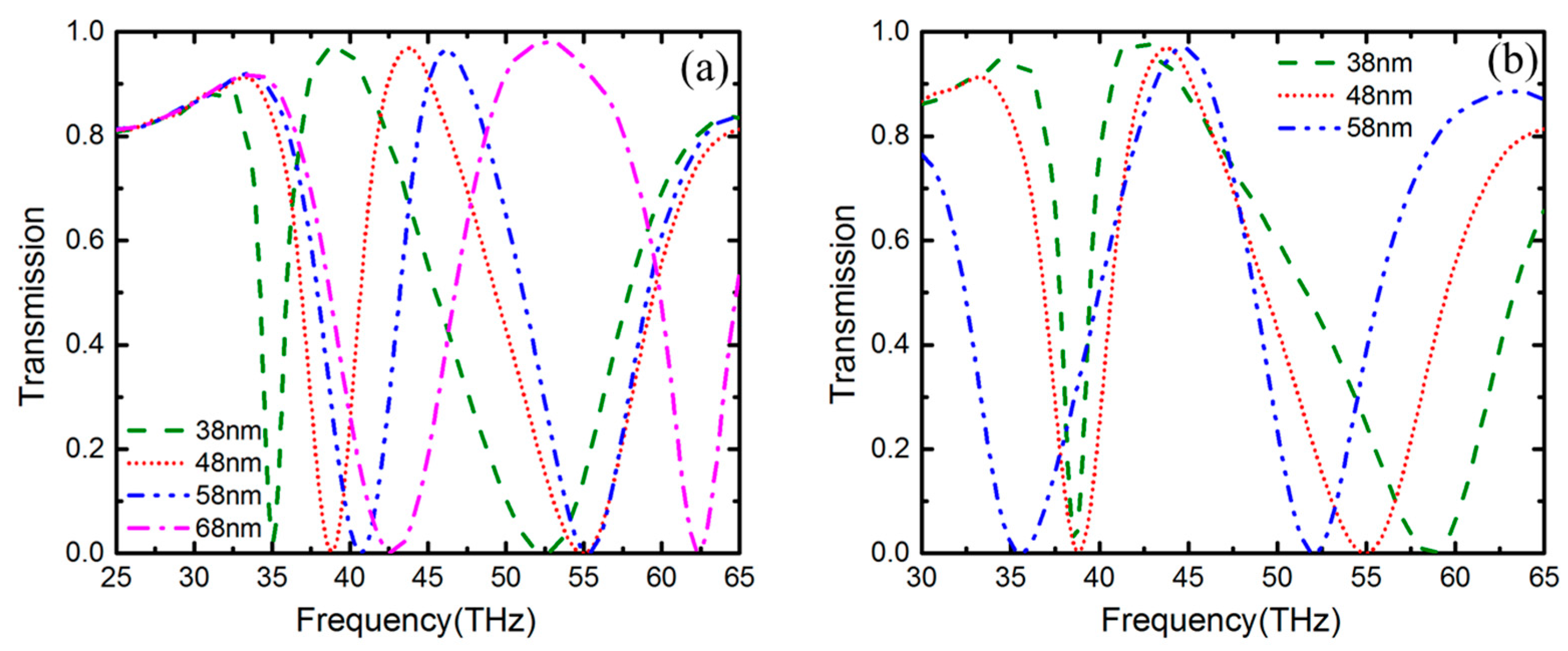
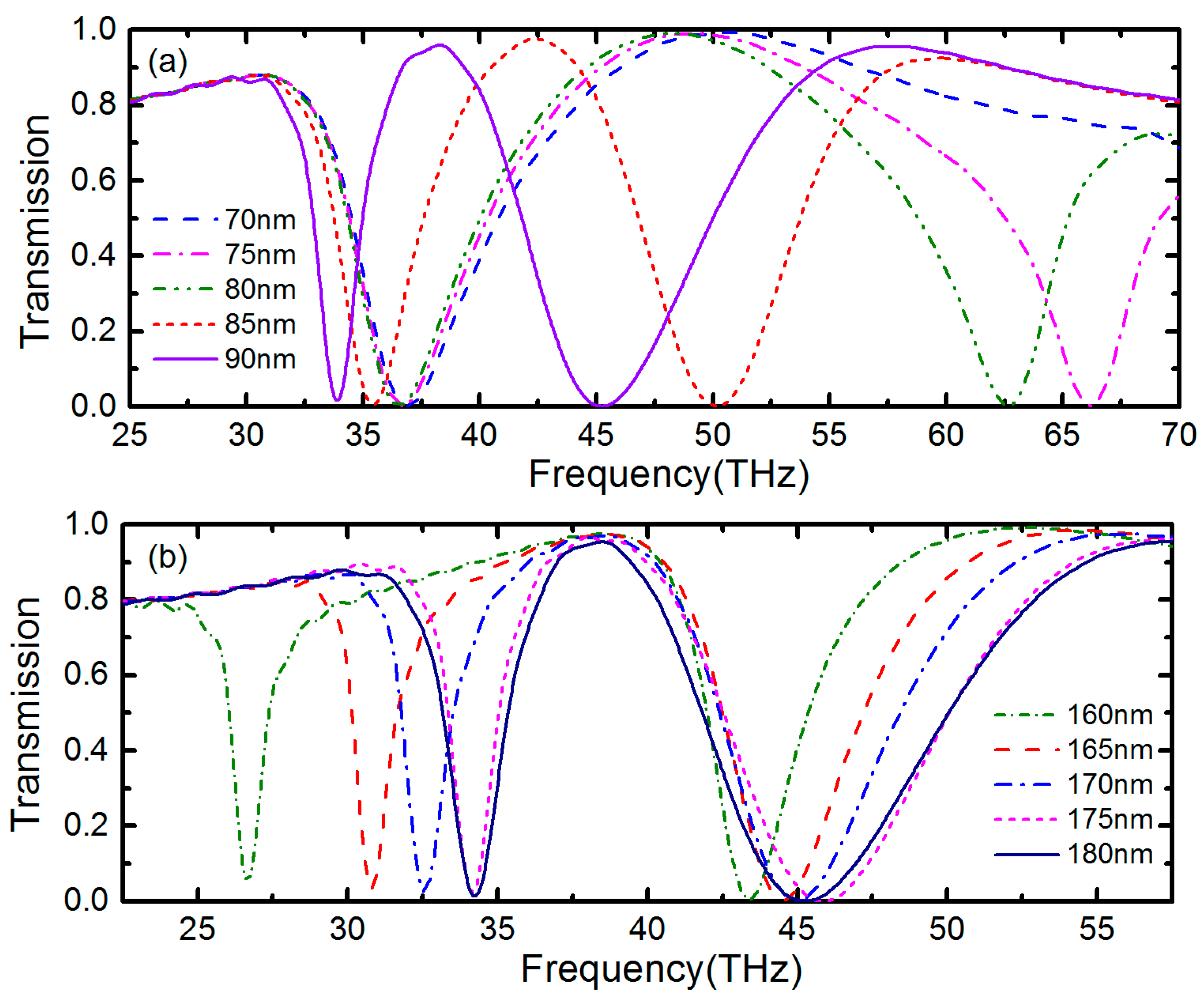
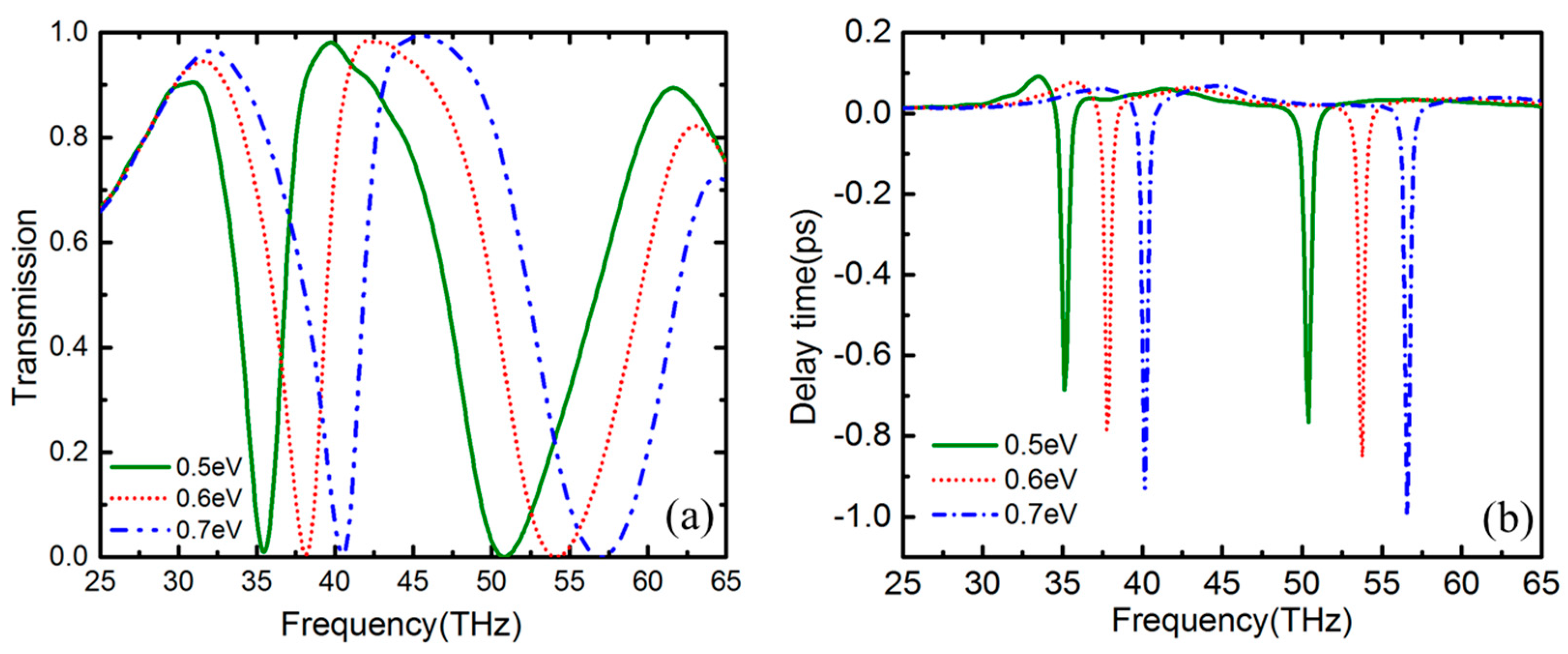
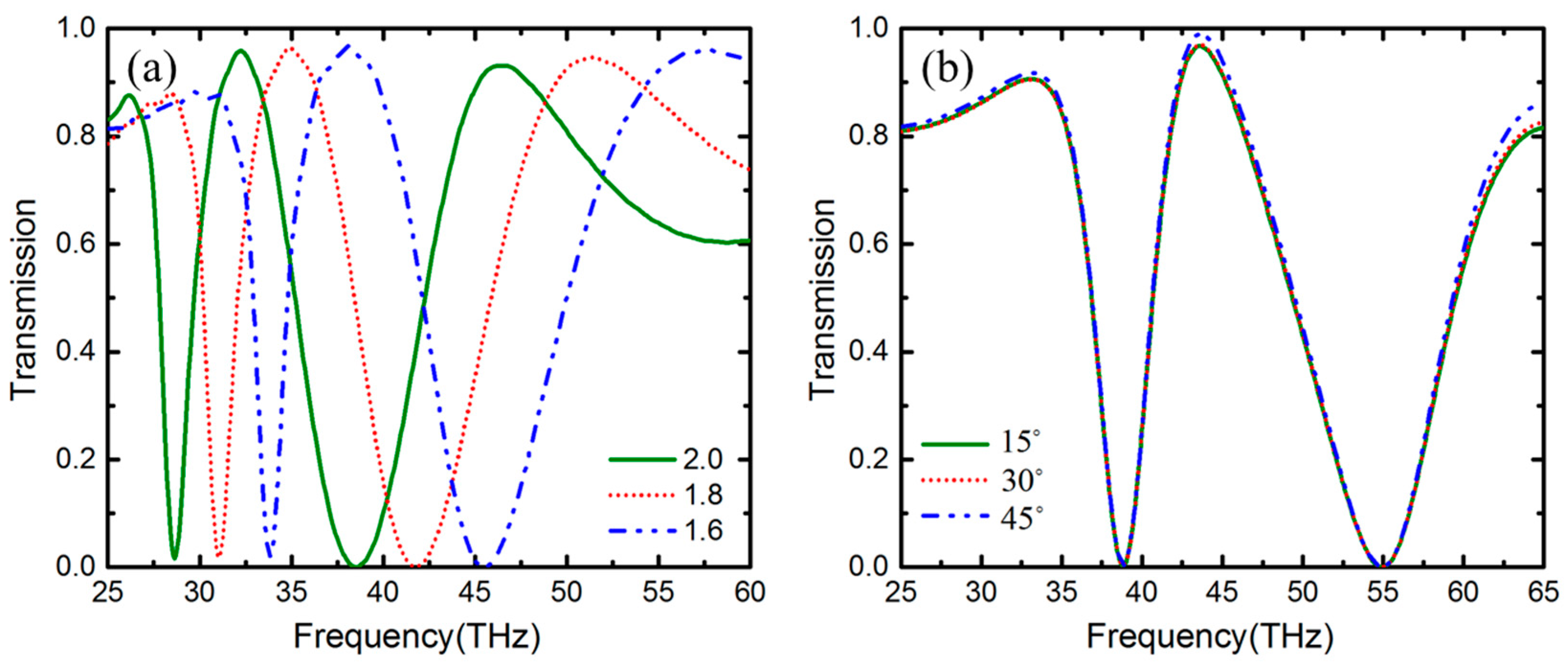
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Deng, G.; Chen, P.; Yang, J.; Yin, Z.; Qiu, L. Graphene-based tunable polarization sensitive terahertz metamaterial absorber. Opt. Commun. 2016, 380, 101–107. [Google Scholar] [CrossRef]
- Fan, Y.; Guo, C.; Zhu, Z.; Xu, W.; Wu, F.; Yuan, X.; Qin, S. Monolayer-graphene-based broadband and wide-angle perfect absorption structures in the near infrared. Sci. Rep. 2018, 8, 13709–13715. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Liu, X.; He, L.; Lin, Y.; Wu, D.; Shi, J. Manipulating graphene mobility and charge neutral point with ligand-bound nanoparticles as charge reservoir. Nano Lett. 2010, 10, 4989–4993. [Google Scholar] [CrossRef] [PubMed]
- Garcia de Abajo, F.J. Graphene Plasmonics: Challenges and Opportunities. ACS Photonics 2014, 1, 135–152. [Google Scholar] [CrossRef]
- Xu, B.; Gu, C.; Li, Z.; Liu, L.; Niu, Z. A Novel Absorber with Tunable Bandwidth Based on Graphene. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 822–825. [Google Scholar]
- Xiong, F.; Zhang, J.; Zhu, Z.; Yuan, X.; Qin, S. Ultrabroadband, More than One Order Absorption Enhancement in Graphene with Plasmonic Light Trapping. Sci. Rep. 2015, 5, 16998. [Google Scholar] [CrossRef]
- He, X.; Zhong, X.; Lin, F.; Shi, W. Investigation of graphene assisted tunable terahertz metamaterials absorber. Opt. Mater. Express 2016, 6, 331–342. [Google Scholar] [CrossRef]
- Hanson, G.W. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys. 2008, 103, 19912–19918. [Google Scholar] [CrossRef]
- Yee, K.J.; Kim, J.H.; Jung, M.H.; Hong, B.H.; Kong, K.J. Ultrafast modulation of optical transitions in monolayer and multilayer graphene. Carbon 2011, 49, 4781–4785. [Google Scholar] [CrossRef]
- Meng, H.; Wang, L.; Liu, G.; Xue, X.; Lin, Q.; Zhai, X. Tunable graphene-based plasmonic multispectral and narrowband perfect metamaterial absorbers at the mid-infrared region. Appl. Opt. 2017, 56, 6022–6027. [Google Scholar] [CrossRef] [PubMed]
- Bonaccorso, F.; Sun, Z.; Hasan, T.; Ferrari, A. Graphene photonics and optoelectronics. Nat. Photonics 2010, 4, 611–622. [Google Scholar] [CrossRef]
- Bao, Q.; Loh, K.P. Graphene photonics, plasmonics, and broadband optoelectronic devices. ACS Nano 2012, 6, 3677–3694. [Google Scholar] [CrossRef] [PubMed]
- Xia, F.; Wang, H.; Xiao, D.; Dubey, M.A. Ramasubramaniam, Two-dimensional material nanophotonics. Nat. Photonics 2014, 8, 899–907. [Google Scholar] [CrossRef]
- Wang, X.; Zhi, L.; Müllen, K. Transparent conductive graphene electrodes for dye-sensitized solar cells. Nano Lett. 2008, 8, 323–327. [Google Scholar] [CrossRef]
- Ma, Q.; Zhan, Y.; Hong, W. Tunable Metamaterial with Gold and Graphene Split-Ring Resonators and Plasmonically Induced Transparency. Nanomaterials 2018, 9, 7. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Zha, S.; Liu, P.; Yang, C.; Zhou, Q. Electrical Manipulation of electromagnetically induced transparency for slow light purpose based on metal-graphene hybrid metamaterial. Appl. Sci. 2018, 8, 2672. [Google Scholar] [CrossRef]
- Chen, J.; Wang, C.; Zhang, R.; Xiao, J. Multiple plasmon-induced transparencies in coupled-resonator systems. Opt. Lett. 2012, 37, 5133–5135. [Google Scholar] [CrossRef]
- Halas, N.J.; Lal, S.; Chang, W.S.; Link, S.; Nordlander, P. Plasmons in strongly coupled metallic nanostructures. Chem. Rev. 2011, 111, 3913–3961. [Google Scholar] [CrossRef]
- Shahamat, Y.; Vahedi, M. Plasmon-induced transparency in a rectangle cavity and an H-shaped structure for sensing and switching applications. J. Nanophotonics 2017, 11, 046012. [Google Scholar] [CrossRef]
- Tang, C.; Niu, Q.; Wang, B.X.; Huang, W.Q. Design of Dual-Band Plasmon-Induced Transparent Effect Based on Composite Structure of Closed-Ring and Square Patch. Plasmonics 2018, 2018, 1–6. [Google Scholar] [CrossRef]
- Nong, J.; Wei, W.; Wang, W.; Lan, G.; Shang, Z.; Yi, J.; Tang, L. Strong coherent coupling between graphene surface plasmons and anisotropic black phosphorus localized surface plasmons. Opt. Express 2018, 26, 1633–1644. [Google Scholar] [CrossRef] [PubMed]
- Habib, M.; Rashed, A.R.; Ozbay, E.; Caglayan, H. Graphene-based tunable plasmon induced transparency in gold strips. Opt. Mater. Express 2018, 8, 1069–1074. [Google Scholar] [CrossRef]
- Verellen, N.; Sonnefraud, Y.; Sobhani, H.; Hao, F.; Moshchalkov, V.V.; Van Dorpe, P.; Nordlander, P.; Maier, S.A. Fano resonances in individual coherent plasmonic nanocavities. Nano Lett. 2009, 9, 1663–1667. [Google Scholar] [CrossRef] [PubMed]
- Cheng, H.; Chen, S.; Yu, P.; Duan, X.; Xie, B.; Tian, J. Dynamically tunable plasmonically induced transparency in periodically patterned graphene nanostrips. Appl. Phys. Lett. 2013, 103, 203112. [Google Scholar] [CrossRef]
- Zare, M.S.; Nozhat, N.; Rashiditabar, R. Tunable graphene based plasmonic absorber with grooved metal film in near infrared region. Opt. Commun. 2017, 398, 56–61. [Google Scholar] [CrossRef]
- Zhang, H.; Cao, Y.; Liu, Y.; Li, Y.; Zhang, Y. Electromagnetically induced transparency based on cascaded π-shaped graphene nanostructure. Plasmonics 2017, 12, 1833–1839. [Google Scholar] [CrossRef]
- Tan, T.C.; Srivastava, Y.K.; Manjappa, M.; Plum, E.; Singh, R. Lattice induced strong coupling and line narrowing of split resonances in metamaterials. Appl. Phys. Lett. 2018, 112, 201111. [Google Scholar] [CrossRef]
- Zhou, F.; Zhang, L.; Wan, M.; Song, Y. Broadband plasmon-induced transparency in terahertz metamaterials via constructive interference of electric and magnetic couplings. Opt. Mater. Express 2015, 23, 27361–27368. [Google Scholar]
- Zhu, Z.; Yang, X.; Gu, J. Broadband plasmon induced transparency in terahertz metamaterials. Nanotechnology 2013, 24, 214003. [Google Scholar] [CrossRef]
- Jin, X.R.; Lu, Y.; Zheng, H.; Lee, Y.; Rhee, J.Y.; Kim, K.W.; Jang, W.H. Plasmonic electromagnetically induced transparency in metamaterial based on second-order plasmonic resonance. Opt. Commun. 2011, 284, 4766–4768. [Google Scholar] [CrossRef]
- Bai, Q.; Liu, C.; Chen, J.; Cheng, C.; Kang, M.; Wang, H.T. Tunable slow light in semiconductor metamaterial in a broad terahertz regime. J. Appl. Phys. 2010, 107, 093104. [Google Scholar]
- Li, C.; Qi, D.; Wang, Y.; Zhang, X. Wideband slow light based on plasmon-induced transparency at telecom frequency. Opt. Commun. 2015, 51, 26–29. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, J.; He, X.; Han, Y.; Zhang, J.; Huang, J.; Chen, D. Active control of broadband plasmon induced transparency in a terahertz hybrid metal graphene metamaterial. RSC Adv. 2018, 8, 27746–27753. [Google Scholar] [CrossRef]
- Han, L.; Wang, L.; Xing, H.; Chen, X. Anisotropic plasmon induced transparency in black phosphorus nanostrip trimer. Opt. Mater. Express 2019, 9, 352–361. [Google Scholar] [CrossRef]
- Jiang, L.; Tang, J.; Xu, J.; Zheng, Z.; Dong, J.; Guo, J.; Qian, S.; Dai, X.; Xiang, Y. Graphene Tamm plasmon-induced low-threshold optical bistability at terahertz frequencies. Opt. Mater. Express 2018, 9, 139–150. [Google Scholar] [CrossRef]
- Cao, W.; Singh, R.; Zhang, C.; Han, J.; Tonouchi, M.W. Zhang, Plasmon-induced transparency in metamaterials: Active near field coupling between bright superconducting and dark metallic mode resonators. Appl. Phys. Lett. 2013, 103, 101106. [Google Scholar] [CrossRef]
- Biabanifard, S.; Biabanifard, M.; Asgari, S.; Asadi, S.; Vagoub, M.C.E. Tunable ultra-wideband terahertz absorber based on graphene disks and ribbons. Opt. Commun. 2018, 427, 418–425. [Google Scholar] [CrossRef]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics, The Finite-Difference Time-Domain Method, 3rd ed.; Artech House: Boston, FL, USA, 2005; pp. 107–112. [Google Scholar]
- Xiao, S.; Wang, T.; Liu, T.; Yan, X.; Li, Z.; Xu, C. Active modulation of electromagnetically induced transparency analogue in terahertz hybrid metal-graphene metamaterials. Carbon 2018, 126, 271–278. [Google Scholar] [CrossRef]
- Cai, Y.; Zhu, J.Q.; Liu, H. Tunable enhanced optical absorption of graphene using plasmonic perfect absorbers. Appl. Phys. Lett. 2015, 106, 043105. [Google Scholar] [CrossRef]
- Prodan, E.; Radloff, C.; Halas, N.J.; Nordlander, P. A Hybridization Model for the Plasmon Response of Complex Nanostructures. Science 2003, 302, 419–422. [Google Scholar] [CrossRef] [PubMed]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Zhang, Z.; Wang, S.; Liu, Y.; Zhang, J.; Chen, D.; Ouyang, J.; Yang, J. Tunable Graphene-Based Plasmon-Induced Transparency Based on Edge Mode in the Mid-Infrared Region. Nanomaterials 2019, 9, 448. https://doi.org/10.3390/nano9030448
Xu H, Zhang Z, Wang S, Liu Y, Zhang J, Chen D, Ouyang J, Yang J. Tunable Graphene-Based Plasmon-Induced Transparency Based on Edge Mode in the Mid-Infrared Region. Nanomaterials. 2019; 9(3):448. https://doi.org/10.3390/nano9030448
Chicago/Turabian StyleXu, Heng, Zhaojian Zhang, Shangwu Wang, Yun Liu, Jingjing Zhang, Dingbo Chen, Jianming Ouyang, and Junbo Yang. 2019. "Tunable Graphene-Based Plasmon-Induced Transparency Based on Edge Mode in the Mid-Infrared Region" Nanomaterials 9, no. 3: 448. https://doi.org/10.3390/nano9030448
APA StyleXu, H., Zhang, Z., Wang, S., Liu, Y., Zhang, J., Chen, D., Ouyang, J., & Yang, J. (2019). Tunable Graphene-Based Plasmon-Induced Transparency Based on Edge Mode in the Mid-Infrared Region. Nanomaterials, 9(3), 448. https://doi.org/10.3390/nano9030448





