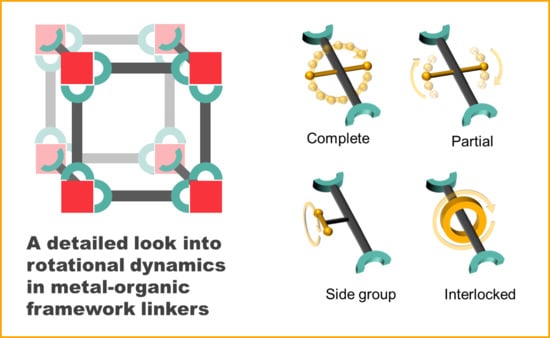
Rotational Dynamics of Linkers in Metal–Organic Frameworks
Abstract
1. Introduction
2. Types of Rotational Linker Dynamics
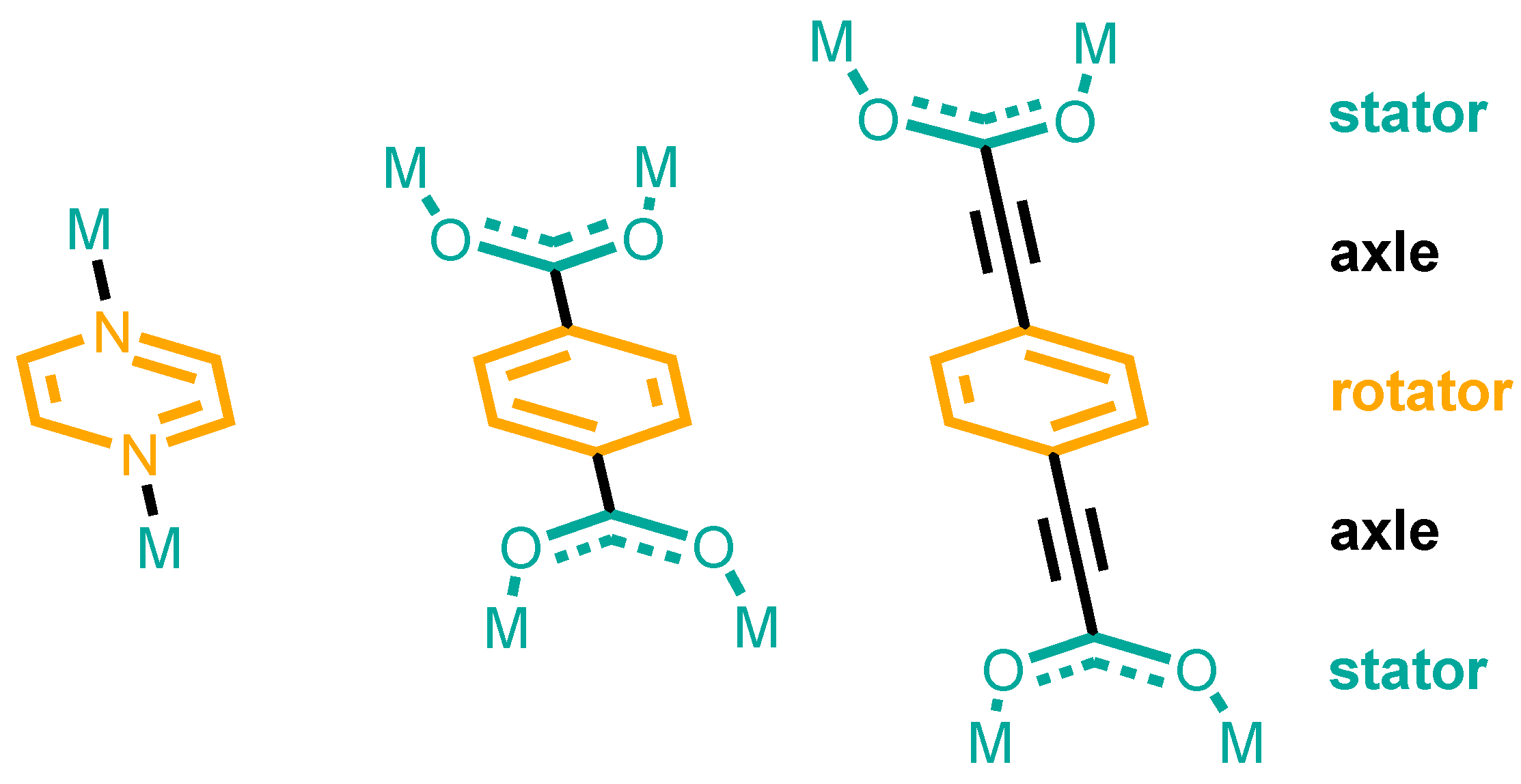
“Molecular rotor: a molecular system in which a molecule or part of a molecule rotates against another part of the moleculeRotator: the part of the molecule or system that rotates against the restStator: the stationary part of the system with respect to which the rotator turnsAxle: the portion of the molecule that carries the rotator and about which the rotator turns”
- Complete rotation
- Partial rotation
- Rotation of side groups
- Mechanically interlocked molecule rotation
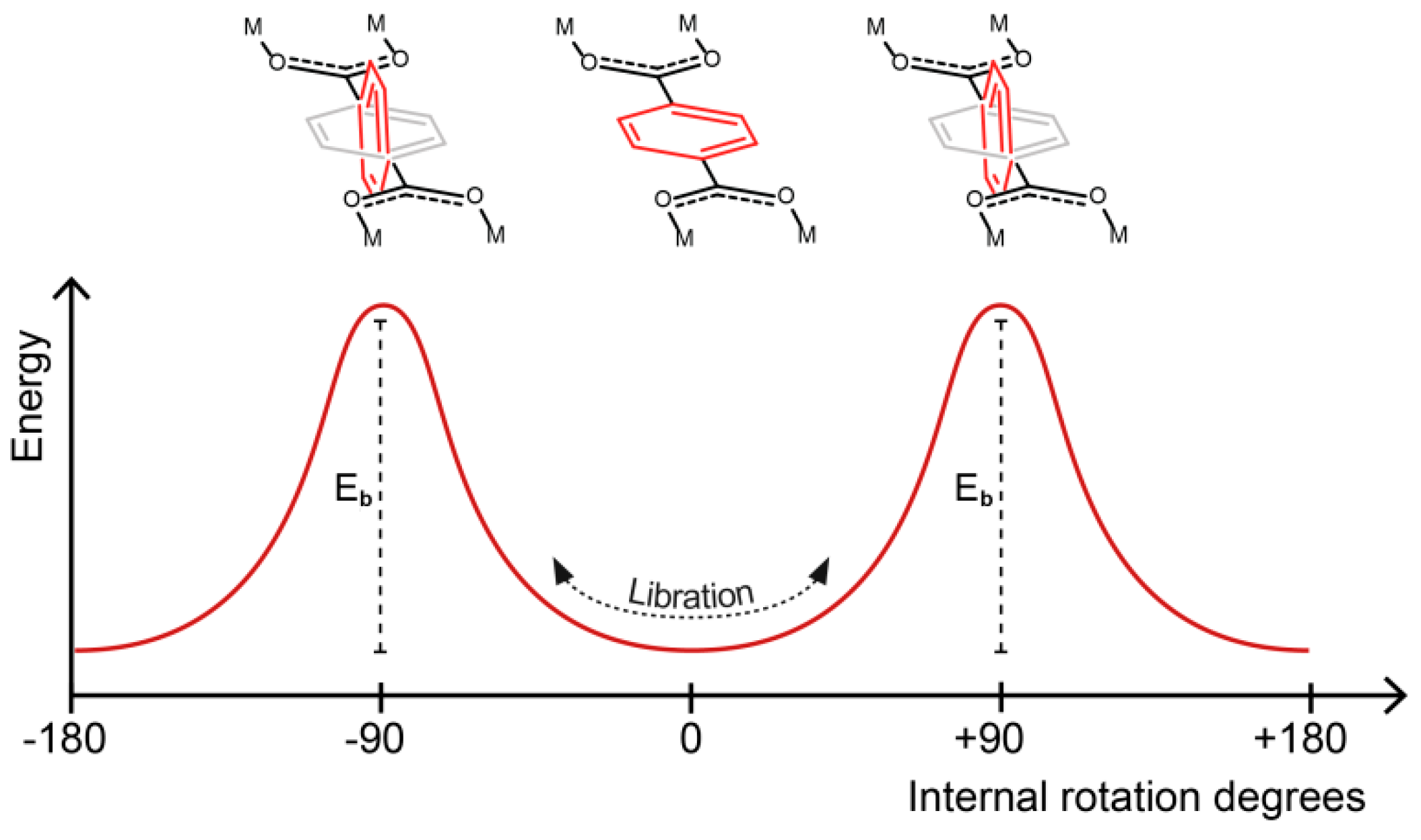
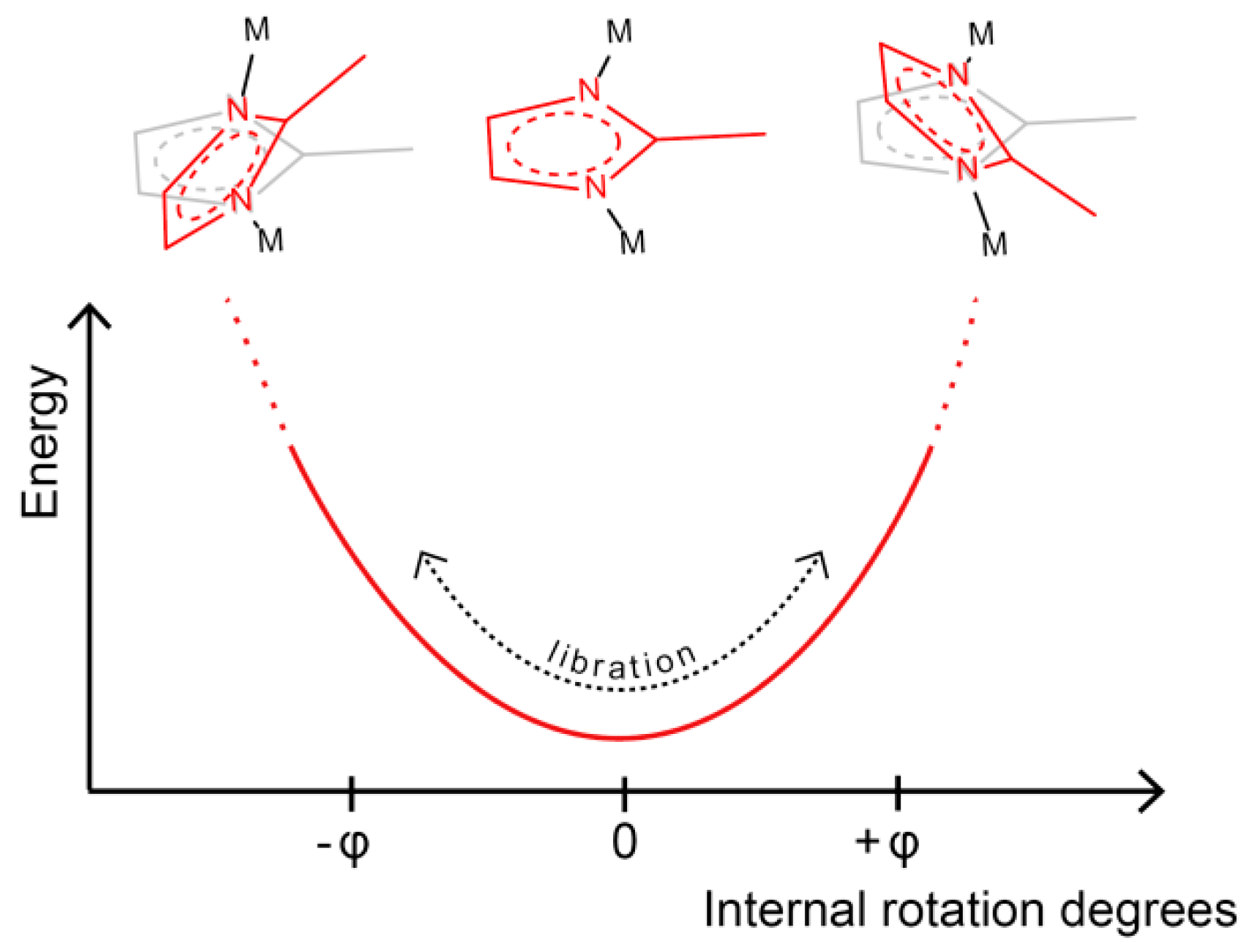
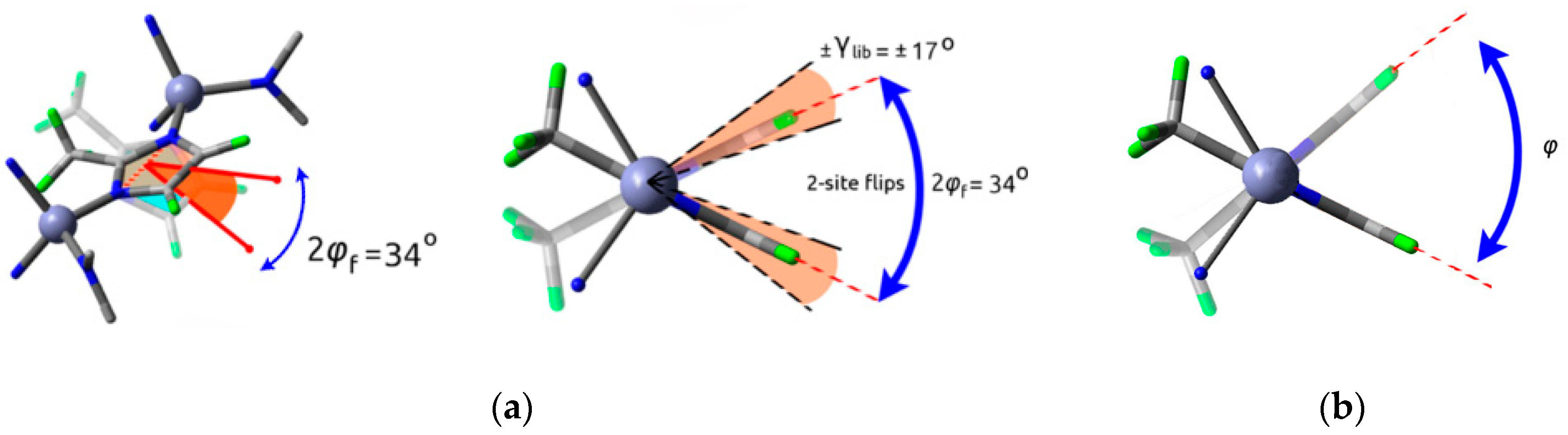
- dynamics where the rotor performs rotational motions about a minimum in a potential energy well, or torsional potential minimum, which are called librations.
- dynamics where the rotor overcomes a maximum in potential energy and reaches a second conformation. For the sake of clarity, they will be referred to as hops in this section.
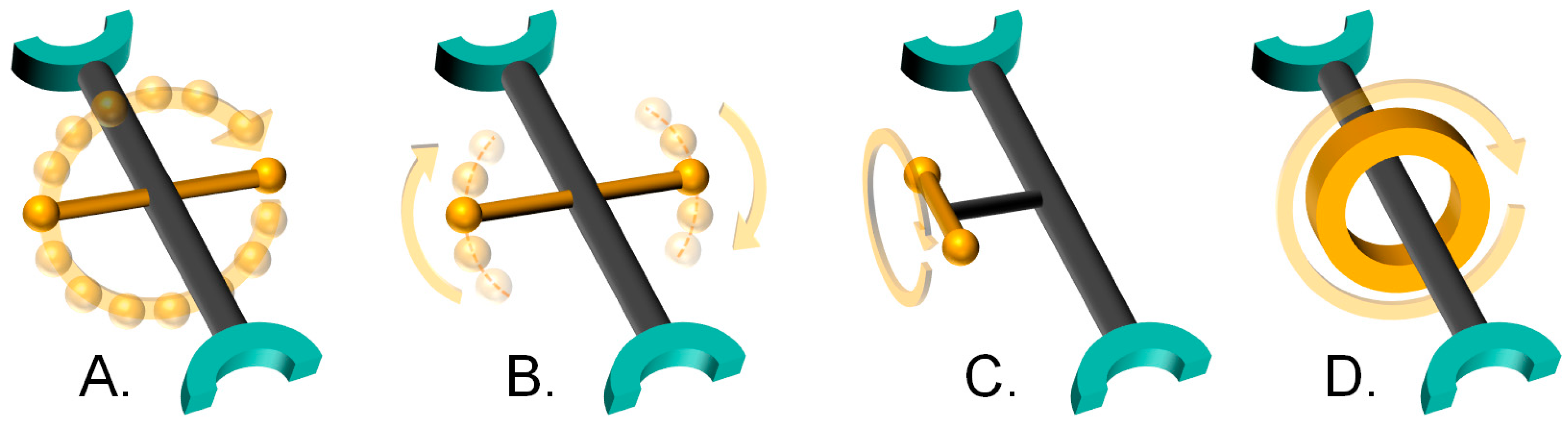
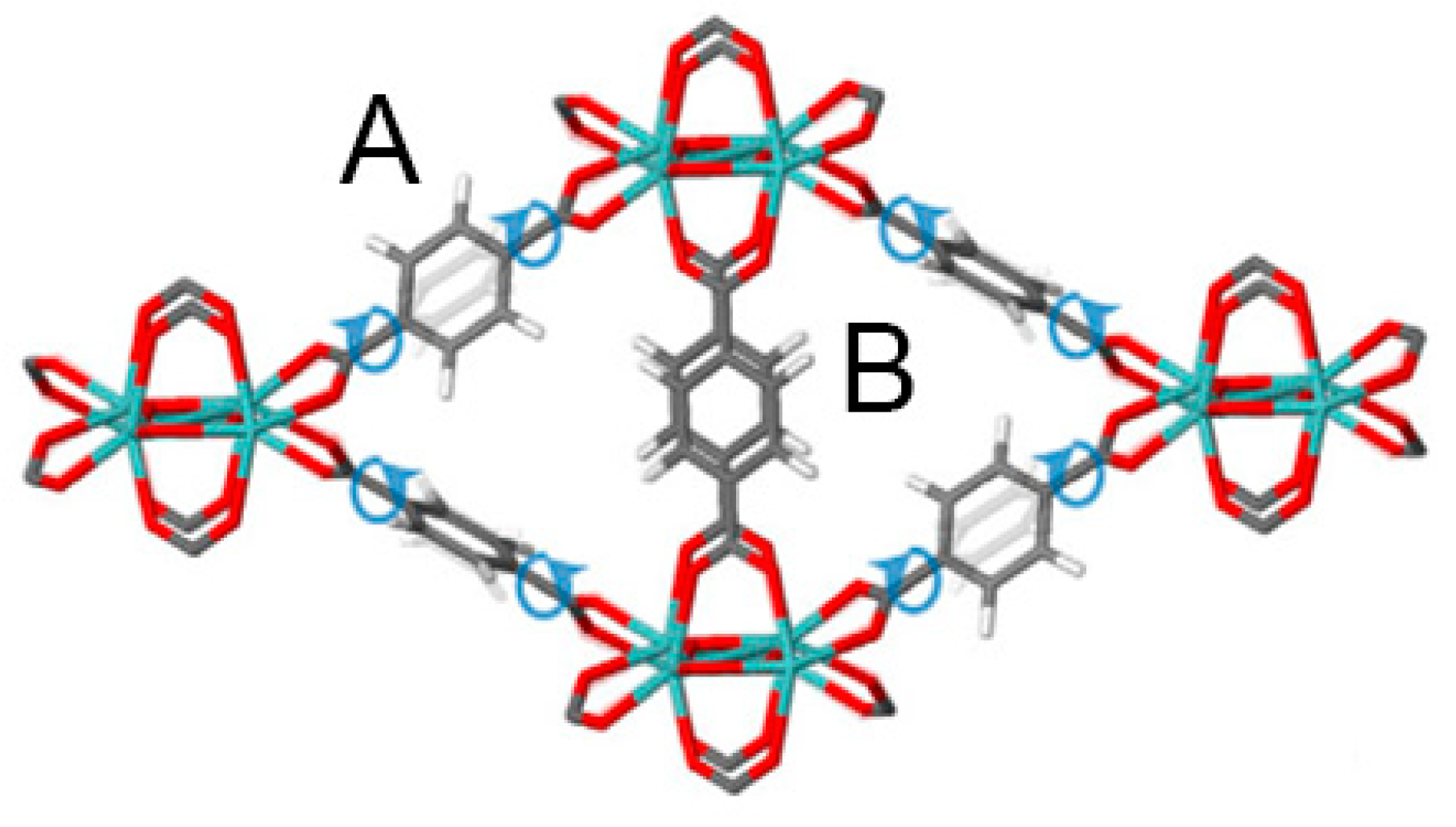
2.1. Type A: Complete Rotation
2.2. Type B: Partial Rotation
2.3. Type C: Rotation of Side Groups
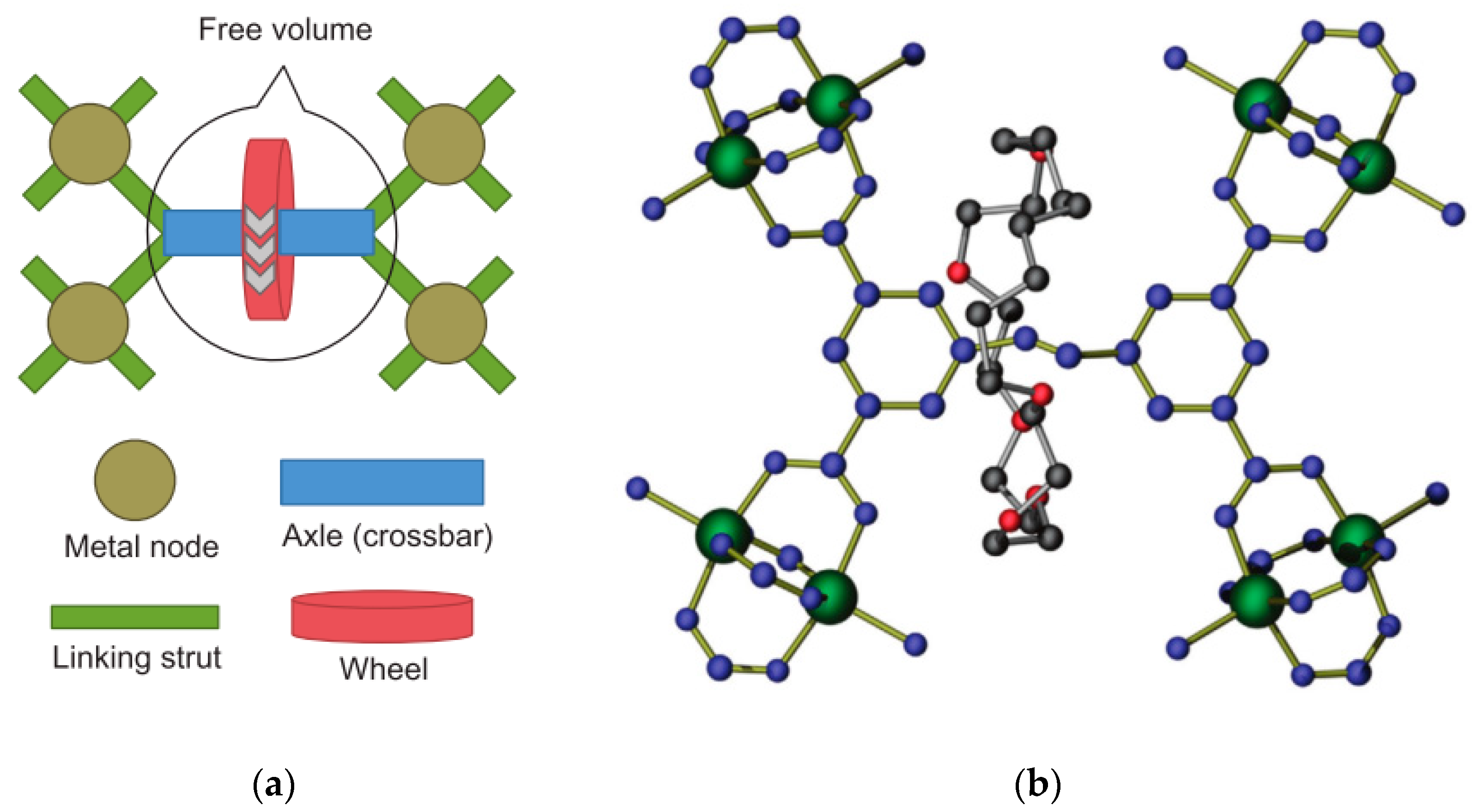
2.4. Type D: Rotation of Mechanically Interlocked Molecules
3. Methods for the Study of Linker Dynamics
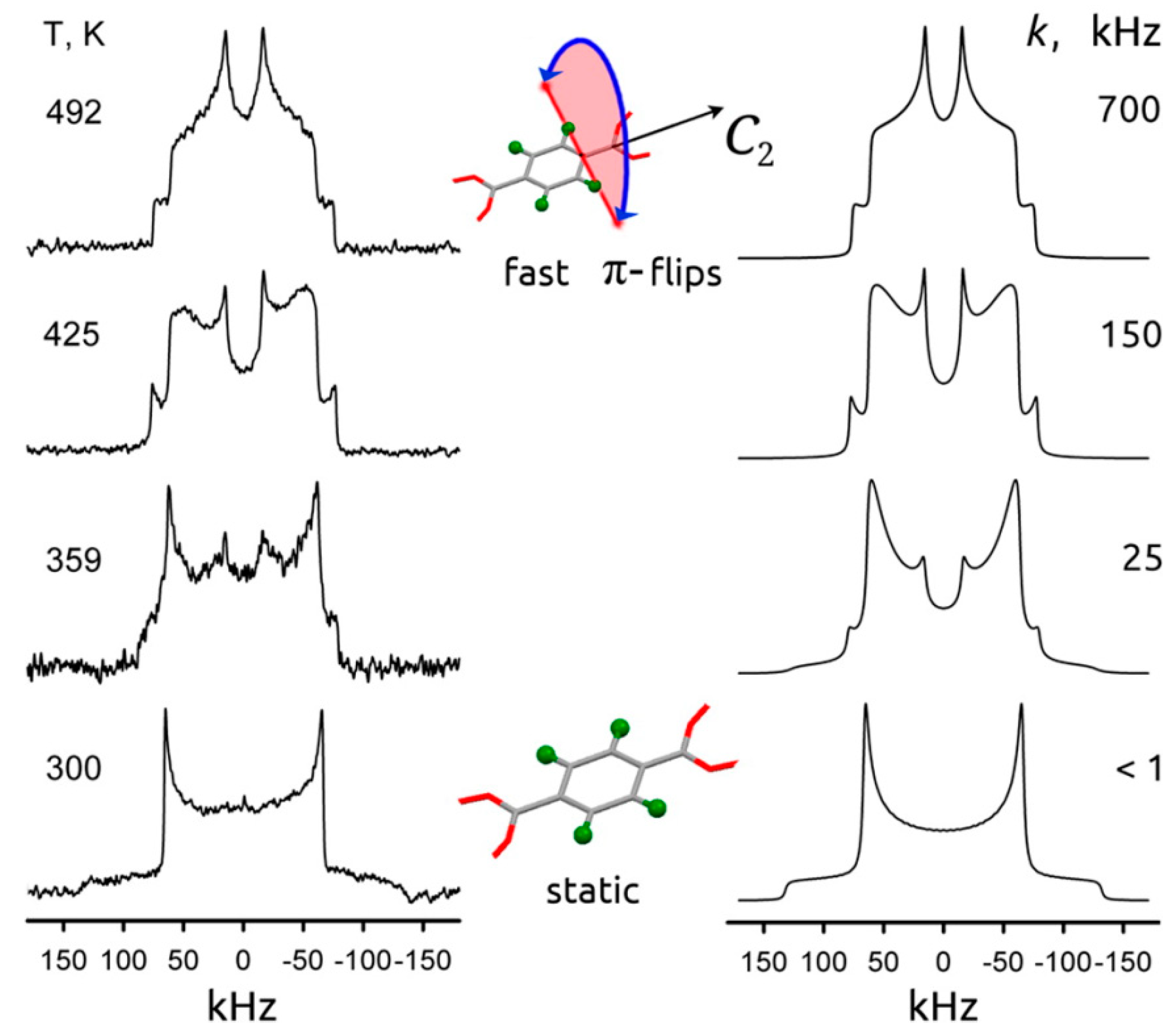
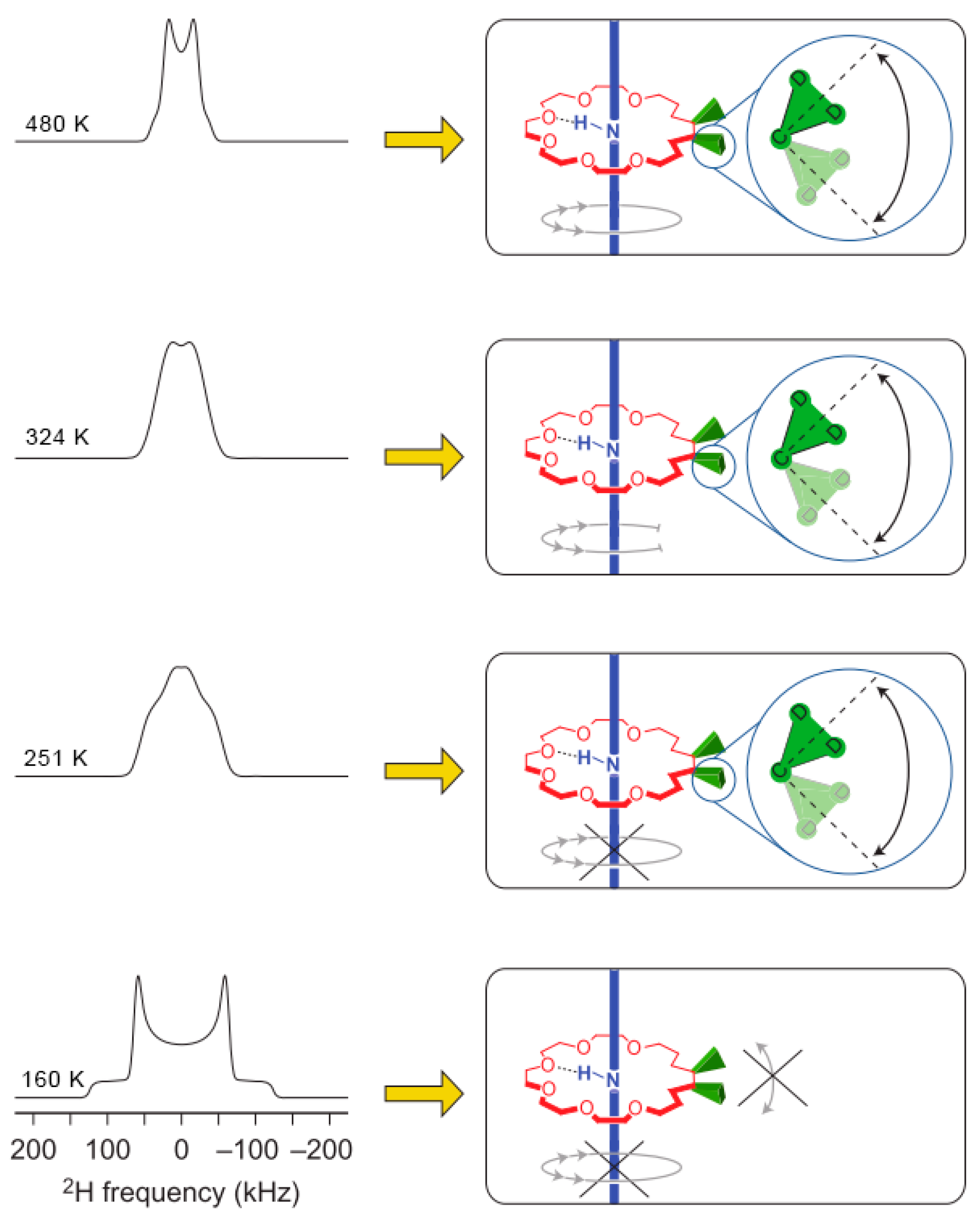
3.1. Solid-State Nuclear Magnetic Resonance (NMR)
3.2. Dielectric Spectroscopy
3.3. Terahertz Spectroscopy
3.4. Computational Methodologies
4. Implications of Rotational Dynamics on Applications of MOFs
4.1. Diffusion and Adsorption
4.2. Optical Properties
4.3. Mechanical Properties
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Furukawa, H.; Cordova, K.E.; O’Keeffe, M.; Yaghi, O.M. The Chemistry and Applications of Metal-Organic Frameworks. Science 2013, 341, 1230444. [Google Scholar] [CrossRef] [PubMed]
- Schneemann, A.; Bon, V.; Schwedler, I.; Senkovska, I.; Kaskel, S.; Fischer, R.A. Flexible Metal–organic Frameworks. Chem. Soc. Rev. 2014, 43, 6062–6096. [Google Scholar] [CrossRef] [PubMed]
- Khuong, T.-A.A.V.; Nunez, J.E.; Godinez, C.E.; Garcia-Garibay, M.A.; Nuñez, J.E.; Godinez, C.E.; Garcia-Garibay, M.A. Crystalline Molecular Machines: A Quest toward Solid-State Dynamics and Function. Acc. Chem. Res. 2006, 39, 413–422. [Google Scholar] [CrossRef] [PubMed]
- Moggach, S.A.; Bennett, T.D.; Cheetham, A.K. The Effect of Pressure on ZIF-8: Increasing Pore Size with Pressure and the Formation of a High-Pressure Phase at 1.47 GPa. Angew. Chemie Int. Ed. 2009, 48, 7087–7089. [Google Scholar] [CrossRef] [PubMed]
- Fairen-Jimenez, D.; Moggach, S.A.; Wharmby, M.T.; Wright, P.A.; Parsons, S.; Düren, T. Opening the Gate: Framework Flexibility in ZIF-8 Explored by Experiments and Simulations. J. Am. Chem. Soc. 2011, 133, 8900–8902. [Google Scholar] [CrossRef] [PubMed]
- Catalano, L.; Naumov, P. Exploiting Rotational Motion in Molecular Crystals. CrystEngComm 2018, 20, 5872–5883. [Google Scholar] [CrossRef]
- Vogelsberg, C.S.; Garcia-Garibay, M.A. Crystalline Molecular Machines: Function, Phase Order, Dimensionality, and Composition. Chem. Soc. Rev. 2012, 41, 1892–1910. [Google Scholar] [CrossRef] [PubMed]
- Khudozhitkov, A.E.; Kolokolov, D.I.; Stepanov, A.G. Characterization of Fast Restricted Librations of Terephthalate Linkers in MOF UiO-66(Zr) by 2H NMR Spin–Lattice Relaxation Analysis. J. Phys. Chem. C 2018, 122, 12956–12962. [Google Scholar] [CrossRef]
- Moreau, F.; Kolokolov, D.I.; Stepanov, A.G.; Easun, T.L.; Dailly, A.; Lewis, W.; Blake, A.J.; Nowell, H.; Lennox, M.J.; Besley, E.; et al. Tailoring Porosity and Rotational Dynamics in a Series of Octacarboxylate Metal-Organic Frameworks. Proc. Natl. Acad. Sci. USA 2017, 114, 3056–3061. [Google Scholar] [CrossRef] [PubMed]
- Vogelsberg, C.S.; Uribe-Romo, F.J.; Lipton, A.S.; Yang, S.; Houk, K.N.; Brown, S.; Garcia-Garibay, M.A. Ultrafast Rotation in an Amphidynamic Crystalline Metal Organic Framework. Proc. Natl. Acad. Sci. USA 2017, 114, 13613–13618. [Google Scholar] [CrossRef] [PubMed]
- Knebel, A.; Geppert, B.; Volgmann, K.; Kolokolov, D.I.; Stepanov, A.G.; Twiefel, J.; Heitjans, P.; Volkmer, D.; Caro, J. Defibrillation of Soft Porous Metal-Organic Frameworks with Electric Fields. Science 2017, 358, 347–351. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Kolokolov, D.I.; da Silva, I.; Stepanov, A.G.; Blake, A.J.; Dailly, A.; Manuel, P.; Tang, C.C.; Yang, S.; Schröder, M. Porous Metal–Organic Polyhedral Frameworks with Optimal Molecular Dynamics and Pore Geometry for Methane Storage. J. Am. Chem. Soc. 2017, 139, 13349–13360. [Google Scholar] [CrossRef] [PubMed]
- Kottas, G.S.; Clarke, L.I.; Horinek, D.; Michl, J. Artificial Molecular Rotors. Chem. Rev. 2005, 105, 1281–1376. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, J.; Nandini Devi, R.; Tunstall, D.P.; Cox, P.A.; Wright, P.A. Deuterium NMR Studies of Framework and Guest Mobility in the Metal–organic Framework Compound MOF-5, Zn4O(O2CC6H4CO2)3. Microporous Mesoporous Mater. 2005, 84, 97–104. [Google Scholar] [CrossRef]
- Spiess, H.W. Molecular Dynamics of Solid Polymers as Revealed by Deuteron NMR. Colloid Polym. Sci. 1983, 261, 193–209. [Google Scholar] [CrossRef]
- Gould, S.L.; Tranchemontagne, D.; Yaghi, O.M.; Garcia-Garibay, M.A. Amphidynamic Character of Crystalline MOF-5: Rotational Dynamics of Terephthalate Phenylenes in a Free-Volume, Sterically Unhindered Environment. J. Am. Chem. Soc. 2008, 130, 3246–3247. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Yildirim, T. Lattice Dynamics of Metal-Organic Frameworks: Neutron Inelastic Scattering and First-Principles Calculations. Phys. Rev. B 2006, 74, 180301. [Google Scholar] [CrossRef]
- Kolokolov, D.I.; Jobic, H.; Stepanov, A.G.; Guillerm, V.; Devic, T.; Serre, C.; Férey, G. Dynamics of Benzene Rings in MIL-53(Cr) and MIL-47(V) Frameworks Studied by 2H NMR Spectroscopy. Angew. Chem. Int. Ed. 2010, 49, 4791–4794. [Google Scholar] [CrossRef] [PubMed]
- Kolokolov, D.I.; Stepanov, A.G.; Jobic, H. Guest Controlled Rotational Dynamics of Terephthalate Phenylenes in Metal-Organic Framework MIL-53(Al): Effect of Different Xylene Loadings. J. Phys. Chem. C 2014, 118, 15978–15984. [Google Scholar] [CrossRef]
- Khudozhitkov, A.E.; Jobic, H.; Freude, D.; Haase, J.; Kolokolov, D.I.; Stepanov, A.G. Ultraslow Dynamics of a Framework Linker in MIL-53 (Al) as a Sensor for Different Isomers of Xylene. J. Phys. Chem. C 2016, 120, 21704–21709. [Google Scholar] [CrossRef]
- Khudozhitkov, A.E.; Jobic, H.; Kolokolov, D.I.; Freude, D.; Haase, J.; Stepanov, A.G. Probing the Guest-Mediated Structural Mobility in the UiO-66(Zr) Framework by 2H NMR Spectroscopy. J. Phys. Chem. C 2017, 66. [Google Scholar] [CrossRef]
- Kolokolov, D.I.; Stepanov, A.G.; Guillerm, V.; Serre, C.; Frick, B.; Jobic, H. Probing the Dynamics of the Porous Zr Terephthalate UiO-66 Framework Using 2H NMR and Neutron Scattering. J. Phys. Chem. C 2012, 116, 12131–12136. [Google Scholar] [CrossRef]
- Khudozhitkov, A.E.; Kolokolov, D.I.; Stepanov, A.G.; Bolotov, V.A.; Dybtsev, D.N. Metal-Cation-Independent Dynamics of Phenylene Ring in Microporous MOFs: A 2H Solid-State NMR Study. J. Phys. Chem. C 2015, 119, 28038–28045. [Google Scholar] [CrossRef]
- Ryder, M.R.; Van De Voorde, B.; Civalleri, B.; Bennett, T.D.; Mukhopadhyay, S.; Cinque, G.; Fernandez-Alonso, F.; De Vos, D.; Rudić, S.; Tan, J.C. Detecting Molecular Rotational Dynamics Complementing the Low-Frequency Terahertz Vibrations in a Zirconium-Based Metal-Organic Framework. Phys. Rev. Lett. 2017, 118, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Shustova, N.B.; Ong, T.-C.; Cozzolino, A.F.; Michaelis, V.K.; Griffin, R.G.; Dincă, M. Phenyl Ring Dynamics in a Tetraphenylethylene-Bridged Metal–Organic Framework: Implications for the Mechanism of Aggregation-Induced Emission. J. Am. Chem. Soc. 2012, 134, 15061–15070. [Google Scholar] [CrossRef] [PubMed]
- Horike, S.; Matsuda, R.; Tanaka, D.; Matsubara, S.; Mizuno, M.; Endo, K.; Kitagawa, S. Dynamic Motion of Building Blocks in Porous Coordination Polymers. Angew. Chem. Int. Ed. 2006, 45, 7226–7230. [Google Scholar] [CrossRef] [PubMed]
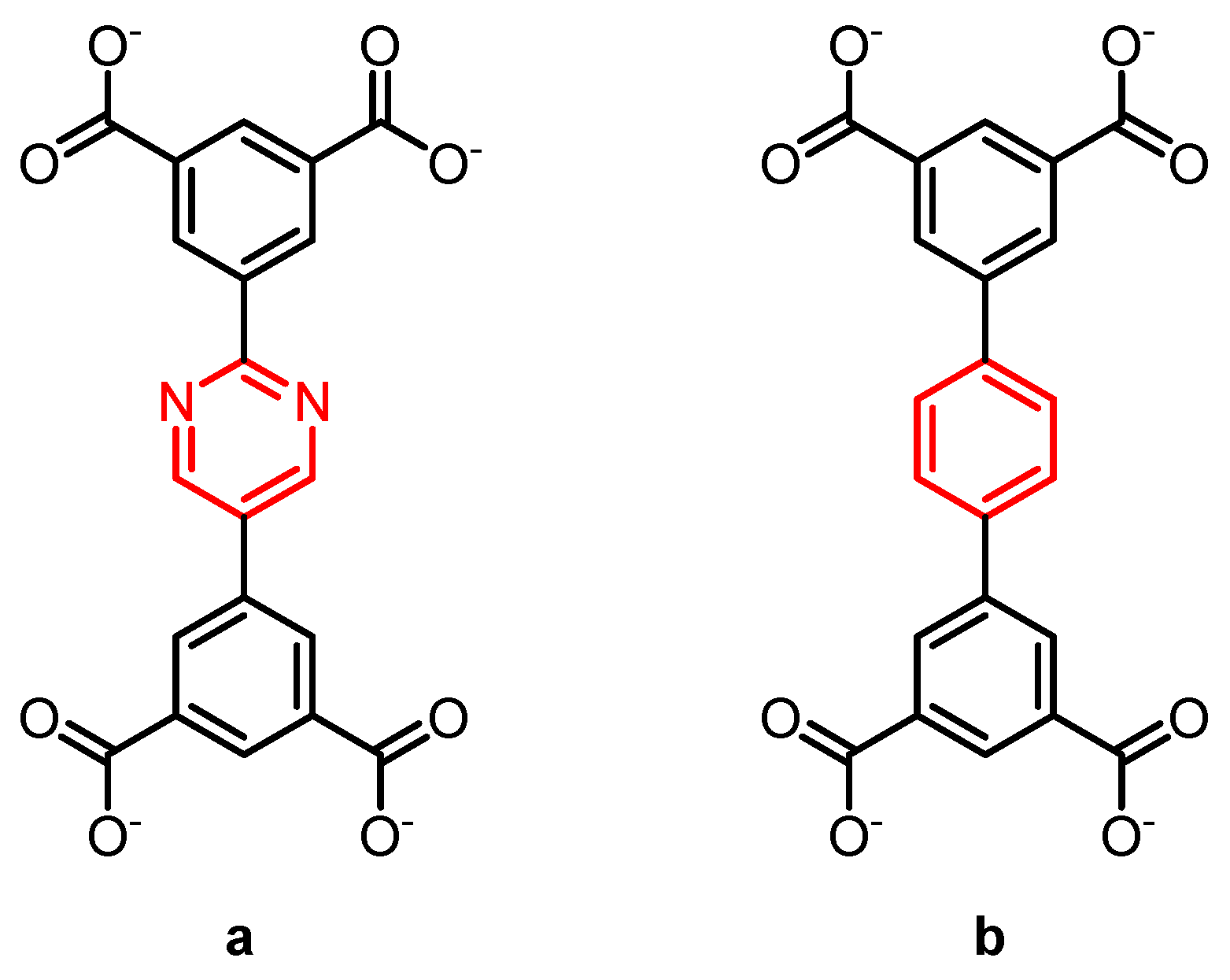
- Li, B.; Wen, H.-M.; Wang, H.; Wu, H.; Tyagi, M.; Yildirim, T.; Zhou, W.; Chen, B. A Porous Metal–Organic Framework with Dynamic Pyrimidine Groups Exhibiting Record High Methane Storage Working Capacity. J. Am. Chem. Soc. 2014, 136, 6207–6210. [Google Scholar] [CrossRef] [PubMed]
- Bastien, G.; Lemouchi, C.; Wzietek, P.; Simonov, S.; Zorina, L.; Rodríguez-Fortea, A.; Canadell, E.; Batail, P. A Crystalline Hybrid of Paddlewheel copper(II) Dimers and Molecular Rotors: Singlet-Triplet Dynamics Revealed by Variable-Temperature Proton Spin-Lattice Relaxation. Z. Anorg. Allg. Chem. 2014, 640, 1127–1133. [Google Scholar] [CrossRef]
- Bracco, S.; Castiglioni, F.; Comotti, A.; Galli, S.; Negroni, M.; Maspero, A.; Sozzani, P. Ultrafast Molecular Rotors and Their CO2 Tuning in MOFs with Rod-Like Ligands. Chem. A Eur. J. 2017, 23, 11210–11215. [Google Scholar] [CrossRef] [PubMed]
- Pakhira, S.; Takayanagi, M.; Nagaoka, M. Diverse Rotational Flexibility of Substituted Dicarboxylate Ligands in Functional Porous Coordination Polymers. J. Phys. Chem. C 2015, 119, 28789–28799. [Google Scholar] [CrossRef]
- Inukai, M.; Tamura, M.; Horike, S.; Higuchi, M.; Kitagawa, S.; Nakamura, K. Storage of CO2 into Porous Coordination Polymer Controlled by Molecular Rotor Dynamics. Angew. Chemie Int. Ed. 2018, 57, 8687–8690. [Google Scholar] [CrossRef] [PubMed]
- Inukai, M.; Fukushima, T.; Hijikata, Y.; Ogiwara, N.; Horike, S.; Kitagawa, S. Control of Molecular Rotor Rotational Frequencies in Porous Coordination Polymers Using a Solid-Solution Approach. J. Am. Chem. Soc. 2015, 137, 12183–12186. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Duan, H.-B.; Khan, S.I.; Garcia-Garibay, M.A. Diffusion-Controlled Rotation of Triptycene in a Metal–Organic Framework (MOF) Sheds Light on the Viscosity of MOF-Confined Solvent. ACS Cent. Sci. 2016, 2, 608–613. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Her, J.H.; Dailly, A.; Ramirez-Cuesta, A.J.; Neumann, D.A.; Brown, C.M. Reversible Structural Transition in MIL-53 with Large Temperature Hysteresis. J. Am. Chem. Soc. 2008, 130, 11813–11818. [Google Scholar] [CrossRef] [PubMed]
- Coudert, F.X. Molecular Mechanism of Swing Effect in Zeolitic Imidazolate Framework ZIF-8: Continuous Deformation upon Adsorption. ChemPhysChem 2017, 18, 2732–2738. [Google Scholar] [CrossRef] [PubMed]
- Kolokolov, D.I.; Stepanov, A.G.; Jobic, H. Mobility of the 2-Methylimidazolate Linkers in ZIF-8 Probed by 2H NMR: Saloon Doors for the Guests. J. Phys. Chem. C 2015, 119, 27512–27520. [Google Scholar] [CrossRef]
- Hobday, C.L.; Bennett, T.D.; Fairen-Jimenez, D.; Graham, A.J.; Morrison, C.A.; Allan, D.R.; Düren, T.; Moggach, S.A. Tuning the Swing Effect by Chemical Functionalization of Zeolitic Imidazolate Frameworks. J. Am. Chem. Soc. 2018, 140, 382–387. [Google Scholar] [CrossRef] [PubMed]
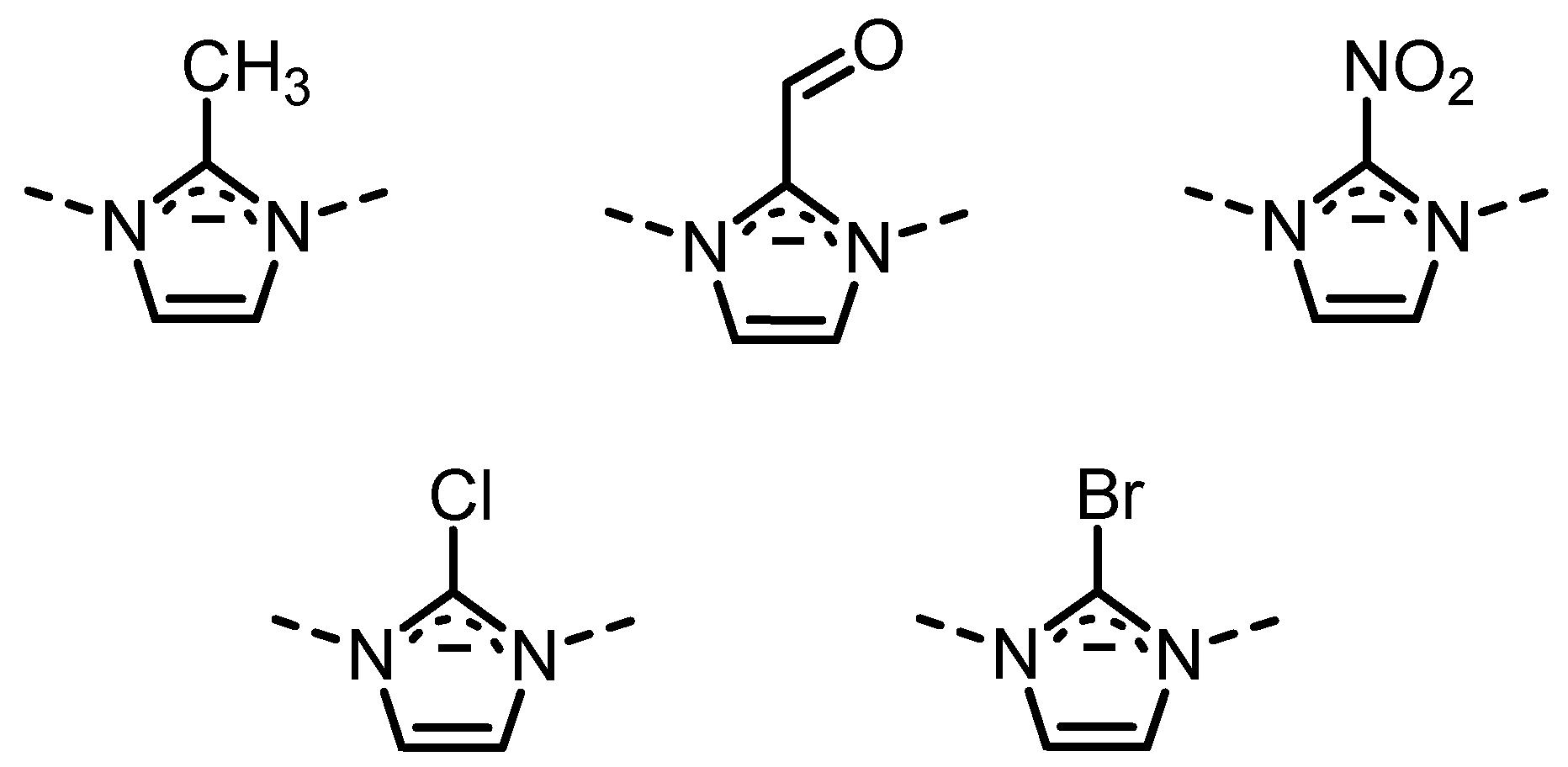
- Chaplais, G.; Fraux, G.; Paillaud, J.-L.; Marichal, C.; Nouali, H.; Fuchs, A.H.; Coudert, F.-X.; Patarin, J. Impacts of the Imidazolate Linker Substitution (CH3, Cl or Br) on the Structural and Adsorptive Properties of ZIF-8. J. Phys. Chem. C 2018. [Google Scholar] [CrossRef]
- Li, Q.; Zaczek, A.J.; Korter, T.M.; Zeitler, J.A.; Ruggiero, M.T. Methyl-Rotation Dynamics in Metal–organic Frameworks Probed with Terahertz Spectroscopy. Chem. Commun. 2018, 54, 5776–5779. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Wu, H.; Udovic, T.J.; Rush, J.J.; Yildirim, T. Quasi-Free Methyl Rotation in Zeolitic Imidazolate Framework-8. J. Phys. Chem. A 2008, 112, 12602–12606. [Google Scholar] [CrossRef] [PubMed]
- Zheng, B.; Fu, F.; Wang, L.L.; Yang, L.; Zhu, Y.; Du, H. Investigation of the Linker Swing Motion in the Zeolitic Imidazolate Framework ZIF-90. J. Phys. Chem. C 2018, 122, 7203–7209. [Google Scholar] [CrossRef]
- Morris, W.; Taylor, R.E.; Dybowski, C.; Yaghi, O.M.; Garcia-Garibay, M.A. Framework Mobility in the Metal-Organic Framework Crystal IRMOF-3: Evidence for Aromatic Ring and Amine Rotation. J. Mol. Struct. 2011, 1004, 94–101. [Google Scholar] [CrossRef]
- Loeb, S.J. Rotaxanes as Ligands: From Molecules to Materials. Chem. Soc. Rev. 2007, 36, 226–235. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.; Olson, M.A.; Stoddart, J.F.; Yaghi, O.M. Robust Dynamics. Nat. Chem. 2010, 2, 439–443. [Google Scholar] [CrossRef] [PubMed]
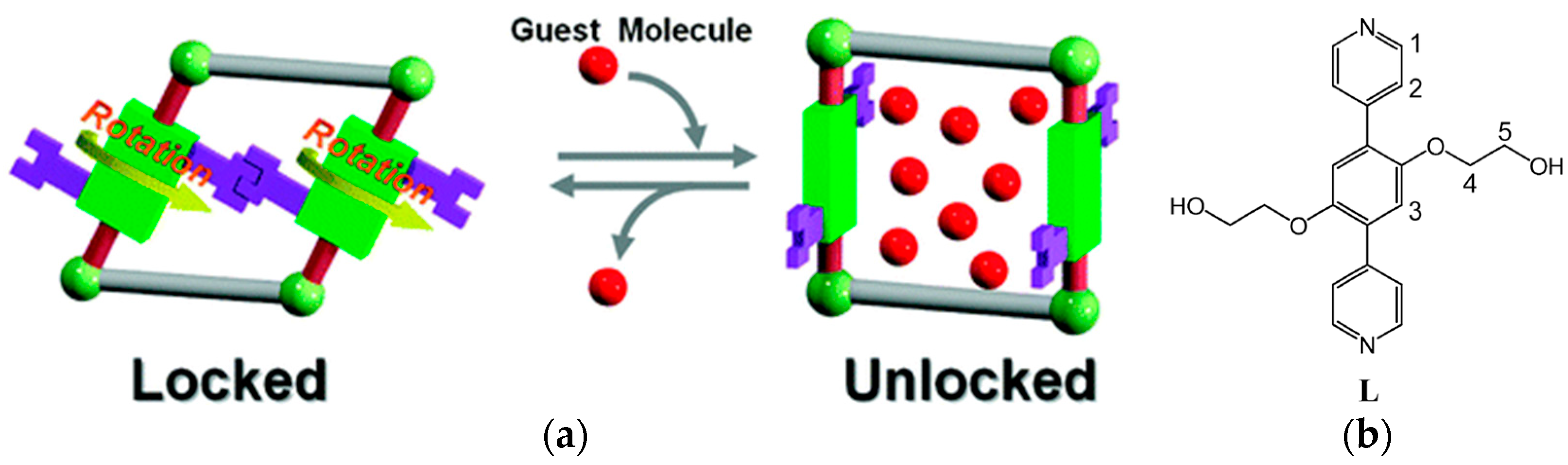
- Vukotic, V.N.; Harris, K.J.; Zhu, K.; Schurko, R.W.; Loeb, S.J. Metal–organic Frameworks with Dynamic Interlocked Components. Nat. Chem. 2012, 4, 456–460. [Google Scholar] [CrossRef] [PubMed]
- Zhu, K.; Vukotic, V.N.; O’Keefe, C.A.; Schurko, R.W.; Loeb, S.J.; Okeefe, C.A.; Schurko, R.W.; Loeb, S.J.; O’Keefe, C.A.; Schurko, R.W.; et al. Metal–Organic Frameworks with Mechanically Interlocked Pillars: Controlling Ring Dynamics in the Solid-State via a Reversible Phase Change. J. Am. Chem. Soc. 2014, 136, 7403–7409. [Google Scholar] [CrossRef] [PubMed]
- Vukotic, V.N.; O’Keefe, C.A.; Zhu, K.; Harris, K.J.; To, C.; Schurko, R.W.; Loeb, S.J. Mechanically Interlocked Linkers inside Metal–Organic Frameworks: Effect of Ring Size on Rotational Dynamics. J. Am. Chem. Soc. 2015, 137, 9643–9651. [Google Scholar] [CrossRef] [PubMed]
- Farahani, N.; Zhu, K.; O’Keefe, C.A.; Schurko, R.W.; Loeb, S.J. Thermally Driven Dynamics of a Rotaxane Wheel about an Imidazolium Axle inside a Metal-Organic Framework. Chempluschem 2016, 81, 836–841. [Google Scholar] [CrossRef]
- Karlen, S.D.; Garcia-Garibay, M.A. yoAmphidynamic Crystals: Structural Blueprints for Molecular Machines. Mol. Mach. 2005, 262, 179–227. [Google Scholar] [CrossRef]
- Wittebort, R.J.; Olejniczak, E.T.; Griffin, R.G. Analysis of Deuterium Nuclear Magnetic Resonance Line Shapes in Anisotropic Media. J. Chem. Phys. 1987, 86, 5411–5420. [Google Scholar] [CrossRef]
- Sutrisno, A.; Huang, Y. Solid-State NMR: A Powerful Tool for Characterization of Metal-Organic Frameworks. Solid State Nucl. Magn. Reson. 2013, 49, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Henrichs, P.M.; Hewitt, J.M.; Linder, M. Experimental Aspects of Deuterium NMR of Solids. J. Magn. Reson. 1984, 60, 280–298. [Google Scholar] [CrossRef]
- Damron, J.T.; Ma, J.; Kurz, R.; Saalwächter, K.; Matzger, A.J.; Ramamoorthy, A. The Influence of Chemical Modification on Linker Rotational Dynamics in Metal–Organic Frameworks. Angew. Chem. Int. Ed. 2018, 57, 8678–8681. [Google Scholar] [CrossRef] [PubMed]
- Broadband Dielectric Spectroscopy; Kremer, F., Schönhals, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Winston, E.B.; Lowell, P.J.; Vacek, J.; Chocholousová, J.; Michl, J.; Price, J.C. Dipolar Molecular Rotors in the Metal-Organic Framework Crystal IRMOF-2. Phys. Chem. Chem. Phys. 2008, 10, 5188–5191. [Google Scholar] [CrossRef] [PubMed]
- Devautour-Vinot, S.; Maurin, G.; Serre, C.; Horcajada, P.; Paula Da Cunha, D.; Guillerm, V.; De Souza Costa, E.; Taulelle, F.; Martineau, C. Structure and Dynamics of the Functionalized MOF Type UiO-66(Zr): NMR and Dielectric Relaxation Spectroscopies Coupled with DFT Calculations. Chem. Mater. 2012, 24, 2168–2177. [Google Scholar] [CrossRef]
- Frunza, S.; Schönhals, A.; Frunza, L.; Ganea, P.; Kosslick, H.; Harloff, J.; Schulz, A. Molecular Relaxation Processes in a MOF-5 Structure Revealed by Broadband Dielectric Spectroscopy: Signature of Phenylene Ring Fluctuations. J. Phys. Chem. B 2010, 114, 12840–12846. [Google Scholar] [CrossRef] [PubMed]
- Balčiūnas, S.; Šimėnas, M.; Pavlovaitė, D.; Kinka, M.; Shieh, F.-K.; Wu, K.C.-W.; Banys, J.; Grigalaitis, R. Low-Frequency Dipolar Dynamics and Atmospheric Effects in ZIF-90 Metal–Organic Framework. J. Phys. Chem. C 2019, 123, 631–636. [Google Scholar] [CrossRef]
- Greaves, G.N.; Meneau, F.; Majérus, O.; Jones, D.G.; Taylor, J. Identifying Vibrations That Destabilize Crystals and Characterize the Glassy State. Science 2005, 308, 1299–1302. [Google Scholar] [CrossRef] [PubMed]
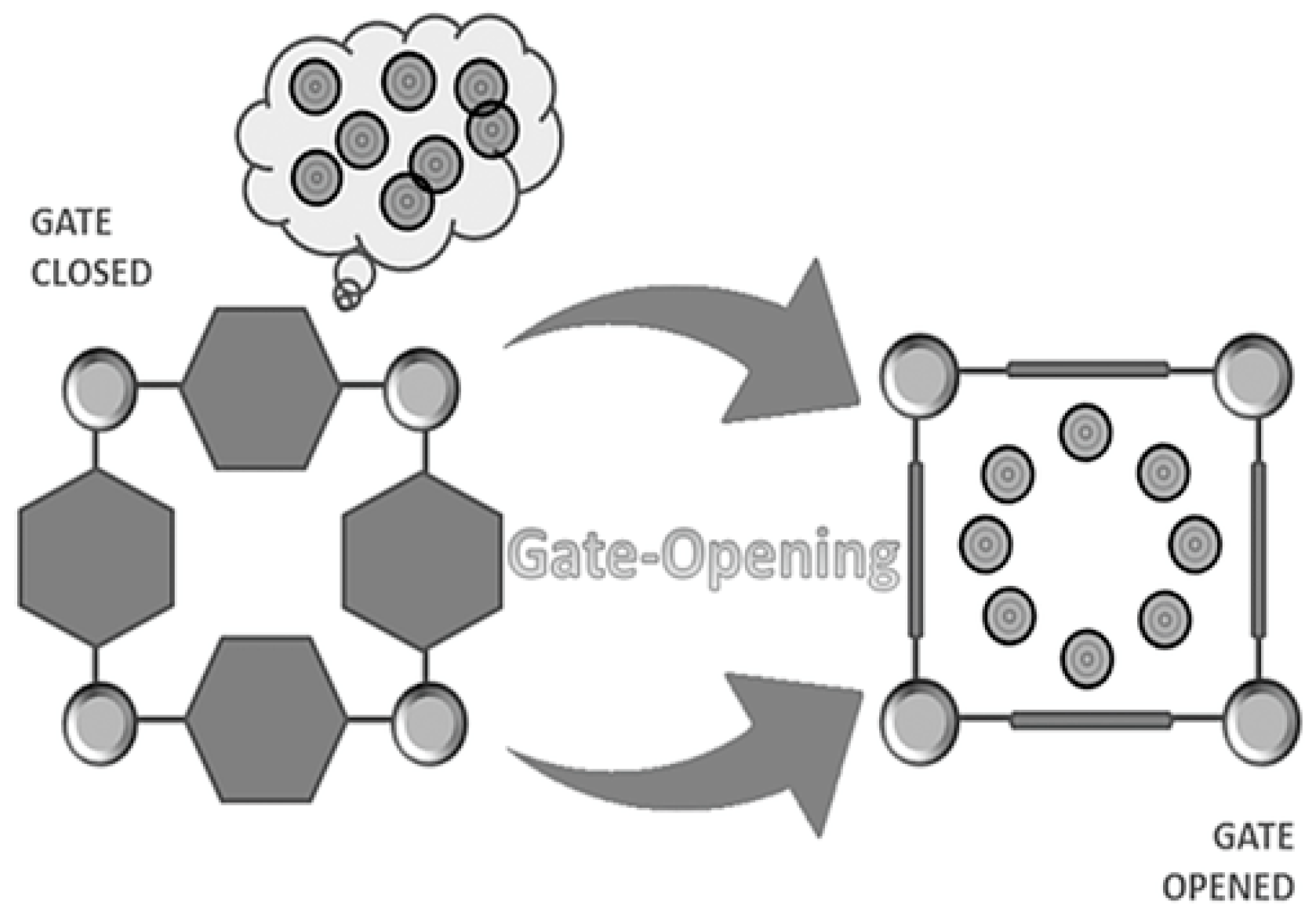
- Ryder, M.R.; Civalleri, B.; Bennett, T.D.; Henke, S.; Rudić, S.; Cinque, G.; Fernandez-Alonso, F.; Tan, J.-C. Identifying the Role of Terahertz Vibrations in Metal-Organic Frameworks: From Gate-Opening Phenomenon to Shear-Driven Structural Destabilization. Phys. Rev. Lett. 2014, 113, 215502. [Google Scholar] [CrossRef] [PubMed]
- Tan, N.Y.; Ruggiero, M.T.; Orellana-Tavra, C.; Tian, T.; Bond, A.D.; Korter, T.M.; Fairen-Jimenez, D.; Axel Zeitler, J. Investigation of the Terahertz Vibrational Modes of ZIF-8 and ZIF-90 with Terahertz Time-Domain Spectroscopy. Chem. Commun. 2015, 51, 16037–16040. [Google Scholar] [CrossRef] [PubMed]
- Kuc, A.; Enyashin, A.; Seifert, G. Metal−Organic Frameworks: Structural, Energetic, Electronic, and Mechanical Properties. J. Phys. Chem. B 2007, 111, 8179–8186. [Google Scholar] [CrossRef] [PubMed]
- Kolokolov, D.I.; Jobic, H.; Stepanov, A.G.; Plazanet, M.; Zbiri, M.; Ollivier, J.; Guillerm, V.; Devic, T.; Serre, C.; Férey, G. Comparison of the Dynamics of MIL-53(Cr) and MIL-47(V) Frameworks Using Neutron Scattering and DFT Methods. Eur. Phys. J. Spec. Top. 2010, 189, 263–271. [Google Scholar] [CrossRef]
- Burtch, N.C.; Torres-Knoop, A.; Foo, G.S.; Leisen, J.; Sievers, C.; Ensing, B.; Dubbeldam, D.; Walton, K.S. Understanding DABCO Nanorotor Dynamics in Isostructural Metal–Organic Frameworks. J. Phys. Chem. Lett. 2015, 6, 812–816. [Google Scholar] [CrossRef] [PubMed]
- Burtch, N.C.; Dubbeldam, D.; Walton, K.S. Investigating Water and Framework Dynamics in Pillared MOFs. Mol. Simul. 2015, 41, 1379–1387. [Google Scholar] [CrossRef]
- Namsani, S.; Yazaydin, A.O. Electric Field Induced Rotation of Halogenated Organic Linkers in Isoreticular Metal–organic Frameworks for Nanofluidic Applications. Mol. Syst. Des. Eng. 2018, 3, 951–958. [Google Scholar] [CrossRef]
- Haldoupis, E.; Watanabe, T.; Nair, S.; Sholl, D.S. Quantifying Large Effects of Framework Flexibility on Diffusion in MOFs: CH4 and CO2 in ZIF-8. ChemPhysChem 2012, 13, 3449–3452. [Google Scholar] [CrossRef] [PubMed]
- Parkes, M.V.; Demir, H.; Teich-McGoldrick, S.L.; Sholl, D.S.; Greathouse, J.A.; Allendorf, M.D. Molecular Dynamics Simulation of Framework Flexibility Effects on Noble Gas Diffusion in HKUST-1 and ZIF-8. Microporous Mesoporous Mater. 2014, 194, 190–199. [Google Scholar] [CrossRef]
- Elsaidi, S.K.; Mohamed, M.H.; Simon, C.M.; Braun, E.; Pham, T.; Forrest, K.A.; Xu, W.; Banerjee, D.; Space, B.; Zaworotko, M.J.; et al. Effect of Ring Rotation upon Gas Adsorption in SIFSIX-3-M (M = Fe, Ni) Pillared Square Grid Networks. Chem. Sci. 2017, 8, 2373–2380. [Google Scholar] [CrossRef] [PubMed]
- Laio, A.; Gervasio, F.L. Metadynamics: A Method to Simulate Rare Events and Reconstruct the Free Energy in Biophysics, Chemistry and Material Science. Rep. Prog. Phys. 2008, 71, 126601. [Google Scholar] [CrossRef]
- Vymětal, J.; Vondrášek, J. Metadynamics As a Tool for Mapping the Conformational and Free-Energy Space of Peptides—The Alanine Dipeptide Case Study. J. Phys. Chem. B 2010, 114, 5632–5642. [Google Scholar] [CrossRef] [PubMed]
- Haigis, V.; Coudert, F.-X.; Vuilleumier, R.; Boutin, A.; Fuchs, A.H. Hydrothermal Breakdown of Flexible Metal–Organic Frameworks: A Study by First-Principles Molecular Dynamics. J. Phys. Chem. Lett. 2015, 6, 4365–4370. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Lucier, B.E.G.; Boyle, P.D.; Huang, Y. Understanding the Fascinating Origins of CO2 Adsorption and Dynamics in MOFs. Chem. Mater. 2016, 28, 5829–5846. [Google Scholar] [CrossRef]
- Katsoulidis, A.P.; Antypov, D.; Whitehead, G.F.S.; Carrington, E.J.; Adams, D.J.; Berry, N.G.; Darling, G.R.; Dyer, M.S.; Rosseinsky, M.J. Chemical Control of Structure and Guest Uptake by a Conformationally Mobile Porous Material. Nature 2019. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Davies, A.J.; Lin, X.; Suyetin, M.; Matsuda, R.; Blake, A.J.; Wilson, C.; Lewis, W.; Parker, J.E.; Tang, C.C.; et al. Selective CO2 Uptake and Inverse CO2/C2H2 Selectivity in a Dynamic Bifunctional Metal–organic Framework. Chem. Sci. 2012, 3, 2993. [Google Scholar] [CrossRef]
- Murdock, C.R.; McNutt, N.W.; Keffer, D.J.; Jenkins, D.M. Rotating Phenyl Rings as a Guest-Dependent Switch in Two-Dimensional Metal–Organic Frameworks. J. Am. Chem. Soc. 2014, 136, 671–678. [Google Scholar] [CrossRef] [PubMed]
- Hyun, S.; Lee, J.H.; Jung, G.Y.; Kim, Y.K.; Kim, T.K.; Jeoung, S.; Kwak, S.K.; Moon, D.; Moon, H.R. Exploration of Gate-Opening and Breathing Phenomena in a Tailored Flexible Metal–Organic Framework. Inorg. Chem. 2016, 55, 1920–1925. [Google Scholar] [CrossRef] [PubMed]
- Yue, Y.; Rabone, J.A.; Liu, H.; Mahurin, S.M.; Li, M.-R.; Wang, H.; Lu, Z.; Chen, B.; Wang, J.; Fang, Y.; et al. A Flexible Metal–Organic Framework: Guest Molecules Controlled Dynamic Gas Adsorption. J. Phys. Chem. C 2015, 119, 9442–9449. [Google Scholar] [CrossRef]
- Sakaida, S.; Otsubo, K.; Sakata, O.; Song, C.; Fujiwara, A.; Takata, M.; Kitagawa, H. Crystalline Coordination Framework Endowed with Dynamic Gate-Opening Behaviour by Being Downsized to a Thin Film. Nat. Chem. 2016, 8, 377–383. [Google Scholar] [CrossRef] [PubMed]
- Serra-Crespo, P.; Gobechiya, E.; Ramos-Fernandez, E.V.; Juan-Alcañiz, J.; Martinez-Joaristi, A.; Stavitski, E.; Kirschhock, C.E.A.; Martens, J.A.; Kapteijn, F.; Gascon, J. Interplay of Metal Node and Amine Functionality in NH2-MIL-53: Modulating Breathing Behavior through Intra-Framework Interactions. Langmuir 2012, 28, 12916–12922. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, D.; Wang, H.; Plonka, A.M.; Emge, T.J.; Parise, J.B.; Li, J. Direct Structural Identification of Gas Induced Gate-Opening Coupled with Commensurate Adsorption in a Microporous Metal-Organic Framework. Chem. A Eur. J. 2016, 22, 11816–11825. [Google Scholar] [CrossRef] [PubMed]
- Bux, H.; Liang, F.; Li, Y.; Cravillon, J.; Wiebcke, M.; Caro, J. Zeolitic Imidazolate Framework Membrane with Molecular Sieving Properties by Microwave-Assisted Solvothermal Synthesis. J. Am. Chem. Soc. 2009, 131, 16000–16001. [Google Scholar] [CrossRef] [PubMed]
- Fairen-Jimenez, D.; Galvelis, R.; Torrisi, A.; Gellan, A.D.; Wharmby, M.T.; Wright, P.A.; Mellot-Draznieks, C.; Düren, T. Flexibility and Swing Effect on the Adsorption of Energy-Related Gases on ZIF-8: Combined Experimental and Simulation Study. Dalt. Trans. 2012, 41, 10752. [Google Scholar] [CrossRef] [PubMed]
- Seo, J.; Matsuda, R.; Sakamoto, H.; Bonneau, C.; Kitagawa, S. A Pillared-Layer Coordination Polymer with a Rotatable Pillar Acting as a Molecular Gate for Guest Molecules. J. Am. Chem. Soc. 2009, 131, 12792–12800. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.-P.; Chen, X.-M. Optimized Acetylene/Carbon Dioxide Sorption in a Dynamic Porous Crystal. J. Am. Chem. Soc. 2009, 131, 5516–5521. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Yang, Q.; Cui, X.; Yang, L.; Bao, Z.; Ren, Q.; Xing, H. Sorting of C4 Olefins with Interpenetrated Hybrid Ultramicroporous Materials by Combining Molecular Recognition and Size-Sieving. Angew. Chemie Int. Ed. 2017, 56, 16282–16287. [Google Scholar] [CrossRef] [PubMed]
- Andres-Garcia, E.; Oar-Arteta, L.; Gascon, J.; Kapteijn, F. ZIF-67 as Silver-Bullet in Adsorptive Propane/propylene Separation. Chem. Eng. J. 2019, 360, 10–14. [Google Scholar] [CrossRef]
- Hartmann, M.; Böhme, U.; Hovestadt, M.; Paula, C. Adsorptive Separation of Olefin/Paraffin Mixtures with ZIF-4. Langmuir 2015, 31, 12382–12389. [Google Scholar] [CrossRef] [PubMed]
- Böhme, U.; Barth, B.; Paula, C.; Kuhnt, A.; Schwieger, W.; Mundstock, A.; Caro, J.; Hartmann, M. Ethene/Ethane and Propene/Propane Separation via the Olefin and Paraffin Selective Metal–Organic Framework Adsorbents CPO-27 and ZIF-8. Langmuir 2013, 29, 8592–8600. [Google Scholar] [CrossRef] [PubMed]
- Luna-Triguero, A.; Vicent-Luna, J.M.; Calero, S. Phase Transition Induced by Gas Adsorption in Metal-Organic Frameworks. Chem. A Eur. J. 2018, 24, 8530–8534. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Jiang, K.; Jiang, M.; Yue, D.; Wan, Y.; Xing, H.; Yang, Y.; Cui, Y.; Chen, B.; Qian, G. A Highly Stable Amino-Coordinated MOF for Unprecedented Block off N2 Adsorption and Extraordinary CO2/N2 Separation. Chem. Commun. 2016, 52, 13568–13571. [Google Scholar] [CrossRef] [PubMed]
- Ania, C.O.; García-Pérez, E.; Haro, M.; Gutiérrez-Sevillano, J.J.; Valdés-Solís, T.; Parra, J.B.; Calero, S. Understanding Gas-Induced Structural Deformation of ZIF-8. J. Phys. Chem. Lett. 2012, 3, 1159–1164. [Google Scholar] [CrossRef] [PubMed]
- Kanoo, P.; Reddy, S.K.; Kumari, G.; Haldar, R.; Narayana, C.; Balasubramanian, S.; Maji, T.K. Unusual Room Temperature CO2 Uptake in a Fluoro-Functionalized MOF: Insight from Raman Spectroscopy and Theoretical Studies. Chem. Commun. 2012, 48, 8487. [Google Scholar] [CrossRef] [PubMed]
- Gee, J.A.; Sholl, D.S. Effect of Framework Flexibility on C8 Aromatic Adsorption at High Loadings in Metal–Organic Frameworks. J. Phys. Chem. C 2016, 120, 370–376. [Google Scholar] [CrossRef]
- Hong, Y.; Lam, J.W.Y.; Tang, B.Z. Aggregation-Induced Emission. Chem. Soc. Rev. 2011, 40, 5361. [Google Scholar] [CrossRef] [PubMed]
- Qin, A.; Jim, C.K.W.; Tang, Y.; Lam, J.W.Y.; Liu, J.; Mahtab, F.; Gao, P.; Tang, B.Z. Aggregation-Enhanced Emissions of Intramolecular Excimers in Disubstituted Polyacetylenes. J. Phys. Chem. B 2008, 112, 9281–9288. [Google Scholar] [CrossRef] [PubMed]
- Dong, Y.; Lam, J.W.Y.; Qin, A.; Liu, J.; Li, Z.; Tang, B.Z.; Sun, J.; Kwok, H.S. Aggregation-Induced Emissions of Tetraphenylethene Derivatives and Their Utilities as Chemical Vapor Sensors and in Organic Light-Emitting Diodes. Appl. Phys. Lett. 2007, 91, 11111. [Google Scholar] [CrossRef]
- Shustova, N.B.; McCarthy, B.D.; Dincă, M. Turn-On Fluorescence in Tetraphenylethylene-Based Metal–Organic Frameworks: An Alternative to Aggregation-Induced Emission. J. Am. Chem. Soc. 2011, 133, 20126–20129. [Google Scholar] [CrossRef] [PubMed]
- Du, T.; Zhang, H.; Ruan, J.; Jiang, H.; Chen, H.-Y.; Wang, X. Adjusting the Linear Range of Au-MOF Fluorescent Probes for Real-Time Analyzing Intracellular GSH in Living Cells. ACS Appl. Mater. Interfaces 2018, 10, 12417–12423. [Google Scholar] [CrossRef] [PubMed]
- Serra-Crespo, P.; Van Der Veen, M.A.; Gobechiya, E.; Houthoofd, K.; Filinchuk, Y.; Kirschhock, C.E.A.; Martens, J.A.; Sels, B.F.; De Vos, D.E.; Kapteijn, F.; et al. NH2-MIL-53(Al): A High-Contrast Reversible Solid-State Nonlinear Optical Switch. J. Am. Chem. Soc. 2012, 134, 8314–8317. [Google Scholar] [CrossRef] [PubMed]
- Balestra, S.R.G.; Bueno-Perez, R.; Hamad, S.; Dubbeldam, D.; Ruiz-Salvador, A.R.; Calero, S. Controlling Thermal Expansion: A Metal–Organic Frameworks Route. Chem. Mater. 2016, 28, 8296–8304. [Google Scholar] [CrossRef] [PubMed]
- Collings, I.E.; Tucker, M.G.; Keen, D.A.; Goodwin, A.L. Geometric Switching of Linear to Area Negative Thermal Expansion in Uniaxial Metal–organic Frameworks. CrystEngComm 2014, 16, 3498–3506. [Google Scholar] [CrossRef]
- Lock, N.; Wu, Y.; Christensen, M.; Cameron, L.J.; Peterson, V.K.; Bridgeman, A.J.; Kepert, C.J.; Iversen, B.B. Elucidating Negative Thermal Expansion in MOF-5. J. Phys. Chem. C 2010, 114, 16181–16186. [Google Scholar] [CrossRef]
- Lock, N.; Christensen, M.; Kepert, C.J.; Iversen, B.B. Effect of Gas Pressure on Negative Thermal Expansion in MOF-5. Chem. Commun. 2013, 49, 789. [Google Scholar] [CrossRef] [PubMed]
- Peterson, V.K.; Kearley, G.J.; Wu, Y.; Ramirez-Cuesta, A.J.; Kemner, E.; Kepert, C.J. Local Vibrational Mechanism for Negative Thermal Expansion: A Combined Neutron Scattering and First-Principles Study. Angew. Chem. Int. Ed. 2010, 49, 585–588. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Wang, C.; Sun, Y.; Shi, K.; Deng, S.; Lu, H. Large Negative Thermal Expansion Provided by Metal-Organic Framework MOF-5: A First-Principles Study. Mater. Chem. Phys. 2016, 175, 138–145. [Google Scholar] [CrossRef]
- Pang, J.; Liu, C.; Huang, Y.; Wu, M.; Jiang, F.; Yuan, D.; Hu, F.; Su, K.; Liu, G.; Hong, M. Visualizing the Dynamics of Temperature- and Solvent-Responsive Soft Crystals. Angew. Chem. Int. Ed. 2016, 55, 7478–7482. [Google Scholar] [CrossRef] [PubMed]
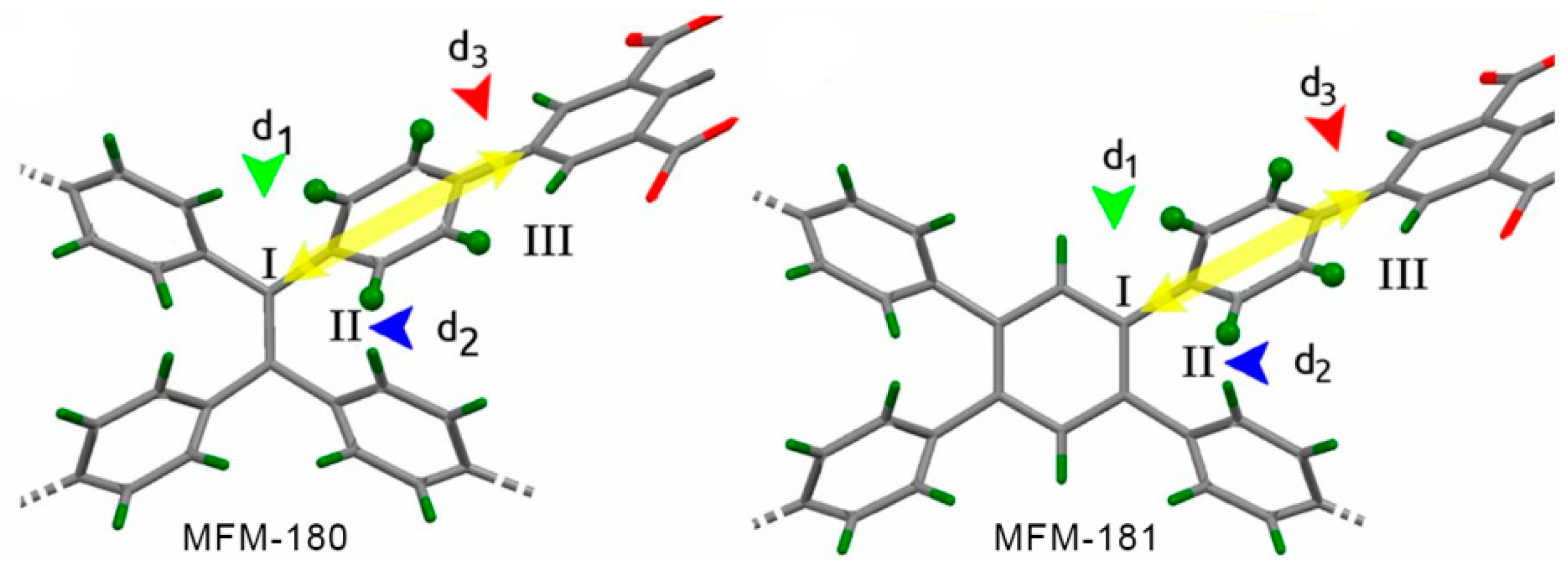
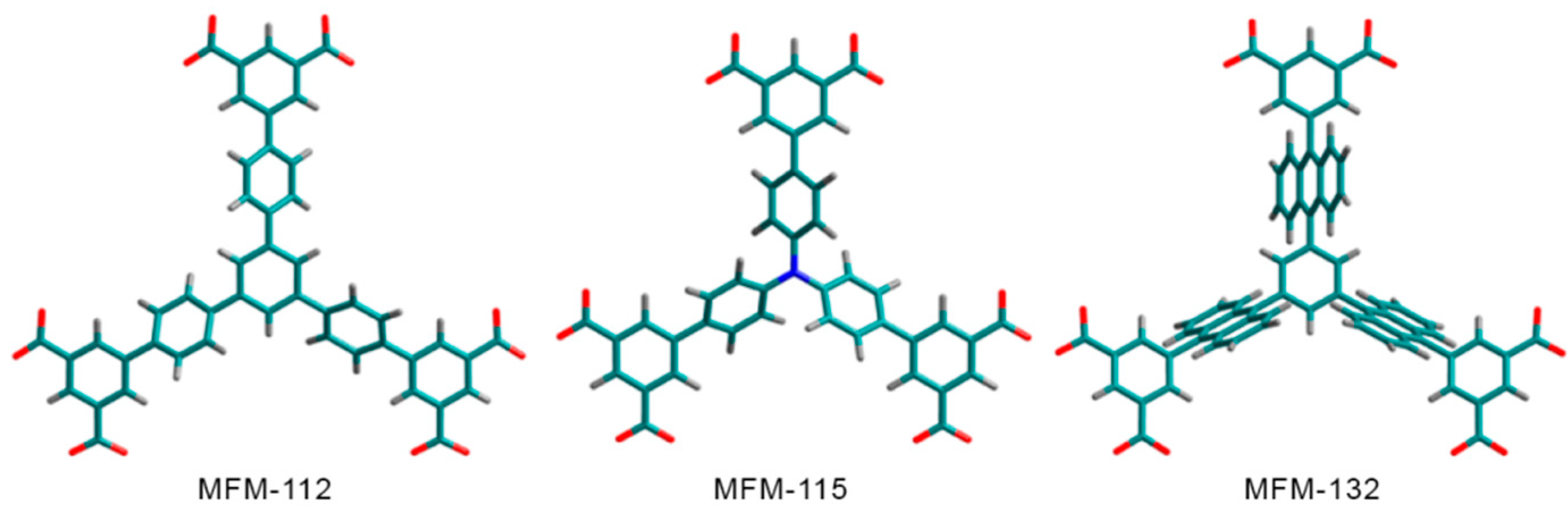
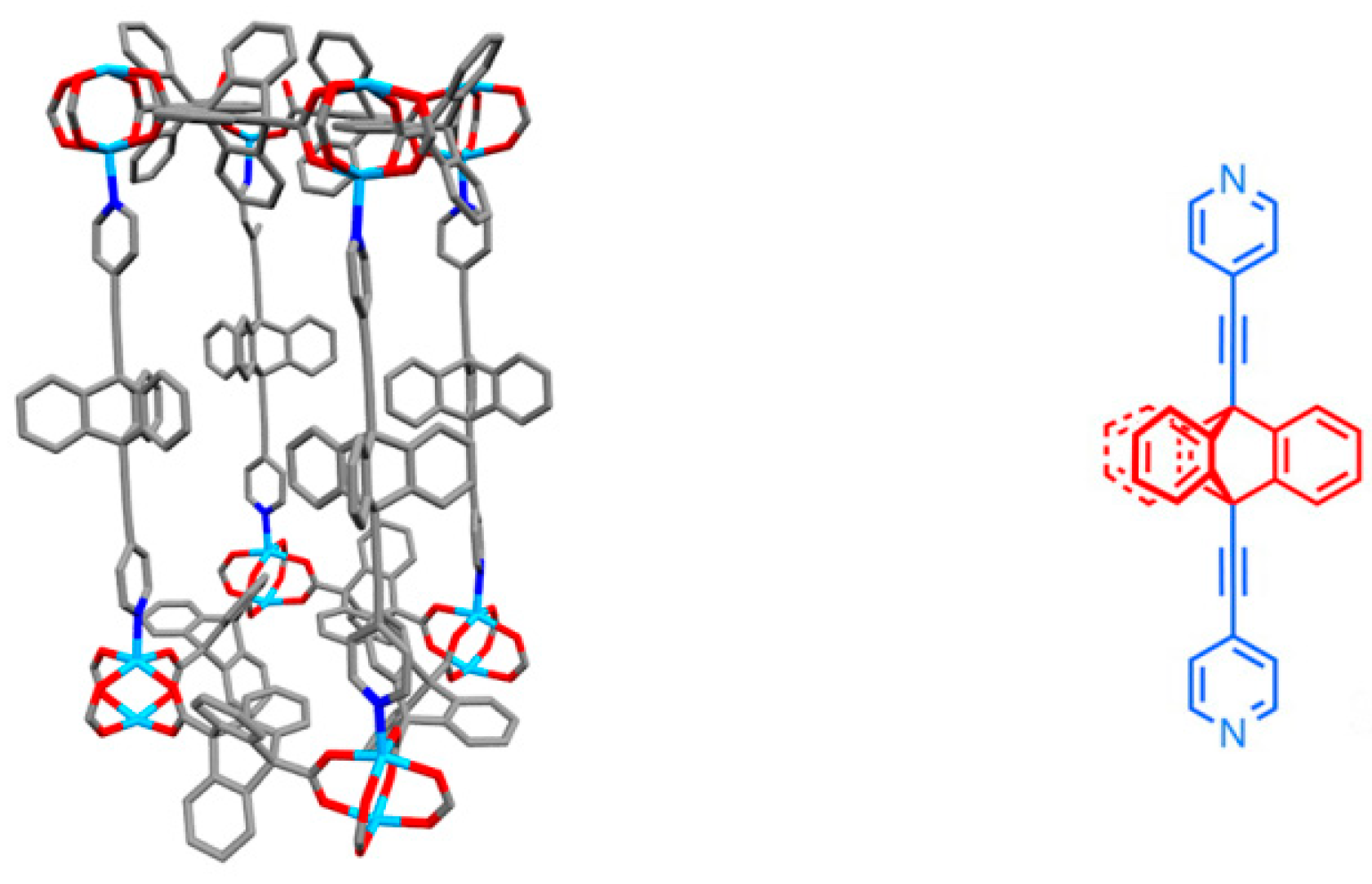
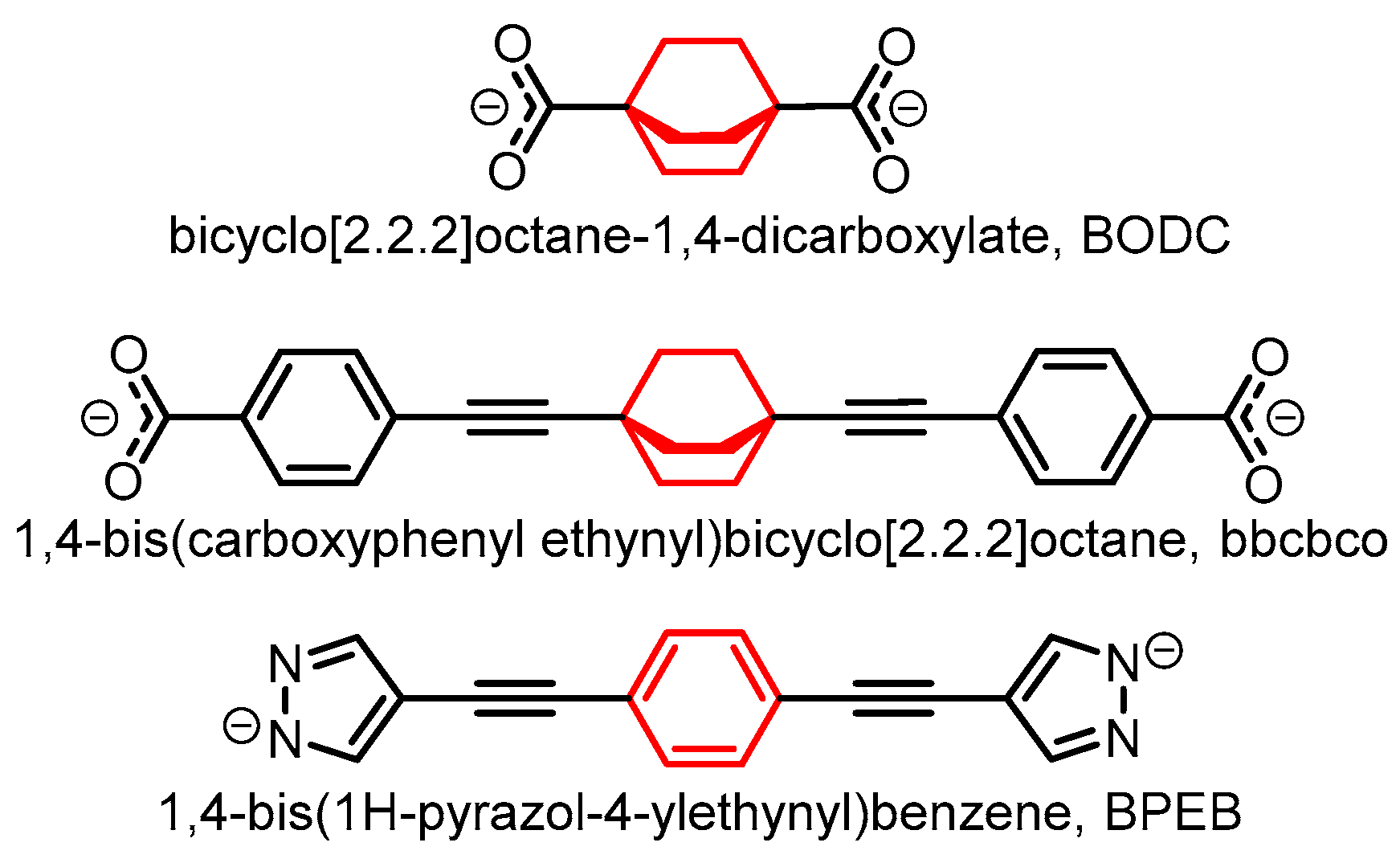
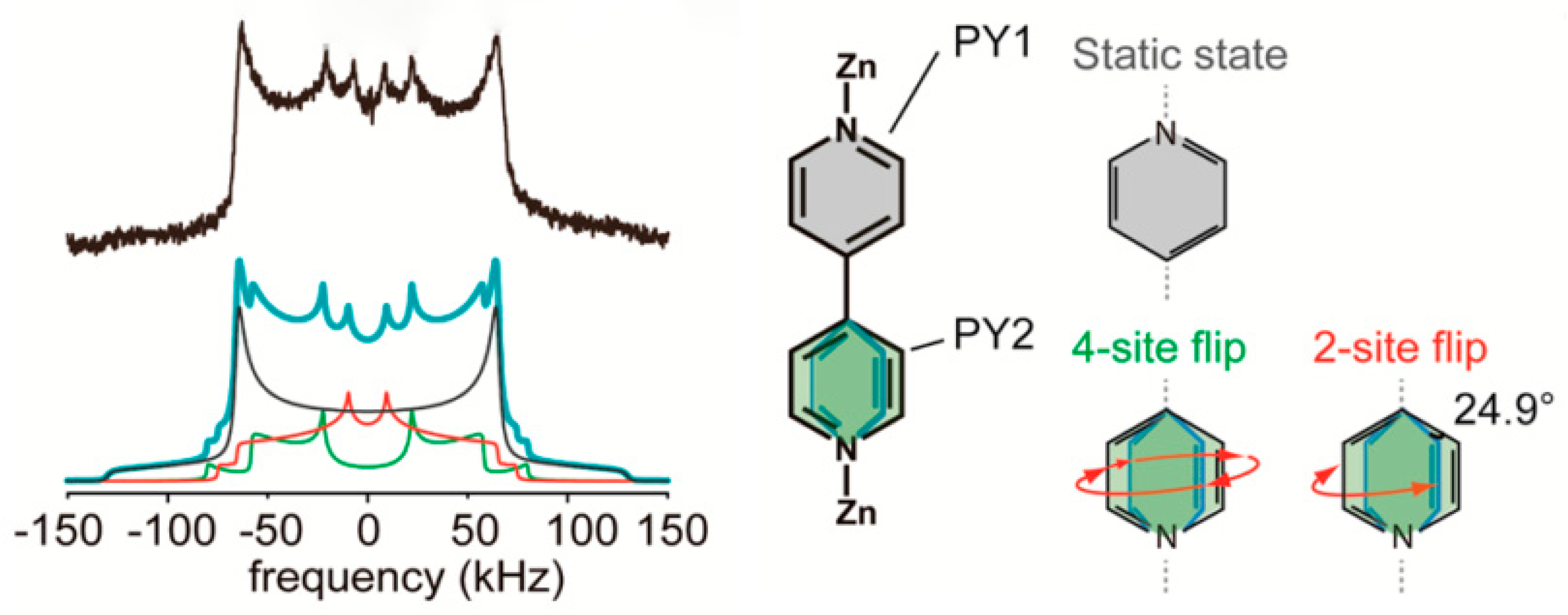
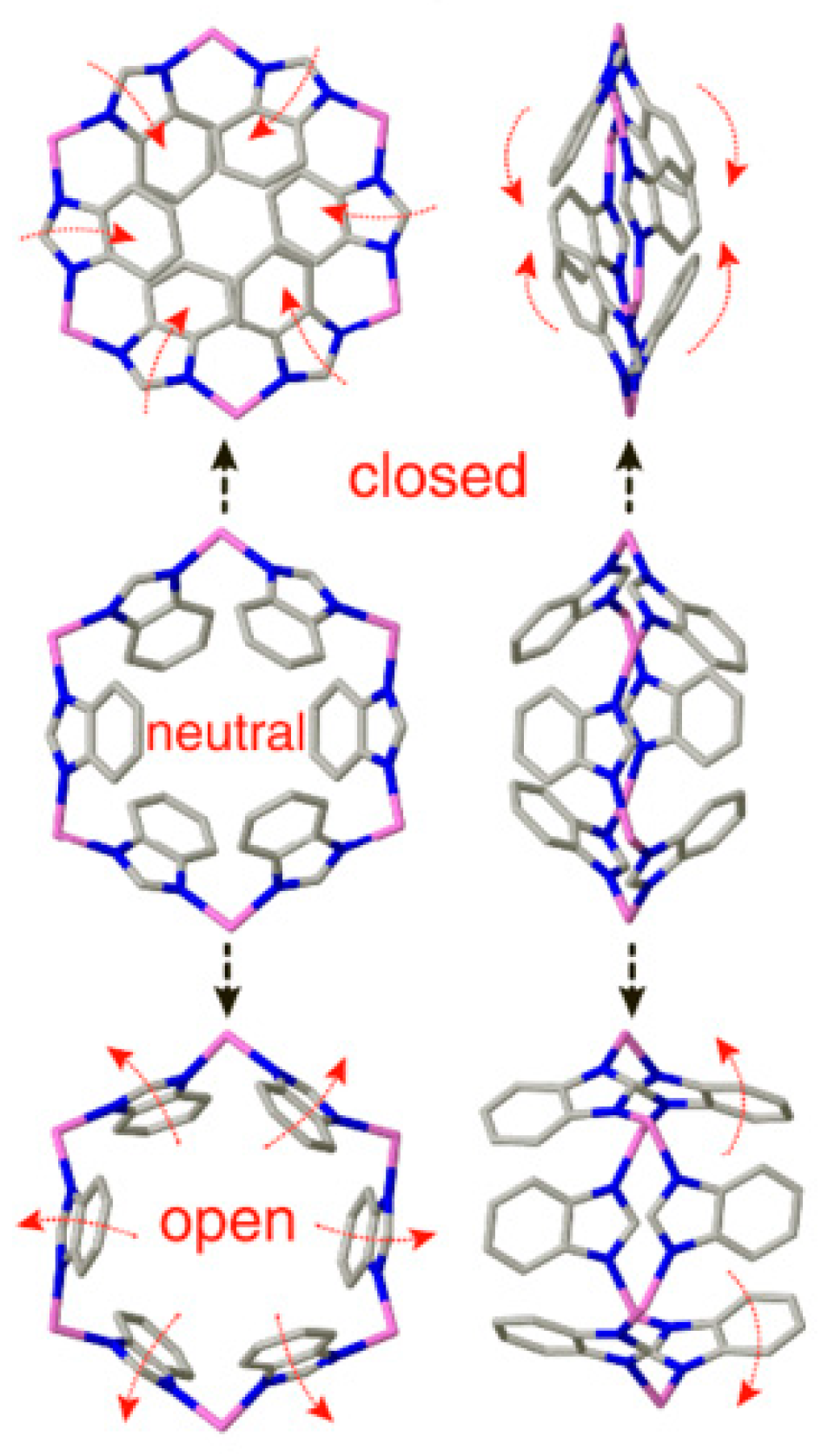
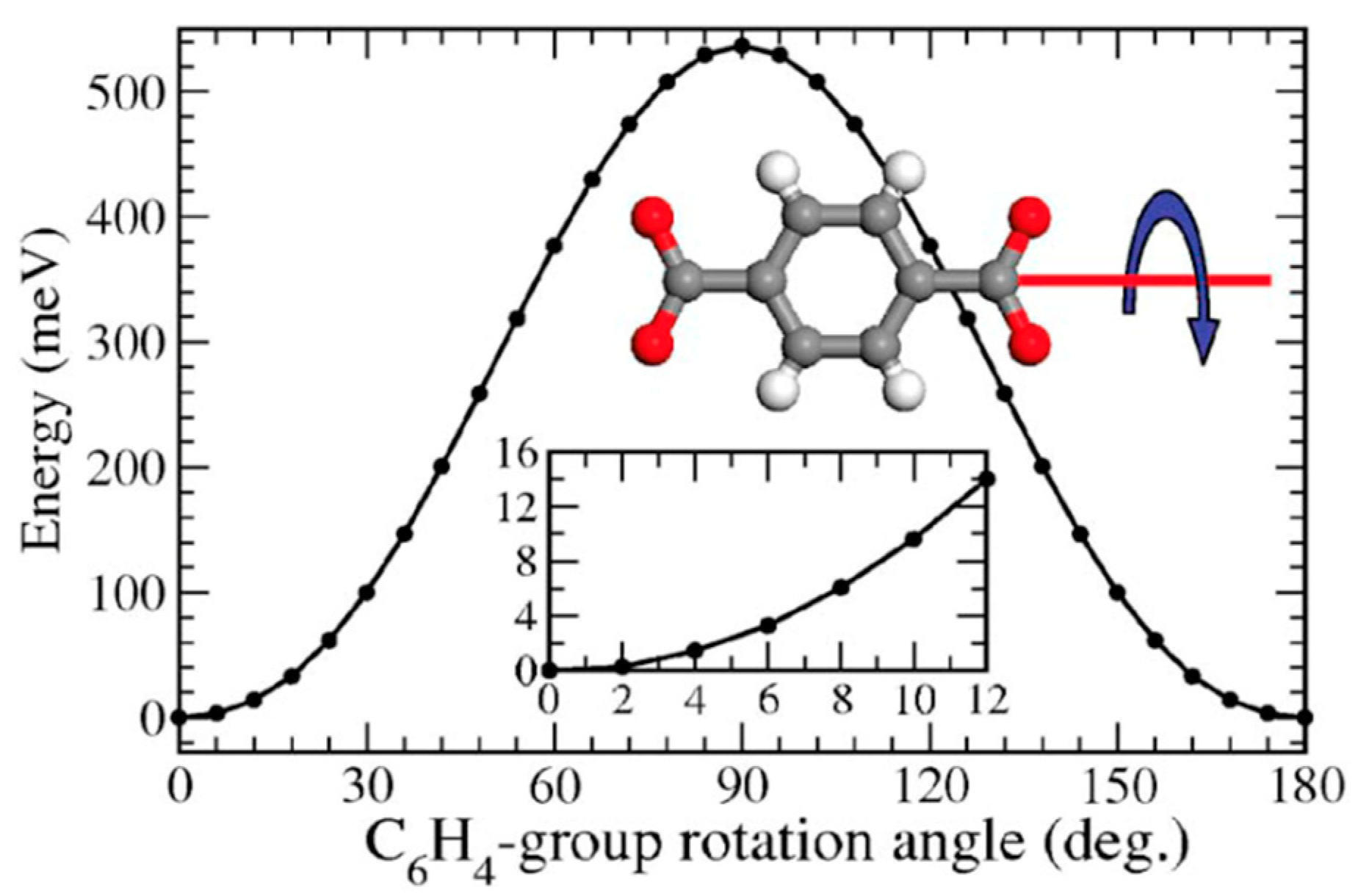
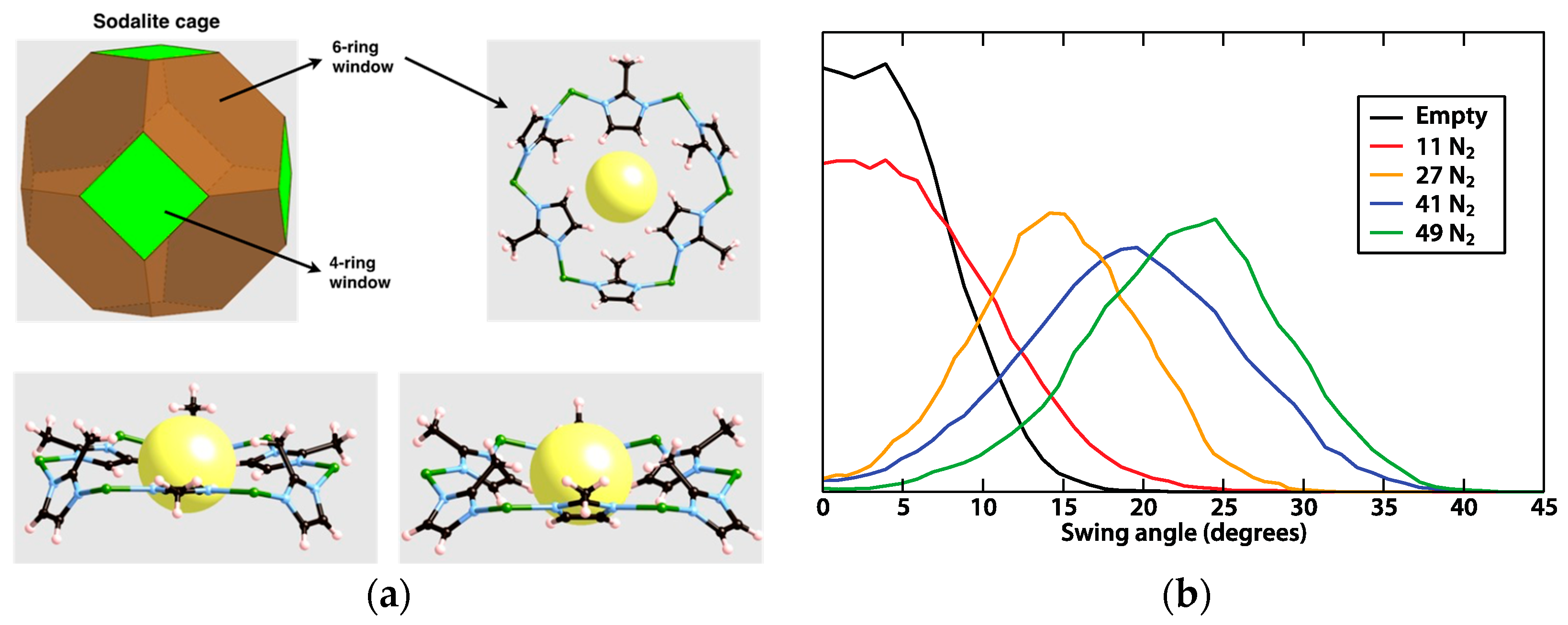

| MOF | Rotator | Type | T/K* | Barrier/kJ mol−1 | ω0/Hz | Method | Ref. |
|---|---|---|---|---|---|---|---|
| MOF-5 |  | π-flip | 363–435 | 47.3 ± 8.4 | 1.60 × 1012 | 2H NMR | [16] |
| MOF-5 | π-flip | - | 51.8 | - | DFT | [17] | |
| MIL-53(Cr) | π-flip | 333–453 | 41 | 1.26 × 1011 | 2H NMR | [18] | |
| MIL-47(V) | π-flip | 373–483 | 45 | 8.80 × 1010 | 2H NMR | [18] | |
| MIL-53(Al) | π-flip | 359–492 | 37 ± 1 | 0.6 × 1010 | 2H NMR | [19] | |
| UiO-66(Zr) | π-flip | 213–403 | 30 ± 2 | 0.5 ± 0.8 × 1012 | 2H NMR | [22] | |
| MIL-140 | π-flip | - | 27.4 | - | DFT | [24] | |
| DMOF | π-flip | 253–359 | 32–36 | 0.3–10 × 1011 | 2H NMR | [23] | |
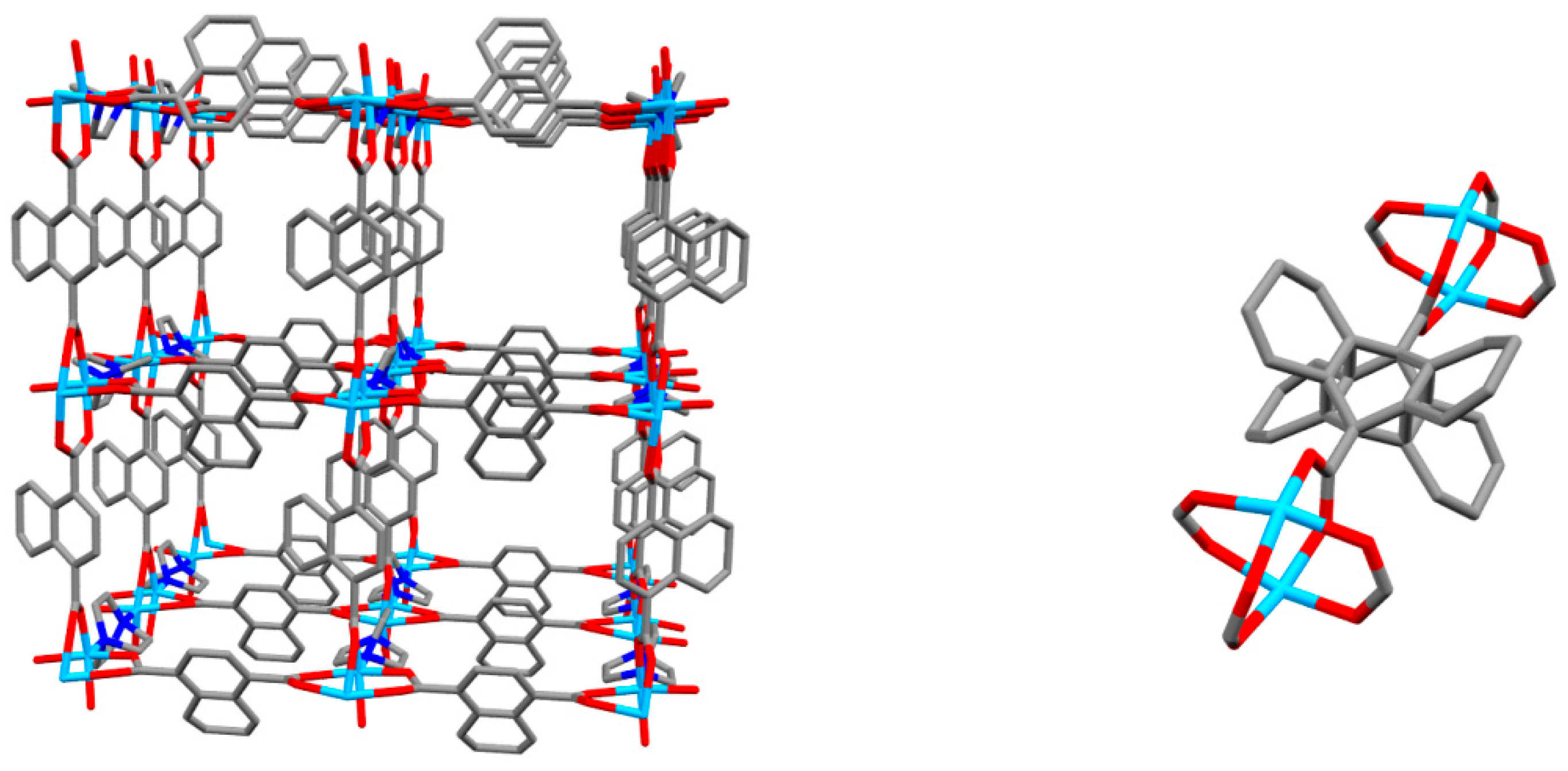
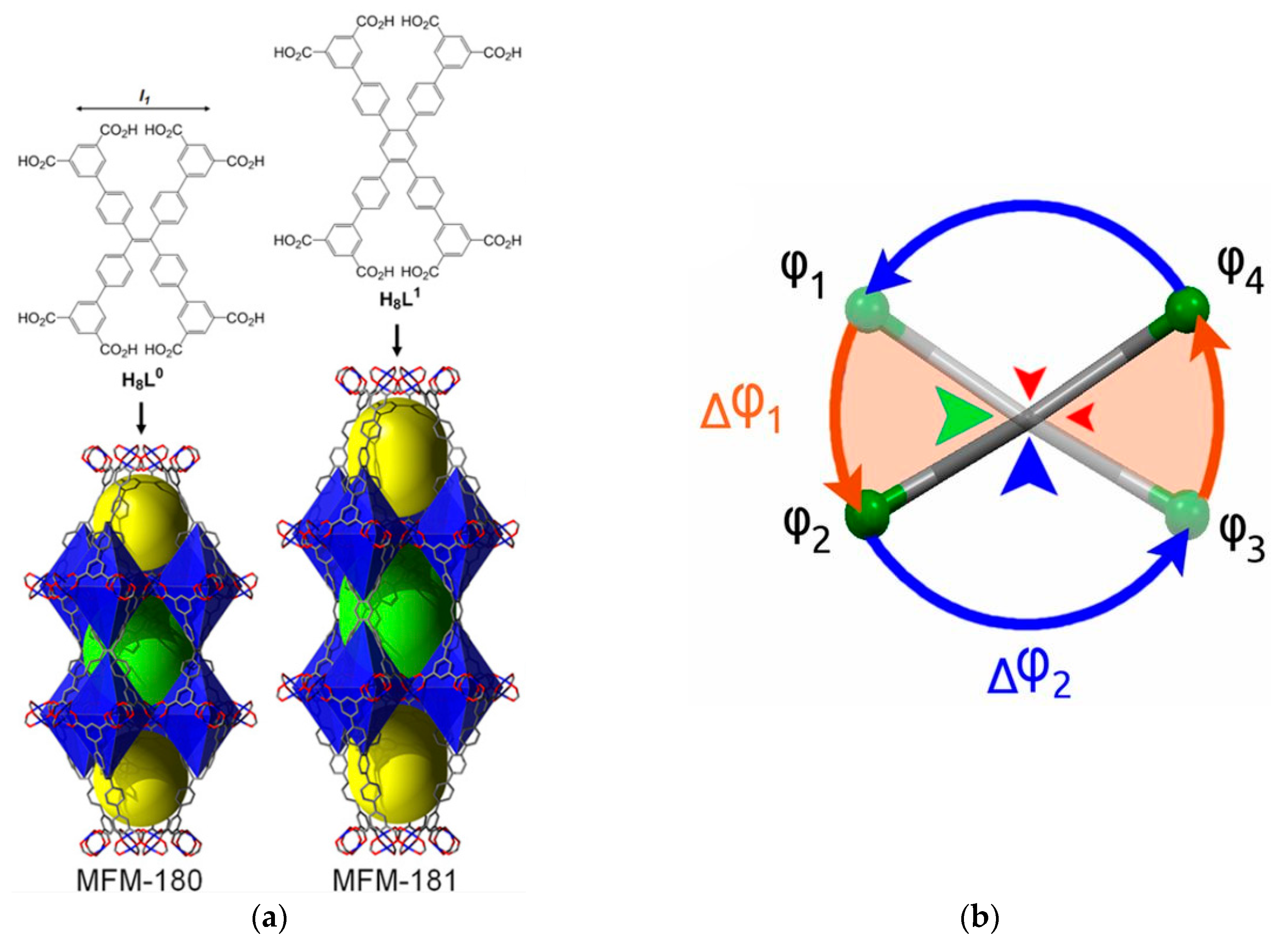
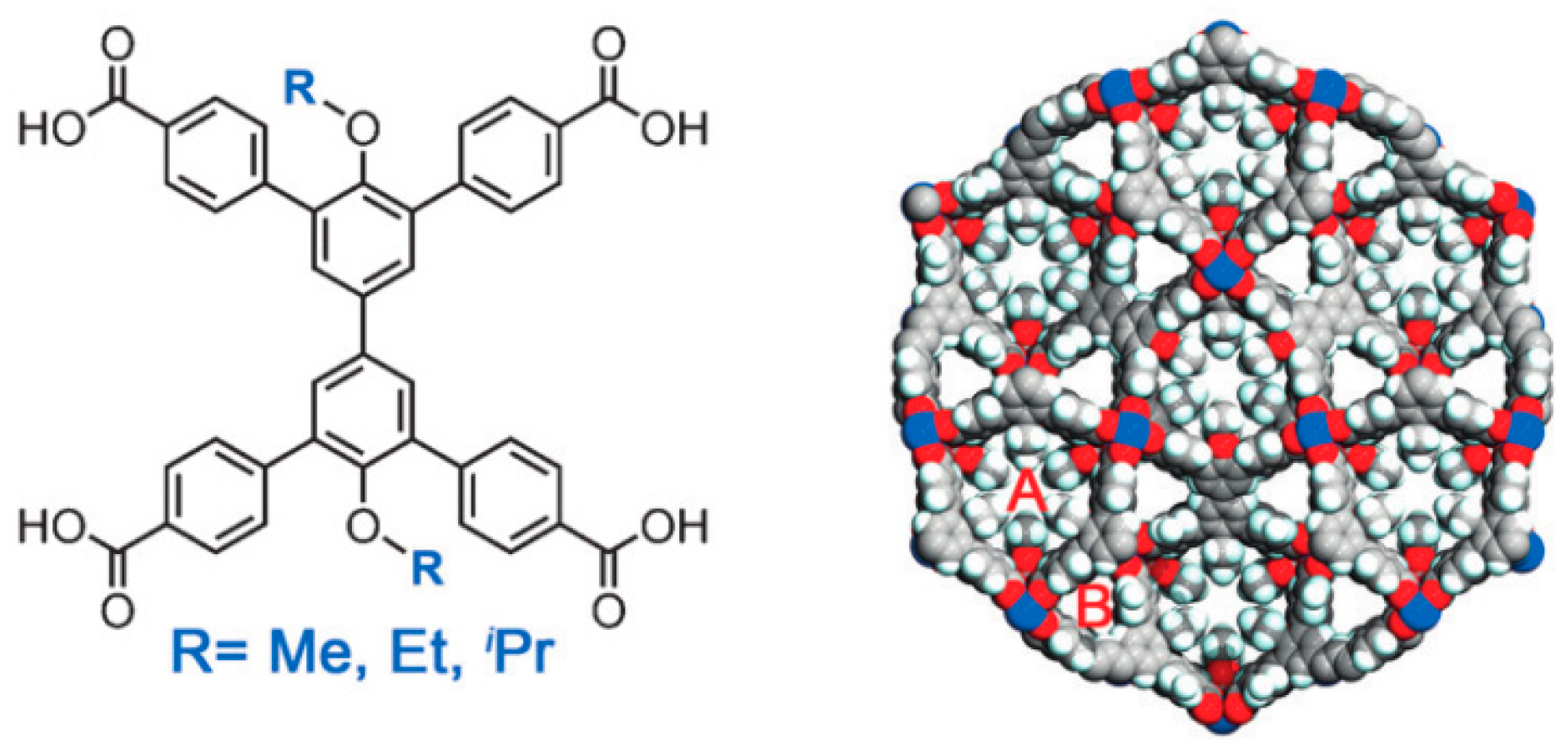
| MFM-180 |  | 4-site | 223–503 | 26; 28 | 1.6 × 1011; 3 × 107 | 2H NMR | [9] |
| MFM-181 |  | 4-site | 153–473 | 20; 34 | 9 × 1011; 4.6 × 108 | 2H NMR | [9] |
| BODCA-MOF |  | 6-site; 3-site; free | 6–12; 12–50; 50–292 | 0.8 | 4.7 × 1010 | 1H T1 relaxation | [10] |
| MFM-112a | 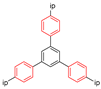 | 4-site | 123–203 | 8.6 | 3 × 108; 18 × 108 | 2H NMR | [12] |
| MFM-115a | 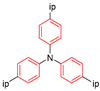 | 4-site; 6-site | 203–315 | 14; 40 | 2 × 108; 5 × 1012 | 2H NMR | [12] |
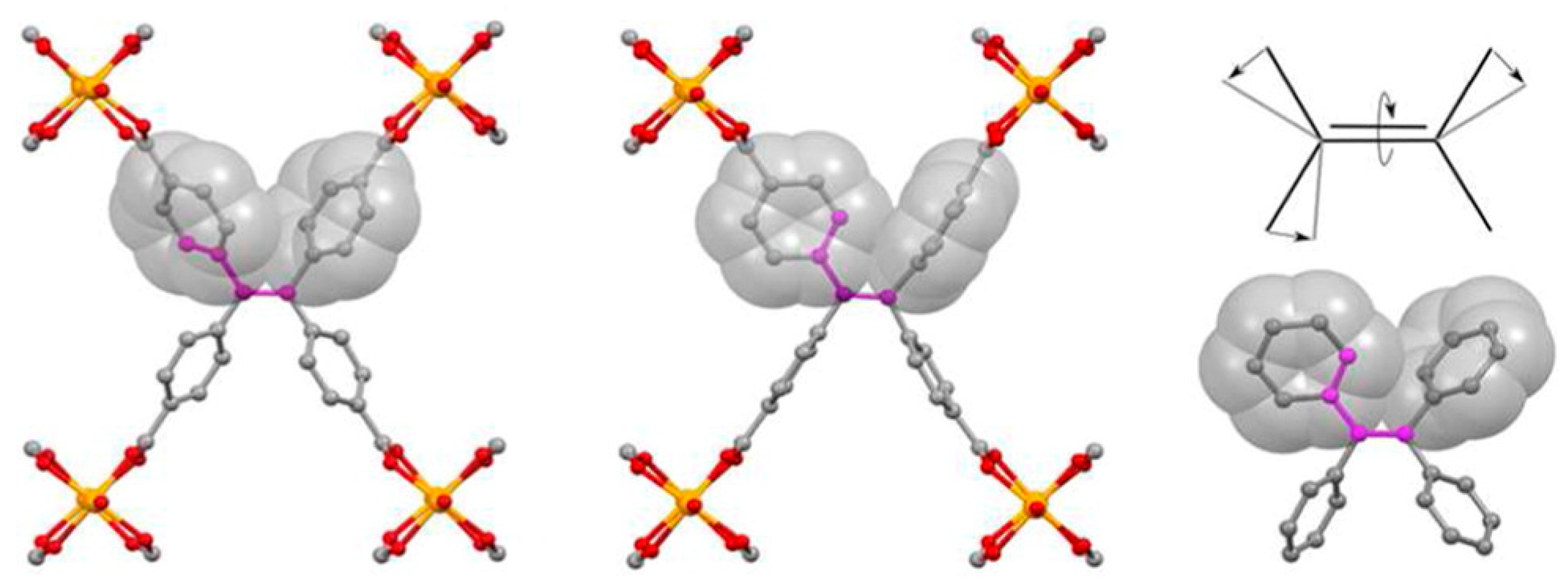
| Zn2(TCPE)(DEF)2 |  | π-flip | 300–421 | 43(6) | 2.2 × 1011 | 2H NMR | [25] |
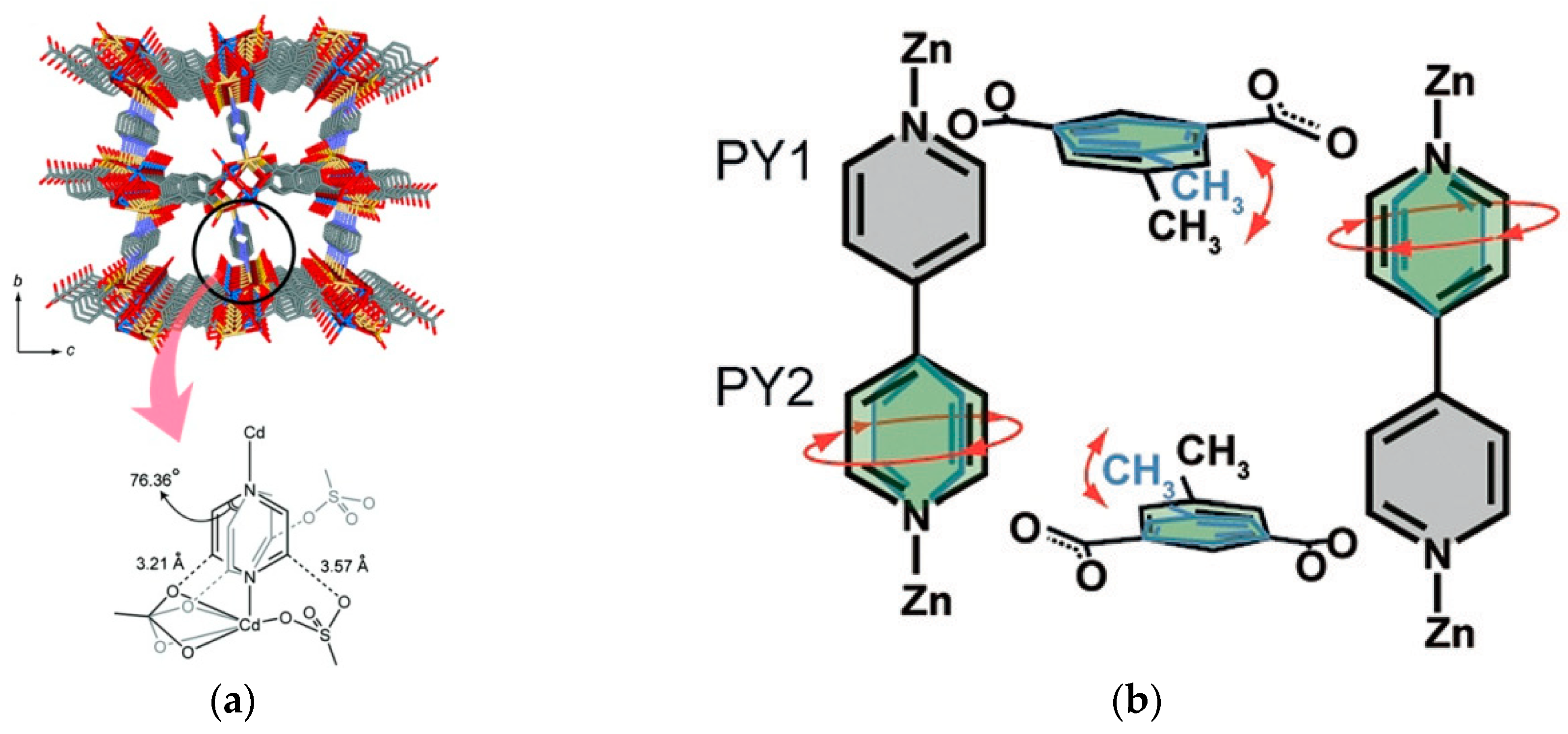
| CdNa(2-stp)(pyz)0.5(H2O) | 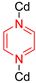 | 4-site | 193–293 | 7.7 | 2.40 × 106 | 2H NMR | [26] |
| Zn2(1,4-ndc)2(DABCO) | 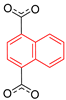 | 4-site | 193–293 | 53 | Not reported | 2H NMR | [26] |
| UTSA-76 |  | π-flip | - | 8.2 | - | DFT | [27] |
| NOTT-101a |  | π-flip | - | 20.2 | - | DFT | [27] |
| UCLA-R3 | Figure 9 | 3-site | - | 56.5 | 8.7 × 1015 | 2H NMR | - |
| Cu(bbcbco)(H2O) | Scheme 2 | - | - | 15.5 | - | DFT | [28] |
| Zn-BPEB | Scheme 2 | free | 150–293 | 2 | 2.2 × 1012 | 1H T1 relaxation | [29] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez-Nelson, A.; Coudert, F.-X.; van der Veen, M.A. Rotational Dynamics of Linkers in Metal–Organic Frameworks. Nanomaterials 2019, 9, 330. https://doi.org/10.3390/nano9030330
Gonzalez-Nelson A, Coudert F-X, van der Veen MA. Rotational Dynamics of Linkers in Metal–Organic Frameworks. Nanomaterials. 2019; 9(3):330. https://doi.org/10.3390/nano9030330
Chicago/Turabian StyleGonzalez-Nelson, Adrian, François-Xavier Coudert, and Monique A. van der Veen. 2019. "Rotational Dynamics of Linkers in Metal–Organic Frameworks" Nanomaterials 9, no. 3: 330. https://doi.org/10.3390/nano9030330
APA StyleGonzalez-Nelson, A., Coudert, F.-X., & van der Veen, M. A. (2019). Rotational Dynamics of Linkers in Metal–Organic Frameworks. Nanomaterials, 9(3), 330. https://doi.org/10.3390/nano9030330