Melt-Mixed 3D Hierarchical Graphene/Polypropylene Nanocomposites with Low Electrical Percolation Threshold
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. Electrical Measurements
2.3. Thermal Analysis
2.4. Thermal Conductivity
2.5. Rheology
2.6. Melt Rheology
2.7. Dynamic Mechanical Analysis (DMTA)
2.8. Morphology
3. Results and Discussion
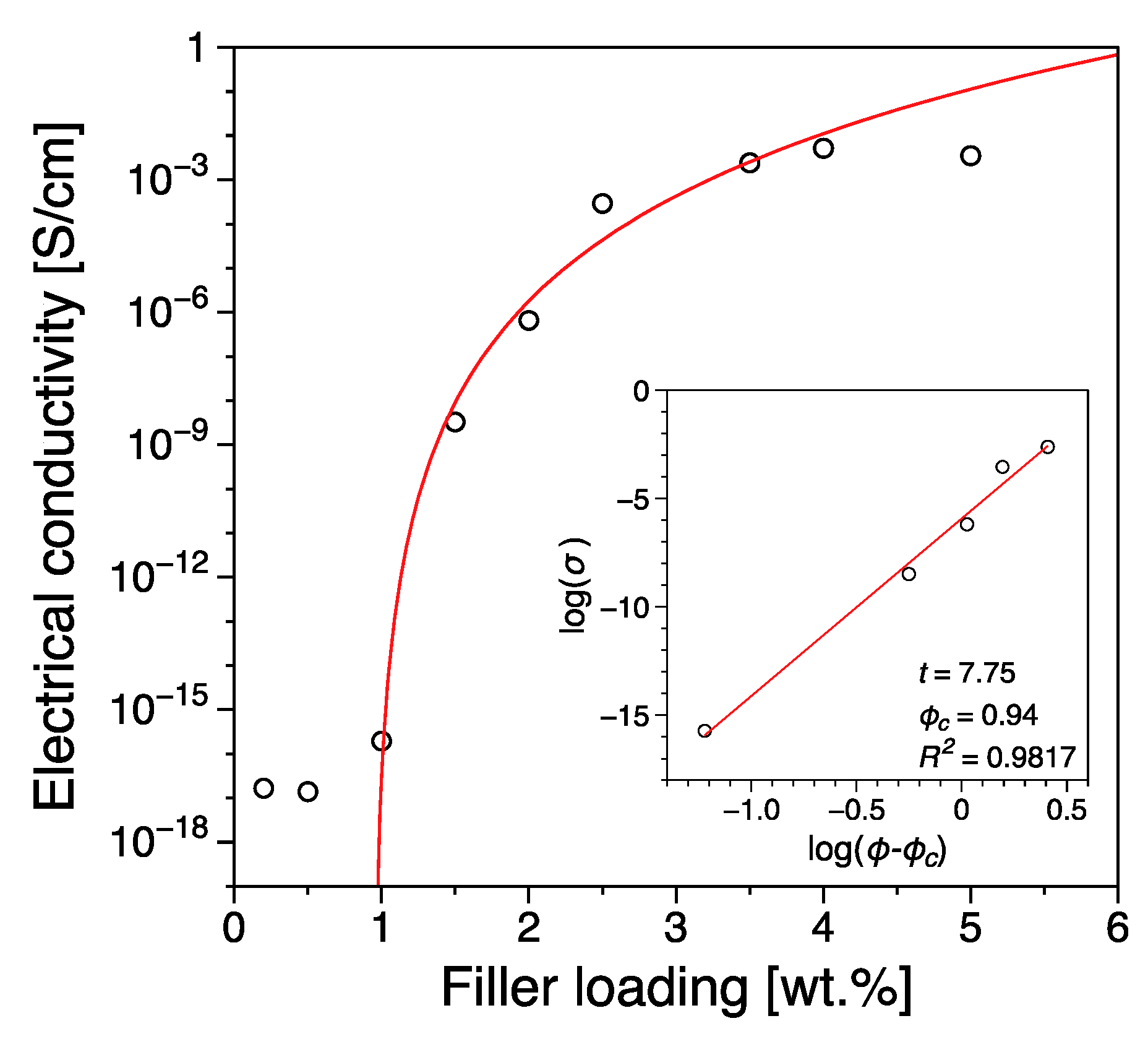
3.1. Electrical Conductivity
3.2. Morphology
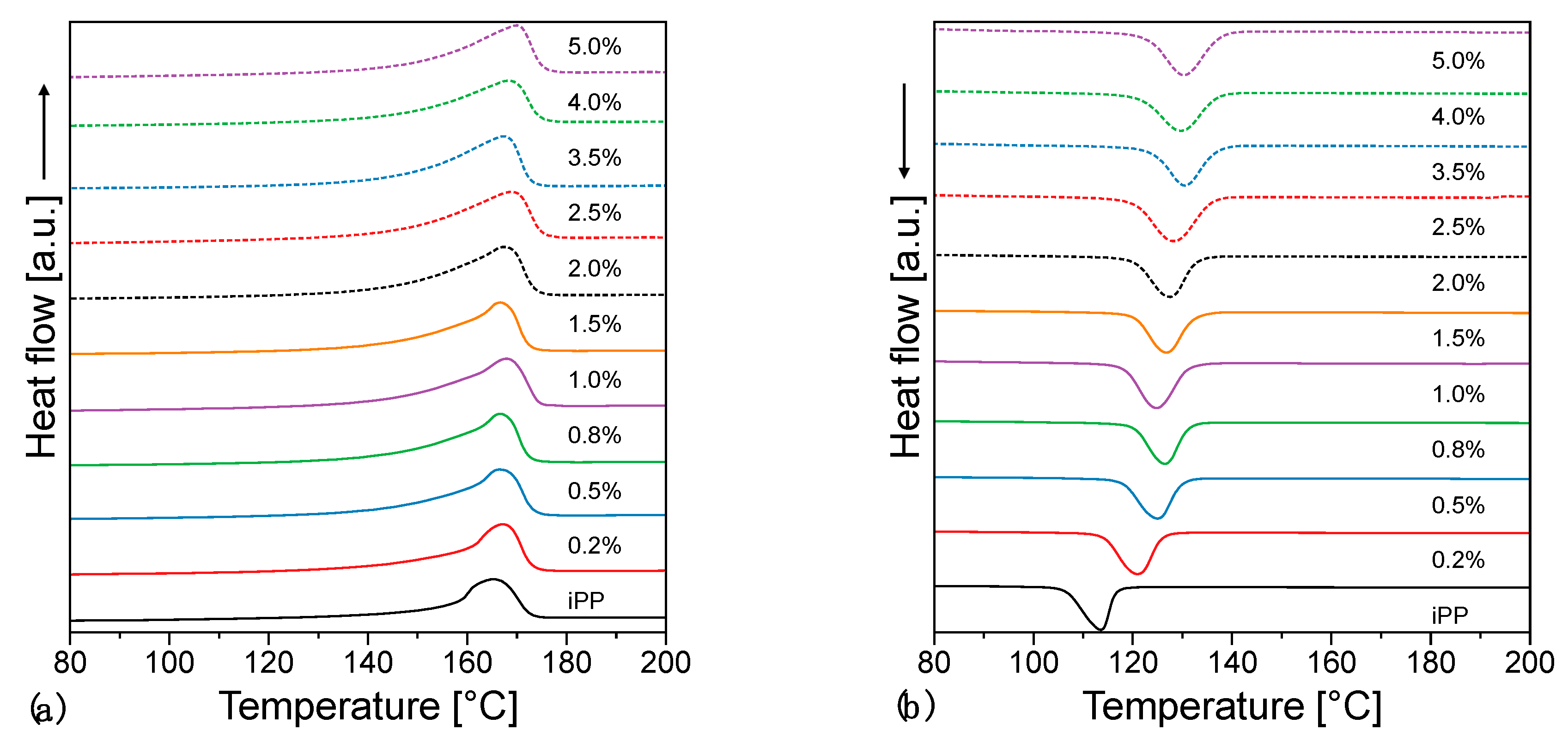
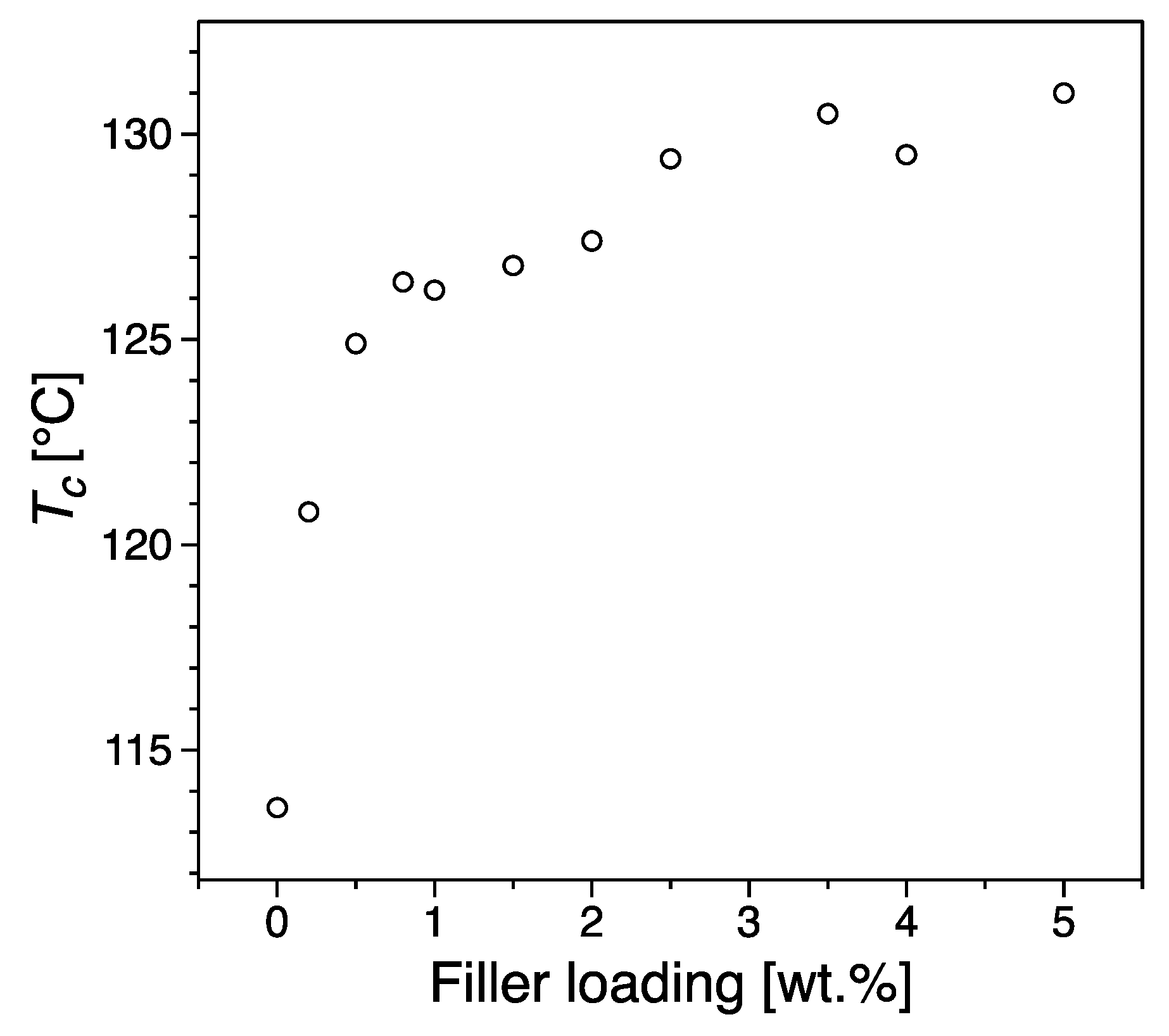
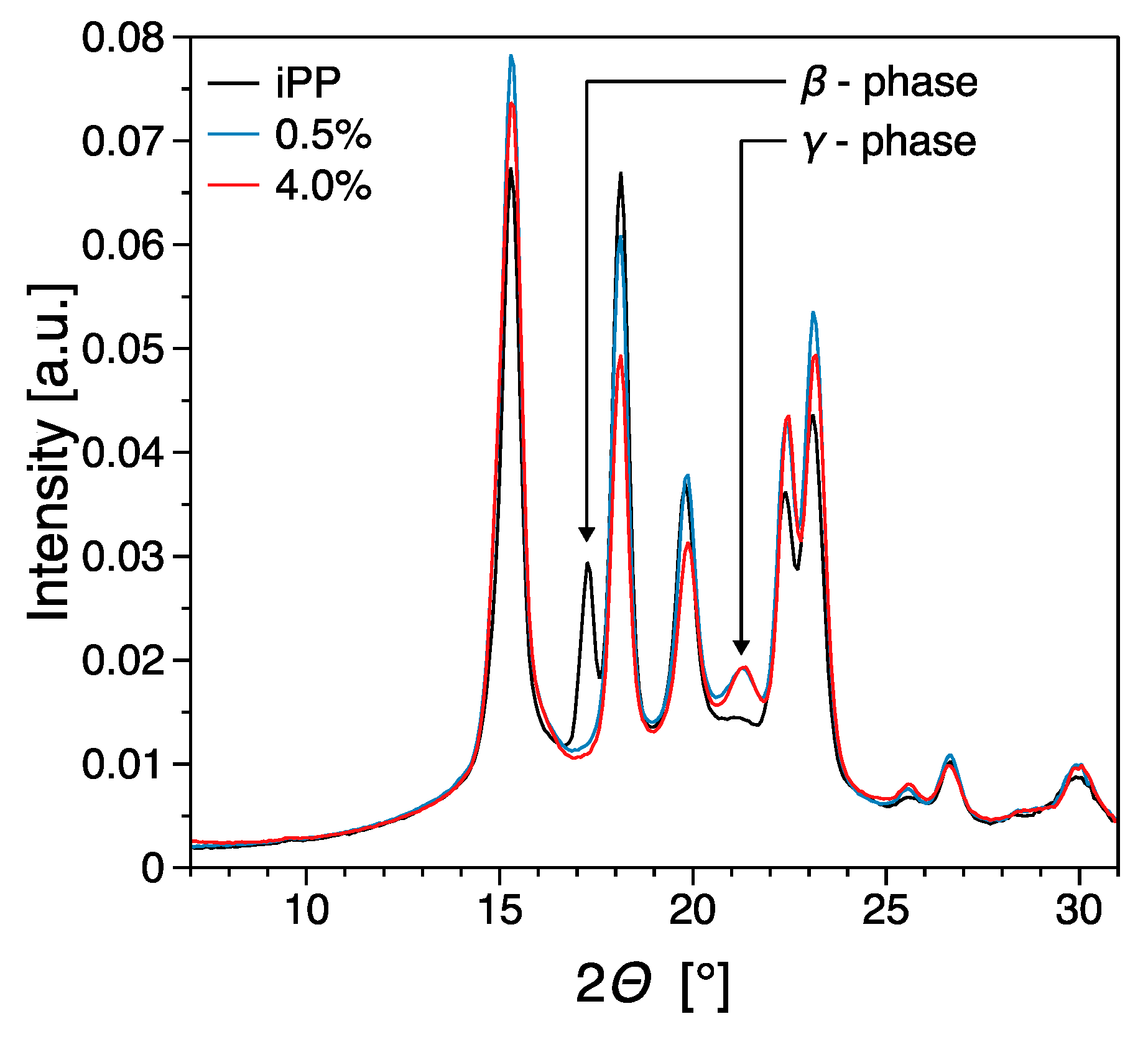
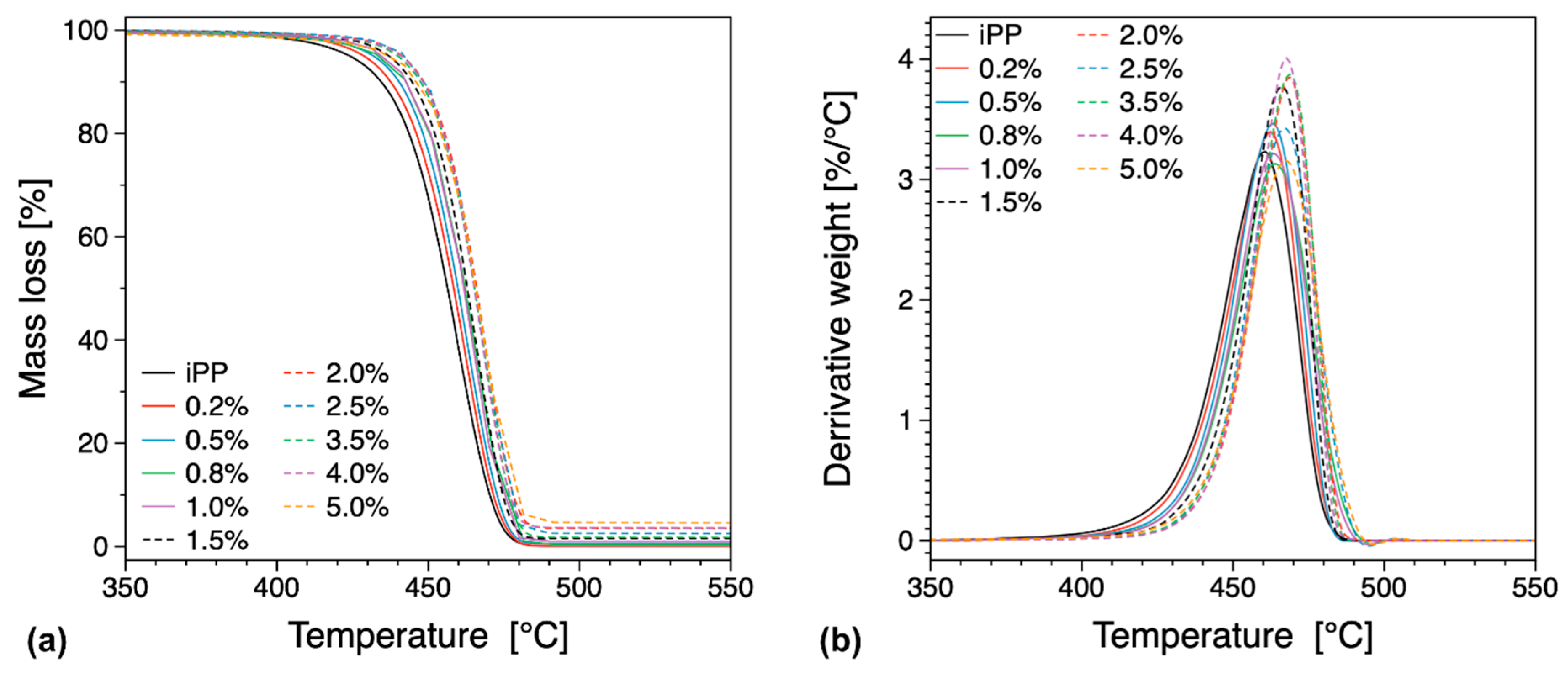
3.3. Thermal Properties
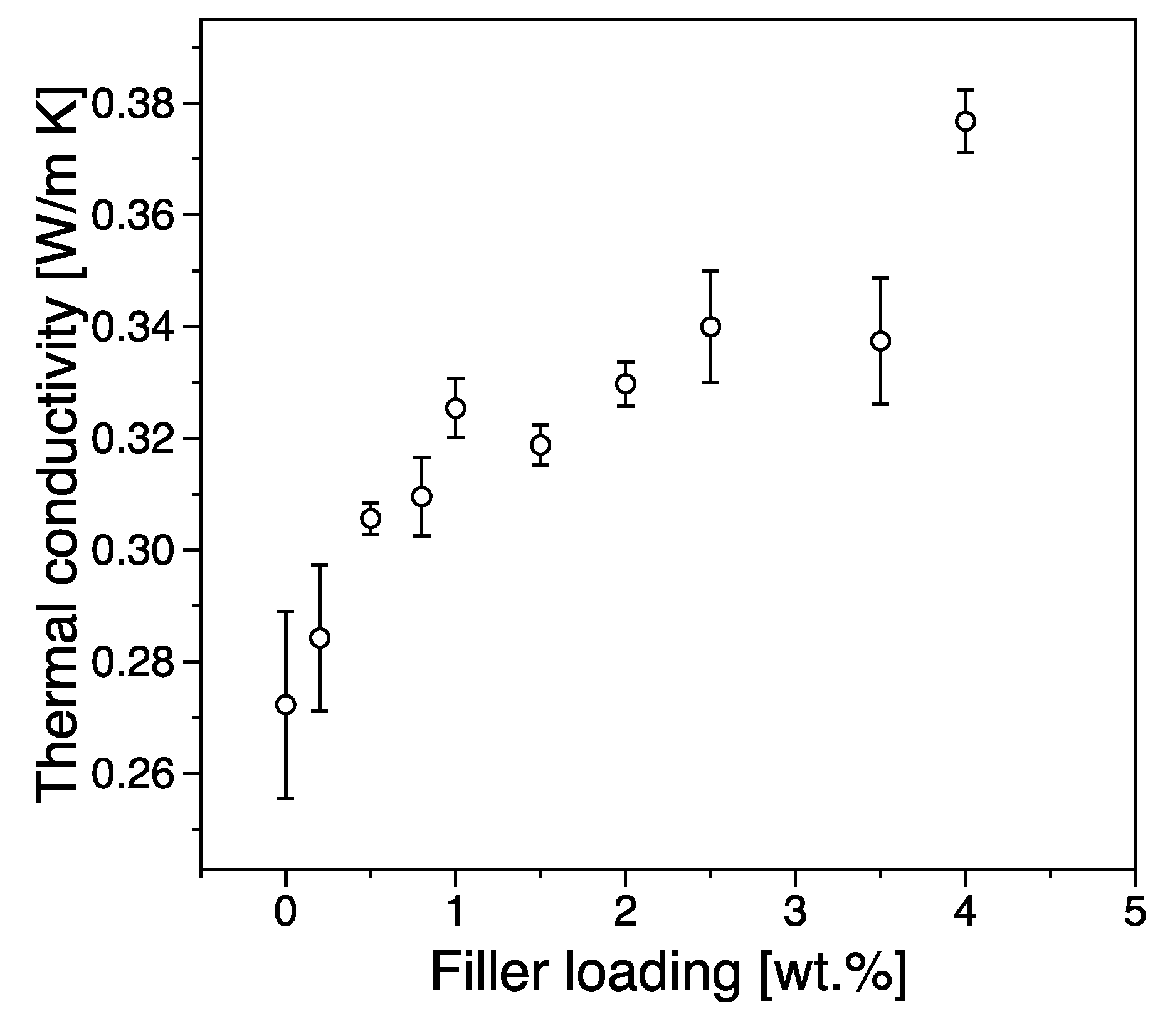
3.4. Thermal Conductivity
3.5. Mechanical Properties
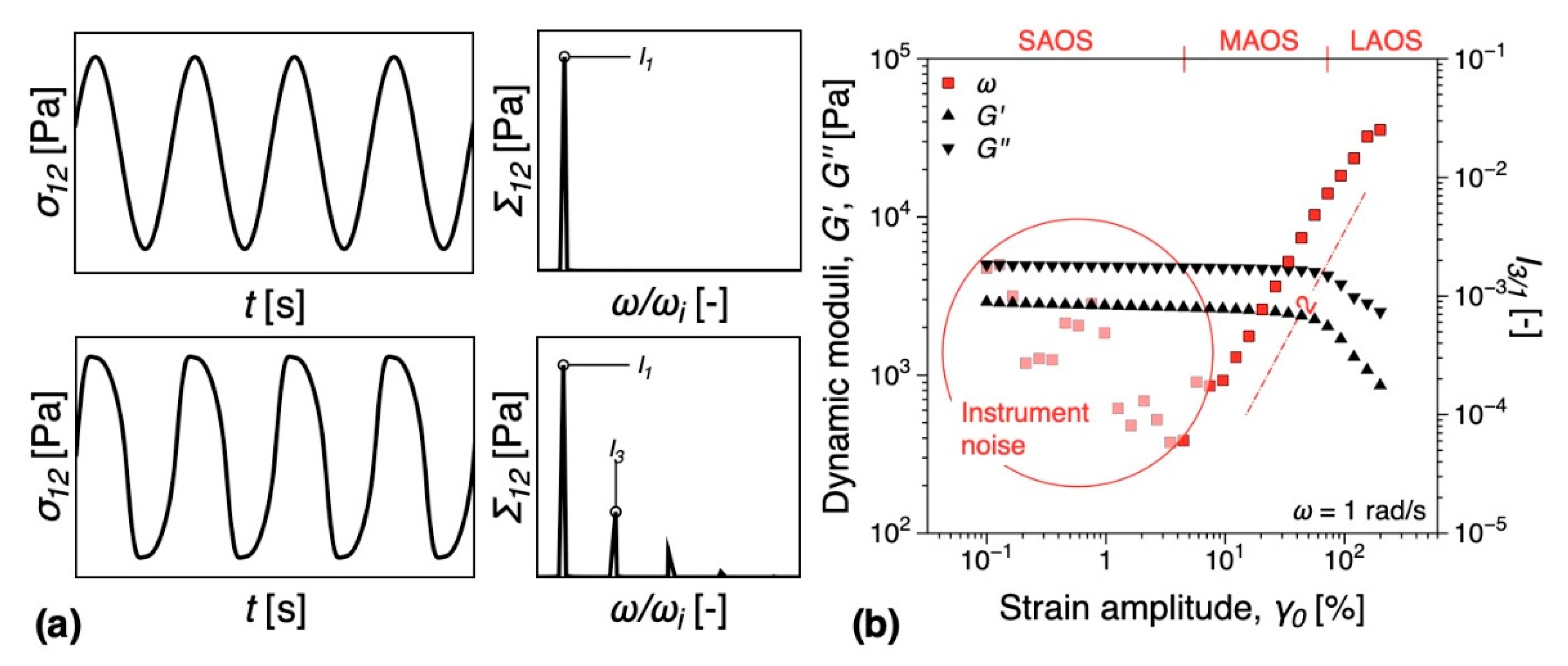
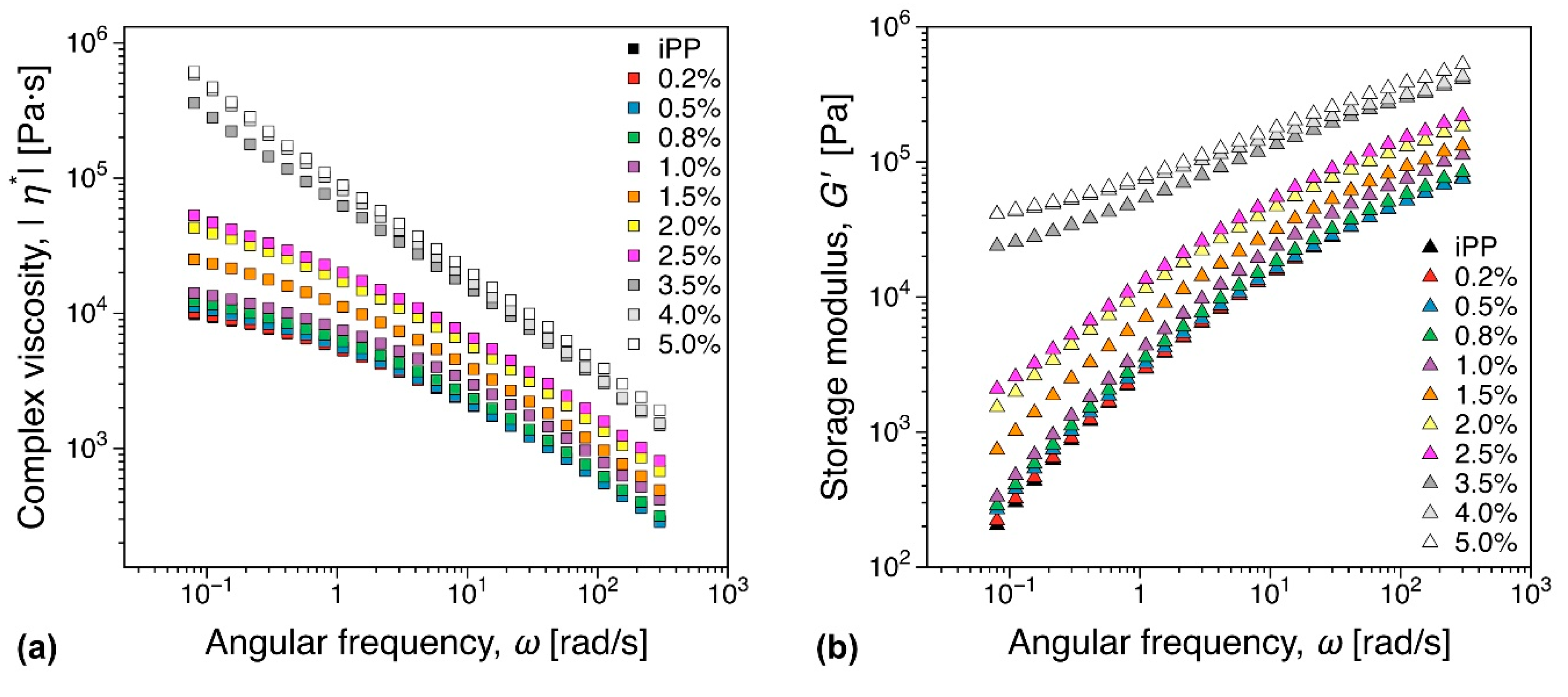
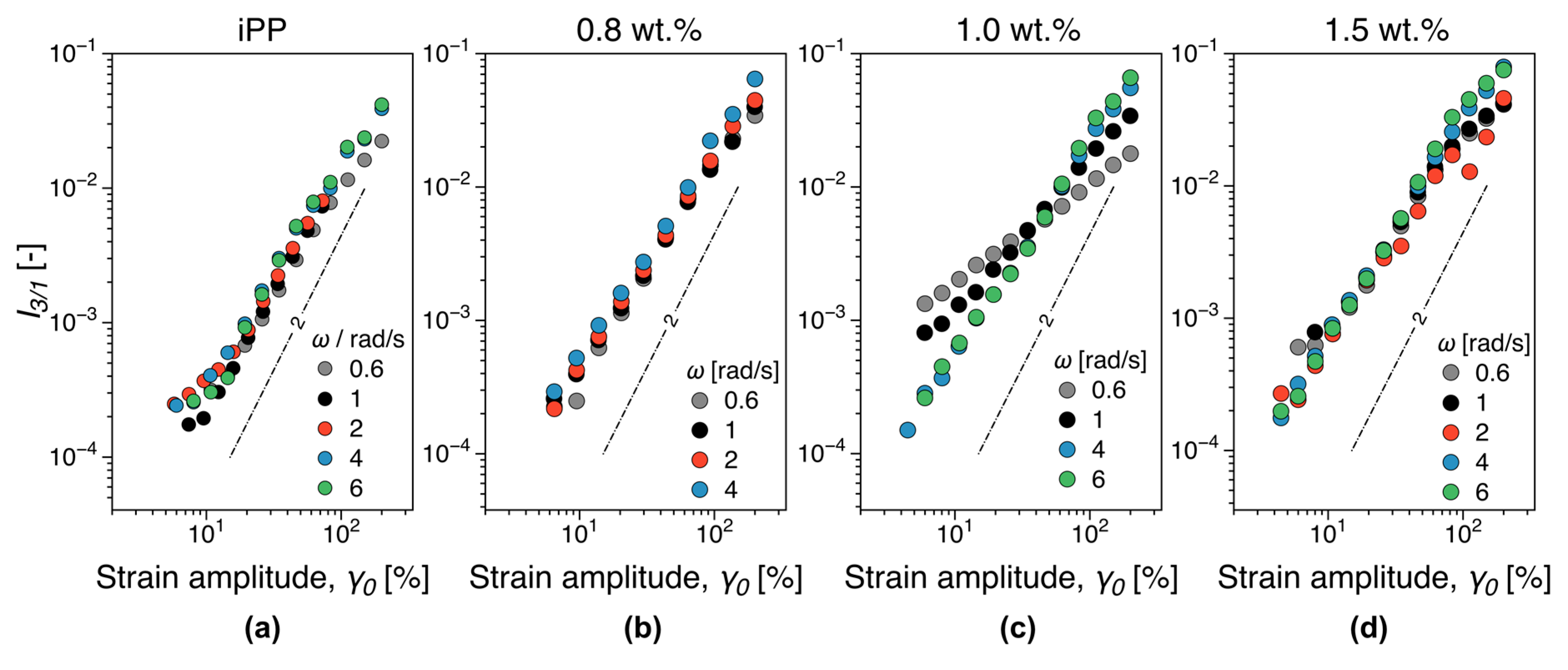
3.5.1. Melt Rheology
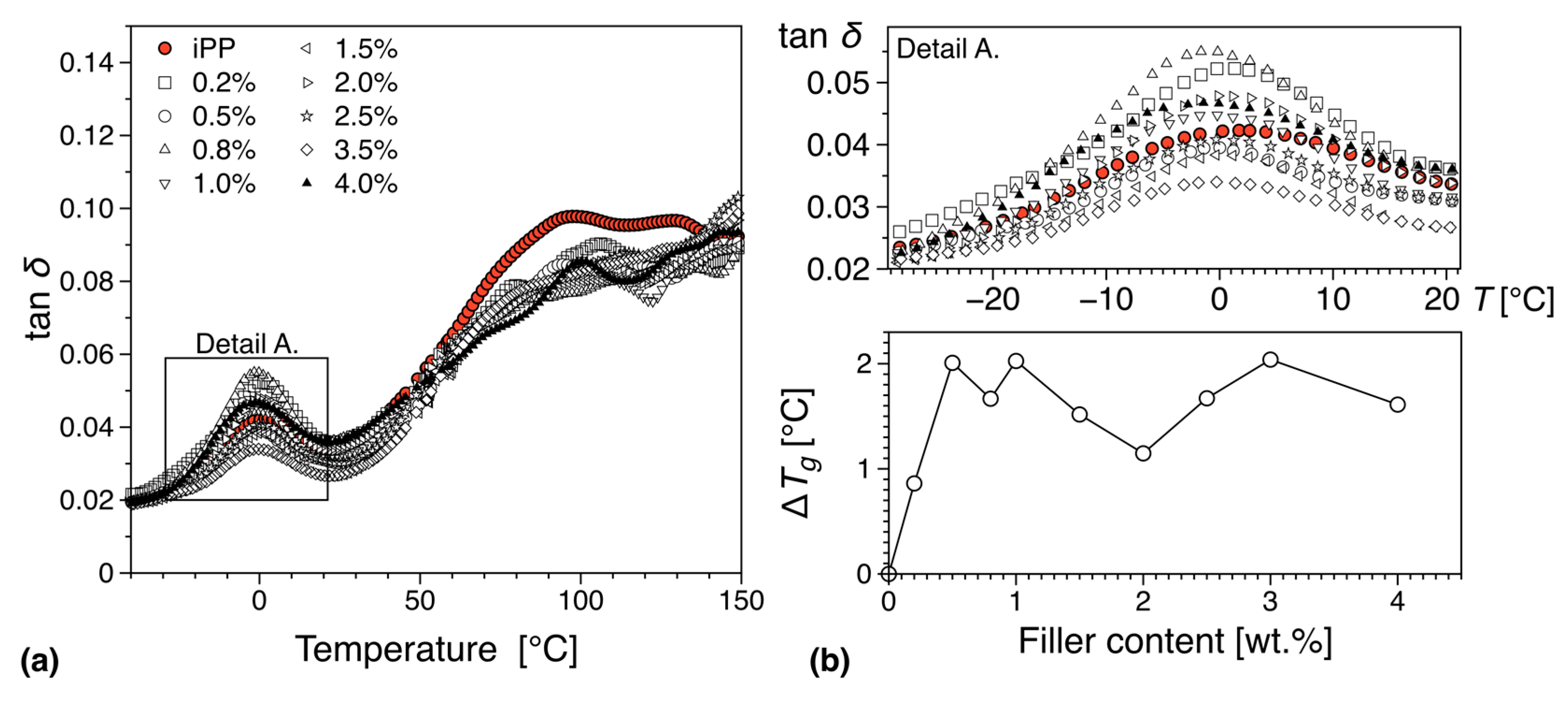
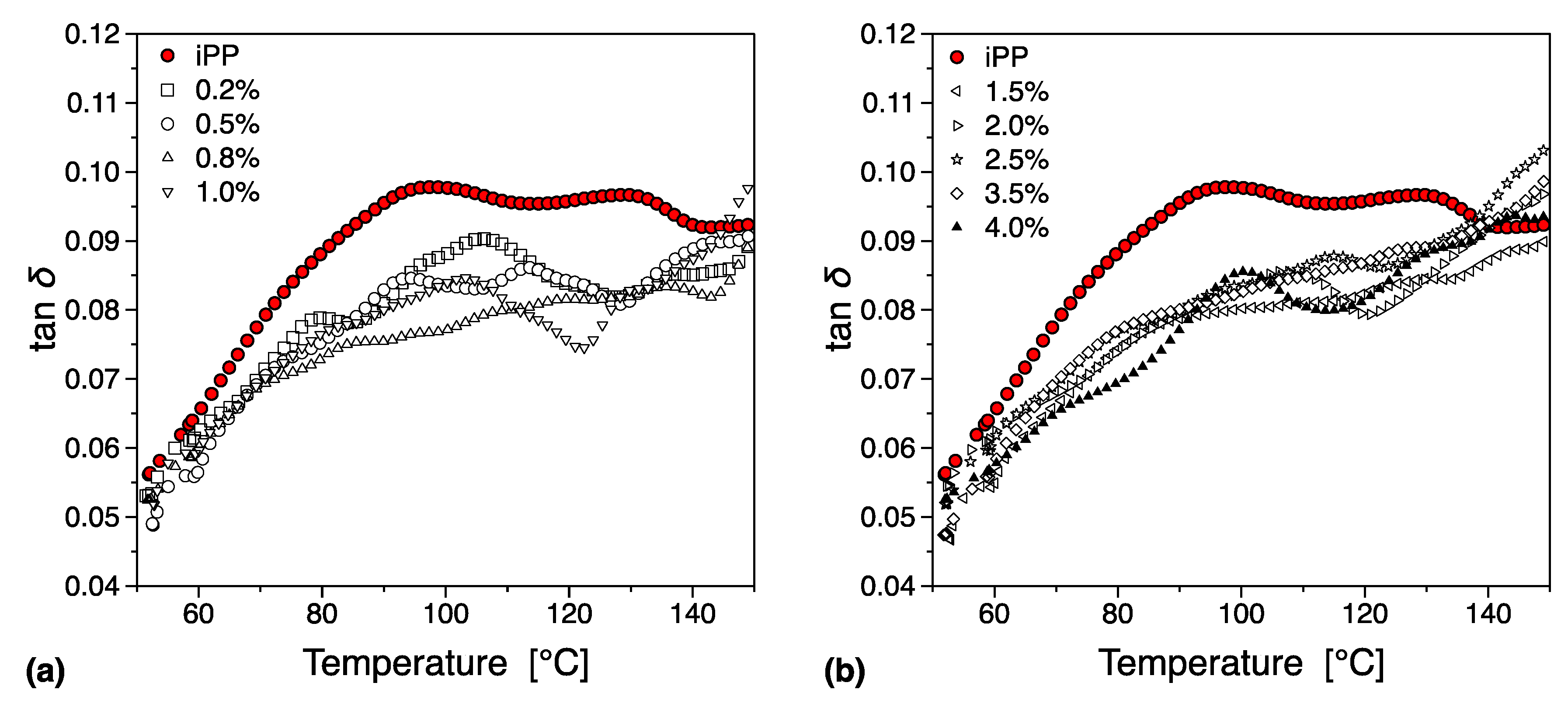
3.5.2. DMTA
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kim, H.; Macosko, C.W. Morphology and Properties of Polyester/Exfoliated Graphite Nanocomposites. Macromolecules 2008, 41, 3317–3327. [Google Scholar] [CrossRef]
- Kim, H.; Abdala, A.A.; Macosko, C.W. Graphene/Polymer Nanocomposites. Macromolecules 2010, 43, 6515–6530. [Google Scholar] [CrossRef]
- Gkourmpis, T. Nanoscience and Computational Chemistry: Research Progress; Mercader, G.A., Haghi, A.K., Eds.; Apple Academic Press: Toronto, ON, Canada, 2014. [Google Scholar]
- Li, B.; Zhong, W.-H. Review on polymer/graphite nanoplatelet nanocomposites. J. Mater. Sci. 2011, 46, 5595–5614. [Google Scholar] [CrossRef]
- Das, T.K.; Prusty, S. Graphene-Based Polymer Composites and Their Applications. Polym. Plast. Technol. Eng. 2013, 52, 319–331. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, M.; He, Q.; Shao, L.; Wei, S.; Guo, Z. An overview of the engineered graphene nanostructures and nanocomposites. RSC Adv. 2013, 3, 22790–22824. [Google Scholar] [CrossRef]
- Paul, D.R.; Robeson, L.M. Polymer nanotechnology: Nanocomposites. Polymer 2008, 49, 3187–3204. [Google Scholar] [CrossRef]
- Potts, J.R.; Dreyer, D.R.; Bielawski, C.W.; Ruoff, R.S. Graphene-based polymer nanocomposites. Polymer 2011, 52, 5–25. [Google Scholar] [CrossRef]
- Stankovich, S.; Dikin, D.A.; Dommett, G.H.B.; Kohlhaas, K.M.; Zimney, E.J.; Stach, E.A.; Piner, R.D.; Nguyen, S.T.; Ruoff, R.S. Graphene-based composite materials. Nature 2006, 442, 282. [Google Scholar] [CrossRef]
- Stankovich, S.; Piner, R.D.; Chen, X.; Wu, N.; Nguyen, S.T.; Ruoff, R.S. Stable aqueous dispersions of graphitic nanoplatelets via the reduction of exfoliated graphite oxide in the presence of poly(sodium 4-styrenesulfonate). J. Mater. Chem. 2006, 16, 155–158. [Google Scholar] [CrossRef]
- Cromer, B.M.; Scheel, S.; Luinstra, G.A.; Coughlin, E.B.; Lesser, A.J. In-situ polymerization of isotactic polypropylene-nanographite nanocomposites. Polymer 2015, 80, 275–281. [Google Scholar] [CrossRef]
- Chee, W.K.; Lim, H.N.; Huang, N.M.; Harrison, I. Nanocomposites of graphene/polymers: A review. RSC Adv. 2015, 5, 68014–68051. [Google Scholar] [CrossRef]
- Wu, H.; Drzal, L.T. Graphene nanoplatelet paper as a light-weight composite with excellent electrical and thermal conductivity and good gas barrier properties. Carbon 2012, 50, 1135–1145. [Google Scholar] [CrossRef]
- Xu, Q.; Yang, G.; Fan, X.; Zheng, W. Improving the Quantum Capacitance of Graphene-Based Supercapacitors by the Doping and Co-Doping: First-Principles Calculations. ACS Omega 2019, 4, 13209–13217. [Google Scholar] [CrossRef] [PubMed]
- Agresti, A.; Pescetelli, S.; Palma, A.L.; Martín-García, B.; Najafi, L.; Bellani, S.; Moreels, I.; Prato, M.; Bonaccorso, F.; Di Carlo, A. Two-Dimensional Material Interface Engineering for Efficient Perovskite Large-Area Modules. ACS Energy Lett. 2019, 4, 1862–1871. [Google Scholar] [CrossRef]
- Jeong, K.-U.; Lim, J.Y.; Lee, J.-Y.; Kang, S.L.; Nah, C. Polymer nanocomposites reinforced with multi-walled carbon nanotubes for semiconducting layers of high-voltage power cables. Polym. Int. 2010, 59, 100–106. [Google Scholar] [CrossRef]
- Alig, I.; Pötschke, P.; Lellinger, D.; Skipa, T.; Pegel, S.; Kasaliwal, G.R.; Villmow, T. Establishment, morphology and properties of carbon nanotube networks in polymer melts. Polymer 2012, 53, 4–28. [Google Scholar] [CrossRef]
- Pötschke, P.; Abdel-Goad, M.; Alig, I.; Dudkin, S.; Lellinger, D. Rheological and dielectrical characterization of melt mixed polycarbonate-multiwalled carbon nanotube composites. Polymer 2004, 45, 8863–8870. [Google Scholar] [CrossRef]
- Probst, N. Carbon Black; Donnet, J.-B., Bansal, R.C., Wang, M.-J., Eds.; Taylor & Francis: London, UK, 1993. [Google Scholar]
- Balberg, I.; Azulay, D.; Toker, D.; Millo, O. Percolation and tunneling in composite materials. Int. J. Mod. Phys. B 2004, 18, 2091–2121. [Google Scholar] [CrossRef]
- Brigandi, P.J.; Cogen, J.M.; Pearson, R.A. Electrically conductive multiphase polymer blend carbon-based composites. Polym. Eng. Sci. 2014, 54, 1–16. [Google Scholar] [CrossRef]
- Huang, J.-C. Carbon black filled conducting polymers and polymer blends. Adv. Polym. Technol. 2002, 21, 299–313. [Google Scholar] [CrossRef]
- Thongruang, W.; Balik, C.M.; Spontak, R.J. Volume-exclusion effects in polyethylene blends filled with carbon black, graphite, or carbon fiber. J. Polym. Sci. Part B Polym. Phys. 2002, 40, 1013–1025. [Google Scholar] [CrossRef]
- Mahapatra, D.; Arun, B.; Revathi, P. Performance evaluation of high structure carbon black in different polymer blends. Rubber World 2004, 231, 33–42. [Google Scholar]
- Gong, T.; Peng, S.-P.; Bao, R.-Y.; Yang, W.; Xie, B.-H.; Yang, M.-B. Low percolation threshold and balanced electrical and mechanical performances in polypropylene/carbon black composites with a continuous segregated structure. Compos. Part B Eng. 2016, 99, 348–357. [Google Scholar] [CrossRef]
- Kim, H.; Macosko, C.W. Processing-property relationships of polycarbonate/graphene composites. Polymer 2009, 50, 3797–3809. [Google Scholar] [CrossRef]
- Kalaitzidou, K.; Fukushima, H.; Drzal, L.T. A new compounding method for exfoliated graphite–polypropylene nanocomposites with enhanced flexural properties and lower percolation threshold. Compos. Sci. Technol. 2007, 67, 2045–2051. [Google Scholar] [CrossRef]
- Kim, S.; Do, I.; Drzal, L.T. Multifunctional xGnP/LLDPE Nanocomposites Prepared by Solution Compounding Using Various Screw Rotating Systems. Macromol. Mater. Eng. 2009, 294, 196–205. [Google Scholar] [CrossRef]
- Kim, H.; Miura, Y.; Macosko, C.W. Graphene/Polyurethane Nanocomposites for Improved Gas Barrier and Electrical Conductivity. Chem. Mater. 2010, 22, 3441–3450. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Zhong, Y.; Zhu, F.; Loh, K.P. Large area, continuous, few-layered graphene as anodes in organic photovoltaic devices. Appl. Phys. Lett. 2009, 95, 063302. [Google Scholar] [CrossRef]
- Rollings, E.; Gweon, G.H.; Zhou, S.Y.; Mun, B.S.; McChesney, J.L.; Hussain, B.S.; Fedorov, A.V.; First, P.N.; de Heer, W.A.; Lanzara, A. Synthesis and characterization of atomically thin graphite films on a silicon carbide substrate. J. Phys. Chem. Solids 2006, 67, 2172–2177. [Google Scholar] [CrossRef]
- Yang, X.; Dou, X.; Rouhanipour, A.; Zhi, L.; Räder, H.J.; Müllen, K. Two-Dimensional Graphene Nanoribbons. J. Am. Chem. Soc. 2008, 130, 4216–4217. [Google Scholar] [CrossRef]
- Kim, C.-D.; Min, B.-K.; Jung, W.-S. Preparation of graphene sheets by the reduction of carbon monoxide. Carbon 2009, 47, 1610–1612. [Google Scholar] [CrossRef]
- Lee, S.; Cho, D.; Drzal, L.T. Real-time observation of the expansion behavior of intercalated graphite flake. J. Mater. Sci. 2005, 40, 231–234. [Google Scholar] [CrossRef]
- Kalaitzidou, K.; Fukushima, H.; Askeland, P.; Drzal, L.T. The nucleating effect of exfoliated graphite nanoplatelets and their influence on the crystal structure and electrical conductivity of polypropylene nanocomposites. J. Mater. Sci. 2008, 43, 2895–2907. [Google Scholar] [CrossRef]
- Staudenmaier, L. Verfahren zur Darstellung der Graphitsäure. Berichte der Deutschen Chemischen Gesellschaft 1898, 31, 1481–1487. [Google Scholar] [CrossRef]
- Bhyan, M.S.A.; Uddin, M.N.; Islam, M.M.; Bipasha, F.A.; Hossain, S.S. Synthesis of graphene. Int. Nano Lett. 2016, 6, 65–83. [Google Scholar] [CrossRef]
- Maddah, H. Polypropylene as a Promising Plastic: A Review. Am. J. Polym. Sci. 2016, 6, 1–11. [Google Scholar]
- Jun, Y.-S.; Um, J.G.; Jiang, G.; Lui, G.; Yu, A. Ultra-large sized graphene nano-platelets (GnPs) incorporated polypropylene (PP)/GnPs composites engineered by melt compounding and its thermal, mechanical, and electrical properties. Compos. Part B Eng. 2018, 133, 218–225. [Google Scholar] [CrossRef]
- Zhang, J.; He, S.; Lv, P.; Chen, Y. Processing–morphology–property relationships of polypropylene–graphene nanoplatelets nanocomposites. J. Appl. Polym. Sci. 2017, 134. [Google Scholar] [CrossRef]
- Kuvardina, E.V.; Novokshonova, L.A.; Lomakin, S.M.; Timan, S.A.; Tchmutin, I.A. Effect of the graphite nanoplatelet size on the mechanical, thermal, and electrical properties of polypropylene/exfoliated graphite nanocomposites. J. Appl. Polym. Sci. 2013, 128, 1417–1424. [Google Scholar] [CrossRef]
- Kalaitzidou, K.; Fukushima, H.; Drzal, L.T. Multifunctional polypropylene composites produced by incorporation of exfoliated graphite nanoplatelets. Carbon 2007, 45, 1446–1452. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, F.; Huang, Y.; Dong, J.-Y.; Han, C.C. Crystallization behaviors in the isotactic polypropylene/graphene composites. Polymer 2014, 55, 4125–4135. [Google Scholar] [CrossRef]
- El Achaby, M.; Arrakhiz, F.-E.; Vaudreuil, S.; el Kacem Qaiss, A.; Bousmina, M.; Fassi-Fehri, O. Mechanical, thermal, and rheological properties of graphene-based polypropylene nanocomposites prepared by melt mixing. Polym. Compos. 2012, 33, 733–744. [Google Scholar] [CrossRef]
- Steurer, P.; Wissert, R.; Thomann, R.; Mülhaupt, R. Functionalized Graphenes and Thermoplastic Nanocomposites Based upon Expanded Graphite Oxide. Macromol. Rapid Commun. 2009, 30, 316–327. [Google Scholar] [CrossRef] [PubMed]
- Gkourmpis, T. Controlling the Morphology of Polymers. In Multiple Scales of Structure and Processing; Mitchell, G.R., Tojeira, A., Eds.; Springer: London, UK, 2016. [Google Scholar]
- Li, J.; Sham, M.L.; Kim, J.-K.; Marom, G. Morphology and properties of UV/ozone treated graphite nanoplatelet/epoxy nanocomposites. Compos. Sci. Technol. 2007, 67, 296–305. [Google Scholar] [CrossRef]
- Lim, H.T.; Ahn, K.H.; Hong, J.S.; Hyun, K. Nonlinear viscoelasticity of polymer nanocomposites under large amplitude oscillatory shear flow. J. Rheol. 2013, 57, 767–789. [Google Scholar] [CrossRef]
- Ahirwal, D.; Palza, H.; Schlatter, G.; Wilhelm, M. New way to characterize the percolation threshold of polyethylene and carbon nanotube polymer composites using Fourier transform (FT) rheology. Korea-Aust. Rheol. J. 2014, 26, 319–326. [Google Scholar] [CrossRef]
- Kádár, R.; Abbasi, M.; Figuli, R.; Rigdahl, M.; Wilhelm, M. Linear and Nonlinear Rheology Combined with Dielectric Spectroscopy of Hybrid Polymer Nanocomposites for Semiconductive Applications. Nanomaterials 2017, 7, 23. [Google Scholar] [CrossRef]
- Gaska, K.; Kádár, R. Evidence of percolated network at the linear—Nonlinear transition in oscillatory shear. AIP Conf. Process. 2019, 2107, 050003. [Google Scholar] [CrossRef]
- Kirkpatrick, S. Percolation and Conduction. Rev. Mod. Phys. 1973, 45, 574–588. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; Taylor & Francis: London, UK, 1992. [Google Scholar]
- Vionnet-Menot, S.; Grimaldi, C.; Maeder, T.; Strässler, S.; Ryser, P. Tunneling-percolation origin of nonuniversality: Theory and experiments. Phys. Rev. B 2005, 71, 064201. [Google Scholar] [CrossRef]
- Balberg, I. Limits on the continuum-percolation transport exponents. Phys. Rev. B 1998, 57, 13351–13354. [Google Scholar] [CrossRef]
- Jun, Y.S.; Um, J.G.; Jiang, G.; Yu, A. A study on the effects of graphene nano-platelets (GnPs) sheet sizes from a few to hundred microns on the thermal, mechanical, and electrical properties of polypropylene (PP)/GnPs composites. Express Polym. Lett. 2018, 12, 885–897. [Google Scholar] [CrossRef]
- Tripathi, S.N.; Rao, G.S.S.; Mathur, A.B.; Jasra, R. Polyolefin/graphene nanocomposites: A review. RSC Adv. 2017, 7, 23615–23632. [Google Scholar] [CrossRef]
- Pionteck, J.; Melchor Valdez, E.M.; Piana, F.; Omastová, M.; Luyt, A.S.; Voit, B. Reduced percolation concentration in polypropylene/expanded graphite composites: Effect of viscosity and polypyrrole. J. Appl. Polym. Sci. 2015, 132. [Google Scholar] [CrossRef]
- Strååt, M.; Toll, S.; Boldizar, A.; Rigdahl, M.; Hagström, B. Melt spinning of conducting polymeric composites containing carbonaceous fillers. J. Appl. Polym. Sci. 2011, 119, 3264–3272. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, J.; Wei, S.; Ryu, J.; Sun, L.; Guo, Z. Poly(propylene)/Graphene Nanoplatelet Nanocomposites: Melt Rheological Behavior and Thermal, Electrical, and Electronic Properties. Macromol. Chem. Phys. 2011, 212, 1951–1959. [Google Scholar] [CrossRef]
- Milani, M.A.; Quijada, R.; Basso, N.R.S.; Graebin, A.P.; Galland, G.B. Influence of the graphite type on the synthesis of polypropylene/graphene nanocomposites. J. Polym. Sci. Part A Polym. Chem. 2012, 50, 3598–3605. [Google Scholar] [CrossRef]
- Pedrazzoli, D.; Pegoretti, A.; Kalaitzidou, K. Understanding the effect of silica nanoparticles and exfoliated graphite nanoplatelets on the crystallization behavior of isotactic polypropylene. Polym. Eng. Sci. 2015, 55, 672–680. [Google Scholar] [CrossRef]
- Mileva, D.; Tranchida, D.; Gahleitner, M. Designing polymer crystallinity: An industrial perspective. Polym. Cryst. 2018, 1, e10009. [Google Scholar] [CrossRef]
- Clerc, J.P.; Podolskiy, V.A.; Sarychev, A.K. Precise determination of the conductivity exponent of 3D percolation using exact numerical renormalization. Eur. Phys. J. B Condens. Matter Complex Syst. 2000, 15, 507–516. [Google Scholar] [CrossRef]
- Beuguel, Q.; Boyer, S.A.E.; Settipani, D.; Monge, G.; Haudin, J.-M.; Vergnes, B.; Peuvrel-Disdier, E. Crystallization behavior of polypropylene/graphene nanoplatelets composites. Polym. Cryst. 2018, 1, e10024. [Google Scholar] [CrossRef]
- Gahleitner, M.; Mileva, D.; Androsch, R.; Gloger, D.; Tranchida, D.; Sandholzer, M.; Doshev, P. Crystallinity-Based Product Design: Utilizing the Polymorphism of Isotactic PP Homo- and Copolymers. Int. Polym. Process. 2016, 31, 618–627. [Google Scholar] [CrossRef]
- Song, P.; Cao, Z.; Cai, Y.; Zhao, L.; Fang, Z.; Fu, S. Fabrication of exfoliated graphene-based polypropylene nanocomposites with enhanced mechanical and thermal properties. Polymer 2011, 52, 4001–4010. [Google Scholar] [CrossRef]
- Gahleitner, M.; Grein, C.; Kheirandish, S.; Wolfschwenger, J. Nucleation of Polypropylene Homo- and Copolymers. Int. Polym. Process. 2011, 26, 2–20. [Google Scholar] [CrossRef]
- Raghu, A.V.; Lee, Y.R.; Jeong, H.M.; Shin, C.M. Preparation and Physical Properties of Waterborne Polyurethane/Functionalized Graphene Sheet Nanocomposites. Macromol. Chem. Phys. 2008, 209, 2487–2493. [Google Scholar] [CrossRef]
- Dealy, J.W.; Kurt, F. Melt Rheology and Its Role in Plastics Processing—Theory and Applications; Van Nostrand Reinhold: New York, NY, USA, 1990. [Google Scholar]
- Krishnamoorti, R.; Banik, I.; Xu, L. Rheology and processing of polymer nanocomposites. In Reviews in Chemical Engineering; Walter de Gruyter GmbH: Berlin, Germany, 2010; Volume 26, p. 3. [Google Scholar]
- Leblanc, J.L. Filled Polymers: Science and Industrial Applications; CRC Press Taylor & Francis: Boca Raton, FL, USA, 2009. [Google Scholar]
- Kádár, R.; Gaska, K.; Gkourmpis, T. Nonlinear Oscillatory Shear Analysis of 3D Hierarchical Polymer Nanocomposites. Manuscript in preparation 2019.
- Read, B.E. Mechanical relaxation in isotactic polypropylene. Polymer 1989, 30, 1439–1445. [Google Scholar] [CrossRef]
- Starkweather, H.W.; Avakian, P.; Matheson, R.R.; Fontanella, J.J.; Wintersgill, M.C. Ultralow temperature dielectric relaxations in polyolefins. Macromolecules 1992, 25, 6871–6875. [Google Scholar] [CrossRef]
- Suljovrujic, E.; Trifunovic, S.; Milicevic, D. The influence of gamma radiation on the dielectric relaxation behaviour of isotactic polypropylene: The α relaxation. Polym. Degrad. Stab. 2010, 95, 164–171. [Google Scholar] [CrossRef]
- Jawad, S.A.; Alhaj-Mohammad, M.H. β-relaxation of drawn isotactic polypropylene in terms of a simplified two phase model. Polym. Int. 1994, 35, 395–398. [Google Scholar] [CrossRef]
- Spieckermann, F.; Polt, G.; Wilhelm, H.; Kerber, M.B.; Schafler, E.; Reinecker, M.; Soprunyuk, V.; Bernstorff, S.; Zehetbauer, M. Dislocation Movement Induced by Molecular Relaxations in Isotactic Polypropylene. Macromolecules 2017, 50, 6362–6368. [Google Scholar] [CrossRef]
- Liao, K.-H.; Aoyama, S.; Abdala, A.A.; Macosko, C. Does Graphene Change Tg of Nanocomposites? Macromolecules 2014, 47, 8311–8319. [Google Scholar] [CrossRef]
- Boyd, R.H. Relaxation processes in crystalline polymers: Molecular interpretation—A review. Polymer 1985, 26, 1123–1133. [Google Scholar] [CrossRef]
- Men, Y.; Rieger, J.; Endeler, H.-F.; Lilge, D. Mechanical α-Process in Polyethylene. Macromolecules 2003, 36, 4689–4691. [Google Scholar] [CrossRef]
- Zubova, E.A.; Balabaev, N.K.; Manevitch, L.I. Molecular mechanisms of the chain diffusion between crystalline and amorphous fractions in polyethylene. Polymer 2007, 48, 1802–1813. [Google Scholar] [CrossRef]
- Saitô, N.; Okano, K.; Iwayanagi, S.; Hideshima, T. Molecular Motion in Solid State Polymers. Solid State Phys. 1963, 14, 343–502. [Google Scholar] [CrossRef]
- Zhou, H.; Wilkes, G.L. Orientation Anisotropy of the Mechanical α Relaxation of High-Density Polyethylene Films Having a Well-Defined Stacked Lamellar Morphology. Macromolecules 1997, 30, 2412–2421. [Google Scholar] [CrossRef]
- Hoyos, M.; Tiemblo, P.; Gómez-Elvira, J.M. The role of microstructure, molar mass and morphology on local relaxations in isotactic polypropylene. The α relaxation. Polymer 2007, 48, 183–194. [Google Scholar] [CrossRef]
- Lezak, E.; Bartczak, Z. Plastic deformation behavior of β phase isotactic polypropylene in plane-strain compression at elevated temperatures. J. Polym. Sci. Part B: Polym. Phys. 2008, 46, 92–108. [Google Scholar] [CrossRef]




| Filler Type | Percolation Threshold [wt.%] | Reference |
|---|---|---|
| Reduced Graphene Oxide | 0.94 | this work |
| Graphite Platelets | 9 | [47] |
| Expanded Graphite | 8–12 | [58] |
| Graphene nanoplatelets | 8–6 | [40] |
| Graphene nanoplatelets | 8 | [59] |
| Graphite nanoplatelets | 12 | [42] |
| Graphene nanoplatelets | 8–12 | [60] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gkourmpis, T.; Gaska, K.; Tranchida, D.; Gitsas, A.; Müller, C.; Matic, A.; Kádár, R. Melt-Mixed 3D Hierarchical Graphene/Polypropylene Nanocomposites with Low Electrical Percolation Threshold. Nanomaterials 2019, 9, 1766. https://doi.org/10.3390/nano9121766
Gkourmpis T, Gaska K, Tranchida D, Gitsas A, Müller C, Matic A, Kádár R. Melt-Mixed 3D Hierarchical Graphene/Polypropylene Nanocomposites with Low Electrical Percolation Threshold. Nanomaterials. 2019; 9(12):1766. https://doi.org/10.3390/nano9121766
Chicago/Turabian StyleGkourmpis, Thomas, Karolina Gaska, Davide Tranchida, Antonis Gitsas, Christian Müller, Aleksandar Matic, and Roland Kádár. 2019. "Melt-Mixed 3D Hierarchical Graphene/Polypropylene Nanocomposites with Low Electrical Percolation Threshold" Nanomaterials 9, no. 12: 1766. https://doi.org/10.3390/nano9121766
APA StyleGkourmpis, T., Gaska, K., Tranchida, D., Gitsas, A., Müller, C., Matic, A., & Kádár, R. (2019). Melt-Mixed 3D Hierarchical Graphene/Polypropylene Nanocomposites with Low Electrical Percolation Threshold. Nanomaterials, 9(12), 1766. https://doi.org/10.3390/nano9121766









