Tunable Electronic Properties of Graphene/g-AlN Heterostructure: The Effect of Vacancy and Strain Engineering
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
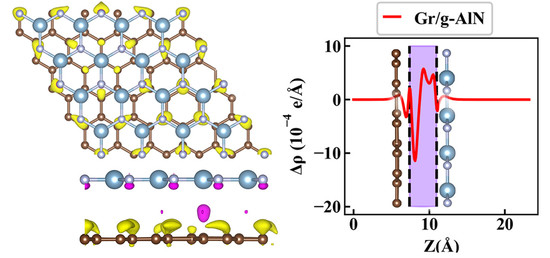
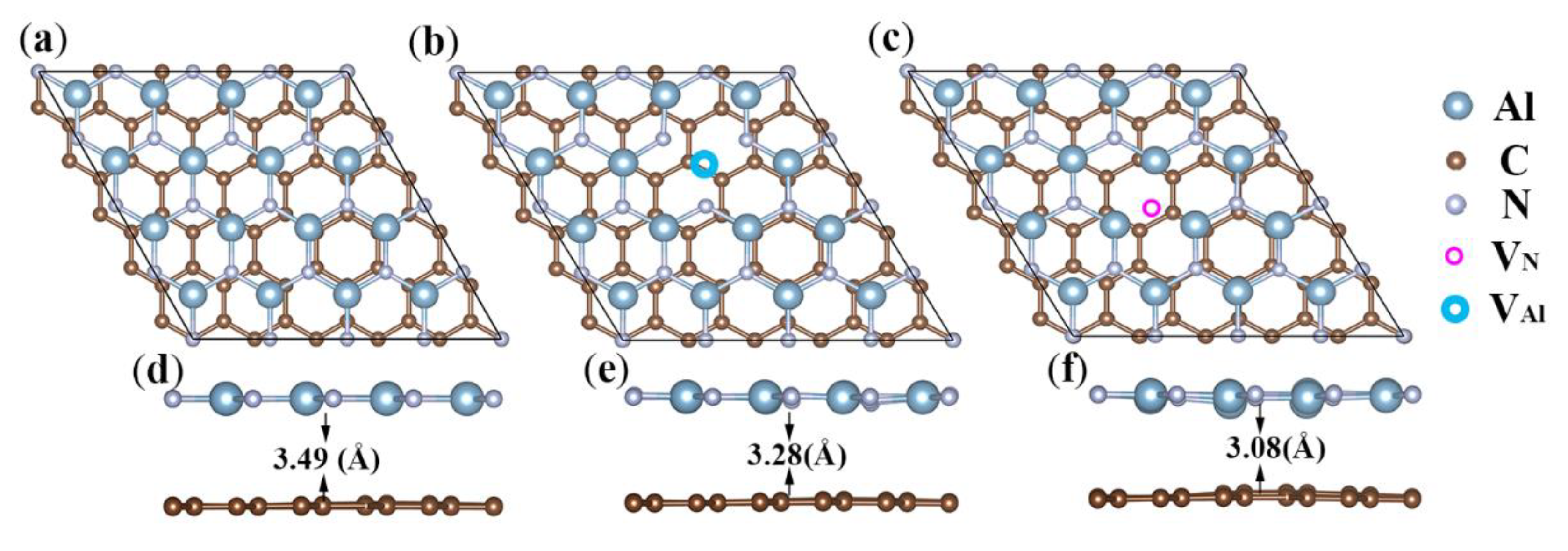
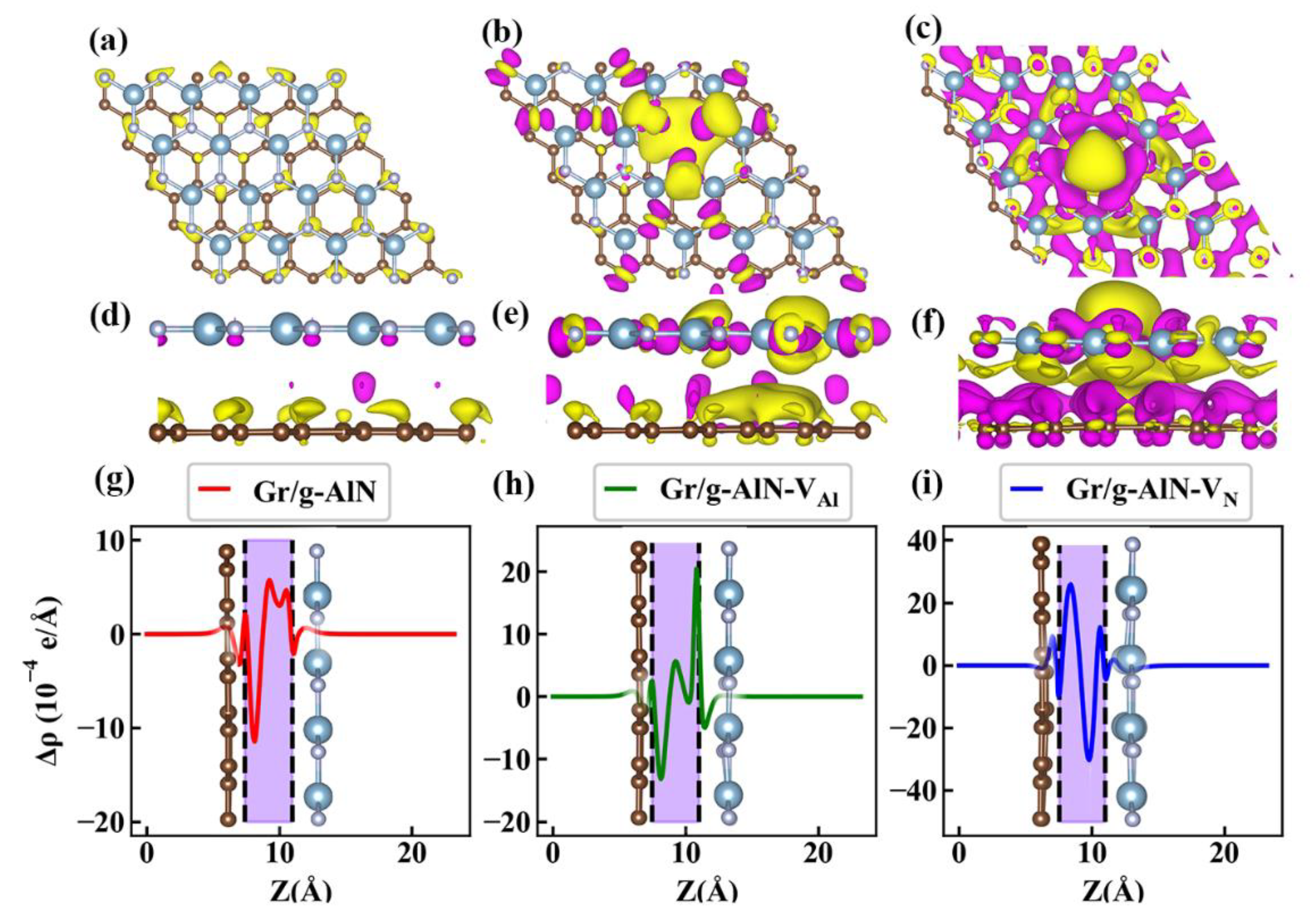
3.1. Sublayers and Heterostructures
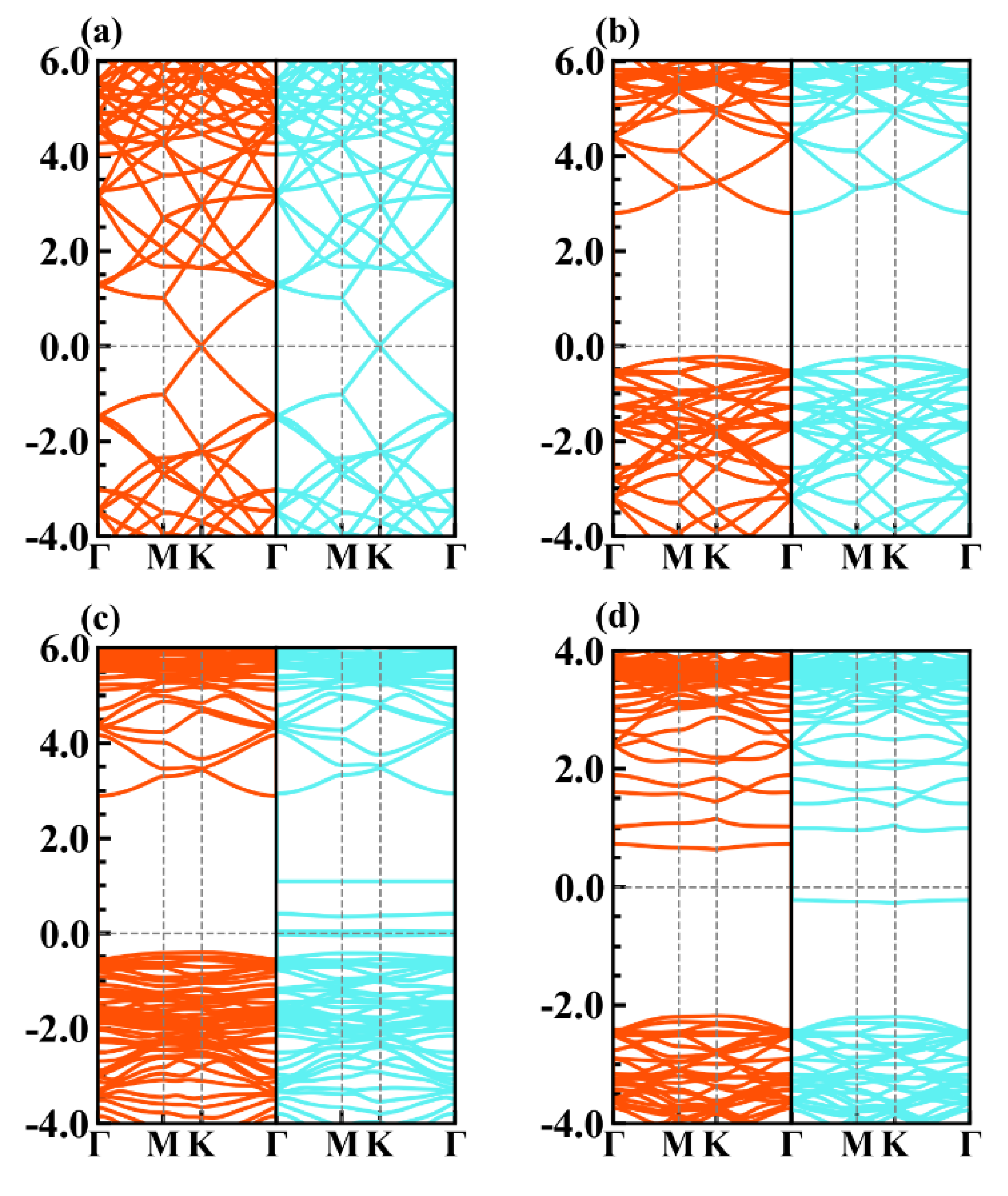
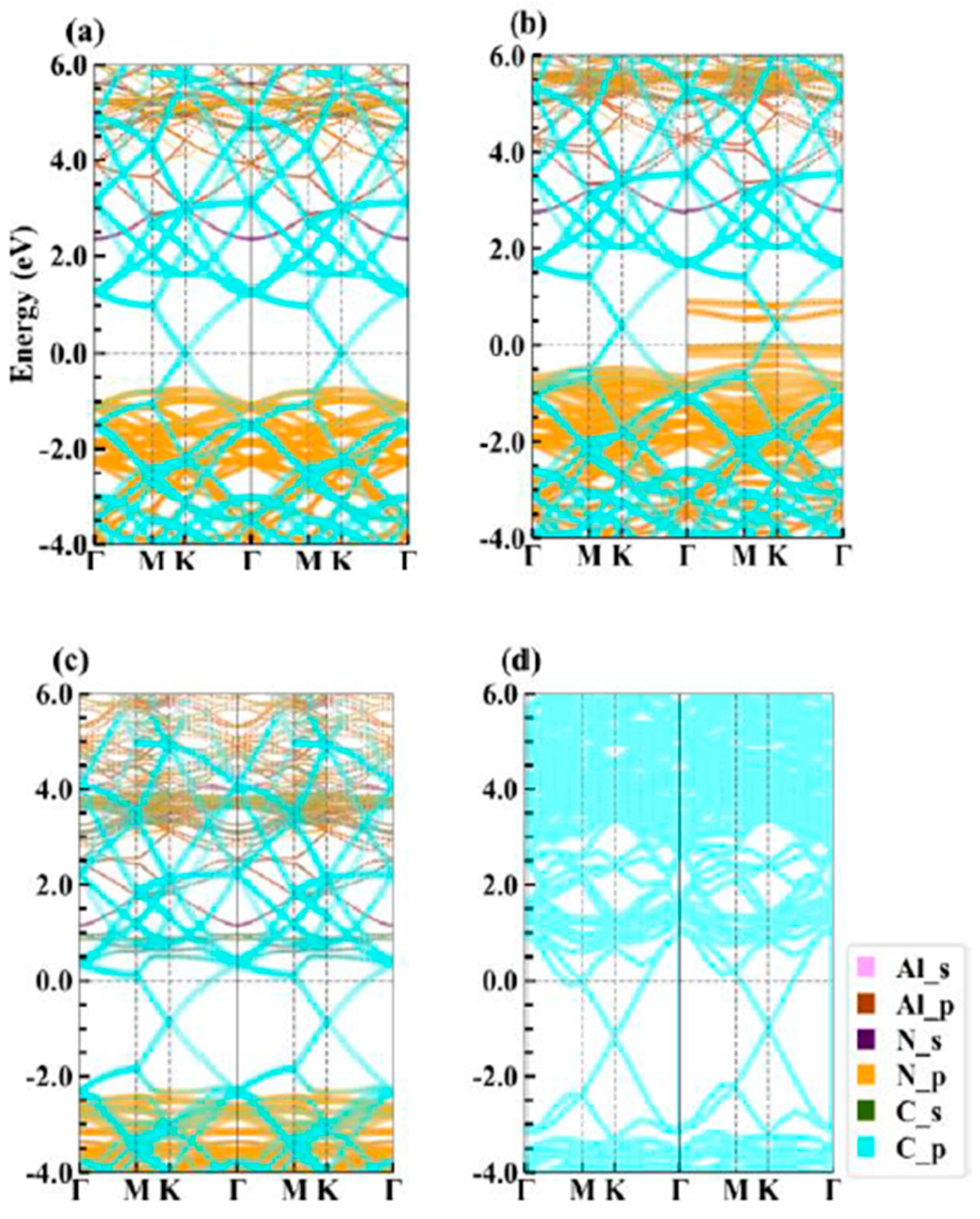
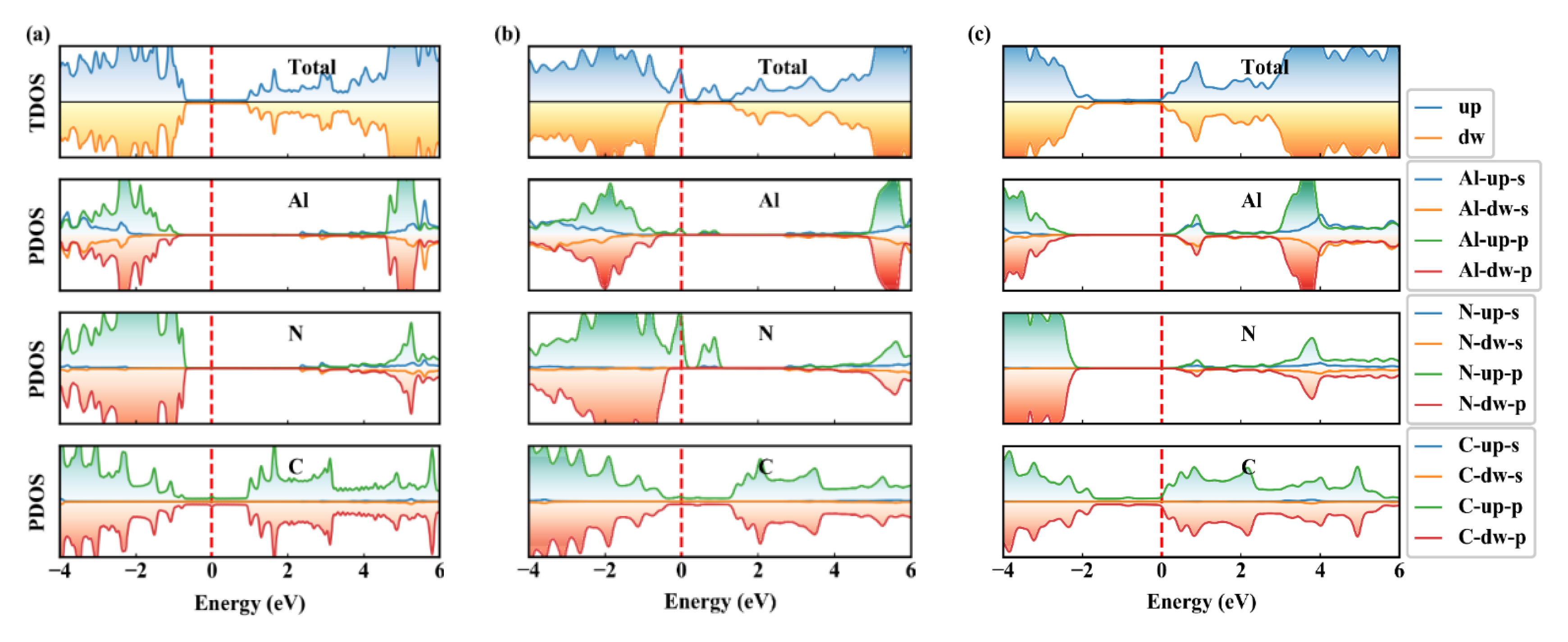
3.2. Electronic Properties
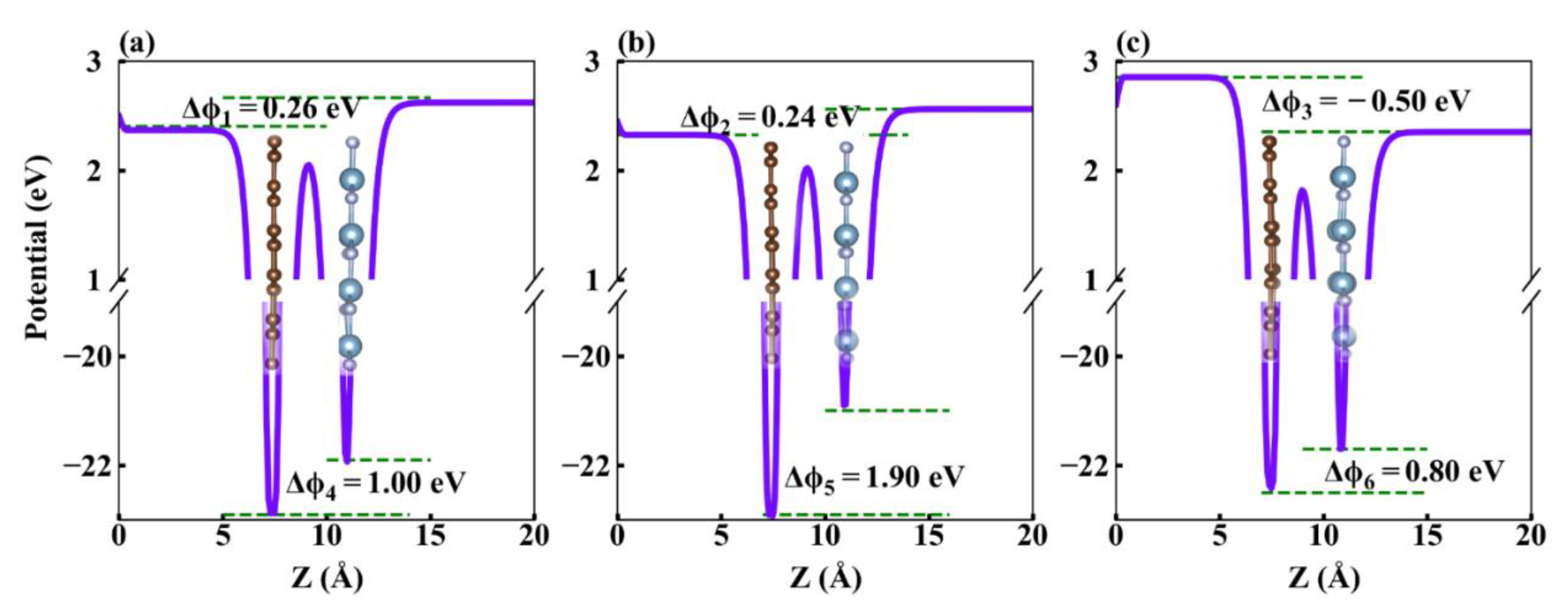
3.3. Schottky Barrier Height
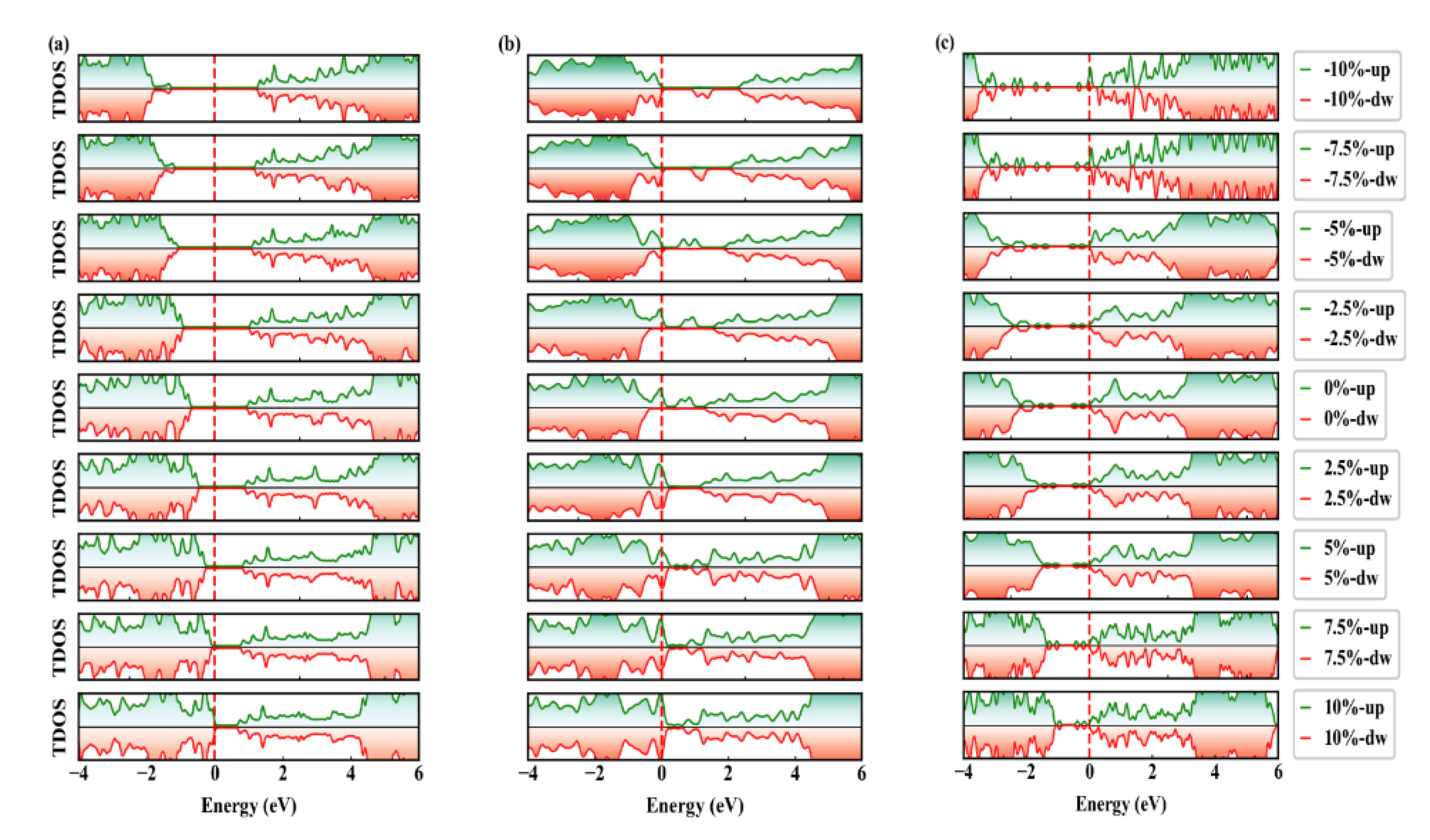
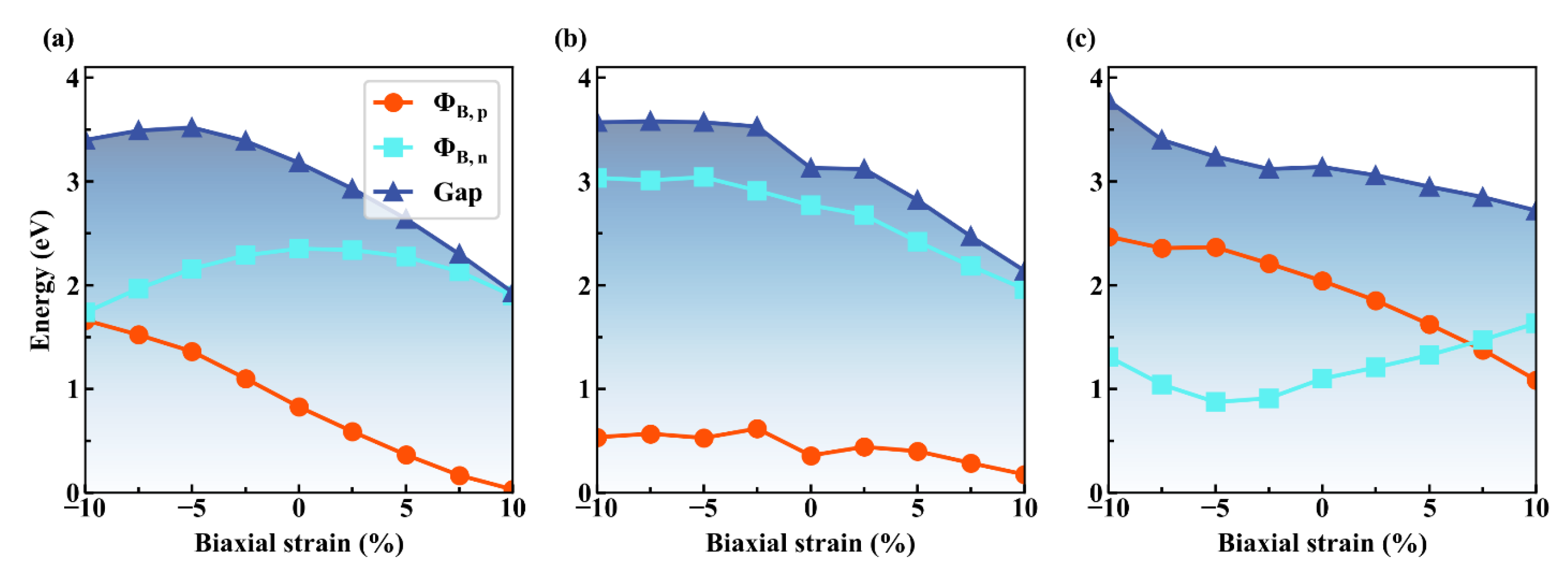
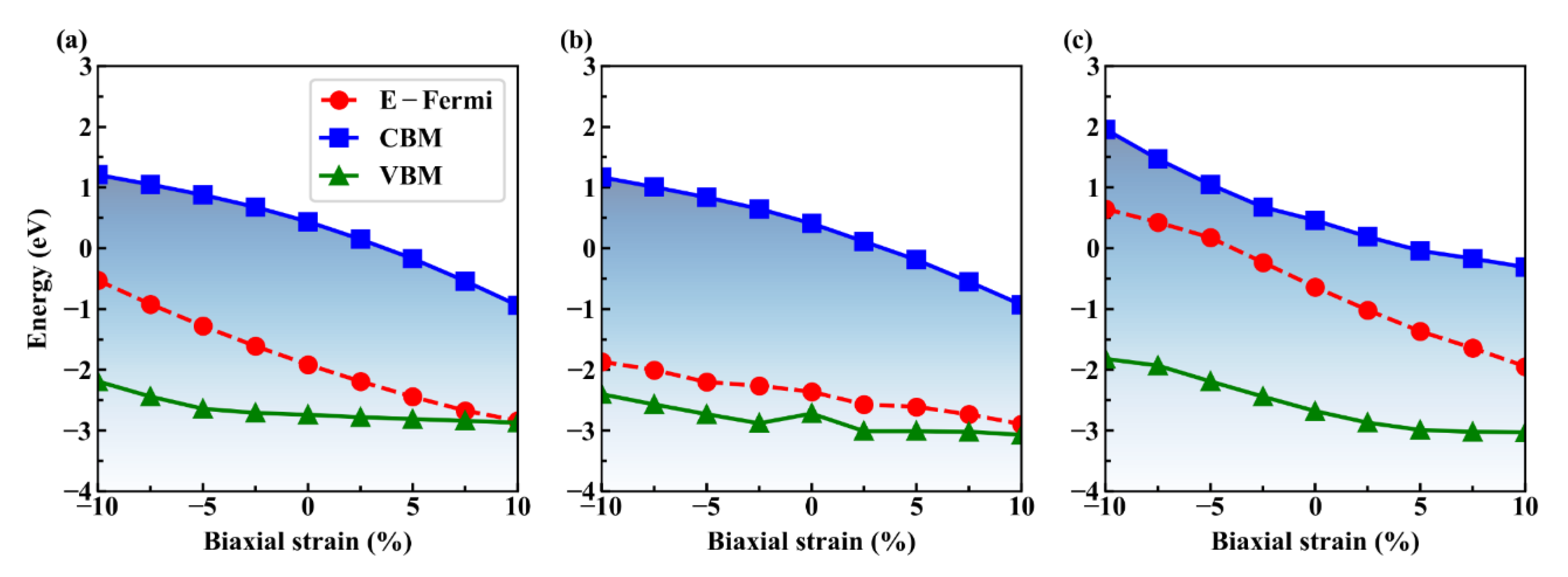
3.4. Effects of Biaxial Strain on SBH
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J.N.; Strano, M.S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 2012, 7, 699–712. [Google Scholar] [CrossRef] [PubMed]
- Duan, X.; Wang, C.; Pan, A.; Yu, R.; Duan, X. Two-dimensional transition metal dichalcogenides as atomically thin semiconductors: Opportunities and challenges. Chem. Soc. Rev. 2015, 44, 8859–8876. [Google Scholar] [CrossRef] [PubMed]
- Choi, W.; Choudhary, N.; Han, G.H.; Park, J.; Akinwande, D.; Lee, Y.H. Recent development of two-dimensional transition metal dichalcogenides and their applications. Mater. Today 2017, 20, 116–130. [Google Scholar] [CrossRef]
- Gao, Z.; Zhou, Z.; Tománek, D. Degenerately Doped Transition Metal Decalcomania as Ohmic Homojunction Contacts to Transition Metal Dichalcogenide Semiconductors. ACS Nano 2019, 13, 5103–5111. [Google Scholar] [CrossRef]
- Liu, H.; Neal, A.T.; Zhu, Z.; Luo, Z.; Xu, X.F.; Tomanek, D.; Ye, P.D. Phosphorene: An Unexplored 2D Semiconductor with a High Hole Mobility. ACS Appl. Nano Mater. 2014, 8, 4033–4041. [Google Scholar] [CrossRef]
- Carvalho, A.; Wang, M.; Zhu, X.; Rodin, A.S.; Su, H.; Castro Neto, A.H. Phosphorene: From theory to applications. Nat. Rev. Mater. 2016, 1, 16061. [Google Scholar] [CrossRef]
- Naseri, A.; Samadi, M.; Pourjavadi, A.; Moshfegh, A.Z.; Ramakrishna, S. Graphitic carbon nitride (g-C3N4)-based photocatalysts for solar hydrogen generation: Recent advances and future development directions. J. Mater. Chem. A 2017, 5, 23406–23433. [Google Scholar] [CrossRef]
- Ong, W.-J.; Tan, L.-L.; Ng, Y.H.; Yong, S.-T.; Chai, S.-P. Graphitic Carbon Nitride (g-C3N4)-Based Photocatalysts for Artificial Photosynthesis and Environmental Remediation: Are We a Step Closer To Achieving Sustainability? Chem. Rev. 2016, 116, 7159–7329. [Google Scholar] [CrossRef]
- Singh, A.K.; Zhuang, H.L.; Hennig, R.G. Ab initio synthesis of single-layer III-V materials. Phys. Rev. B 2014, 89, 245431. [Google Scholar] [CrossRef]
- Zhang, Z.; Geng, Z.; Cai, D.; Pan, T.; Chen, Y.; Dong, L.; Zhou, T. Structure, electronic and magnetic properties of hexagonal boron nitride sheets doped by 5d transition metal atoms: First-principles calculations and molecular orbital analysis. Phys. E (Amsterdam, Neth.) 2015, 65, 24–29. [Google Scholar] [CrossRef]
- Onen, A.; Kecik, D.; Durgun, E.; Ciraci, S. GaN: From three- to two-dimensional single-layer crystal and its multilayer van der Waals solids. Phys. Rev. B 2016, 93, 085431. [Google Scholar] [CrossRef]
- Kecik, D.; Onen, A.; Konuk, M.; Gürbüz, E.; Ersan, F.; Cahangirov, S.; Aktürk, E.; Durgun, E.; Ciraci, S. Fundamentals, progress, and future directions of nitride-based semiconductors and their composites in two-dimensional limit: A first-principles perspective to recent synthesis. Appl. Phys. Rev. 2018, 5, 011105. [Google Scholar] [CrossRef]
- Al Balushi, Z.Y.; Wang, K.; Ghosh, R.K.; Vila, R.A.; Eichfeld, S.M.; Caldwell, J.D.; Qin, X.; Lin, Y.C.; DeSario, P.A.; Stone, G.; et al. Two-dimensional gallium nitride realized via graphene encapsulation. Nat. Mater. 2016, 15, 1166–1171. [Google Scholar] [CrossRef]
- Young, A.F.; Kim, P. Quantum interference and Klein tunnelling in graphene heterojunctions. Nat. Phys. 2009, 5, 222. [Google Scholar] [CrossRef]
- Kwak, J.Y.; Hwang, J.; Calderon, B.; Alsalman, H.; Munoz, N.; Schutter, B.; Spencer, M.G. Electrical characteristics of multilayer MoS2 FET’s with MoS2/graphene heterojunction contacts. Nano Lett. 2014, 14, 4511–4516. [Google Scholar] [CrossRef]
- Deng, Z.; Wang, X. Strain engineering on the electronic states of two-dimensional GaN/graphene heterostructure. RSC Adv. 2019, 9, 26024–26029. [Google Scholar] [CrossRef]
- Deng, Z.; Wang, X.; Cui, J. Effect of interfacial defects on the electronic properties of graphene/g-GaN heterostructures. RSC Adv. 2019, 9, 13418–13423. [Google Scholar] [CrossRef]
- Ahmad, H.; Thandavan, T.M.K. Influence of boron nitride nanoparticles in the electrical and photoconduction characteristics of planar boron nitride-graphene oxide composite layer. Mater. Express 2019, 9, 265–272. [Google Scholar] [CrossRef]
- Tsipas, P.; Kassavetis, S.; Tsoutsou, D.; Xenogiannopoulou, E.; Golias, E.; Giamini, S.A.; Grazianetti, C.; Chiappe, D.; Molle, A.; Fanciulli, M.; et al. Evidence for graphite-like hexagonal AlN nanosheets epitaxially grown on single crystal Ag(111). Appl. Phys. Lett. 2013, 103, 251605. [Google Scholar] [CrossRef]
- Wang, W.; Zheng, Y.; Li, X.; Li, Y.; Zhao, H.; Huang, L.; Yang, Z.; Zhang, X.; Li, G. 2D AlN Layers Sandwiched Between Graphene and Si Substrates. Adv. Mater. 2019, 31, 1803448. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Yang, Y.; Zhang, Z.; Gong, Y.; Zhou, W.; Hu, Z.; Ye, G.; Zhang, X.; Bianco, E.; Lei, S. Strain-induced electronic structure changes in stacked van der Waals heterostructures. Nano Lett. 2016, 16, 3314–3320. [Google Scholar] [CrossRef] [PubMed]
- Deng, S.; Sumant, A.V.; Berry, V. Strain engineering in two-dimensional nanomaterials beyond graphene. Nano Today 2018, 22, 14–35. [Google Scholar] [CrossRef]
- Huang, T.; Wei, W.; Chen, X.; Dai, N. Strained 2D Layered Materials and Heterojunctions. Ann. Phys. 2019, 531. [Google Scholar] [CrossRef]
- Xia, W.; Dai, L.; Yu, P.; Tong, X.; Song, W.; Zhang, G.; Wang, Z. Recent progress in van der Waals heterojunctions. Nanoscale 2017, 9, 4324–4365. [Google Scholar] [CrossRef]
- Yu, Q.; Luo, Y.; Mahmood, A.; Liu, B.; Cheng, H.-M. Engineering Two-Dimensional Materials and Their Heterostructures as High-Performance Electrocatalysts. Electrochem. Energy Rev. 2019, 2, 1–22. [Google Scholar] [CrossRef]
- Sciuto, A.; La Magna, A.; Angilella, G.G.N.; Pucci, R.; Greco, G.; Roccaforte, F.; Giannazzo, F.; Deretzis, I. Extensive Fermi-Level Engineering for Graphene through the Interaction with Aluminum Nitrides and Oxides. Phys. Status Solidi RRL 2019, 1900399. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B. 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Wang, V.; Xu, N.; Liu, J.-C.; Tang, G.; Geng, W.-T. VASPKIT: A Pre- and Post-Processing Program for VASP code. arXiv 2019, arXiv:1908.08269. Available online: https://arxiv.org/abs/1908.08269 (accessed on 25 August 2019).
- Hu, J.-S.; Duan, W.; He, H.; Lv, H.; Huang, C.; Ma, X. A Promising Strategy to Tune the Schottky Barrier of MoS2 (1-x) Se2x/graphene Heterostructure by Asymmetric Se Doping. J. Mater. Chem. C 2019, 7, 7798–7805. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, R.; Wang, C.; Li, H.-B.; Dong, H.; Wang, W.-H.; Lu, F.; Cheng, Y.; Xie, X.; Liu, H. GaN as an Interfacial Passivation Layer: Tuning Band Offset and Removing Fermi Level Pinning for III–V MOS Devices. ACS Appl. Mater. Interfaces 2015, 7, 5141–5149. [Google Scholar] [CrossRef]
- Sun, M.; Chou, J.-P.; Yu, J.; Tang, W. Effects of structural imperfection on the electronic properties of graphene/WSe2 heterostructures. J. Mater. Chem. C 2017, 5, 10383–10390. [Google Scholar] [CrossRef]
- Mansurov, V.; Malin, T.; Galitsyn, Y.; Zhuravlev, K. Graphene-like AlN layer formation on (111)Si surface by ammonia molecular beam epitaxy. J. Cryst. Growth 2015, 428, 93–97. [Google Scholar] [CrossRef]
- Liu, X.-F.; Luo, Z.-J.; Zhou, X.; Wei, J.-M.; Wang, Y.; Guo, X.; Lv, B.; Ding, Z. Structural, mechanical, and electronic properties of 25 kinds of III–V binary monolayers: A computational study with first-principles calculation. Chin. Phys. B 2019, 28, 086105. [Google Scholar] [CrossRef]
- Zhang, Z.-F.; Zhou, T.-G.; Zhao, H.-Y.; Wei, X.-L. First-principles calculations of 5d atoms doped hexagonal-AlN sheets: Geometry, magnetic property and the influence of symmetry and symmetry-breaking on the electronic structure. Chin. Phys. B 2013, 23, 016801. [Google Scholar] [CrossRef]
- Liao, J.; Sa, B.; Zhou, J.; Ahuja, R.; Sun, Z. Design of High-Efficiency Visible-Light Photocatalysts for Water Splitting: MoS2/AlN(GaN) Heterostructures. J. Phys. Chem. C 2014, 118, 17594–17599. [Google Scholar] [CrossRef]
- Phuc, H.V.; Hieu, N.N.; Hoi, B.D.; Phuong, L.T.T.; Hieu, N.V.; Nguyen, C.V. Out-of-plane strain and electric field tunable electronic properties and Schottky contact of graphene/antimonene heterostructure. Superlattices Microstruct. 2017, 112, 554–560. [Google Scholar] [CrossRef]
- Zhang, F.; Li, W.; Ma, Y.; Dai, X. Strain effects on the Schottky contacts of graphene and MoSe2 heterobilayers. Phys. E (Amsterdam Neth.) 2018, 103, 284–288. [Google Scholar] [CrossRef]
- Komsa, H.-P.; Kotakoski, J.; Kurasch, S.; Lehtinen, O.; Kaiser, U.; Krasheninnikov, A.V. Two-Dimensional Transition Metal Dichalcogenides under Electron Irradiation: Defect Production and Doping. Phys. Rev. Lett. 2012, 109, 035503. [Google Scholar] [CrossRef] [PubMed]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- González, R.; López-Pérez, W.; González-García, Á.; Moreno-Armenta, M.G.; González-Hernández, R. Vacancy charged defects in two-dimensional GaN. Appl. Surf. Sci. 2018, 433, 1049–1055. [Google Scholar] [CrossRef]
- Si, C.; Lin, Z.; Zhou, J.; Sun, Z. Controllable Schottky barrier in GaSe/graphene heterostructure: The role of interface dipole. 2D Mater. 2016, 4, 015027. [Google Scholar] [CrossRef]
- Gao, X.; Shen, Y.; Ma, Y.; Wu, S.; Zhou, Z. Graphene/g-GeC bilayer heterostructure: Modulated electronic properties and interface contact via external vertical strains and electric fileds. Carbon 2019, 146, 337–347. [Google Scholar] [CrossRef]
- Padilha, J.E.; Fazzio, A.; da Silva, A.J. Van der Waals heterostructure of phosphorene and graphene: Tuning the Schottky barrier and doping by electrostatic gating. Phys. Rev. Lett. 2015, 114, 066803. [Google Scholar] [CrossRef]
- Yun, W.S.; Han, S.; Hong, S.C.; Kim, I.G.; Lee, J. Thickness and strain effects on electronic structures of transition metal dichalcogenides: 2H-M X 2 semiconductors (M = Mo, W.; X = S, Se, Te). Phys. Rev. B 2012, 85, 033305. [Google Scholar] [CrossRef]
- Wang, H.; Liu, F.; Fu, W.; Fang, Z.; Zhou, W.; Liu, Z. Two-dimensional heterostructures: Fabrication, characterization, and application. Nanoscale 2014, 6, 12250–12272. [Google Scholar] [CrossRef]
- Liu, Y.; Weiss, N.O.; Duan, X.; Cheng, H.-C.; Huang, Y.; Duan, X.-F. Van der Waals heterostructures and devices. Nat. Rev. Mater. 2016, 1, 1–15. [Google Scholar] [CrossRef]
| Structures | d (Å) | Gap (eV) | WF (eV) | SBH (eV) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PBE | HSE | PBE | HSE | |||||||||
| PBE | HSE | PBE | HSE | |||||||||
| Graphene | - | 1.43 | - | - | - | - | 4.26 | - | - | - | - | - |
| g-AlN | - | - | 1.78 | 3.07 | - | - | 5.10 | - | - | - | - | - |
| g-AlN-VAl | - | - | 1.80 | 3.15 | - | - | 5.44 | - | - | - | - | - |
| g-AlN-VN | - | - | 1.81 | 3.40 | - | - | 3.29 | - | - | - | - | - |
| Gr/g-AlN | 3.49 | 1.42 | 1.78 | 3.18 | 3.93 | −2.15 | 4.41 | 5.67 | 2.35 | 3.69 | 0.83 | 0.24 |
| Gr/g-AlN- | 3.28 | 1.42 | 1.78 | 3.13 | 3.98 | −2.89 | 4.80 | 5.12 | 2.77 | 3.23 | 0.36 | 0.75 |
| Gr/g-AlN- | 3.08 | 1.43 | 1.78 | 3.14 | 4.11 | −2.90 | 3.27 | 3.16 | 1.10 | 0.98 | 2.04 | 3.13 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhang, Z.; Luo, Z.; Lv, B.; Ding, Z. Tunable Electronic Properties of Graphene/g-AlN Heterostructure: The Effect of Vacancy and Strain Engineering. Nanomaterials 2019, 9, 1674. https://doi.org/10.3390/nano9121674
Liu X, Zhang Z, Luo Z, Lv B, Ding Z. Tunable Electronic Properties of Graphene/g-AlN Heterostructure: The Effect of Vacancy and Strain Engineering. Nanomaterials. 2019; 9(12):1674. https://doi.org/10.3390/nano9121674
Chicago/Turabian StyleLiu, Xuefei, Zhaofu Zhang, Zijiang Luo, Bing Lv, and Zhao Ding. 2019. "Tunable Electronic Properties of Graphene/g-AlN Heterostructure: The Effect of Vacancy and Strain Engineering" Nanomaterials 9, no. 12: 1674. https://doi.org/10.3390/nano9121674
APA StyleLiu, X., Zhang, Z., Luo, Z., Lv, B., & Ding, Z. (2019). Tunable Electronic Properties of Graphene/g-AlN Heterostructure: The Effect of Vacancy and Strain Engineering. Nanomaterials, 9(12), 1674. https://doi.org/10.3390/nano9121674