A Review on Electrical Conductivity of Nanoparticle-Enhanced Fluids
Abstract
:1. Introduction
2. Theoretical Models for Electrical Conductivity
3. Literature Overview
3.1. Nanofluids with Ethylene Glycol (EG) as Base Fluid
3.2. Nanofluids with Water as Base Fluid
3.3. Nanofluids with Water-Ethylene Glycol Mixture as Base Fluid
3.4. Nanofluids Based on Other Liquids
3.4.1. Bioglycol-Based Nanofluids
3.4.2. Oil-Based Nanofluids
4. Discussion on Experimental Results
4.1. Nanoparticle Concentration Influence on Electrical Conductivity
4.2. Base Fluid Influence on Electrical Conductivity
4.3. Temperature Influence on Electrical Conductivity
4.4. Other Factors Influence on Electrical Conductivity
4.5. Electrical Conductivity—A Method for Stability Estimation?
5. Conclusions
Challenges and Future Directions for Research
Funding
Conflicts of Interest
| Nomenclature | |
| K0 | fitting parameter in Hill equation, - |
| L | Avogadro constant, L = 6.02214086 × 1023 mol−1 |
| n | fitting parameter in Hill equation, - |
| r | radius of nanoparticles, nm |
| R | thermodynamic constant, R = 8.314 kJ/kmol K |
| t | temperature, °C |
| T | temperature, K |
| U0 | zeta potential, mV |
| Greek Symbols | |
| α | ratio of electrical conductivity, - |
| ε0 | dielectric constant of vacuum, - |
| εr | dielectric constant of base fluid, - |
| φ | volume fraction of nanoparticles, - |
| η | viscosity, Pa.s |
| ρ | density, kg/m3 |
| σ | electrical conductivity, µS/cm |
| Subscripts | |
| B | refers to Brownian motion |
| bf | refers to base-fluid |
| E | refers to electrophoretic mobility |
| M | refers to Maxwell model |
| nf | refers to nanofluid |
| p | refers to nanoparticles |
| Abbreviations | |
| ANN | artificial neural network model |
| BG | Bio glycol |
| CNT | carbon nanotubes |
| EDL | electrical double layer |
| EHD | electro hydrodynamics |
| EG | ethylene glycol |
| MHD | magneto hydrodynamics |
| MWCNT | multi-wall carbon nanotubes |
| NEIL | ionic liquids enhanced nanofluids |
| PG | propylene glycol |
| RDB | refined, bleached and deodorized (refers to oils) |
| SDBS | Sodium dodecyl benzenesulfonate |
| SDS | Sodium dodecyl sulfate |
| TEC | thermo-electrical conductivity |
| W | water |
References
- Pordanjani, A.H.; Aghakhani, S.; Afrand, M.; Mahmoudi, B.; Mahian, O.; Wongwises, S. An updated review on application of nanofluids in heat exchangers for saving energy. Energy Convers. Manag. 2019, 198, 111886. [Google Scholar] [CrossRef]
- Sharafeldin, M.A.; Gróf, G.; Abu-Nada, E.; Mahian, O. Evacuated tube solar collector performance using copper nanofluid: Energy and environmental analysis. Appl. Therm. Eng. 2019, 162, 114205. [Google Scholar] [CrossRef]
- Das, P.K. A review based on the effect and mechanism of thermal conductivity of normal nanofluids and hybrid nanofluids. J. Mol. Liq. 2017, 240, 420–446. [Google Scholar] [CrossRef]
- Cabaleiro, D.; Pastoriza-Gallego, M.J.; Piñeiro, M.M.; Lugo, L. Characterization and measurements of thermal conductivity, density and rheological properties of zinc oxide nanoparticles dispersed in (ethane-1,2-diol + water) mixture. J. Chem. Thermodyn. 2013, 58, 405–415. [Google Scholar] [CrossRef]
- Vallejo, J.P.; Gómez-Barreiro, S.; Cabaleiro, D.; Gracia-Fernández, C.; Fernández-Seara, J.; Lugo, L. Flow behaviour of suspensions of functionalized graphene nanoplatelets in propylene glycol–water mixtures. Int. Commun. Heat Mass 2018, 91, 150–157. [Google Scholar] [CrossRef]
- Radhakrishnan, A.K.; Aishwarya, V.; Suganthi, K.; Rajan, K. How better are propylene glycol-based nanofluids compared to propylene glycol? A study in small, jacketed vessel. Asian J. Sci. Res. 2014, 7, 328–334. [Google Scholar]
- Eastman, J.A.; Choi, U.S.; Li, S.; Thompson, L.J.; Lee, S. Enhanced Thermal Conductivity Through the Development of Nanofluids. In Proceedings of the Symposium on Nanophase and Nanocomposite Materials II, Boston, MA, USA, 2–5 December 1997; pp. 3–11. [Google Scholar]
- Guo, W.; Li, G.; Zheng, Y.; Dong, C. Measurement of the thermal conductivity of SiO2 nanofluids with an optimized transient hot wire method. Thermochim. Acta 2018, 661, 84–97. [Google Scholar] [CrossRef]
- Manna, O.; Singh, S.; Paul, G. Enhanced thermal conductivity of nano-SiC dispersed water based nanofluid. Bull. Mater. Sci. 2012, 35, 707–712. [Google Scholar]
- Das, P.K.; Mallik, A.K.; Ganguly, R.; Santra, A.K. Synthesis and characterization of TiO2–water nanofluids with different surfactants. Int. Commun. Heat Mass 2016, 75, 341–348. [Google Scholar] [CrossRef]
- Nikkam, N.; Saleemi, M.; Haghighi, E.B.; Ghanbarpour, M.; Khodabandeh, R.; Muhammed, M. Fabrication, characterization and thermophysical property evaluation of SiC nanofluids for heat transfer applications. Nano-Micro Lett. 2014, 6, 178–189. [Google Scholar] [CrossRef]
- Chen, W.; Zou, C.; Li, X.; Li, L. Experimental investigation of SiC nanofluids for solar distillation system: Stability, optical properties and thermal conductivity with saline water-based fluid. Int. J. Heat Mass Trans. 2017, 107, 264–270. [Google Scholar] [CrossRef]
- Mudagi, B.S. The Study of Some Problems of Magneto Hydrodynamic Flow in Presence of Transverse Magnetic Field. Ph.D. Thesis, University of Pune, Maharashtra, India, 2011; pp. 21–38. [Google Scholar]
- Nakhla, D.; Thompson, E.; Lacroix, B.; Cotton, J.S. Measurement of heat transfer enhancement in melting of n-Octadecane under gravitational and electro hydrodynamics (EHD) forces. J. Electrost. 2018, 92, 31–37. [Google Scholar] [CrossRef]
- Ghoshal, U.; Miner, A.C. Cooling of Electronics by Electrically Conducting Fluids. Patent No. US 6,708,501 B1, 23 March 2004. [Google Scholar]
- Semat, H.; Katz, R. Electrical Conduction in Liquids and Solids. In Physics; University of Nebraska: Linkoln, NB, USA, 1958; p. 154. [Google Scholar]
- Banisi, S.; Finch, J.A.; Laplante, A.R. Electrical conductivity of dispersions: A review. Miner. Eng. 1993, 6, 369–385. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise of Electricity and Magnetism, 3rd ed.; Oxford University Press: London, UK, 1892; Volume 1, Part II, Chapter IX; pp. 435–449. [Google Scholar]
- Bruggeman, D.A.G. Berechnung Verschiedener Physicalischer Konstanten yon Heterogenen Substanzen. Annalen Physik 1935, 24, 639–664. [Google Scholar]
- Fricke, H. A Mathematical Treatment of the Electric Conductivity and Capacity of Dispersed Systems, I. The Electric Conductivity of a Suspension of Homogeneous Spheroids. Phys. Rev. 1924, 24, 575–585. [Google Scholar] [CrossRef]
- Cruz, R.C.D.; Reinshagen, J.; Oberacker, R.; Segadães, A.M.; Hoffmann, M.J. Electrical conductivity and stability of concentrated aqueous alumina suspensions. J. Colloid Interface Sci. 2005, 286, 579–588. [Google Scholar] [CrossRef]
- Shirazi, S.F.S.; Gharehkhani, S.; Yarmand, H.; Badarudin, A.; Metselaar, H.S.C.; Kazi, S.N. Nitrogen doped activated carbon/graphene with high nitrogen level: Green synthesis and thermo-electrical properties of its nanofluid. Mater. Lett. 2015, 152, 192–195. [Google Scholar] [CrossRef]
- Mohamed, R.A. Modeling electrical properties of nanofluids using artificial neural network. Phys. Scripta 2019, 94, 10522. [Google Scholar] [CrossRef]
- Akilu, S.; Baheta, A.T.; Kadirgama, K.; Padmanabhan, E.; Sharma, K.V. Viscosity, electrical and thermal conductivities of ethylene and propylene glycol-based β-SiCnanofluids. J. Mol. Liq. 2019, 284, 780–792. [Google Scholar] [CrossRef]
- Fal, J.; Wanic, M.; Malick, M.; Oleksy, M.; Zyła, G. Experimental Investigation of Electrical Conductivity of Ethylene Glycol Containing Indium Oxide Nanoparticles. Actaphysica Polonica A 2019, 135, 1237–1239. [Google Scholar] [CrossRef]
- Baby, T.T.; Ramaprabhu, S. Investigation of thermal and electrical conductivity of graphene based nanofluids. J. Appl. Phys. 2010, 108, 124308. [Google Scholar] [CrossRef]
- Zyła, G.; Vallejo, J.P.; Fal, J.; Lugo, L. Nanodiamonds—Ethylene Glycol nanofluids: Experimental investigation of fundamental physical properties. Int. J. Heat Mass Trans. 2018, 121, 1201–1213. [Google Scholar] [CrossRef]
- Zyła, G.; Fal, J. Experimental studies on viscosity, thermal and electrical conductivity of aluminum nitride–ethylene glycol (AlN–EG) nanofluids. Thermoch. Acta 2016, 637, 11–16. [Google Scholar] [CrossRef]
- Zyła, G.; Fal, J. Viscosity, thermal and electrical conductivity of silicon dioxide–ethylene glycol transparent nanofluids: An experimental studies. Thermoch. Acta 2017, 650, 106–113. [Google Scholar] [CrossRef]
- Fal, J.; Wanic, M.; Budzik, G.; Oleksy, M.; Żyła, G. Electrical Conductivity and Dielectric Properties of Ethylene Glycol-Based Nanofluids Containing Silicon Oxide–Lignin Hybrid Particles. Nanomaterials 2019, 9, 1008. [Google Scholar] [CrossRef]
- Żyła, G.; Fal, J.; Bikić, S.; Wanic, M. Ethylene glycol based silicon nitride nanofluids: An experimental study on their thermophysical, electrical and optical properties. Phys. E Low-Dimens. Syst. Nanostruct. 2018, 104, 82–90. [Google Scholar] [CrossRef]
- Zawrah, M.F.; Khattab, R.M.; Girgis, L.G.; El Daidamony, H.; Abdel Aziz Rehab, E. Stability and electrical conductivity of water-base Al2O3 nanofluids for different applications. HBRC J. 2016, 12, 227–234. [Google Scholar] [CrossRef]
- Bagheli, S.; Fadafan, H.K.; LotfiOrimi, R.; Ghaemi, M. Synthesis and experimental investigation of the electrical conductivity of water based magnetite nanofluids. Power Technol. 2015, 274, 426–430. [Google Scholar] [CrossRef]
- Coelho, M.F.; Rivas, M.A.; Vilão, G.; Nogueira, E.M.; Iglesias, T.P. Permittivity and electrical conductivity of copper oxide nanofluid (12 nm) in water at different temperatures. J. Chem. Thermodyn. 2019, 132, 164–173. [Google Scholar] [CrossRef]
- Anu, K.; Hemalatha, J. Magnetic and electrical conductivity studies of zinc doped cobalt ferrite nanofluids. J. Mol. Liq. 2019, 284, 445–453. [Google Scholar] [CrossRef]
- Shoghl, S.N.; Jamali, J.; Moraveji, M.K. Electrical conductivity, viscosity, and density of different nanofluids: An experimental study. Exp. Therm. Fluid Sci. 2016, 74, 339–346. [Google Scholar] [CrossRef]
- Heyhat, M.M.; Irannezhad, A. Experimental investigation on the competition between enhancement of electrical and thermal conductivities in water-based nanofluids. J. Mol. Liq. 2018, 268, 169–175. [Google Scholar] [CrossRef]
- Satriananda, I.N. Satriananda, Investigation on Electrical Conductivity Enhancement of Water Based Maghemite (γ-Fe2O3) Nanofluids. Int. J. Mater. Sci. Appl. 2017, 6, 32–36. [Google Scholar]
- Mashali, F.; Languri, E.; Mirshekari, G.; Davidson, J.; Kerns, D. Nano diamond nanofluid microstructural and thermo-electrical characterization. Int. Commun. Heat Mass 2019, 101, 82–88. [Google Scholar] [CrossRef]
- Modesto-Lopez, L.B.; Biswas, P. Role of the effective electrical conductivity of nano suspensions in the generation of TiO2 agglomerates with electrospray. J. Aerosol Sci. 2010, 41, 790–804. [Google Scholar] [CrossRef]
- Zakaria, I.; Mohamed, W.A.N.W.; Azmi, W.H.; Mamat, A.M.I.; Mamat, R.; Daud, W.R.W. Thermo-electrical performance of PEM fuel cell using Al2O3 nanofluids. Int. J. Heat Mass Trans. 2018, 119, 460–471. [Google Scholar] [CrossRef]
- Hadadian, M.; Goharshadi, E.K.; Youssefi, A.J. Electrical conductivity, thermal conductivity, and rheological properties of graphene oxide-based nanofluids. Nanopart. Res. 2014, 16, 2788. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Modeling and optimization of MHD mixed convection in a lid-driven trapezoidal cavity filled with alumina–water nanofluid: Effects of electrical conductivity models. Int. J. Mech. Sci. 2018, 136, 264–278. [Google Scholar] [CrossRef]
- Ganguly, S.; Sikdar, S.; Basu, S. Experimental investigation of the effective electrical conductivity of aluminum oxide nanofluids. Power Technol. 2009, 196, 326–330. [Google Scholar] [CrossRef]
- Minea, A.A.; Luciu, R.S. Investigations on electrical conductivity of stabilized water based Al2O3 nanofluids. Microfluid Nanofluid 2012, 13, 977–985. [Google Scholar] [CrossRef]
- Minea, A.A. Electrical and rheological behavior of stabilized Al2O3 nanofluids. Curr. Nanosci. 2013, 9, 81–88. [Google Scholar]
- Sundar, L.S.; Shusmitha, K.; Singh, M.K.; Sousa, A.C.M. Electrical conductivity enhancement of nanodiamond–nickel (ND–Ni) nanocomposite based magnetic nanofluids. Int. Commun. Heat Mass 2014, 57, 1–7. [Google Scholar] [CrossRef]
- Chereches, E.I.; Minea, A.A. Electrical conductivity of new nanoparticle enhanced fluids: An experimental study. Nanomaterials 2019, 9, 1228. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.R.; Shabani, B.; Rosengarten, G. Electrical and thermal conductivities of 50/50 water-ethylene glycol based TiO2 nanofluids to be used as coolants in PEM fuel cells. Energy Proc. 2017, 110, 101–108. [Google Scholar] [CrossRef]
- Islam, R.; Shabani, B. Prediction of electrical conductivity of TiO2 water and ethylene glycol-based nanofluids for cooling application in low temperature PEM fuel cells. Energy Proc. 2019, 160, 550–557. [Google Scholar] [CrossRef]
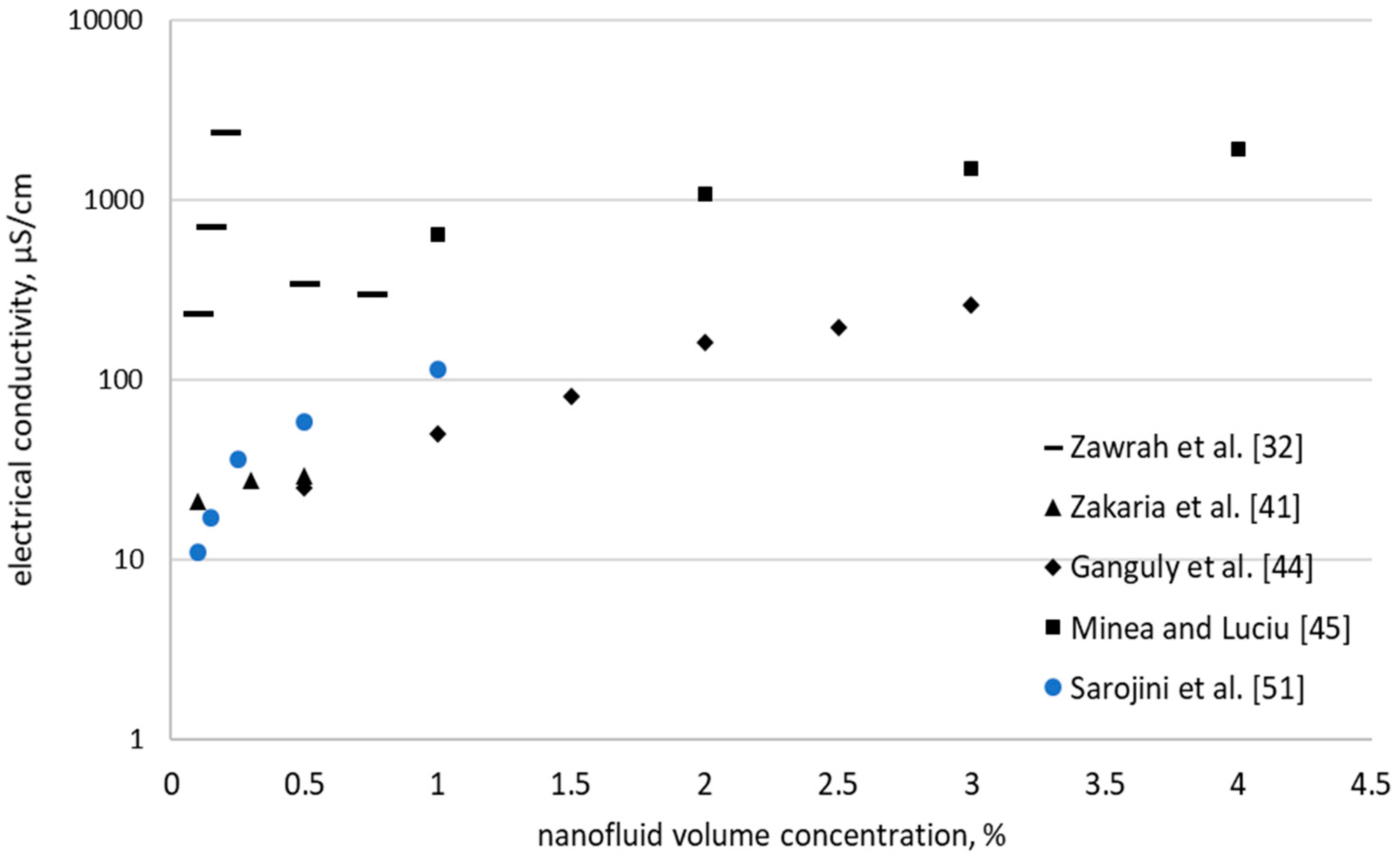
- Sarojini, K.G.K.; Manoja, S.V.; Singha, P.K.; Pradeepb, T.; Das, S.K. Electrical conductivity of ceramic and metallic nanofluids. Colloids Surf. A Phys. Eng. Asp. 2013, 417, 39–46. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, T.; Zhang, D.; Wang, Q. Experimental investigation of thermal and electrical conductivity of silicon oxide nanofluids in ethylene glycol/water mixture. Int. J. Heat Mass Trans. 2018, 117, 280–286. [Google Scholar] [CrossRef]
- Ijam, I.; Saidur, R.; Ganesan, P.; Golsheikh, A.M. Stability, thermo-physical properties, and electrical conductivity of graphene oxide-deionized water/ethylene glycol based nanofluid. Int. J. Heat Mass Trans. 2015, 87, 92–103. [Google Scholar] [CrossRef]
- Kole, M.; Dey, T.K. Investigation of thermal conductivity, viscosity, and electrical conductivity of graphene based nanofluids. J. Appl. Phys. 2013, 113, 084307. [Google Scholar] [CrossRef]
- Khdher, M.; CheSidik, N.A.; Hamzah, W.A.W.; Mamat, R. An experimental determination of thermal conductivity and electrical conductivity of bio glycol based Al2O3 nanofluids and development of new correlation. Int. Commun. Heat Mass 2016, 73, 75–83. [Google Scholar] [CrossRef]
- Abdolbaqi, M.K.; Azmi, W.H.; Mamat, R.; Sharma, K.V.; Najafi, G. Experimental investigation of thermal conductivity and electrical conductivity of BioGlycol–water mixture based Al2O3 nanofluid. Appl. Therm. Eng. 2016, 102, 932–941. [Google Scholar] [CrossRef]
- Naddaf, P.; Heris, S.Z. Experimental study on thermal conductivity and electrical conductivity of diesel oil-based nanofluids of graphene nanoplatelets and carbon nanotubes. Int. Comm. Heat Mass Trans. 2018, 95, 116–122. [Google Scholar] [CrossRef]
- Shen, L.P.; Wang, H.; Dong, M.; Ma, Z.C.; Wang, H.B. Solvothermal synthesis and electrical conductivity model for the zinc oxide-insulated oil nanofluid. Phys. Lett. A 2012, 376, 1053. [Google Scholar] [CrossRef]
- Hill, A.V. The possible effects of the aggregation of the molecules of hemoglobin on its dissociation curves. J. Physiol. 1910, 40, iv–viii. [Google Scholar]
- Goutelle, S.; Maurin, M.; Rougier, F.; Barbaut, X.; Bourguignon, L.; Ducher, M.; Maire, P. The Hill equation: A review of its capabilities in pharmacological modelling. Fundam. Clin. Pharmacol. 2008, 22, 633–648. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, F.; Wang, Q.; Yao, W.; Sun, K.; Zhang, R.; Zhao, J.; Lou, Z.; Li, J. Significantly Enhanced Electrical Performances of Eco-Friendly Dielectric Liquids for Harsh Conditions with Fullerene. Nanomaterials 2019, 9, 989. [Google Scholar] [CrossRef]
- Konakanchi, H.; Vajjha, R.; Misra, D.; Das, D. Electrical conductivity measurements of nanofluids and development of new correlations. J. Nanosci. Nanotechnol. 2011, 8, 6788–6795. [Google Scholar] [CrossRef]
- Glover, B.; Whites, K.W.; Hong, H.; Mukherjee, A.; Billups, W.E. Effective electrical conductivity of functional single-wall carbon nanotubes in aqueous fluids. Synth. Met. 2008, 158, 506–508. [Google Scholar] [CrossRef]
- Dong, M.; Shen, L.P.; Wang, H.; Wang, H.B.; Miao, J. Investigation on the electrical conductivity of transformer oil-Based AlN nanofluid. J. Nano Mater. 2013, 7, 842963. [Google Scholar] [CrossRef]
| Base Fluid | Nanoparticle Type | Observation | Relevance as a Conductive Fluid, if Compared to the Base Fluid | Equipment Used for Electrical Conductivity Measurement | Reference |
|---|---|---|---|---|---|
| ethylene glycol (EG) | nitrogen doped activated carbon/graphene (NACG) | Increase was noticed while the samples concentration increases. | yes | AB200, Fisher scientific | Shirazi et al. [22] |
| MgO and Si-TiO | Theoretical study using an artificial neural network (ANN) model. | no information provided | – | Mohamed [23] | |
| β-SiC | The variation with volume concentration was found to be linear. | yes | SG 23 SevenGo Duo, Mettler Toledo | Akilu et al. [24] | |
| In2O3 | Maximum growth in electrical conductivity of In2O3–EG nanofluids was detected for 0.0081% concentration at 333.15 K, 27,300%. | yes | MultiLine 363 | Fal et al. [25] | |
| graphene | Enhancement up to 220%. | yes | not declared | Baby and Ramaprabhu [26] | |
| nanodiamond | Maximum electrical conductivity enhancement was for 0.0338 volume fraction of nanoparticles (98 times higher than EG). | yes | Multiline 3630 (WTW GmbH, Weilheim, Germany) | Zyla et al. [27] | |
| aluminum nitride | Increase of up to 600 times in electrical conductivity with the upsurge in nanoparticles concentration. | yes | MultiLine 3410 | Zyla and Fal [28] | |
| SiO2 | Thermo-electrical conductivity (TEC) analysis revealed that there are no benefits from using this nanofluid in heat transfer processes. | yes | MultiLine 3410 | Zyla and Fal [29] | |
| silicon oxide lignin (SiO2-L) | Increasing mass fraction, the conductivity increases. | yes | MultiLine 3410 | Fal et al. [30] | |
| Si3N4 | High progression in electrical conductivity due to several factors and especially due to concentration increase. | yes | MultiLine 3630m | Zyla et al. [31] | |
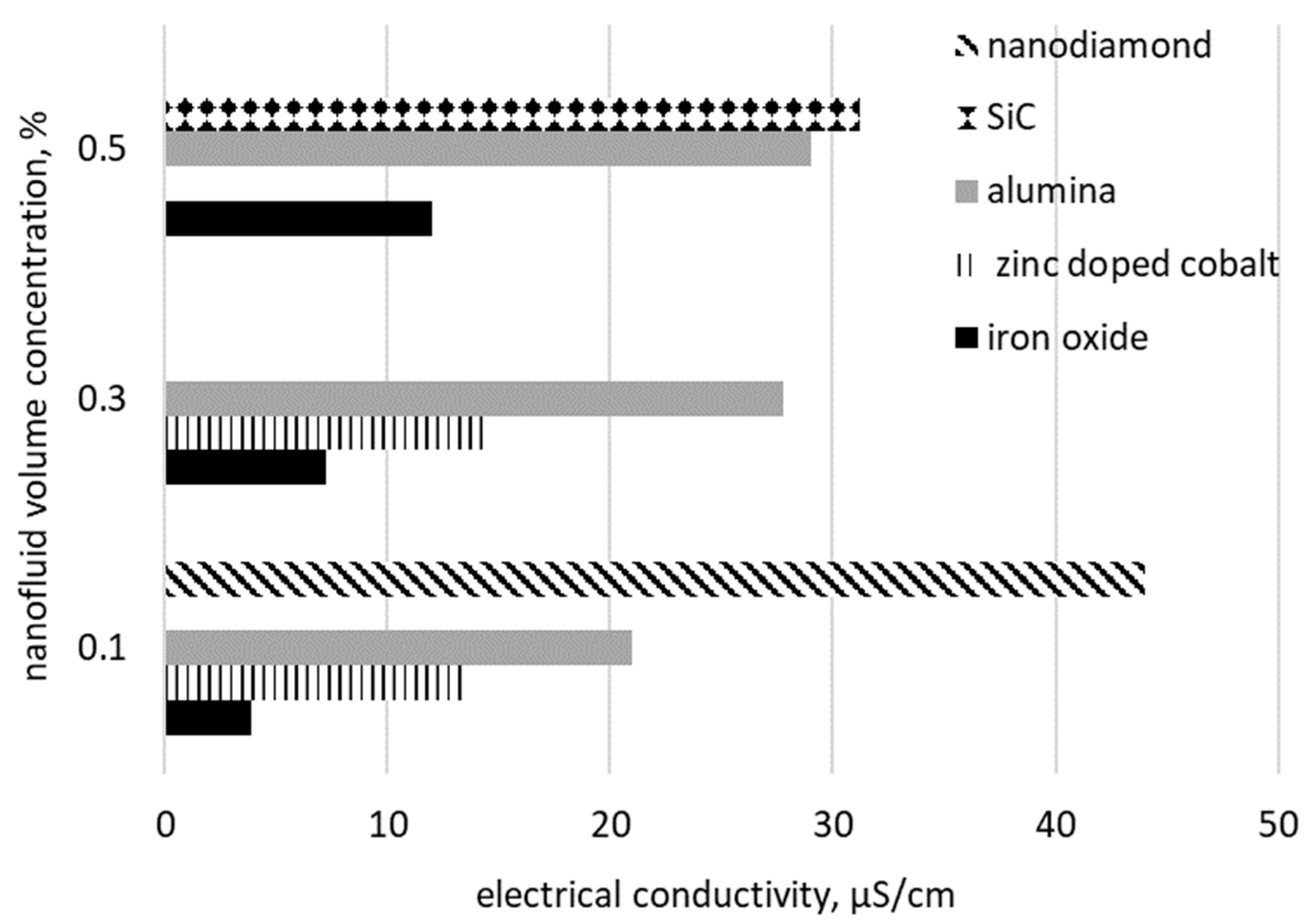
| water | Al2O3 | Highest value of electrical conductivity, 2370 µS/cm, was logged for 0.2% concentration at a temperature of 25.9 °C. | yes | not declared | Zawrah et al. [32] |
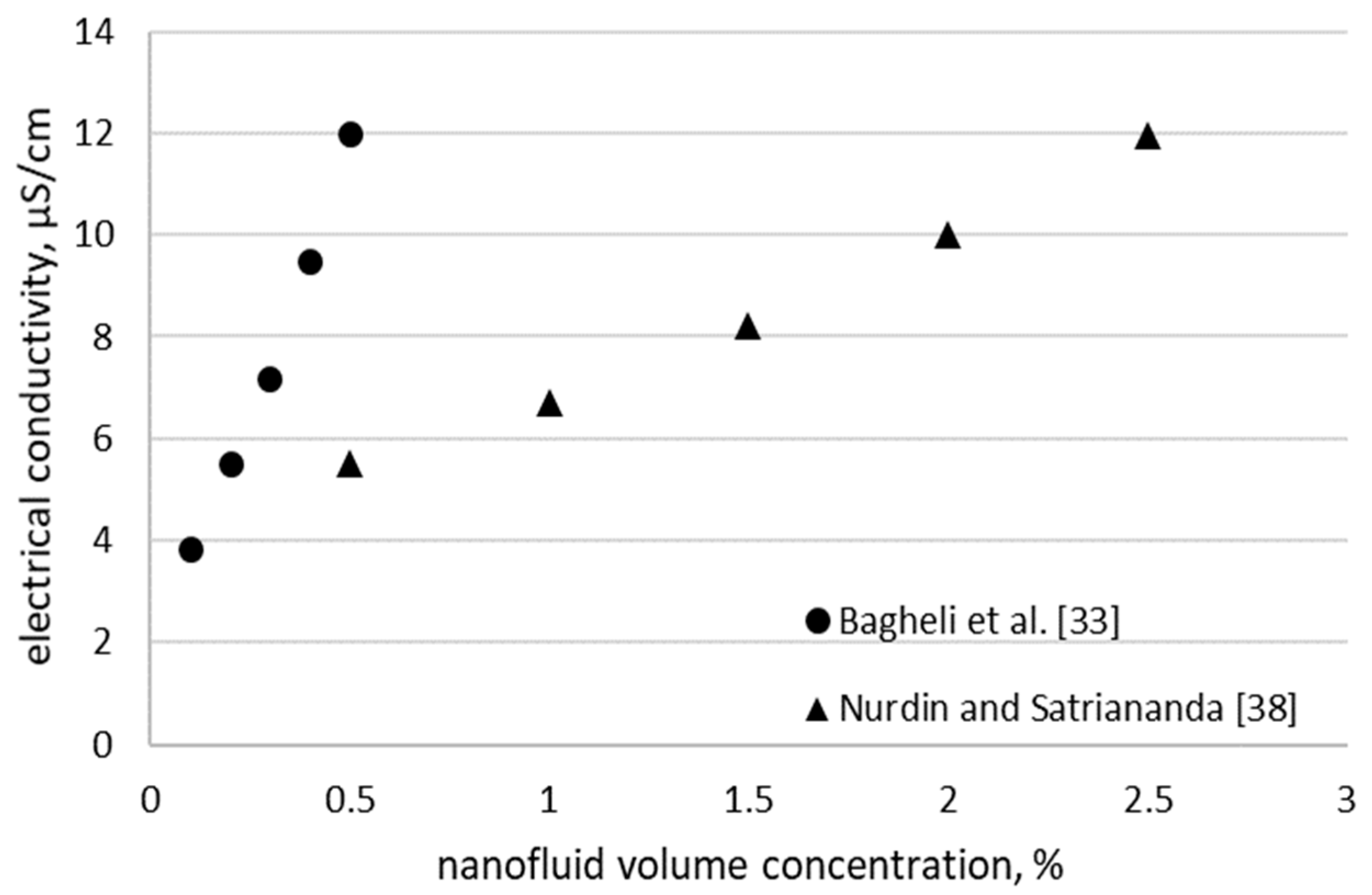
| Fe3O4 | A considerable enhancement of electrical conductivity with the upsurge in concentration and temperature. | yes | WagtechEc-meter model Con 11 | Bagheli et al. [33] | |
| CuO | Enhancement of electrical conductivity with the increase in temperature and volume concentration. | yes | EC-Meter GLP 31 from CRISON | Coelho et al. [34] | |
| un-doped and zinc doped cobalt ferrite | Maxwell model is not suitable. | no information provided | Cyberscan CON110 | Anu and Hemalatha [35] | |
| Alumina CuO MgO CNT titania ZnO | Linear correlations were proposed by authors. | yes | JENWAY 4520 | Shoghl et al. [36] | |
| Ag SiC Graphene oxide (GO) | Electrical conductivities of nanofluids is linearly increasing with temperature and concentration. | yes | AZ86505 benchtop multi-meter | Heyhat and Irannezhad [37] | |
| Fe2O3 | Enhancement of electrical conductivity with the increase in temperature and volume concentration. | yes | Eutech instrument PC 2700 | Nurdin and Satriananda [38] | |
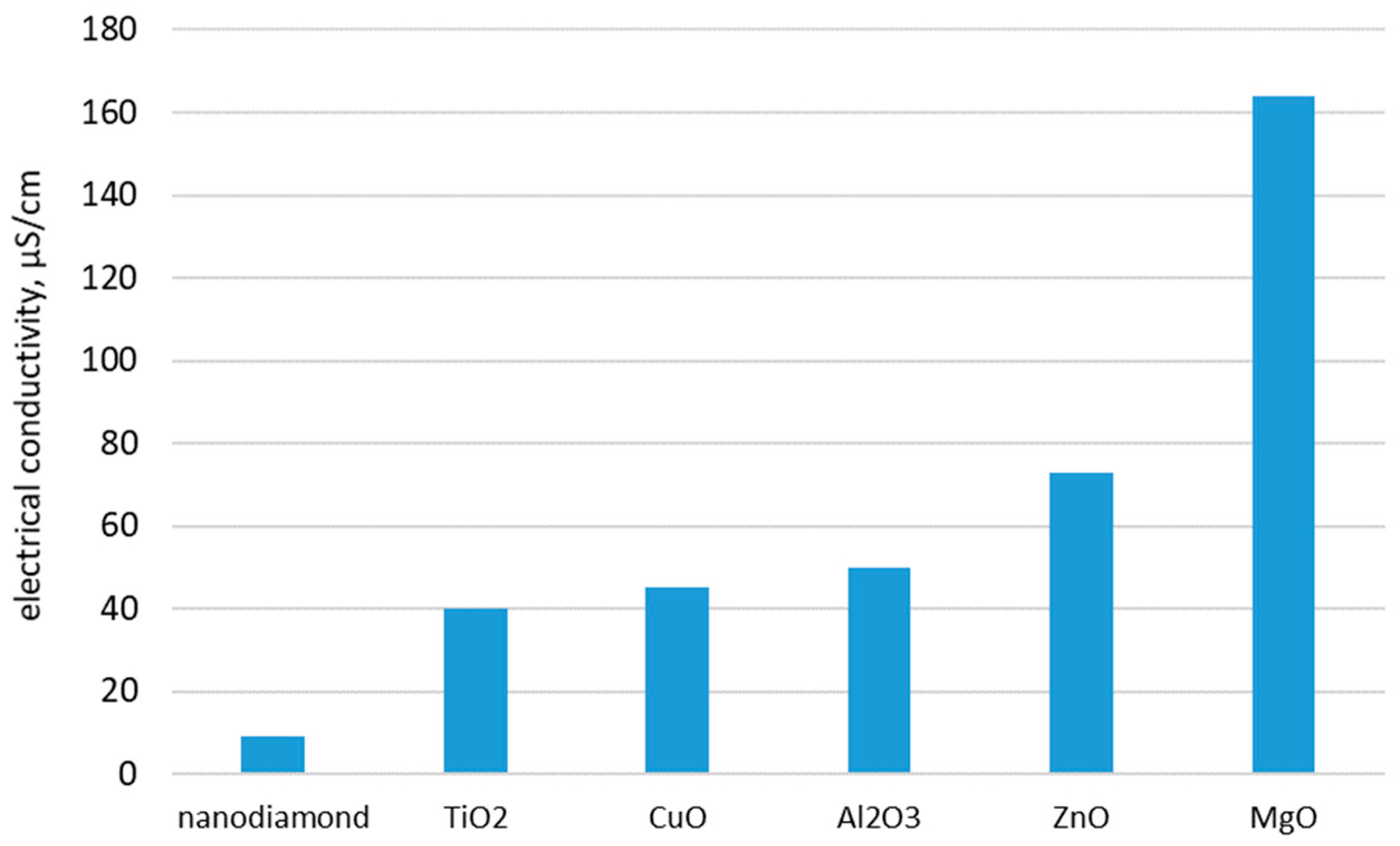
| diamond | Electrical conductivity was found lower than similar concentrations of other nanoparticles. | no | Orion A122 Conductivity Meter (Thermo-Orion, Boston, USA) | Mashali et al. [39] | |
| TiO2 | Enhancement in electrical conductivity in dependence with nanoparticle addition. | yes | digital conductivity meter (Dip cell, Pt plate surface, Model 1054, Amber Science Inc., OR, US) | Modesto-Lopez and Biswas [40] | |
| graphene | Enhancement up to 1400%. | yes | – | Baby and Ramaprabhu [26] | |
| Al2O3 | An increase in electrical conductivity of about 5.5. times compared to water. | yes | CyberScan PC10 | Zakaria et al. [41] | |
| graphene oxide (GO) | Enhancement of electrical conductivity. | yes | BA 380 | Hadadian et al. [42] | |
| Al2O3 | A disagreement was noticed between diverse electrical conductivity models for upper values of Richardson number. | no information provided | – | Selimefendigil and Öztop [43] | |
| Al2O3 | Considerable augmentation of electrical conductivity with volume fraction. | yes | Tetracon | Ganguly et al. [44] | |
| Al2O3 | At room temperature an increase of 379.6% in effective electrical conductivity of nanofluid is detected for 4% alumina. | yes | Multiparameter Consort C 831 | Minea and Luciu [45] Minea [46] | |
| ND-Ni nano-composite | A disagreement was noticed between experimental results and conventional models. | no information provided | two-pole conductivity electrode meter (Mettler-Toledo, USA) | Sundar et al. [47] | |
| TiO2 SiO2 Alumina + titania hybrid alumina + silica hybrid | Large enhancement of electrical conductivity was noticed, depending also on the nanoparticles synergy. | yes | Edge® Multiparameter HI 2030 (Hanna Instruments) | Chereches and Minea [48] | |
| EG–water mixture | TiO2 | Experimental results point out that the Maxwell model is not capable to foretell the electrical conductivity. | yes | IntelliCALTM CDC401 | Islam et al. [49] Islam and Shabani [50] |
| Cu Al2O3 CuO | The Maxwell model under predicts the experiment. | yes | CYBERSCAN CON 11 | Sarojini et al. [51] | |
| SiO2 | The electrical conductivity rises by about 10 times. | yes | Jenco Instruments Inc | Guo et al. [52] | |
| graphene | Electrical conductivity rapidly increased with loading of GONs until 0.07 wt.%. | depending on concentration | Orion™ VERSA STAR™ Multiparameter Benchtop Meter | Ijam et al. [53] | |
| functionalized graphene nanosheets | Electrical conductivity enhanced to a percentage up to 8620%. | yes | – | Kole and Dey [54] | |
| Al2O3 | The change in electrical conductivity is rather low. | no | CyberScan PC10 | Zakaria et al. [41] | |
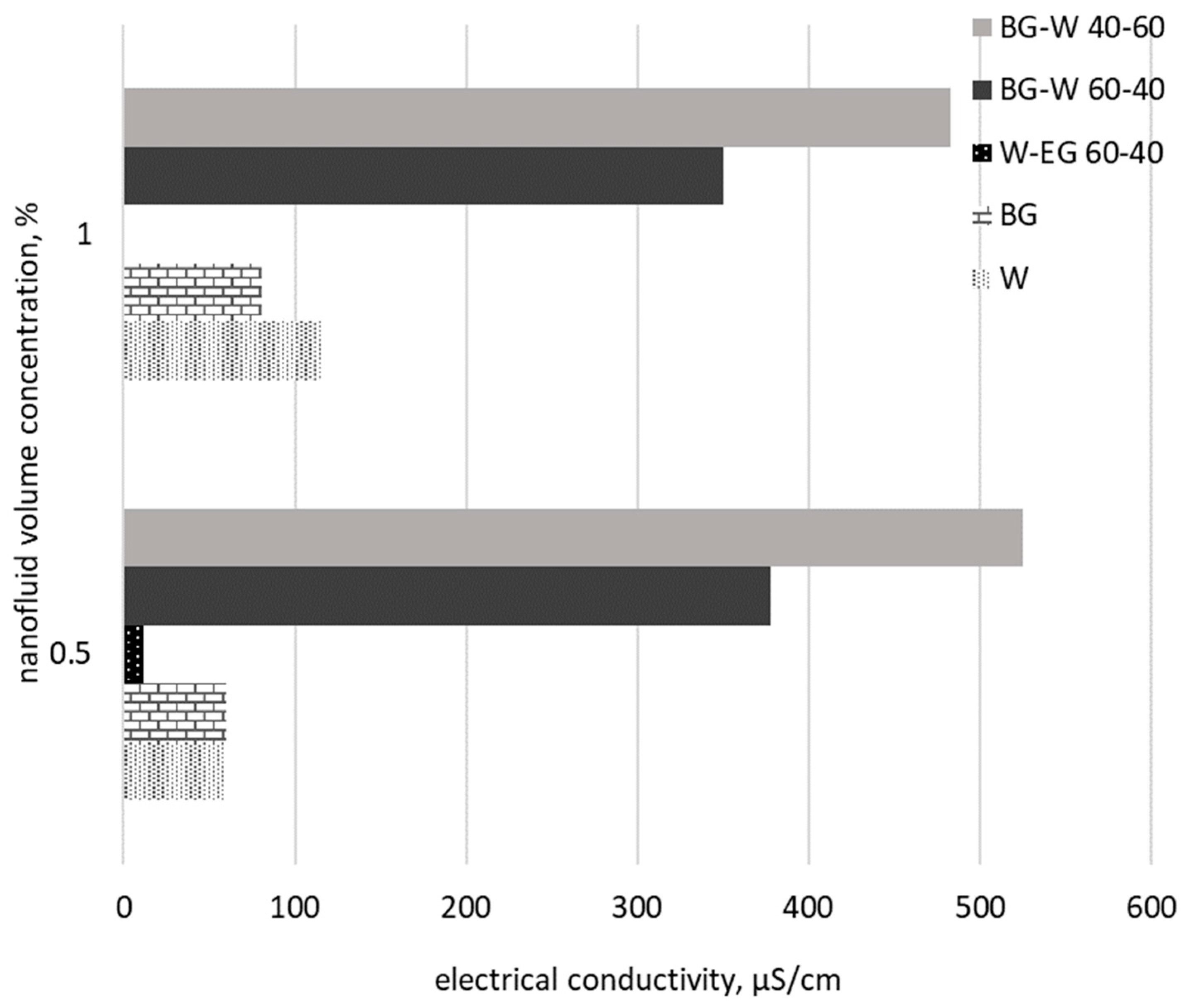
| bio glycol (BG) | Al2O3 | Electrical conductivity increases with temperature. | yes, even if the alumina addition decreases slightly the electrical conductivity of BG | Cyberscan PC-10 | Khdher et al. [55] |
| bio glycol–water mixture | Al2O3 | Electrical conductivity of BG:W in 40%:60% decreased progressively while adding nanoparticles. | no | Cyberscan PC-10 | Abdolbaqi et al. [56] |
| diesel oil | Graphene multi-wall carbon nanotubes (MWCNT) | Nanofluids with functional nanomaterials have inferior electrical conductivity compared to those with non-functional ones. | no, because Diesel has extremely low electrical conductivity | non declared electrical property analyzer | Naddaf and Heris [57] |
| Base Fluid | Electrical Conductivity (µS/cm) | Reference |
|---|---|---|
| EG | 0.12 | Akilu et al. [24] |
| PG | 0.10 | |
| Distilled water | 6 | Zakaria et al. [41] |
| EG | 1.07 | |
| EG | 3.14 | Islam et al. [49] |
| EG-Water 50:50 | 5.03 | |
| Water | 5.44 | Guo et al. [52] |
| EG-Water 20:80 | 4.22 | |
| EG-Water 40:60 | 1.9 | |
| EG-Water 60:40 | 1.47 | |
| EG-Water 80:20 | 1.36 | |
| EG | 0.33 | |
| Distilled water-EG 60:40 | 12.7 | Ijam et al. [53] |
| Distilled water | 6 | Abdolbaqi et al. [56] |
| BG | 45 | |
| BG | 53 | Khdher et al. [55] |
| BG-Water 60:40 | 389 | Abdolbaqi et al. [56] |
| BG-Water 40:60 | 620 | |
| Diesel oil | authors cannot measure it | Naddaf and Heris [57] |
| Base Fluid | Nanoparticle Type | Temperature Influence over Electrical Conductivities Values | Reference |
|---|---|---|---|
| EG | nitrogen doped activated carbon/graphene (NACG) | • maximum enhancement of 11,000% at 30 °C for 0.06%. temperature does not linearly influence the electrical conductivity values, a decrease was noticed at 35 °C and no explanation was provided | Shirazi et al. [22] |
| β-SiC | • maximum enhancement of 53.5% for 1 vol.% the dependence of β-SiC NFs electrical conductivity on temperature can be modelled using an Arrhenius-type equation | Akilu et al. [24] | |
| In2O3 | • the highest increase in electrical conductivity was achieved for 0.0081 vol.% at temperature of 333.15 K and it was 272 times higher than that in case of pure ethylene glycol at 298.15 K. | Fal et al. [25] | |
| water | Fe3O4 | • maximum enhancement of 360% at 65 °C | Bagheli et al. [33] |
| CuO | • The conductivity increases with increasing temperature | Coelho et al. [34] | |
| un-doped and zinc doped cobalt ferrite | • up to 94% enhancement at 308 K the percentage enhancement in electrical conductivity decreases with the increase in temperature, as thermal agitation hinders the percolation behavior | Anu and Hemalatha [35] | |
| Ag SiC Graphene oxide (GO) | • the maximum augmentation occurred in temperature of 25 °C and weight fraction of 0.05% GO maximum enhancement of 15 times higher at 50 °C for 1% SiC | Heyhat and Irannezhad [37] | |
| Fe2O3 | • up to 22% enhancement for 2.5% at 60 °C | Nurdin and Satriananda [38] | |
| Al2O3 | • up to 115% for 3% at 45 °C | Ganguly et al. [44] | |
| Al2O3 | • linear increase with temperature | Minea and Luciu [45] | |
| ND-Ni nano-composite | • linear increase with temperature maximum electrical conductivity enhancement for 0.1% ND–Ni is 1339.81% at 24 °C | Sundar et al. [47] | |
| TiO2 SiO2 alumina + titania hybrid alumina + silica hybrid | • linear increase with temperature | Chereches and Minea [48] | |
| EG-water mixture | TiO2 | • maximum enhancement of 13 times higher for 0.5% at 70 °C | Islam et al. [49] Islam and Shabani [50] |
| Cu Al2O3 CuO | • linear increase of electrical conductivity with temperature. no appreciable improvement of electrical conductivity with temperature for low volume fractions (less than 0.5%) | Sarojini et al. [51] | |
| SiO2 | • up to 10 times at 45 °C for the nanofluid with water | Guo et al. [52] | |
| graphene | • at 25 °C, maximum improvement in electrical conductivity is 1664% at 0.10% concentration | Ijam et al. [53] | |
| bio glycol | Al2O3 | • maximum enhancement of 5112% was obtained by 0.1% Al2O3 at 30 °C temperature linearly influences electrical conductivity | Khdher et al. [55] |
| diesel oil | Graphene MWCNT | • temperature linearly influences electrical conductivity in the range 5–100 °C | Naddaf and Heris [57] |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minea, A.A. A Review on Electrical Conductivity of Nanoparticle-Enhanced Fluids. Nanomaterials 2019, 9, 1592. https://doi.org/10.3390/nano9111592
Minea AA. A Review on Electrical Conductivity of Nanoparticle-Enhanced Fluids. Nanomaterials. 2019; 9(11):1592. https://doi.org/10.3390/nano9111592
Chicago/Turabian StyleMinea, Alina Adriana. 2019. "A Review on Electrical Conductivity of Nanoparticle-Enhanced Fluids" Nanomaterials 9, no. 11: 1592. https://doi.org/10.3390/nano9111592
APA StyleMinea, A. A. (2019). A Review on Electrical Conductivity of Nanoparticle-Enhanced Fluids. Nanomaterials, 9(11), 1592. https://doi.org/10.3390/nano9111592