Hybrid Au/Si Disk-Shaped Nanoresonators on Gold Film for Amplified SERS Chemical Sensing
Abstract
1. Introduction
2. Experimental Details
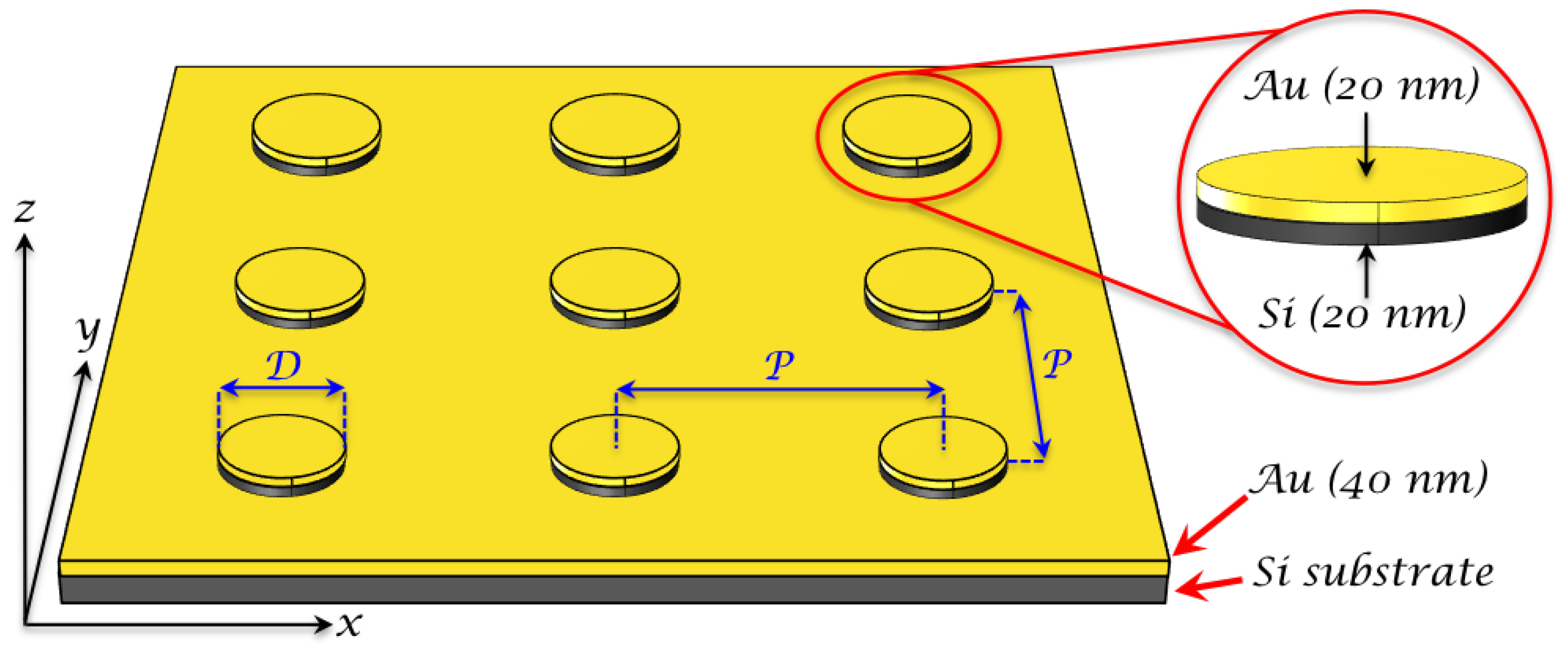
2.1. Fabrication of Hybrid Au/Si Nanodisks
2.2. Thiophenol Functionalization of the Hybrid Au/Si Nanodisks
2.3. Raman Spectroscopy of Hybrid Nanodisks on Gold Film
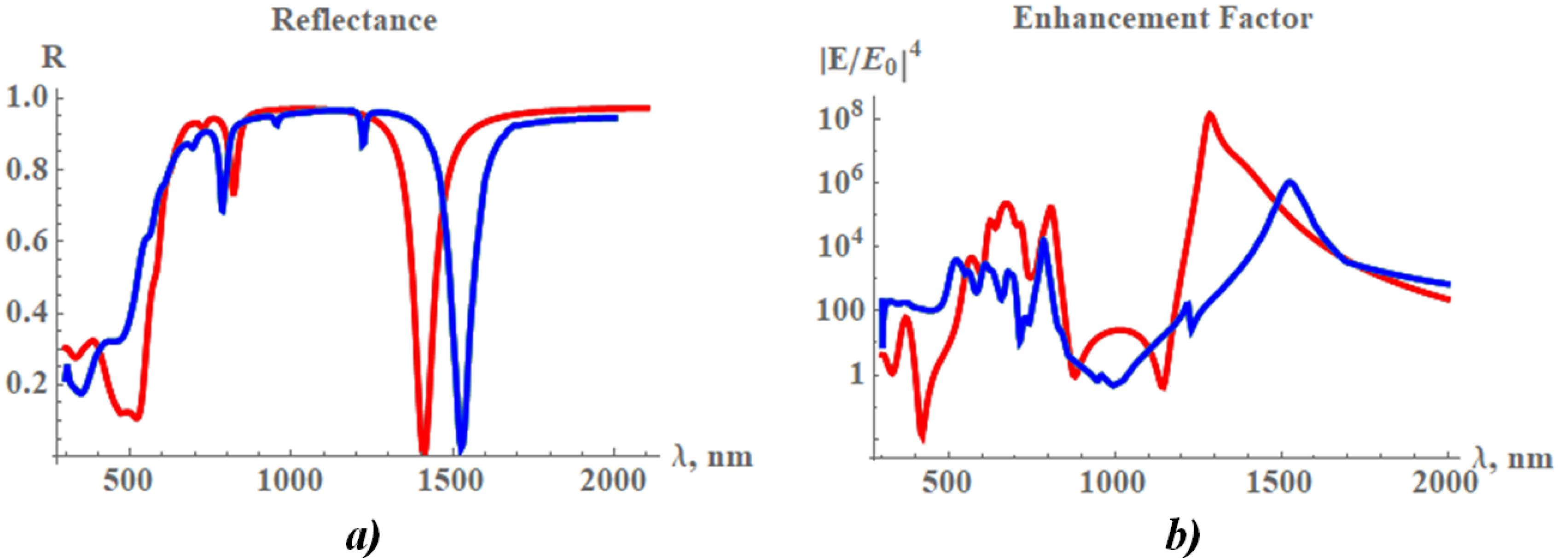
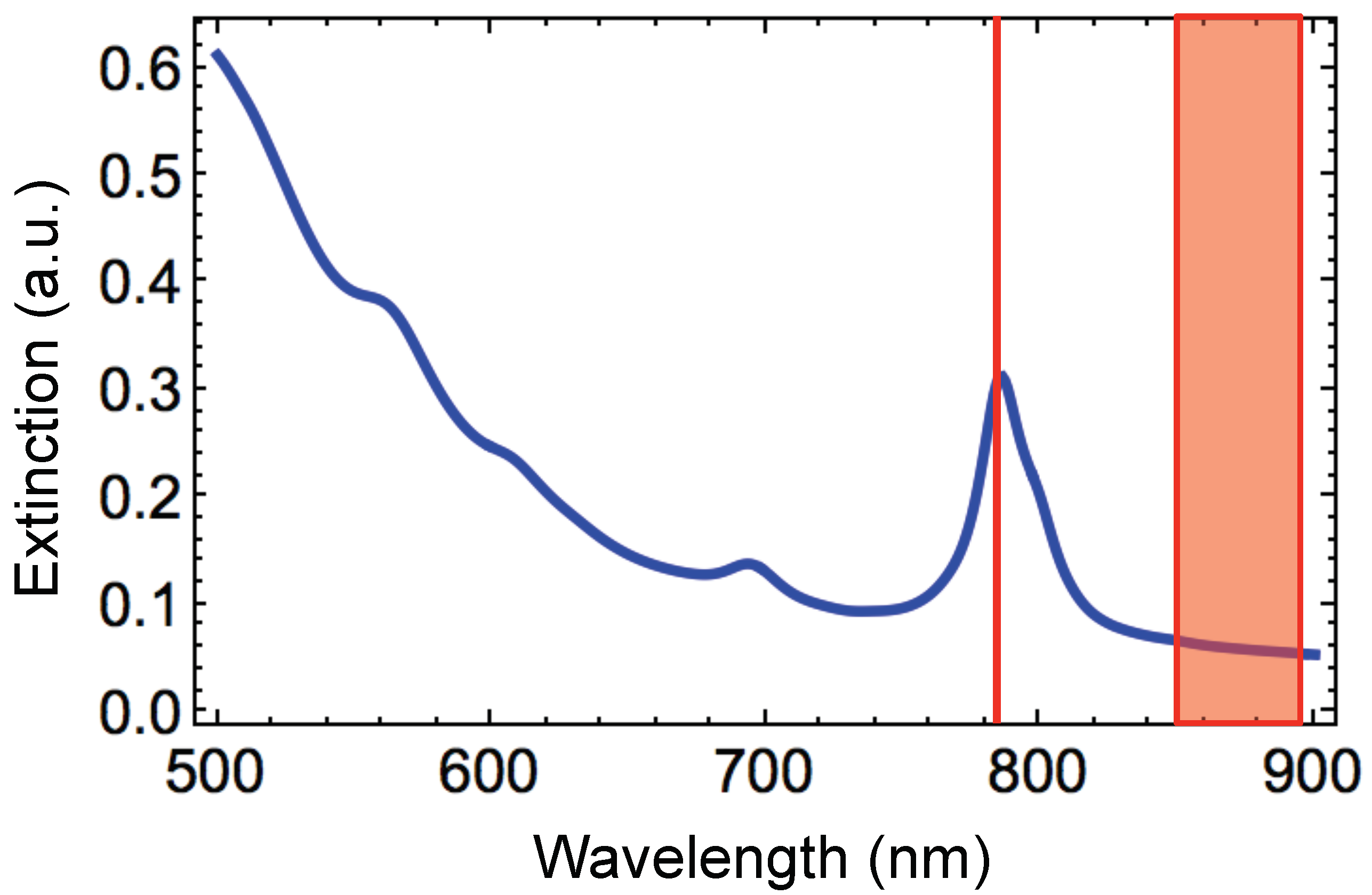
2.4. Plasmon Resonances in Hybrid Nanodisks on Gold Film
3. Results and Discussion
3.1. Fabrication and Functionalization of the Hybrid Disk-Shaped Nanoresonators on Gold Film
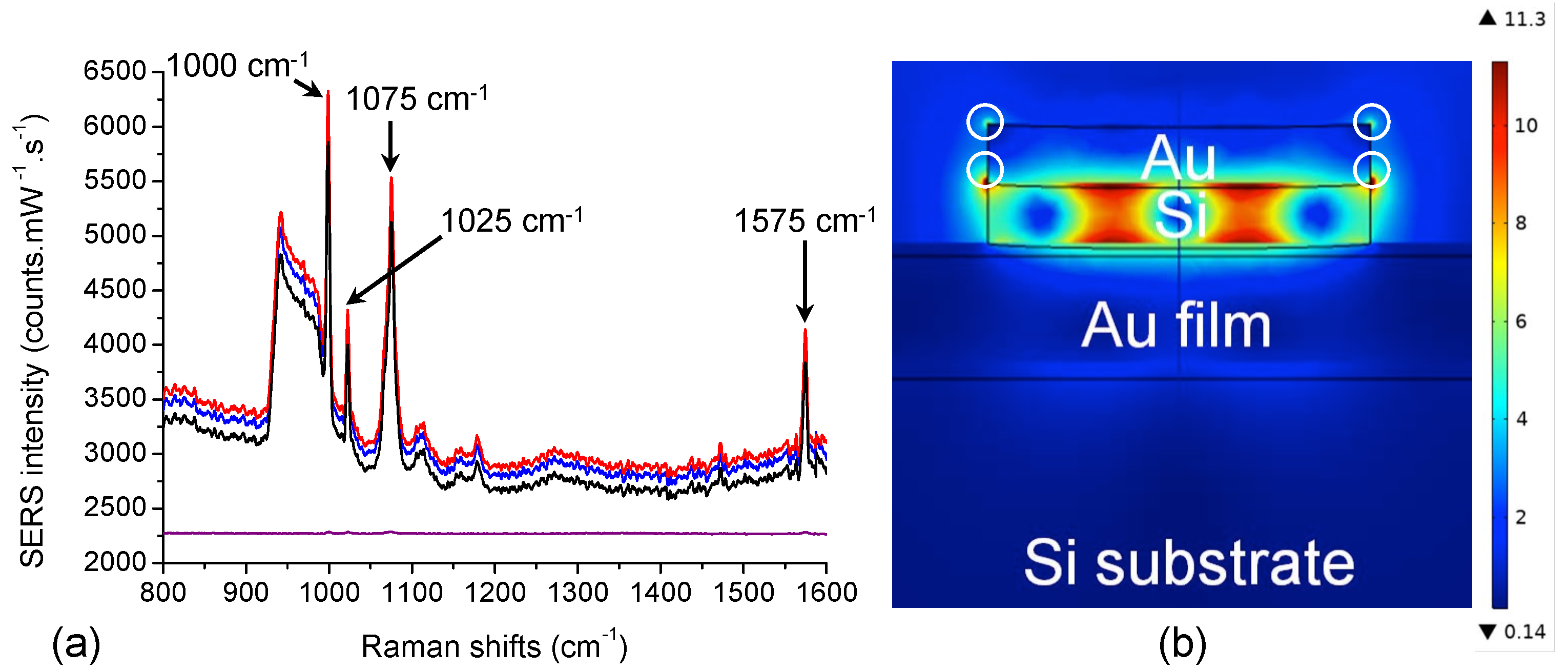
3.2. Sensitivity of the Hybrid Disk-Shaped Nanoresonators and Reproducibility of SERS Signal
3.3. Spectral Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sharma, B.; Frontiera, R.R.; Henry, A.-I.; Ringe, E.; Van Duyne, R.P. SERS: Materials, applications, and the future. Mater. Today 2012, 15, 16–25. [Google Scholar] [CrossRef]
- Ding, S.-Y.; Yi, J.; Li, J.-F.; Ren, B.; Wu, D.-Y.; Panneerselvam, R.; Tian, Z.-Q. Nanostructure-based plasmon-enhanced Raman spectroscopy for surface analysis of materials. Nat. Rev. Mater. 2016, 1, 16021. [Google Scholar] [CrossRef]
- Barbillon, G. Nanoplasmonics-Fundamentals and Applications; InTech: Rijeka, Croatia, 2017; pp. 3–481. [Google Scholar]
- Wustholz, K.L.; Henri, A.-I.; McMahon, J.M.; Freeman, R.G.; Valley, N.; Piotti, M.E.; Natan, M.J.; Schatz, G.C.; Van Duyne, R.P. Structure–Activity Relationships in Gold Nanoparticle Dimers and Trimers for Surface-Enhanced Raman Spectroscopy. J. Am. Chem. Soc. 2010, 132, 10903–10910. [Google Scholar] [CrossRef]
- Itoh, T.; Yamamoto, Y.S.; Ozaki, Y. Plasmon-enhanced spectroscopy of absorption and spontaneous emissions explained using cavity quantum optics. Chem. Soc. Rev. 2017, 49, 3904–3921. [Google Scholar] [CrossRef] [PubMed]
- Ding, S.-Y.; You, E.-M.; Tian, Z.-Q.; Moskovits, M. Electromagnetic theories of surface-enhanced Raman spectroscopy. Chem. Soc. Rev. 2017, 46, 4042–4076. [Google Scholar] [CrossRef] [PubMed]
- Henzie, J.; Lee, J.; Lee, M.H.; Hasan, W.; Odom, T.W. Nanofabrication of Plasmonic Structures. Annu. Rev. Phys. Chem. 2009, 60, 147–165. [Google Scholar] [CrossRef] [PubMed]
- Yu, Q.; Guan, P.; Qin, D.; Golden, G.; Wallace, P.M. Inverted size-dependence of surface-enhanced Raman scattering on gold nanohole and nanodisk arrays. Nano Lett. 2008, 8, 1923–1928. [Google Scholar] [CrossRef]
- Faure, A.C.; Barbillon, G.; Ou, M.; Ledoux, G.; Tillement, O.; Roux, S.; Fabregue, D.; Descamps, A.; Bijeon, J.-L.; Marquette, C.A.; et al. Core/shell nanoparticles for multiple biological detection with enhanced sensitivity and kinetics. Nanotechnology 2008, 19, 485103. [Google Scholar] [CrossRef]
- Bryche, J.-F.; Gillibert, R.; Barbillon, G.; Sarkar, M.; Coutrot, A.-L.; Hamouda, F.; Aassime, A.; Moreau, J.; Lamy de la Chapelle, M.; Bartenlian, B.; et al. Density effect of gold nanodisks on the SERS intensity for a highly sensitive detection of chemical molecules. J. Mater. Sci. 2015, 50, 6601–6607. [Google Scholar] [CrossRef]
- Bryche, J.-F.; Gillibert, R.; Barbillon, G.; Gogol, P.; Moreau, J.; Lamy de la Chapelle, M.; Bartenlian, B.; Canva, M. Plasmonic enhancement by a continuous gold underlayer: Application to SERS sensing. Plasmonics 2016, 11, 601–608. [Google Scholar] [CrossRef]
- Zhang, P.; Yang, S.; Wang, L.; Zhao, J.; Zhu, Z.; Liu, B.; Zhong, J.; Sun, X. Large-scale uniform Au nanodisk arrays fabricated via X-ray interference lithography for reproducible and sensitive SERS substrate. Nanotechnology 2014, 25, 245301. [Google Scholar] [CrossRef] [PubMed]
- Barbillon, G.; Bijeon, J.-L.; Lérondel, G.; Plain, J.; Royer, P. Detection of chemical molecules with integrated plasmonic glass nanotips. Surf. Sci. 2008, 602, L119–L122. [Google Scholar] [CrossRef]
- Dhawan, A.; Duval, A.; Nakkach, M.; Barbillon, G.; Moreau, J.; Canva, M.; Vo-Dinh, T. Deep UV nano-microstructuring of substrates for surface plasmon resonance imaging. Nanotechnology 2011, 22, 165301. [Google Scholar] [CrossRef] [PubMed]
- Guisbert Quilis, N.; Lequeux, M.; Venugopalan, P.; Khan, I.; Knoll, W.; Boujday, S.; Lamy de la Chapelle, M.; Dostalek, J. Tunable laser interference lithography preparation of plasmonic nanoparticle arrays tailored for SERS. Nanoscale 2018, 10, 10268. [Google Scholar] [CrossRef] [PubMed]
- Hwang, J.S.; Yang, M. Sensitive and Reproducible Gold SERS Sensor Based on Interference Lithography and Electrophoretic Deposition. Sensors 2018, 18, 4076. [Google Scholar] [CrossRef] [PubMed]
- Ding, T.; Sigle, D.O.; Herrmann, L.O.; Wolverson, D.; Baumberg, J.J. Nanoimprint lithography of Al Nanovoids for Deep-UV SERS. ACS Appl. Mater. Interfaces 2014, 6, 17358–17363. [Google Scholar] [CrossRef]
- Cottat, M.; Lidgi-Guigui, N.; Tijunelyte, I.; Barbillon, G.; Hamouda, F.; Gogol, P.; Aassime, A.; Lourtioz, J.-M.; Bartenlian, B.; de la Lamy Chapelle, M. Soft UV nanoimprint lithography-designed highly sensitive substrates for SERS detection. Nanoscale Res. Lett. 2014, 9, 623. [Google Scholar] [CrossRef]
- Masson, J.F.; Gibson, K.F.; Provencher-Girard, A. Surface-enhanced Raman spectroscopy amplification with film over etched nanospheres. J. Phys. Chem. C 2010, 114, 22406–22412. [Google Scholar] [CrossRef]
- Bechelany, M.; Brodard, P.; Elias, J.; Brioude, A.; Michler, J.; Philippe, L. Simple Synthetic Route for SERS-Active Gold Nanoparticles Substrate with Controlled Shape and Organization. Langmuir 2010, 26, 14364–14371. [Google Scholar] [CrossRef]
- Bryche, J.-F.; Tsigara, A.; Bélier, B.; Lamy de la Chapelle, M.; Canva, M.; Bartenlian, B.; Barbillon, G. Surface enhanced Raman scattering improvement of gold triangular nanoprisms by a gold reflective underlayer for chemical sensing. Sens. Actuators B 2016, 228, 31–35. [Google Scholar] [CrossRef]
- Barbillon, G.; Noblet, T.; Busson, B.; Tadjeddine, A.; Humbert, C. Localised detection of thiophenol with gold nanotriangles highly structured as honeycombs by nonlinear sum frequency generation spectroscopy. J. Mater. Sci. 2018, 53, 4554–4562. [Google Scholar] [CrossRef]
- Brolo, A.G.; Arctander, E.; Gordon, R.; Leathem, B.; Kavanagh, K.L. Nanohole-Enhanced Raman Scattering. Nano Lett. 2004, 4, 2015–2018. [Google Scholar] [CrossRef]
- Suh, J.Y.; Odom, T.W. Nonlinear properties of nanoscale antennas. Nano Today 2013, 8, 469–479. [Google Scholar] [CrossRef]
- Lim, D.-K.; Jeon, K.-S.; Kim, H.M.; Nam, J.-M.; Suh, Y.D. Nanogop-engineerable Raman-active nanodumbbells for single-molecule detection. Nat. Mater. 2010, 9, 60–67. [Google Scholar] [CrossRef] [PubMed]
- Félidj, N.; Aubard, J.; Lévi, G.; Krenn, J.R.; Hohenau, A.; Schider, G.; Leitner, A.; Aussenegg, F.R. Optimized surface-enhanced Raman scattering on gold nanoparticle arrays. Appl. Phys. Lett. 2003, 82, 3095–3097. [Google Scholar] [CrossRef]
- Guillot, N.; Shen, H.; Frémaux, B.; Péron, O.; Rinnert, E.; Toury, T.; Lamy de la Chapelle, M. Surface enhanced Raman scattering optimization of gold nanocylinder arrays: Influence of the localized surface plasmon resonance and excitation wavelength. Appl. Phys. Lett. 2010, 97, 023113. [Google Scholar] [CrossRef]
- Li, Z.; Butun, S.; Aydin, K. Ultranarrow Band Absorbers Based on Surface Lattice Resonances in Nanostructured Metal Surfaces. ACS Nano 2014, 8, 8242–8248. [Google Scholar] [CrossRef]
- Sarkar, M.; Besbes, M.; Moreau, J.; Bryche, J.-F.; Olivéro, A.; Barbillon, G.; Coutrot, A.-L.; Bartenlian, B.; Canva, M. Hybrid Plasmonic Mode by Resonant Coupling of Localized Plasmons to Propagating Plasmons in a Kretschmann Configuration. ACS Photonics 2015, 2, 237–245. [Google Scholar] [CrossRef]
- Sobhani, A.; Manjavacas, A.; Cao, Y.; McClain, M.J.; Javier Garcia de Abajo, F.; Nordlander, P.; Halas, N.J. Pronounced Linewidth Narrowing of an Aluminum Nanoparticle Plasmon Resonance by Interaction with an Aluminum Metallic Film. Nano Lett. 2015, 15, 6946–6951. [Google Scholar] [CrossRef]
- Yue, W.; Wang, Z.; Whittaker, J.; Lopez-Royo, F.; Yang, Y.; Zayats, A.V. Amplification of surface-enhanced Raman scattering due to substrate-mediated localized surface plasmons in gold nanodimers. J. Mater. Chem. C 2017, 5, 4075–4084. [Google Scholar] [CrossRef]
- Zhou, Q.; Liu, Y.; He, Y.; Zhang, Z.; Zhao, Y. The effect of underlayer thin films on the surface-enhanced Raman scattering response of Ag nanorod substrates. Appl. Phys. Lett. 2010, 97, 121902. [Google Scholar] [CrossRef]
- Driskell, J.D.; Lipert, R.J.; Porter, M.D. Labeled Gold Nanoparticles Immobilized at Smooth Metallic Substrates: Systematic Investigation of Surface Plasmon Resonance and Surface-Enhanced Raman Scattering. J. Phys. Chem. B 2006, 110, 17444–17451. [Google Scholar] [CrossRef] [PubMed]
- Mulvaney, S.P.; He, L.; Natan, M.J.; Keating, C.D. Three-layer substrates for surface-enhanced Raman scattering: Prepartion and preliminary evaluation. J. Raman Spectrosc. 2003, 34, 163–171. [Google Scholar] [CrossRef]
- Galopin, E.; Barbillat, J.; Coffinier, Y.; Szunerits, S.; Patriarche, G.; Boukherroub, R. Silicon nanowires coated with silver nanostructures as ultrasensitive interfaces for surface-enhanced Raman spectroscopy. ACS Appl. Mater. Interfaces 2009, 1, 1396–1403. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.L.; Fan, X.; Zhou, H.W.; Shao, M.W.; Zapien, J.A.; Wong, N.B.; Lee, S.T. A high-efficiency surface-enhanced Raman scattering substrate based on silicon nanowires array decorated with silver nanoparticles. J. Phys. Chem. C 2010, 114, 1969–1975. [Google Scholar] [CrossRef]
- He, Y.; Su, S.; Xu, T.T.; Zhong, Y.L.; Zapien, J.A.; Li, J.; Fan, C.H.; Lee, S.T. Silicon nanowires-based highly-efficient SERS-active platform for ultrasensitive DNA detection. Nano Today 2011, 6, 122–130. [Google Scholar] [CrossRef]
- Schmidt, M.S.; Hübner, J.; Boisen, A. Large area fabrication of leaning silicon nanopillars for surface enhanced Raman spectroscopy. Adv. Mater. 2012, 24, OP11–OP18. [Google Scholar] [CrossRef]
- Akin, M.S.; Yilmaz, M.; Babur, E.; Ozdemir, B.; Erdogan, H.; Tamer, U.; Demirel, G. Large area uniform deposition of silver nanoparticles through bio-inspired polydopamine coating on silicon nanowire arrays for pratical SERS applications. J. Mater. Chem. B 2014, 2, 4894–4900. [Google Scholar] [CrossRef]
- Bryche, J.-F.; Bélier, B.; Bartenlian, B.; Barbillon, G. Low-cost SERS substrates composed of hybrid nanoskittles for a highly sensitive sensing of chemical molecules. Sens. Actuators B 2017, 239, 795–799. [Google Scholar] [CrossRef]
- Magno, G.; Bélier, B.; Barbillon, G. Gold thickness impact on the enhancement of SERS detection in low-cost Au/Si nanosensors. J. Mater. Sci. 2017, 52, 13650–13656. [Google Scholar] [CrossRef]
- Magno, G.; Bélier, B.; Barbillon, G. Al/Si nanopillars as very sensitive SERS substrates. Materials 2018, 11, 1534. [Google Scholar] [CrossRef] [PubMed]
- Barbillon, G. Fabrication and SERS Performances of Metal/Si and Metal/ZnO Nanosensors: A Review. Coatings 2019, 9, 86. [Google Scholar] [CrossRef]
- Lagarkov, A.; Boginkaya, I.; Bykov, I.; Budashov, I.; Ivanov, A.; Kurochkin, I.; Ryzhikov, I.; Rodionov, I.; Sedova, M.; Zverev, A.; et al. Light localization and SERS in tip-shaped silicon metasurface. Opt. Express 2017, 25, 17021–17038. [Google Scholar] [CrossRef] [PubMed]
- Sarychev, A.K.; Ivanov, A.; Lagarkov, A.; Barbillon, G. Light Concentration by Metal-Dielectric Micro-Resonators for SERS Sensing. Materials 2019, 12, 103. [Google Scholar] [CrossRef]
- Kanipe, K.N.; Chidester, P.P.F.; Stucky, G.D.; Meinhart, C.D.; Moskovits, M. Properly Structured, Any Metal Can Produce Intense Surface Enhanced Raman Spectra. J. Phys. Chem. C 2017, 121, 14269–14273. [Google Scholar] [CrossRef]
- Whelan, C.M.; Smyth, M.R.; Barnes, C.J. HREELS, XPS, and Electrochemical Study of Benzenethiol Adsorption on Au(111). Langmuir 1999, 15, 116–126. [Google Scholar] [CrossRef]
- Lu, G.; Xu, J.; Wen, T.; Zhang, W.; Zhao, J.; Hu, A.; Barbillon, G.; Gong, Q. Hybrid Metal-Dielectric Nano-Aperture Antenna for Surface Enhanced Fluorescence. Materials 2018, 11, 1435. [Google Scholar] [CrossRef]
- Zambrana-Puyalto, X.; Ponzellini, P.; Maccaferri, N.; Tessarolo, E.; Pelizzo, M.G.; Zhang, W.; Barbillon, G.; Lu, G.; Garoli, D. A hybrid metal-dielectric zero mode waveguide for enhanced single molecule detection. Chem. Commun. 2019, 55, 9725–9728. [Google Scholar] [CrossRef]
- Colas, F.; Barchiesi, D.; Kessentini, S.; Toury, T.; Lamy de la Chapelle, M. Comparison of adhesion layers of gold on silicate glasses for SERS detection. J. Opt. 2015, 17, 114010. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- McPeak, K.M.; Jayanti, S.V.; Kress, S.J.P.; Meyer, S.; Iotti, S.; Rossinelli, A.; Norris, D.J. Plasmonic Films Can Easily Be Better: Rules and Recipes. ACS Photonics 2015, 2, 326–333. [Google Scholar] [CrossRef] [PubMed]
- Schinke, C.; Peest, P.C.; Schmidt, J.; Brendel, R.; Bothe, K.; Vogt, M.R.; Kröger, I.; Winter, S.; Schirmacher, A.; Lim, S.; et al. Uncertainty analysis for the coefficient of band-to-band absorption of crystalline silicon. AIP Adv. 2015, 5, 067168. [Google Scholar] [CrossRef]
- Manjare, M.; Wang, F.; Rodrigo, S.G.; Harutyunyan, H. Exposing optical near fields of plasmonic patch nanoantennas. Appl. Phys. Lett. 2017, 111, 221106. [Google Scholar] [CrossRef]
- Scalora, M.; Vincenti, M.A.; de Ceglia, D.; Grande, M.; Haus, J.W. Raman scattering near metal nanostructures. J. Opt. Soc. Am. B 2012, 29, 2035–2045. [Google Scholar] [CrossRef]
- Tetsassi Feugmo, C.G.; Liégeois, V. Analyzing the vibrational signatures of thiophenol adsorbed on small gold clusters by DFT calculations. ChemPhysChem 2013, 14, 1633–1645. [Google Scholar] [CrossRef]
- Li, S.; Wu, D.; Xu, X.; Gu, R. Theoretical and experimental studies on the adsorption behavior of thiophenol on gold nanoparticles. J. Raman Spectrosc. 2007, 38, 1436–1443. [Google Scholar] [CrossRef]
- Temple, P.A.; Hathaway, C.E. Multiphonon Raman Spectrum of Silicon. Phys. Rev. B 1973, 7, 3685–3697. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Walia, J.; Saini, S.S. Enhanced first-order Raman scattering from arrays of vertical silicon nanowires. Nanotechnology 2012, 23, 275706. [Google Scholar] [CrossRef]
- Stern, D.A.; Wellner, E.; Salaita, G.N.; Laguren-Davidson, L.; Lu, F.; Batina, N.; Frank, D.G.; Zapien, D.C.; Walton, N.; Hubbard, A.T. Adsorbed Thiophenol and Related-Compounds Studied at Pt(111) Electrodes by EELS, Auger Spectroscopy and Cyclic Voltammetry. J. Am. Chem. Soc. 1988, 110, 4885–4893. [Google Scholar] [CrossRef]
- Caldwell, J.D.; Glembocki, O.; Bezares, F.J.; Bassim, N.D.; Rendell, R.W.; Feygelson, M.; Ukaegbu, M.; Kasica, R.; Shirey, L.; Hosten, C. Plasmonic Nanopillar Arrays for Large-Area, High-Enhancement Surface-Enhanced Raman Scattering Sensors. ACS Nano 2011, 5, 4046–4055. [Google Scholar] [CrossRef]
- Alvarez-Puebla, R.A. Effects of the Excitation Wavelength on the SERS Spectrum. J. Phys. Chem. Lett. 2012, 3, 857–866. [Google Scholar] [CrossRef] [PubMed]
- Le Ru, E.C.; Blackie, E.J.; Meyer, M.; Etchegoin, P.G. Surface enhanced Raman scattering enhancement factors: A comprehensive study. J. Phys. Chem. C 2007, 111, 13794–13803. [Google Scholar] [CrossRef]
- Zheng, M.; Zhu, X.; Chen, Y.; Xiang, Q.; Duan, H. Three-dimensional donut-like gold nanorings with multiple hot spots for surface-enhanced Raman spectroscopy. Nanotechnology 2017, 28, 0453503. [Google Scholar] [CrossRef] [PubMed]
- Etchegoin, P.G.; Le Ru, E.C. Basic Electromagnetic Theory of SERS. In Surface Enhanced Raman Spectroscopy: Analytical, Biophysical and Life Science Applications; Schlücker, S., Ed.; Wiley-VCH: Weinheim, Germany, 2011; pp. 1–34. ISBN 978-3-527-32567-2. [Google Scholar]

| Number | RS (cm) | RSD (%) | EF | EF (a.u.) | |||
|---|---|---|---|---|---|---|---|
| 1 | 1000 | 852 | 79 | 3533 | 4.9 | 5.9 × 10 | 0.0198 |
| 2 | 1025 | 854 | 32 | 1402 | 4.1 | 5.8 × 10 | 0.0192 |
| 3 | 1075 | 857 | 55 | 2350 | 4.7 | 5.6 × 10 | 0.0186 |
| 4 | 1575 | 896 | 18 | 724 | 5.0 | 5.3 × 10 | 0.0170 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbillon, G.; Ivanov, A.; Sarychev, A.K. Hybrid Au/Si Disk-Shaped Nanoresonators on Gold Film for Amplified SERS Chemical Sensing. Nanomaterials 2019, 9, 1588. https://doi.org/10.3390/nano9111588
Barbillon G, Ivanov A, Sarychev AK. Hybrid Au/Si Disk-Shaped Nanoresonators on Gold Film for Amplified SERS Chemical Sensing. Nanomaterials. 2019; 9(11):1588. https://doi.org/10.3390/nano9111588
Chicago/Turabian StyleBarbillon, Grégory, Andrey Ivanov, and Andrey K. Sarychev. 2019. "Hybrid Au/Si Disk-Shaped Nanoresonators on Gold Film for Amplified SERS Chemical Sensing" Nanomaterials 9, no. 11: 1588. https://doi.org/10.3390/nano9111588
APA StyleBarbillon, G., Ivanov, A., & Sarychev, A. K. (2019). Hybrid Au/Si Disk-Shaped Nanoresonators on Gold Film for Amplified SERS Chemical Sensing. Nanomaterials, 9(11), 1588. https://doi.org/10.3390/nano9111588






