A Diamond Temperature Sensor Based on the Energy Level Shift of Nitrogen-Vacancy Color Centers
Abstract
1. Introduction
2. Experiments and Methods
3. Results and Discussion
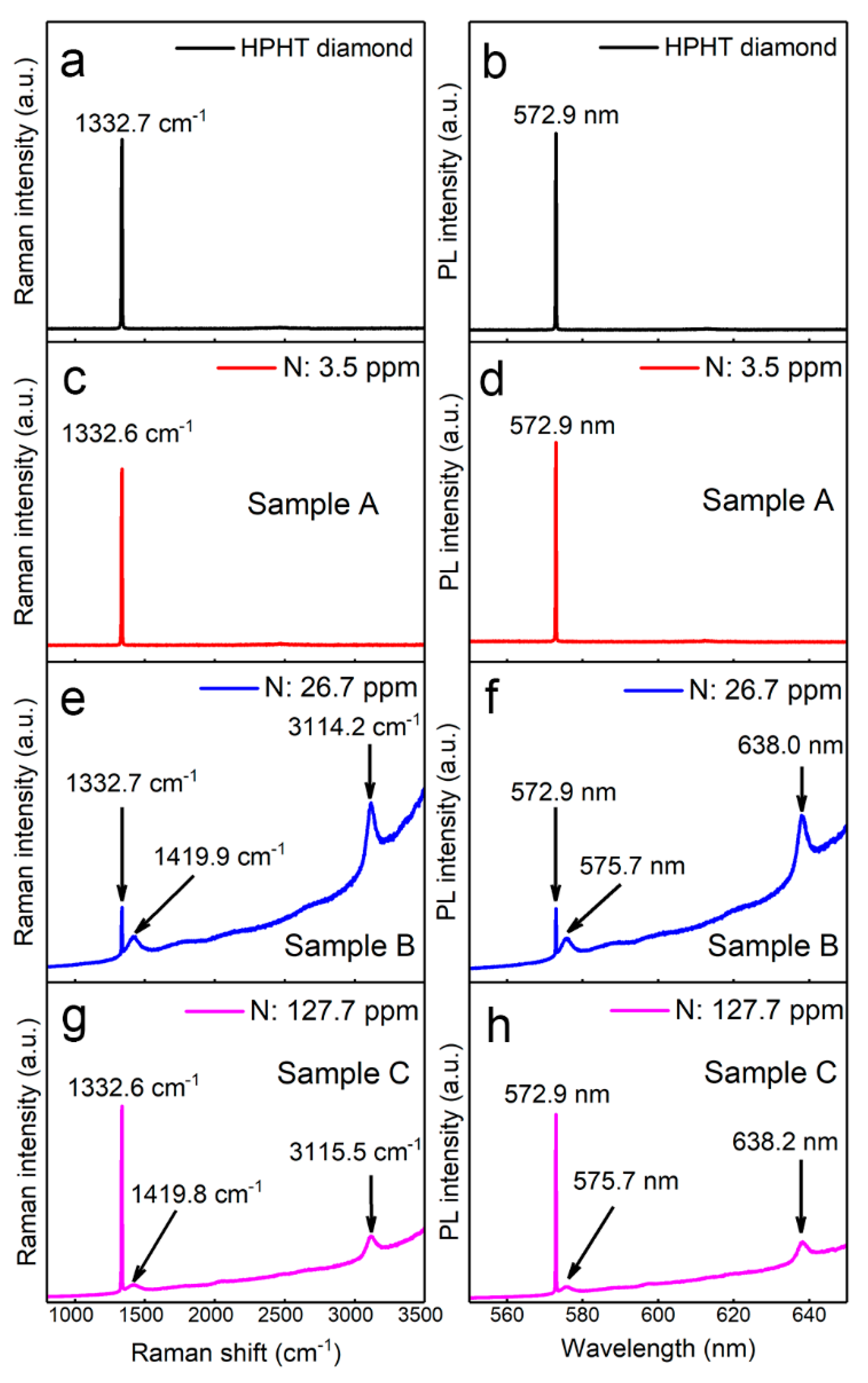
3.1. Raman and PL Spectroscopy of Different Diamond Samples
3.2. Raman and PL Characterization of NV Centers under Different Temperatures
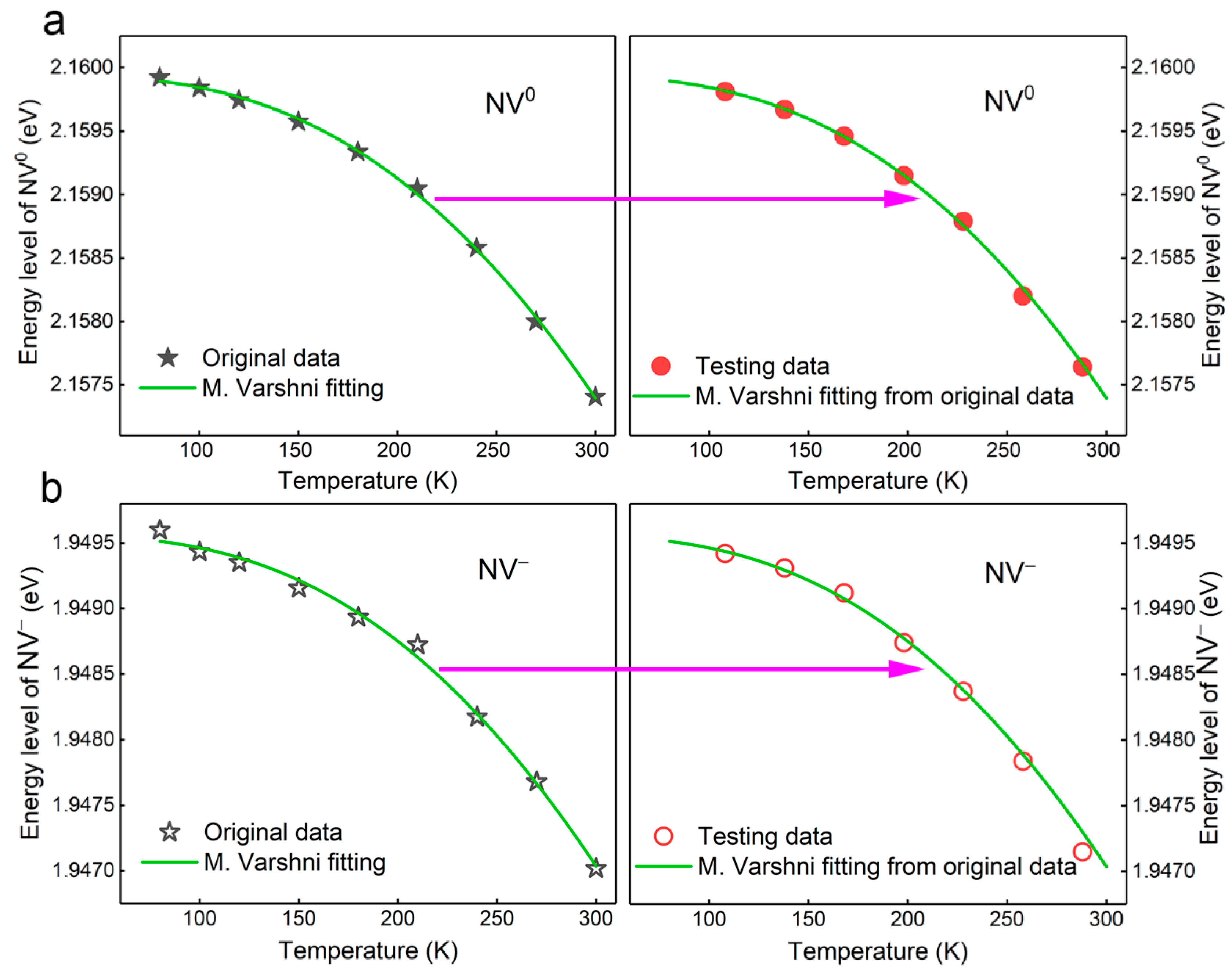
3.3. The Dependence of Energy Level Shifts of NV Centers to Temperature
3.4. The Determination of NV Centers in Temperature Measurement
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Wrachtrup, J.; Jelezko, F. Processing quantum information in diamond. J. Phys. Condens. Matter 2006, 18, S807–S824. [Google Scholar] [CrossRef]
- Liu, G.Q.; Pan, X.Y. Quantum information processing with nitrogen-vacancy centers in diamond. Chin. Phys. B 2018, 27, 020304. [Google Scholar] [CrossRef]
- Gruber, A.; Drabenstedt, A.; Tietz, C.; Fleury, L.; Wrachtrup, J.; von Borczyskowski, C. Scanning confocal optical microscopy and magnetic resonance on single defect centers. Science 1997, 276, 2012–2014. [Google Scholar] [CrossRef]
- Fuchs, G.D.; Dobrovitski, V.V.; Toyli, D.M.; Heremans, F.J.; Awschalom, D.D. Gigahertz Dynamics of a Strongly Driven Single Quantum Spin. Science 2009, 326, 1520–1522. [Google Scholar] [CrossRef]
- Jelezko, F.; Gaebel, T.; Popa, I.; Domhan, M.; Gruber, A.; Wrachtrup, J. Observation of coherent oscillation of a single nuclear spin and realization of a two-qubit conditional quantum gate. Phys. Rev. Lett. 2004, 93, 130501. [Google Scholar] [CrossRef]
- Jelezko, F.; Wrachtrup, J. Read-out of single spins by optical spectroscopy. J. Phys. Condens. Matter 2004, 16, R1089–R1104. [Google Scholar] [CrossRef]
- Gurudev Dutt, M.V.; Childress, L.; Jiang, L.; Togan, E.; Maze, J.; Jelezko, F.; Zibrov, A.S.; Hemmer, P.R.; Lukin, M.D. Quantum register based on individual electronic and nuclear spin qubits in diamond. Science 2007, 316, 1312–1316. [Google Scholar] [CrossRef]
- Maze, J.R.; Stanwix, P.L.; Hodges, J.S.; Hong, S.; Taylor, J.M.; Cappellaro, P.; Jiang, L.; Dutt, M.V.G.; Togan, E.; Zibrov, A.S.; et al. Nanoscale magnetic sensing with an individual electronic spin in diamond. Nature 2008, 455, 644–647. [Google Scholar] [CrossRef]
- Acosta, V.M.; Bauch, E.; Ledbetter, M.P.; Waxman, A.; Bouchard, L.S.; Budker, D. Temperature dependence of the nitrogen-vacancy magnetic resonance in diamond. Phys. Rev. Lett. 2010, 104, 070801. [Google Scholar] [CrossRef]
- Acosta, V.M.; Bauch, E.; Ledbetter, M.P.; Santori, C.; Fu, K.M.C.; Barclay, P.E.; Beausoleil, R.G.; Linget, H.; Roch, J.F.; Treussart, F.; et al. Diamonds with a high density of nitrogen-vacancy centers for magnetometry applications. Phys. Rev. B 2009, 80, 115202. [Google Scholar] [CrossRef]
- Tetienne, J.P.; Hingant, T.; Kim, J.V.; Diez, L.H.; Adam, J.P.; Garcia, K.; Roch, J.F.; Rohart, S.; Thiaville, A.; Ravelosona, D.; et al. Nanoscale imaging and control of domain-wall hopping with a nitrogen-vacancy center microscope. Science 2014, 344, 1366–1369. [Google Scholar] [CrossRef] [PubMed]
- Beams, R.; Smith, D.; Johnson, T.W.; Oh, S.H.; Novotny, L.; Vamivakas, A.N. Nanoscale Fluorescence Lifetime Imaging of an Optical Antenna with a Single Diamond NV Center. Nano Lett. 2013, 13, 3807–3811. [Google Scholar] [CrossRef] [PubMed]
- Pfaff, W.; Hensen, B.J.; Bernien, H.; van Dam, S.B.; Blok, M.S.; Taminiau, T.H.; Tiggelman, M.J.; Schouten, R.N.; Markham, M.; Twitchen, D.J.; et al. Unconditional quantum teleportation between distant solid-state quantum bits. Science 2014, 345, 532–535. [Google Scholar] [CrossRef]
- Doherty, M.W.; Struzhkin, V.V.; Simpson, D.A.; McGuinness, L.P.; Meng, Y.; Stacey, A.; Karle, T.J.; Hemley, R.J.; Manson, N.B.; Hollenberg, L.C.; et al. Electronic properties and metrology applications of the diamond NV− center under pressure. Phys. Rev. Lett. 2014, 112, 047601. [Google Scholar] [CrossRef]
- Sotoma, S.; Epperla, C.P.; Chang, H.C. Diamond Nanothermometry. Chemnanomat 2018, 4, 15–27. [Google Scholar] [CrossRef]
- Davies, G.; Hamer, M.F. Optical Studies of the 1.945 eV Vibronic Band in Diamond. Proc. R. Soc. A Math. Phys. Eng. Sci. 1976, 348, 285–298. [Google Scholar] [CrossRef]
- Mita, Y. Change of absorption spectra in type-Ib diamond with heavy neutron irradiation. Phys. Rev. B 1996, 53, 11360–11364. [Google Scholar] [CrossRef]
- Loubser, J.; Vanwyk, J.A. Electron-Spin Resonance in Study of Diamond. Rep. Prog. Phys. 1978, 41, 1201–1248. [Google Scholar] [CrossRef]
- Davies, G. Dynamic Jahn-Teller distortions at trigonal optical-centers in diamond. J. Phys. C Solid State Phys. 1979, 12, 2551–2566. [Google Scholar] [CrossRef]
- Breeding, C.M.; Shigley, J.E. The “TYPE” Classification System of Diamonds and its Importance in Gemology. Gems Gemol. 2009, 45, 96–111. [Google Scholar] [CrossRef]
- Meijer, J.; Burchard, B.; Domhan, M.; Wittmann, C.; Gaebel, T.; Popa, I.; Jelezko, F.; Wrachtrup, J. Generation of single-color centers by focused nitrogen implantation. Appl. Phys. Lett. 2005, 87, 261909. [Google Scholar] [CrossRef]
- Dyer, H.B.; Preez, L.D. Irradiation Damage in Type I Diamond. J. Chem. Phys. 1965, 42, 1898–1906. [Google Scholar] [CrossRef]
- Ermakova, A.; Pramanik, G.; Cai, J.M.; Algara-Siller, G.; Kaiser, U.; Weil, T.; Tzeng, Y.K.; Chang, H.C.; McGuinness, L.P.; Plenio, M.B.; et al. Detection of a Few Metallo-Protein Molecules Using Color Centers in Nanodiamonds. Nano Lett. 2013, 13, 3305–3309. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, W.W.W.; Hui, Y.Y.; Tsai, P.C.; Chang, H.C. Fluorescent Nanodiamond: A Versatile Tool for Long-Term Cell Tracking, Super-Resolution Imaging, and Nanoscale Temperature Sensing. Acc. Chem. Res. 2016, 49, 400–407. [Google Scholar] [CrossRef] [PubMed]
- Kask, P.; Palo, K.; Ullmann, D.; Gall, K. Fluorescence-intensity distribution analysis and its application in biomolecular detection technology. Proc. Natl. Acad. Sci. USA 1999, 96, 13756–13761. [Google Scholar] [CrossRef] [PubMed]
- Doherty, M.W.; Acosta, V.M.; Jarmola, A.; Barson, M.S.J.; Manson, N.B.; Budker, D.; Hollenberg, L.C.L. Temperature shifts of the resonances of the NV− center in diamond. Phys. Rev. B 2014, 90, 041201. [Google Scholar] [CrossRef]
- Plakhotnik, T.; Doherty, M.W.; Cole, J.H.; Chapman, R.; Manson, N.B. All-Optical Thermometry and Thermal Properties of the Optically Detected Spin Resonances of the NV− Center in Nanodiamond. Nano Lett. 2014, 14, 4989–4996. [Google Scholar] [CrossRef]
- Chen, X.D.; Dong, C.H.; Sun, F.W.; Zou, C.L.; Cui, J.M.; Han, Z.F.; Guo, G.C. Temperature dependent energy level shifts of nitrogen-vacancy centers in diamond. Appl. Phys. Lett. 2011, 99, 161903. [Google Scholar] [CrossRef]
- Bhosale, J.; Ramdas, A.K.; Burger, A.; Munoz, A.; Romero, A.H.; Cardona, M.; Lauck, R.; Kremer, R.K. Temperature dependence of band gaps in semiconductors: Electron-phonon interaction. Phys. Rev. B 2012, 86, 195208. [Google Scholar] [CrossRef]
- Odonnell, K.P.; Chen, X. Temperature dependence of semiconductor band gaps. Appl. Phys. Lett. 1991, 58, 2924–2926. [Google Scholar] [CrossRef]
- Kingsmith, R.D.; Needs, R.J.; Heine, V.; Hodgson, M.J. A First-Principle Calculation of the Temperature Dependence of the Indirect Band-Gap of Silicon. EPL (Europhys. Lett.) 1989, 10, 569–574. [Google Scholar] [CrossRef]
- Lautenschlager, P.; Allen, P.B.; Cardona, M. Temperature Dependence of Band Gaps in Si and Ge. Phys. Rev. B 1985, 31, 2163–2171. [Google Scholar] [CrossRef] [PubMed]
- Varshni, Y.P. Temperature dependence of energy gap in semiconductors. Physica 1967, 34, 149–154. [Google Scholar] [CrossRef]
- Klein, C.A.; Hartnett, T.M.; Robinson, C.J. Critical-point phonon frequencies of diamond. Phys. Rev. B 1992, 45, 12854–12863. [Google Scholar] [CrossRef]
- Sato, T.; Ohashi, K.; Sudoh, T.; Haruna, K.; Maeta, H. Thermal expansion of a high purity synthetic diamond single crystal at low temperatures. Phys. Rev. B 2002, 65, 092102. [Google Scholar] [CrossRef]
- Nath, N.N. The dynamical theory of the diamond lattice. I. Proc. Indian Acad. Sci. Sect. A 1935, 2, 143–152. [Google Scholar] [CrossRef]
- Wang, K.Y.; Li, Z.H.; Zhang, B.; Zhu, Y.M. Investigation of vibronic structures of optical centres in diamond by photoluminescence spectra. Acta Phys. Sin. 2012, 61, 127804. [Google Scholar]
- Wang, K.; Steeds, J.W.; Li, Z.; Tian, Y. Photoluminescence Studies of Both the Neutral and Negatively Charged Nitrogen-Vacancy Center in Diamond. Microsc. Microanal. 2016, 22, 108–112. [Google Scholar] [CrossRef]
- Li, C.C.; Gong, M.; Chen, X.D.; Li, S.; Zhao, B.W.; Dong, Y.; Guo, G.C.; Sun, F.W. Temperature dependent energy gap shifts of single color center in diamond based on modified Varshni equation. Diam. Relat. Mater. 2017, 74, 119–124. [Google Scholar] [CrossRef]


| Varshni Model | E0 (eV) | α (eV/K) | β (K) | R2 | |
| NV0 | 2.16021 | 1.68396 × 105 | 5.64457 × 1012 | 0.98848 | |
| NV− | 1.94983 | 1.79467 × 105 | 6.06312 × 1012 | 0.98676 | |
| Modified Varshni Model | E0 (eV) | A (eV/K2) | B (K) | R2 | |
| NV0 | 2.15994 | 6.94965 × 10−8 | 170.30905 | 0.99918 | |
| NV− | 1.94956 | 6.72722 × 10−8 | 164.62925 | 0.99605 |
| Setting temperature (K) | 108 | 138 | 168 | 198 | 228 | 258 | 288 | |
| NV0 | Calculated temperature (K) | 110.1 | 138.8 | 167.6 | 198.2 | 225.7 | 261.3 | 289.1 |
| Error | 1.94% | 0.58% | −0.24% | 0.10% | −1.01% | 1.28% | 0.38% | |
| NV− | Calculated temperature (K) | 109.8 | 135.6 | 162.7 | 200.9 | 228.7 | 260.8 | 294.9 |
| Error | −1.67% | −1.74% | −3.15% | 1.46% | 0.31% | 1.08% | 2.40% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Yuan, Q.; Gao, J.; Shu, S.; Chen, F.; Sun, H.; Nishimura, K.; Wang, S.; Yi, J.; Lin, C.-T.; et al. A Diamond Temperature Sensor Based on the Energy Level Shift of Nitrogen-Vacancy Color Centers. Nanomaterials 2019, 9, 1576. https://doi.org/10.3390/nano9111576
Yang M, Yuan Q, Gao J, Shu S, Chen F, Sun H, Nishimura K, Wang S, Yi J, Lin C-T, et al. A Diamond Temperature Sensor Based on the Energy Level Shift of Nitrogen-Vacancy Color Centers. Nanomaterials. 2019; 9(11):1576. https://doi.org/10.3390/nano9111576
Chicago/Turabian StyleYang, Mingyang, Qilong Yuan, Jingyao Gao, Shengcheng Shu, Feiyue Chen, Huifang Sun, Kazuhito Nishimura, Shaolong Wang, Jian Yi, Cheng-Te Lin, and et al. 2019. "A Diamond Temperature Sensor Based on the Energy Level Shift of Nitrogen-Vacancy Color Centers" Nanomaterials 9, no. 11: 1576. https://doi.org/10.3390/nano9111576
APA StyleYang, M., Yuan, Q., Gao, J., Shu, S., Chen, F., Sun, H., Nishimura, K., Wang, S., Yi, J., Lin, C.-T., & Jiang, N. (2019). A Diamond Temperature Sensor Based on the Energy Level Shift of Nitrogen-Vacancy Color Centers. Nanomaterials, 9(11), 1576. https://doi.org/10.3390/nano9111576






