Simultaneous Generation of Complex Structured Curve Beam
Abstract
1. Introduction
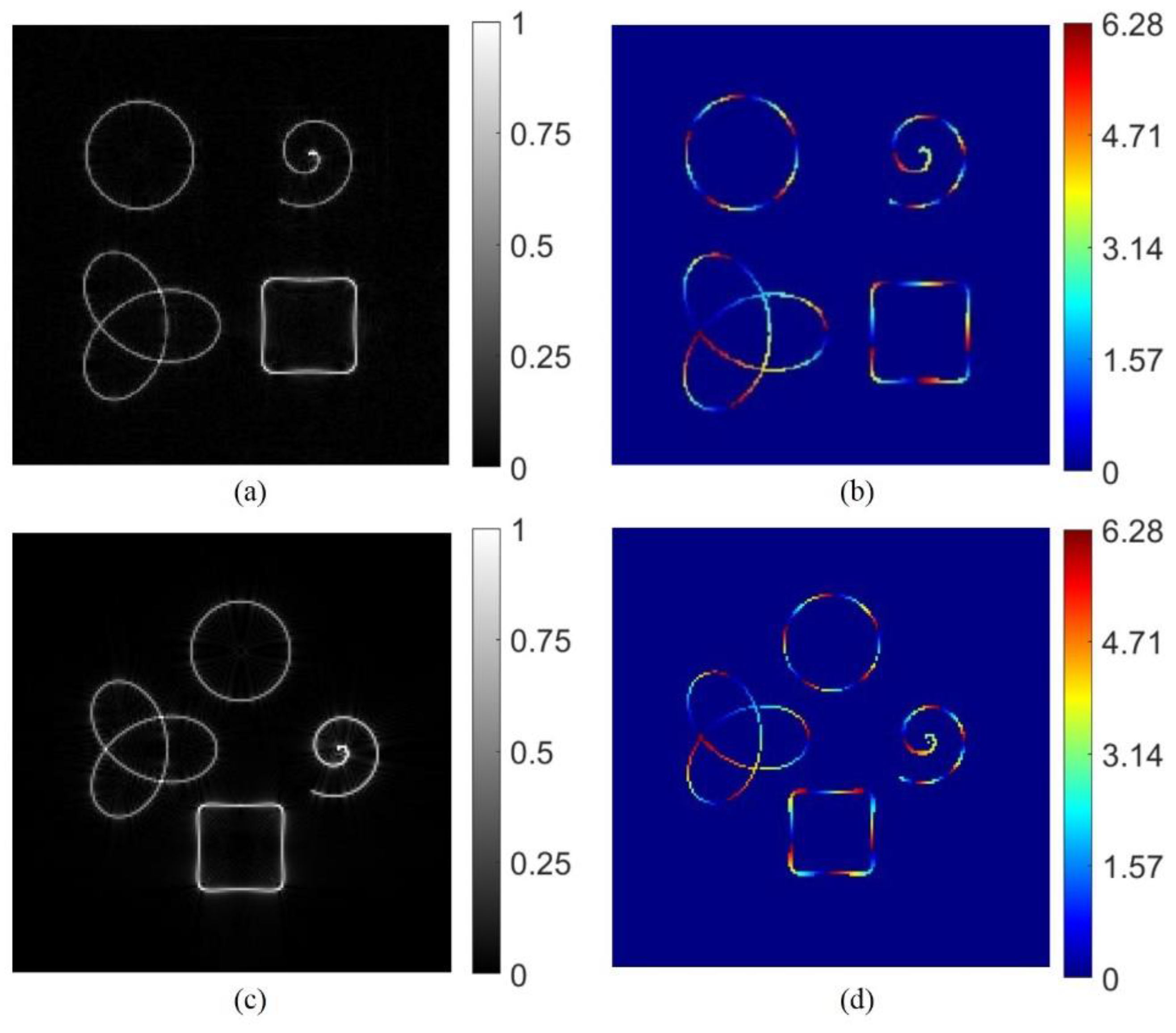
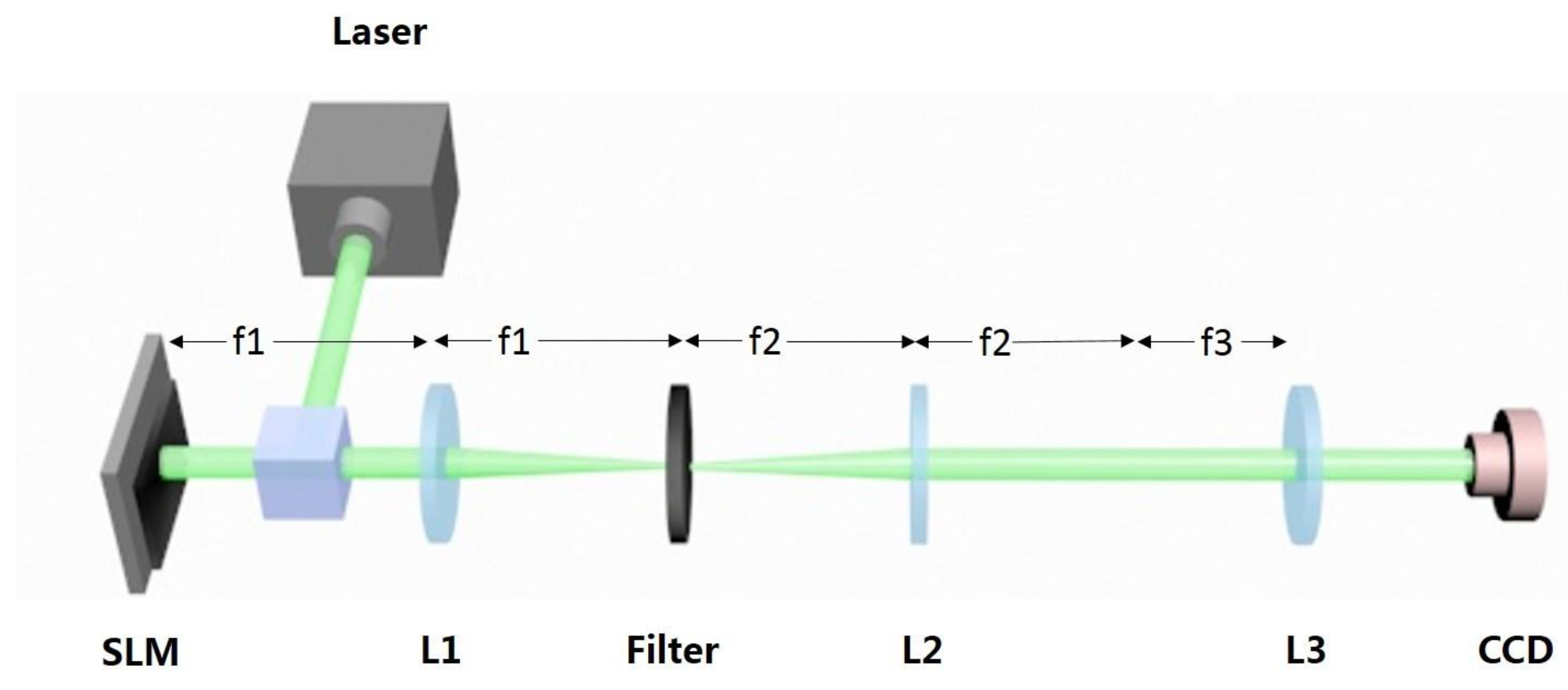
2. Materials and Methods
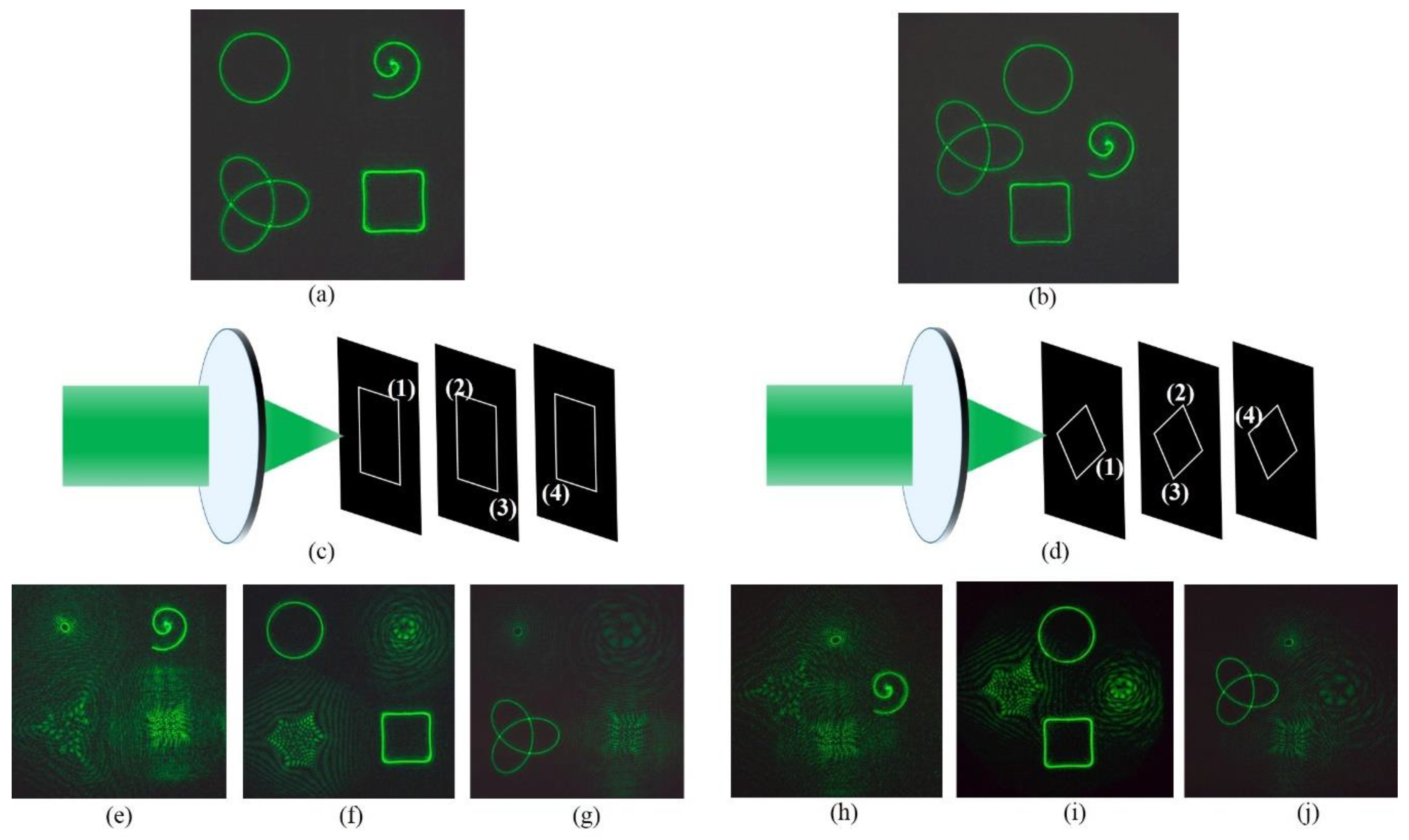
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vaughan, J.M.; Willetts, D.V. Interference properties of a light beam having a helical wave surface. Opt. Commun. 1979, 30, 263–267. [Google Scholar] [CrossRef]
- Coullet, P.; Gil, L.; Rocca, F. Optical vortices. Opt. Commun. 1989, 73, 403–408. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185. [Google Scholar] [CrossRef]
- Shvedov, V.G.; Desyatnikov, A.S.; Rode, A.V.; Izdebskaya, Y.V.; Krolikowski, W.Z.; Kivshar, Y.S. Optical vortex beams for trapping and transport of particles in air. Appl. Phys. A 2010, 100, 327–331. [Google Scholar] [CrossRef]
- Liu, C.X.; Guo, Z.Y.; Li, Y.; Wang, X.S.; Qu, S.L. Manipulating ellipsoidal micro-particles by femtosecond vortex tweezers. J. Opt. 2015, 17, 035402. [Google Scholar] [CrossRef]
- Caullet, V.; Marsal, N.; Wolfersberger, D.; Sciamanna, M. Optical patterns using vortex beams. Proc. SPIE 2012, 8434, 46. [Google Scholar]
- Li, X.Z.; Tai, Y.P.; Nie, Z.G. Digital speckle correlation method based on phase vortices. Opt. Eng. 2012, 51, 077004. [Google Scholar] [CrossRef]
- Chen, D.; Zhao, S.H.; Shi, L.; Liu, Y. Measurement-device-independent quantum key distribution with pairs of vector vortex beams. Phys. Rev. A 2016, 93, 032320. [Google Scholar] [CrossRef]
- Rotschild, C.; Zommer, S.; Moed, S.; Hershcovitz, O.; Lipson, S.G. Adjustable spiral phase plate. Appl. Opt. 2004, 43, 2397–2399. [Google Scholar] [CrossRef] [PubMed]
- Izdebskaya, Y.; Shvedov, V.; Volyar, A. Generation of higher-order optical vortices by a dielectric wedge. Opt. Lett. 2005, 30, 2472–2474. [Google Scholar] [CrossRef] [PubMed]
- Sarenac, D.; Cory, D.G.; Nsofini, J.; Hincks, I.; Miguel, P.; Arif, M.; Clark, C.W.; Huber, M.G.; Pushin, D.A. Generation of a Lattice of Spin-Orbit Beams via Coherent Averaging. Phys. Rev. Lett. 2017, 121, 183602. [Google Scholar] [CrossRef] [PubMed]
- Deng, D.; Li, Y.; Han, Y.H.; Su, X.Y.; Ye, J.F.; Gao, J.M.; Sun, Q.Q.; Qu, S.L. Perfect vortex in three-dimensional multifocal array. Opt. Express 2016, 24, 28270–28278. [Google Scholar] [CrossRef] [PubMed]
- Rodrigo, J.A.; Alieva, T.; Abramochkin, E.; Castrol, I. Shaping of light beams along crves in three dimensions. Opt. Express 2013, 21, 20544. [Google Scholar] [CrossRef] [PubMed]
- Rodrigo, J.A.; Alieva, T. Freestyle 3D laser traps: Tools for studying light-driven particle dynamics and beyond. Optica 2015, 2, 812–815. [Google Scholar] [CrossRef]
- Chang, C.L.; Gao, Y.; Xia, J.P.; Nie, S.P.; Ding, J.P. Shaping of optical vector beams in three dimensions. Opt. Lett. 2017, 42, 3884–3887. [Google Scholar] [CrossRef] [PubMed]
- Omel, M.; Mínguezvega, G.; Lancis, J. Encoding complex fields by using a phase-only optical element. Opt. Lett. 2014, 39, 1740–1743. [Google Scholar]
- Qi, Y.J.; Chang, C.L.; Xia, J. Speckleless holographic display by complex modulation based on double-phase method. Opt. Express 2016, 24, 30368–30378. [Google Scholar] [CrossRef] [PubMed]



| Type of Curve | x0(t) | y0(t) |
|---|---|---|
| ring curve | Rcos(t) | Rsin(t) |
| Archimedean spiral | −Rtcos(10t) | −Rtsin(10t) |
| trefoil-knotted curve | Rcos(t) − 2Rcos(2t) | Rsin(t) + 2Rsin(2t) |
| square curve | −2Rcos(t) + 0.3Rcos(kt) | −2Rsin(t) + 0.3Rsin(kt) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Tang, X.; Xia, J. Simultaneous Generation of Complex Structured Curve Beam. Nanomaterials 2019, 9, 87. https://doi.org/10.3390/nano9010087
Wu J, Tang X, Xia J. Simultaneous Generation of Complex Structured Curve Beam. Nanomaterials. 2019; 9(1):87. https://doi.org/10.3390/nano9010087
Chicago/Turabian StyleWu, Jun, Xinquan Tang, and Jun Xia. 2019. "Simultaneous Generation of Complex Structured Curve Beam" Nanomaterials 9, no. 1: 87. https://doi.org/10.3390/nano9010087
APA StyleWu, J., Tang, X., & Xia, J. (2019). Simultaneous Generation of Complex Structured Curve Beam. Nanomaterials, 9(1), 87. https://doi.org/10.3390/nano9010087




