Realization of the Kohn’s Theorem in Ge/Si Quantum Dots with Hole Gas: Theory and Experiment
Abstract
1. Introduction
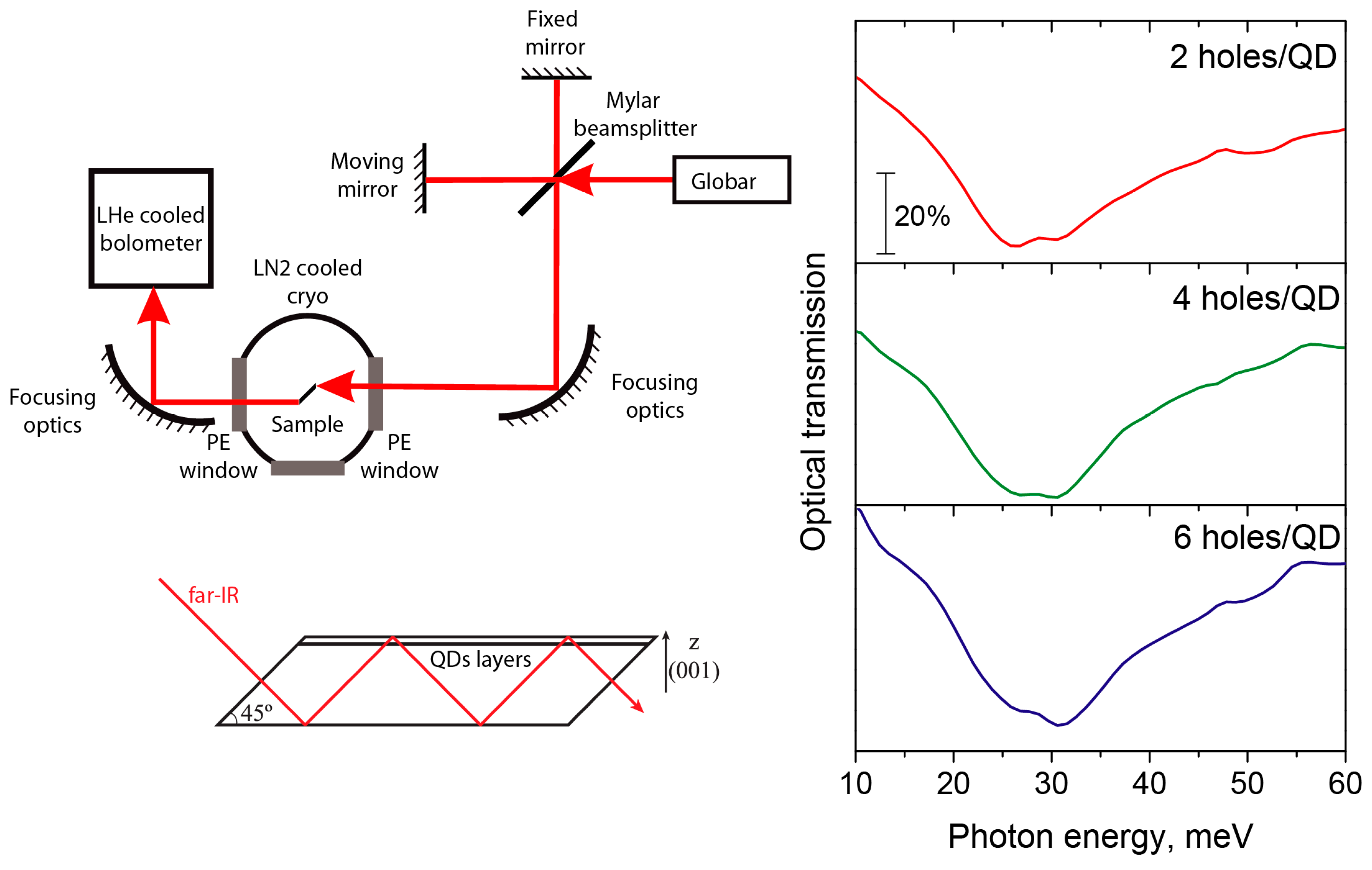
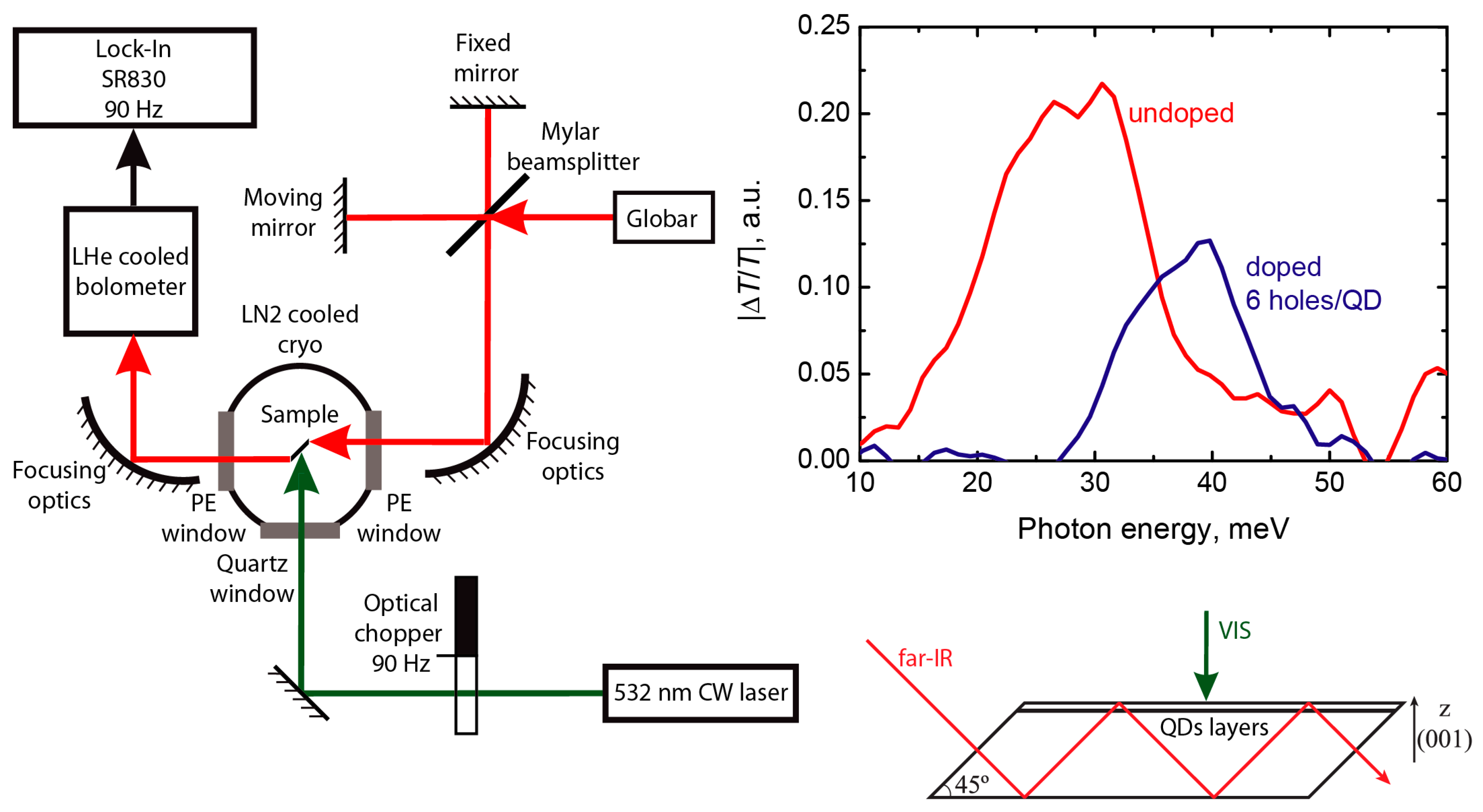
2. Materials and Methods
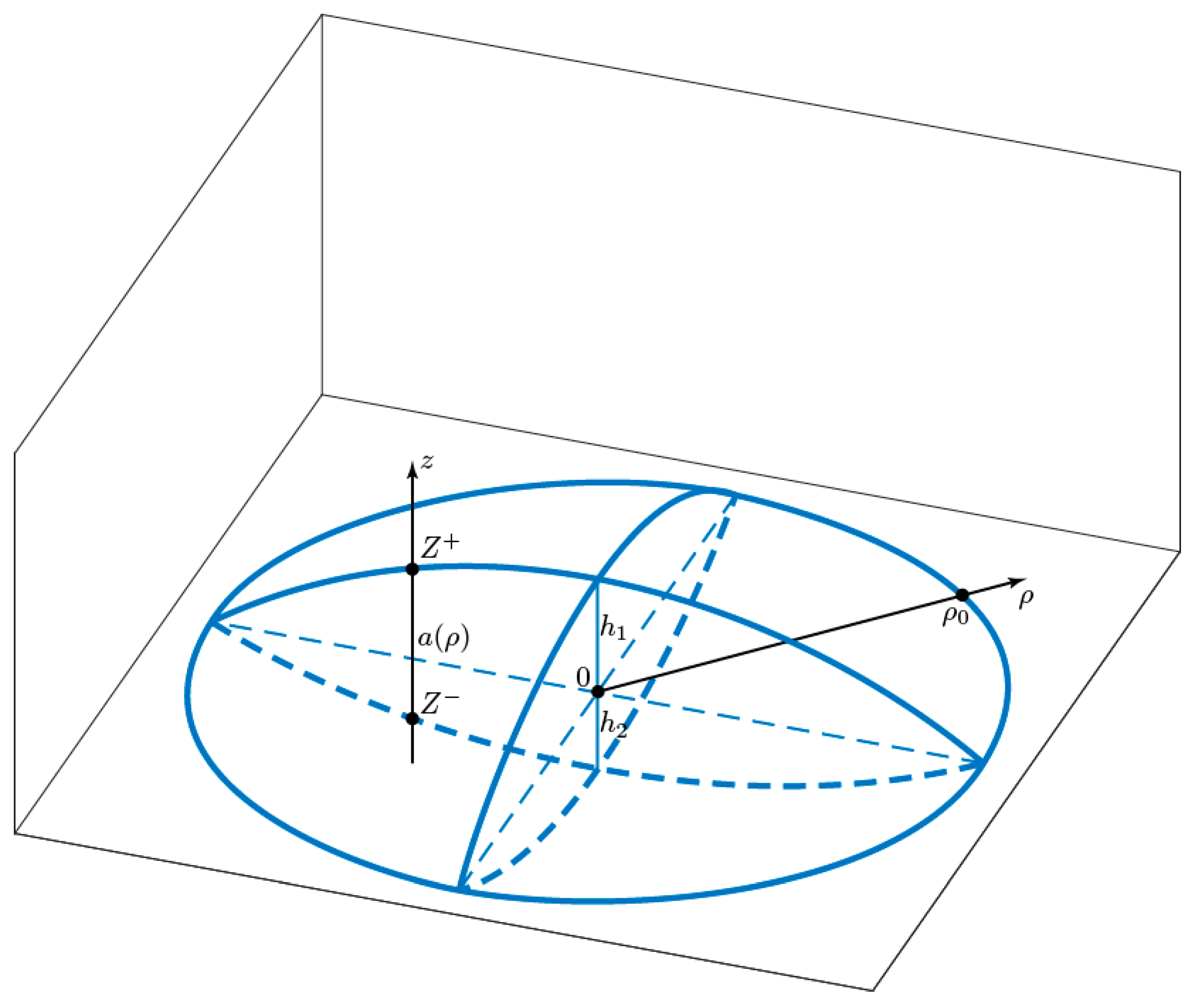
3. Theoretical Model for Asymmetric Biconvex Quantum Lens
- (1)
- QD contains few-particle gas (particularly, gas of heavy holes);
- (2)
- The effective mass of particles is scalar;
- (3)
- The QD has specific geometry, which allows dividing the particle’s motion into “fast” and “slow”;
- (4)
- The incident perturbation on the system is long-wavelength.
- First we will consider single-particle states in ABCQL.
- On the basis of the single-particle model we will describe pair-interacting gas.
3.1. Single-Particle States in ABCQL
3.2. Multiparticle States in ABSQL
4. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chakraborty, T. Quantum Dots: A Survey of the Properties of Artificial Atoms; Elsevier: New York, NY, USA, 1999. [Google Scholar]
- Bimberg, D.; Grundmann, M.; Ledetsov, N. Quantum Dot Heterostructures; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Wang, Z. (Ed.) Quantum Dot Devices; Springer: New York, NY, USA, 2012. [Google Scholar]
- Wang, Z. (Ed.) Self-Assembled Quantum Dots; Springer: New York, NY, USA, 2008. [Google Scholar]
- Choi, I.; Lee, H.; Lee, C.-R.; Jeong, K.-U.; Kim, J.S. Formation of spherical-shaped GaN and InN quantum dots on curved SiN/Si surface. Nanotechnology 2018, 29, 315603. [Google Scholar] [CrossRef] [PubMed]
- Hasanirokh, K.; Asgari, A. Modeling and studying of white light emitting diodes based on CdS/ZnS spherical quantum dots. Opt. Mater. 2018, 81, 129–133. [Google Scholar] [CrossRef]
- Portacio, A.A.; Rodríguez, B.A.; Villamil, P. Influence of the position of a donor impurity on the second-order nonlinear optical susceptibility in a cylindrical quantum dot. Superlattices Microstruct. 2018, 113, 550–557. [Google Scholar] [CrossRef]
- Duque, C.M.; Morales, A.L.; Duque, C.A.; Mora-Ramos, M.E. Electron-related Raman scattering in dilute nitride GaAs/InxGa1-xNyAs1-y cylindrically shaped quantum dots. Superlattices Microstruct. 2015, 87, 83–88. [Google Scholar] [CrossRef]
- Gambaryan, K.M.; Harutyunyan, V.G.; Aroutiounian, V.M.; Ai, Y.; Ashalley, E.; Wang, Z.M. Magnetoresistance and capacitance oscillations and hysteresis in type-II InAsSbP ellipsoidal quantum dots. J. Phys. D 2015, 48, 275302. [Google Scholar] [CrossRef]
- Hayrapetyan, D.B.; Ohanyan, G.L.; Baghdasaryan, D.A.; Sarkisyan, H.A.; Baskoutas, S.; Kazaryan, E.M. Binding energy and photoionization cross-section of hydrogen-like donor impurity in strongly oblate ellipsoidal quantum dot. Phys. E Low-Dimens. Syst. Nanostruct. 2018, 95, 27–31. [Google Scholar] [CrossRef]
- Marín, J.H.; Betancur, F.J.; Mikhailov, I.D. Effect of magnetic field on the formation of D- ions in lens-shape quantum dot. J. Phys. Condens. Matter 2006, 18, 1005–1019. [Google Scholar] [CrossRef]
- Williamson, A.J.; Wang, L.W.; Zunger, A. Theoretical interpretation of the experimental electronic structure of lens-shaped self-assembled InAs/GaAs quantum dots. Phys. Rev. B 2000, 62, 12963–12977. [Google Scholar] [CrossRef]
- Gioia, L.; Zülicke, U.; Governale, M.; Winkler, R. Dirac electrons in quantum rings. Phys. Rev. B 2018, 97, 205421. [Google Scholar] [CrossRef]
- Kozin, V.K.; Iorsh, I.V.; Kibis, O.V.; Shelykh, I.A. Periodic array of quantum rings strongly coupled to circularly polarized light as a topological insulator. Phys. Rev. B 2018, 97, 035416. [Google Scholar] [CrossRef]
- Zhu, J.L.; Xiong, J.J.; Gu, B.L. Confined electron and hydrogenic donor states in a spherical quantum dot of GaAs-Ga1-xAlxAs. Phys. Rev. B 1990, 41, 6001–6007. [Google Scholar] [CrossRef]
- Chuu, D.S.; Hsiao, C.M.; Mei, W.N. Hydrogenic impurity states in quantum dots and quantum wires. Phys. Rev. B 1992, 46, 3898–3905. [Google Scholar] [CrossRef]
- Sarkisyan, H.A. Direct optical absorption in cylindrical quantum dot. Mod. Phys. Lett. B 2004, 18, 443–452. [Google Scholar] [CrossRef]
- Hayrapetyan, D.B.; Chalyan, A.V.; Kazaryan, E.M.; Sarkisyan, H.A. Direct interband light absorption in conical quantum dot. J. Nanomater. 2015, 16, 915742. [Google Scholar] [CrossRef]
- Li, W.; Belling, S.W. Symmetric analysis, categorization, and optical spectrum of ideal pyramid quantum dots. J. Phys. D 2017, 50, 435102. [Google Scholar] [CrossRef]
- Kaczmarkiewicz, P.; Machnikowski, P.; Kuhn, T. Double quantum dot in a quantum dash: Optical properties. J. Appl. Phys. 2013, 114, 183108. [Google Scholar] [CrossRef]
- Karabulut, I.; Baskoutas, S. Linear and nonlinear optical absorption coefficients and refractive index changes in spherical quantum dots: Effects of impurities, electric field, size, and optical intensity. J. Appl. Phys. 2008, 103, 073512. [Google Scholar] [CrossRef]
- Beckel, A.; Kurzmann, A.; Geller, M.; Ludwig, A.; Wieck, A.D.; König, J.; Lorke, A. Asymmetry of charge relaxation times in quantum dots: The influence of degeneracy. Europhys. Lett. 2014, 106, 47002. [Google Scholar] [CrossRef]
- Chen, R.; Zheng, X.; Jiang, T. Broadband ultrafast nonlinear absorption and ultra-long exciton relaxation time of black phosphorus quantum dots. Opt. Express 2017, 25, 7507–7519. [Google Scholar] [CrossRef]
- Aghekyan, N.G.; Amirkhanyan, S.M.; Kazaryan, E.M.; Sarkisyan, H.A. Spin magnetic moment and persistent orbital currents in cylindrical nanolayer. Superlattices Microstruct. 2014, 69, 87–98. [Google Scholar] [CrossRef]
- Van Bree, J.; Silov, A.Y.; van Maasakkers, M.L.; Pryor, C.E.; Flatté, M.E.; Koenraad, P.M. Anisotropy of electron and hole g tensors of quantum dots: An intuitive picture based on spin-correlated orbital currents. Phys. Rev. B 2016, 93, 035311. [Google Scholar] [CrossRef]
- Grundmann, M.; Stier, O.; Bimberg, D. InAs/GaAs pyramidal quantum dots: Strain distribution, optical phonons, and electronic structure. Phys. Rev. B 1995, 52, 11969–11981. [Google Scholar] [CrossRef]
- Grundmann, M.; Heitz, R.; Ledentsov, N.; Stier, O.; Bimberg, D.; Ustinov, V.M.; Kop’ev, P.S.; Alferov, Z.I.; Ruvimov, S.S.; Werner, P.; et al. Electronic structure and energy relaxation in strained InAs/GaAs quantum pyramids. Superlattices Microstruct. 1996, 19, 81–95. [Google Scholar] [CrossRef]
- Barker, J.A.; O’Reilly, E.P. The influence of inter-diffusion on electron states in quantum dots. Phys. E Low-Dimens. Syst. Nanostruct. 1999, 4, 231–237. [Google Scholar] [CrossRef]
- Petrosyan, L.S. Electron states in spherical quantum dots with Wood-Saxon’s confinement potential. J. Contemp. Phys. 2002, 37, 173–176. [Google Scholar]
- Aziz Aghchegala, V.L.; Mughnetsyan, V.N.; Kirakosyan, A.A. Effect of interdiffusion on impurity states in quantum dots of spherical symmetry. Phys. E Low-Dimens. Syst. Nanostruct. 2010, 42, 1567–1570. [Google Scholar] [CrossRef]
- Hayrapetyan, D.B.; Kazaryan, E.M.; Petrosyan, L.S.; Sarkisyan, H.A. Core/shell/shell spherical quantum dot with Kratzer confining potential: Impurity states and electrostatic multipoles. Phys. E Low-Dimens. Syst. Nanostruct. 2015, 66, 7–12. [Google Scholar] [CrossRef]
- Johnson, N.F.; Payne, M.C. Exactly solvable model of interacting particles in a quantum dot. Phys. Rev. Lett. 1991, 67, 1157–1160. [Google Scholar] [CrossRef]
- Madhav, A.V.; Chakraborty, T. Electronic properties of anisotropic quantum dots in a magnetic field. Phys. Rev. B 1994, 49, 8163–8168. [Google Scholar] [CrossRef]
- Atoyan, M.S.; Kazaryan, E.M.; Sarkisyan, H.A. Direct interband light absorption in a cylindrical quantum dot in quantizing magnetic field. Phys. E Low-Dimens. Syst. Nanostruct. 2004, 22, 860–866. [Google Scholar] [CrossRef]
- Atoyan, M.S.; Kazaryan, E.M.; Sarkisyan, H.A. Interband light absorption in parabolic quantum dot in the presence of electrical and magnetic fields. Phys. E Low-Dimens. Syst. Nanostruct. 2006, 31, 83–85. [Google Scholar] [CrossRef]
- Maksym, P.A.; Chakraborty, T. Quantum dots in a magnetic field: Role of electron-electron interactions. Phys. Rev. Lett. 1990, 65, 108–111. [Google Scholar] [CrossRef] [PubMed]
- Peeters, F. Magneto-optics in parabolic quantum dots. Phys. Rev. B 1990, 42, 1486–1487. [Google Scholar] [CrossRef]
- Govorov, A.O.; Chaplik, A.V. Magnetoabsorption at quantum points. JETP Lett. 1990, 52, 31–33. [Google Scholar]
- Li, Q.P.; Karraï, K.; Yip, S.K.; Das Sarma, S.; Drew, H.D. Electrodynamic response of a harmonic atom in an external magnetic field. Phys. Rev. B 1991, 43, 5151–5154. [Google Scholar] [CrossRef]
- Pfannkuche, D.; Gerhardts, R.R.; Maksym, P.A.; Gudmundsson, V. Theory of quantum dot helium. Phys. B Condens. Matter 1993, 189, 6–15. [Google Scholar] [CrossRef]
- Kohn, W. Cyclotron resonance and de Haas-van Alphen oscillations of an interacting electron gas. Phys. Rev. 1961, 123, 1242–1244. [Google Scholar] [CrossRef]
- Brey, L.; Johnson, N.F.; Halperin, B.I. Optical and magneto-optical absorption in parabolic quantum wells. Phys. Rev. B 1989, 40, 10647–10649. [Google Scholar] [CrossRef]
- Hayrapetyan, D.B.; Kazaryan, E.M.; Sarkisyan, H.A. On the possibility of implementation of Kohn’s theorem in the case of ellipsoidal quantum dots. J. Contemp. Phys. 2013, 48, 32–36. [Google Scholar] [CrossRef]
- Hayrapetyan, D.B.; Kazaryan, E.M.; Sarkisyan, H.A. Implementation of Kohn’s theorem for the ellipsoidal quantum dot in the presence of external magnetic field. Phys. E Low-Dimens. Syst. Nanostruct. 2016, 75, 353–357. [Google Scholar] [CrossRef]
- Ghaltaghchyan, H.T.; Hayrapetyan, D.B.; Kazaryan, E.M.; Sarkisyan, H.A. Few-body magneto-absorption in prolate ellipsoidal quantum dot. Phys. At. Nucl. 2017, 80, 769–773. [Google Scholar] [CrossRef]
- Galitski, V.; Karnakov, B.; Kogan, V. Exploring Quantum Mechanics: A Collection of 700+ Solved Problems for Students, Lecturers, and Researchers; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Yuryev, V.A.; Arapkina, L.V. Ge quantum dot arrays grown by ultrahigh vacuum molecular-beam epitaxy on the Si(001) surface: Nucleation, morphology, and CMOS compatibility. Nanoscale Res. Lett. 2011, 6, 522. [Google Scholar] [CrossRef] [PubMed]
- Lobanov, D.N.; Novikov, A.V.; Kudryavtsev, K.E.; Yablonskiy, A.N.; Antonov, A.V.; Drozdov, Y.N.; Shengurov, D.V.; Shmagin, V.B.; Krasilnik, Z.F.; Zakharov, N.D.; et al. Electroluminescence and photoconductivity of GeSi heterostructures with self-assembled islands in the wavelength range 1.3–1.55 μm. Phys. E Low-Dimens. Syst. Nanostruct. 2009, 41, 935–938. [Google Scholar] [CrossRef]
- Krasilnik, Z.F.; Novikov, A.V.; Lobanov, D.N.; Kudryavtsev, K.E.; Antonov, A.V.; Obolenskiy, S.V.; Zakharov, N.D.; Werner, P. SiGe nanostructures with self-assembled islands for Si-based optoelectronics. Semicond. Sci. Technol. 2011, 26, 014029. [Google Scholar] [CrossRef]
- Yakimov, A.I.; Kirienko, V.V.; Bloshkin, A.A.; Armbrister, V.A.; Kuchinskaya, P.A.; Dvurechenskii, A.V. Localization of electrons in dome-shaped GeSi/Si islands. Appl. Phys. Lett. 2015, 106, 032104. [Google Scholar] [CrossRef]
- Yakimov, A.I.; Kirienko, V.V.; Armbrister, V.A.; Bloshkin, A.A.; Dvurechenskii, A.V. Phonon bottleneck in p-type Ge/Si quantum dots. Appl. Phys. Lett. 2015, 107, 213502. [Google Scholar] [CrossRef]
- Yakimov, A.I.; Kirienko, V.V.; Armbrister, V.A.; Bloshkin, A.A.; Dvurechenskii, A.V.; Shklyaev, A.A. Photoconductive gain and quantum efficiency of remotely doped Ge/Si quantum dot photodetectors. Mater. Res. Express 2016, 3, 105032. [Google Scholar] [CrossRef]
- Yakimov, A.I.; Kirienko, V.V.; Bloshkin, A.A.; Armbrister, V.A.; Dvurechenskii, A.V. Plasmon polariton enhanced mid-infrared photodetectors based on Ge quantum dots in Si. J. Appl. Phys. 2017, 122, 133101. [Google Scholar] [CrossRef]
- Yakimov, A.I.; Kirienko, V.V.; Bloshkin, A.A.; Armbrister, V.A.; Dvurechenskii, A.V.; Hartmann, J.-M. Photovoltaic Ge/SiGe quantum dot mid-infrared photodetector enhanced by surface plasmons. Opt. Express 2017, 25, 25602. [Google Scholar] [CrossRef]
- Tonkikh, A.; Zakharov, N.; Talalaev, V.; Werner, P. Ge/Si(100) quantum dots grown via a thin Sb layer. Phys. Status Solidi Rapid Res. Lett. 2010, 4, 224. [Google Scholar] [CrossRef]
- Tonkikh, A.; Werner, P. Surfactant-mediated Stranski—Krastanov islands. Phys. Status Solidi B 2013, 250, 1795. [Google Scholar] [CrossRef]
- Levinshtein, M.; Rumyantsev, S.; Shur, M. Handbook Series on Semiconductor Parameters; World Scientific Publishing: Singapore, 1996; Volume 1. [Google Scholar]
- Sofronov, A.; Vorobjev, L.; Firsov, D.; Panevin, V.; Balagula, R.; Werner, P.; Tonkikh, A. Photoinduced mid-infrared intraband light absorption and photoconductivity in Ge/Si quantum dots. Superlattices Microstruct. 2015, 87, 53. [Google Scholar] [CrossRef]
- Darnhofer, T.; Rossler, U.; Broido, D.A. Far-infrared response of holes in quantum dots: Band structure effects and the generalized Kohn’s theorem. Phys. Rev. B 1995, 52, R14376. [Google Scholar] [CrossRef]
- Jacak, L.; Hawrylak, P.; Wojs, A. Quantum Dots; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Kurdi, M.E.; Sauvage, S.; Fishman, G.; Boucaud, P. Band-edge alignment of SiGe/Si quantum wells and SiGe/Si self-assembled islands. Phys. Rev. B 2006, 73, 195327. [Google Scholar] [CrossRef]
- Balagula, R.M.; Sofronov, A.N.; Vorobjev, L.E.; Firsov, D.A.; Tonkikh, A.A. Temperature evolution of the photoexcited charge carriers dynamics in Ge/Si quantum dots. Phys. E Low-Dimens. Syst. Nanostruct. 2019, 106, 85. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarkisyan, H.A.; Hayrapetyan, D.B.; Petrosyan, L.S.; Kazaryan, E.M.; Sofronov, A.N.; Balagula, R.M.; Firsov, D.A.; Vorobjev, L.E.; Tonkikh, A.A. Realization of the Kohn’s Theorem in Ge/Si Quantum Dots with Hole Gas: Theory and Experiment. Nanomaterials 2019, 9, 56. https://doi.org/10.3390/nano9010056
Sarkisyan HA, Hayrapetyan DB, Petrosyan LS, Kazaryan EM, Sofronov AN, Balagula RM, Firsov DA, Vorobjev LE, Tonkikh AA. Realization of the Kohn’s Theorem in Ge/Si Quantum Dots with Hole Gas: Theory and Experiment. Nanomaterials. 2019; 9(1):56. https://doi.org/10.3390/nano9010056
Chicago/Turabian StyleSarkisyan, Hayk A., David B. Hayrapetyan, Lyudvig S. Petrosyan, Eduard M. Kazaryan, Anton N. Sofronov, Roman M. Balagula, Dmitry A. Firsov, Leonid E. Vorobjev, and Alexander A. Tonkikh. 2019. "Realization of the Kohn’s Theorem in Ge/Si Quantum Dots with Hole Gas: Theory and Experiment" Nanomaterials 9, no. 1: 56. https://doi.org/10.3390/nano9010056
APA StyleSarkisyan, H. A., Hayrapetyan, D. B., Petrosyan, L. S., Kazaryan, E. M., Sofronov, A. N., Balagula, R. M., Firsov, D. A., Vorobjev, L. E., & Tonkikh, A. A. (2019). Realization of the Kohn’s Theorem in Ge/Si Quantum Dots with Hole Gas: Theory and Experiment. Nanomaterials, 9(1), 56. https://doi.org/10.3390/nano9010056





