Tin, The Enabler—Hydrogen Diffusion into Ruthenium
Abstract
1. Introduction
2. Computational Methods
2.1. DFT Calculations
2.2. Electronic Structure and Bonding Analysis
3. Results
3.1. Hydrogen and Ruthenium
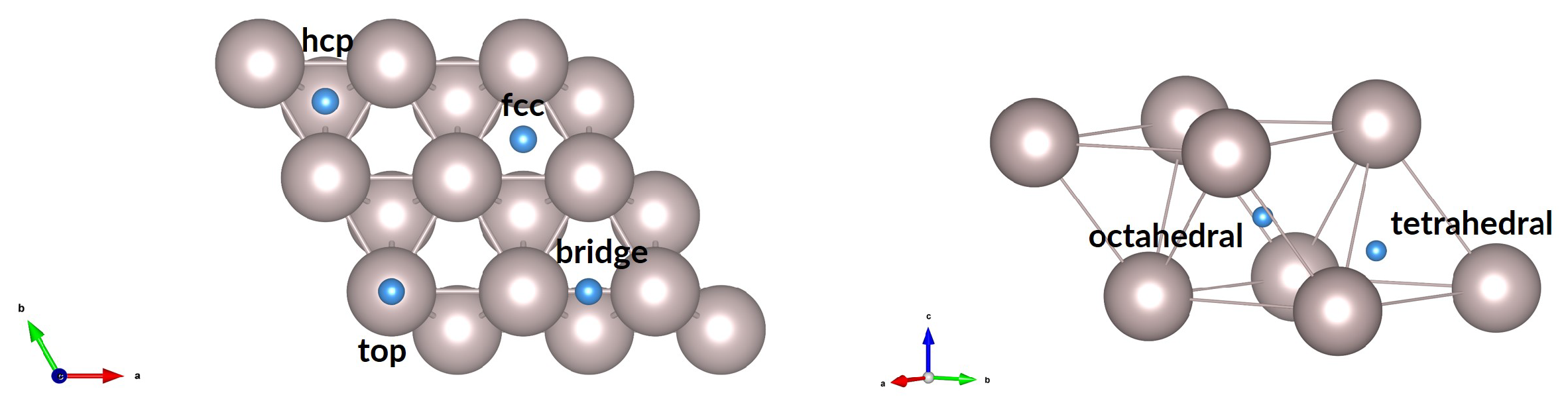
3.1.1. Surface, Subsurface, and Bulk
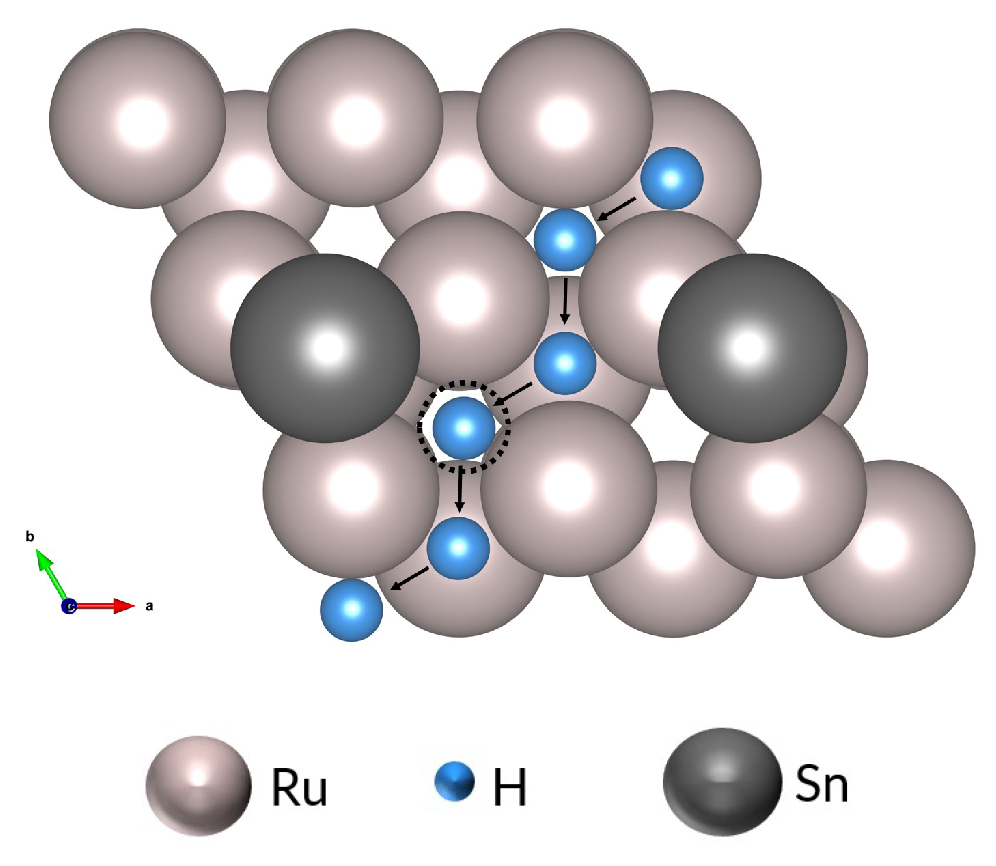
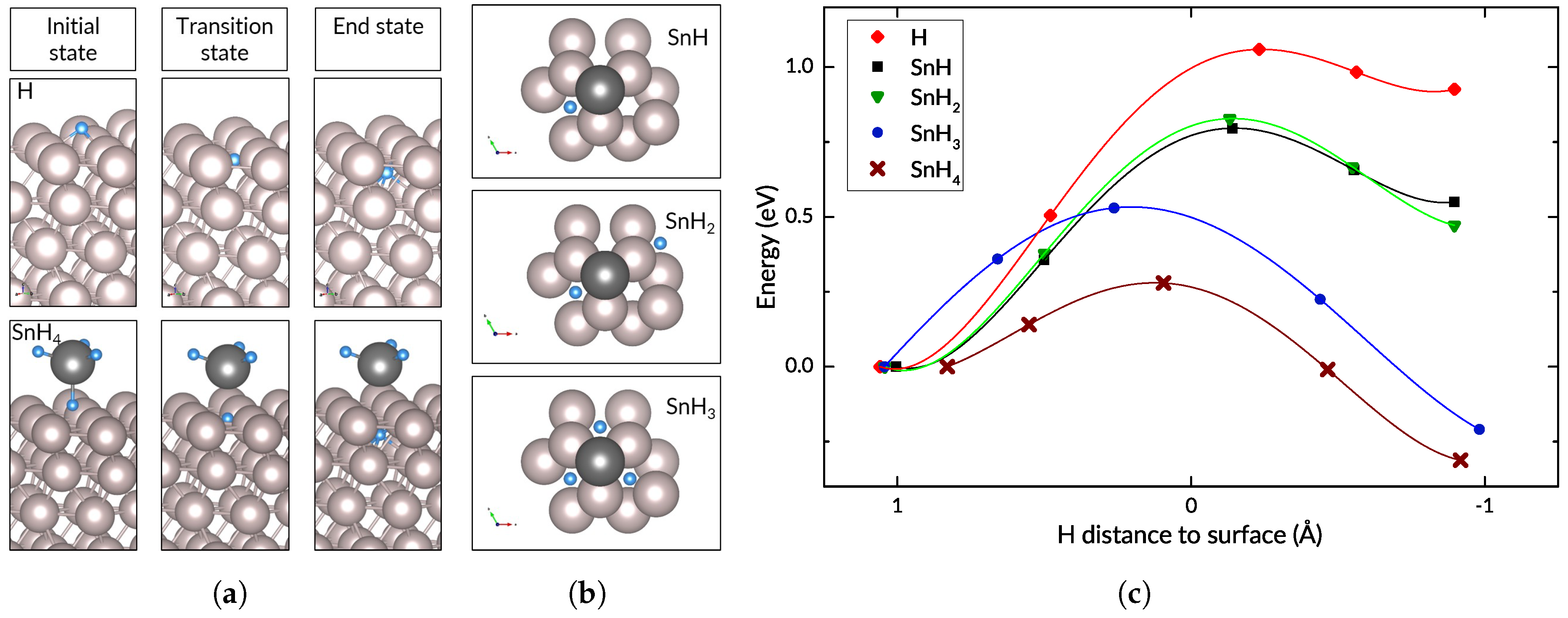
3.1.2. Diffusion
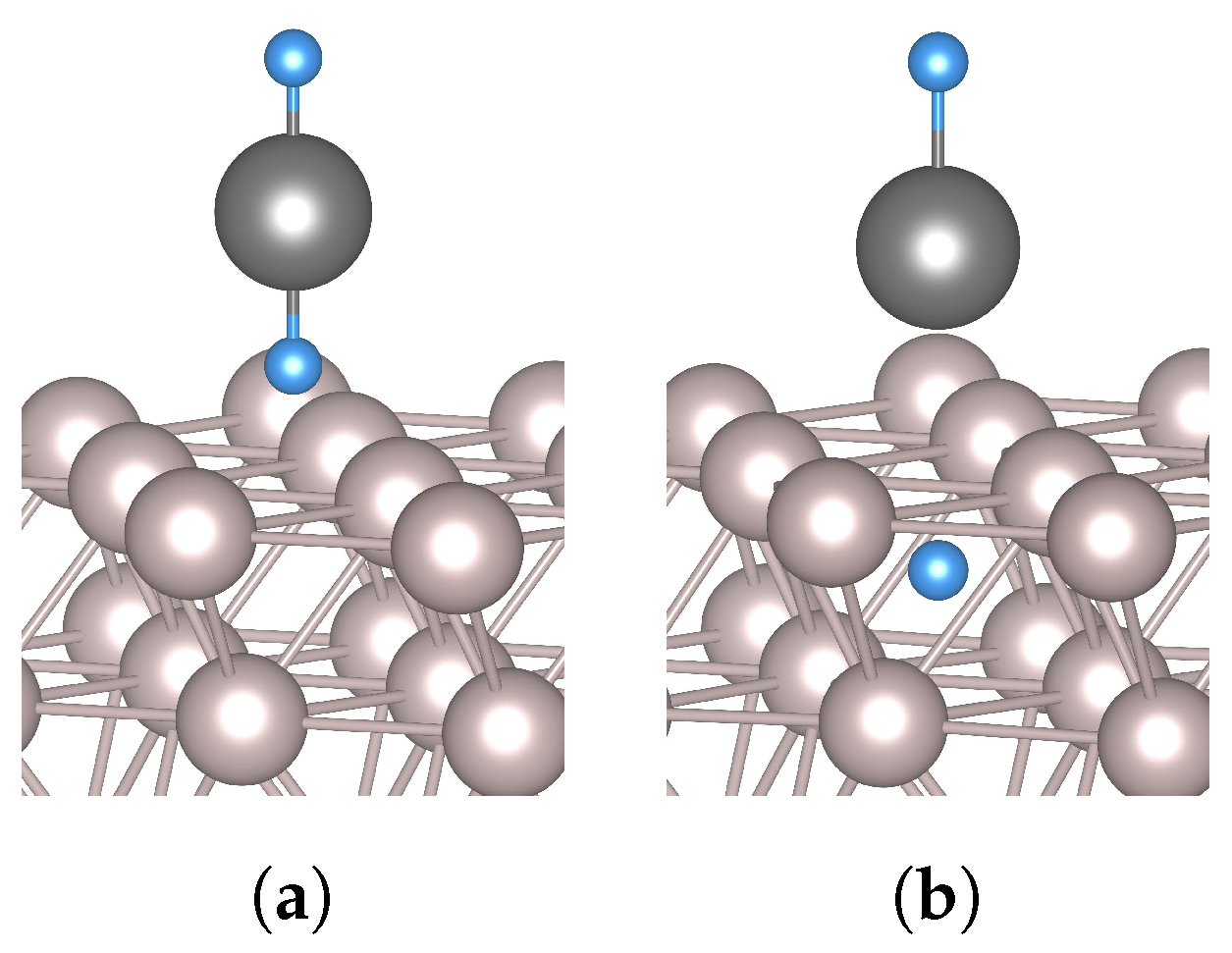
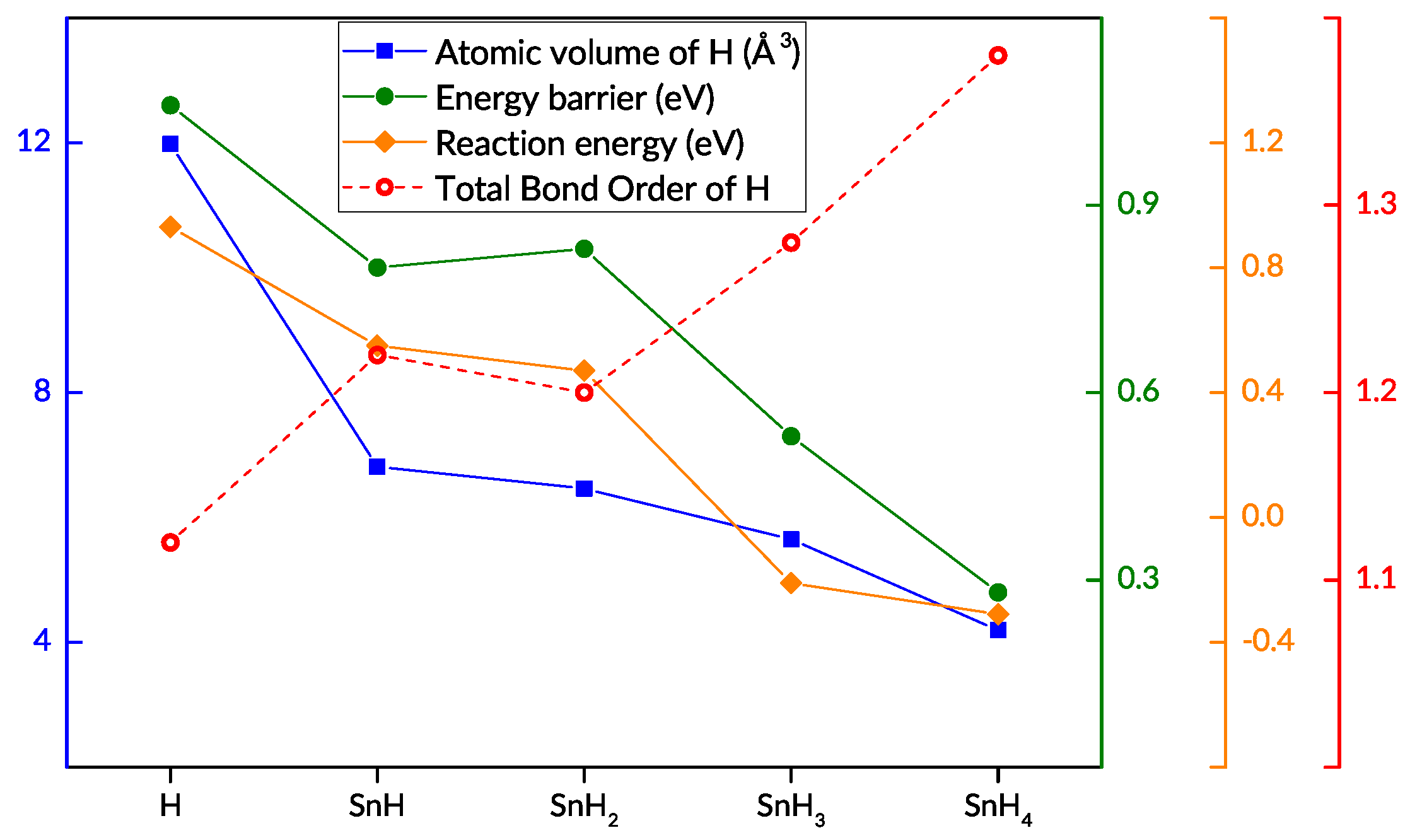
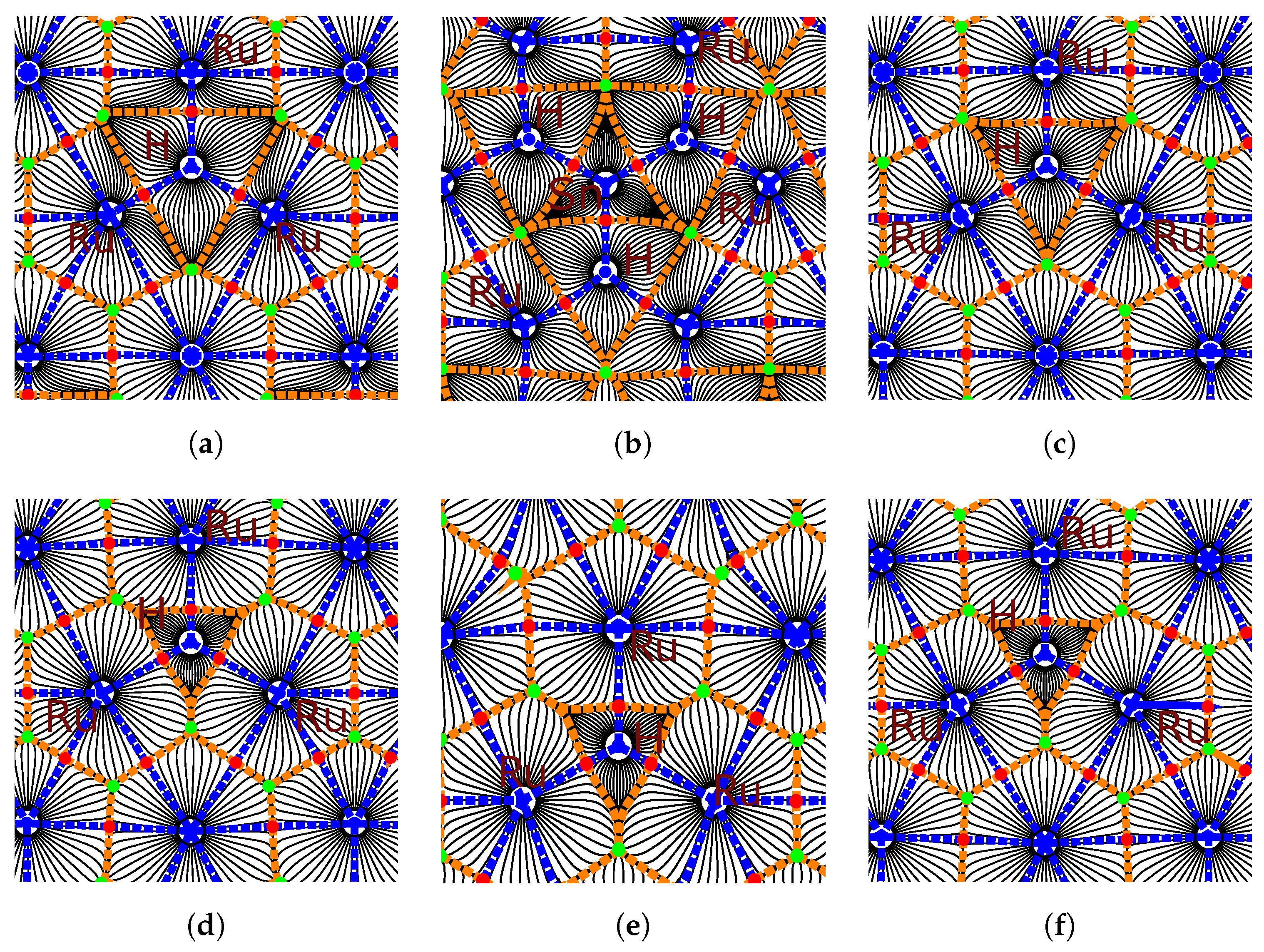
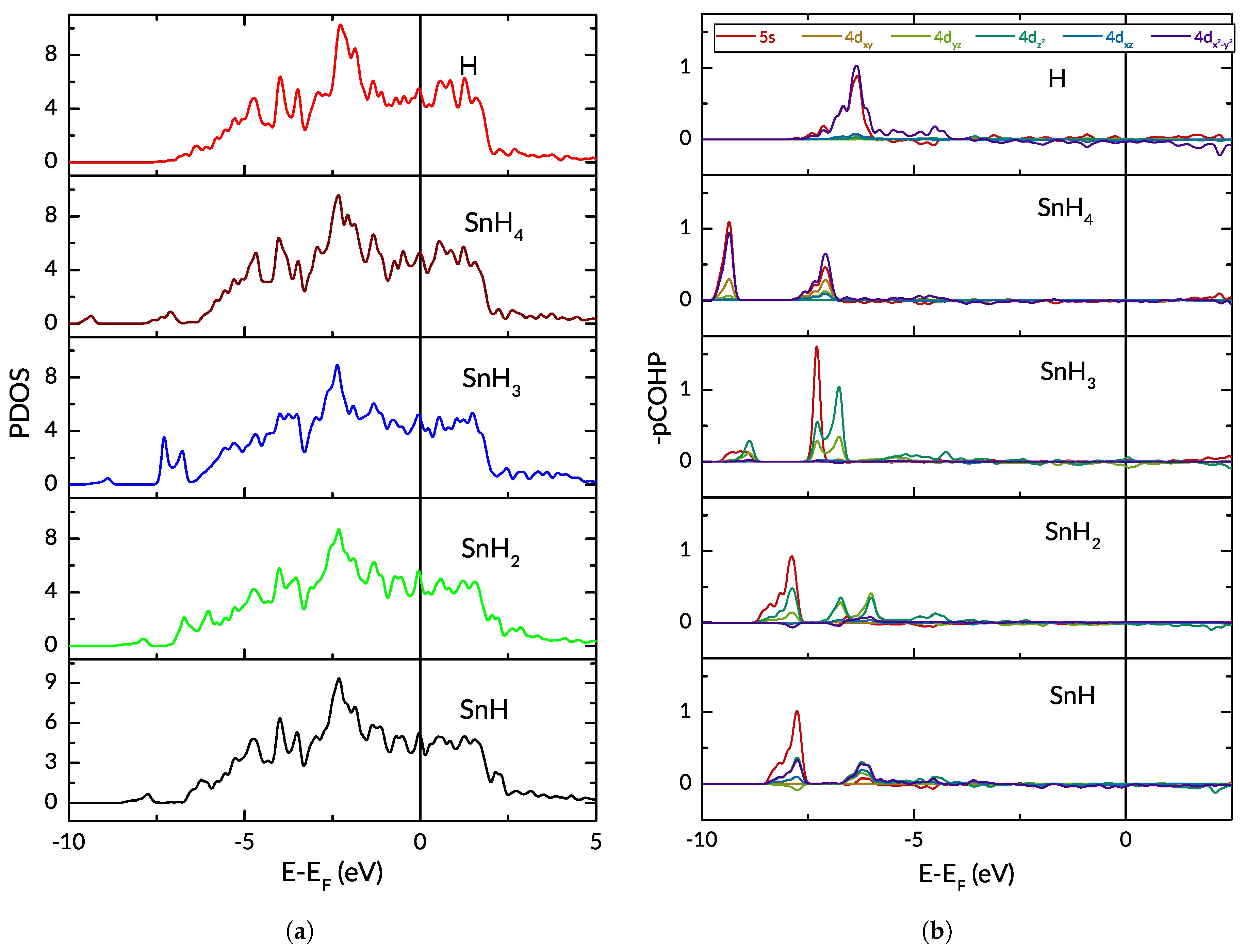
3.2. Hydrogen and Tin
3.3. The Effect of Tin
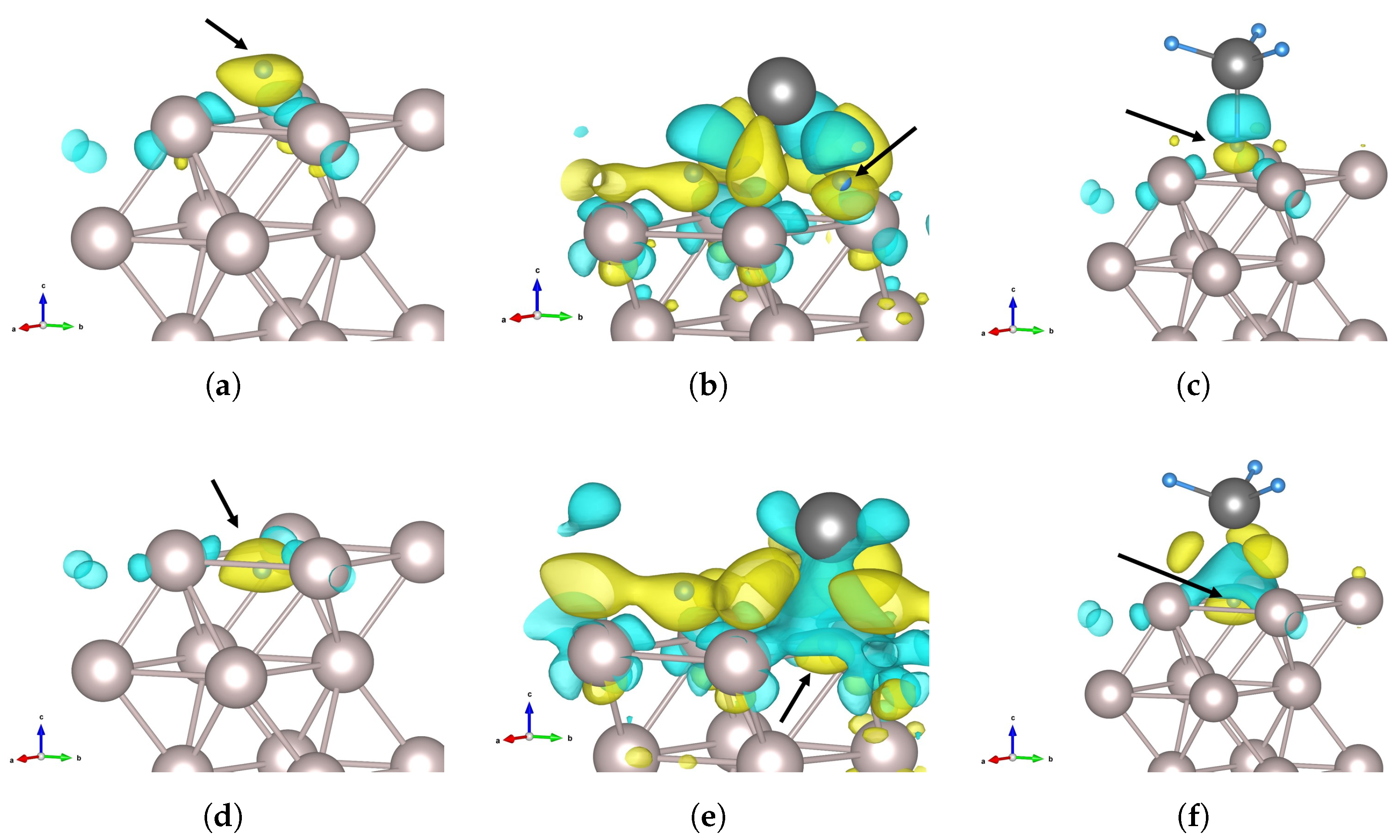
3.4. Charge Density Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bond, G.C.; Webb, G.; Wells, P.B.; Winterbottom, J.M. Patterns of behavior in catalysis by metals. J. Catal. 1962, 1, 74–84. [Google Scholar] [CrossRef]
- Sinfelt, J.H. Heterogeneous catalysis by metals. Prog. Solid-State Chem. 1975, 10, 55–69. [Google Scholar] [CrossRef]
- Knapton, A.G. Palladium Alloys for Hydrogen Diffusion Membranes. Platinum Met. Rev. 1977, 21, 44–50. [Google Scholar]
- Al-Mufachi, N.A.; Rees, N.V.; Steinberger-Wilkens, R. Hydrogen selective membranes: A review of palladium-based dense metal membranes. Renew. Sustain. Energy Rev. 2015, 47, 540–551. [Google Scholar] [CrossRef]
- Sakintuna, B.; Lamari-Darkrim, F.; Hirscher, M. Metal hydride materials for solid hydrogen storage: A review. Int. J. Hydrog. Energy 2007, 32, 1121–1140. [Google Scholar] [CrossRef]
- Hübert, T.; Boon-Brett, L.; Black, G.; Banach, U. Hydrogen sensors—A review. Sens. Actuators B Chem. 2011, 157, 329–352. [Google Scholar] [CrossRef]
- Herlach, D.; Kottler, C.; Wider, T.; Maier, K. Hydrogen embrittlement of metals. Phys. B Condens. Matter 2000, 290, 443–446. [Google Scholar] [CrossRef]
- Nanninga, N.E.; Levy, Y.S.; Drexler, E.S.; Condon, R.T.; Stevenson, A.E.; Slifka, A.J. Comparison of hydrogen embrittlement in three pipeline steels in high pressure gaseous hydrogen environments. Corros. Sci. 2012, 59, 1–9. [Google Scholar] [CrossRef]
- Muschiol, U.; Schmidt, P.K.; Christmann, K. Adsorption and absorption of hydrogen on a palladium (210) surface: A combined LEEDS, TDS, ΔΦ and HREELS study. Surf. Sci. 1998, 395, 182–204. [Google Scholar] [CrossRef]
- Nordlander, P.; Holloway, S.; Nørskov, J.K. Hydrogen adsorption on metal surfaces. Surf. Sci. 1984, 136, 59–81. [Google Scholar] [CrossRef]
- Pick, M.A.; Sonnenberg, K. A model for atomic hydrogen-metal interactions—Application to recycling, recombination and permeation. J. Nucl. Mater. 1985, 131, 208–220. [Google Scholar] [CrossRef]
- Myers, S.M.; Richards, P.M.; Wampler, W.R.; Besenbacher, F. Ion-beam studies of hydrogen-metal interactions. J. Nucl. Mater. 1989, 165, 9–64. [Google Scholar] [CrossRef]
- Van Santen, R.A.; Tranca, I. How molecular is the chemisorptive bond? Phys. Chem. Chem. Phys. 2016, 18, 20868–20894. [Google Scholar] [CrossRef] [PubMed]
- Sinfelt, J.H. Catalysis by Alloys and Bimetallic Clusters. Acc. Chem. Res. 1977, 10, 15–20. [Google Scholar] [CrossRef]
- Rodriguez, J.A. Electronic and chemical properties of Pt, Pd and Ni in bimetallic surfaces. Surf. Sci. 1996, 345, 347–362. [Google Scholar] [CrossRef]
- Ruban, A.; Hammer, B.; Stoltze, P.; Skriver, H.L.; Nørskov, J.K. Surface electronic structure and reactivity of transition and noble metals. J. Mol. Catal. A Chem. 1997, 115, 421–429. [Google Scholar] [CrossRef]
- Chen, J.G.; Menning, C.A.; Zellner, M.B. Monolayer bimetallic surfaces: Experimental and theoretical studies of trends in electronic and chemical properties. Surf. Sci. Rep. 2008, 63, 201–254. [Google Scholar] [CrossRef]
- He, Y.B.; Goriachko, A.; Korte, C.; Farkas, A.; Mellau, G.; Dudin, P.; Gregoratti, L.; Barinov, A.; Kiskinova, M.; Stierle, A.; et al. Oxidation and reduction of ultrathin nanocrystalline Ru films on silicon: Model system for Ru-capped extreme ultraviolet lithography optics. J. Phys. Chem. C 2007, 111, 10988–10992. [Google Scholar] [CrossRef]
- Bajt, S.; Chapman, H.N.; Nguyen, N.; Alameda, J.B.; Robinson, J.C.; Malinowski, M.E.; Gullikson, E.; Aquila, A.; Tarrio, C.; Grantham, S. Design and performance of capping layers for EUV multilayer mirrors. Proc. SPIE 2003, 5037, 236–248. [Google Scholar] [CrossRef]
- Kuznetsov, A.S.; van de Kruijs, R.W.E.; Gleeson, M.A.; Schmid, K.; Bijkerk, F. Hydrogen interaction with EUVL-relevant optical materials. J. Surf. Investig. X-ray Synchrotron Neutron Tech. 2010, 4, 563–566. [Google Scholar] [CrossRef]
- Kuznetsov, A.S.; Gleeson, M.A.; Bijkerk, F. Temperature dependencies of hydrogen-induced blistering of thin film multilayers. J. Appl. Phys. 2014, 115, 173510. [Google Scholar] [CrossRef]
- Faradzhev, N.; Sidorkin, V. Hydrogen mediated transport of Sn to Ru film surface. J. Vac. Sci. Technol. A Vac. Surf. Films 2009, 27, 306–314. [Google Scholar] [CrossRef]
- Bruneau, C.; Dixneuf, P.H. Volume 48, Topics in Organometallic Chemistry. In Ruthenium in Catalysis; Springer International Publishing: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Adams, R.D.; Trufan, E. Ruthenium-tin cluster complexes and their applications as bimetallic nanoscale heterogeneous hydrogenation catalysts. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 1473–1493. [Google Scholar] [CrossRef]
- Bonnefille, E.; Novio, F.; Gutmann, T.; Poteau, R.; Lecante, P.; Jumas, J.C.; Philippot, K.; Chaudret, B. Tin-decorated ruthenium nanoparticles: A way to tune selectivity in hydrogenation reaction. Nanoscale 2014, 6, 9806–9816. [Google Scholar] [CrossRef]
- Galvagno, S.; Donato, A.; Neri, G.; Pietropaolo, R.; Capannelli, G. Selective hydrogenation of cinnamaldehyde over Ru-Sn catalysts. J. Mol. Catal. 1993, 78, 227–236. [Google Scholar] [CrossRef]
- Gallo, A.; Pirovano, C.; Marelli, M.; Psaro, R.; Dal Santo, V. Hydrogen production by glycerol steam reforming with ru-based catalysts: A study on sn doping. Chem. Vap. Depos. 2010, 16, 305–310. [Google Scholar] [CrossRef]
- Driessen, A.; Sanger, P.; Hemmes, H.; Griessen, R. Metal hydride formation at pressures up to 1 Mbar. J. Phys. Condens. Matter 1990, 2, 9797–9814. [Google Scholar] [CrossRef]
- Yates, J.T.; Peden, C.H.; Houston, J.E.; Goodman, D.W. Subsurface penetration of chemisorbed hydrogen isotopes into the Ru(0001) crystal surface. Surf. Sci. 1985, 160, 37–45. [Google Scholar] [CrossRef]
- Peden, C.H.F.; Goodman, D.W.; Houston, J.E.; Yates, J.T. Subsurface hydrogen on Ru(0001): Quantification by Cu titration. Surf. Sci. 1988, 194, 92–100. [Google Scholar] [CrossRef]
- Lagos, M. Subsurface bonding of hydrogen to metallic surfaces. Surf. Sci. 1982, 122, L601–L607. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metalamorphous- semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.D.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Henkelman, G.; Uberuaga, B.P.; Jónsson, H. Climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
- King, H.W. Crystal structures and lattice parameters of allotropes of the elements. In CRC Handbook of Chemistry and Physics; CRC: Boca Raton, FL, USA, 2012; pp. 15–18. [Google Scholar]
- Vineyard, G.H. Frequency factors and isotope effects in solid state rate processes. J. Phys. Chem. Solids 1957, 3, 121–127. [Google Scholar] [CrossRef]
- Irikura, K.K. Experimental Vibrational Zero-Point Energies: Diatomic Molecules. J. Phys. Chem. Ref. Data 2007, 36, 389–397. [Google Scholar] [CrossRef]
- Tang, W.; Sanville, E.; Henkelman, G. A grid-based Bader analysis algorithm without lattice bias. J. Phys. Condens. Matter 2009, 21, 084204. [Google Scholar] [CrossRef]
- Sanville, E.; Kenny, S.D.; Smith, R.; Henkelman, G. Improved grid-based algorithm for Bader charge allocation. J. Comput. Chem. 2007, 28, 899–908. [Google Scholar] [CrossRef]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Yu, M.; Trinkle, D.R. Accurate and efficient algorithm for Bader charge integration. J. Chem. Phys. 2011, 134, 064111. [Google Scholar] [CrossRef] [PubMed]
- Manz, T.A.; Limas, N.G. Introducing DDEC6 atomic population analysis: Part 1. Charge partitioning theory and methodology. RSC Adv. 2016, 6, 47771–47801. [Google Scholar] [CrossRef]
- Manz, T.A. Introducing DDEC6 atomic population analysis: Part 3. Comprehensive method to compute bond orders. RSC Adv. 2017, 7, 45552–45581. [Google Scholar] [CrossRef]
- Vega, D.; Almeida, D. AIM-UC: An application for QTAIM analysis. J. Comput. Methods Sci. Eng. 2014, 14, 131–136. [Google Scholar] [CrossRef]
- Hoffmann, R. Interaction of Orbitals through Space and through Bonds. Acc. Chem. Res. 1971, 4, 1–9. [Google Scholar] [CrossRef]
- Dronskowski, R.; Blöchl, P.E. Crystal orbital hamilton populations (COHP). Energy-resolved visualization of chemical bonding in solids based on density-functional calculations. J. Phys. Chem. 1993, 97, 8617–8624. [Google Scholar] [CrossRef]
- Deringer, V.L.; Tchougréeff, A.L.; Dronskowski, R. Crystal orbital Hamilton population (COHP) analysis as projected from plane-wave basis sets. J. Phys. Chem. A 2011, 115, 5461–5466. [Google Scholar] [CrossRef]
- Maintz, S.; Deringer, V.L.; Tchougréeff, A.L.; Dronskowski, R. LOBSTER: A tool to extract chemical bonding from plane-wave based DFT. J. Comput. Chem. 2016, 37, 1030–1035. [Google Scholar] [CrossRef]
- Matta, C.F.; Boyd, R.J. An Introduction to the Quantum Theory of Atoms in Molecules; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2007; pp. 1–34. [Google Scholar] [CrossRef]
- Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Ciobica, I.M.; Kleyn, A.W.; Van Santen, R.A. Adsorption and coadsorption of CO and H on ruthenium surfaces. J. Phys. Chem. B 2003, 107, 164–172. [Google Scholar] [CrossRef]
- Del Rosal, I.; Truflandier, L.; Poteau, R.; Gerber, I.C. A density functional theory study of spectroscopic and thermodynamic properties of surfacic hydrides on Ru (0001) model surface: The influence of the coordination modes and the coverage. J. Phys. Chem. C 2011, 115, 2169–2178. [Google Scholar] [CrossRef]
- Luppi, M.; Olsen, R.A.; Baerends, E.J. Six-dimensional potential energy surface for H2 at Ru(0001). Phys. Chem. Chem. Phys. 2006, 8, 688–696. [Google Scholar] [CrossRef] [PubMed]
- Kristinsdóttir, L.; Skúlason, E. A systematic DFT study of hydrogen diffusion on transition metal surfaces. Surf. Sci. 2012, 606, 1400–1404. [Google Scholar] [CrossRef]
- McIntosh, E.M.; Wikfeldt, K.T.; Ellis, J.; Michaelides, A.; Allison, W. Quantum Effects in the Diffusion of Hydrogen on Ru(0001). J. Phys. Chem. Lett. 2013, 4, 1565–1569. [Google Scholar] [CrossRef] [PubMed]
- Van Herpen, M.M.J.W.; Klunder, D.J.W.; Soer, W.A.; Moors, R.; Banine, V. Sn etching with hydrogen radicals to clean EUV optics. Chem. Phys. Lett. 2010, 484, 197–199. [Google Scholar] [CrossRef]
- Pachecka, M.; Sturm, J.M.; van de Kruijs, R.W.E.; Lee, C.J.; Bijkerk, F. Electronegativity-dependent tin etching from thin films. AIP Adv. 2016, 6, 075222. [Google Scholar] [CrossRef]
- Fearon, J.; Watson, G.W. Hydrogen adsorption and diffusion on Pt {111} and PtSn {111}. J. Mater. Chem. 2006, 16, 1989–1996. [Google Scholar] [CrossRef]

| [eV] | [eV] | |||||
|---|---|---|---|---|---|---|
| This Work | Other | This Work | Other | |||
| top | −0.15 | −0.14 [55], −0.09 [54] | Tbulk | 0.76 | ||
| bridge | −0.45 | −0.44 [55], −0.43 [54] | Obulk | 0.21 | ||
| hcp | −0.58 | −0.50 [55], −0.52 [54] | Tsub | 0.90 | 1.04 [55] | |
| fcc | −0.64 | −0.59 [55], −0.55 [54] | Osub | 0.15 | 0.37 [55] | |
| top * | 0.01 | |||||
| hcp * | −0.52 | |||||
| fcc * | −0.58 | |||||
| fcc_Sn * | −0.33 | |||||
| / [Å] | Total Bond Order | Electron Density | Laplacian | Bader Volume [Å3] | NAC | Reaction Energy [eV] | Barrier [eV] | |||
|---|---|---|---|---|---|---|---|---|---|---|
| H | Ru | Sn | ||||||||
| H | 1.90/0.69 | 1.12 | 0.50 | 2.79 | 11.98 | −0.051 | −0.01 | - | 0.93 | 1.06 |
| SnH | 1.89/0.68 | 1.22 | 0.50 | 3.59 | 6.81 | −0.059 | −0.26 | 0.22 | 0.55 | 0.80 |
| SnH2 | 1.88/0.68 | 1.20 | 0.52 | 3.56 | 6.46 | −0.061 | −0.20 | 0.25 | 0.47 | 0.83 |
| SnH3 | 1.89/0.68 | 1.28 | 0.51 | 3.53 | 5.65 | −0.075 | −0.14 | 0.33 | −0.21 | 0.53 |
| SnH4 | 1.82/0.63 | 1.38 | 0.56 | 3.86 | 4.19 | −0.062 | −0.23 | 0.57 | −0.31 | 0.28 |
| SnH2 * | 1.93/0.70 | 1.54 | 0.45 | 3.54 | 3.54 | −0.061 | −0.20 | 0.25 | - | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Onwudinanti, C.; Tranca, I.; Morgan, T.; Tao, S. Tin, The Enabler—Hydrogen Diffusion into Ruthenium. Nanomaterials 2019, 9, 129. https://doi.org/10.3390/nano9010129
Onwudinanti C, Tranca I, Morgan T, Tao S. Tin, The Enabler—Hydrogen Diffusion into Ruthenium. Nanomaterials. 2019; 9(1):129. https://doi.org/10.3390/nano9010129
Chicago/Turabian StyleOnwudinanti, Chidozie, Ionuţ Tranca, Thomas Morgan, and Shuxia Tao. 2019. "Tin, The Enabler—Hydrogen Diffusion into Ruthenium" Nanomaterials 9, no. 1: 129. https://doi.org/10.3390/nano9010129
APA StyleOnwudinanti, C., Tranca, I., Morgan, T., & Tao, S. (2019). Tin, The Enabler—Hydrogen Diffusion into Ruthenium. Nanomaterials, 9(1), 129. https://doi.org/10.3390/nano9010129







