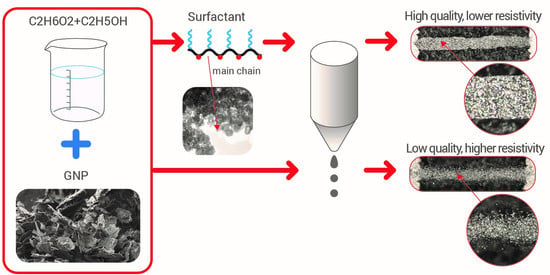
Efficient Inkjet Printing of Graphene-Based Elements: Influence of Dispersing Agent on Ink Viscosity
Abstract
:1. Introduction
2. Materials and Methods
2.1. Ink Formulation
2.2. Rheology Measurements and Printing Process
3. Results and Discussion
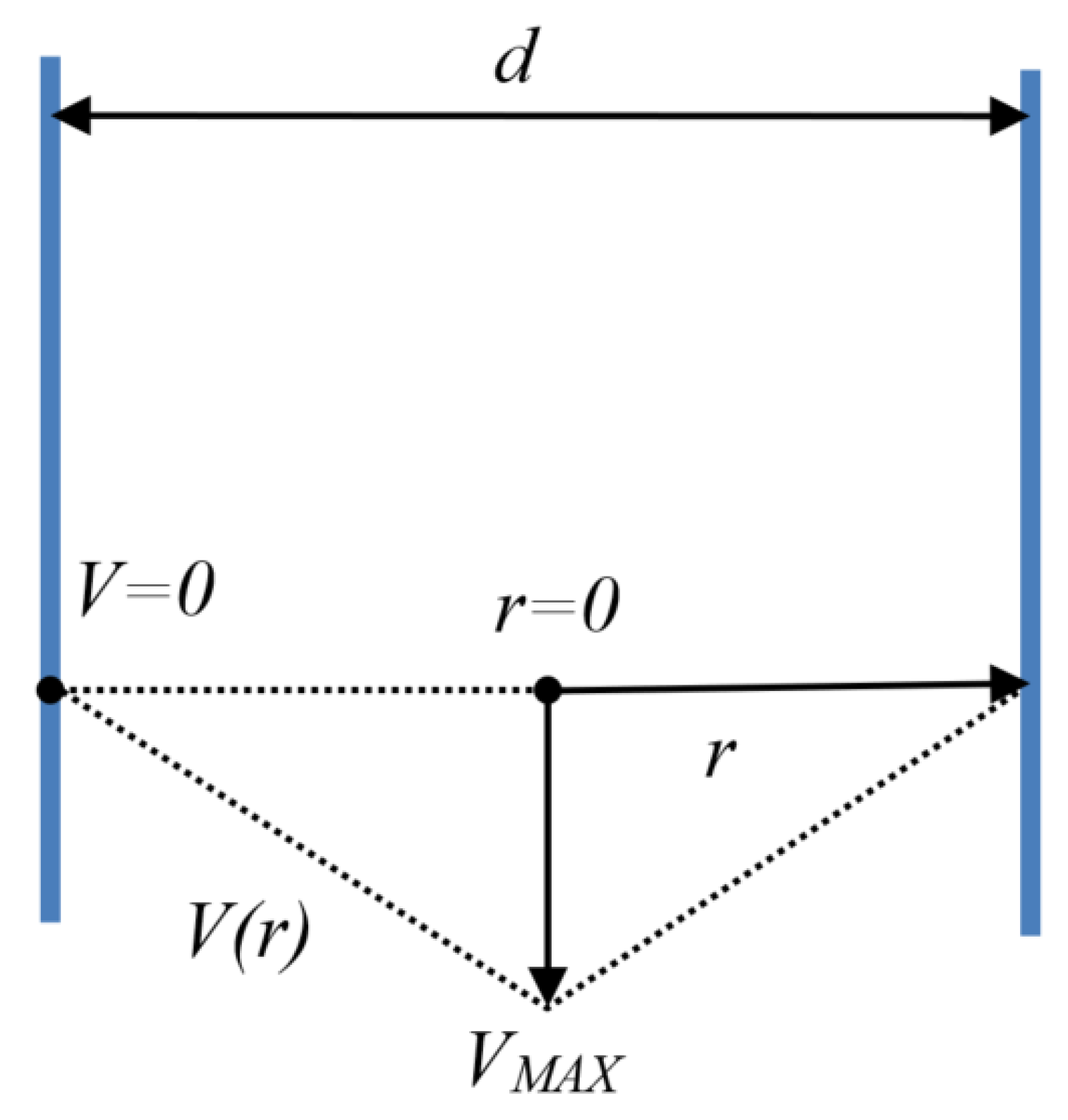
3.1. Calculation of the Shear Rate Acting on the Ink Inside the Nozzle
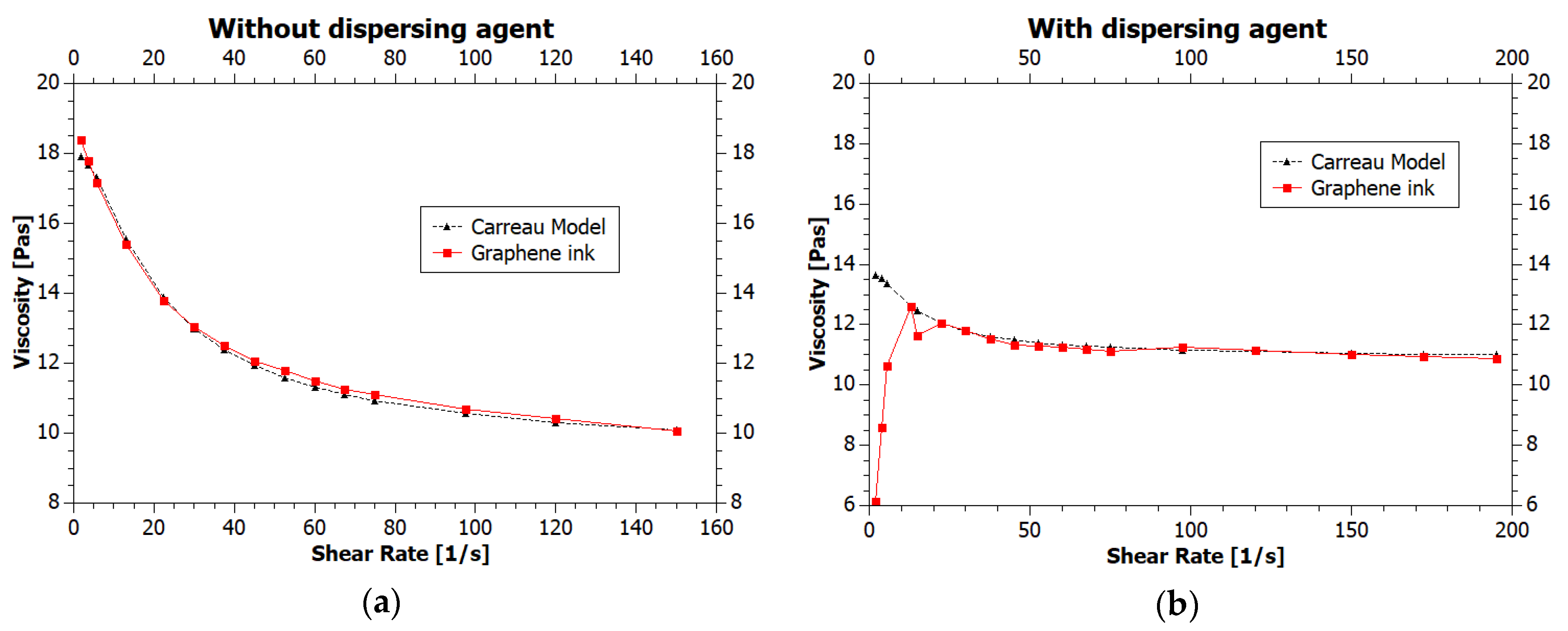
3.2. The Viscosity of Inks
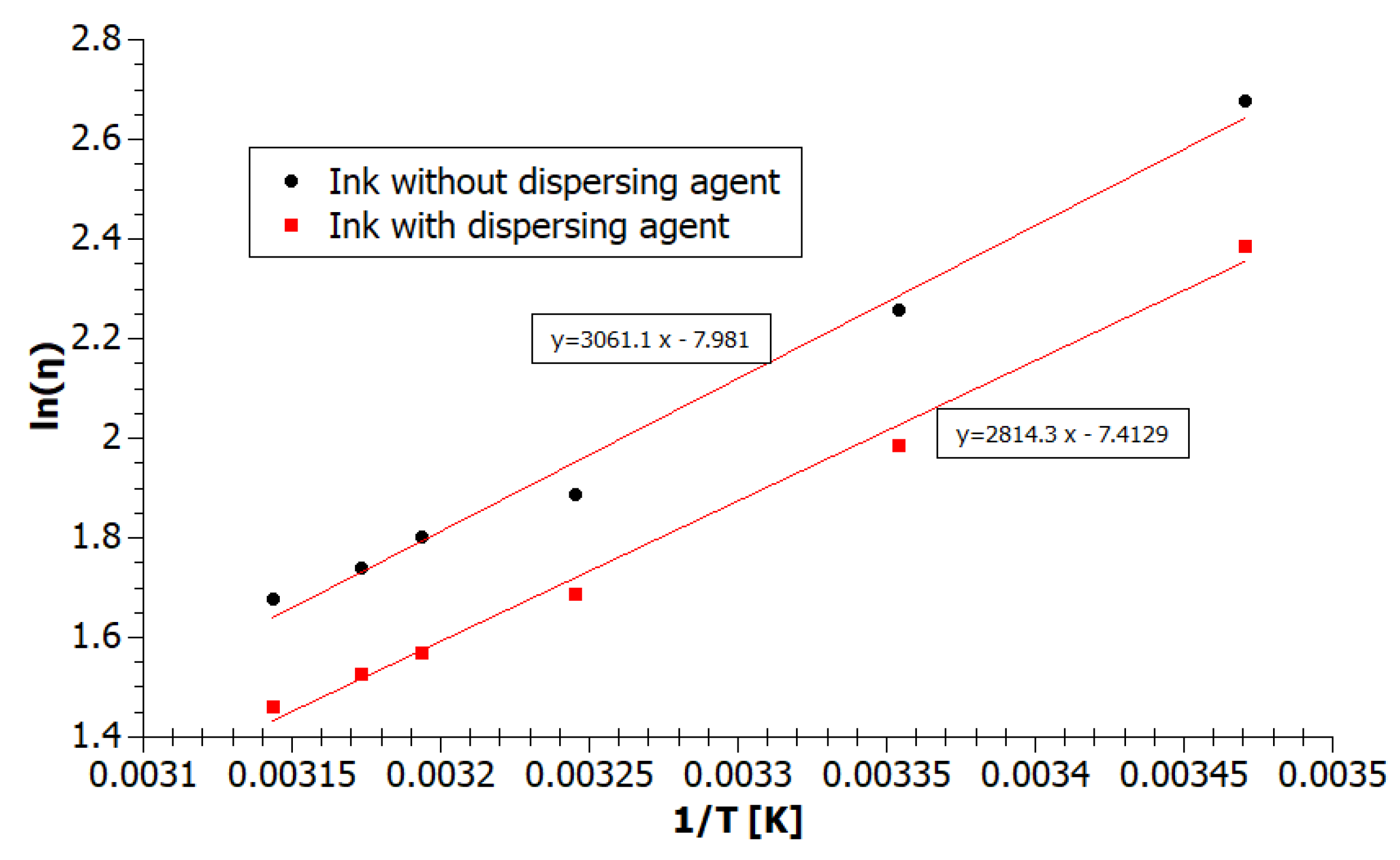
3.3. Calculation of the Temperature Dependence of Inks Viscosity Parameters
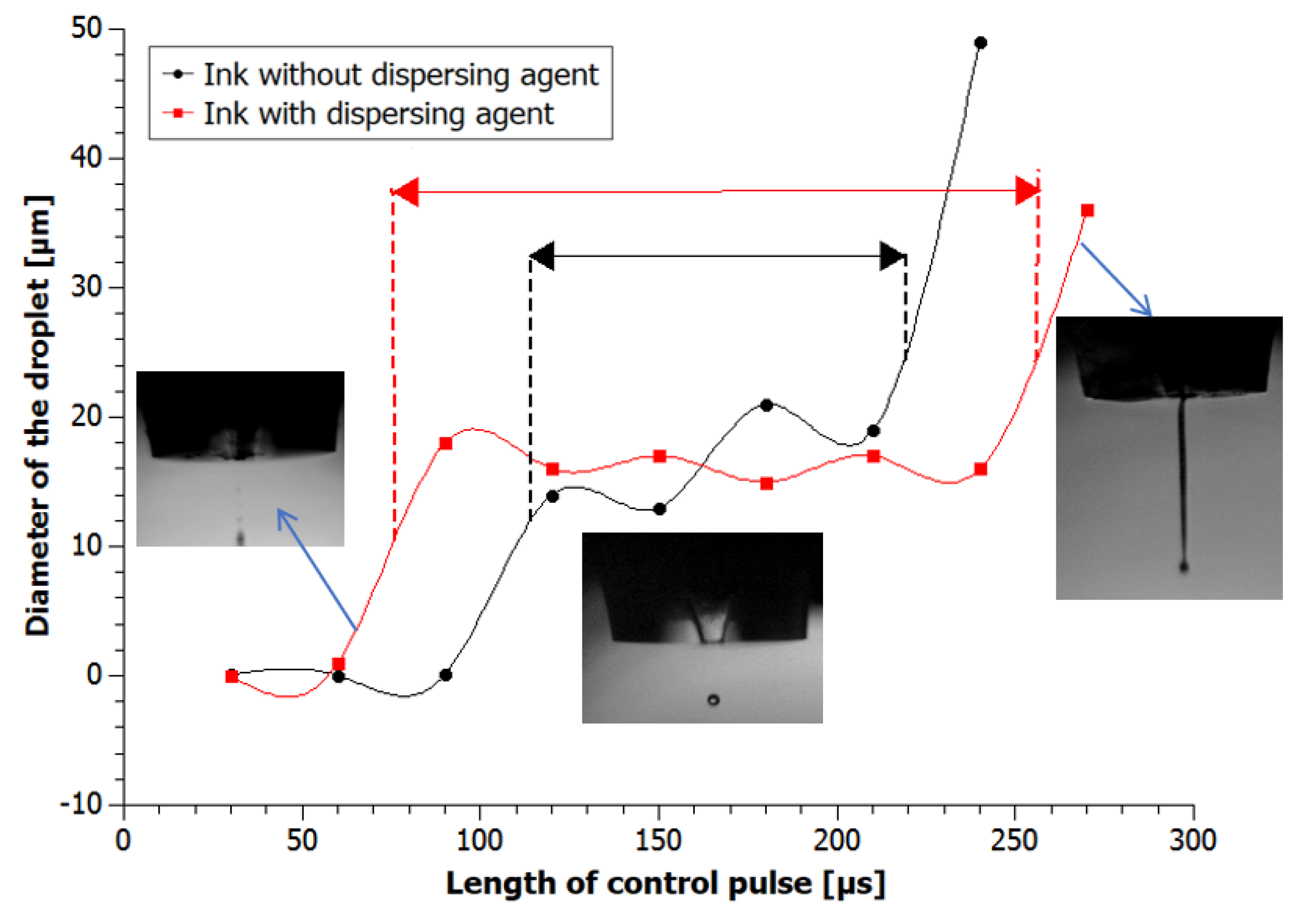
3.4. Influence of Pulse Length on Drop Formation
3.5. Printing Paths
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Huang, L.; Huang, Y.; Liang, J.; Wan, X.; Chen, Y. Graphene-based conducting inks for direct inkjet printing of flexible conductive patterns and their applications in electric circuits and chemical sensors. Nano Res. 2011, 4, 675–684. [Google Scholar] [CrossRef]
- Woo, K.; Jang, D.; Kim, Y.; Moon, J. Relationship between printability and rheological behavior of inkjet conductive inks. Ceram. Int. 2013, 39, 7015–7021. [Google Scholar] [CrossRef]
- Zhang, W.L.; Choi, H.J.; Ko, H.S.; Kwon, K.S. Inkjetting and rheological behavior of a silica particle suspension. J. Ind. Eng. Chem. 2015, 22, 120–126. [Google Scholar] [CrossRef]
- Scoutaris, N.; Alexander, M.R.; Gellert, P.R.; Roberts, C.J. Inkjet printing as a novel medicine formulation technique. J. Control. Release 2011, 156, 179–185. [Google Scholar] [CrossRef] [PubMed]
- Tricomi, B.J.; Dias, A.D.; Corr, D.T. Stem cell bioprinting for applications in regenerative medicine. Ann. N. Y. Acad. Sci. 2016, 1383, 115–124. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Wang, L.; Huang, Y.; Meng, Y.; Sun, G.; Fan, Q.; Shao, J. Fabrication of reactive pigment composite particles for blue-light curable inkjet printing of textiles. RSC Adv. 2017, 7, 36175–36184. [Google Scholar] [CrossRef] [Green Version]
- Stempien, Z.; Rybicki, E.; Rybicki, T.; Lesnikowski, J. Inkjet-printing deposition of silver electro-conductive layers on textile substrates at low sintering temperature by using an aqueous silver ions-containing ink for textronic applications. Sens. Actuators B Chem. 2015, 224, 714–725. [Google Scholar] [CrossRef]
- Mao, H.Y.; Laurent, S.; Chen, W.; Akhavan, O.; Imani, M.; Ashkarran, A.A.; Mahmoudi, M. Graphene: Promises, Facts, Opportunities, and Challenges in Nanomedicine. Chem. Rev. 2013, 113, 3407–3424. [Google Scholar] [CrossRef] [PubMed]
- Shin, K.Y.; Hong, J.Y.; Jang, J. Micropatterning of graphene sheets by inkjet printing and its wideband dipole-antenna application. Adv. Mater. 2011, 23, 2113–2118. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.L.; Chen, C.H.; Chen, C.W. Graphene nanosheets as ink particles for inkjet printing on flexible board. Chem. Eng. J. 2013, 230, 296–302. [Google Scholar] [CrossRef]
- Wang, J.; Fang, Z.; Zhu, H.; Gao, B.; Garner, S.; Cimo, P.; Barcikowski, Z.; Mignerey, A.; Hu, L. Flexible, transparent, and conductive defrosting glass. Thin Solid Films 2014, 556, 13–17. [Google Scholar] [CrossRef]
- Le, L.T.; Ervin, M.H.; Qiu, H.; Fuchs, B.E.; Lee, W.Y. Graphene supercapacitor electrodes fabricated by inkjet printing and thermal reduction of graphene oxide. Electrochem. Commun. 2011, 13, 355–358. [Google Scholar] [CrossRef]
- Dua, V.; Surwade, S.P.; Ammu, S.; Agnihotra, S.R.; Jain, S.; Roberts, K.E.; Park, S.; Ruoff, R.S.; Manohar, S.K. All-organic vapor sensor using inkjet-printed reduced graphene oxide. Angew. Chem. Int. Ed. 2010, 49, 2154–2157. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Liu, H.; Zhao, Y.; Sun, X.; Wen, Y.; Guo, Y.; Gao, X.; Di, C.A.; Yu, G.; Liu, Y. Inkjet printing high-resolution, large-area graphene patterns by coffee-ring lithography. Adv. Mater. 2012, 24, 436–440. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Ye, F.; Vaziri, S.; Muhammed, M.; Lemme, M.C.; Östling, M. Efficient inkjet printing of graphene. Adv. Mater. 2013, 25, 3985–3992. [Google Scholar] [CrossRef] [PubMed]
- Torrisi, F.; Torrisi, T.; Hasan, W.; Wu, Z.; Sun, A.; Lombardo, T.; Kulmala, G.-W.; Hsieh, S.; Jung, F.; Bonaccorso, P.; et al. Inkjet-Printed Graphene Electronics. ACS Nano 2012, 6, 2992–3006. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Secor, E.B.; Gao, T.Z.; Islam, A.E.; Rao, R.; Wallace, S.G.; Zhu, J.; Putz, K.W.; Maruyama, B.; Hersam, M.C. Enhanced Conductivity, Adhesion, and Environmental Stability of Printed Graphene Inks with Nitrocellulose. Chem. Mater. 2017, 29, 2332–2340. [Google Scholar] [CrossRef]
- Secor, E.B.; Prabhumirashi, P.L.; Puntambekar, K.; Geier, M.L.; Hersam, M.C. Inkjet printing of high conductivity, flexible graphene patterns. J. Phys. Chem. Lett. 2013, 4, 1347–1351. [Google Scholar] [CrossRef] [PubMed]
- Caglar, U. Studies of Inkjet Printing Technology with Focus on Electronic Materials; Tampere University of Technology: Tampere, Finland, 2009; ISBN 9789521523021. [Google Scholar]
- Nelo, M.; Sowpati, A.; Palukuru, V.K.; Juuti, J.; Jantunen, H. Formulation of Screen Printable Cobalt Nanoparticle Ink for High Frequency Applications. Prog. Electromagn. Res. 2010, 110, 253–266. [Google Scholar] [CrossRef]
- Kamyshny, A. Metal-based Inkjet Inks for Printed Electronics. Open Appl. Phys. J. 2011, 4, 19–36. [Google Scholar] [CrossRef]
- Gamota, D.; Brazis, P.; Kalyanasundaram, K.; Zhang, J. Printed Organic and Molecular Electronics; Springer Science + Business Media: New York, NY, USA, 2004; ISBN 9781461347835. [Google Scholar]
- Chen, C.N.; Huang, C.T.; Tseng, W.J.; Wei, M.H. Dispersion and rheology of surfactant-mediated silver nanoparticle suspensions. Appl. Surf. Sci. 2010, 257, 650–655. [Google Scholar] [CrossRef]
- Tseng, W.J.; Chen, C.N. Dispersion and rheology of nickel nanoparticle inks. J. Mater. Sci. 2006, 41, 1213–1219. [Google Scholar] [CrossRef]
- Moore, V.C.; Strano, M.S.; Haroz, E.H.; Hauge, R.H.; Smalley, R.E.; Schmidt, J.; Talmon, Y. Individually wuspended wingle-walled carbon nanotubes in various surfactants. Nano Lett. 2003, 3, 1379–1382. [Google Scholar] [CrossRef]
- Wajid, A.S.; Das, S.; Irin, F.; Ahmed, H.S.T.; Shelburne, J.L.; Parviz, D.; Fullerton, R.J.; Jankowski, A.F.; Hedden, R.C.; Green, M.J. Polymer-stabilized graphene dispersions at high concentrations in organic solvents for composite production. Carbon N. Y. 2012, 50, 526–534. [Google Scholar] [CrossRef]
- Heinzl, J.; Hertz, C.H. Inkjet Printing. Adv. Eletron. Electron Phys. 1985, 65, 91–171. [Google Scholar]
- McIlroy, C.; Harlen, O.G. Modelling capillary break-up of particulate suspensions. Phys. Fluids 2014, 26, 033010. [Google Scholar] [CrossRef]
- Derby, B.; Reis, N. Inkjet Printing of Highly Loaded Particulate Suspensions. MRS Bull. 2003, 28, 815–818. [Google Scholar] [CrossRef]
- Tuladhar, T.R.; Mackley, M.R. Filament stretching rheometry and break-up behaviour of low viscosity polymer solutions and inkjet fluids. J. Nonnewton. Fluid Mech. 2008, 148, 97–108. [Google Scholar] [CrossRef]
- De Gans, B.-J.; Duineveld, P.C.; Schubert, U.S. Inkjet printing of polymers: State of the art and future developments. Adv. Mater. 2004, 16, 203–213. [Google Scholar] [CrossRef]
- Dong, H.; Carr, W.W.; Morris, J.F. An experimental study of drop-on-demand drop formation. Phys. Fluids 2006, 18, 072102. [Google Scholar] [CrossRef]
- Castrejón-Pita, J.R.; Martin, G.D.; Hoath, S.D.; Hutchings, I.M. A simple large-scale droplet generator for studies of inkjet printing. Rev. Sci. Instrum. 2008, 79, 075108. [Google Scholar] [CrossRef] [PubMed]
- Messaâdi, A.; Dhouibi, N.; Hamda, H.; Belgacem, F.B.M.; Adbelkader, Y.H.; Ouerfelli, N.; Hamzaoui, A.H. A New Equation Relating the Viscosity Arrhenius Temperature and the Activation Energy for Some Newtonian Classical Solvents. J. Chem. 2015, 2015, 7–10. [Google Scholar] [CrossRef]
- Dyre, J.C.; Olsen, N.B.; Christensen, T. Local elastic expansion model for viscous-flow activation energies of glass-forming molecular liquids. Phys. Rev. B 1996, 53, 2171–2174. [Google Scholar] [CrossRef]

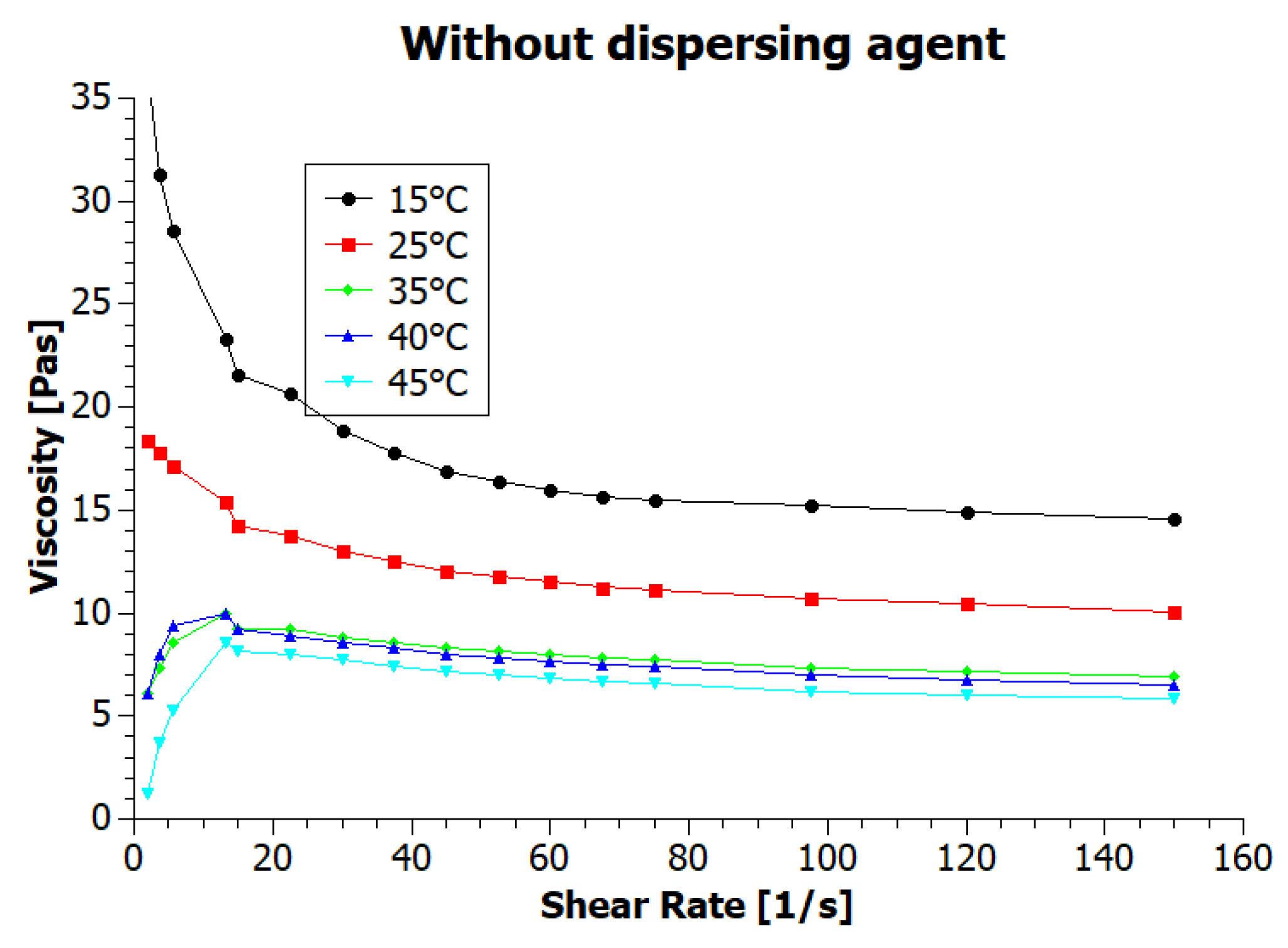
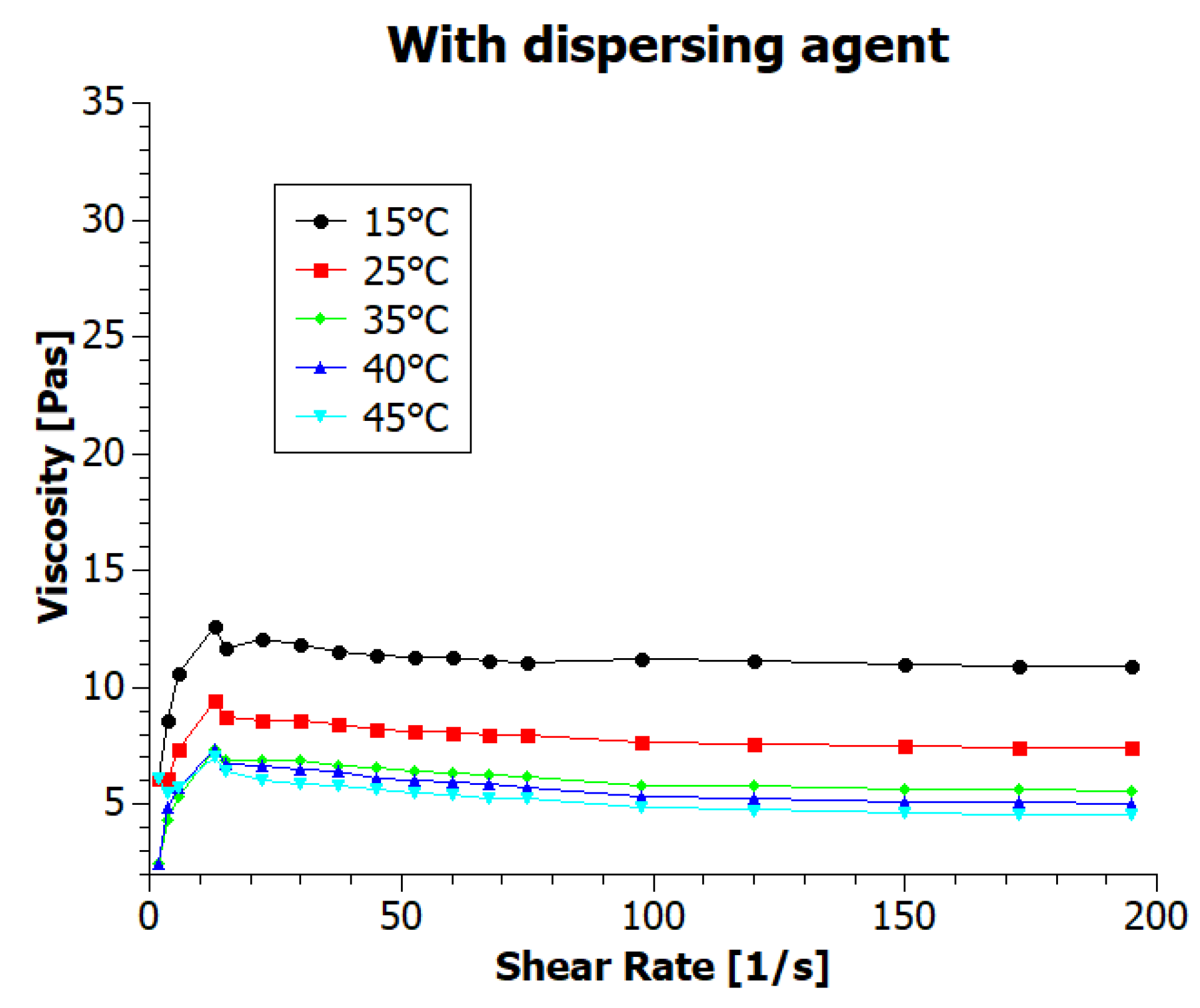


| Temperature (°C) | GNP1 Ink Viscosity (mPas) | GNP2 Ink Viscosity (mPas) |
|---|---|---|
| 15 | 14.56 | 11.00 |
| 25 | 10.07 | 7.48 |
| 35 | 6.54 | 5.06 |
| 45 | 5.82 | 4.46 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dybowska-Sarapuk, L.; Kielbasinski, K.; Arazna, A.; Futera, K.; Skalski, A.; Janczak, D.; Sloma, M.; Jakubowska, M. Efficient Inkjet Printing of Graphene-Based Elements: Influence of Dispersing Agent on Ink Viscosity. Nanomaterials 2018, 8, 602. https://doi.org/10.3390/nano8080602
Dybowska-Sarapuk L, Kielbasinski K, Arazna A, Futera K, Skalski A, Janczak D, Sloma M, Jakubowska M. Efficient Inkjet Printing of Graphene-Based Elements: Influence of Dispersing Agent on Ink Viscosity. Nanomaterials. 2018; 8(8):602. https://doi.org/10.3390/nano8080602
Chicago/Turabian StyleDybowska-Sarapuk, Lucja, Konrad Kielbasinski, Aneta Arazna, Konrad Futera, Andrzej Skalski, Daniel Janczak, Marcin Sloma, and Malgorzata Jakubowska. 2018. "Efficient Inkjet Printing of Graphene-Based Elements: Influence of Dispersing Agent on Ink Viscosity" Nanomaterials 8, no. 8: 602. https://doi.org/10.3390/nano8080602
APA StyleDybowska-Sarapuk, L., Kielbasinski, K., Arazna, A., Futera, K., Skalski, A., Janczak, D., Sloma, M., & Jakubowska, M. (2018). Efficient Inkjet Printing of Graphene-Based Elements: Influence of Dispersing Agent on Ink Viscosity. Nanomaterials, 8(8), 602. https://doi.org/10.3390/nano8080602