Extreme Energy Density Confined Inside a Transparent Crystal: Status and Perspectives of Solid-Plasma-Solid Transformations
Abstract
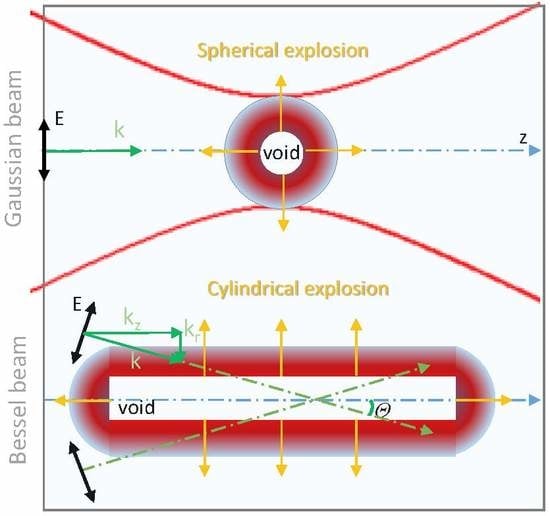
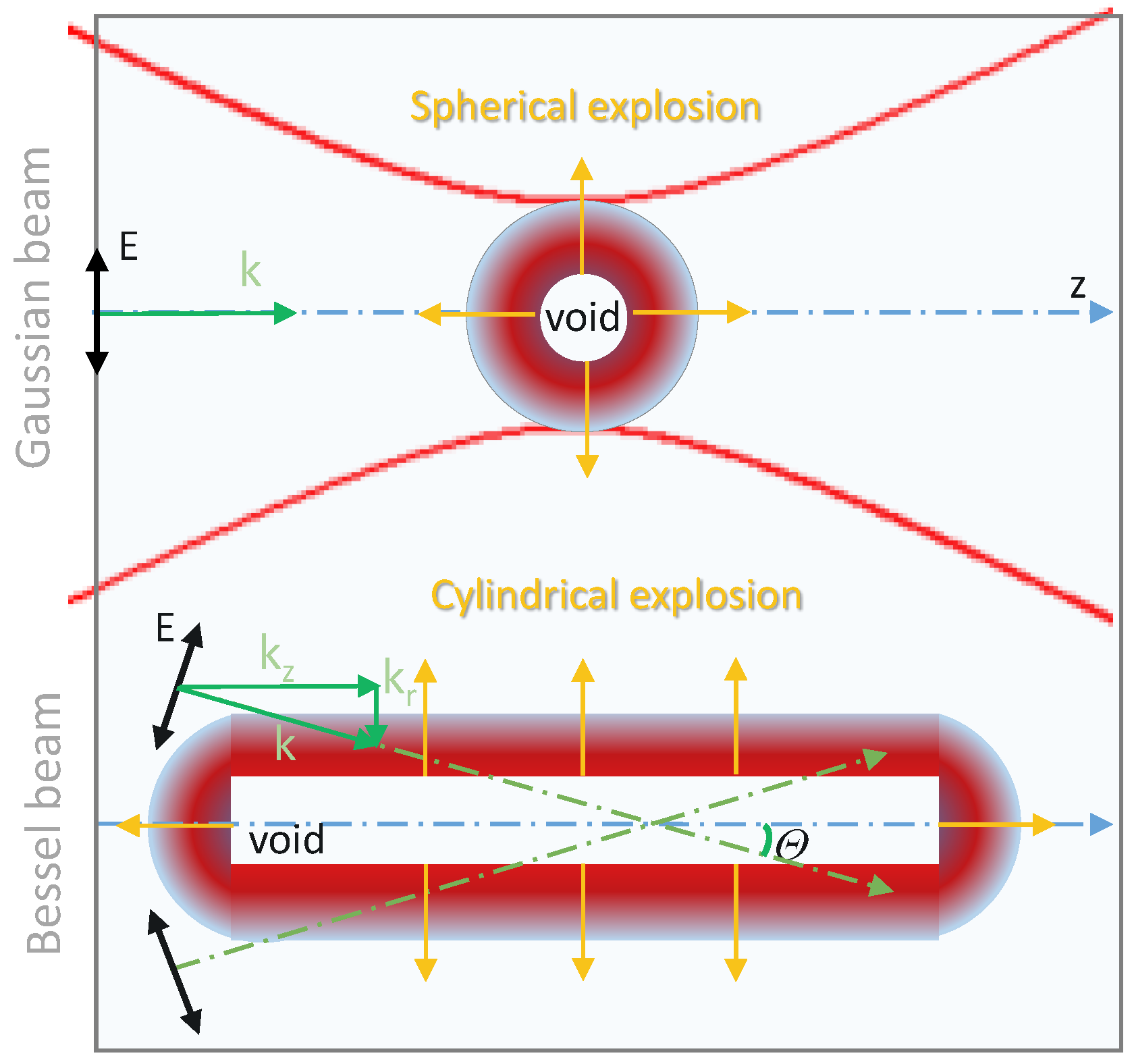
1. Microexplosion Studies with Gauss-Shaped Beam
1.1. Novelty of the Phase Transformation Path during and after Confined Microexplosion
1.2. Limitations of the Confined Microexplosion Method with the GB
2. Status of the BB-Transparent Crystal Interactions
Control of Energy Deposition by BB Pulses
3. Conclusions and Outlook
- The low intensity stage before ionisation threshold lasts a few fs at the beginning of the pulse;
- As the ionisation threshold is attained, the cylindrical plasma region is created at the axis of the focal region with a diameter less than a micron. One should note that the full length of the focal region of m is reached at the end of the pulse, assuming that light propagates as in unaffected sapphire with a speed of cm/s;
- The cylinder diameter of the energy absorption region to the end of the pulse allegedly might be around the doubled absorption length in a dense plasma ∼60 nm;
- The shock wave is created after the energy transfer from electrons to ions in a 7–10-ps time span;
- The shock wave propagates during another 4–6 ps until it is converted into the acoustic wave, effectively stopped by the cold pressure of the crystal (∼Young modulus of sapphire). The void surrounded by the shell of compressed material is formed by the rarefaction wave;
- The thermal wave of conventional heat conduction spreads into the laser-unaffected crystal, cooling the laser-affected area down to the ambient conditions during tens of nanoseconds. The material re-structuring occurs most probably during Stages 5 and 6. The whole area affected by the heat from the laser-heated region is a cylinder with a length of around 32–34 microns with a diameter of about 2–4 micrometers.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Juodkazis, S.; Nishimura, K.; Tanaka, S.; Misawa, H.; Gamaly, E.E.; Luther-Davies, B.; Hallo, L.; Nicolai, P.; Tikhonchuk, V. Laser-induced microexplosion confined in the bulk of a sapphire crystal: Evidence of multimegabar pressures. Phys. Rev. Lett. 2006, 96, 166101. [Google Scholar] [CrossRef] [PubMed]
- Gamaly, E.E.; Juodkazis, S.; Nishimura, K.; Misawa, H.; Luther-Davies, B.; Hallo, L.; Nicolai, P.; Tikhonchuk, V. Laser-matter interaction in a bulk of a transparent solid: confined microexplosion and void formation. Phys. Rev. B 2006, 73, 214101. [Google Scholar] [CrossRef]
- Vailionis, A.; Gamaly, E.G.; Mizeikis, V.; Yang, W.; Rode, A.; Juodkazis, S. Evidence of super-dense Aluminum synthesized by ultra-fast microexplosion. Nat. Commun. 2011, 2, 445. [Google Scholar] [CrossRef] [PubMed]
- Rapp, L.; Haberl, B.; Pickard, C.J.; Bradby, J.E.; Gamaly, E.G.; Williams, J.S.; Rode, A.V. Experimental evidence of new tetragonal polymorphs of silicon formed through ultrafast laser-induced confined microexplosion. Nat. Commun. 2015, 6, 7555. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; He, C.; Pickard, C.J.; Tang, C.; Zhong, J. Stochastic generation of complex crystal structures combining group and graph theory with application to carbon. Phys. Rev. B 2018, 97, 014104. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Gamaly, E.G.; Rapp, L.; Roppo, V.; Juodkazis, S.; Rode, A.V. Generation of high energy density by fs-laser induced confined microexplosion. New J. Phys. 2013, 15, 025018. [Google Scholar] [CrossRef]
- Rapp, L.; Meyer, R.; Giust, R.; Furfaro, L.; Jacquot, M.; Lacourt, P.A.; Dudley, J.M.; Courvoisier, F. High aspect ratio microexplosions in the bulk of sapphire generated by femtosecond Bessel beams. Sci. Rep. 2016, 6, 34286. [Google Scholar] [CrossRef] [PubMed]
- Gamaly, E.G.; Rode, A.V.; Rapp, L.; Giust, R.; Furfaro, L.; Lacourt, P.A.; Dudley, J.M.; Courvoisier, F.; Juodkazis, S. Interaction of the ultra-short Bessel beam with transparent dielectrics: Evidence of high-energy concentration and multi-TPa pressure. arXiv, 2017; arXiv:1708.07630. [Google Scholar]
- Durnin, J.; Miceli, J.J.; Eberly, J.H. Diffraction-free beams. Phys. Rev. Lett. 1987, 58, 1499. [Google Scholar] [CrossRef] [PubMed]
- Marcinkevičius, A.; Juodkazis, S.; Matsuo, S.; Mizeikis, V.; Misawa, H. Application of Bessel Beams for microfabrication of dielectrics by femtosecond laser. Jpn. J. Appl. Phys. 2001, 40, L1197–L1199. [Google Scholar] [CrossRef]
- Mikutis, M.; Kudrius, T.; Šlekys, G.; Paipulas, D.; Juodkazis, S. High 90% efficiency Bragg gratings formed in fused silica by femtosecond Gauss-Bessel laser beams. Opt. Mat. Express 2013, 11, 1862–1871. [Google Scholar] [CrossRef]
- Buividas, R.; Gervinskas, G.; Tadich, A.; Cowie, B.; Mizeikis, V.; Vailionis, A.; de Ligny, D.; Gamaly, E.G.; Rode, A.; Juodkazis, S. Phase transformation in laser-induced microexplosion in olivine (Fe,Mg)2SiO4. Adv. Eng. Mater. 2014, 16, 767–773. [Google Scholar] [CrossRef]
- Liu, H.; Lalanne, P. Microscopic theory of the extraordinary optical transmission. Nature 2008, 452, 728–731. [Google Scholar] [CrossRef] [PubMed]
- Morse, P.; Feshbach, H. Methods of Theoretical Physics; McGraw Hill: New York, NY, USA, 1953; Volume 1–2. [Google Scholar]
- Salo, J.; Fagerholm, J.; Friberg, A.T.; Salomaa, M.M. Unified description of nondiffracting X and Y waves. Phys. Rev. E 2000, 62, 4261. [Google Scholar] [CrossRef]
- Porras, M.A.; Parola, A.; Faccio, D.; Dubietis, A.; Trapani, P.D. Nonlinear Unbalanced Bessel Beams: Stationary Conical Waves Supported by Nonlinear Losses. Phys. Rev. Lett. 2004, 93, 153902. [Google Scholar] [CrossRef] [PubMed]
- Hu, J. High throughput micro/nano manufacturing by femtosecond laser temporal pulse shaping. In Proceedings of the 9th International Conference on Information Optics and Photonics, Harbin, China, 17–20 July 2017. [Google Scholar]
- Wang, G.; Yu, Y.; Jiang, L.; Li, X.; Xie, Q.; Lu, Y. Cylindrical shockwave-induced compression mechanism in femtosecond laser Bessel pulse micro-drilling of PMMA. Appl. Phys. Lett. 2017, 110, 161907. [Google Scholar] [CrossRef]
- Dharmavarapu, R.; Bhattacharya, S.; Juodkazis, S. Diffractive optics for axial intensity shaping of Bessel beams. J. Opt. 2018, 20, 085606. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gamaly, E.G.; Juodkazis, S.; Rode, A.V. Extreme Energy Density Confined Inside a Transparent Crystal: Status and Perspectives of Solid-Plasma-Solid Transformations. Nanomaterials 2018, 8, 555. https://doi.org/10.3390/nano8070555
Gamaly EG, Juodkazis S, Rode AV. Extreme Energy Density Confined Inside a Transparent Crystal: Status and Perspectives of Solid-Plasma-Solid Transformations. Nanomaterials. 2018; 8(7):555. https://doi.org/10.3390/nano8070555
Chicago/Turabian StyleGamaly, Eugene G., Saulius Juodkazis, and Andrei V. Rode. 2018. "Extreme Energy Density Confined Inside a Transparent Crystal: Status and Perspectives of Solid-Plasma-Solid Transformations" Nanomaterials 8, no. 7: 555. https://doi.org/10.3390/nano8070555
APA StyleGamaly, E. G., Juodkazis, S., & Rode, A. V. (2018). Extreme Energy Density Confined Inside a Transparent Crystal: Status and Perspectives of Solid-Plasma-Solid Transformations. Nanomaterials, 8(7), 555. https://doi.org/10.3390/nano8070555