High Frequency Hysteresis Losses on γ-Fe2O3 and Fe3O4: Susceptibility as a Magnetic Stamp for Chain Formation
Abstract
1. Introduction
2. Materials and Methods
2.1. Synthesis of the Iron Oxide Nanoparticles
2.2. Structural and Colloidal Characterization
2.3. Magnetic Characterization
3. Results and Discussion
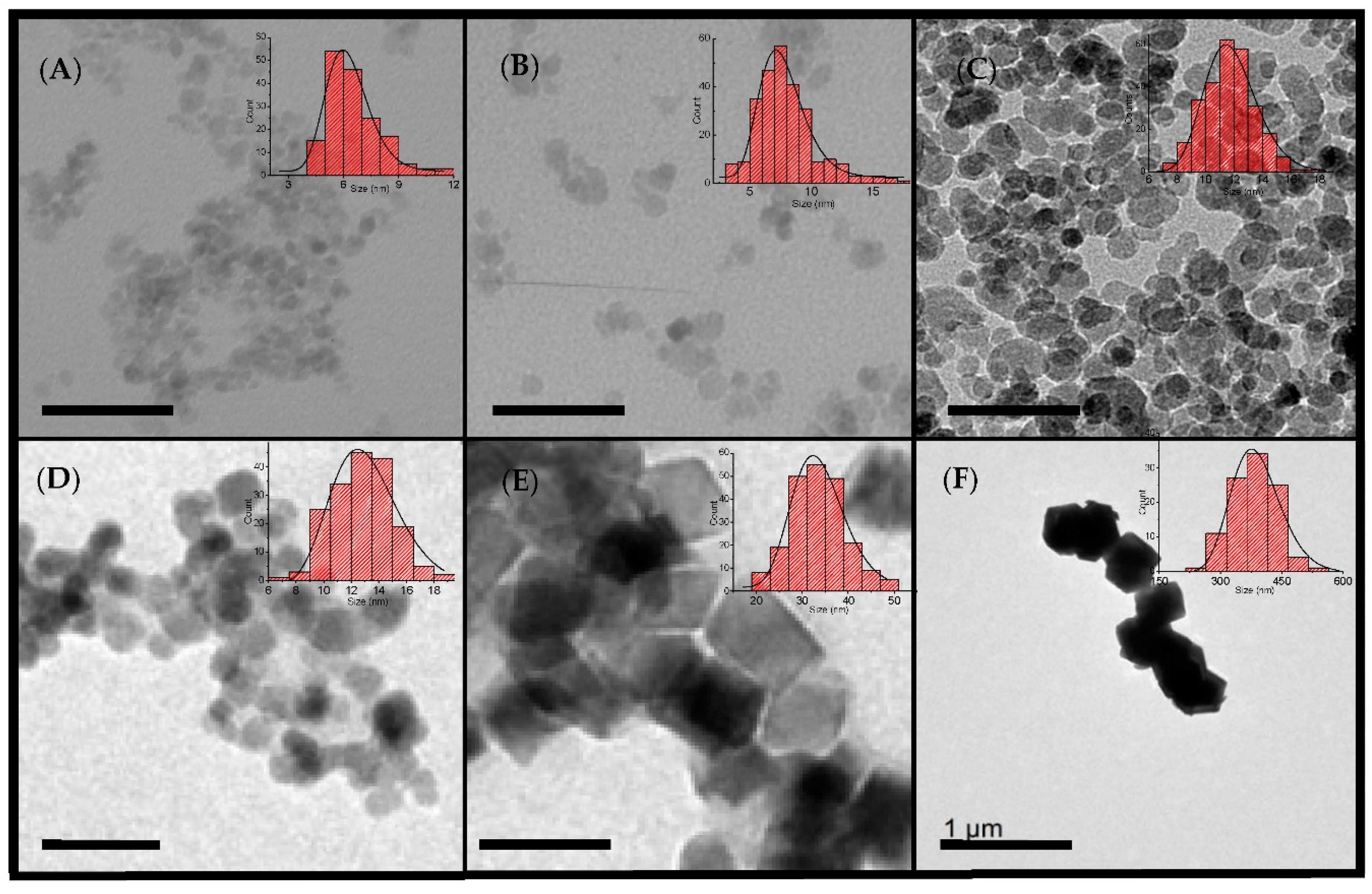
3.1. Structural and Colloidal Characterization
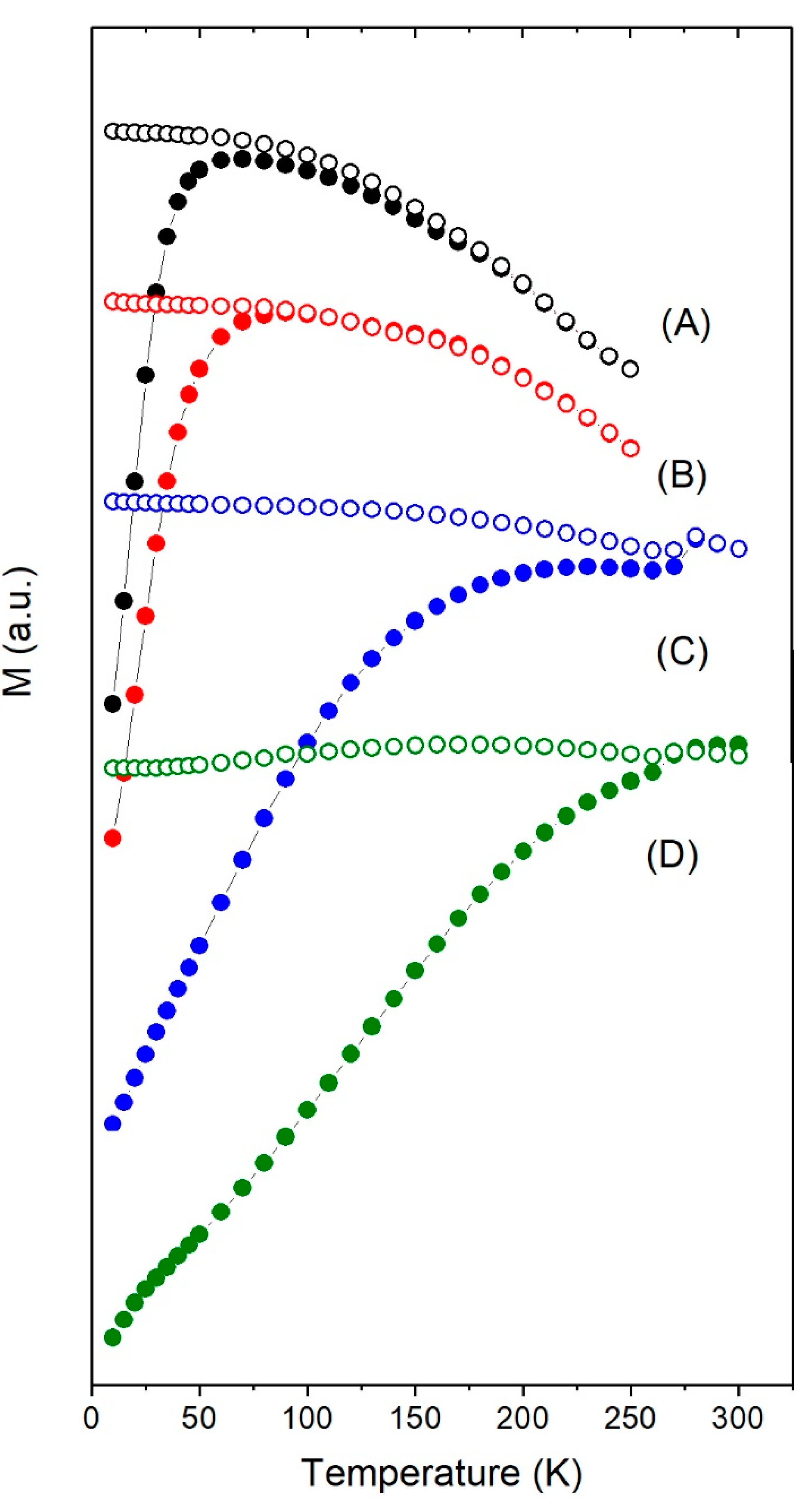
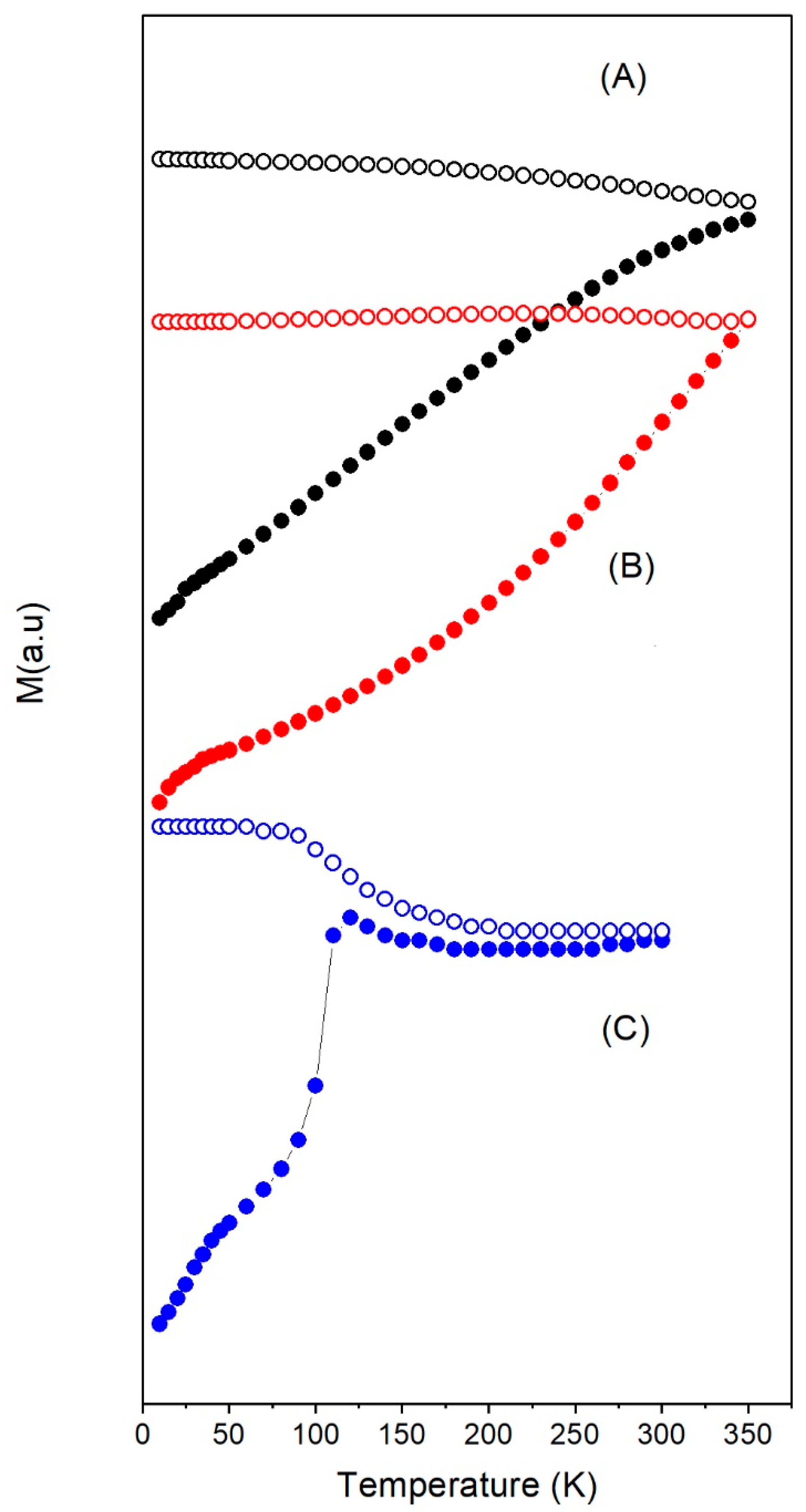
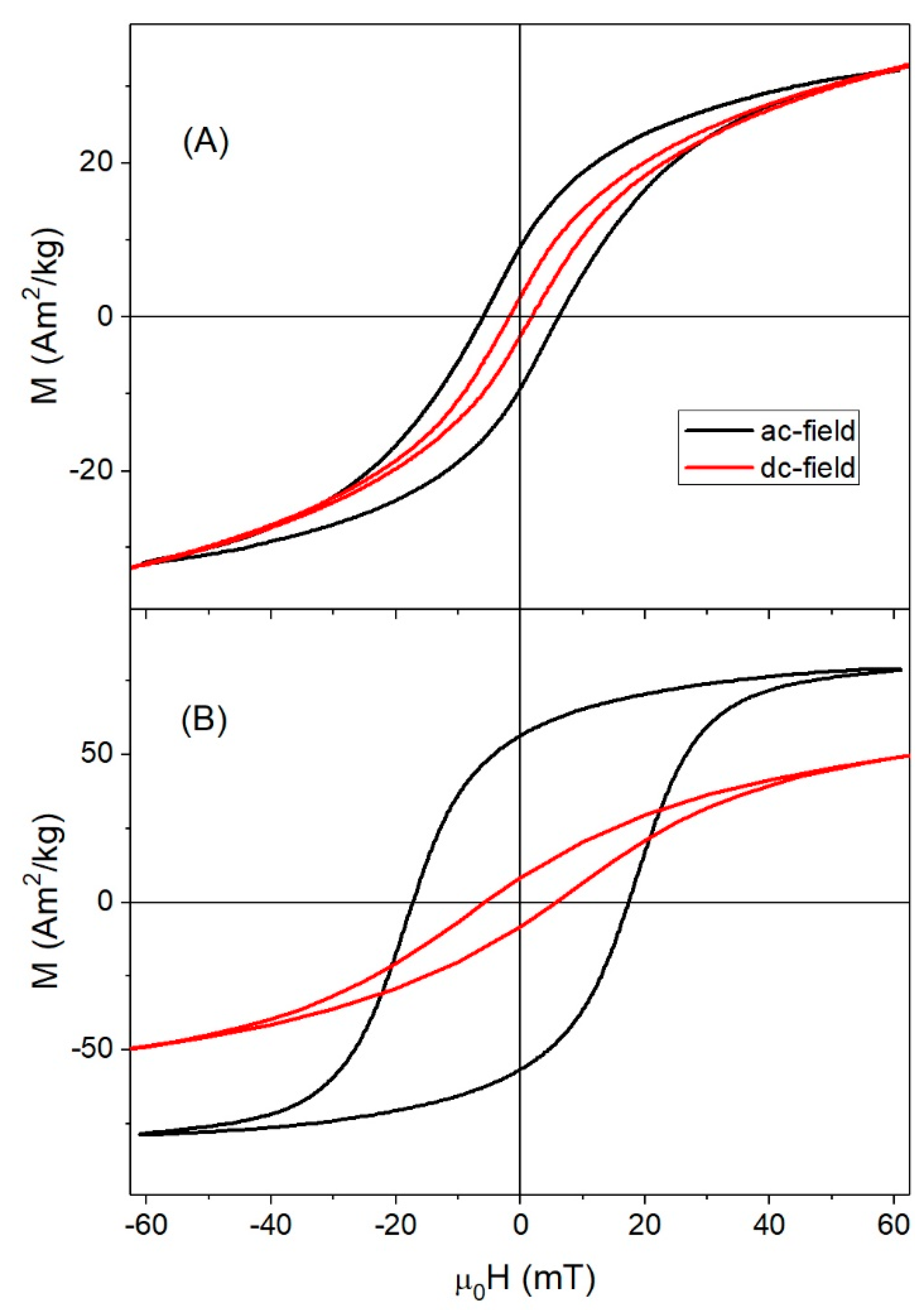
3.2. Magnetic Properties under dc-Field
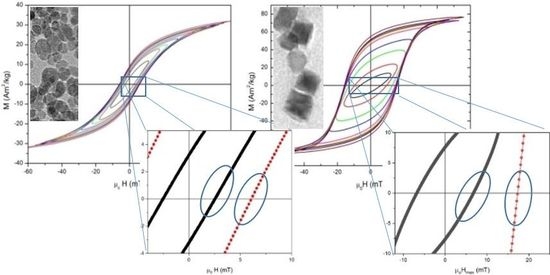
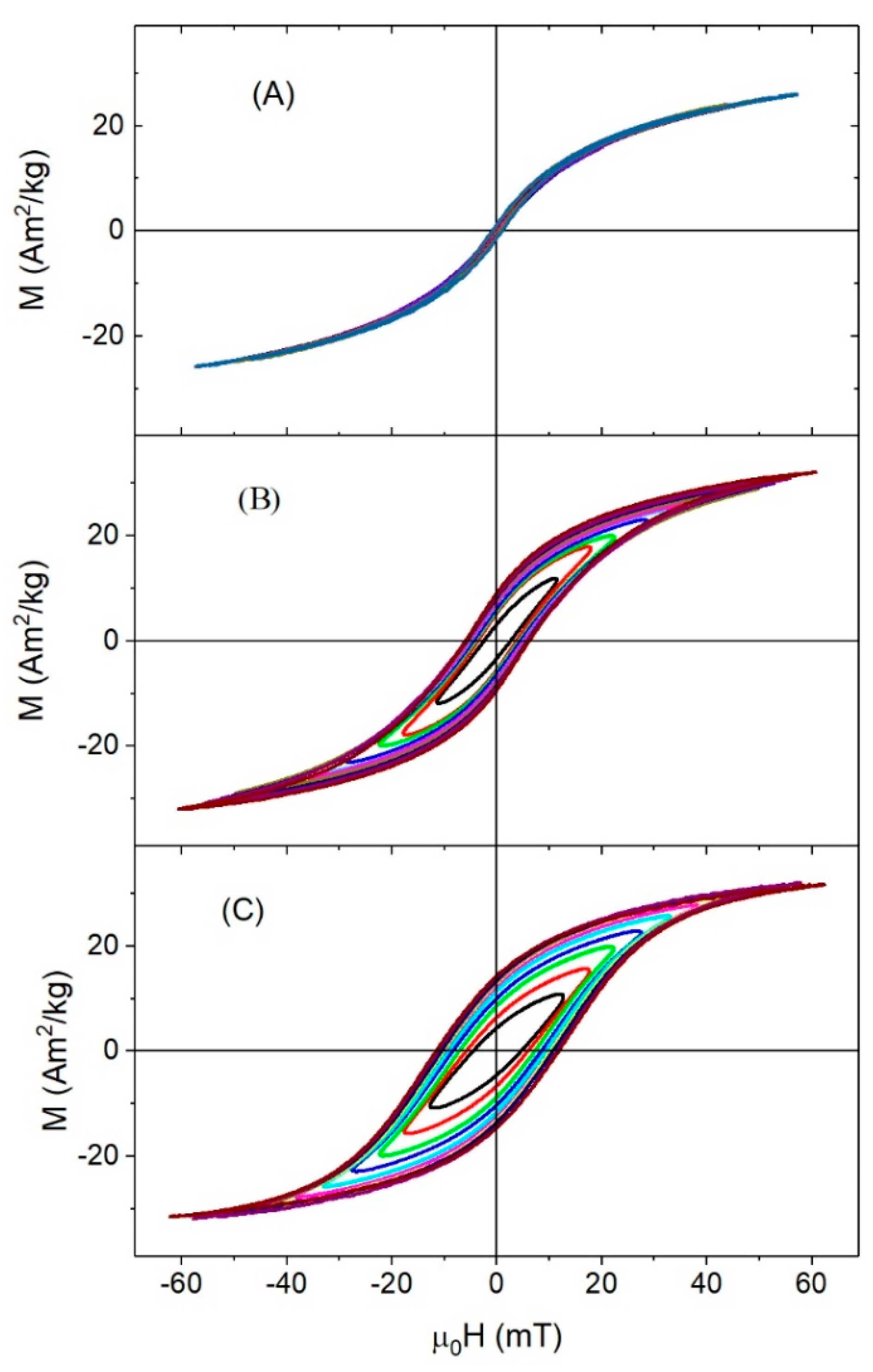
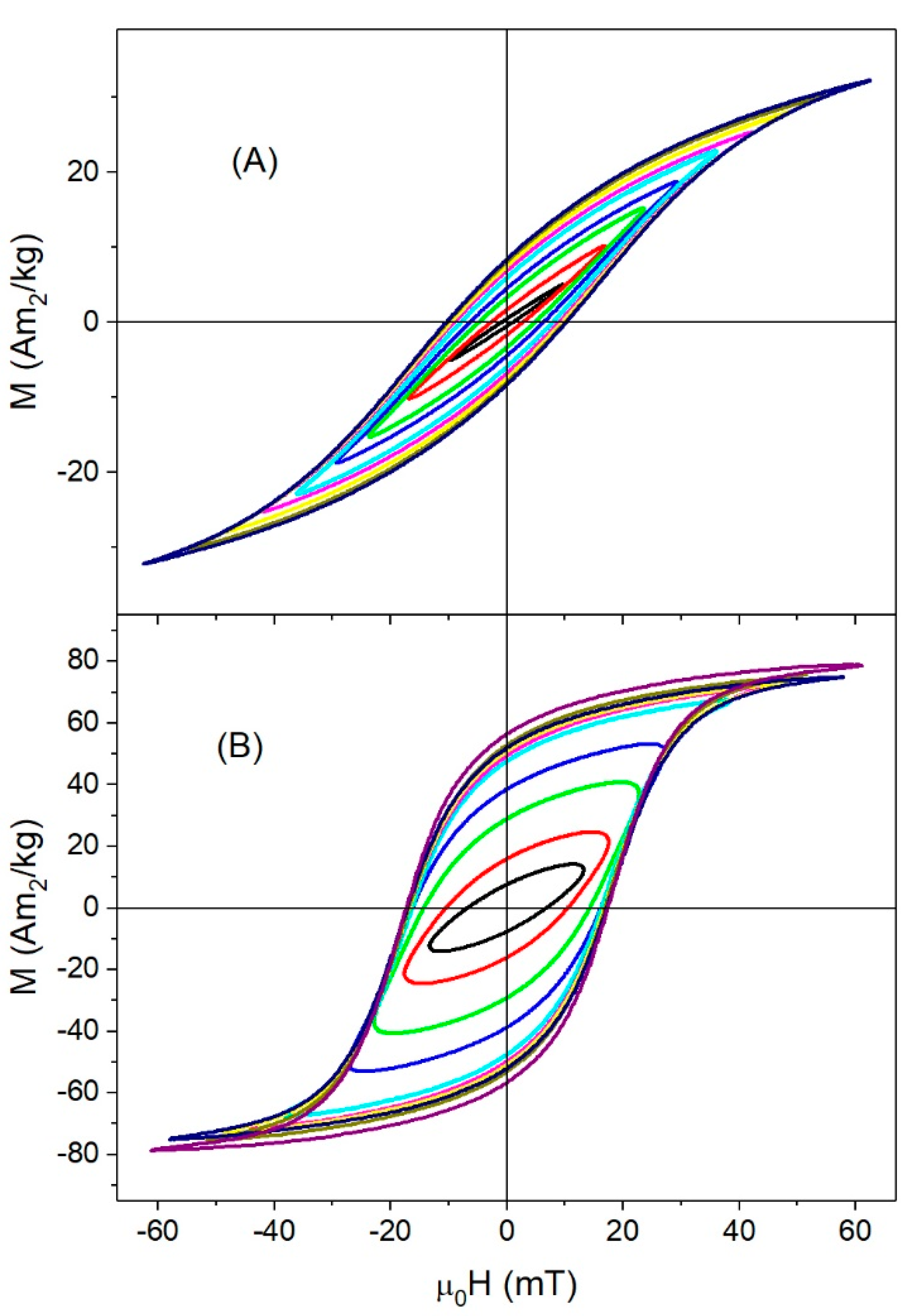
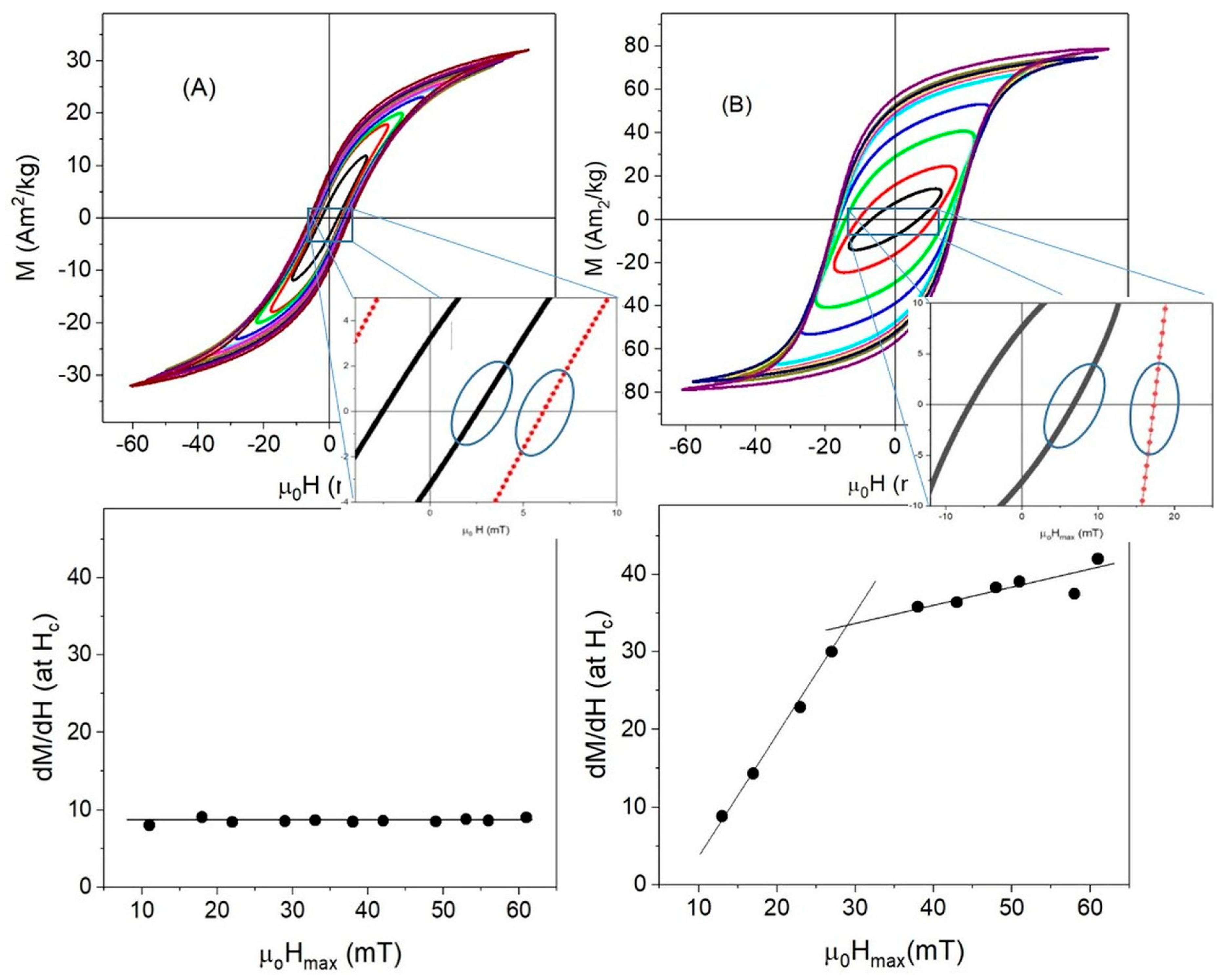
3.3. High-Frequency Hysteresis Loop Measurements
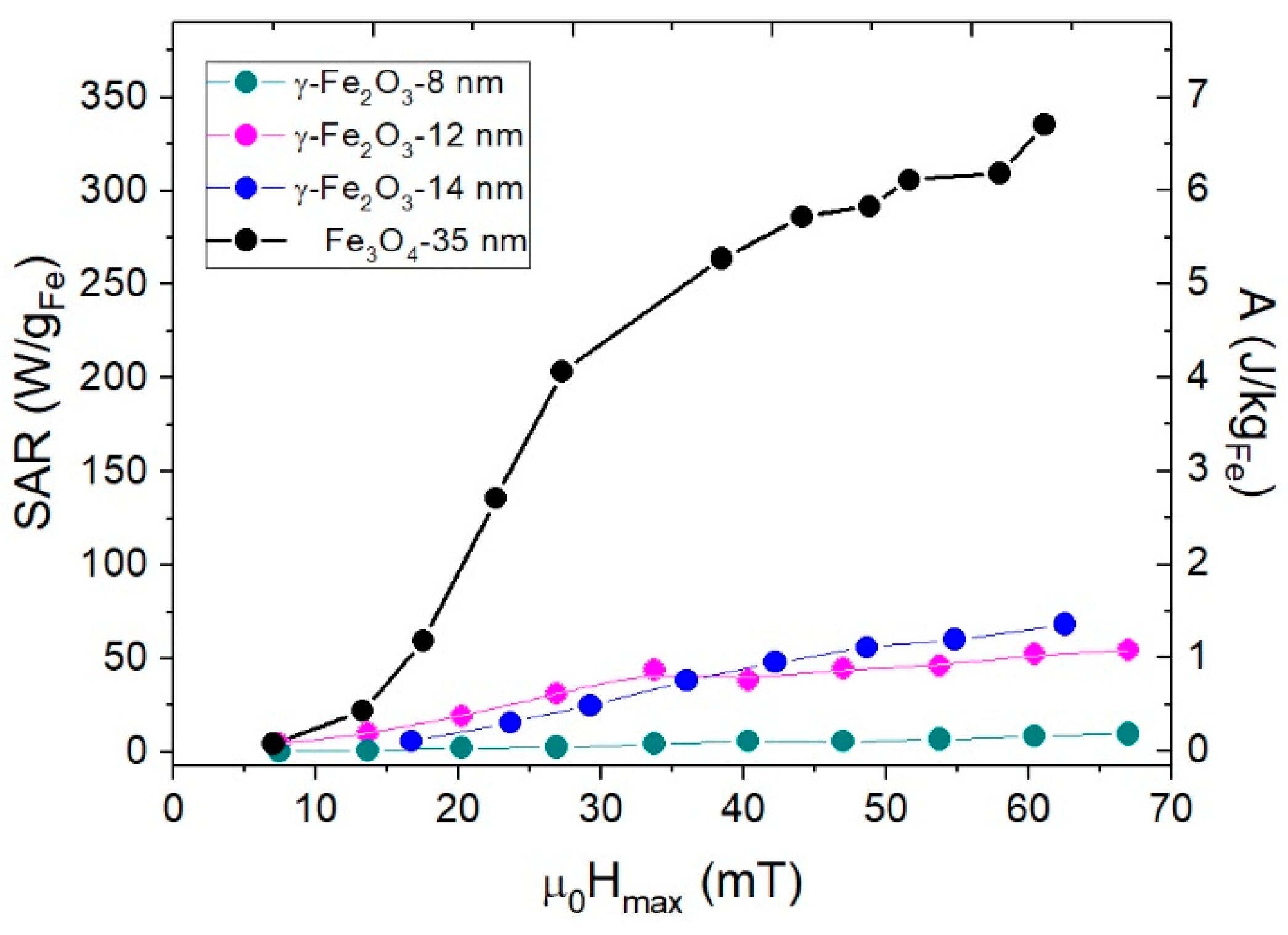
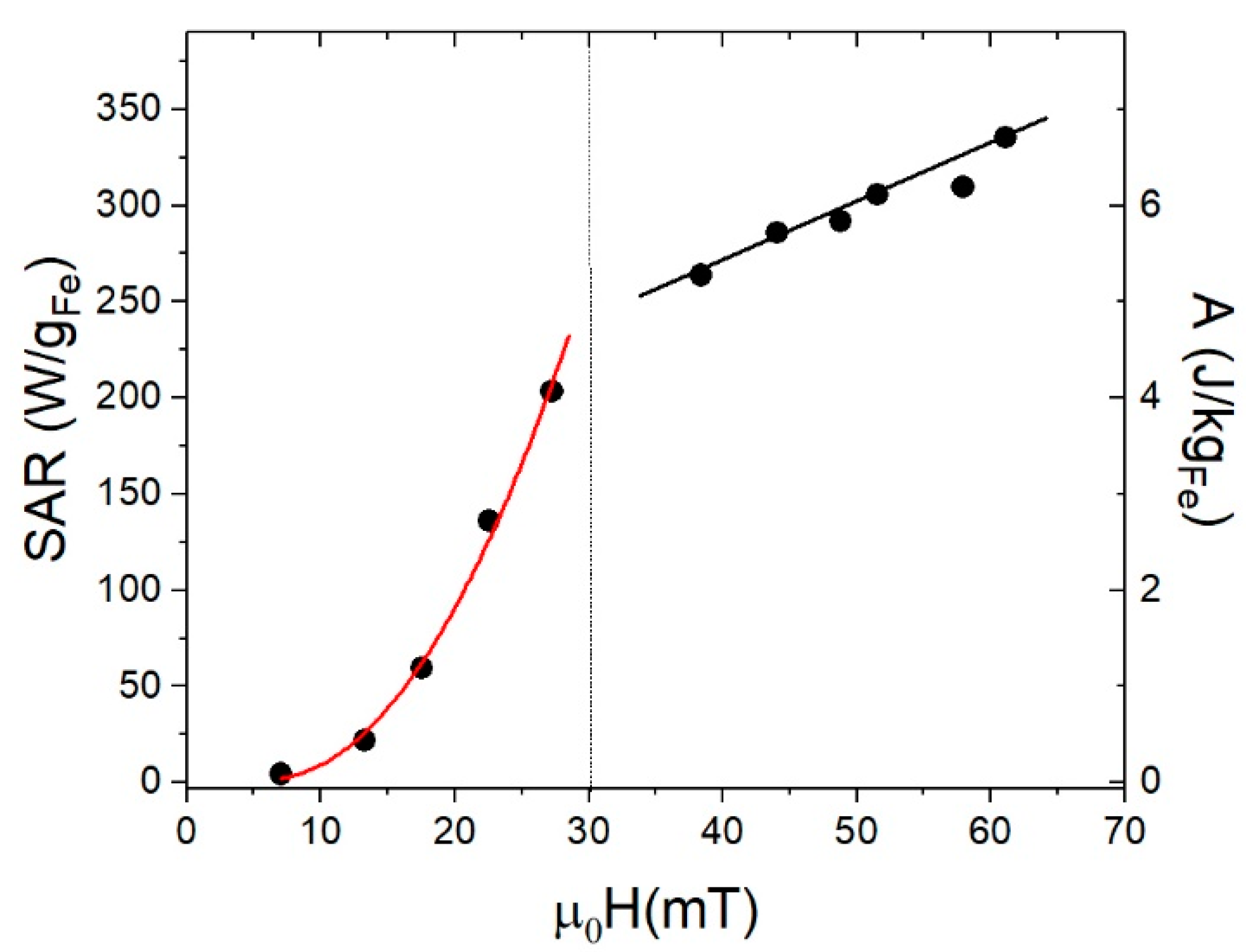
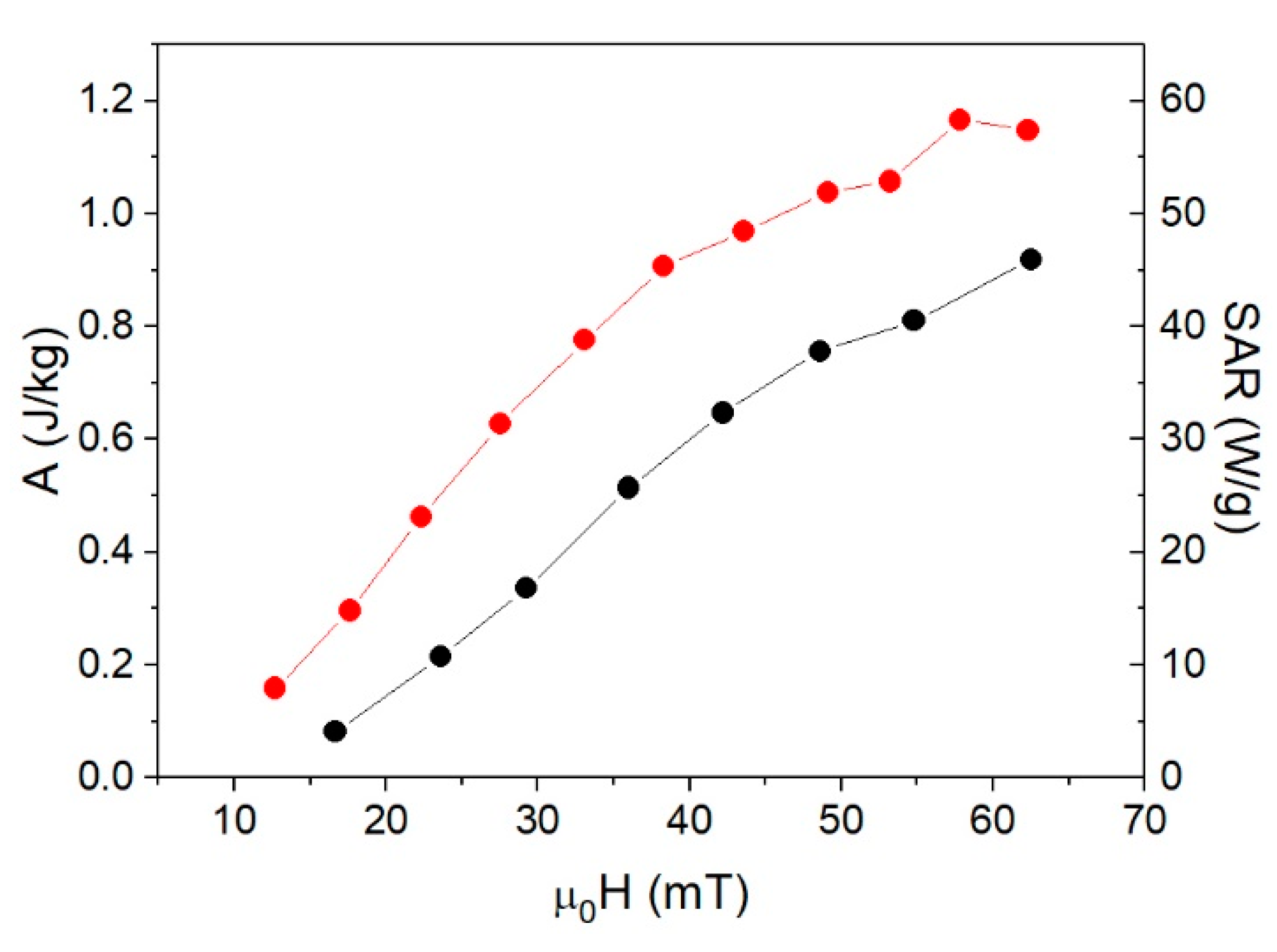
3.4. Specific Absorption Rate (SAR)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jordan, A.; Wust, P.; Fahling, H.; John, W.; Hinz, A.; Felix, R. Inductive heating of ferrimagnetic particles ad magnetic fluids: Physical evaluation of their potential for hyperthermia. Int. J. Hyperth. 1993, 9, 51–68. [Google Scholar] [CrossRef]
- Gupta, A.K.; Gupta, M. Synthesis and surface engineering of iron oxide nanoparticles for biomedical applications. Biomaterials 2005, 26, 3995–4021. [Google Scholar] [CrossRef] [PubMed]
- Simeonidis, K.; Morales, M.P.; Marciello, M.; Angelakeris, M.; de la Presa, P.; Lazaro-Carrillo, A.; Tabero, A.; Villanueva, A.; Chubykalo-Fesenko, O.; Serantes, D. In-situ particles reorientation during magnetic hyperthermia application: Shape matters twice. Sci. Rep. 2016, 6, 38382. [Google Scholar] [CrossRef] [PubMed]
- Das, R.; Alonso, J.; Porshokouh, Z.N.; Kalappattil, V.; Torres, D.; Phan, M.H.; Garaio, E.; Garcia, J.A.; Llamazares, J.L.S.; Srikanth, H. Tunable High Aspect Ratio Iron Oxide Nanorods for Enhanced Hyperthermia. J. Phys. Chem. C 2016, 120, 10086–10093. [Google Scholar] [CrossRef]
- Wetterskog, E.; Jonasson, C.; Smilgies, D.-M.; Schaller, V.; Johansson, C.; Svedlindh, P. Colossal Anisotropy of the Dynamic Magnetic Susceptibility in Low-Dimensional Nanocube Assemblies. ACS Nano 2018, 12, 1403–1412. [Google Scholar] [CrossRef] [PubMed]
- Tartaj, P.; Morales, M.D.; Veintemillas-Verdaguer, S.; Gonzalez-Carreno, T.; Serna, C.J. The preparation of magnetic nanoparticles for applications in biomedicine. J. Phys. D Appl. Phys. 2003, 36, R182–R197. [Google Scholar] [CrossRef]
- Wilhelm, C.; Billotey, C.; Roger, J.; Pons, J.N.; Bacri, J.C.; Gazeau, F. Intracellular uptake of anionic superparamagnetic nanoparticles as a function of their surface coating. Biomaterials 2003, 24, 1001–1011. [Google Scholar] [CrossRef]
- Berry, C.C.; Curtis, A.S.G. Functionalisation of magnetic nanoparticles for applications in biomedicine. J. Phys. D Appl. Phys. 2003, 36, R198–R206. [Google Scholar] [CrossRef]
- Goya, G.F.; Grazu, V.; Ibarra, M.R. Magnetic nanoparticles for cancer therapy. Curr. Nanosci. 2008, 4, 1–16. [Google Scholar] [CrossRef]
- de la Presa, P.; Luengo, Y.; Multigner, M.; Costo, R.; Morales, M.P.; Rivero, G.; Hernando, A. Study of Heating Efficiency as a Function of Concentration, Size, and Applied Field in gamma-Fe2O3 Nanoparticles. J. Phys. Chem. C 2012, 116, 25602–25610. [Google Scholar] [CrossRef]
- Fortin, J.P.; Wilhelm, C.; Servais, J.; Menager, C.; Bacri, J.C.; Gazeau, F. Size-sorted anionic iron oxide nanomagnets as colloidal mediators for magnetic hyperthermia. J. Am. Chem. Soc. 2007, 129, 2628–2635. [Google Scholar] [CrossRef] [PubMed]
- Cabrera, D.; Lak, A.; Yoshida, T.; Materia, M.E.; Ortega, D.; Ludwig, F.; Guardia, P.; Sathya, A.; Pellegrino, T.; Teran, F.J. Unraveling viscosity effects on the hysteresis losses of magnetic nanocubes. Nanoscale 2017, 9, 5094–5101. [Google Scholar] [CrossRef] [PubMed]
- Ota, S.; Kitaguchi, R.; Takeda, R.; Yamada, T.; Takemura, Y. Rotation of Magnetization Derived from Brownian Relaxation in Magnetic Fluids of Different Viscosity Evaluated by Dynamic Hysteresis Measurements over a Wide Frequency Range. Nanomaterials 2016, 6, 170. [Google Scholar] [CrossRef] [PubMed]
- Rosensweig, R.E. Heating magnetic fluid with alternating magnetic field. J. Magn. Magn. Mater. 2002, 252, 370–374. [Google Scholar] [CrossRef]
- Ma, M.; Wu, Y.; Zhou, H.; Sun, Y.K.; Zhang, Y.; Gu, N. Size dependence of specific power absorption of Fe3O4 particles in AC magnetic field. J. Magn. Magn. Mater. 2004, 268, 33–39. [Google Scholar] [CrossRef]
- Carrey, J.; Mehdaoui, B.; Respaud, M. Simple models for dynamic hysteresis loop calculations of magnetic single-domain nanoparticles: Application to magnetic hyperthermia optimization. J. Appl. Phys. 2011, 109, 083921. [Google Scholar] [CrossRef]
- Mornet, S.; Vasseur, S.; Grasset, F.; Duguet, E. Magnetic nanoparticle design for medical diagnosis and therapy. J. Mater. Chem. 2004, 14, 2161–2175. [Google Scholar] [CrossRef]
- Gupta, A.K.; Naregalkar, R.R.; Vaidya, V.D.; Gupta, M. Recent advances on surface engineering of magnetic iron oxide nanoparticles and their biomedical applications. Nanomedicine 2007, 2, 23–39. [Google Scholar] [CrossRef] [PubMed]
- Hergt, R.; Dutz, S.; Muller, R.; Zeisberger, M. Magnetic particle hyperthermia: Nanoparticle magnetism and materials development for cancer therapy. J. Phys. Condes. Matter 2006, 18, S2919–S2934. [Google Scholar] [CrossRef]
- Dobson, J. Magnetic nanoparticles for drug delivery. Drug Dev. Res. 2006, 67, 55–60. [Google Scholar] [CrossRef]
- Asin, L.; Ibarra, M.R.; Tres, A.; Goya, G.F. Controlled Cell Death by Magnetic Hyperthermia: Effects of Exposure Time, Field Amplitude, and Nanoparticle Concentration. Pharm. Res. 2012, 29, 1319–1327. [Google Scholar] [CrossRef] [PubMed]
- Villanueva, A.; de la Presa, P.; Alonso, J.M.; Rueda, T.; Martínez, A.; Crespo, P.; Morales, M.P.; Gonzalez-Fernandez, M.A.; Valdés, J.; Rivero, G. Hyperthermia HeLa Cell Treatment with Silica-Coated Manganese Oxide Nanoparticles. J. Phys. Chem. C 2010, 114, 1976–1981. [Google Scholar] [CrossRef]
- Jordan, A.; Scholz, R.; Maier-Hauff, K.; Johannsen, M.; Wust, P.; Nadobny, J.; Schirra, H.; Schmidt, H.; Deger, S.; Loening, S.; et al. Presentation of a new magnetic field therapy system for the treatment of human solid tumors with magnetic fluid hyperthermia. J. Magn. Magn. Mater. 2001, 225, 118–126. [Google Scholar] [CrossRef]
- Johannsen, M.; Gneveckow, U.; Eckelt, L.; Feussner, A.; Waldofner, N.; Scholz, R.; Deger, S.; Wust, P.; Loening, S.A.; Jordan, A. Clinical hyperthermia of prostate cancer using magnetic nanoparticles: Presentation of a new interstitial technique. Int. J. Hyperth. 2005, 21, 637–647. [Google Scholar] [CrossRef]
- Natividad, E.; Castro, M.; Mediano, A. Accurate measurement of the specific absorption rate using a suitable adiabatic magnetothermal setup. Appl. Phys. Lett. 2008, 92, 093116. [Google Scholar] [CrossRef]
- Lahiri, B.B.; Ranoo, S.; Philip, J. Uncertainties in the estimation of specific absorption rate during radiofrequency alternating magnetic field induced non-adiabatic heating of ferrofluids. J. Phys. D Appl. Phys. 2017, 50, 455005. [Google Scholar] [CrossRef]
- Natividad, E.; Castro, M.; Mediano, A. Adiabatic vs. non-adiabatic determination of specific absorption rate of ferrofluids. J. Magn. Magn. Mater. 2009, 321, 1497–1500. [Google Scholar] [CrossRef]
- Garaio, E.; Collantes, J.M.; Garcia, J.A.; Plazaola, F.; Mornet, S.; Couillaud, F.; Sandre, O. A wide-frequency range AC magnetometer to measure the specific absorption rate in nanoparticles for magnetic hyperthermia. J. Magn. Magn. Mater. 2014, 368, 432–437. [Google Scholar] [CrossRef]
- Connord, V.; Mehdaoui, B.; Tan, R.P.; Carrey, J.; Respaud, M. An air-cooled Litz wire coil for measuring the high frequency hysteresis loops of magnetic samples-A useful setup for magnetic hyperthermia applications. Rev. Sci. Instrum. 2014, 85, 093904. [Google Scholar] [CrossRef] [PubMed]
- Le, A.T.; Giang, C.D.; Tam, L.T.; Tuan, T.Q.; Phan, V.N.; Alonso, J.; Devkota, J.; Garaio, E.; Garcia, J.A.; Martin-Rodriguez, R.; et al. Enhanced magnetic anisotropy and heating efficiency in multi-functional manganese ferrite/graphene oxide nanostructures. Nanotechnology 2016, 27, 155707. [Google Scholar] [CrossRef] [PubMed]
- Mehdaoui, B.; Tan, R.P.; Meffre, A.; Carrey, J.; Lachaize, S.; Chaudret, B.; Respaud, M. Increase of magnetic hyperthermia efficiency due to dipolar interactions in low-anisotropy magnetic nanoparticles: Theoretical and experimental results. Phys. Rev. B 2013, 87, 174419. [Google Scholar] [CrossRef]
- Ovejero, J.G.; Cabrera, D.; Carrey, J.; Valdivielso, T.; Salas, G.; Teran, F.J. Effects of inter- and intra-aggregate magnetic dipolar interactions on the magnetic heating efficiency of iron oxide nanoparticles. Phys. Chem. Chem. Phys. 2016, 18, 10954–10963. [Google Scholar] [CrossRef] [PubMed]
- Nemati, Z.; Alonso, J.; Rodrigo, I.; Das, R.; Garaio, E.; García, J.Á.; Orue, I.; Phan, M.-H.; Srikanth, H. Improving the Heating Efficiency of Iron Oxide Nanoparticles by Tuning Their Shape and Size. J. Phys. Chem. C 2018, 122, 2367–2381. [Google Scholar] [CrossRef]
- Cabrera, D.; Coene, A.; Leliaert, J.; Artés-Ibáñez, E.J.; Dupré, L.; Telling, N.D.; Teran, F.J. Dynamical Magnetic Response of Iron Oxide Nanoparticles Inside Live Cells. ACS Nano 2018, 12, 2741–2752. [Google Scholar] [CrossRef] [PubMed]
- Ovejero, J.G.; Morales, I.; de la Presa, P.; Mille, N.; Carrey, J.; Garcia, M.A.; Hernando, A.; Herrasti, P. Hybrid nanoparticles for magnetic and plasmonic hyperthermia. Phys. Chem. Chem. Phys. 2018, 20, 24065–24073. [Google Scholar] [CrossRef] [PubMed]
- Mehdaoui, B.; Meffre, A.; Carrey, J.; Lachaize, S.; Lacroix, L.-M.; Gougeon, M.; Chaudret, B.; Respaud, M. Optimal Size of Nanoparticles for Magnetic Hyperthermia: A Combined Theoretical and Experimental Study. Adv. Funct. Mater. 2011, 21, 4573–4581. [Google Scholar] [CrossRef]
- Vergés, M.A.; Costo, R.; Roca, A.G.; Marco, J.F.; Goya, G.F.; Serna, C.J.; Morales, M.P. Uniform and water stable magnetite nanoparticles with diameters around the monodomain–multidomain limit. J. Phys. D Appl. Phys. 2008, 41, 134003. [Google Scholar] [CrossRef]
- Massart, R.; Cabuil, V. Efect of some parameters on the formation of colloidal magnetite in alkaline medium-yield and particle size control. J. Chim. Phys. Chim. Biol. 1987, 84, 967–973. [Google Scholar] [CrossRef]
- Costo, R.; Bello, V.; Robic, C.; Port, M.; Marco, J.F.; Morales, M.P.; Veintemillas-Verdaguer, S. Ultrasmall Iron Oxide Nanoparticles for Biomedical Applications: Improving the Colloidal and Magnetic Properties. Langmuir 2012, 28, 178–185. [Google Scholar] [CrossRef] [PubMed]
- Cornell, R.; Schwertmann, U. The Iron Oxides: Structure, Properties, Reactions, Occurrences and Uses, 2nd ed.; Wiley: Weinheim, Geramny, 2006; p. 706. [Google Scholar]
- Morales, M.P.; Veintemillas-Verdaguer, S.; Montero, M.I.; Serna, C.J.; Roig, A.; Casas, L.; Martinez, B.; Sandiumenge, F. Surface and internal spin canting in γ-Fe2O3 nanoparticles. Chem. Mater. 1999, 11, 3058–3064. [Google Scholar] [CrossRef]
- Stoner, E.C.; Wohlfarth, E.P. A mechanism of magnetic hysteresis in heterogenous alloys. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 240, 599–642. [Google Scholar] [CrossRef]
- Serna, C.J.; Morales, M.P. Maghemite (γ-Fe2O3): A Versatile Magnetic Colloidal Material. In Surface and Colloid Science; Matijević, E., Borkovec, M., Eds.; Springer: Boston, MA, USA, 2004; pp. 27–81. [Google Scholar]
- Serantes, D.; Simeonidis, K.; Angelakeris, M.; Chubykalo-Fesenko, O.; Marciello, M.; Morales, M.D.; Baldomir, D.; Martinez-Boubeta, C. Multiplying Magnetic Hyperthermia Response by Nanoparticle Assembling. J. Phys. Chem. C 2014, 118, 5927–5934. [Google Scholar] [CrossRef]
- Alphandery, E.; Ding, Y.; Ngo, A.T.; Wang, Z.L.; Wu, L.F.; Pileni, M.P. Assemblies of Aligned Magnetotactic Bacteria and Extracted Magnetosomes: What Is the Main Factor Responsible for the Magnetic Anisotropy? ACS Nano 2009, 3, 1539–1547. [Google Scholar] [CrossRef] [PubMed]
- Lemine, O.M.; Omri, K.; Iglesias, M.; Velasco, V.; Crespo, P.; de la Presa, P.; El Mir, L.; Bouzid, H.; Yousif, A.; Al-Hajry, A. γ-Fe2O3 by sol-gel with large nanoparticles size for magnetic hyperthermia application. J. Alloys Compd. 2014, 607, 125–131. [Google Scholar] [CrossRef]
- Maldonado, K.L.L.; de la Presa, P.; de la Rubia, M.A.; Crespo, P.; de Frutos, J.; Hernando, A.; Aquino, J.A.M.; Galindo, J.T.E. Effects of grain boundary width and crystallite size on conductivity and magnetic properties of magnetite nanoparticles. J. Nanopart. Res. 2014, 16, 2482. [Google Scholar] [CrossRef]
- Colombo, M.; Carregal-Romero, S.; Casula, M.F.; Gutierrez, L.; Morales, M.P.; Bohm, I.B.; Heverhagen, J.T.; Prosperi, D.; Parak, W.J. Biological applications of magnetic nanoparticles. Chem. Soc. Rev. 2012, 41, 4306–4334. [Google Scholar] [CrossRef] [PubMed]
- Mehdaoui, B.; Meffre, A.; Lacroix, L.M.; Carrey, J.; Lachaize, S.; Gougeon, M.; Respaud, M.; Chaudret, B. Large specific absorption rates in the magnetic hyperthermia properties of metallic iron nanocubes. J. Magn. Magn. Mater. 2010, 322, L49–L52. [Google Scholar] [CrossRef]
- de la Presa, P.; Luengo, Y.; Velasco, V.; Morales, M.P.; Iglesias, M.; Veintemillas-Verdaguer, S.; Crespo, P.; Hernando, A. Particle Interactions in Liquid Magnetic Colloids by Zero Field Cooled Measurements: Effects on Heating Efficiency. J. Phys. Chem. C 2015, 119, 11022–11030. [Google Scholar] [CrossRef]
- Andreu, I.; Natividad, E.; Solozábal, L.; Roubeau, O. Nano-objects for Addressing the Control of Nanoparticle Arrangement and Performance in Magnetic Hyperthermia. ACS Nano 2015, 9, 1408–1419. [Google Scholar] [CrossRef] [PubMed]
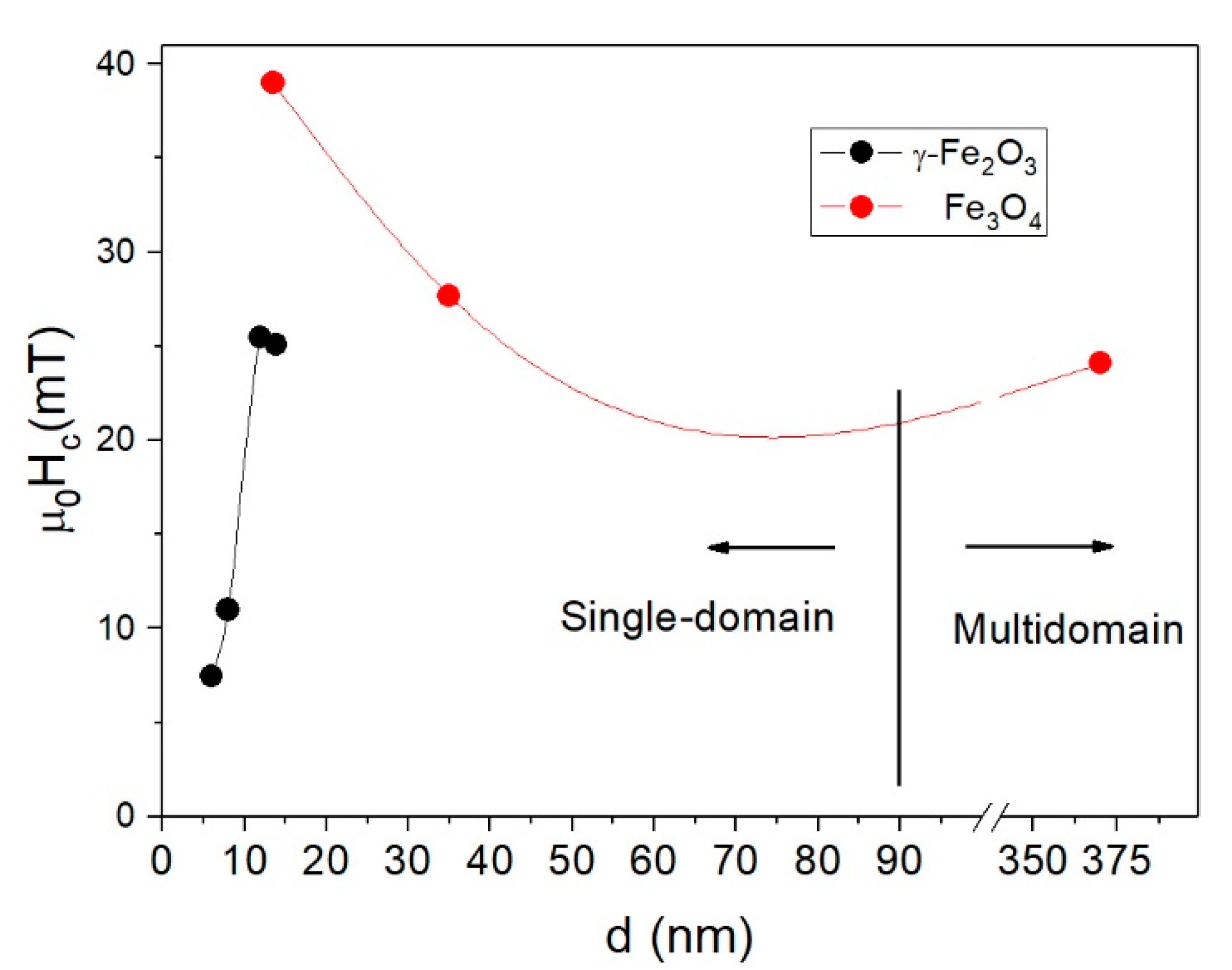
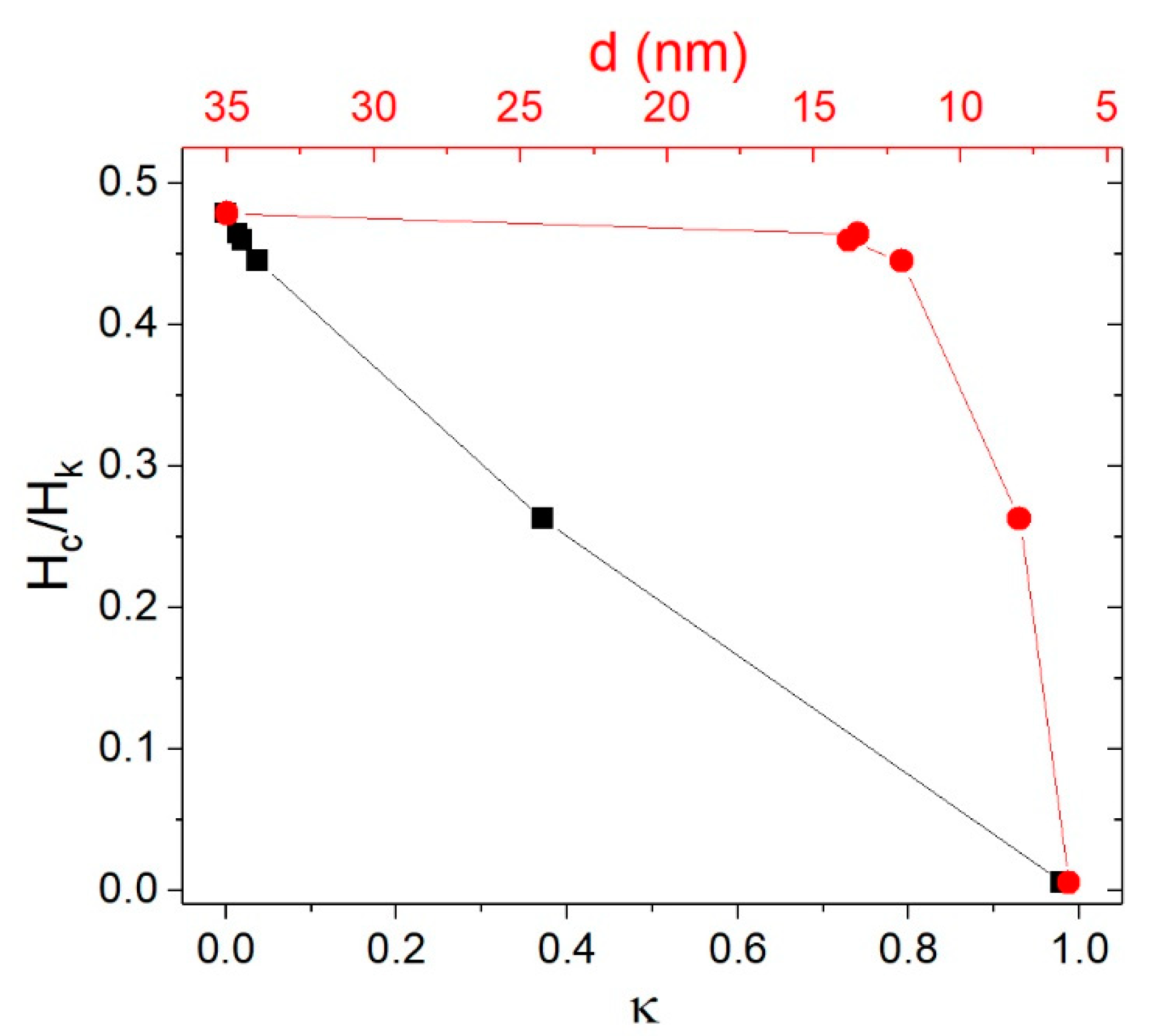
| f ≈ 10−4 Hz | T = 10 K, f ≈ 10−4 Hz | T = 300 K, f = 50 kHz | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sample Name | TEM Particle Size d (nm) (σ) | Hydrodynamic Size Dh (nm) (σ) | Iron Oxide Majority Phase | TB (K) | μ0HC (mT) | μ0HK (mT) | Ms (Am2/kg) | Mr/Ms | μ0Hc (mT) | MS (Am2/kg) | Mr/Ms |
| γFe2O3-6nm | 6.3 (0.19) | 25.4 (0.27) | γ-Fe2O3 | ~70 | 7.5 | 55 | 0.16 | — | — | — | |
| γFe2O3-8nm | 7.6 (0.20) | 29.9 (0.23) | γ-Fe2O3 | ~90 | 11.0 | 42 | 59 | 0.20 | 0.9 | 26 | 0.05 |
| γFe2O3-12nm | 11.7 (0.16) | 58.4 (0.25) | γ-Fe2O3 | ~220 K | 25.5 | 57.3 | 65 | 0.30 | 5.5 | 32 | 0.28 |
| γFe2O3-14nm | 13.8 (0.18) | 96.8 (0.19) | γ-Fe2O3 | ~300 K | 25.1 | 54.7 | 79 | 0.29 | 10.6 | 32 | 0.45 |
| Fe3O4-14nm | 13.5 (0.19) | 160.7 (0.20) | Fe3O4/γ-Fe2O3 | >300 K | 39.0 | 84.1 | 71 | 0.31 | 10.0 | 32 | 0.26 |
| Fe3O4-35nm | 35 (0.20) | 88.1 (0.18) | Fe3O4 | >300 K | 27.7 | 57.9 | 80 | 0.29 | 15.8 | 77 | 0.72 |
| Fe3O4-350nm | 350 (0.24) | 2751 (0.45) | Fe3O4 | >>300 K | 24.1 | 90 | 0.17 | — | — | — | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morales, I.; Costo, R.; Mille, N.; Da Silva, G.B.; Carrey, J.; Hernando, A.; De la Presa, P. High Frequency Hysteresis Losses on γ-Fe2O3 and Fe3O4: Susceptibility as a Magnetic Stamp for Chain Formation. Nanomaterials 2018, 8, 970. https://doi.org/10.3390/nano8120970
Morales I, Costo R, Mille N, Da Silva GB, Carrey J, Hernando A, De la Presa P. High Frequency Hysteresis Losses on γ-Fe2O3 and Fe3O4: Susceptibility as a Magnetic Stamp for Chain Formation. Nanomaterials. 2018; 8(12):970. https://doi.org/10.3390/nano8120970
Chicago/Turabian StyleMorales, Irene, Rocio Costo, Nicolas Mille, Gustavo B. Da Silva, Julian Carrey, Antonio Hernando, and Patricia De la Presa. 2018. "High Frequency Hysteresis Losses on γ-Fe2O3 and Fe3O4: Susceptibility as a Magnetic Stamp for Chain Formation" Nanomaterials 8, no. 12: 970. https://doi.org/10.3390/nano8120970
APA StyleMorales, I., Costo, R., Mille, N., Da Silva, G. B., Carrey, J., Hernando, A., & De la Presa, P. (2018). High Frequency Hysteresis Losses on γ-Fe2O3 and Fe3O4: Susceptibility as a Magnetic Stamp for Chain Formation. Nanomaterials, 8(12), 970. https://doi.org/10.3390/nano8120970