Light-Tuned DC Conductance of Anatase TiO2 Nanotubular Arrays: Features of Long-Range Charge Transport
Abstract
:1. Introduction
2. Experimental Techniques and Results
2.1. Synthesis and Characterization of Partially Ordered Assemblies of Densely Packed aTNTAs
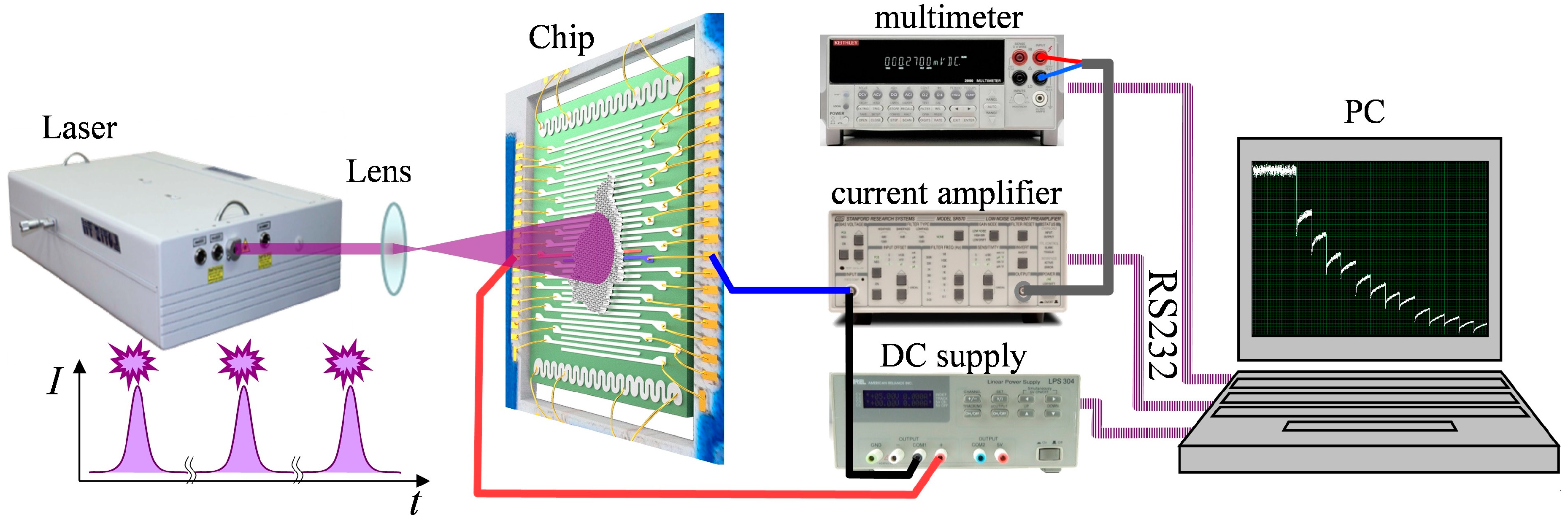
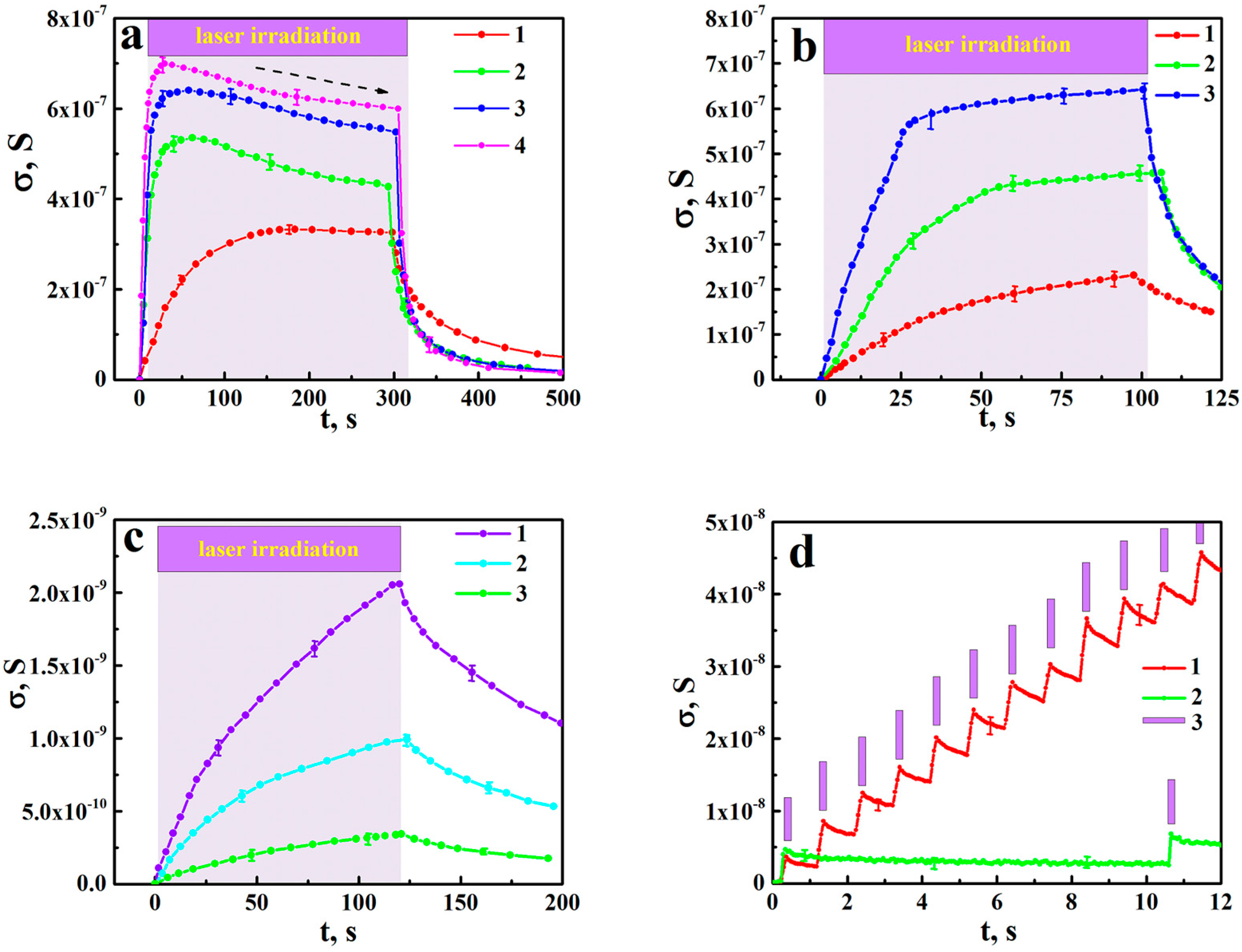
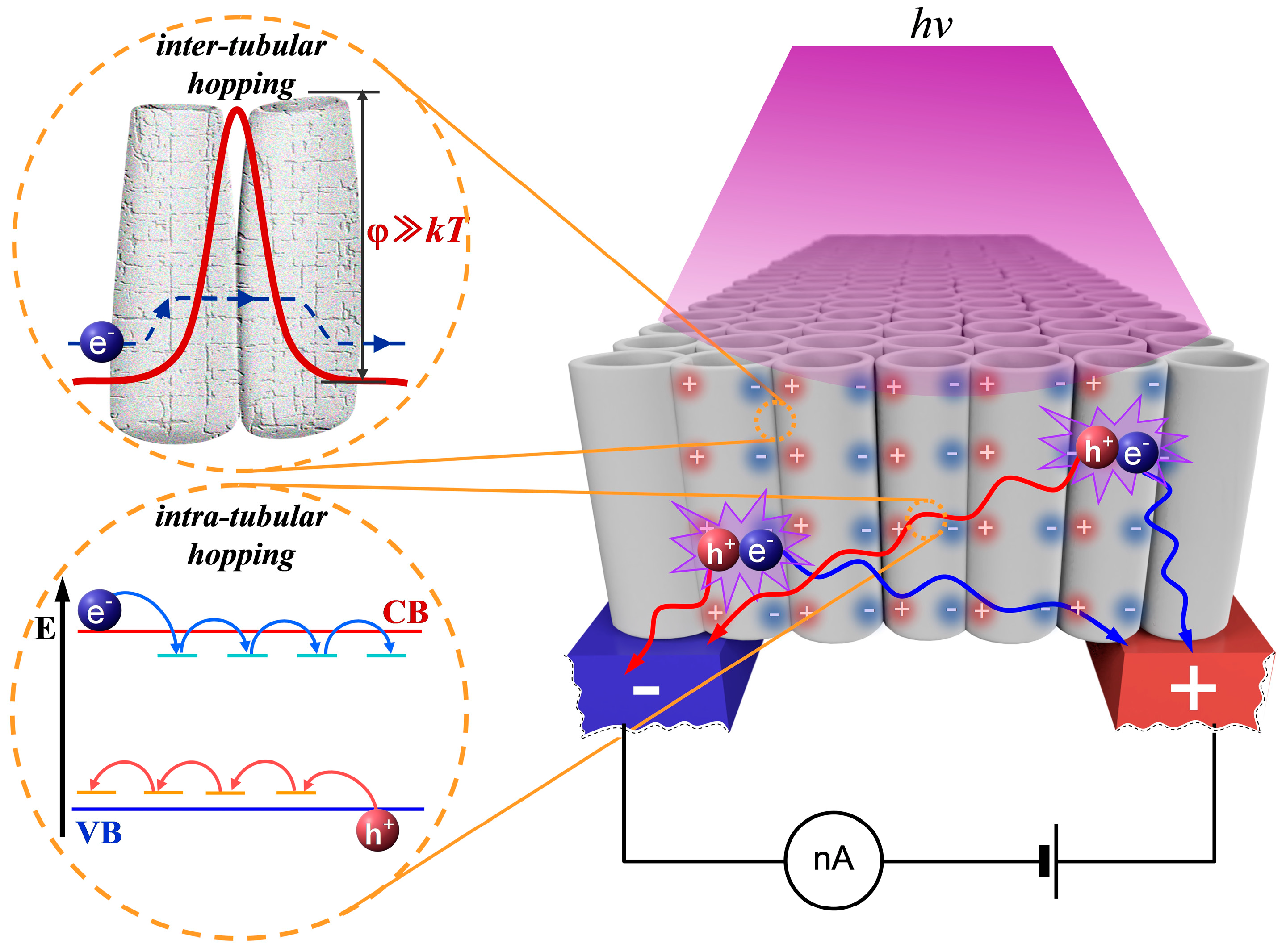
2.2. Measurements of the Photo-Induced DC Conductance of aTNTA
3. Interpretation of Experimental Results
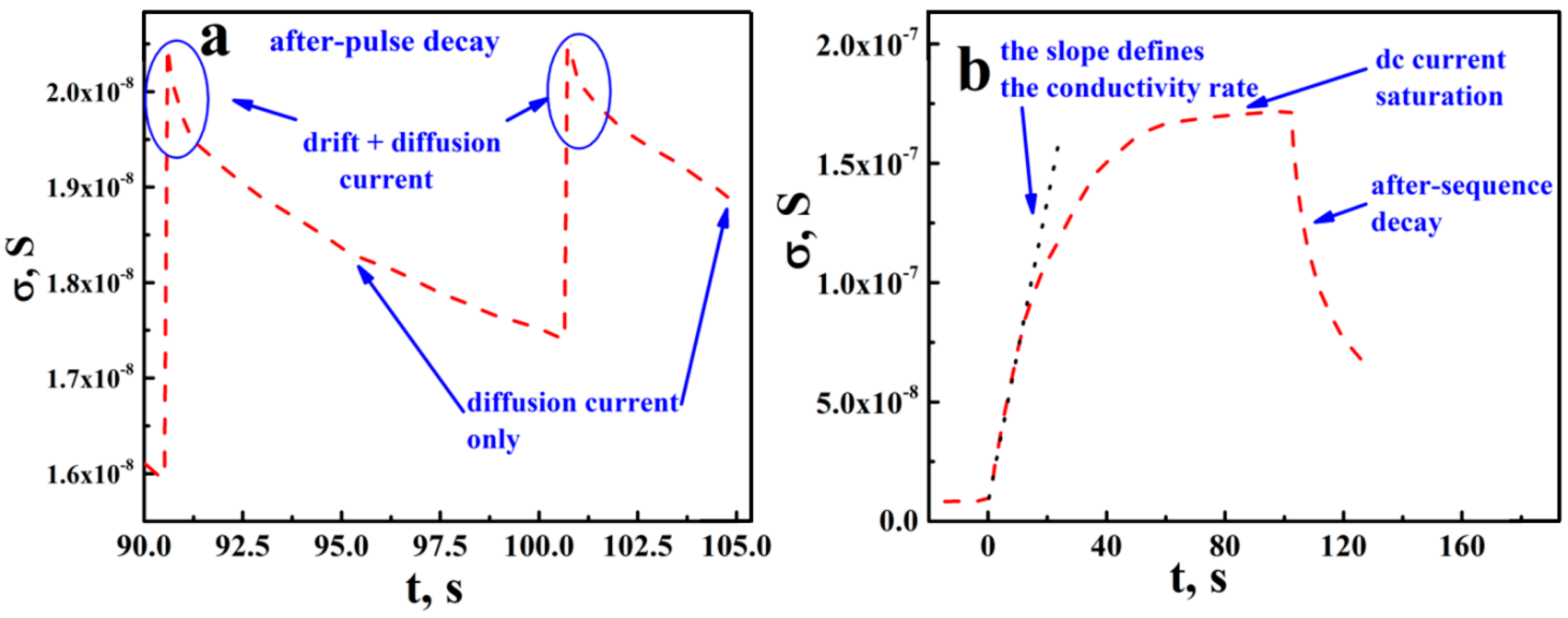
3.1. Kinetics of DC Conductance Decay in aTNTA
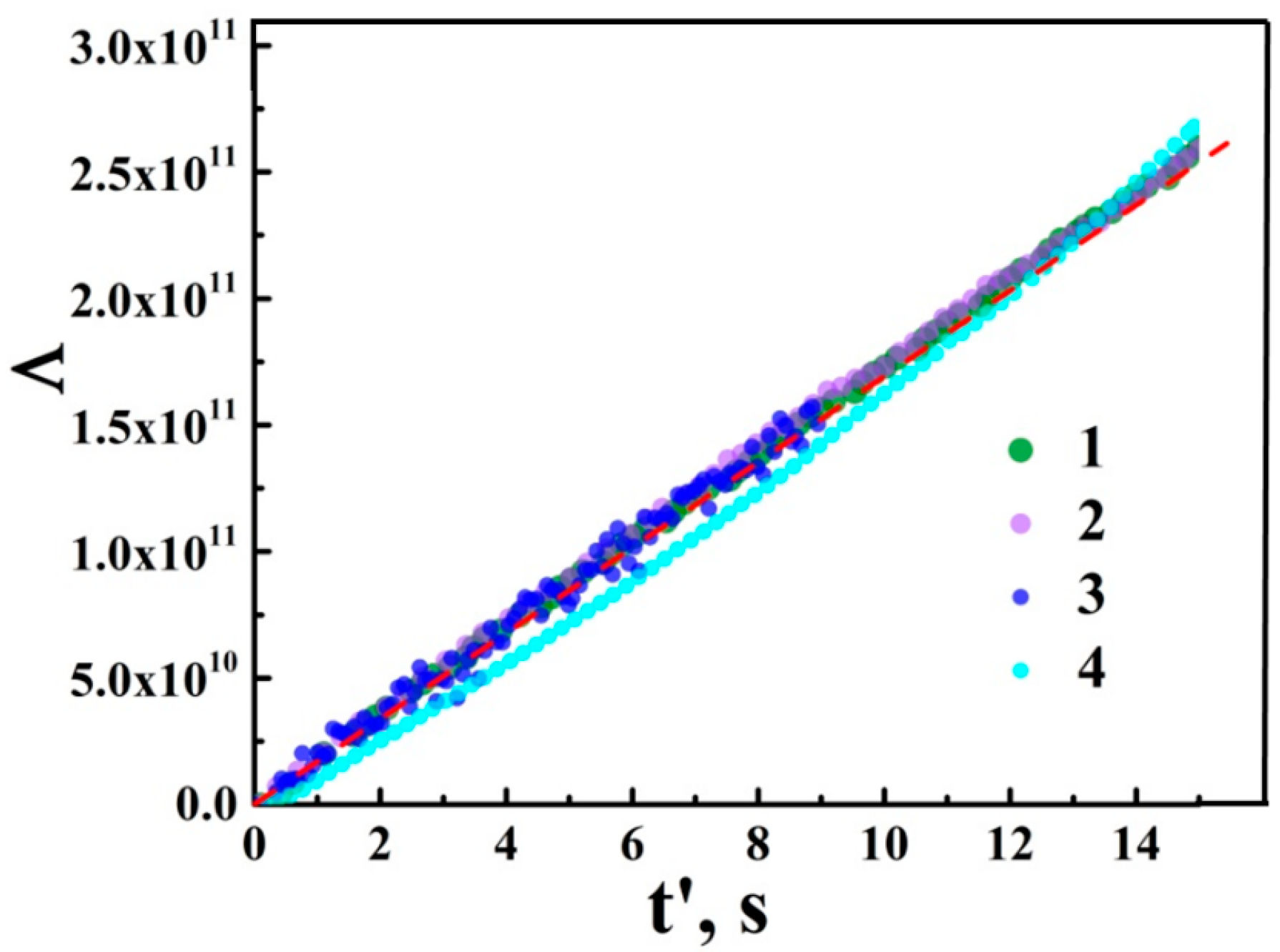
3.2. The Quantum Yield of Photo-Activation and Mobility of Charge Carriers in aTNTA
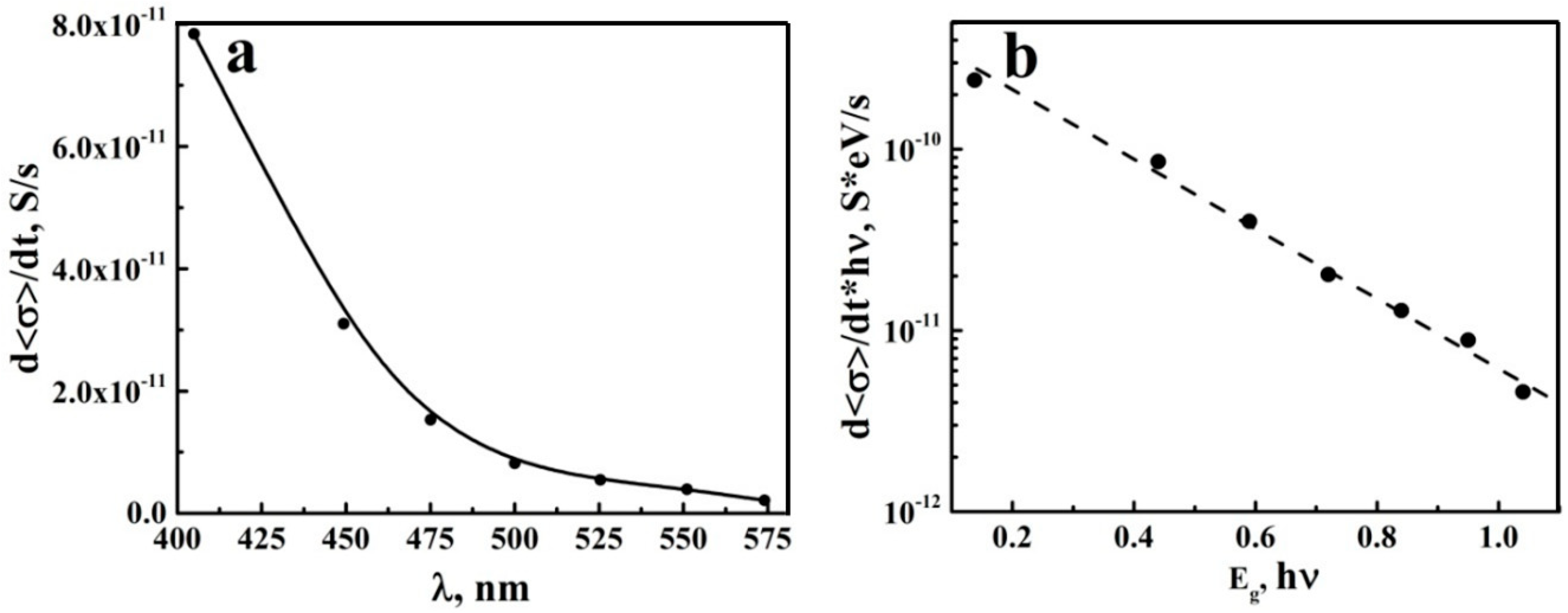
3.3. Photo-Activated DC Conductance of aTNTA Outside the Fundamental Absorption Band
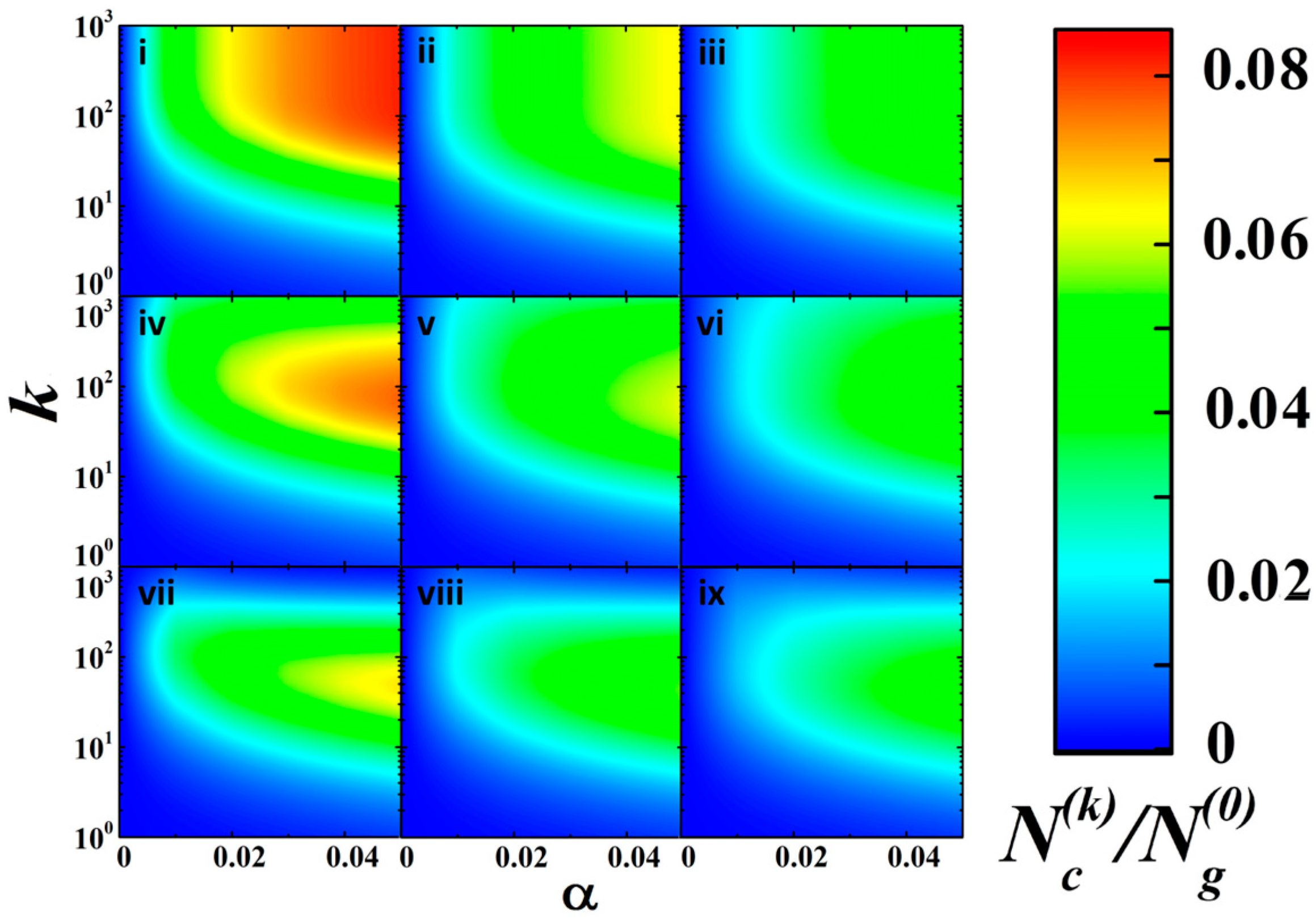
3.4. A Recurrent Kinetic Model for Photo-Activated Evolution of DC Conductivity of aTNTA
- -
- The photo-induced conductance of the examined aTNTA is proportional to the current population ;
- -
- the time lapse after beginning the photoactivation process is defined as , where is the repetition rate of laser pulses;
- -
- the influence of the population on the photo-ionization efficiency is assumed to be a monotonically decaying function of ; we have assumed a linear decay in described by the following relationshipwhere the critical population is assumed equal to ;
- -
- the recombination efficiency and the trapping efficiency are assumed to be independent from the population .
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, X.; Mao, S.S. Titanium dioxide nanomaterials: Synthesis, properties, modifications, and applications. Chem. Rev. 2007, 107, 2891–2959. [Google Scholar] [CrossRef] [PubMed]
- Hagfeldt, A.; Boschloo, G.; Sun, L.; Kloo, L.; Pettersson, H. Dye-sensitized solar cells. Chem. Rev. 2010, 110, 6595–6663. [Google Scholar] [CrossRef] [PubMed]
- Anpo, M.; Takeuchi, M. The design and development of highly reactive titanium oxide photocatalysts operating under visible light irradiation. J. Catal. 2003, 216, 505–516. [Google Scholar] [CrossRef]
- Schneider, J.; Matsuoka, M.; Takeuchi, M.; Zhang, J.; Horiuchi, Y.; Anpo, M.; Bahnemann, D.W. Understanding TiO2 photocatalysis: Mechanisms and materials. Chem. Rev. 2014, 114, 9919–9986. [Google Scholar] [CrossRef] [PubMed]
- Henderson, M.A. A surface science perspective on TiO2 photocatalysis. Surf. Sci. Rep. 2011, 66, 185–297. [Google Scholar] [CrossRef]
- Gutierrez-Fujishima, A.; Zhang, X.; Tryk, D.A. TiO2 photocatalysis and related surface phenomena. Surf. Sci. Rep. 2008, 63, 515–582. [Google Scholar] [CrossRef]
- Grätzel, M. Photoelectrochemical cells. Nature 2001, 414, 338–344. [Google Scholar] [CrossRef] [PubMed]
- Dittrich, T.; Lebedev, A.N.; Weidmann, J. Electron drift mobility in porous TiO2 (anatase). Phys. Stat. Sol. A 1998, 165, R5–R6. [Google Scholar] [CrossRef]
- Wehrenfennig, C.; Palumbiny, C.M.; Snaith, H.J.; Johnston, M.B.; Schmidt-Mende, L.; Herz, L.M. Fast charge-carrier trapping in TiO2 nanotubes. J. Phys. Chem. C 2015, 119, 9159–9168. [Google Scholar] [CrossRef]
- Fravventura, M.C.; Deligiannis, D.; Schins, J.M.; Siebbeles, L.D.A.; Savenije, T.J. What limits photoconductance in anatase TiO2 nanostructures? A real and imaginary microwave conductance study. J. Phys. Chem. C 2013, 117, 8032–8040. [Google Scholar] [CrossRef]
- Fravventura, M.C.; Siebbeles, L.D.A.; Savenije, T.J. Mechanisms of photogeneration and relaxation of excitons and mobile carriers in anatase TiO2. J. Phys. Chem. C 2014, 118, 7337–7343. [Google Scholar] [CrossRef]
- Moser, S.; Moreschini, L.; Jaćimović, J.; Barišić, O.S.; Berger, H.; Magrez, A.; Chang, Y.J.; Kim, K.S.; Bostwick, A.; Rotenberg, E.; et al. Tunable polaronic conduction in anatase TiO2. Phys. Rev. Lett. 2013, 110, 196403. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Wang, F.; Zhang, J.; Wang, K.; Qiu, Y.; Liang, Q.; Chen, Z. Efficient photoelectrochemical water splitting by g-C3N4/TiO2nanotube array heterostructures. Nano-Micro Lett. 2018, 10, 37. [Google Scholar] [CrossRef] [PubMed]
- Erdem, E.; Kiraz, K.; Somer, M.; Eichel, R.-A. Size effects in Fe3+-doped PbTiO3 nanocrystals—Formation and orientation of (FeTi-VO) defect-dipoles. J. Eur. Ceram. Soc. 2010, 30, 289–293. [Google Scholar] [CrossRef]
- Kment, S.; Riboni, F.; Pausova, S.; Wang, L.; Wang, L.; Han, H.; Hubicka, Z.; Krysa, J.; Schmuki, P.; Zboril, R. Photoanodes based on TiO2 and alpha-Fe2O3 for solar water splitting-superior role of 1D nanoarchitectures and of combined heterostructures. Chem. Soc. Rev. 2017, 46, 3716–3769. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Feng, Y.P. Review on charge transfer and chemical activity of TiO2: Mechanism and applications. Prog. Surf. Sci. 2016, 91, 183–202. [Google Scholar] [CrossRef]
- Espid, E.; Taghipour, F. UV-LED photo-activated chemical gas sensors: A review. Crit. Rev. Solid State Mater. Sci. 2017, 42, 416–432. [Google Scholar] [CrossRef]
- Espinosa, E.H.; Ionescu, R.; Chambon, B.; Bedis, G.; Sotter, E.; Bittencourt, C.; Felten, A.; Pireaux, J.-J.; Correig, X.; Llobet, E. Hybrid metal oxide and multiwall carbon nanotube films for low temperature gas sensing. Sens. Actuators B Chem. 2007, 127, 137–142. [Google Scholar] [CrossRef]
- Enachi, M.; Lupan, O.; Braniste, T.; Sarua, A.; Chow, L.; Mishra, Y.K.; Gedamu, D.; Adelung, R.; Tiginyanu, I. Integration of individual TiO2 nanotube on the chip: Nanodevice for hydrogen sensing. Phys. Status Solidi Rapid Res. Lett. 2015, 9, 171–174. [Google Scholar] [CrossRef]
- Plecenik, T.; Moško, M.; Haidry, A.A.; Durina, P.; Truchlý, M.; Grancic, B.; Gregor, M.; Roch, T.; Satrapinskyy, L.; Mošková, A.; et al. Fast highly-sensitive room-temperature semiconductor gas sensor based on the nanoscale Pt-TiO2-Pt sandwich. Sens. Actuators B Chem. 2015, 207, 351–361. [Google Scholar] [CrossRef]
- Varezhnikov, A.S.; Fedorov, F.S.; Burmistrov, I.N.; Plugin, I.A.; Sommer, M.; Lashkov, A.V.; Gorokhovsky, A.V.; Nasibulin, A.G.; Kuznecov, D.V.; Gorshenkov, M.V.; et al. The room-temperature chemiresistive properties of potassium titanate whiskers versus organic vapors. Nanomaterials 2017, 7, 455. [Google Scholar] [CrossRef] [PubMed]
- Mor, G.K.; Varghese, O.K.; Paulose, M.; Shankar, K.; Grimes, C.A. A review on highly ordered, vertically oriented TiO2 nanotube arrays: Fabrication, material properties, and solar energy applications. Sol. Energy Mater. Sol. Cells 2006, 90, 2011–2075. [Google Scholar] [CrossRef]
- Huang, J.; Wan, Q. Gas sensors based on semiconducting metal oxide one-dimensional nanostructures. Sensors 2009, 9, 9903–9924. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Ma, T.; Pinna, N.; Zhang, J. Two-dimensional nanostructured materials for gas sensing. Adv. Funct. Mater. 2017, 27, 1702168. [Google Scholar] [CrossRef]
- Roy, P.; Berger, S.; Schmuki, P. TiO2 nanotubes: Synthesis and applications. Angew. Chem. Int. Ed. 2011, 50, 2904–2939. [Google Scholar] [CrossRef] [PubMed]
- Comini, E.; Galstyan, V.; Faglia, G.; Bontempi, E.; Sberveglieri, G. Highly conductive titanium oxide nanotubes chemical sensors. Microporous Mesoporous Mater. 2015, 208, 165–170. [Google Scholar] [CrossRef]
- Fedorov, F.; Vasilkov, M.; Lashkov, A.; Varezhnikov, A.; Fuchs, D.; Kübel, C.; Bruns, M.; Sommer, M.; Sysoev, V. Toward new gas-analytical multisensor chips based on titanium oxide nanotube array. Sci. Rep. 2017, 7, 9732. [Google Scholar] [CrossRef] [PubMed]
- Albu, S.P.; Ghicov, A.; Macak, J.M.; Hahn, R.; Schmuki, P. Self-organized, free-standing TiO2 nanotube membrane for flow-through photocatalytic applications. Nano Lett. 2007, 7, 1286–1289. [Google Scholar] [CrossRef] [PubMed]
- Goschnick, J. An electronic nose for intelligent consumer products based on a gas analytical gradient microarray. Microelectron. Eng. 2001, 57–58, 693–704. [Google Scholar] [CrossRef]
- Fang, D.; Luo, Z.; Huang, K.; Lagoudas, D.C. Effect of heat treatment on morphology, crystalline structure and photocatalysisproperties of TiO2 nanotubes on Ti substrate and freestanding membrane. Appl. Surf. Sci. 2011, 257, 6451–6461. [Google Scholar] [CrossRef]
- Allam, N.K.; El-Sayed, M.A. Photoelectrochemical water oxidation characteristics of anodically fabricated TiO2 nanotube arrays: Structural and optical properties. J. Phys. Chem. C 2010, 114, 12024–12029. [Google Scholar] [CrossRef]
- Munirathinam, B.; Pydimukkala, H.; Ramaswamy, N.; Neelakantan, L. Influence of crystallite size and surface morphology on electrochemical properties of annealed TiO2 nanotubes. Appl. Surf. Sci. 2015, 355, 1245–1253. [Google Scholar] [CrossRef]
- Likodimos, V.; Stergiopoulos, T.; Falaras, P.; Kunze, J.; Schmuki, P. Phase composition, size, orientation, and antenna effects of self-assembled anodized titania nanotube arrays: A polarized micro-Raman investigation. J. Phys. Chem. C 2008, 112, 12687–12696. [Google Scholar] [CrossRef]
- Fisher, S.; Shierbaum, K.-D.; Goepel, W. Submonolayer Pt on TiO2 (110) surfaces: Electronic and geometric effects. Sens. Actuators B 1996, 31, 13–18. [Google Scholar] [CrossRef]
- Di Valentin, C.; Selloni, A. Bulk and surface polarons in photoexcited anatase TiO2. J. Phys. Chem. Lett. 2011, 2, 2223–2228. [Google Scholar] [CrossRef]
- Zimnyakov, D.A.; Yuvchenko, S.A. Effective dielectric function of TiO2 nanoparticles under laser pumping in the fundamental absorption band. Quantum Electron. 2017, 47, 547–552. [Google Scholar] [CrossRef]
- Song, K.S.; Williams, R.T. Self-Trapped Excitons; Springer: Berlin, Germany, 1993. [Google Scholar]
- Tang, H.; Lévy, F.; Berger, H.; Schmid, P.E. Urbach tail of anatase TiO2. Phys. Rev. B 1995, 52, 7771–7774. [Google Scholar] [CrossRef]
- Soci, C.; Moses, D.; Xu, Q.-H.; Heeger, A.J. Charge-carrier relaxation dynamics in highly ordered poly (p-phenylenevinylene): Effects of carrier bimolecular recombination and trapping. Phys. Rev. B 2005, 72, 245204. [Google Scholar] [CrossRef]
- Esaki, L.; Chang, L.L. New transport phenomenon in a semiconductor “superlattice”. Phys. Rev. Lett. 1974, 33, 495–498. [Google Scholar] [CrossRef]
- Grünevald, M.; Thomas, P. Percolation and effective medium theory of conductivity and thermopower in the hopping transport regime. Phys. Stat. Sol. B 1979, 93, K17–K20. [Google Scholar] [CrossRef]
- Kumar, S.; Murthy, J.Y.; Alam, M.A. Percolating conduction in finite nanotube networks. Phys. Rev. Lett. 2005, 95, 066802. [Google Scholar] [CrossRef] [PubMed]
- Go, J.; Sysoev, V.V.; Kolmakov, A.; Pimparkar, N.; Alam, M.A. A novel model for (percolating) nanonet chemical sensors for microarray-based E-nose application. In Proceedings of the 2009 IEEE International Electron Devices Meeting (IEDM), Baltimore, MD, USA, 7–9 December 2009. [Google Scholar] [CrossRef]
- Shuttle, C.G.; O’Regan, B.; Ballantyne, A.M.; Nelson, J.; Bradley, D.D.C.; de Mello, J.; Durrant, J.R. Experimental determination of the rate law for charge carrier decay in a polythiophene: Fullerene solar cell. Appl. Phys. Lett. 2008, 92, 093311. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zimnyakov, D.A.; Vasilkov, M.Y.; Yuvchenko, S.A.; Varezhnikov, A.S.; Sommer, M.; Sysoev, V.V. Light-Tuned DC Conductance of Anatase TiO2 Nanotubular Arrays: Features of Long-Range Charge Transport. Nanomaterials 2018, 8, 915. https://doi.org/10.3390/nano8110915
Zimnyakov DA, Vasilkov MY, Yuvchenko SA, Varezhnikov AS, Sommer M, Sysoev VV. Light-Tuned DC Conductance of Anatase TiO2 Nanotubular Arrays: Features of Long-Range Charge Transport. Nanomaterials. 2018; 8(11):915. https://doi.org/10.3390/nano8110915
Chicago/Turabian StyleZimnyakov, Dmitry A., Michail Yu. Vasilkov, Sergey A. Yuvchenko, Alexey S. Varezhnikov, Martin Sommer, and Victor V. Sysoev. 2018. "Light-Tuned DC Conductance of Anatase TiO2 Nanotubular Arrays: Features of Long-Range Charge Transport" Nanomaterials 8, no. 11: 915. https://doi.org/10.3390/nano8110915
APA StyleZimnyakov, D. A., Vasilkov, M. Y., Yuvchenko, S. A., Varezhnikov, A. S., Sommer, M., & Sysoev, V. V. (2018). Light-Tuned DC Conductance of Anatase TiO2 Nanotubular Arrays: Features of Long-Range Charge Transport. Nanomaterials, 8(11), 915. https://doi.org/10.3390/nano8110915








