1. Introduction. Magnetic Polymersomes
The science of magnetic nano-objects in recent decades has been developing at high rate due to their prospects, first of all, in nanomedicine and theranostics. By now, the nomenclature of those entities is really vast including microferrohydrogels, magnetic liposomes, magnetic micelles, magnetic vesicles, and a great many others. In view of that, in order not to confuse the subject of the present work with other similar ones, we begin with definitions. The more so that
magnetic polymersomes or
magnetopolymersomes (MPSs) is not yet a customary term in comparison with: (1)
magnetosomes, and (2)
magnetic endosomes often encountered in the literature on magnetic soft matter. The objects of type (1) are the iron oxide nanograins (their size in the range of 20–40 nm) synthesised by pelobiont magnetotactic bacteria [
1]. Therefore, magnetosomes are completely biogenic entities. They self-organise in chain-like aggregates inside the cytosol, thus making the magnetotactic bacteria sensitive to terrestrial field. Such a “compass” is vital for their normal life. The objects of type (2) are also biogenic: those are small vesicles formed by the cell membrane in the process of endocytosis (uptake) of magnetic nanoparticles from the surrounding medium [
2,
3]. As the content of endosomes is magnetic, their motion inside the cytosol could be put under external control [
4].
Among the artificial magnetically controlled microcontainers, a more subtle but important difference could be established between MPS’s and
magnetic colloidosomes [
5,
6] which are microcapsules whose inner content is surrounded by a nanosize magnetically active shell (membrane). In both types of objects the membrane builds up in result of self-assembling of amphiphilic diblock co-polymer molecules and is modified by embedding their magnetic nanoparticles. The difference is that in colloidosomes the nanoparticles are chemically bonded to the membrane, whereas in MPSs, due to appropriate functionalisation of the particles, even though they are confined inside the hydrophobic shell layer, they retain their ability to move inside it [
7,
8,
9,
10].
The above-mentioned structure details entail the differences in the object responses to an external field. In colloidosomes (microcapsules) the magnetic nanoparticles are “glued” to their sites within the shell. Because of that, when the interparticle dipole-dipole forces are modulated by an external field and the particles are compelled to regroup, each particle has to entrain in this motion its local polymer environment.
The structure of the MPS membrane could be presented as follows. In an MPS with the overall size (diameter)
nm) [
10], the nanoparticles of diameter
nm are confined in a closed thin layer made of the hydrophobic tails of the polymer molecules whose polar heads form the inner and outer interfaces of the MPS’s membrane. As the particles are covered with an appropriate surfactant, they are not chemically bonded to the hydrophobic “fluid” and are free to diffuse through it. The only restriction on that motion stems from the fact that the thickness of the intra-membrane layer but slightly exceeds the size of a nanoparticle, and so it should rather resemble not 3D but 2D diffusion.
Had the particles been non-magnetic, the thermofluctuational motion would have resulted just in additional isotropic osmotic pressure acting on the membrane boundaries. For magnetic particles the situation is different. First, the particles interact with each other via dipole-dipole potential and tend to form chain-like aggregates; second, under an applied field
the chains unwind and strive to align. Taking
as a polar axis, one finds that those chains tend to position themselves in meridional direction, thus stretching the MPS along the field. Assuming that the shell is strong enough as to conserve its area—see justification in
Section 2.5 below—one finds that this would mean its simultaneous shrinking in the perpendicular direction. This tendency is opposed, however, by two mechanisms. The first one is the high-elasticity (entropy) resistance of all the polymer component of the membrane. Another mechanism, working to the same effect, is the consequence of anisotropic nature of the magnetostatic interaction and requires that every two magnetised chains set in parallel repel each other in the lateral direction. Therefore, in the confined intra-membrane geometry, the neighbouring meridional nanoparticle chains would strive to move away from one another and, thus, to shrink the MPS in direction transverse to the field. For completeness, we note also an exception from this rule. When the inter-chain distances are very short and the chains are positioned in a “zipper” pattern with respect to one another, their lateral interaction might turn into attraction [
11]. However, such a case should really matter only for the systems with high filling factor, and this is not the case for the situations discussed below.
The above-presented considerations, even though providing a general qualitative view, cannot predict the overall deformation of a particular MPS, neither sign nor its magnitude. As follows, those characteristics would depend on the material parameters of a real system: the nanoparticle substance, size and concentration as well as on the polymer shell deformational properties.
As an MPS is a small soft object comprising a countable number of nanoparticles, the coarse-grained molecular dynamics (MD) turns out to be a very appropriate modelling tool to study its basic state and field-induced equilibrium deformation behaviour. Such an approach is successfully used to investigate similar systems, where the magnetic nanoparticles are embedded in the bulk of a loose polymer mesh (ferrogel). The structural elements of the mesh (their scales are different from that of the particles) are described in various ways. For example, in References [
12,
13,
14] each polymer string that connects neighbouring magnetic particles is a sequence of beads (blobs) linked by springs. Another approximation [
15] is more close to continual representation and presents the elastic medium as a network (triangular or other), in which the nodes are coupled to each other by entropic springs subjected to some spatial and angular constraints. Here both the nanoparticles and the blobs are the entities of finite size, to which the potentials excluding their overlaps are ascribed. Considering this way as a most prospective, we approximate the magnetic phase of an MPS as an assembly of structureless particles confined in a layer between two concentric borders made of a polymer (in the above-mentioned model sense). Those borders are impermeable for the particles but deform in response to the pressure generated by the latter.
3. Results and Discussion
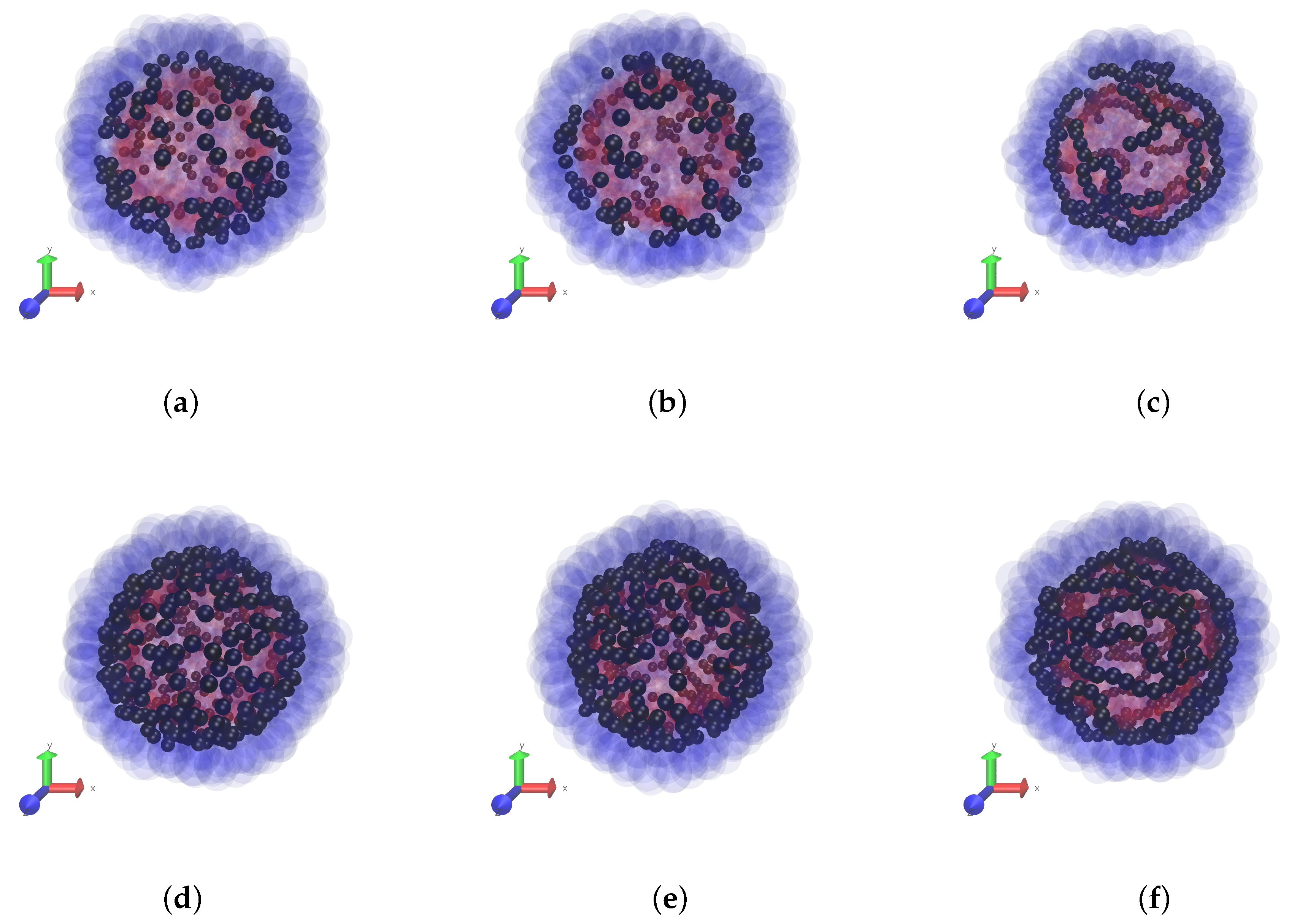
In this paper we keep the elastic properties of the polar layers (boundaries) of the membrane fixed, and vary the magnetic characteristics of the MPS: the interparticle dipole-dipole interaction and the concentration of the particles. The snapshots of
Figure 2 give a clear notion of the initial magnetic structures inherent to non-magnetised MPSs with different intensities of the interparticle interaction
for two fixed volume concentrations
of the particles, see series of panes (a–c) and (d,e). We remark that clotting of the particles at the periphery of the snapshots is illusional and is due simply to the fact that there the line of view is tangential to the MPS surface.
Strictly speaking, the change of corresponds to either variation of temperature or variation of the magnetic substance (different ), which the particles are made of. Although such a test is difficult (or impossible) to realise experimentally, it is instructive from the theoretical viewpoint as it shows that, depending on , the ground (zero-field) states of the MPSs are qualitatively different. At a low-to-moderate dipole interaction (up to ), only short particle chains, di- and trimers, could be distinguished at the snapshots. Note that the enhancement of concentration does not seem to substantially affect the aggregate length, it just increases their number. It is at a high level of interaction (), when non-directed chains whose contour length is of the order of that of the MPS are clearly visible.
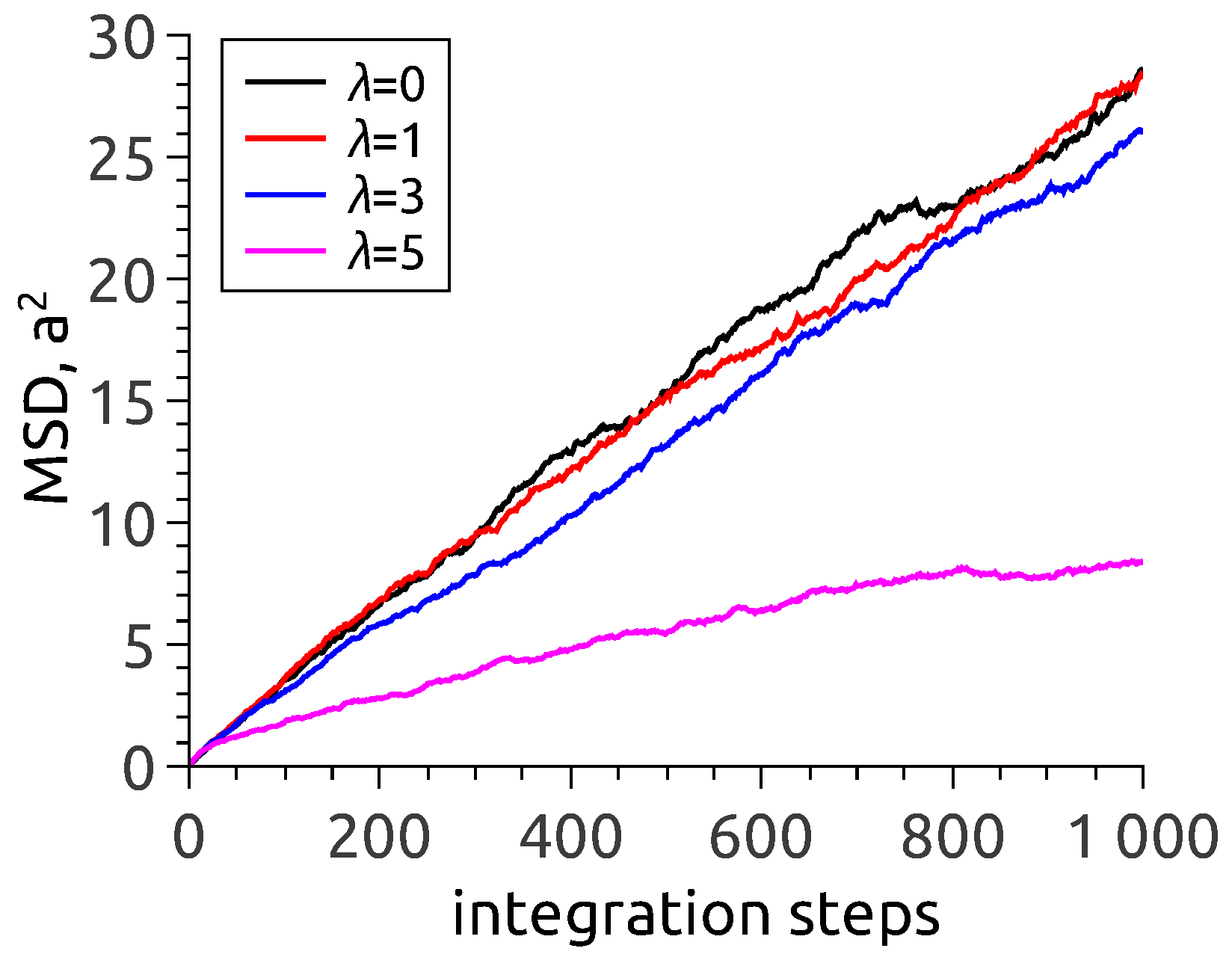
One arrives at the same conclusion when analysing the dependence of mean-square displacement (MSD) of nanoparticles in zero-field situation, see
Figure 3. To interpret the data, one has to recall that in an MD simulation with a fixed time step, the number of steps is a direct analog of observation time. As follows from
Figure 3, the MSD lines corresponding to
(no interparticle interaction at all) and
and 3 virtually coincide and quite well follow the usual free diffusion law
. It is at
that the dependence is different. The evident reason is that under those conditions, the particles are by no means isolated: in vast majority they are incorporated in chain aggregates where their motion is to a high extent hindered.
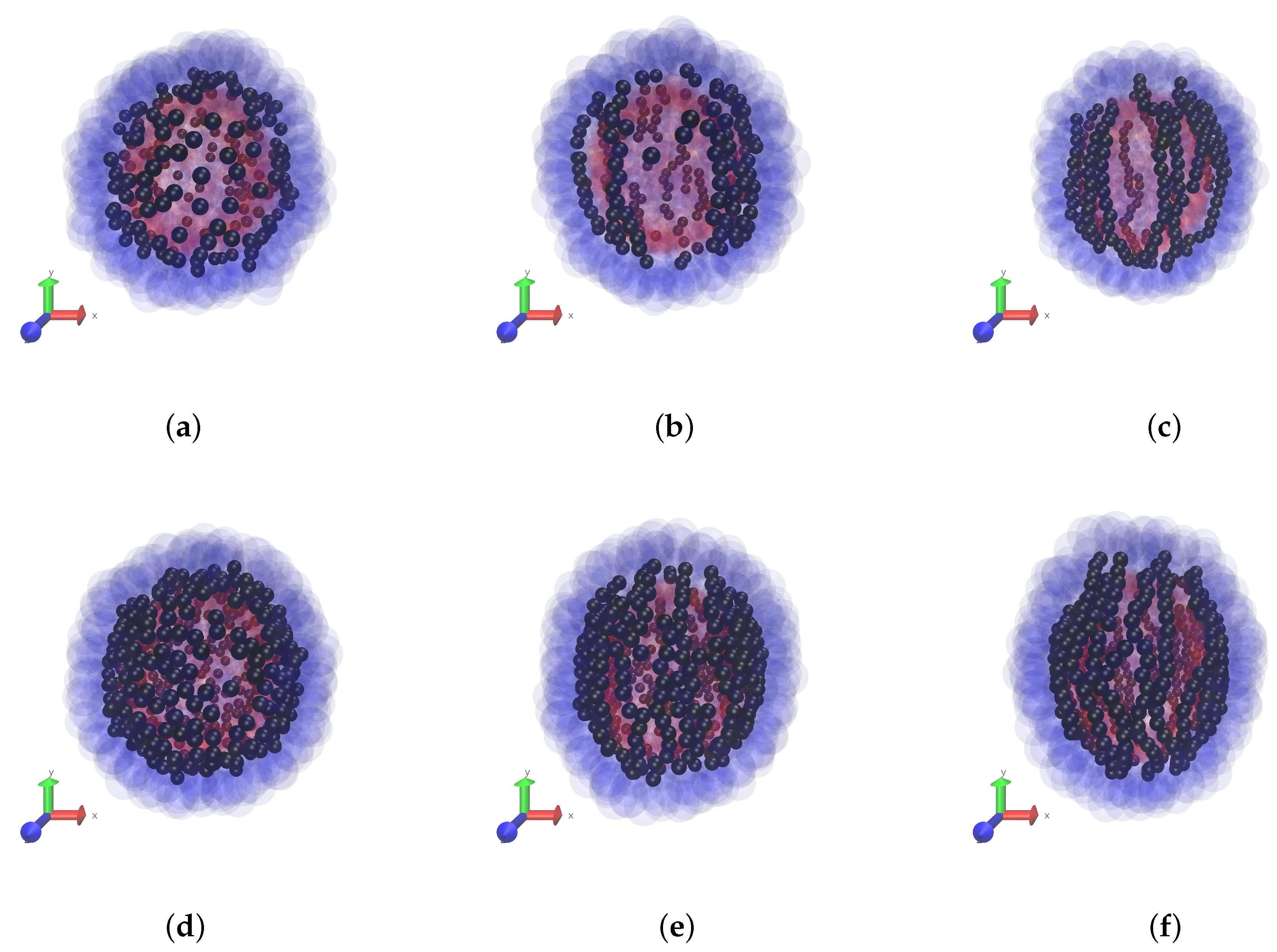
The effect of interparticle interaction on the magnetodeformational response of the MPS is illustrated by the snapshots of
Figure 4, which correspond to the situation under a strong field:
. We remind that parameter
measures the ratio of Zeeman to thermal energy for an MNP. Thus, for
, fluctuations of the magnetic moments are relatively weak, and vectors
of the particles readily align with the field. This strongly enhances their magnetic attraction in the “head-to-tail” direction, i.e., the direction of
, and this favors appearance of long erect chains. In their striving to full straightening, the chains work against the confinement imposed by the shell and this results in the MPS elongation. This is visible in
Figure 4, and, as seen, the elongation increases with the enhancement of the particle concentration and the more so with the magneto-dipole interaction parameter.
As the snapshots show, the emerging chain structure is not perfect, and this could be attributed to several reasons. First, those are kinetic restrictions: too much time is necessary for the already formed long chains to change their conformations. Second, as mentioned, the concept of laterally repulsive particle strings is entirely valid only for the system with very low concentration of the particles. Otherwise, the “zipper”-like attachment of neighbouring chains becomes energetically favorable. The spots where such patterns are present one could easily distinguish in
Figure 4, especially in panes (c,f).
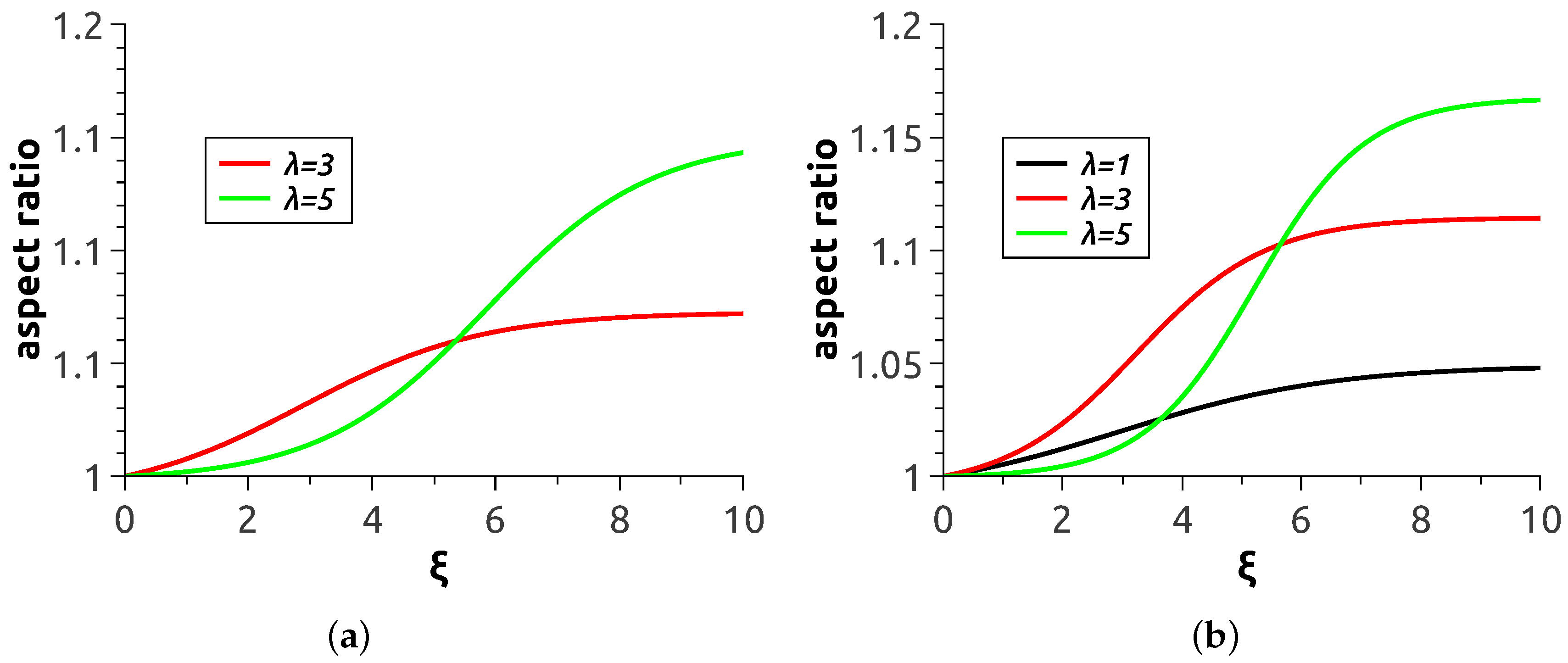
Quantitative characterisation of the magnetodeformational behaviour of MPS’s is presented in
Figure 5, where the aspect ratio of the polymersome cross-section by the plane parallel to the direction of
is plotted as a function of applied field strength. Each curve there was obtained by averaging over ten realisations of the magnetisation process with the same material parameters and same initial conditions. Expectedly, the greater the magnetic content of the shell and the level of magnetic interaction of the particles the more pronounced is the elongation effect of the field. It should be noted that the presented smooth curves were carried out with the aid of sigmoid fitting of calculation data points. Because of that, the curve corresponding to
at
wt.% is not presented: for it, the set of ten realisations does not suffice to reduce the uncertainty to a reasonable level.
All the presented curves display the tendency to saturation. The cause of that is clear: as soon as all magnetic moments in a chain are aligned with the field (at
), the magnetostatic force that the chain generates ceases to grow. However, at intermediate stages of magnetisation, the system undergoes complex structure evolution. For example, the non-directed chains in
Figure 2e are apparently shorter than those in
Figure 4e, whereas comparison of respective panes (f) of the same Figures reveals the opposite tendency. In our view, the rules governing such rearrangements could hardly be derived analytically. Indeed, to evaluate the number of the emerging chains as well as their length and curvature one has to carry out minimisation of the total (magnetic + elastic) energy of a multi-particle assembly subjected to such a complicated restriction as closeness of the layer and conservation of the areas of its surfaces. Therefore, numerical experiment seems the only adequate way to investigate MPS’s.
The main issue of interest is the overall deformation of an MPS as it determines its ability to work in numerous previewed applications. As
Figure 5 shows, the aspect ratios attainable with the model are about 1.17 maximum. This is much lower than those (about 2) for experimentally prepared large-size (about 500 μm) magnetic colloidosomes reported in [
6]. To understand the difference, we recall the results of References [
23,
24] where a continuum model of an MPS has been studied. It has been shown that the aspect ratio of a ferrovesicle in a given field grows substantially as the ratio of the shell thickness to the overall size of the vesicle goes down. For illustration, we remark that In Reference [
6] this ratio was about 1/50 whereas for the present model, see Equation (
6) it is
= 1/6, i.e., in our case is about ten times greater. Given that, the difference in the attained aspect ratios is quite understandable.
We remark, however, that comparison of the continuum model to the present one could not be other than qualitative. From structural viewpoint, the essence of the continuum approach is that local magnetic properties of any part of the membrane do not depend on the applied field. On the contrary, in the MD model of MPS, application of the field strongly affects the spatial distribution of the magnetic particles.
Finally we remark that the family of magnetic polymersomes is growing, and these objects are getting specialised for particular purposes. In this connection, we point out the idea to modulate permeability of the shell for the inner content of the MPS (e.g., a drug) with the aid of an applied field either mechanically [
6] or via inductive heating [
10]. A possible way to that goal, is the effect of field-driven spatial redistribution of nanoparticles in the MPS shell that we demonstrate here.
4. Conclusions
Magnetic polymersomes (MPS’s) are micro-objects with high potential impact in applications, the essence of which is the field control over their structure and deformational behaviour. Physically, the MPS’s are complex systems with a hierarchy of their intra- and inter-component interactions. Due to the presence of that many degrees of freedom, analytical description of MPS’s basic state and field-dependent properties cannot go very far. On the other hand, with allowance for the reference magnitudes of their inner and outer scales, MPS’s are very well fit for molecular dynamics modelling.
In this paper we apply one of the schemes of coarse-grained molecular dynamics for a detailed analysis of an isolated MPS. As far as we know, this is the first attempt of such a kind. The object considered here is a model one and as such cannot be directly associated with any real MPS known insofar. However, that is not the purpose of the work. Our goal is to formulate a consistent generic model for the problem in such a way that the model would be well prone for extending and detailing. Here the developed framework is applied to a quite particular situation, where just some magnetic parameters of an MPS with a given size, elasticity, etc. are varied. However, in our view, even this limited example suffices to demonstrate good workability of the molecular dynamics approach and proves its high potential for further studies. There are a number of interesting tasks to be accomplished in order to facilitate the use of the model and to bring it closer to real systems. Firstly, the description of equilibrium properties should be advanced: one needs to have a clear correlation between the potentials coupling the non-magnetic elements and the customary elastic characteristics of the membranes. In particular, the occurred rather low deformability of the studied MPS might be due just to a too high rigidity of the model membrane. As well the pre-simulation scheme should be made more flexible and comprehensible in choosing all the geometry parameters of the MPS’s.
Yet untouched, although quite attainable, is the whole scope of dynamic (kinetic) problems concerning time-dependent response of the MPS’s; there the interplay of viscosity effects would be of vital importance. For example, the assumption that the fluid that fills the membrane and in which the magnetic nanoparticles move through, is a Newtonian one, is evidently very naive. Indeed, the viscoelastic nature of the solution of hydrophobic polymer blocks separating the polar interfaces of the membrane should manifest itself in full when the behaviour of an MPS under a time-varying field comes in question.