Effect of Alkali Metal Atoms Doping on Structural and Nonlinear Optical Properties of the Gold-Germanium Bimetallic Clusters
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussion
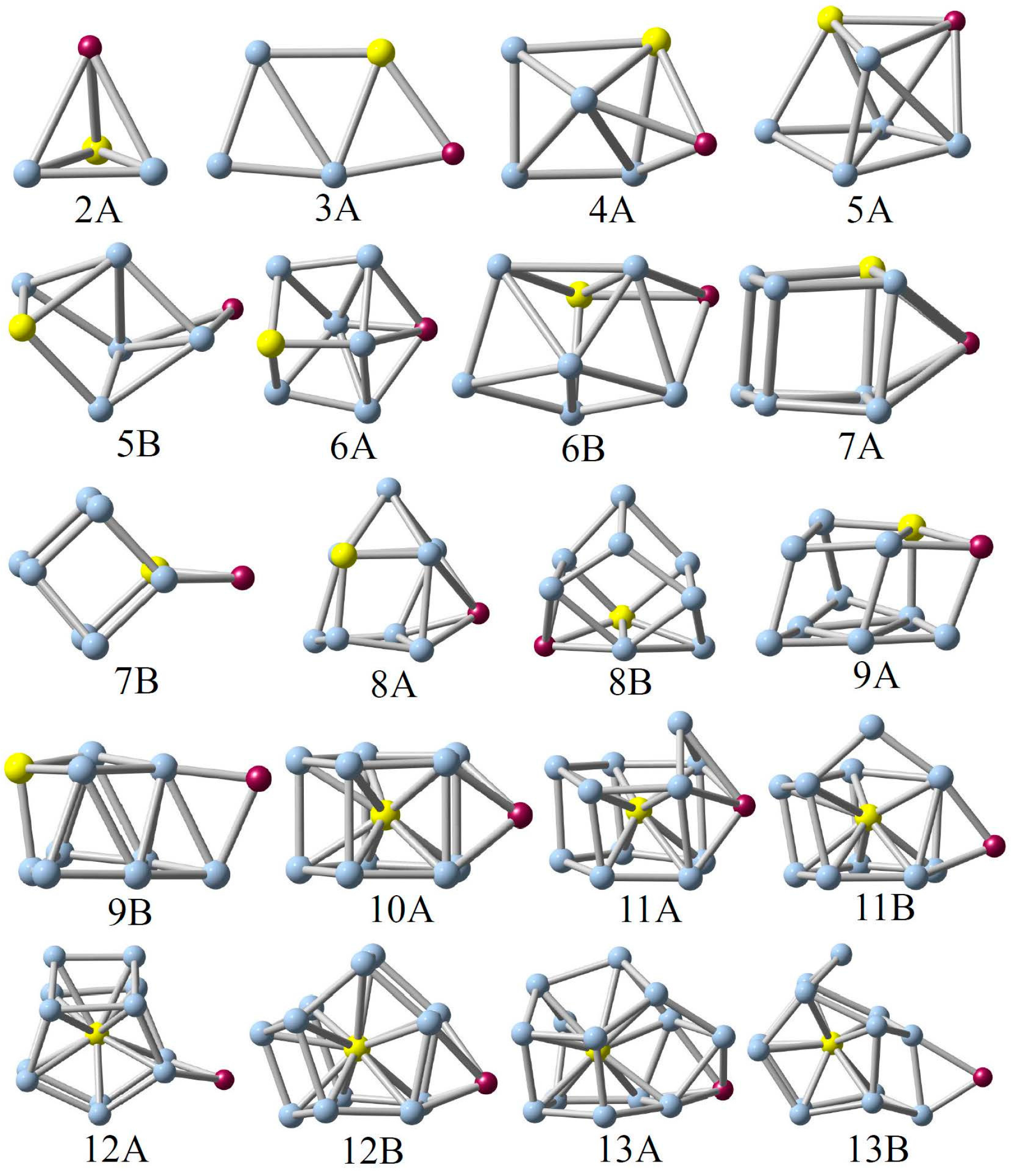
3.1. Geometric Structures
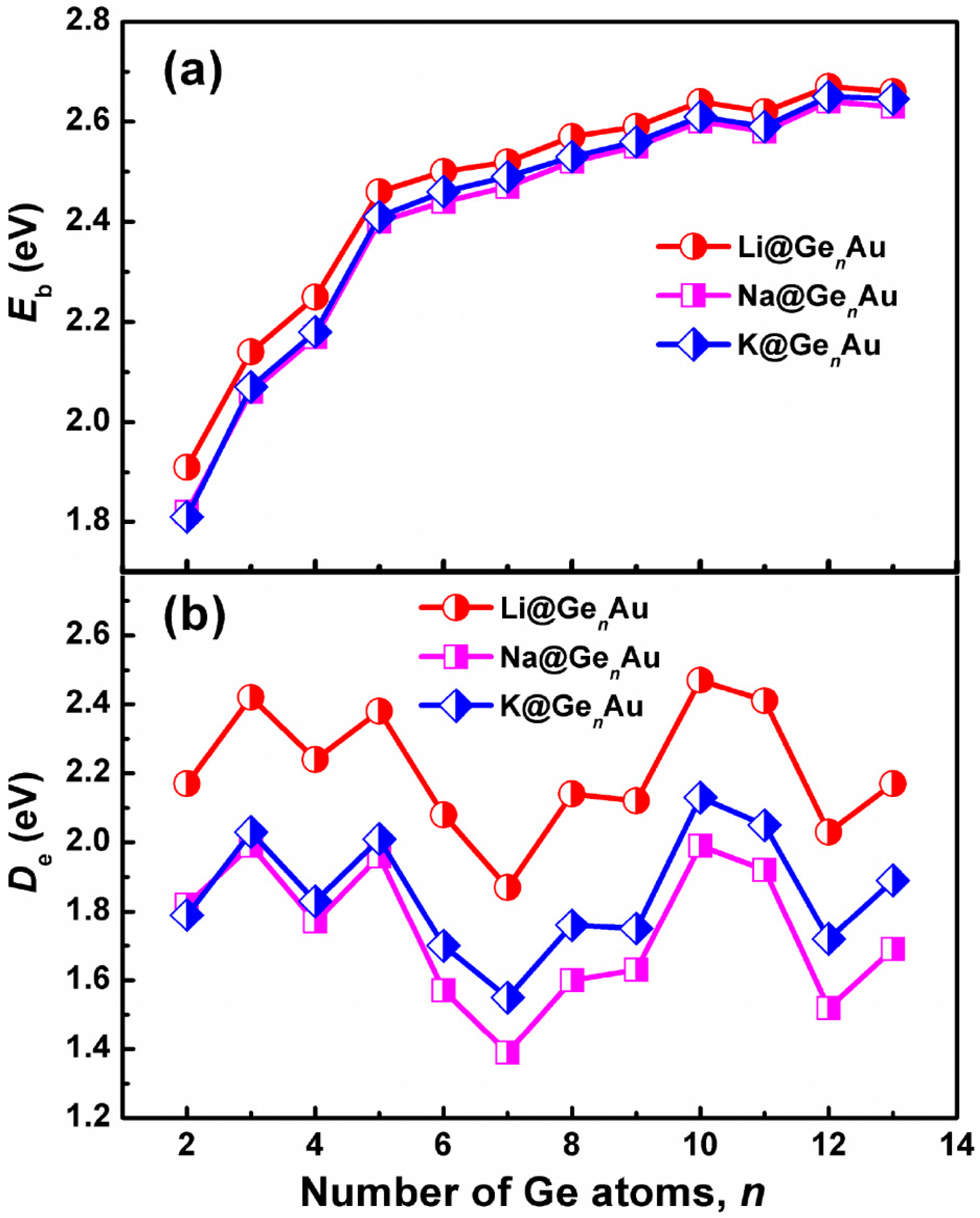
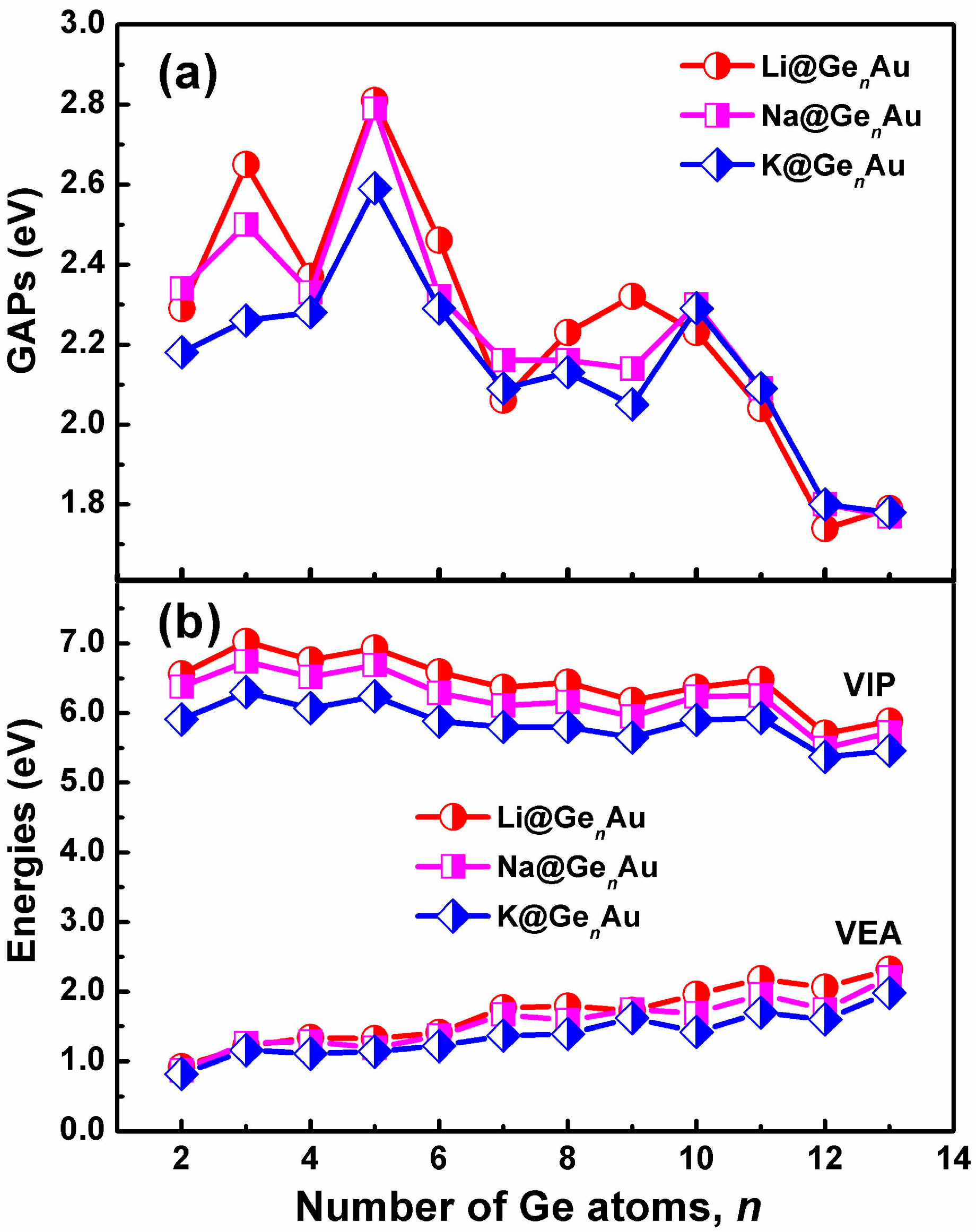
3.2. Chemical Stability and Electronic Structures
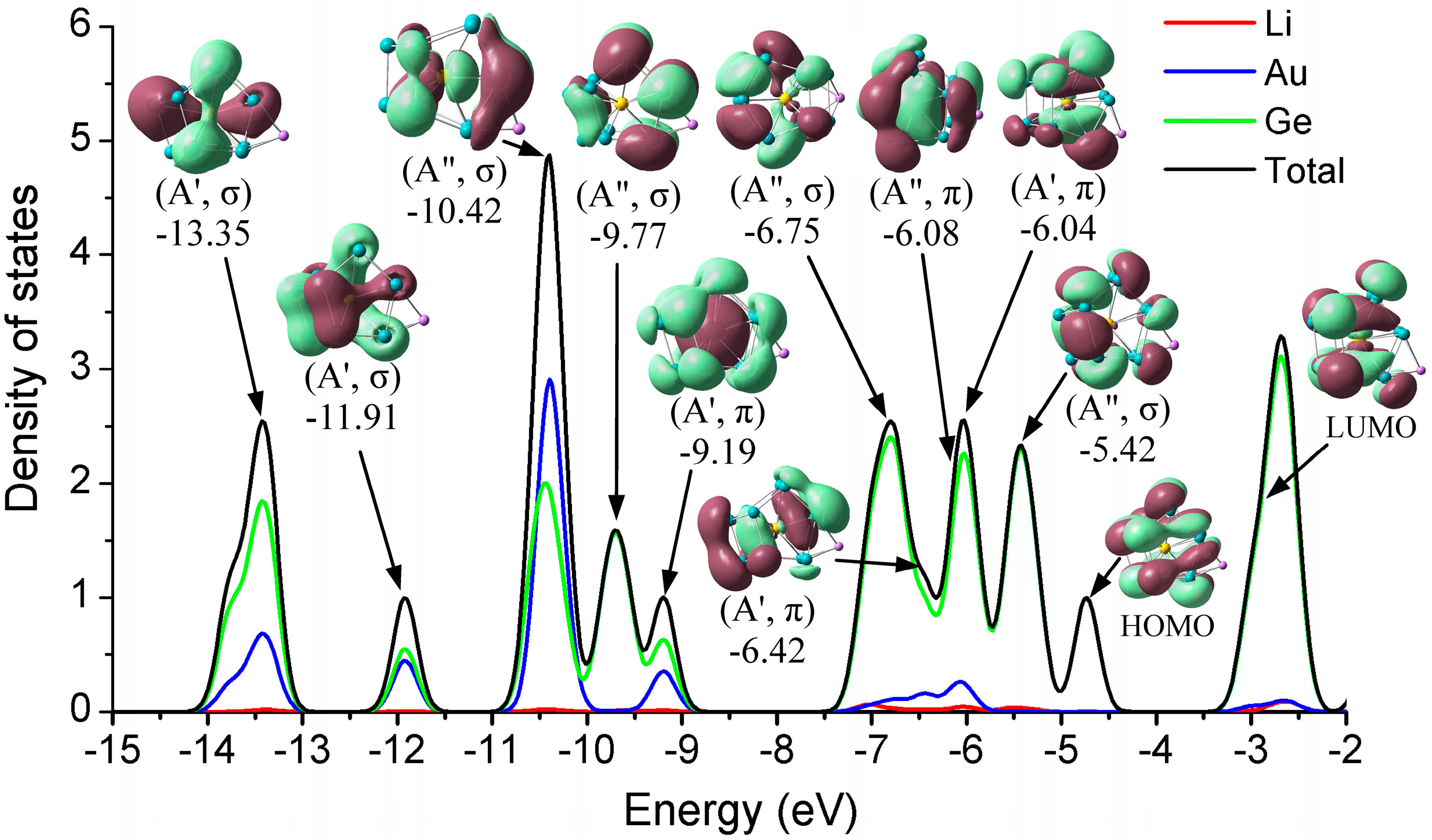
3.3. Density of States
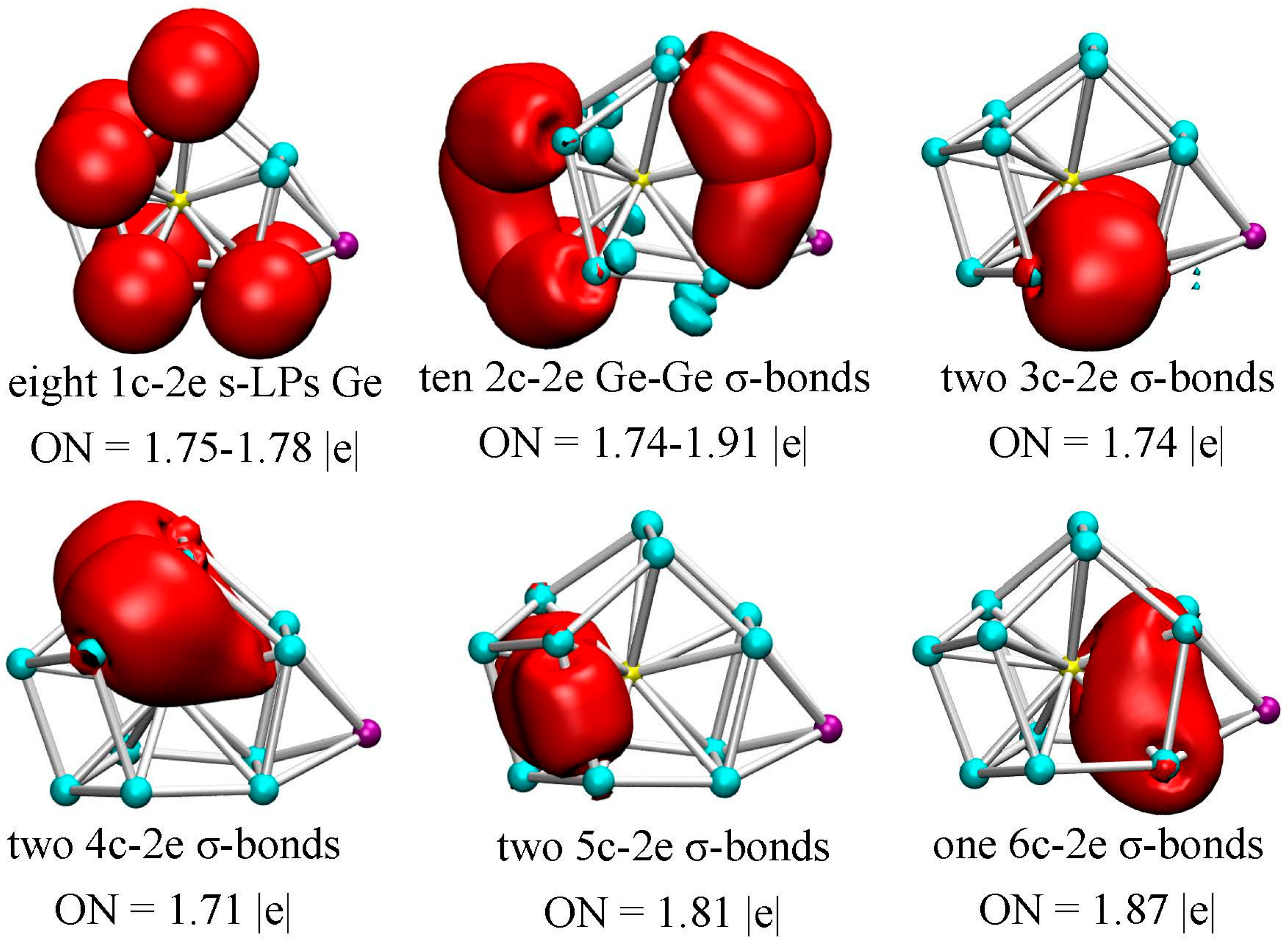
3.4. Chemical Bonding Analysis
3.5. Spherical Aromaticity
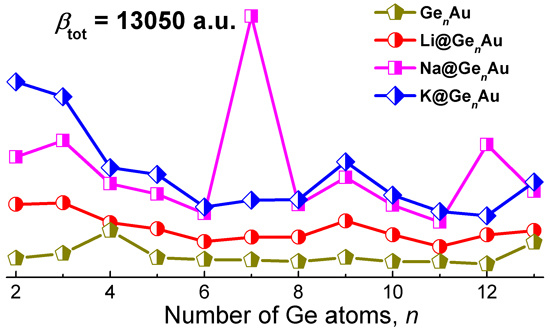
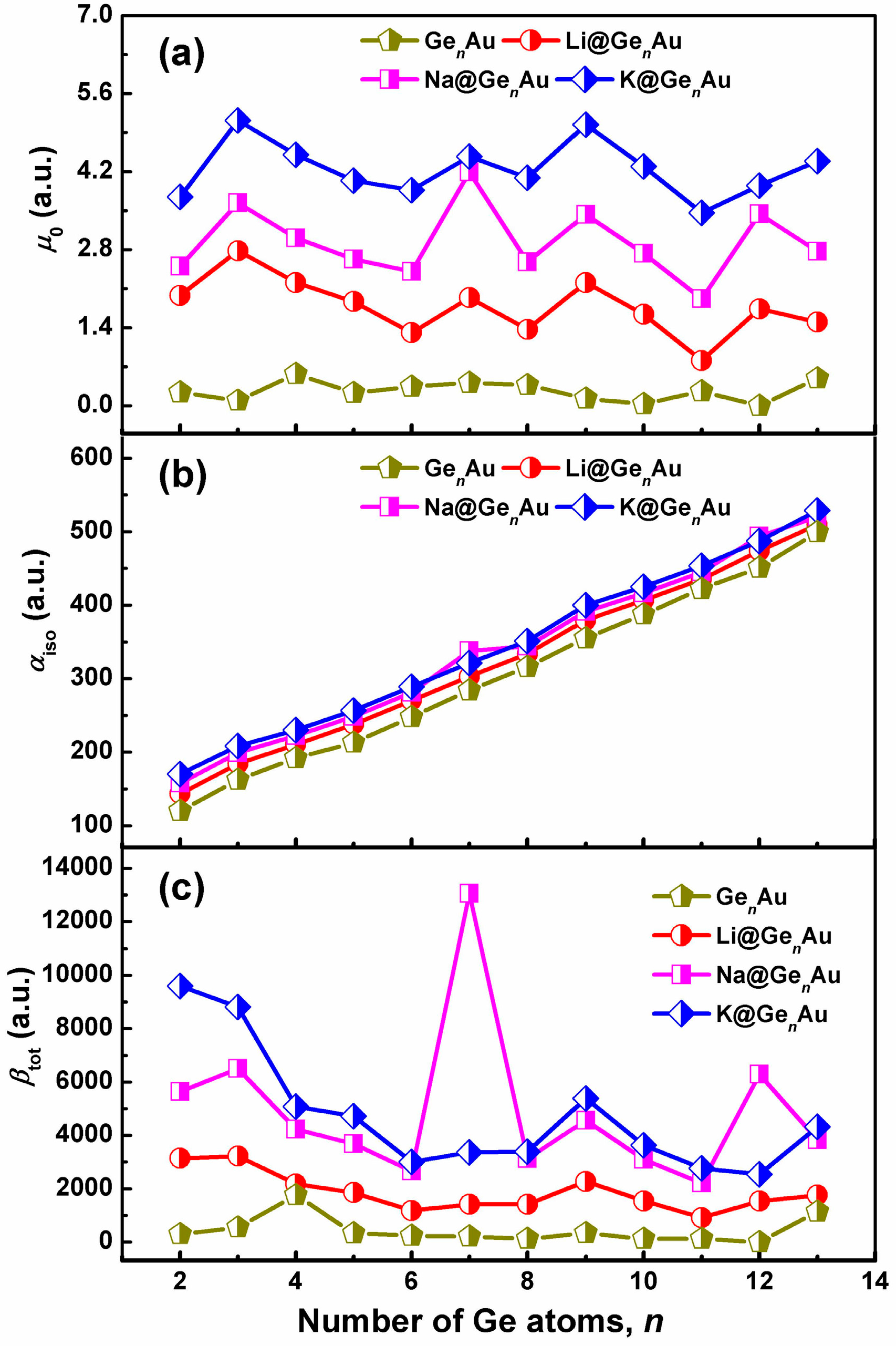
3.6. Linear and Nonlinear Optical Properties
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Khanna, S.N.; Jena, P. Atomic clusters: Building blocks for a class of solids. Phys. Rev. B 1995, 51, 13705. [Google Scholar] [CrossRef]
- Hou, N.; Wu, D.; Li, Y.; Li, Z.-R. Lower the electron affinity by halogenation: An unusual strategy to design superalkali cations. J. Am. Chem. Soc. 2014, 136, 2921–2927. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.-C.; Xu, H.-L.; Hu, Y.-Y.; Sun, S.-L.; Su, Z.-M. Quantum chemical research on structures, linear and nonlinear optical properties of the Li@n-acenes salt (n = 1, 2, 3, and 4). J. Phys. Chem. A 2011, 115, 2035–2040. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.-M.; Wu, D.; Li, Y.; Li, Z.-R. Theoretical study on superalkali (Li3) in ammonia: Novel alkalides with considerably large first hyperpolarizabilities. Dalton Trans. 2014, 43, 486–494. [Google Scholar] [CrossRef] [PubMed]
- Yaghobi, M.; Rafie, R.; Koohi, A. Optical and structural properties of the endohedral complexes M@C60 (M = Cs, Li, and Na). J. Mol. Struct. THEOCHEM 2009, 905, 48–50. [Google Scholar] [CrossRef]
- Wang, S.-J.; Li, Y.; Wang, Y.-F.; Wu, D.; Li, Z.-R. Structures and nonlinear optical properties of the endohedral metallofullerene-superhalogen compounds Li@C60–BX4 (X = F, Cl, Br). Phys. Chem. Chem. Phys. 2013, 15, 12903–12910. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, A.K.; Misra, N. Nonlinear optical behavior of LinF (n = 2–5) superalkali clusters. J. Mol. Model. 2015, 21, 305. [Google Scholar] [CrossRef] [PubMed]
- Ma, F.; Zhou, Z.-J.; Liu, Y.-T. Li2 trapped inside tubiform [n] boron nitride clusters (n = 4–8): Structures and first hyperpolarizability. ChemPhysChem 2012, 13, 1307–1312. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, A.K.; Misra, N. Competition between alkalide characteristics and nonlinear optical properties in OLi3-M-Li3O (M = Li, Na, and K) complexes. Int. J. Quantum Chem. 2017, 117, 208–212. [Google Scholar] [CrossRef]
- Sun, W.-M.; Fan, L.-T.; Li, Y.; Liu, J.-Y.; Wu, D.; Li, Z.-R. On the potential application of superalkali clusters in designing novel alkalides with large nonlinear optical properties. Inorg. Chem. 2014, 53, 6170–6178. [Google Scholar] [CrossRef] [PubMed]
- Jing, Y.-Q.; Li, Z.-R.; Wu, D.; Li, Y.; Wang, B.-Q.; Gu, F.L.; Aoki, Y. Effect of the complexant shape on the large first hyperpolarizability of alkalides Li+(NH3)4M−. ChemPhysChem 2006, 7, 1759–1763. [Google Scholar] [CrossRef] [PubMed]
- DeBacker, M.G.; Mkadmi, E.B.; Sauvage, F.X.; Lelieur, J.-P.; Wagner, M.J.; Concepcion, R.; Kim, J.; McMills, L.E.H.; Dye, J.L. The lithium-sodium-methylamine system: Does a low-melting sodide become a liquid metal? J. Am. Chem. Soc. 1996, 118, 1997–2003. [Google Scholar] [CrossRef]
- Muhammad, S.; Xu, H.; Liao, Y.; Kan, Y.; Su, Z. Quantum mechanical design and structure of the Li@B10H14 basket with a remarkably enhanced electro-optical response. J. Am. Chem. Soc. 2009, 131, 11833–11840. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.-L.; Li, Z.-R.; Su, Z.-M.; Muhammad, S.; Gu, F.L.; Harigaya, K. Knot-isomers of möbius cyclacene: How does the number of knots influence the structure and first hyperpolarizability? J. Phys. Chem. C 2009, 113, 15380–15383. [Google Scholar] [CrossRef]
- Karamanis, P.; Marchal, R.; Carbonniére, P.; Pouchan, C. Doping-enhanced hyperpolarizabilities of silicon clusters: A global ab initio and density functional theory study of Si10 (Li, Na, K)n (n = 1, 2) clusters. J. Chem. Phys. 2011, 135, 044511. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Han, Q.; Yang, X.; Song, R.; Song, L. Modification of alkali metals on silicon-based nanoclusters: An enhanced nonlinear optical response. Chem. Phys. Lett. 2016, 659, 93–99. [Google Scholar] [CrossRef]
- Donoso-Tauda, O.; Yepes, D.; Jaque, P.; Santos, J.C. Stability analysis of lithio-silicon si10li8 clusters: Planar bicyclic ring vs. Three-dimensional structures. Chem. Phys. Lett. 2014, 604, 72–76. [Google Scholar] [CrossRef]
- Li, X.; Su, K.; Yang, X.; Song, L.; Yang, L. Size-selective effects of geometry and electronic property on bimetallic au-ge nanoclusters. Comput. Theor. Chem. 2013, 1010, 32–37. [Google Scholar] [CrossRef]
- Deng, X.-J.; Kong, X.-Y.; Xu, X.-L.; Xu, H.-G.; Zheng, W.-J. Structural and magnetic properties of CoGen− (n = 2–11) clusters: Photoelectron spectroscopy and density functional calculations. ChemPhysChem 2014, 15, 3987–3993. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Claes, P.; Haertelt, M.; Lievens, P.; Janssens, E.; Fielicke, A. Structural determination of niobium-doped silicon clusters by far-infrared spectroscopy and theory. Phys. Chem. Chem. Phys. 2016, 18, 6291–6300. [Google Scholar] [CrossRef] [PubMed]
- Ngan, V.T.; Haeck, J.D.; Le, H.T.; Gopakumar, G.; Lievens, P.; Nguyen, M.T. Experimental detection and theoretical characterization of germanium-doped lithium clusters LinGe (n = 1–7). J. Phys. Chem. A 2009, 113, 9080–9091. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Yan, Z.; Li, S. The nature of structure and bonding between transition metal and mixed si-ge tetramers: A 20-electron superatom system. J. Comput. Chem. 2016, 37, 2316–2323. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.-J.; Xu, X.-L.; Feng, G.; Xu, H.-G.; Zheng, W.-J. Structural and electronic properties of AuSin− (n = 4–12) clusters: Photoelectron spectroscopy and ab initio calculations. J. Phys. Chem. C 2016, 120, 25628–25637. [Google Scholar] [CrossRef]
- Li, X.; Su, K. Structure, stability and electronic property of the gold-doped germanium clusters: AuGen (n = 2–13). Theor. Chem. Acc. 2009, 124, 345–354. [Google Scholar] [CrossRef]
- Li, X.; Li, C.; Yang, J.; Jalbout, A.F. The structures, thermochemistry, and electron affinities of hydrogenated silicon clusters Si6Hn/Si6Hn− (n = 3–14). Int. J. Quantum Chem. 2009, 109, 1283–1301. [Google Scholar] [CrossRef]
- Xenides, D.; Karamanis, P.; Pouchan, C. A critical analysis of the performance of new generation functionals on the calculation of the (hyper) polarizabilities of clusters of varying stoichiometry: Test case the SimGen (m + n = 7, n = 0–7) clusters. Chem. Phys. Lett. 2010, 498, 134–139. [Google Scholar] [CrossRef]
- Knoppe, S.; Hakkinen, H.; Verbiest, T. Nonlinear optical properties of thiolate-protected gold clusters: A theoretical survey of the first hyperpolarizabilities. J. Phys. Chem. C 2015, 119, 27676–27682. [Google Scholar] [CrossRef]
- Knoppe, S.; Vanbel, M.; van Cleuvenbergen, S.; Vanpraet, L.; Buergi, T.; Verbiest, T. Nonlinear optical properties of thiolate-protected gold clusters. J. Phys. Chem. C 2015, 119, 6221–6226. [Google Scholar] [CrossRef]
- Ozga, K.; Kawaharamura, T.; Umar, A.A.; Oyama, M.; Nouneh, K.; Slezak, A.; Fujita, S.; Piasecki, M.; Reshak, A.H.; Kityk, I.V. Second order optical effects in Au nanoparticle-deposited ZnO nanocrystallite films. Nanotechnology 2008, 19, 185709. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the colle-salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D. 01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Ngan, V.T.; Nguyen, M.T. The aromatic 8-electron cubic silicon clusters Be@Si8, B@Si8+, and C@Si82+. J. Phys. Chem. A 2010, 114, 7609–7615. [Google Scholar] [CrossRef] [PubMed]
- Bauschlicher, C.W. A comparison of the accuracy of different functionals. Chem. Phys. Lett. 1995, 246, 40–44. [Google Scholar] [CrossRef]
- Garoufalis, C.S.; Zdetsis, A.D.; Grimme, S. High level ab initio calculations of the optical gap of small silicon quantum dots. Phys. Rev. Lett. 2001, 87, 276402. [Google Scholar] [CrossRef] [PubMed]
- Hay, P.J.; Wadt, W.R. Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg. J. Chem. Phys. 1985, 82, 270–283. [Google Scholar] [CrossRef]
- Wadt, W.R.; Hay, P.J. Ab initio effective core potentials for molecular calculations. Potentials for main group elements Na to Bi. J. Chem. Phys. 1985, 82, 284–298. [Google Scholar] [CrossRef]
- Hay, P.J.; Wadt, W.R. Ab initio effective core potentials for molecular calculations. Potentials for K to Au including the outermost core orbitals. J. Chem. Phys. 1985, 82, 299–310. [Google Scholar] [CrossRef]
- Lu, S.-J.; Hu, L.-R.; Xu, X.-L.; Xu, H.-G.; Chen, H.; Zheng, W.-J. Transition from exohedral to endohedral structures of AuGen− (n = 2–12) clusters: Photoelectron spectroscopy and ab initio calculations. Phys. Chem. Chem. Phys. 2016, 18, 20321–20329. [Google Scholar] [CrossRef] [PubMed]
- Kanis, D.R.; Ratner, M.A.; Marks, T.J. Design and construction of molecular assemblies with large second-order optical nonlinearities. Quantum chemical aspects. Chem. Rev. 1994, 94, 195–242. [Google Scholar] [CrossRef]
- Li, X.; Ren, H.; Yang, X.; Song, J. Exploring the chemical bonding, infrared and UV–vis absorption spectra of oh radicals adsorption on the smallest fullerene. Spectrochim. Acta Part A 2015, 144, 258–265. [Google Scholar] [CrossRef] [PubMed]
- Cohen, H.D.; Roothaan, C.C.J. Electric dipole polarizability of atoms by the hartree-fock method. I. Theory for closed-shell systems. J. Chem. Phys. 1965, 43, S34–S39. [Google Scholar] [CrossRef]
- O’Boyle, N.M.; Tenderholt, A.L.; Langner, K.M. Cclib: A library for packageindependent computational chemistry algorithms. J. Comp. Chem. 2008, 29, 839–845. [Google Scholar] [CrossRef] [PubMed]
- Zubarev, D.Y.; Boldyrev, A.I. Developing paradigms of chemical bonding: Adaptive natural density partitioning. Phys. Chem. Chem. Phys. 2008, 10, 5207–5217. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. Vmd: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Yanaia, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange—Correlation functional using the coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Li, X.; Hopmann, K.H.; Hudecová, J.; Isaksson, J.; Novotná, J.; Stensen, W.; Andrushchenko, V.; Urbanová, M.; Svendsen, J.-S.; Bouř, P.; et al. Determination of absolute configuration and conformation of a cyclic dipeptide by nmr and chiral spectroscopic methods. J. Phys. Chem. A 2013, 117, 1721–1736. [Google Scholar] [CrossRef] [PubMed]
- Kumar, V.; Kawazoe, Y. Metal-encapsulated icosahedral superatoms of germanium and tin with large gaps: Zn@Ge12 and Cd@Sn12. Appl. Phys. Lett. 2002, 80, 859–861. [Google Scholar] [CrossRef]
- Mahtout, S.; Tariket, Y. Electronic and magnetic properties of CrGen (15 ≤ n ≤ 29) clusters: A DFT study. Chem. Phys. 2016, 472, 270–277. [Google Scholar] [CrossRef]
- Tai, T.B.; Nguyen, M.T. A stochastic search for the structures of small germanium clusters and their anions: Enhanced stability by spherical aromaticity of the Ge10 and Ge122− systems. J. Chem. Theory Comput. 2011, 7, 1119–1130. [Google Scholar] [CrossRef] [PubMed]
- Brack, M. The physics of simple metal clusters: Self-consistent jellium model and semiclassical approaches. Rev. Mod. Phys. 1993, 65, 677–732. [Google Scholar] [CrossRef]
- Zhai, H.-J.; Zhao, Y.-F.; Li, W.-L.; Chen, Q.; Bai, H.; Hu, H.-S.; Piazza, Z.A.; Tian, W.-J.; Lu, H.-G.; Wu, Y.-B.; et al. Observation of an all-boron fullerene. Nat. Chem. 2014, 6, 727–731. [Google Scholar] [CrossRef] [PubMed]
- Popov, I.A.; Li, W.-L.; Piazza, Z.A.; Boldyrev, A.I.; Wang, L.-S. Complexes between planar boron clusters and transition metals: A photoelectron spectroscopy and ab initio study of CoB12− and RhB12−. J. Phys. Chem. A 2014, 118, 8098–8105. [Google Scholar] [CrossRef] [PubMed]
- Boldyrev, A.; Wang, L.-S. Beyond organic chemistry: Aromaticity in atomic clusters. Phys. Chem. Chem. Phys. 2016, 18, 11589–11605. [Google Scholar] [CrossRef] [PubMed]
- Popov, I.A.; Jian, T.; Lopez, G.V.; Boldyrev, A.I.; Wang, L.-S. Cobalt-centred boron molecular drums with the highest coordination number in the cob16− cluster. Nat. Commun. 2015, 6, 8654. [Google Scholar] [CrossRef] [PubMed]
- Boldyrev, A.I.; Wang, L.-S. All-metal aromaticity and antiaromaticity. Chem. Rev. 2005, 105, 3716–3757. [Google Scholar] [CrossRef] [PubMed]
- Hirsch, A.; Chen, Z.; Jiao, H. Spherical aromaticity in ih symmetrical fullerenes: The 2(n + 1)2 rule. Angew. Chem. Int. Ed. 2000, 39, 3915–3917. [Google Scholar] [CrossRef]
- Hirsch, A.; Chen, Z.; Jiao, H. Spherical aromaticity of inorganic cage molecules. Angew. Chem. Int. Ed. 2001, 40, 2834–2838. [Google Scholar] [CrossRef]
- Tai, T.B.; Nguyen, M.T. Lithium atom can be doped at the center of a germanium cage: The stable icosahedral ge12li− cluster and derivatives. Chem. Phys. Lett. 2010, 492, 290–296. [Google Scholar] [CrossRef]
- King, R.B.; Heine, T.; Corminboeuf, C.; Schleyer, P.v.R. Antiaromaticity in bare deltahedral silicon clusters satisfying wade’s and hirsch’s rules: An apparent correlation of antiaromaticity with high symmetry. J. Am. Chem. Soc. 2004, 126, 430–431. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; Schleyer, P.v.R. Nucleus-independent chemical shifts (NICS) as an aromaticity criterion. Chem. Rev. 2005, 105, 3842–3888. [Google Scholar] [CrossRef] [PubMed]
- Pearson, R.G. Hard and soft acids and bases. J. Am. Chem. Soc. 1963, 85, 3533–3539. [Google Scholar] [CrossRef]
- Oudar, J.L. Optical nonlinearities of conjugated molecules. Stilbene derivatives and highly polar aromatic compounds. J. Chem. Phys. 1977, 67, 446–457. [Google Scholar] [CrossRef]
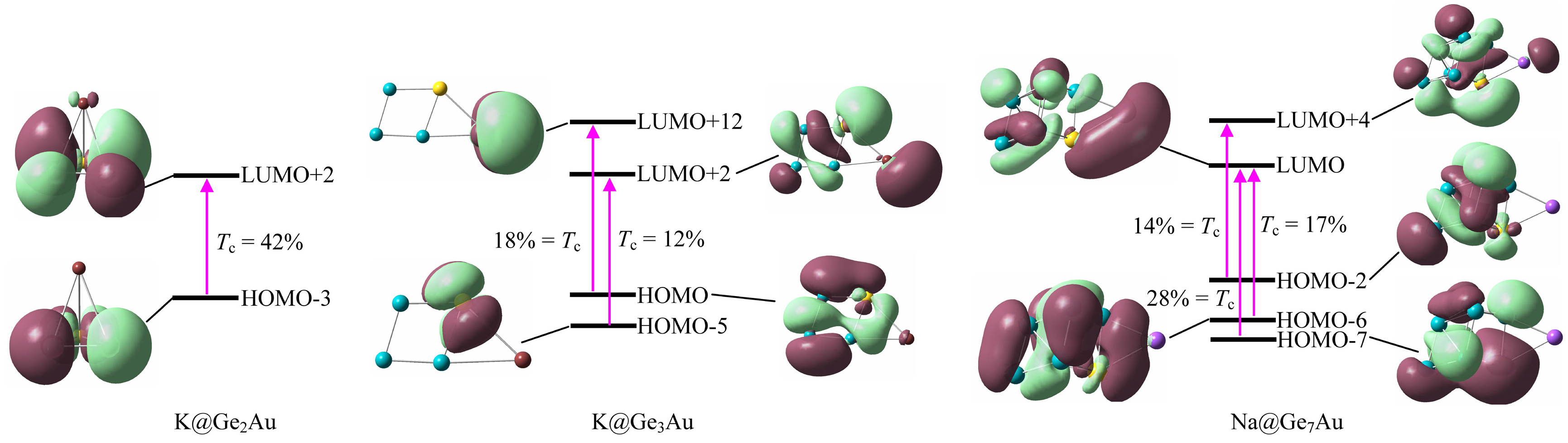
| Clusters | αiso | βtot | ∆E | f0 | ∆μ | Crucial Transitions * (%) |
|---|---|---|---|---|---|---|
| K@Ge2Au | 170 | 9602 | 6.056 | 0.358 | 0.371 | H-3 → L+2 (42%) |
| K@Ge3Au | 209 | 8812 | 5.702 | 0.297 | 0.623 | H → L+12 (18%), H-5 → L+2 (12%) |
| Na@Ge7Au | 338 | 13050 | 3.798 | 0.128 | 3.245 | H-7 → L (28%), H-6 → L (17%), H-2 → L+4 (14%) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Li, S.; Ren, H.; Yang, J.; Tang, Y. Effect of Alkali Metal Atoms Doping on Structural and Nonlinear Optical Properties of the Gold-Germanium Bimetallic Clusters. Nanomaterials 2017, 7, 184. https://doi.org/10.3390/nano7070184
Li X, Li S, Ren H, Yang J, Tang Y. Effect of Alkali Metal Atoms Doping on Structural and Nonlinear Optical Properties of the Gold-Germanium Bimetallic Clusters. Nanomaterials. 2017; 7(7):184. https://doi.org/10.3390/nano7070184
Chicago/Turabian StyleLi, Xiaojun, Shuna Li, Hongjiang Ren, Juxiang Yang, and Yongqiang Tang. 2017. "Effect of Alkali Metal Atoms Doping on Structural and Nonlinear Optical Properties of the Gold-Germanium Bimetallic Clusters" Nanomaterials 7, no. 7: 184. https://doi.org/10.3390/nano7070184