Mesoporous Silica Matrix as a Tool for Minimizing Dipolar Interactions in NiFe2O4 and ZnFe2O4 Nanoparticles
Abstract
:1. Introduction
2. Results and Discussion
3. Experimental Section
3.1. Synthesis of the MCM-41 Type Mesoporous Matrix
3.2. Preparation of Ferrite Nanoparticles Encapsulated in the Silica Mesoporous Matrix
3.3. Preparation of Ferrite Nanoparticles through Solvothermal Conditions
3.4. Preparation of Ferrite Nanoparticles Embedded in Amorphous Silica
3.5. Characterization Techniques
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dupré De Baubigny, J.; Benzaquen, M.; Fabié, L.; Delmas, M.; Aimé, J.P.; Legros, M.; Ondarçuhu, T. Shape and Effective Spring Constant of Liquid Interfaces Probed at the Nanometer Scale: Finite Size Effects. Langmuir 2015, 31, 9790–9798. [Google Scholar] [CrossRef] [PubMed]
- Yao, H.; Ishikawa, Y. Finite Size Effect on Magneto-Optical Responses of Chemically Modified Fe3O4 Nanoparticles Studied by MCD Spectroscopy. J. Phys. Chem. C 2015, 119, 13224–13230. [Google Scholar] [CrossRef]
- Guidi, T.; Gillon, B.; Mason, S.A.; Garlatti, E.; Carretta, S.; Santini, P.; Stunault, A.; Caciuffo, R.; van Slageren, J.; Klemke, B.; et al. Direct observation of finite size effects in chains of antiferromagnetically coupled spins. Nat. Commun. 2015, 6, 7061. [Google Scholar] [CrossRef] [PubMed]
- Silva, J.P.O.; Da Oliveira, M.J.T.; Lanceros-Mendez, S.; Nogueira, F. Finite-Size Effects in the Absorption Spectra of a Single-Wall Carbon Nanotube. J. Phys. Chem. C 2016, 120, 18268. [Google Scholar] [CrossRef]
- Geneste, G.; Bousquet, E.; Junquera, J.; Ghosez, P. Finite-size effects in BaTiO3 nanowires. Appl. Phys. Lett. 2006, 88, 112906. [Google Scholar] [CrossRef]
- Fukuhara, M. Lattice expansion of nanoscale compound particles. Phys. Lett. A 2003, 313, 427–430. [Google Scholar] [CrossRef]
- Petracic, O. Superparamagnetic nanoparticle ensembles. Superlattices Microstruct. 2010, 47, 569–578. [Google Scholar] [CrossRef]
- Knobel, M.; Nunes, W.C.; Socolovsky, L.M.; De Biasi, E.; Vargas, J.M.; Denardin, J.C. Superparamagnetism and other magnetic features in granular materials: A review on ideal and real systems. J. Nanosci. Nanotechnol. 2008, 8, 2836–2857. [Google Scholar] [CrossRef] [PubMed]
- Tartaj, P. Superparamagnetic composites: Magnetism with no memory. Eur. J. Inorg. Chem. 2009, 3, 333–343. [Google Scholar] [CrossRef]
- Blanco-Gutiérrez, V.; Torralvo-Fernández, M.J.; Sáez-Puche, R. Magnetic Behavior of ZnFe2O4 Nanoparticles: Effects of a Solid Matrix and the Particle Size. J. Phys. Chem. C 2010, 114, 1789–1795. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, Z.J. Size-dependent superparamagnetic properties of MgFe2O4 spinel ferrite nanocrystallites. Appl. Phys. Lett. 1998, 73, 3156–3158. [Google Scholar] [CrossRef]
- Bean, C.P.; Livingston, J.D. Superparamagnetism. J. Appl. Phys. 1959, 30, S120. [Google Scholar] [CrossRef]
- Gubbala, S.; Nathani, H.; Koizol, K.; Misra, R.D.K. Magnetic properties of nanocrystalline Ni-Zn, Zn-Mn, and Ni-Mn ferrites synthesized by reverse micelle technique. Phys. B Condens. Matter 2004, 348, 317–328. [Google Scholar] [CrossRef]
- Carta, D.; Casula, M.F.; Falqui, A.; Loche, D.; Mountjoy, G.; Sangregorio, C.; Corrias, A. Structural and Magnetic Investigation of the Inversion Degree in Ferrite Nanocrystals MFe2O4 (M = Mn, Co, Ni). J. Phys. Chem. C 2009, 113, 8606–8615. [Google Scholar] [CrossRef]
- Liu, C.; Zou, B.; Rondinone, A.J.; Zhang, Z.J. Chemical control of superparamagnetic properties of magnesium and cobalt spinel ferrite nanoparticles through atomic level magnetic couplings. J. Am. Chem. Soc. 2000, 122, 6263–6267. [Google Scholar] [CrossRef]
- Song, Q.; Zhang, Z.J. Correlation between spin-orbital coupling and the superparamagnetic properties in magnetite and cobalt ferrite spinel nanocrystals. J. Phys. Chem. B 2006, 110, 11205–11209. [Google Scholar] [CrossRef] [PubMed]
- Jacob, J.; Khadar, M.A. Investigation of mixed spinel structure of nanostructured nickel ferrite. J. Appl. Phys. 2010, 107, 114310. [Google Scholar] [CrossRef]
- Blanco-Gutiérrez, V.; Gallastegui, J.A.; Bonville, P.; Torralvo-Fernández, M.J.; Sáez-Puche, R. MFe2O4 (M: Co2+, Ni2+) Nanoparticles: Mössbauer and X-ray Absorption Spectroscopies Studies and High-Temperature Superparamagnetic Behavior. J. Phys. Chem. C 2012, 116, 24331–24339. [Google Scholar] [CrossRef]
- Blanco-Gutierrez, V.; Climent-Pascual, E.; Sáez-Puche, R.; Torralvo-Fernández, M.J. Temperature dependence of superparamagnetism in CoFe2O4 nanoparticles and CoFe2O4/SiO2 nanocomposites. Phys. Chem. Chem. Phys. 2016, 18, 9186–9193. [Google Scholar] [CrossRef] [PubMed]
- Kremenović, A.; Antić, B.; Vulić, P.; Blanuša, J.; Tomic, A. ZnFe2O4 antiferromagnetic structure redetermination. J. Magn. Magn. Mater. 2017, 426, 264–266. [Google Scholar] [CrossRef]
- Mørup, S.; Hansen, M.F.; Frandsen, C. Magnetic interactions between nanoparticles. Beilstein J. Nanotechnol. 2010, 1, 182–190. [Google Scholar] [CrossRef] [PubMed]
- Blanco-Gutierrez, V.; Saez-Puche, R.; Torralvo-Fernandez, M.J. Superparamagnetism and interparticle interactions in ZnFe2O4 nanocrystals. J. Mater. Chem. 2012, 22, 2992–3003. [Google Scholar] [CrossRef]
- Sun, X.; Ma, Y.Q.; Xu, S.T.; Xu, Y.F.; Geng, B.Q. The stress, surface spin and dipolar interaction in the diluted NiFe2O4 nanoparticles by the SiO2 matrix: Characterization and analyses. Mater. Charact. 2015, 107, 343–349. [Google Scholar] [CrossRef]
- Tartaj, P. Nanomagnets-From fundamental physics to biomedicine. Curr. Nanosci. 2006, 2, 43–53. [Google Scholar] [CrossRef]
- Coral, D.F.; Zélis, P.M.; Marciello, M.; Morales, M.P.; Craievich, A.; Sánchez, F.H.; Fernández Van Raap, M.B. Effect of Nanoclustering and Dipolar Interactions in Heat Generation for Magnetic Hyperthermia. Langmuir 2016, 32, 1201–1213. [Google Scholar] [CrossRef] [PubMed]
- Castellanos-Rubio, I.; Insausti, M.; Garaio, E.; Gil de Muro, I.; Plazaola, F.; Rojo, T.; Lezama, L. Fe3O4 nanoparticles prepared by the seeded-growth route for hyperthermia: Electron magnetic resonance as a key tool to evaluate size distribution in magnetic nanoparticles. Nanoscale 2014, 6, 7542–7552. [Google Scholar] [CrossRef] [PubMed]
- Mestrom, L.; Lenders, J.J.; de Groot, R.; Hooghoudt, T.; Sommerdijk, N.A.; Artigas, M.V. Stable ferrofluids of magnetite nanoparticles in hydrophobic ionic liquids. Nanotechnology 2015, 26, 285602. [Google Scholar] [CrossRef] [PubMed]
- Blanco-Gutiérrez, V.; Torralvo-Fernandez, M.J.; Saez-Puche, R. Innovative study of superparamagnetism in 3 nm CoFe2O4 particles. RSC Adv. 2016, 6, 87995–88000. [Google Scholar] [CrossRef]
- Peddis, D.; Orru, F.; Ardu, A.; Cannas, C.; Musinu, A. Piccaluga G Interparticle Interactions and Magnetic Anisotropy in Cobalt Ferrite Nanoparticles: Influence of Molecular Coating. Chem. Mater. 2012, 24, 1062–1071. [Google Scholar] [CrossRef]
- Blanco-Gutiérrez, V.; Virumbrales, M.; Saez-Puche, R.; Torralvo-Fernandez, M.J. Superparamagnetic behavior of MFe2O4 nanoparticles and MFe2O4/SiO2 composites (M:Co, Ni). J. Phys. Chem. C 2013, 117, 20927–20935. [Google Scholar] [CrossRef]
- Blanco-Gutiérrez, V.; Urones-Garrote, E.; Torralvo-Fernández, M.J.; Sáez-Puche, R. ZnFe2O4 nanoparticles: Different magnetic behavior when they are hosted in porous structures. Chem. Mater. 2010, 22, 6130–6137. [Google Scholar] [CrossRef]
- Chen, J.; Feng, Z.; Ying, P.; Li, C. ZnO clusters encapsulated inside micropores of zeolites studied by UV Raman and laser-induced luminescence spectroscopies. J. Phys. Chem. B 2004, 108, 12669–12676. [Google Scholar] [CrossRef]
- Neimark, A.V.; Ravikovitch, P.I.; Grün, M.; Schüth, F.; Unger, K.K. Pore Size Analysis of MCM-41 Type Adsorbents by Means of Nitrogen and Argon Adsorption. J. Colloid Interface Sci. 1998, 207, 159–169. [Google Scholar] [CrossRef] [PubMed]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of Gases in Multimolecular Layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Barrett, E.P.; Joyner, L.G.; Halenda, P.P. The Determination of Pore Volume and Area Distributions in Porous Substances. I. Computations from Nitrogen Isotherms. J. Am. Chem. Soc. 1951, 73, 373–380. [Google Scholar] [CrossRef]
- Broekhoff, J.C.P.; De Boer, J.H. Studies on Pore Systems in Catalysts: XII. Pore Distributions from the Desorption Branch of a Nitrogen Sorption Isotherm in the Case of Cylindrical Pores A. An Analysis of the Capillary Evaporation Process. J. Catal. 1968, 10, 368–374. [Google Scholar] [CrossRef]
- Mitra, S.; Mandal, K.; Anil Kumar, P. Temperature dependence of magnetic properties of NiFe2O4 nanoparticles embeded in SiO2 matrix. J. Magn. Magn. Mater. 2006, 306, 254–259. [Google Scholar] [CrossRef]
- Gubin, S.P.; Koksharov, Y.A.; Khomutov, G.B.; Yurkov, G.Y. Magnetic nanoparticles: Preparation, structure and properties. Russ. Chem. Rev. 2005, 74, 489–520. [Google Scholar] [CrossRef]
- Fiorani, D. Surface Effects in Magnetic Nanoparticles; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Limaye, M.V.; Singh, S.B.; Date, S.K.; Kothari, D.; Reddy, V.; Raghavendra, G.; Ajay, S.; Vasant, C.; Ram Jane, K.; Sulabha, K. High Coercivity of Oleic Acid Capped CoFe2O4 Nanoparticles at Room Temperature. J. Phys. Chem. B 2009, 113, 9070–9076. [Google Scholar] [CrossRef] [PubMed]
- Vestal, C.R.; Zhang, Z.J. Effects of surface coordination chemistry on the magnetic properties of MnFe2O4 spinel ferrite nanoparticles. J. Am. Chem. Soc. 2003, 125, 9828–9833. [Google Scholar] [CrossRef] [PubMed]
- Nadeem, K.; Krenn, H.; Traussnig, T.; Würschum, R.; Szabó, D.V.; Letofsky-Papst, I. Effect of dipolar and exchange interactions on magnetic blocking of maghemite nanoparticles. J. Magn. Magn. Mater. 2011, 323, 1998–2004. [Google Scholar] [CrossRef]
- Virumbrales, M.; Delgado-Cabello, A.; Andrada, A.; Sanchez-Benitez, J.; Urones-Garrote, E.; Blanco-Gutiérrez, V.; Torralvo-Fernandez, M.J.; Saez-Puche, R. Effect of composition and coating on the interparticle interactions and magnetic hardness of MFe2O4 (M = Fe, Co, Zn) nanoparticles. Phys. Chem. Chem. Phys. 2017, 4, 8363–8372. [Google Scholar] [CrossRef] [PubMed]
- Cai, C.; Wang, H.; Han, J. Synthesis and characterization of ionic liquid-functionalized alumino-silicate MCM-41 hybrid mesoporous materials. Appl. Surf. Sci. 2011, 257, 9802–9808. [Google Scholar] [CrossRef]

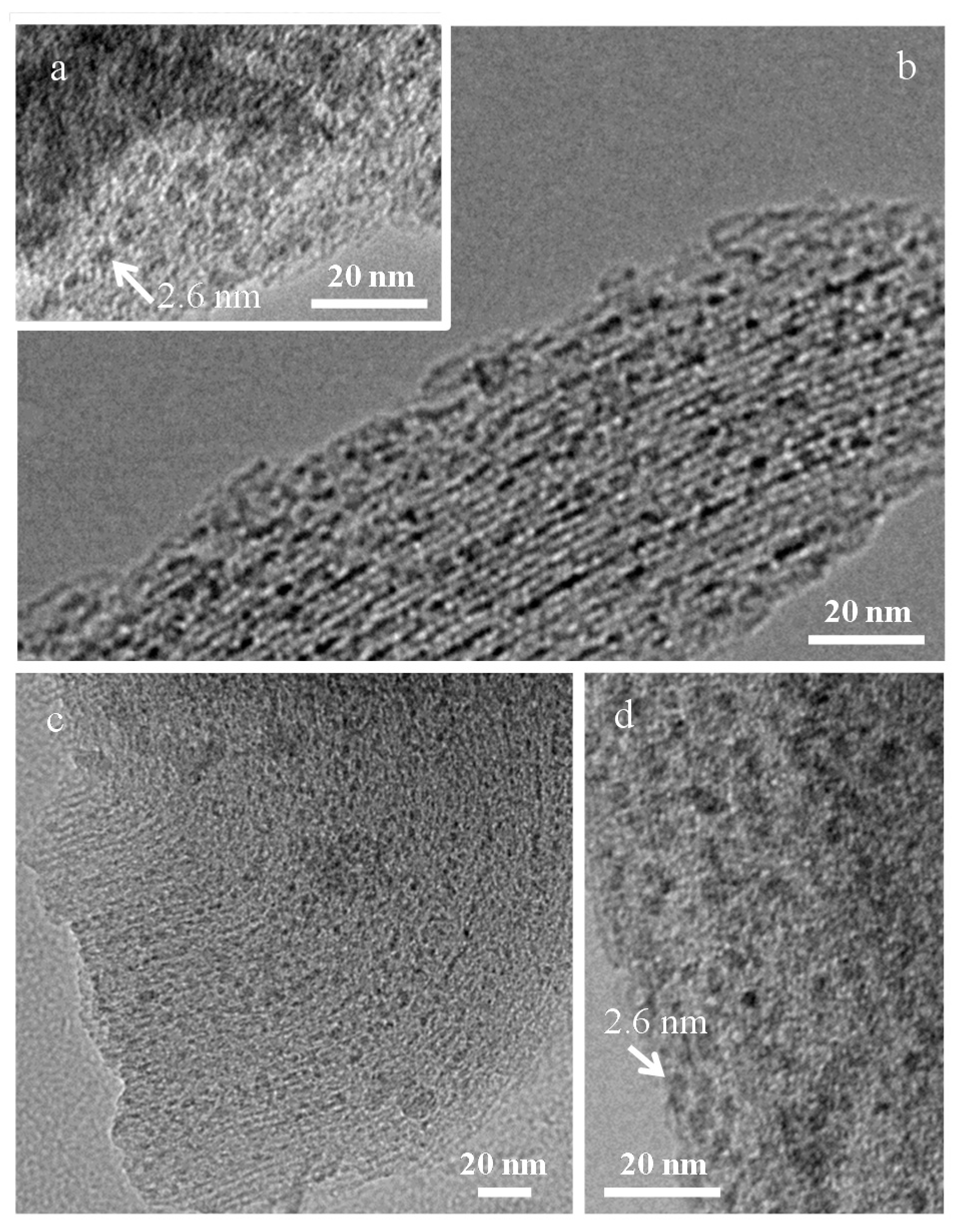
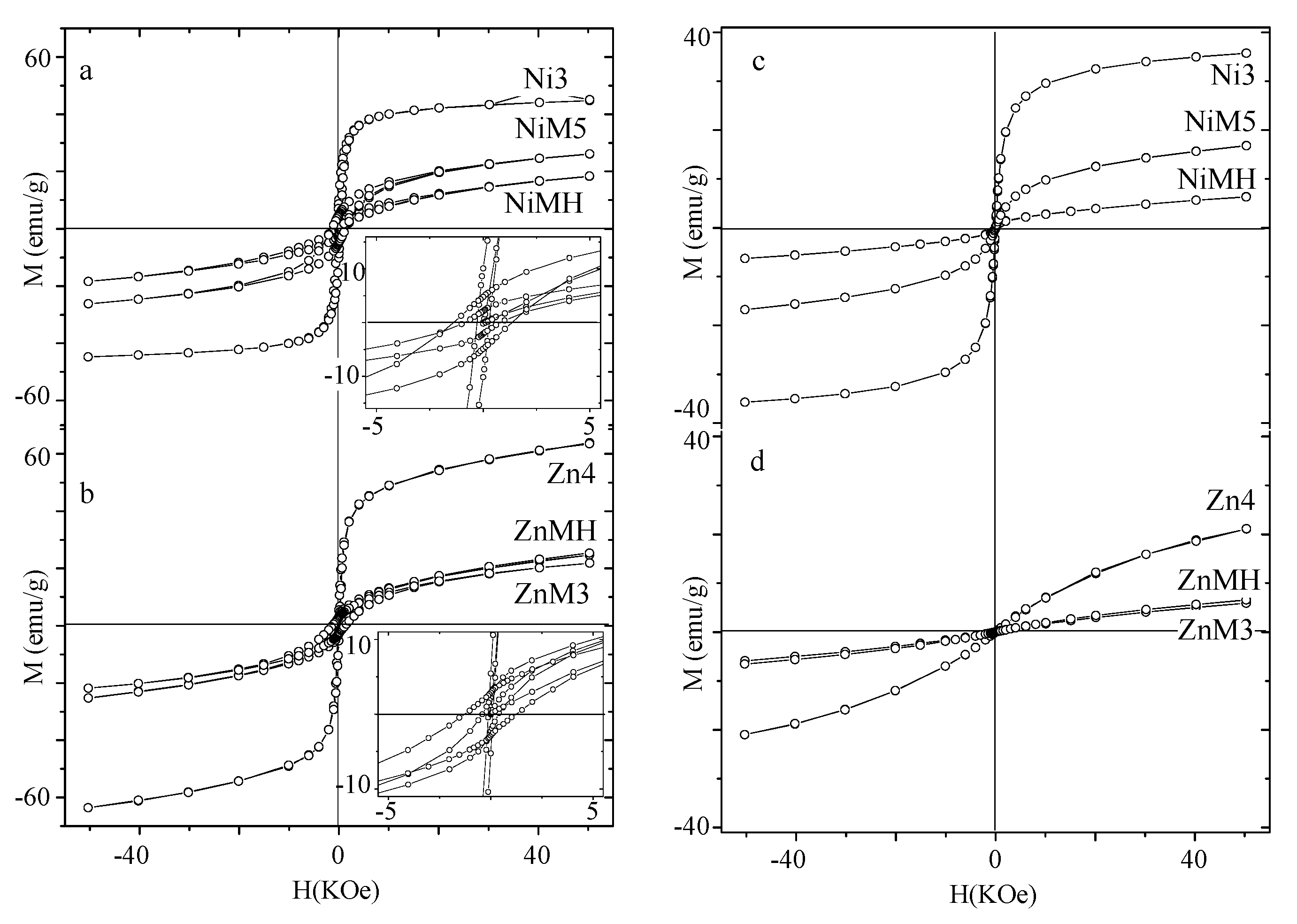
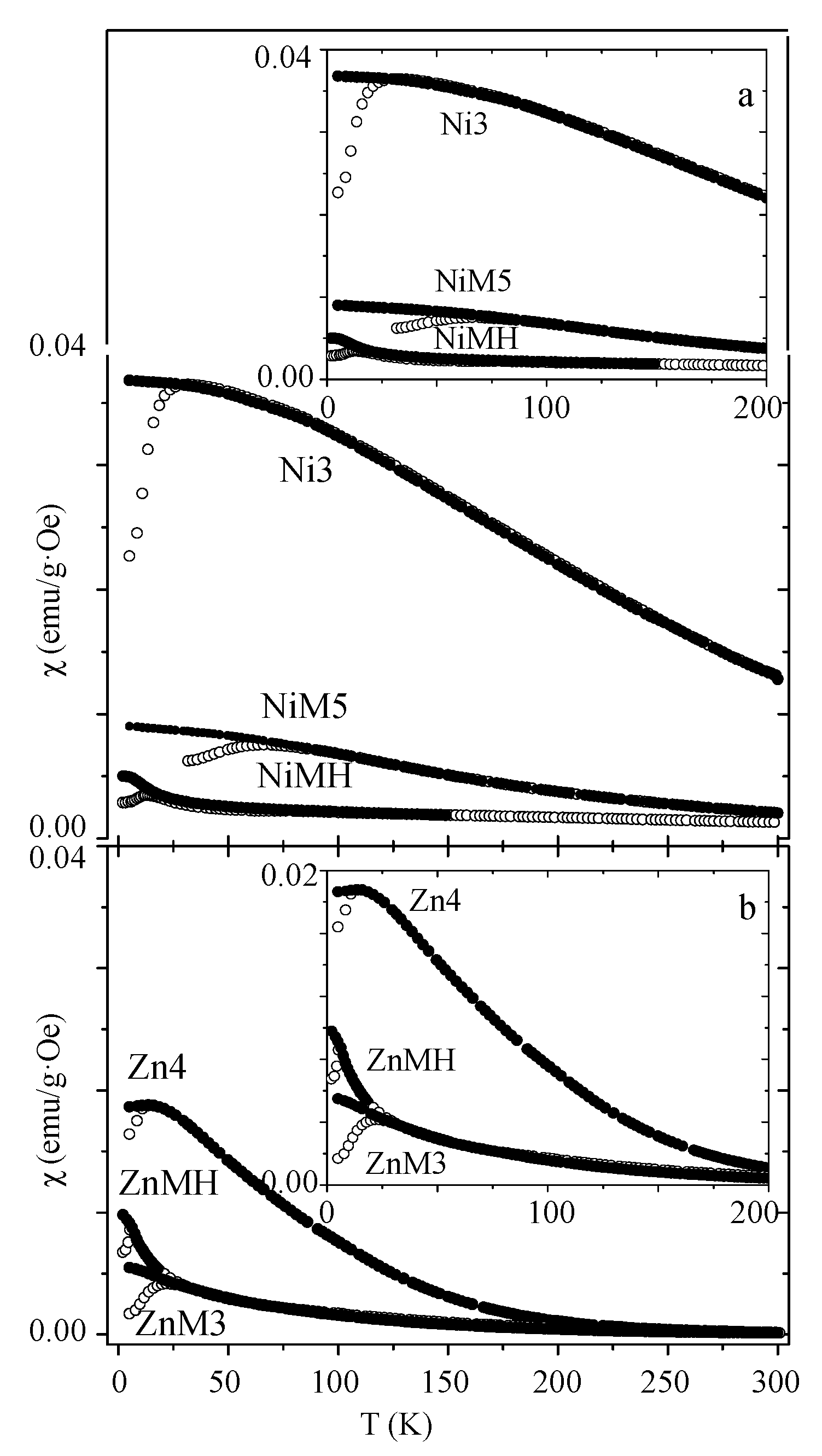
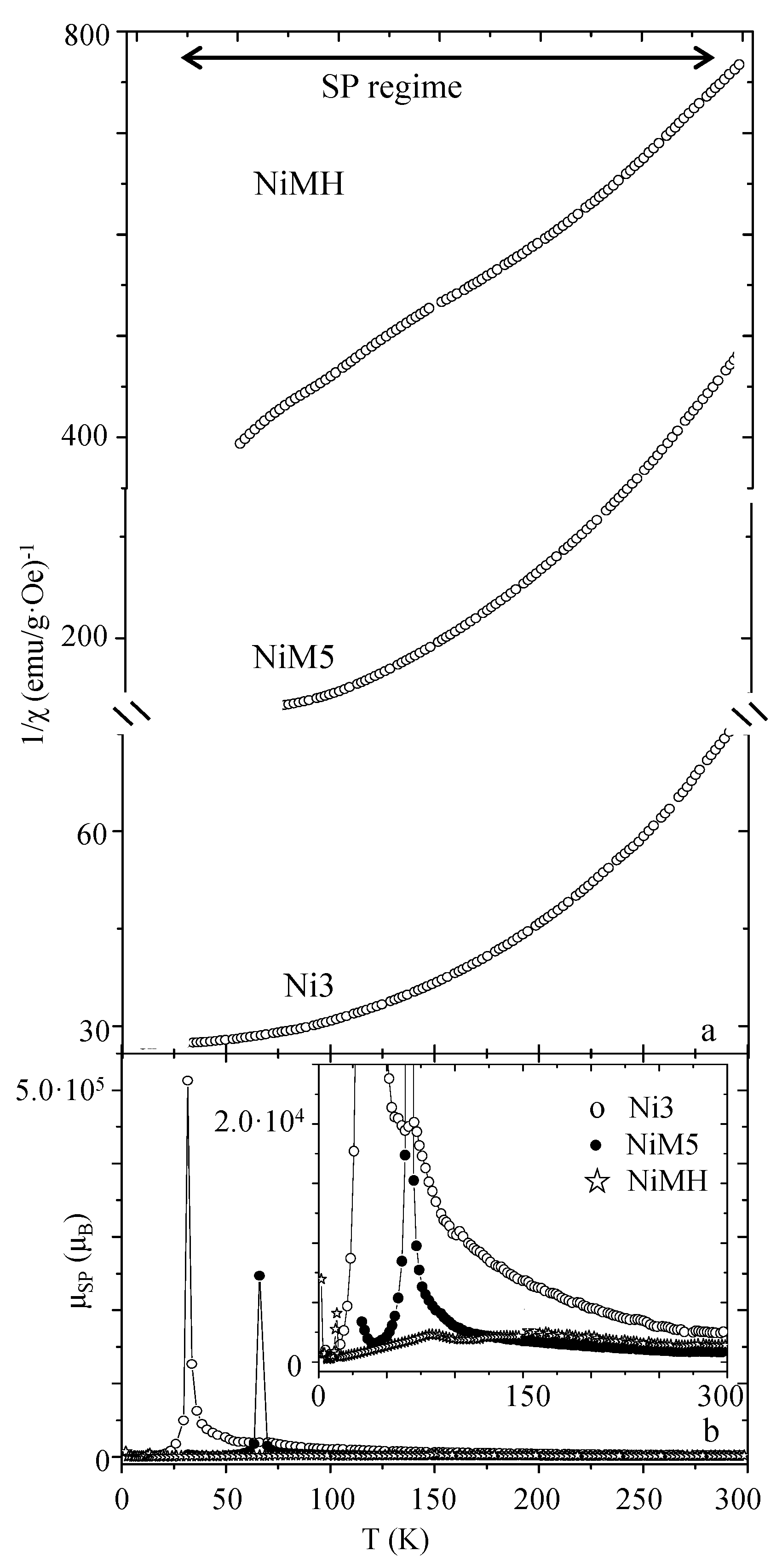
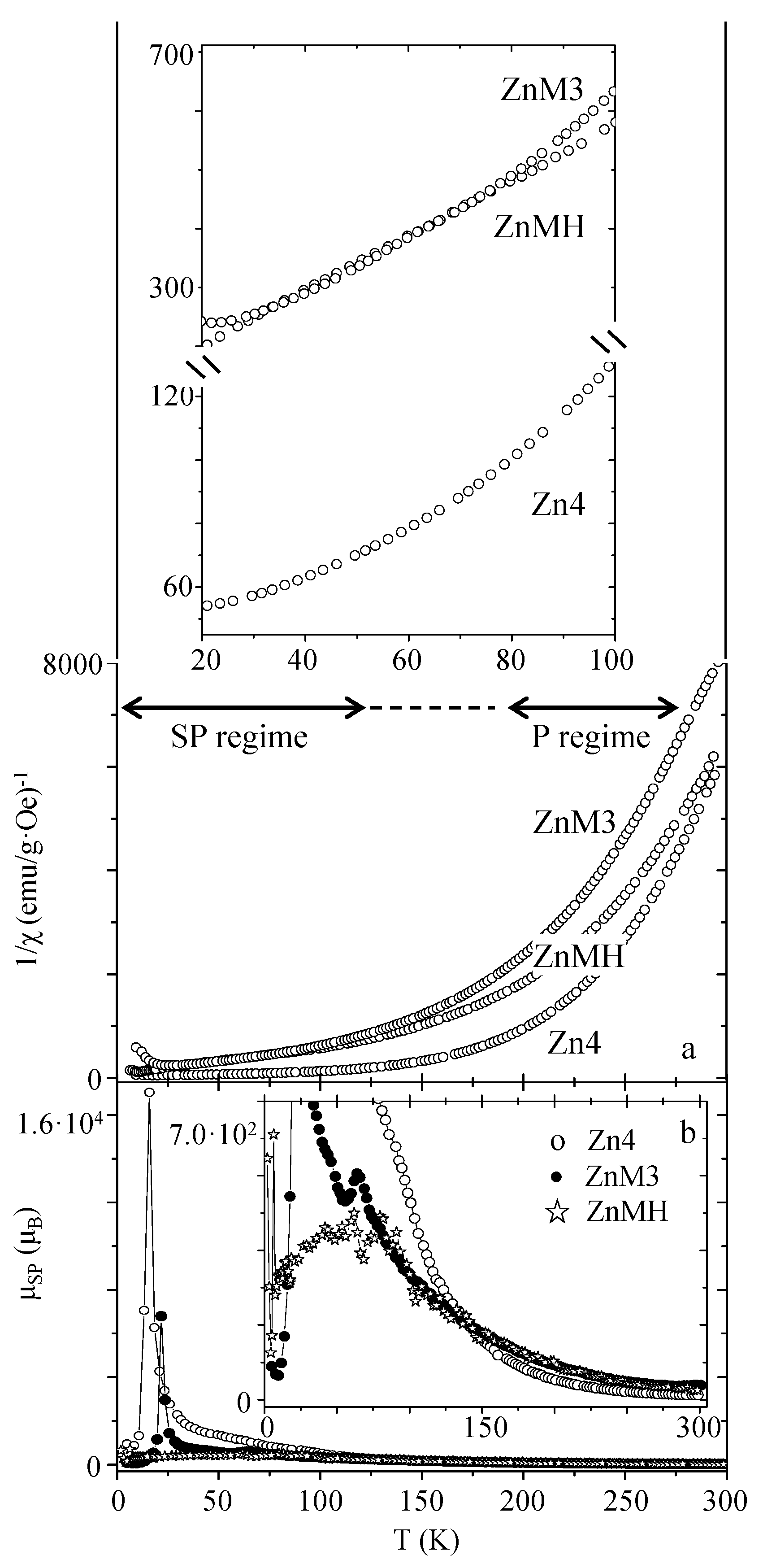
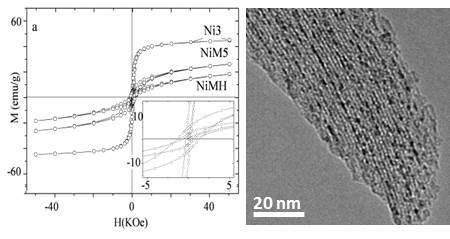
| Sample | MS (emu/g) | K (erg/cm3) | HK (Oe) | HC,5K (Oe) | TB (K) | |
|---|---|---|---|---|---|---|
| Ni3 | 3 nm bare particles | 46.8 | 1.7 × 105 | 1312 | 286 | 27 |
| NiMH | 2.6 nm particles in the MCM-type matrix | 16.0 | 7.1 × 105 | 16492 | 880 | 13 |
| NiM5 | 5 nm particles in amorphous SiO2 | 20.9 | 2.3 × 105 | 3912 | 1390 | 63 |
| Zn4 | 4 nm bare particles | 43.1 | 2.5 × 105 | 1722 | 125 | 14 |
| ZnMH | 2.6 nm particles in the MCM-type matrix | 22.0 | 9.1 × 105 | 15516 | 400 | 6.5 |
| ZnM3 | 3 nm particles in amorphous SiO2 | 15.9 | 2.3 × 105 | 5311 | 1300 | 23 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Virumbrales, M.; Saez-Puche, R.; Torralvo, M.J.; Blanco-Gutierrez, V. Mesoporous Silica Matrix as a Tool for Minimizing Dipolar Interactions in NiFe2O4 and ZnFe2O4 Nanoparticles. Nanomaterials 2017, 7, 151. https://doi.org/10.3390/nano7070151
Virumbrales M, Saez-Puche R, Torralvo MJ, Blanco-Gutierrez V. Mesoporous Silica Matrix as a Tool for Minimizing Dipolar Interactions in NiFe2O4 and ZnFe2O4 Nanoparticles. Nanomaterials. 2017; 7(7):151. https://doi.org/10.3390/nano7070151
Chicago/Turabian StyleVirumbrales, Maider, Regino Saez-Puche, María José Torralvo, and Veronica Blanco-Gutierrez. 2017. "Mesoporous Silica Matrix as a Tool for Minimizing Dipolar Interactions in NiFe2O4 and ZnFe2O4 Nanoparticles" Nanomaterials 7, no. 7: 151. https://doi.org/10.3390/nano7070151
APA StyleVirumbrales, M., Saez-Puche, R., Torralvo, M. J., & Blanco-Gutierrez, V. (2017). Mesoporous Silica Matrix as a Tool for Minimizing Dipolar Interactions in NiFe2O4 and ZnFe2O4 Nanoparticles. Nanomaterials, 7(7), 151. https://doi.org/10.3390/nano7070151