Compact Nonvolatile Reconfigurable Mode Converter by Sb2S3 Embedded in 4H-Silicon-Carbide-on-Insulator Platform
Abstract
1. Introduction
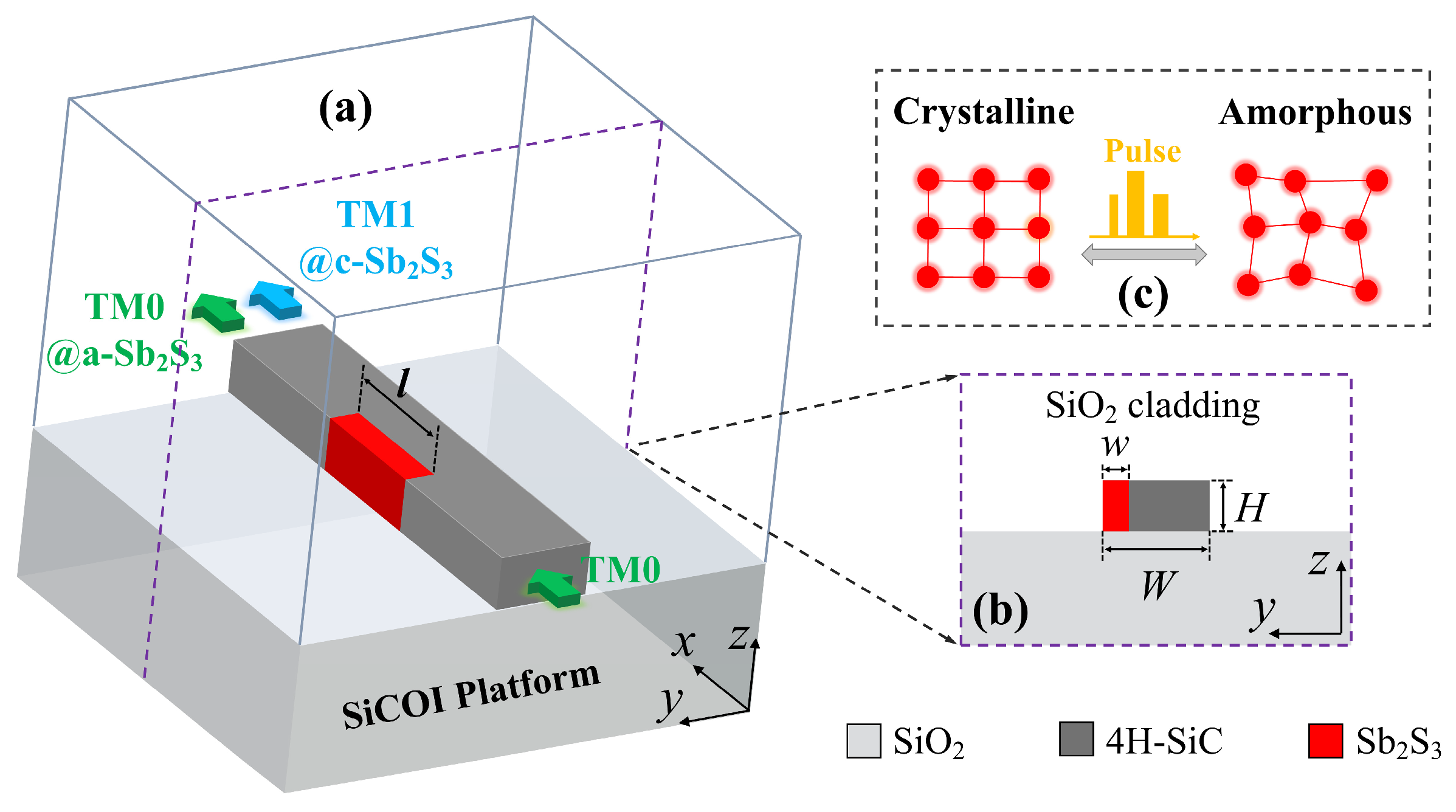
2. Design and Principle
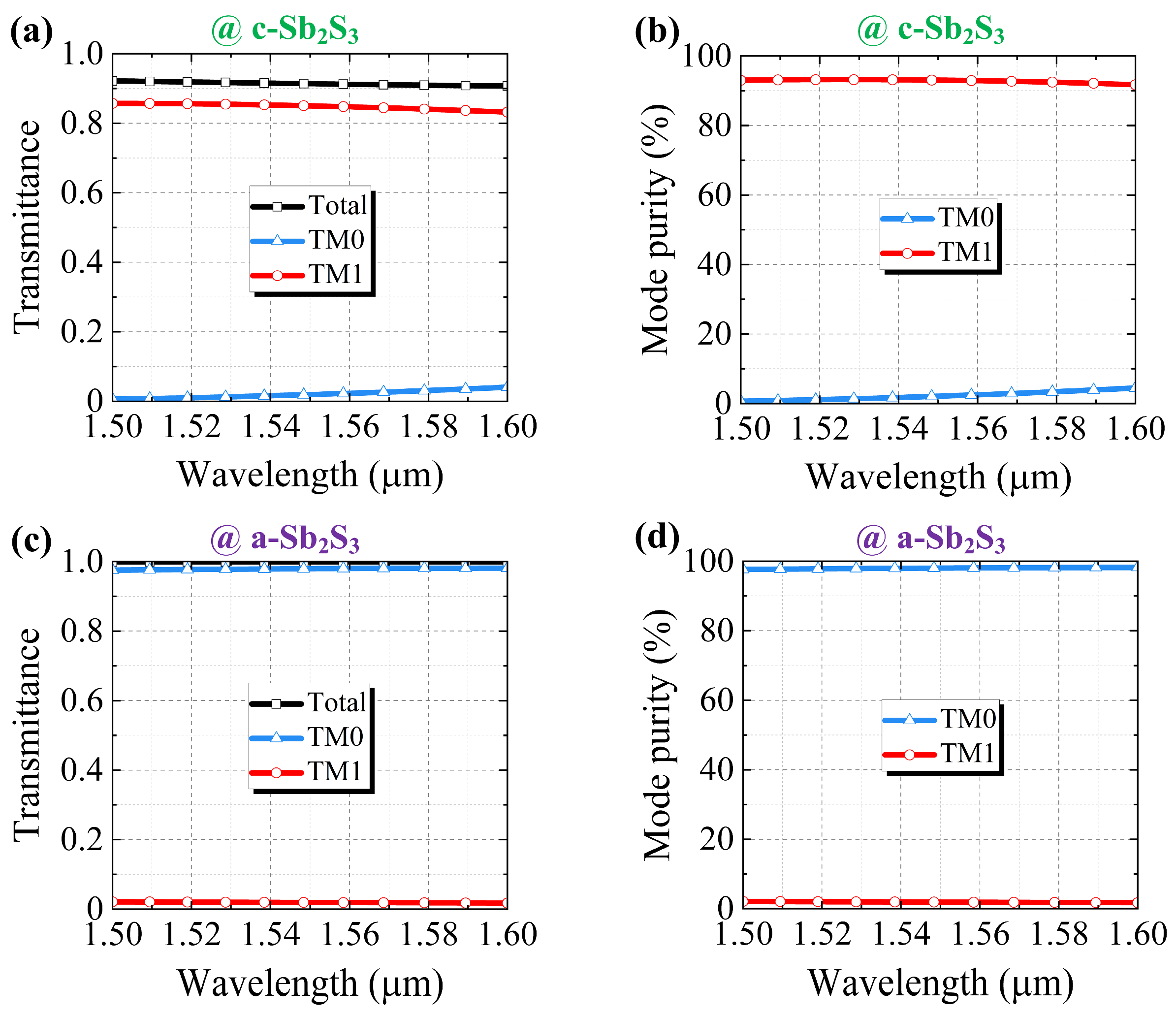
3. Simulation and Performance
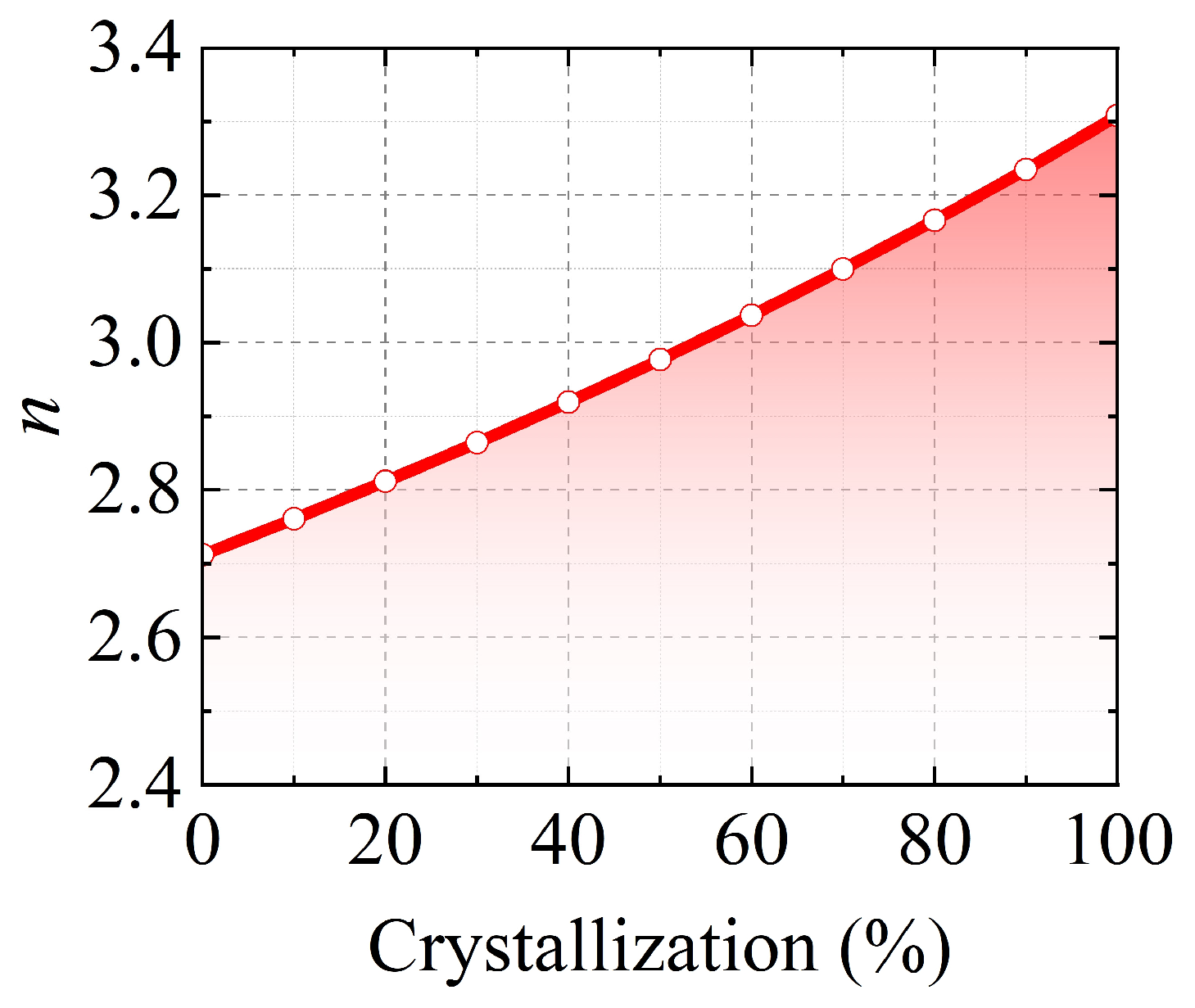
4. Discussion of the Partially Crystallized States of Sb2S3
5. Robustness Analysis and Suggested Fabrication
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wuttig, M.; Bhaskaran, H.; Taubner, T. Phase-change materials for non-volatile photonic applications. Nat. Photonics 2017, 11, 465–476. [Google Scholar] [CrossRef]
- Parra, J.; Olivares, I.; Brimont, A.; Sanchis, P. Toward nonvolatile switching in silicon photonic devices. Laser Photonics Rev. 2021, 15, 2000501. [Google Scholar] [CrossRef]
- Wu, C.; Yu, H.; Lee, S.; Peng, R.; Takeuchi, I.; Li, M. Programmable phase-change metasurfaces on waveguides for multimode photonic convolutional neural network. Nat. Commun. 2021, 12, 96. [Google Scholar] [CrossRef]
- Zhang, Y.; Chou, J.B.; Li, J.; Li, H.; Du, Q.; Yadav, A.; Zhou, S.; Shalaginov, M.Y.; Fang, Z.; Zhong, H.; et al. Broadband transparent optical phase change materials for high-performance nonvolatile photonics. Nat. Commun. 2019, 10, 4279. [Google Scholar] [CrossRef]
- Delaney, M.; Zeimpekis, I.; Lawson, D.; Hewak, D.W.; Muskens, O.L. A new family of ultralow loss reversible phase-change materials for photonic integrated circuits: Sb2S3 and Sb2Se3. Adv. Funct. Mater. 2020, 30, 2002447. [Google Scholar] [CrossRef]
- Li, C.; Liu, D.; Dai, D. Multimode silicon photonics. Nanophotonics 2019, 8, 227–247. [Google Scholar] [CrossRef]
- Memon, A.K.; Chen, K.X. Recent advances in mode converters for a mode division multiplex transmission system. Opto-Electron. Rev. 2021, 29, 13–32. [Google Scholar]
- Huang, Y.; Xu, G.; Ho, S.T. An ultracompact optical mode order converter. IEEE Photonics Technol. Lett. 2006, 18, 2281–2283. [Google Scholar] [CrossRef]
- Oner, B.B.; Üstün, K.; Kurt, H.; Okyay, A.K.; Turhan-Sayan, G. Large bandwidth mode order converter by differential waveguides. Opt. Express 2015, 23, 3186–3195. [Google Scholar] [CrossRef]
- Guo, J.; Ye, C.; Liu, C.; Zhang, M.; Li, C.; Li, J.; Shi, Y.; Dai, D. Ultra-compact and ultra-broadband guided-mode exchangers on silicon. Laser Photonics Rev. 2020, 14, 2000058. [Google Scholar] [CrossRef]
- Guo, Z.; Xiao, J.; Wu, S. Experimental demonstration of a flexible and high-performance mode-order converter using subwavelength grating metamaterials. Opt. Express 2023, 31, 10744–10757. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Qiu, P.; He, R.; Song, X.; Dai, Z.; Liu, Y.; Pan, D.; Yang, J.; Guo, K. Compact mode converters in thin-film lithium niobate integrated platforms. Opt. Lett. 2024, 49, 2958–2961. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Guo, X.; Zhang, Y.; Xiang, J.; Wang, K.; Wang, H.; Su, Y. Ultra-compact silicon mode-order converters based on dielectric slots. Opt. Lett. 2020, 45, 3797–3800. [Google Scholar] [CrossRef]
- Lu, J.; Vučković, J. Objective-first design of high-efficiency, small-footprint couplers between arbitrary nanophotonic waveguide modes. Opt. Express 2012, 20, 7221–7236. [Google Scholar] [CrossRef] [PubMed]
- Liao, J.; Huang, D.; Lu, Y.; Li, Y.; Tian, Y. Low-loss and compact arbitrary-order silicon mode converter based on hybrid shape optimization. Nanophotonics 2024, 13, 4137–4148. [Google Scholar] [CrossRef]
- Garcia-Rodriguez, D.; Corral, J.L.; Griol, A.; Llorente, R. Dimensional variation tolerant mode converter/multiplexer fabricated in SOI technology for two-mode transmission at 1550 nm. Opt. Lett. 2017, 42, 1221–1224. [Google Scholar] [CrossRef]
- Zhu, D.; Ye, H.; Liu, Y.; Li, J.; Wang, Y.; Yu, Z. Silicon subwavelength grating-assisted asymmetric directional coupler around 2 μm and its applications. Opt. Laser Technol. 2021, 136, 106789. [Google Scholar] [CrossRef]
- Xiao, R.; Shi, Y.; Li, J.; Dai, P.; Zhao, Y.; Li, L.; Lu, J.; Chen, X. On-chip mode converter based on two cascaded Bragg gratings. Opt. Express 2019, 27, 1941–1957. [Google Scholar] [CrossRef]
- He, Y.; Zhang, Y.; Wang, H.; Sun, L.; Su, Y. Design and experimental demonstration of a silicon multi-dimensional (de) multiplexer for wavelength-, mode-and polarization-division (de) multiplexing. Opt. Lett. 2020, 45, 2846–2849. [Google Scholar] [CrossRef]
- Li, Z.; Kim, M.-H.; Wang, C.; Han, Z.; Shrestha, S.; Overvig, A.C.; Lu, M.; Stein, A.; Agarwal, A.M.; Lončar, M.; et al. Controlling propagation and coupling of waveguide modes using phase-gradient metasurfaces. Nat. Nanotechnol. 2017, 12, 675–683. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; He, Y.; Zhu, Q.; Sun, L.; Su, Y. Compact silicon waveguide mode converter employing dielectric metasurface structure. Adv. Opt. Mater. 2019, 7, 1801191. [Google Scholar] [CrossRef]
- Lee, B.T.; Shin, S.Y. Mode-order converter in a multimode waveguide. Opt. Lett. 2003, 28, 1660–1662. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Zhang, D.; Xu, Y.; Ji, L.; Chen, W.; Wang, X.; Gao, W.; Sun, X. Compact six-mode (de) multiplexer based on cascaded asymmetric Y-junctions with mode rotators. Opt. Commun. 2019, 451, 41–45. [Google Scholar] [CrossRef]
- Dai, D.; Tang, Y.; Bowers, J.E. Mode conversion in tapered submicron silicon ridge optical waveguides. Opt. Express 2012, 20, 13425–13439. [Google Scholar] [CrossRef]
- Dai, D.; Mao, M. Mode converter based on an inverse taper for multimode silicon nanophotonic integrated circuits. Opt. Express 2015, 23, 28376–28388. [Google Scholar] [CrossRef]
- Jiang, W. Reconfigurable mode (de) multiplexer via 3-D triple-waveguide directional coupler with optical phase change material. J. Light. Technol. 2019, 37, 1000–1007. [Google Scholar] [CrossRef]
- Liu, T.; Xu, Y.; Liu, S.; Sun, X.; Zhang, D. Ge2Sb2Se4Te1-assisted non-volatile silicon mode selective switch. Opt. Mater. Express 2022, 12, 2584–2593. [Google Scholar] [CrossRef]
- Chen, H.; Wang, T.; Yang, J.; Jia, H. Ultra-compact Sb 2 S 3-silicon hybrid integrated arbitrarily cascaded tunable mode converter. IEEE Photonics J. 2022, 14, 1–7. [Google Scholar]
- Fei, Y.; Xu, Y.; Dong, Y.; Zhang, B.; Ni, Y. Nonvolatile phase change material based multifunctional silicon waveguide mode converters. Opt. Laser Technol. 2024, 168, 110006. [Google Scholar] [CrossRef]
- Guo, J.; Zhao, Y. Analysis of mode hybridization in tapered waveguides. IEEE Photonics Technol. Lett. 2015, 27, 2441–2444. [Google Scholar] [CrossRef]
- Lumerical Inc. Ansys Lumerical MODE. Available online: https://www.ansys.com/products/optics/mode (accessed on 17 March 2024).
- Yariv, A. Coupled-mode theory for guided-wave optics. IEEE J. Quantum Electron. 2003, 9, 919–933. [Google Scholar] [CrossRef]
- Soldano, L.B.; Pennings, E.C.M. Optical multi-mode interference devices based on self-imaging: Principles and applications. J. Light. Technol. 1995, 13, 615–627. [Google Scholar] [CrossRef]
- Lumerical Inc. Ansys Lumerical FDTD. Available online: https://www.ansys.com/products/optics/fdtd (accessed on 1 May 2024).
- Lumerical Inc. Using and Understanding Mode Expansion Monitors. Available online: https://optics.ansys.com/hc/en-us/articles/360034902433-Using-and-understanding-Mode-Expansion-Monitors (accessed on 1 May 2024).
- Ríos, C.; Stegmaier, M.; Hosseini, P.; Wang, D.; Scherer, T.; Wright, C.D.; Bhaskaran, H.; Pernice, W.H.P. Integrated all-photonic non-volatile multi-level memory. Nat. Photonics 2015, 9, 725–732. [Google Scholar] [CrossRef]
- Wang, Q.; Maddock, J.; Rogers, E.T.F.; Roy, T.; Craig, C.; Macdonald, K.F.; Hewak, D.W.; Zheludev, N.I. 1.7 Gbit/in. 2 gray-scale continuous-phase-change femtosecond image storage. Appl. Phys. Lett. 2014, 104, 121105. [Google Scholar] [CrossRef]
- Lei, K.; Wang, Y.; Jiang, M.; Wu, Y. Refractive index modulation of Sb70Te30 phase-change thin films by multiple femtosecond laser pulses. J. Appl. Phys. 2016, 119, 173105. [Google Scholar] [CrossRef]
- Chu, C.H.; Tseng, M.L.; Chen, J.; Wu, P.C.; Chen, Y.-H.; Wang, H.-C.; Chen, T.-Y.; Hsieh, W.T.; Wu, H.J.; Sun, G.; et al. Active dielectric metasurface based on phase-change medium. Laser Photonics Rev. 2016, 10, 986–994. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Sonnefraud, Y.; Fernández-Domínguez, A.I.; Luo, X.; Hong, M.; Maier, S.A. Engineering the phase front of light with phase-change material based planar lenses. Sci. Rep. 2015, 5, 8660. [Google Scholar] [CrossRef]
- Guidry, M.A.; Yang, K.Y.; Lukin, D.M.; Markosyan, A.; Yang, J.; Fejer, M.M.; Vučković, J. Optical parametric oscillation in silicon carbide nanophotonics. Optica 2020, 7, 1139–1142. [Google Scholar] [CrossRef]
- Chen, R.; Fang, Z.; Perez, C.; Miller, F.; Kumari, K.; Saxena, A.; Zheng, J.; Geiger, S.J.; Goodson, K.E.; Majumdar, A. Non-volatile electrically programmable integrated photonics with a 5-bit operation. Nat. Commun. 2023, 14, 3465. [Google Scholar] [CrossRef]
- Chen, W.; Liu, S.; Zhu, J. Pixelated non-volatile programmable photonic integrated circuits with 20-level intermediate states. Int. J. Extrem. Manuf. 2024, 6, 035501. [Google Scholar] [CrossRef]
- Chen, F.; Liu, Y.; Liu, X.; Zheng, Y. Multistate spectral-tunable manipulation of mid-infrared emissivity using Sb2S3/GST/VO2. Appl. Phys. Lett. 2023, 122, 191702. [Google Scholar] [CrossRef]
- Miller, F.; Chen, R.; Fröch, J.; Fang, Z.; Tara, V.; Geiger, S.; Majumdar, A. Rewritable photonic integrated circuit canvas based on low-loss phase change material and nanosecond pulsed lasers. Nano Lett. 2024, 24, 6844–6849. [Google Scholar] [CrossRef] [PubMed]
- Laprais, C.; Zrounba, C.; Bouvier, J.; Blanchard, N.; Bugnet, M.; Gassenq, A.; Gutiérrez, Y.; Vazquez-Miranda, S.; Espinoza, S.; Thiesen, P.; et al. Reversible Single-Pulse Laser-Induced Phase Change of Sb2S3 Thin Films: Multi-Physics Modeling and Experimental Demonstrations. Adv. Opt. Mater. 2024, 12, 2401214. [Google Scholar] [CrossRef]
- Gao, K.; Du, K.; Tian, S.; Wang, H.; Zhang, L.; Guo, Y.; Luo, B.; Zhang, W.; Mei, T. Intermediate Phase-Change States with Improved Cycling Durability of Sb2S3 by Femtosecond Multi-Pulse Laser Irradiation. Adv. Funct. Mater. 2021, 31, 2103327. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, D.; Chen, J.; Qiu, S.; Deng, D.; Luo, J. Compact Nonvolatile Reconfigurable Mode Converter by Sb2S3 Embedded in 4H-Silicon-Carbide-on-Insulator Platform. Nanomaterials 2025, 15, 689. https://doi.org/10.3390/nano15090689
Zhu D, Chen J, Qiu S, Deng D, Luo J. Compact Nonvolatile Reconfigurable Mode Converter by Sb2S3 Embedded in 4H-Silicon-Carbide-on-Insulator Platform. Nanomaterials. 2025; 15(9):689. https://doi.org/10.3390/nano15090689
Chicago/Turabian StyleZhu, Danfeng, Junbo Chen, Shaobin Qiu, Dingnan Deng, and Jinming Luo. 2025. "Compact Nonvolatile Reconfigurable Mode Converter by Sb2S3 Embedded in 4H-Silicon-Carbide-on-Insulator Platform" Nanomaterials 15, no. 9: 689. https://doi.org/10.3390/nano15090689
APA StyleZhu, D., Chen, J., Qiu, S., Deng, D., & Luo, J. (2025). Compact Nonvolatile Reconfigurable Mode Converter by Sb2S3 Embedded in 4H-Silicon-Carbide-on-Insulator Platform. Nanomaterials, 15(9), 689. https://doi.org/10.3390/nano15090689





