NaOH as an Aqueous Electrolyte to Improve the Performance of Electric Double-Layer Capacitors—A Molecular Dynamics Study
Abstract
1. Introduction
2. Model and Methodology
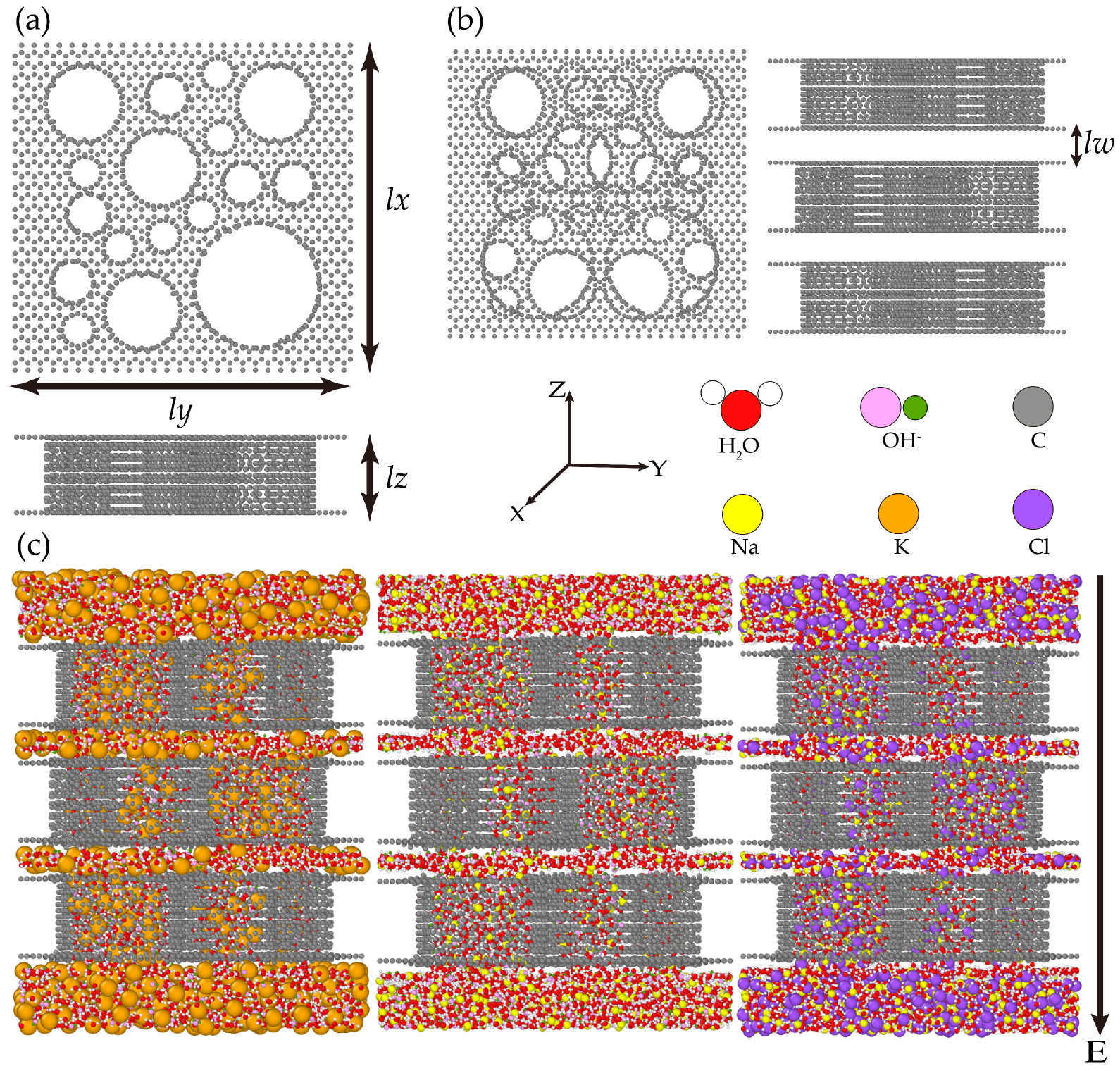
2.1. Physical Model
2.2. Force Field
| Atom | M (g/mol) | q (e) | (Å) | (eV) | (Å) | (eV) |
|---|---|---|---|---|---|---|
| C | 12.0107 | 0.0000 | 3.4000 | 0.00373 | 3.1900 | 0.00406 |
| Na(NaOH) | 22.9898 | 0.7500 | 2.2174 | 0.01526 | 2.6084 | 0.00822 |
| Na(NaCl) | 22.9898 | 0.8500 | 2.2174 | 0.01526 | 2.3872 | 0.00822 |
| K | 39.0983 | 0.7500 | 2.3014 | 0.02058 | 2.8954 | 0.01451 |
| H | 1.00794 | 0.4681 | 1.4430 | 0.00191 | 2.3009 | 0.00391 |
| O | 15.9994 | −1.2181 | 3.6500 | 0.00260 | 3.4044 | 0.00457 |
| Cl | 35.4529 | −0.8500 | 4.6991 | 0.00080 | 3.9290 | 0.00253 |
2.3. MD Simulations
3. Result and Discussion
3.1. Effect of Concentration on the Diffusion of Na+ and K+
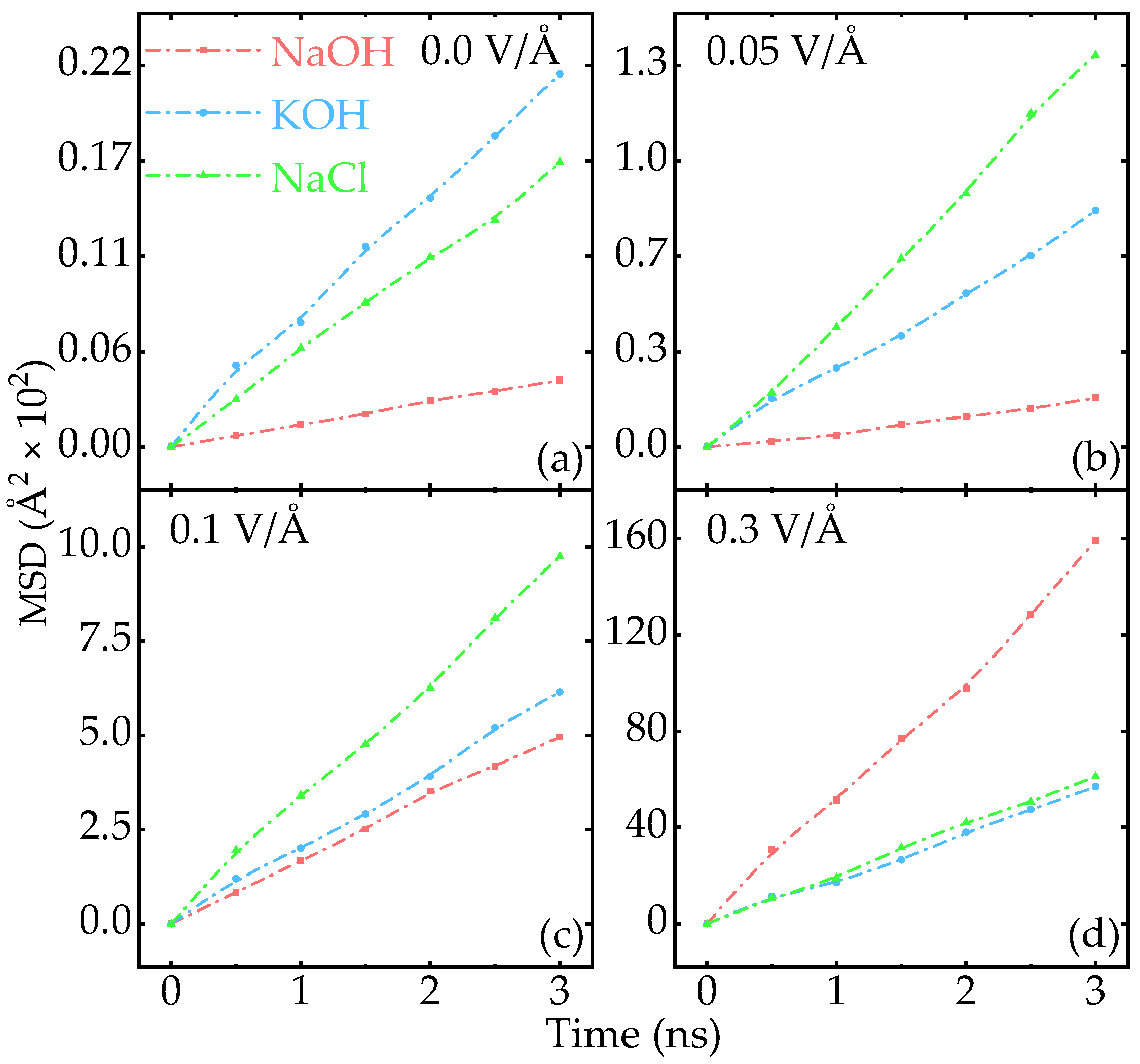
3.2. Effect of Electric Field on the Diffusion of Na+ and K+
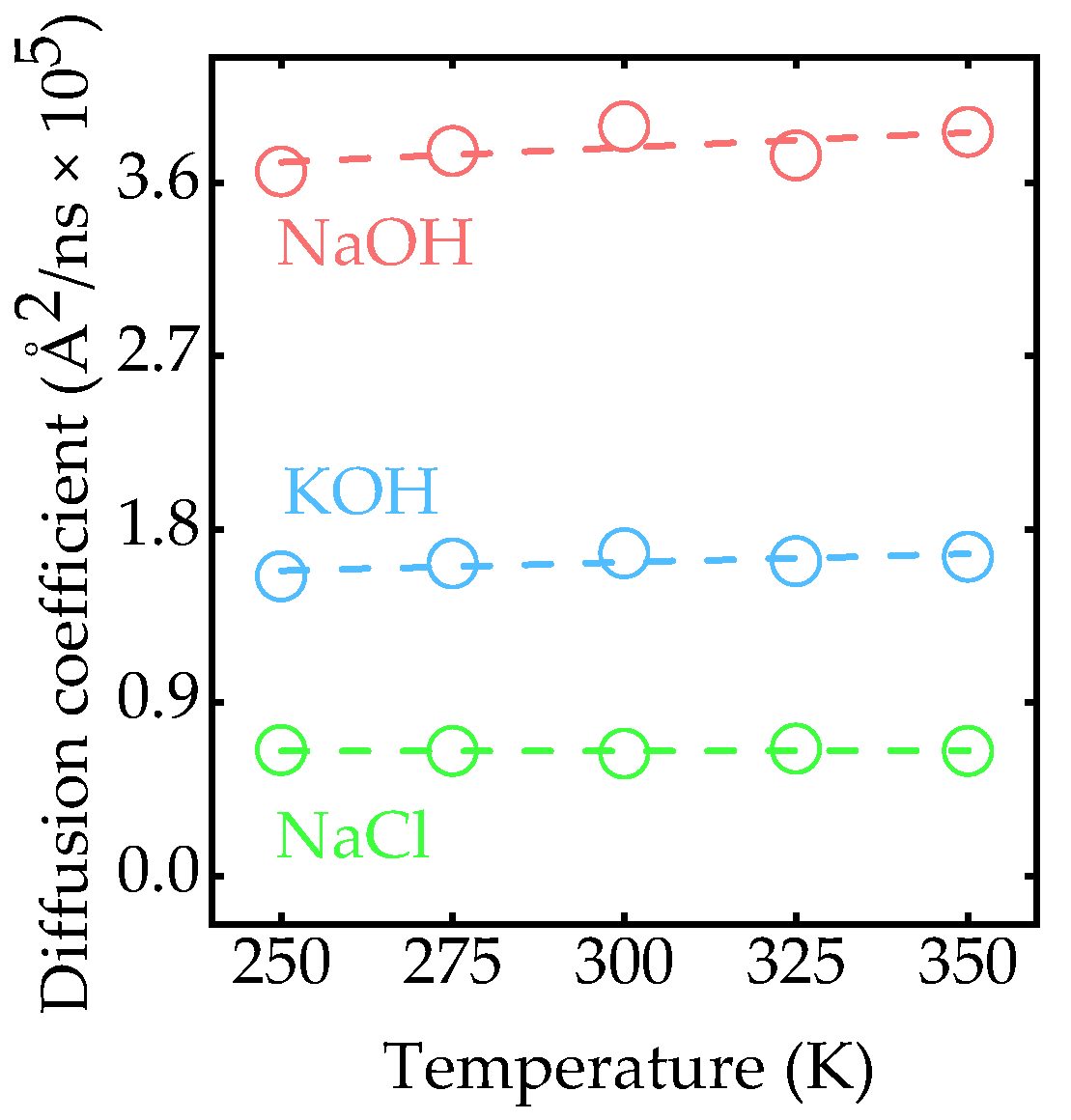
3.3. Effect of Temperature on the Diffusion of Na+ and K+
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SCs | supercapacitors |
| EDLCs | Electric Double-Layer Capacitors |
| AC | Activated carbon |
| MD | molecular dynamics |
| LAMMPS | Large-scale Atomic/Molecular Massively Parallel Simulator |
| PPPM | Particle–Particle Particle–Mesh |
| MSD | mean square displacement |
Appendix A. Supplementary Information
Appendix A.1. Kinetic Energy of System
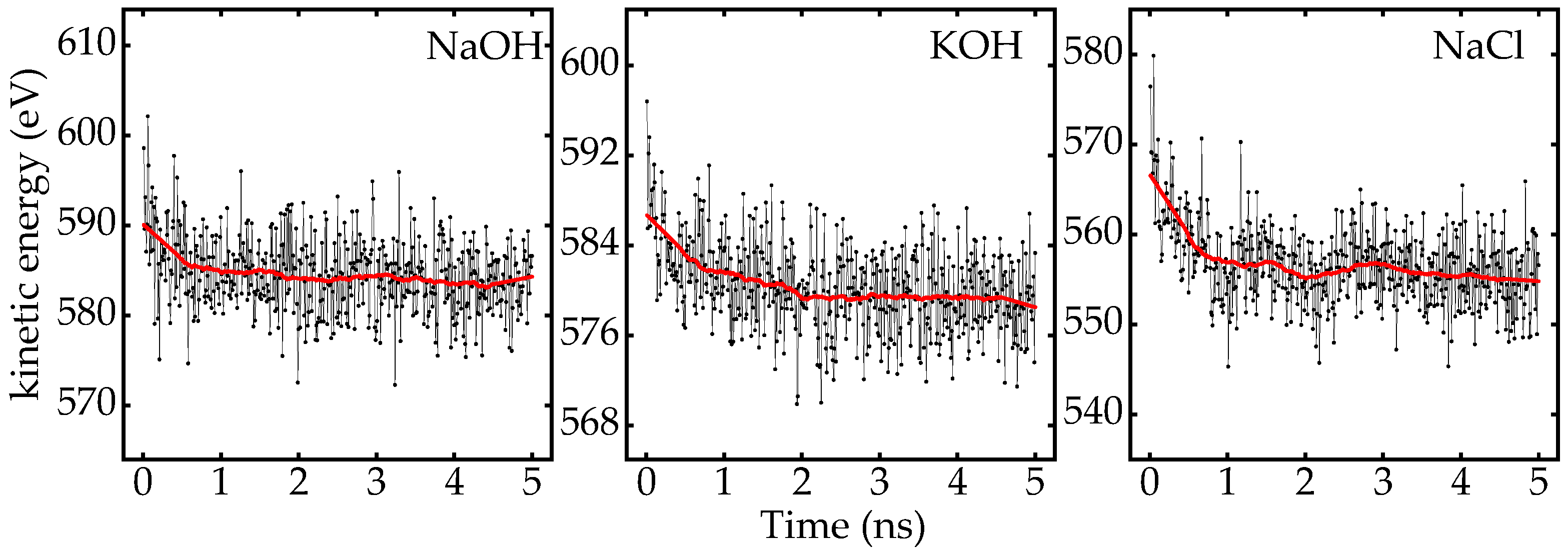
Appendix A.2. MSD of Ions Along Different Axis
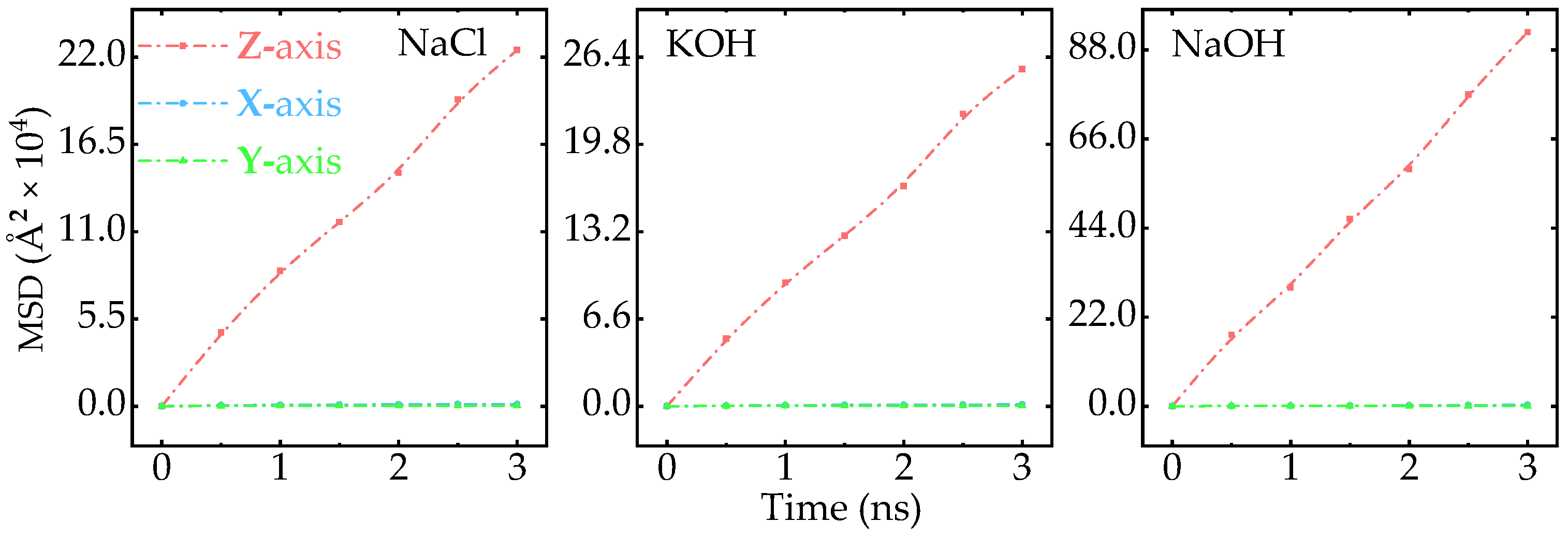
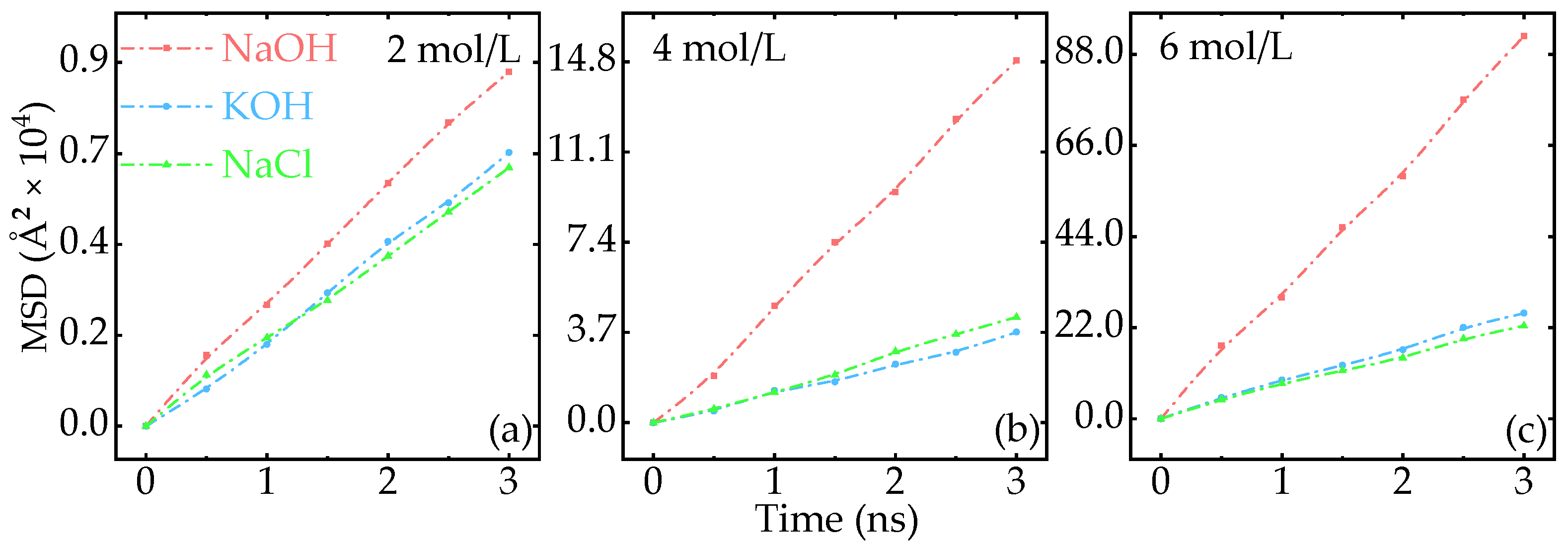
Appendix A.3. Effect of Aqueous Concentration on the MSD
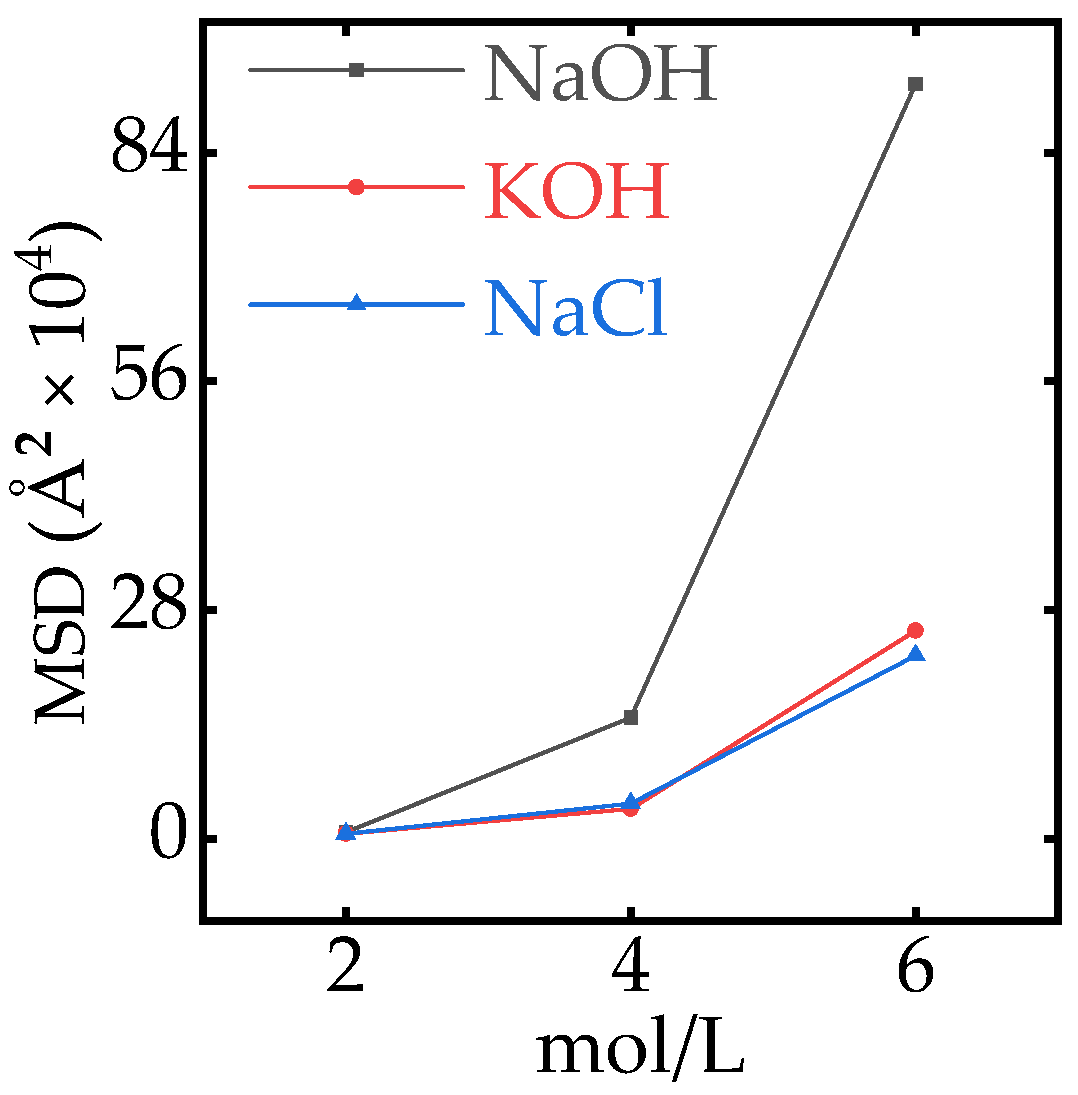
Appendix A.4. Mass Density Profile of Ions
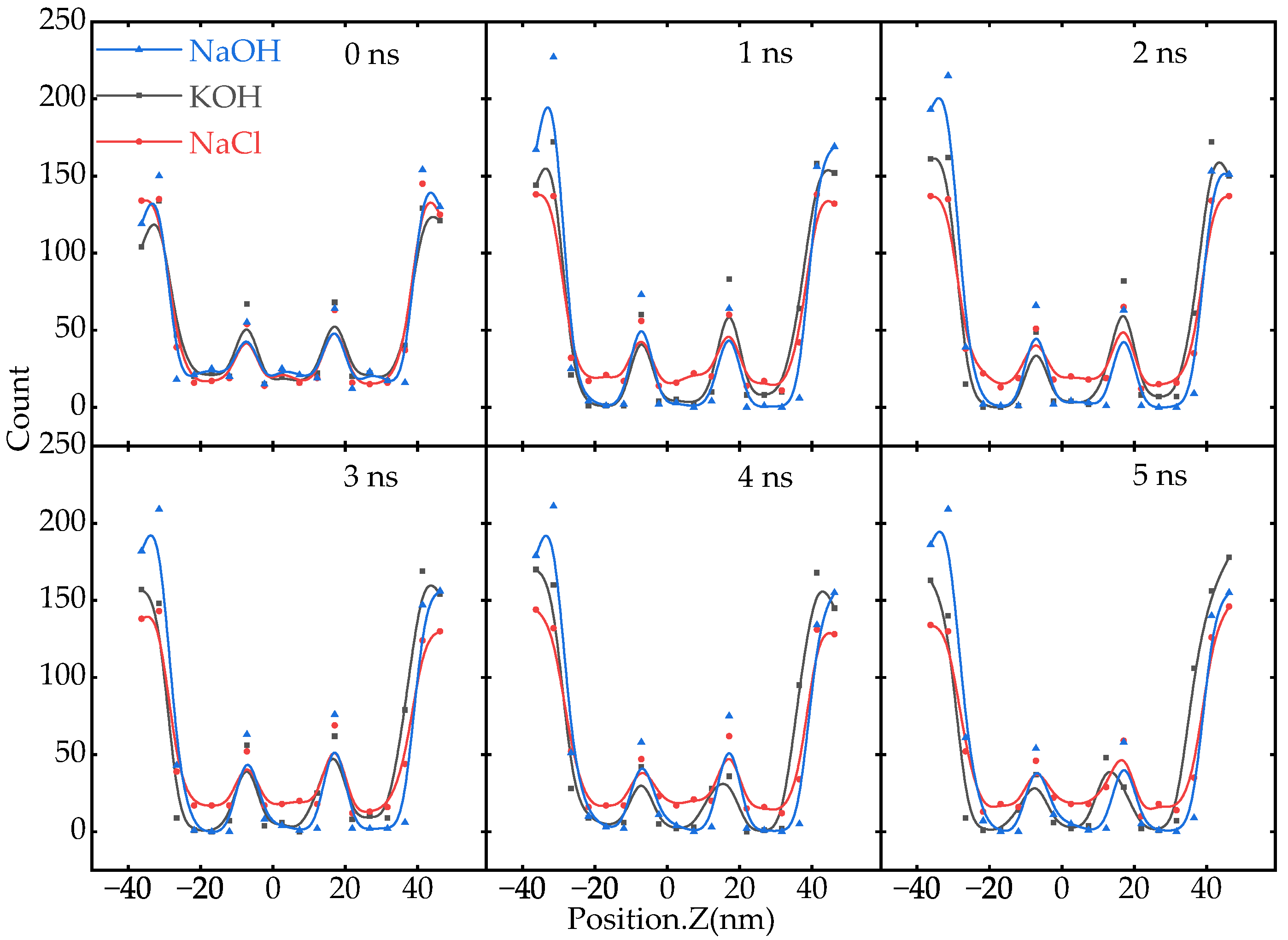
Appendix A.5. Comparison of Carbon-Based SCs with Different Electrolytes
| Material Used | Measurement Protocol | Electrolyte | Maximum Specific Capacitance |
|---|---|---|---|
| Graphene | GCD (1 ) | 3 NaOH | 596 [18] |
| Graphene | GCD (1 ) | 6 KOH | 355 [43] |
| Carbon | GCD (1 ) | 6 KOH | 331 [44] |
| Carbon | GCD (1 ) | 6 KOH | 222.92 [45] |
Appendix A.6. Self-Diffusion of Ions in FHWSAC-3
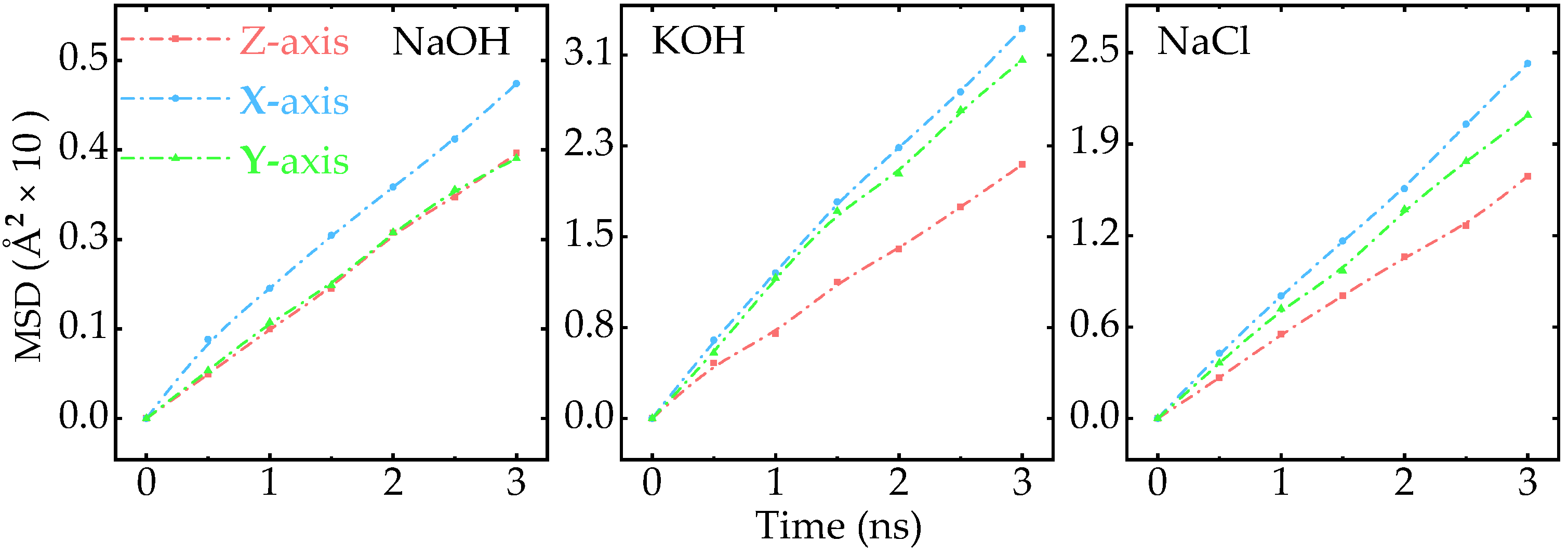
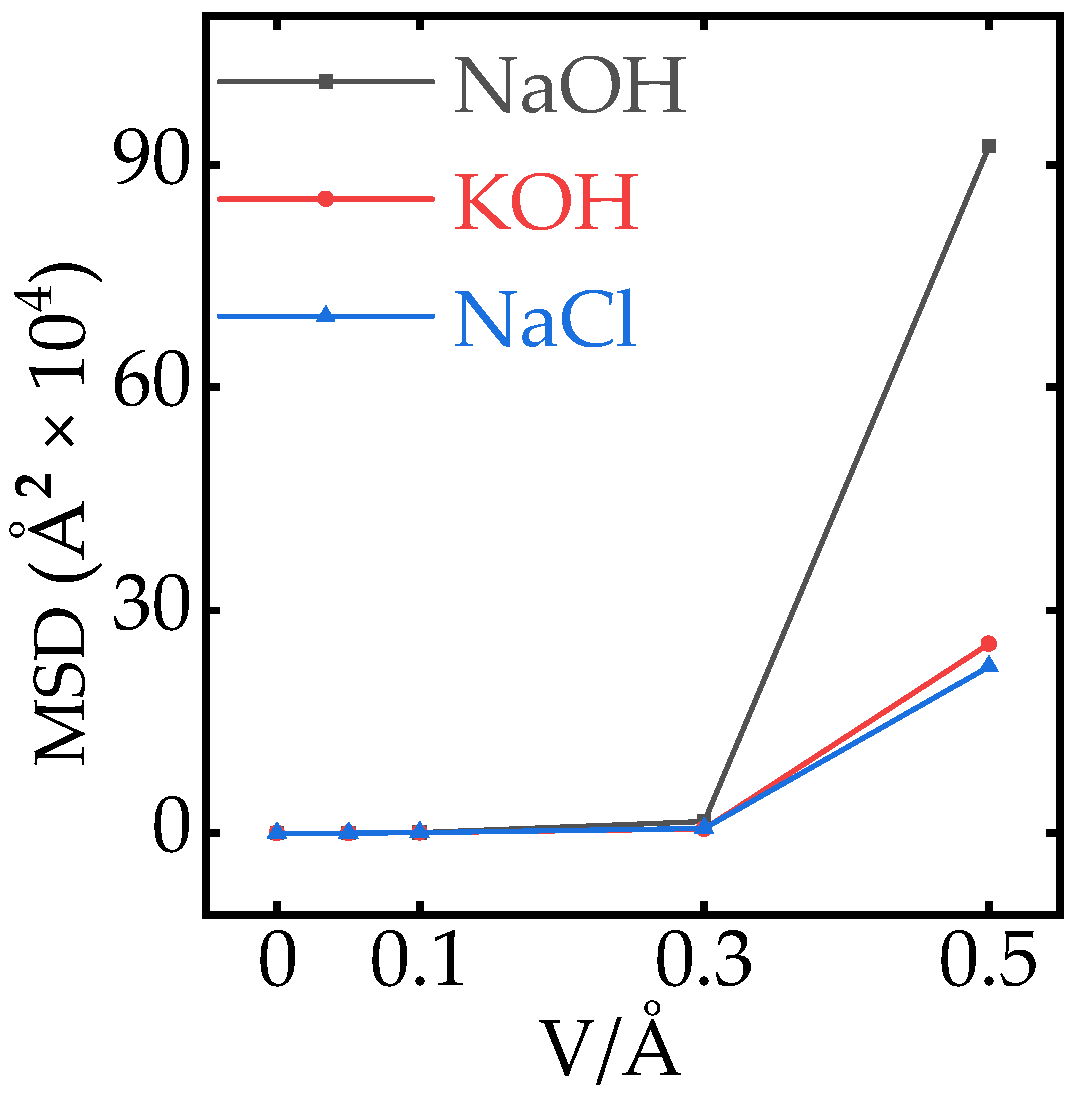
Appendix A.7. Effect of Electric Field on the MSD
References
- Chu, S.; Cui, Y.; Liu, N. The path towards sustainable energy. Nat. Mater. 2017, 16, 16–22. [Google Scholar] [CrossRef] [PubMed]
- Sütterlin, B.; Siegrist, M. Public acceptance of renewable energy technologies from an abstract versus concrete perspective and the positive imagery of solar power. Energy Policy 2017, 106, 356–366. [Google Scholar] [CrossRef]
- Hashemi, M.; Rahmanifar, M.S.; El-Kady, M.F.; Noori, A.; Mousavi, M.F.; Kaner, R.B. The use of an electrocatalytic redox electrolyte for pushing the energy density boundary of a flexible polyaniline electrode to a new limit. Nano Energy 2018, 44, 489–498. [Google Scholar] [CrossRef]
- Pandolfo, A.G.; Hollenkamp, A.F. Carbon properties and their role in supercapacitors. J. Power Sources 2006, 157, 11–27. [Google Scholar] [CrossRef]
- Yadav, A.A.; Hunge, Y.M.; Majumder, S.; Mourad, A.-H.I.; Islam, M.M.; Sakurai, T.; Kang, S.-W. Multiplicative rGO/Cu-BDC MOF for 4-nitrophenol reduction and supercapacitor applications. J. Colloid Interface Sci. 2025, 677, 161–170. [Google Scholar] [CrossRef]
- Yadav, A.A.; Hunge, Y.M.; Kim, B.-K.; Kang, S.-W. Hierarchically designed NiCo2O4 nanowire/NiCo2O4 nanosheet electrodes for high-performance energy storage applications. Surf. Interf. 2022, 34, 102340. [Google Scholar] [CrossRef]
- Yadav, A.A.; Hunge, Y.M.; Ko, S.; Kang, S.-W. Chemically synthesized iron-oxide-based pure negative electrode for solid-state asymmetric supercapacitor devices. Materials 2022, 15, 6133. [Google Scholar] [CrossRef]
- Zhang, S.; Pan, N. Supercapacitors Performance Evaluation. Adv. Energy Mater. 2015, 5, 1401401. [Google Scholar] [CrossRef]
- Cakici, M.; Kakarla, R.R.; Alonso-Marroquin, F. Advanced electrochemical energy storage supercapacitors based on the flexible carbon fiber fabric-coated with uniform coral-like MnO2 structured electrodes. Chem. Eng. J. 2017, 309, 151–158. [Google Scholar] [CrossRef]
- Jayaseelan, S.S.; Radhakrishnan, S.; Saravanakumar, B.; Seo, M.-K.; Khil, M.-S.; Kim, H.-Y.; Kim, B.-S. Mesoporous 3D NiCo2O4/MWCNT nanocomposite aerogels prepared by a supercritical CO2 drying method for high performance hybrid supercapacitor electrodes. Colloids Surfaces A Physicochem. Eng. Asp. 2018, 538, 451–459. [Google Scholar] [CrossRef]
- Qu, D.; Shi, H. Studies of activated carbons used in double-layer capacitors. J. Power Sources 1998, 74, 99–107. [Google Scholar] [CrossRef]
- Barbieri, O.; Hahn, M.; Herzog, A.; Kötz, R. Capacitance limits of high surface area activated carbons for double layer capacitors. Carbon 2005, 43, 1303–1310. [Google Scholar] [CrossRef]
- Raza, W.; Ali, F.; Raza, N.; Luo, Y.; Kim, K.-H.; Yang, J.; Kumar, S.; Mehmood, A.; Kwon, E.E. Recent advancements in supercapacitor technology. Nano Energy 2018, 52, 441–473. [Google Scholar] [CrossRef]
- de Araujo Chagas, H.; Oliveira, L.B.A.; Fonseca, T.L.; Colherinhas, G. Systematic analysis to evaluate the impact of hydration on electrolytes [emim][BF4] and [cho][gly] in supercapacitors formed by graphene or graphyne electrodes. J. Mol. Liq. 2024, 415, 126280. [Google Scholar] [CrossRef]
- Fileti, E.E.; Colherinhas, G. Investigating the asymmetry in the EDL response of C 60/graphene supercapacitors. J. Phys. Chem. Chem. Phys. 2019, 21, 15362–15371. [Google Scholar] [CrossRef]
- Wang, H.; Guo, Z.; Yao, S.; Li, Z.; Zhang, W. Design and synthesis of ternary graphene/polyaniline/Co3O4 hierarchical nanocomposites for supercapacitors. Int. J. Electrochem. Sci. 2017, 12, 3721–3731. [Google Scholar] [CrossRef]
- Kim, D.J.; Yoon, J.W.; Lee, C.S.; Bae, Y.-S.; Kim, J.H. Covalent organic framework-derived microporous carbon nanoparticles coated with conducting polypyrrole as an electrochemical capacitor. Appl. Surf. Sci. 2018, 439, 833–838. [Google Scholar] [CrossRef]
- Zheng, F.; Kotobuki, M.; Song, S.; Lai, M.O.; Lu, L. Review on solid electrolytes for all-solid-state lithium-ion batteries. J. Power Sources 2018, 389, 198–213. [Google Scholar] [CrossRef]
- Song, Z.; Duan, H.; Li, L.; Zhu, D.; Cao, T.; Lv, Y.; Xiong, W.; Wang, Z.; Liu, M.; Gan, L. High-energy flexible solid-state supercapacitors based on O, N, S-tridoped carbon electrodes and a 3.5 V gel-type electrolyte. Chem. Eng. J. 2019, 372, 1216–1225. [Google Scholar] [CrossRef]
- Li, Y.; Ni, L.; Luo, J.; Zhu, L.; Zhang, X.; Li, H.; Zada, I.; Yu, J.; Zhu, S.; Lian, K. Fenton reaction doubled biomass carbon activation efficiency for high-performance supercapacitors. Adv. Funct. Mater. 2024, 34, 2403448. [Google Scholar] [CrossRef]
- Tang, L.; Yang, Z.; Duan, F.; Chen, M. Fabrication of graphene sheets/polyaniline nanofibers composite for enhanced supercapacitor properties. Colloids Surf. A Physicochem. Eng. Asp. 2017, 520, 184–192. [Google Scholar] [CrossRef]
- Raut, S.S.; Sankapal, B.R.; Hossain, M.S.A.; Pradhan, S.; Salunkhe, R.R.; Yamauchi, Y. Zinc ferrite anchored multiwalled carbon nanotubes for high-performance supercapacitor applications. Eur. J. Inorg. Chem. 2018, 2018, 137–142. [Google Scholar] [CrossRef]
- Chae, J.H.; Chen, G.Z. Influences of ions and temperature on performance of carbon nano-particulates in supercapacitors with neutral aqueous electrolytes. Particuology 2014, 15, 9–17. [Google Scholar] [CrossRef]
- Fic, K.; Lota, G.; Meller, M.; Frackowiak, E. Novel insight into neutral medium as electrolyte for high-voltage supercapacitors. Energy Environ. Sci. 2012, 5, 5842–5850. [Google Scholar] [CrossRef]
- Abascal, J.L.F.; Vega, C. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 2005, 123, 234505. [Google Scholar] [CrossRef]
- Zeron, I.M.; Abascal, J.L.F.; Vega, C. A force field of Li+, Na+, K+, Mg2+, Ca2+, Cl−, and SO42− in aqueous solution based on the TIP4P/2005 water model and scaled charges for the ions. J. Chem. Phys. 2019, 151, 134504. [Google Scholar] [CrossRef]
- Blazquez, S.; Vega, C.; Conde, M.M. Three phase equilibria of the methane hydrate in NaCl solutions: A simulation study. J. Mol. Liq. 2023, 383, 122031. [Google Scholar] [CrossRef]
- Habibi, P.; Rahbari, A.; Blazquez, S.; Vega, C.; Dey, P.; Vlugt, T.J.H.; Moultos, O.A. A new force field for OH- for computing thermodynamic and transport properties of H2 and O2 in aqueous NaOH and KOH solutions. J. Phys. Chem. B 2022, 126, 9376–93871. [Google Scholar] [CrossRef]
- Werder, T.; Walther, J.H.; Jaffe, R.L.; Halicioglu, T.; Koumoutsakos, P. On the water- carbon interaction for use in molecular dynamics simulations of graphite and carbon nanotubes. J. Phys. Chem. B 2008, 112, 14090. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; In’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Verlet, L. Computer “experiments” on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules. Phys. Rev. 1967, 159, 98–103. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Ryckaert, J.-P.; Ciccotti, G.; Berendsen, H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Miller Iii, T.F.; Eleftheriou, M.; Pattnaik, P.; Ndirango, A.; Newns, D.; Martyna, G.J. Symplectic quaternion scheme for biophysical molecular dynamics. J. Comput. Phys. 2002, 116, 8649–8659. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N log (N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Kamberaj, H.; Low, R.J.; Neal, M.P. Time reversible and symplectic integrators for molecular dynamics simulations of rigid molecules. J. Chem. Phys. 2005, 122, 224114. [Google Scholar] [CrossRef] [PubMed]
- Malaspina, T.; Colherinhas, G.; Weitzner, S.E.; Wood, B.C.; Fileti, E.E. Unraveling local structures of Salt-in-Water and Water-in-Salt electrolytes via ab initio molecular dynamics. J. Mol. Liq. 2023, 383, 122097. [Google Scholar] [CrossRef]
- Kumar, P.; Yashonath, S. Ionic conductivity in aqueous electrolyte solutions: Insights from computer simulations. J. Mol. Liq. 2019, 277, 506–515. [Google Scholar] [CrossRef]
- He, Z.; Cui, H.; Hao, S.; Wang, L.; Zhou, J. Electric-field effects on ionic hydration: A molecular dynamics study. J. Phys. Chem. B 2018, 122, 5991–5998. [Google Scholar] [CrossRef] [PubMed]
- Jamali, S.H.; Wolff, L.; Becker, T.M.; De Groen, M.; Ramdin, M.; Hartkamp, R.; Bardow, A.; Vlugt, T.J.H.; Moultos, O.A. OCTP: A tool for on-the-fly calculation of transport properties of fluids with the order-n algorithm in LAMMPS. J. Chem. Inf. Model. 2019, 59, 1290–1294. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Shi, M.; Lu, W.; Zhu, D.; Li, L.; Gan, L. Core–shell reduced graphene oxide/MnOx@ carbon hollow nanospheres for high performance supercapacitor electrodes. Chem. Eng. J. 2017, 313, 518–526. [Google Scholar] [CrossRef]
- Liu, W.; Tang, Y.; Sun, Z.; Gao, S.; Ma, J.; Liu, L. A simple approach of constructing sulfur-containing porous carbon nanotubes for high-performance supercapacitors. Carbon 2017, 115, 754–762. [Google Scholar] [CrossRef]
- Silva, A.A.; Pinheiro, R.A.; Rodrigues, A.C.; Baldan, M.R.; Trava-Airoldi, V.J.; Corat, E.J. Graphene sheets produced by carbon nanotubes unzipping and their performance as supercapacitor. Appl. Surf. Sci. 2018, 446, 201–208. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, L.; Yu, J. NaOH as an Aqueous Electrolyte to Improve the Performance of Electric Double-Layer Capacitors—A Molecular Dynamics Study. Nanomaterials 2025, 15, 649. https://doi.org/10.3390/nano15090649
Ni L, Yu J. NaOH as an Aqueous Electrolyte to Improve the Performance of Electric Double-Layer Capacitors—A Molecular Dynamics Study. Nanomaterials. 2025; 15(9):649. https://doi.org/10.3390/nano15090649
Chicago/Turabian StyleNi, Lifeng, and Jin Yu. 2025. "NaOH as an Aqueous Electrolyte to Improve the Performance of Electric Double-Layer Capacitors—A Molecular Dynamics Study" Nanomaterials 15, no. 9: 649. https://doi.org/10.3390/nano15090649
APA StyleNi, L., & Yu, J. (2025). NaOH as an Aqueous Electrolyte to Improve the Performance of Electric Double-Layer Capacitors—A Molecular Dynamics Study. Nanomaterials, 15(9), 649. https://doi.org/10.3390/nano15090649







