Design of Real-Time Demodulation for FBG Sensing Signals Based on All-Dielectric Subwavelength Gratings Edge Filters
Abstract
1. Introduction
2. Methods
3. Results and Discussion
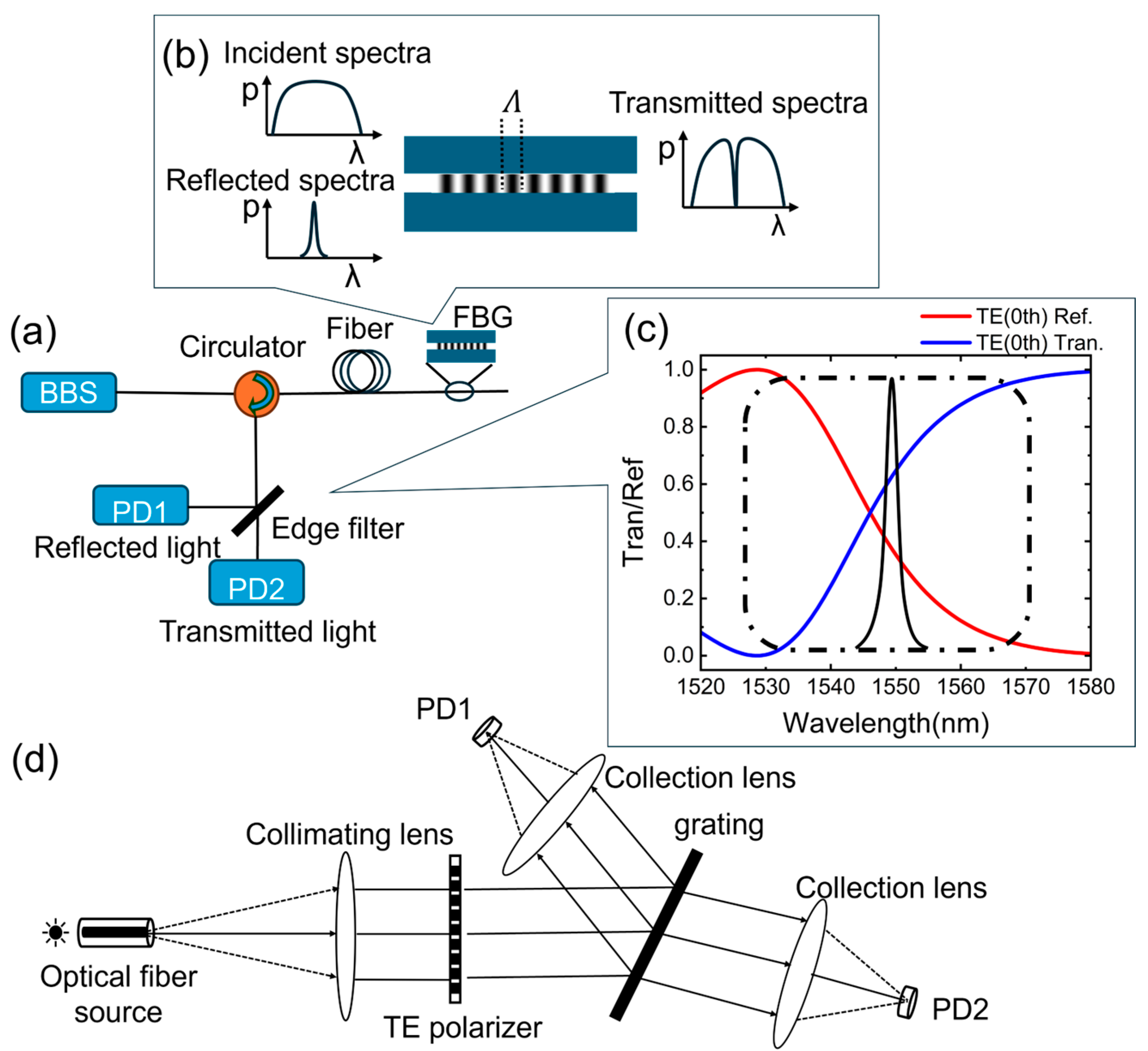
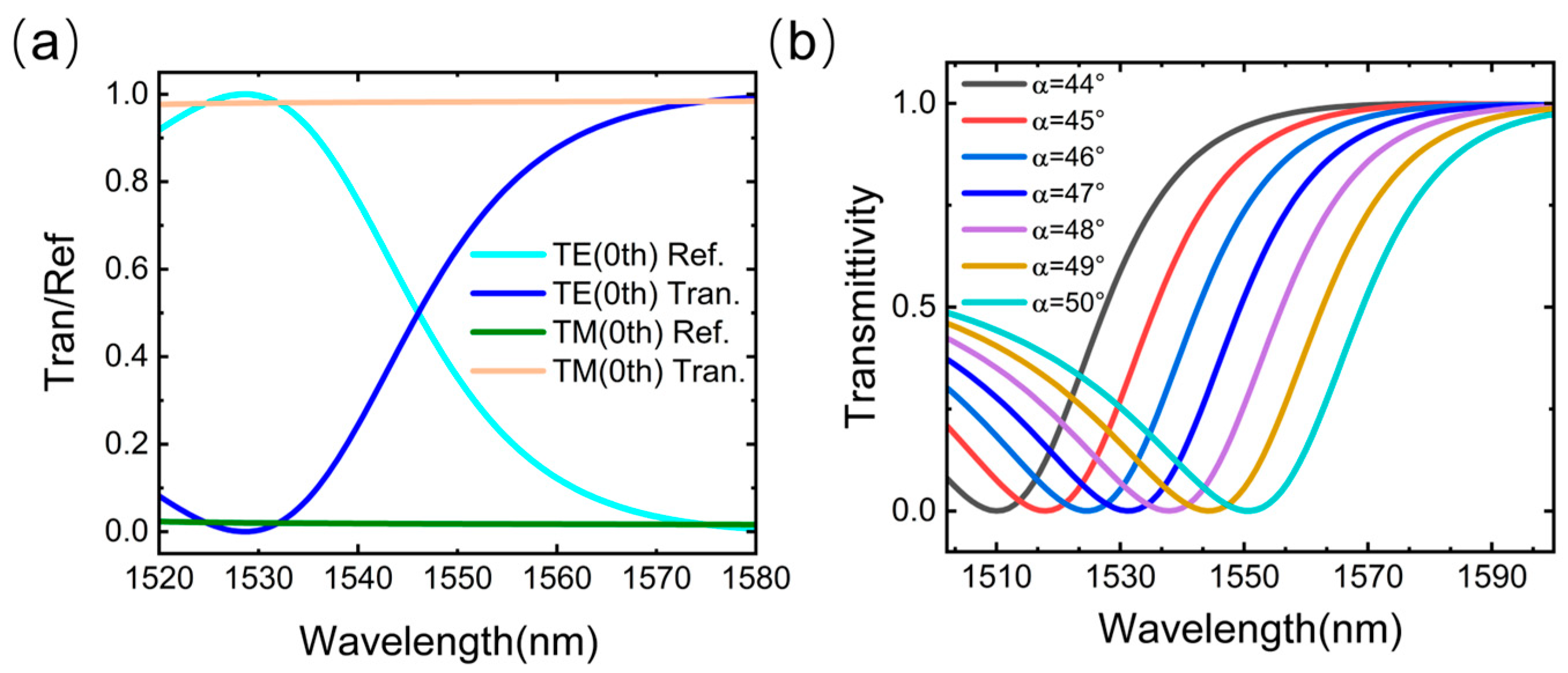
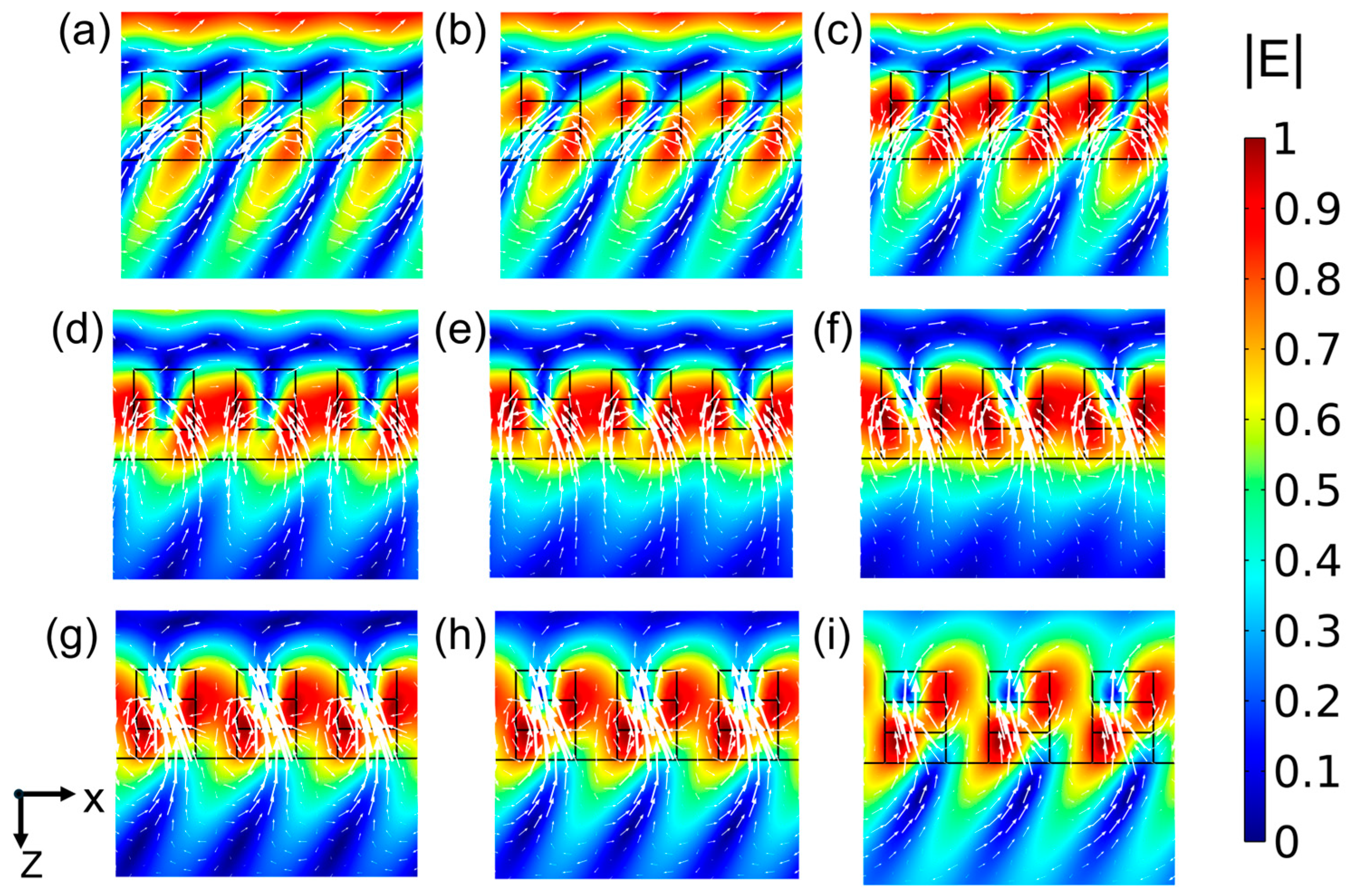
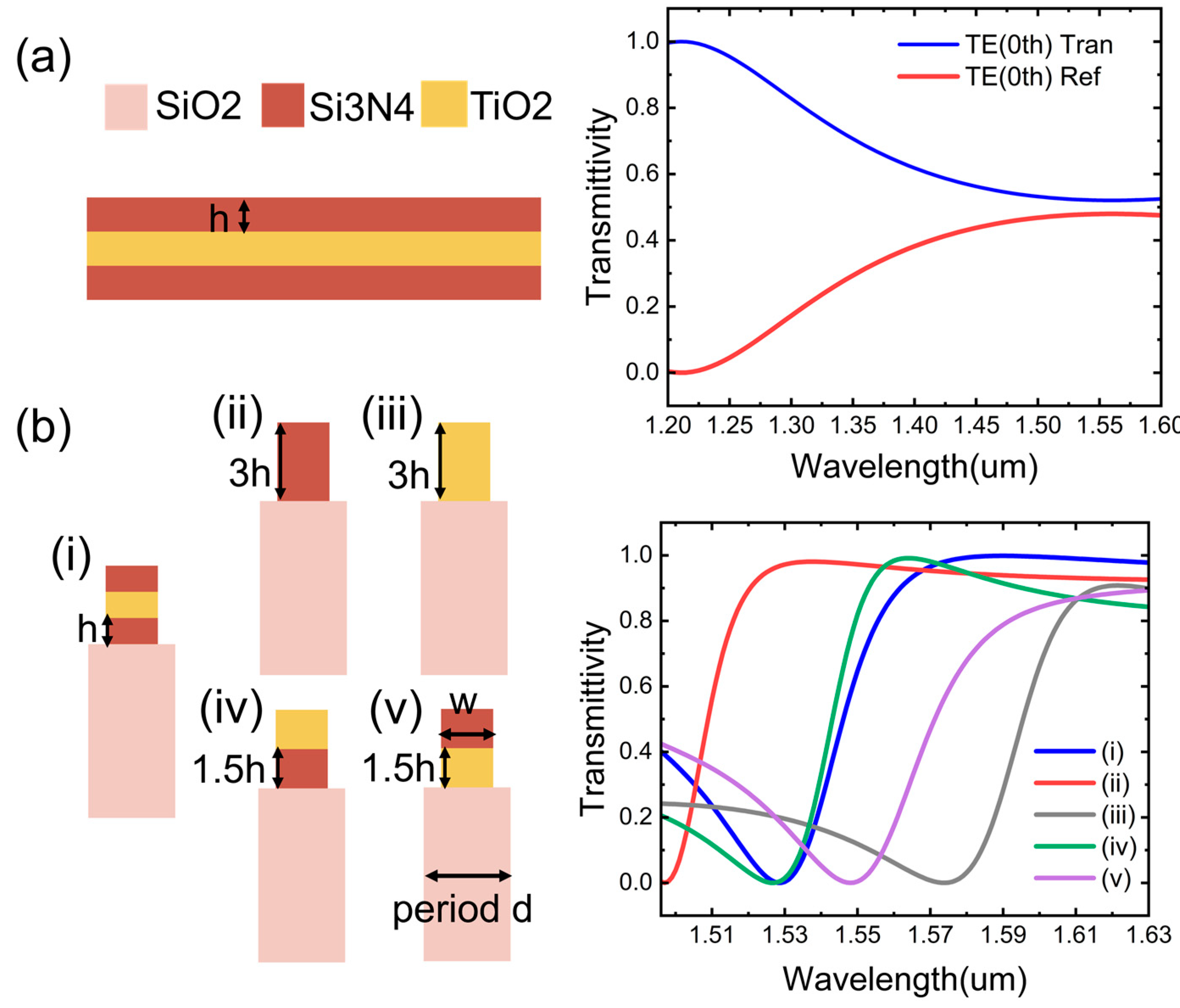
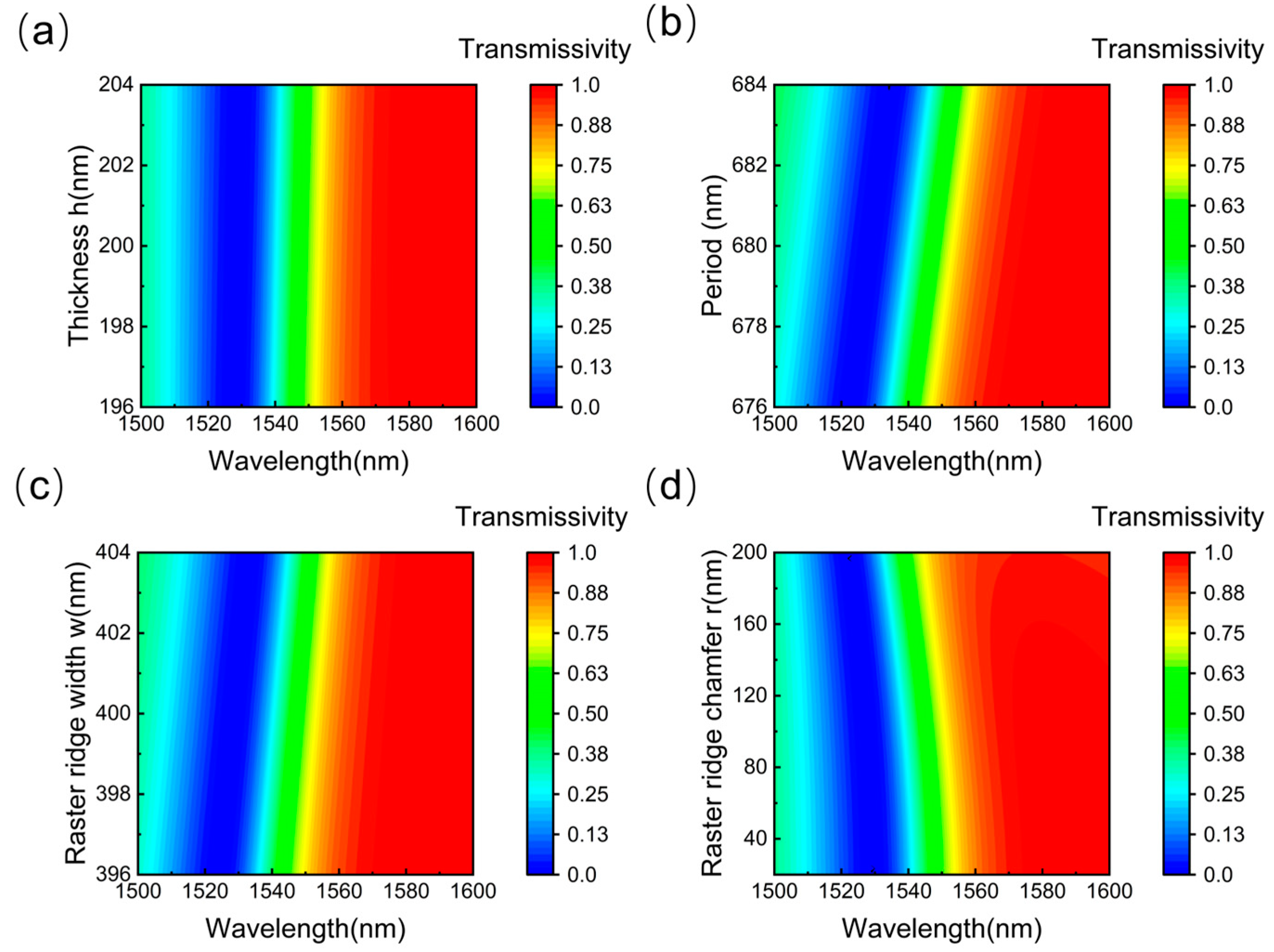
3.1. Design of the Subwavelength Grating Edge Filter
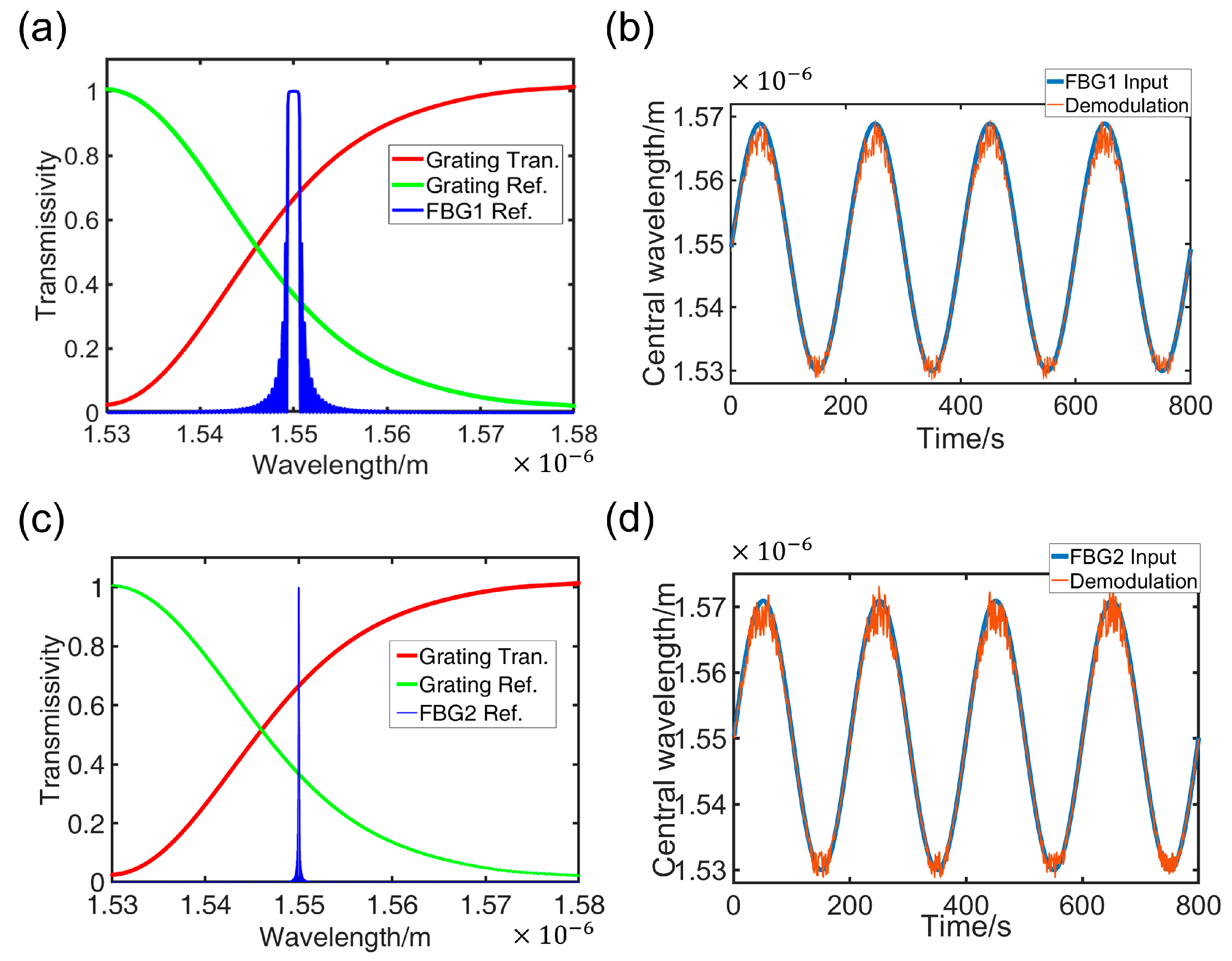
3.2. FBG Demodulation Based on Subwavelength Grating Edge Filters
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Q.; Wei, Q.; Luo, J.; Li, Z.; Zhou, Z.; Fang, Y. A Bi-Mode State Monitoring System for Aero-Engine Components Based on FBG Sensing. In Proceedings of the 2014 International Conference on Innovative Design and Manufacturing (ICIDM), Montreal, QC, Canada, 13–15 August 2014; pp. 100–104. [Google Scholar]
- Zeng, F.; Tong, X.; Huang, W.; Li, C.; Wang, Y.; Zou, Q.; Zhang, H. Multipoint Temperature Measurement System for Aero-Engine External Piping Based on Arrayed Fiber Bragg Grating Temperature Sensors. IEEE Sens. J. 2024, 24, 11102–11112. [Google Scholar] [CrossRef]
- Scervini, M.; Rae, C. An Improved Nickel Based MIMS Thermocouple for High Temperature Gas Turbine Applications. J. Eng. Gas Turbines Power 2013, 135, 091601. [Google Scholar] [CrossRef]
- Mihailov, S.J. Fiber Bragg Grating Sensors for Harsh Environments. Sensors 2012, 12, 1898–1918. [Google Scholar] [CrossRef]
- Khan, R.Y.M.; Ullah, R.; Faisal, M. Design and Development of Type-1 FBG Based High Temperature Sensor. Phys. Scr. 2023, 98, 045515. [Google Scholar] [CrossRef]
- Habisreuther, T. Sapphire Fiber Bragg Gratings for High Temperature and Dynamic Temperature Diagnostics. Appl. Therm. Eng. 2015, 91, 860–865. [Google Scholar] [CrossRef]
- Zhu, C.; Gerald, R.E.; Huang, J. Progress Toward Sapphire Optical Fiber Sensors for High-Temperature Applications. IEEE Trans. Instrum. Meas. 2020, 69, 8639–8655. [Google Scholar] [CrossRef]
- Khan, R.Y.M.; Faisal, M. Fiber Bragg Grating Temperature Sensor and Its Interrogation Techniques. J. Brill. Eng. 2023, 3, 4840. [Google Scholar]
- Melle, S.M.; Liu, K.; Measures, R.M. A Passive Wavelength Demodulation System for Guided-Wave Bragg Grating Sensors. IEEE Photonics Technol. Lett. 1992, 4, 516–518. [Google Scholar] [CrossRef]
- Davis, M.A.; Kersey, A.D. All-Fibre Bragg Grating Strain-Sensor Demodulationtechnique Using a Wavelength Division Coupler. Electron. Lett. 1994, 30, 75–77. [Google Scholar] [CrossRef]
- Trita, A.; Voet, E.; Vermeiren, J.; Delbeke, D.; Dumon, P.; Pathak, S.; Van Thourhout, D. Simultaneous Interrogation of Multiple Fiber Bragg Grating Sensors Using an Arrayed Waveguide Grating Filter Fabricated in SOI Platform. IEEE Photonics J. 2015, 7, 1–11. [Google Scholar]
- Moon, H.-M.; Kwak, S.-C.; Im, K.; Kim, J.-B.; Kim, S. Wavelength Interrogation System for Quasi-Distributed Fiber Bragg Grating Temperature Sensors Based on a 50-GHz Array Waveguide Grating. IEEE Sens. J. 2019, 19, 2598–2604. [Google Scholar]
- Díaz, C.A.R.; Leitão, C.; Marques, C.A.; Domingues, M.F.; Alberto, N.; Pontes, M.J.; Frizera, A.; Ribeiro, M.R.N.; André, P.S.B.; Antunes, P.F.C. Low-Cost Interrogation Technique for Dynamic Measurements with FBG-Based Devices. Sensors 2017, 17, 2414. [Google Scholar] [CrossRef]
- Cui, J.; Hu, Y.; Feng, K.; Li, J.; Tan, J. FBG Interrogation Method with High Resolution and Response Speed Based on a Reflective-Matched FBG Scheme. Sensors 2015, 15, 16516–16535. [Google Scholar] [CrossRef]
- Mamidi, V.R.; Kamineni, S. Fiber Bragg Grating-Based High Temperature Sensor and Its Low Cost Interrogation System with Enhanced Resolution. Opt. Appl. 2014, 44, 299–308. [Google Scholar]
- Srivastava, D.; Bhatnagar, R.; Kumar, A.; Parmar, V. Intensity Modulation Using Chirped Fiber Bragg Grating as an Edge Filter for Temperature Sensing. Microw. Opt. Technol. Lett. 2014, 56, 2913–2915. [Google Scholar] [CrossRef]
- Ogawa, K.; Koyama, S.; Haseda, Y.; Fujita, K.; Ishizawa, H.; Fujimoto, K. Wireless, Portable Fiber Bragg Grating Interrogation System Employing Optical Edge Filter. Sensors 2019, 19, 3222. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Zhou, J.; Tsai, D.P.; Xiao, S. Advanced Manufacturing of Dielectric Meta-Devices. Photonics Insights 2024, 3, R04. [Google Scholar]
- Pimbi, D.; Mia, B.; Jaidye, N.; Hasan, M.; Ahmed, S.Z. Integrated Polarization-Free Bragg Filters with Subwavelength Gratings for Photonic Sensing. Opt. Express 2024, 32, 2147. [Google Scholar] [PubMed]
- Lin, H.-A.; Huang, C.-S. Linear Variable Filter Based on a Gradient Grating Period Guided-Mode Resonance Filter. IEEE Photonics Technol. Lett. 2016, 28, 1042–1045. [Google Scholar] [CrossRef]
- Liu, D.; He, J.; Zhu, M.; Xiang, Y.; Zhang, L.; Zhang, M.; Xu, Y.; Dai, D. High-Performance Silicon Photonic Filter Using Subwavelength-Structure Multimode Waveguide Gratings. Laser Photonics Rev. 2023, 17, 2300485. [Google Scholar]
- Xiong, Z.; Wang, B.; Zhou, J. Triple-Layer Array Splitter for Zeroth-Order Suppressing under Normal Incidence. Optik 2022, 267, 169743. [Google Scholar]
- Luke, K. Parametric Frequency Comb Generation in Visible and Mid-Infrared Wavelengths with Integrated Silicon Nitride Ring Resonators. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 2016. [Google Scholar]
- Siefke, T.; Kroker, S.; Pfeiffer, K.; Puffky, O.; Dietrich, K.; Franta, D.; Ohlídal, I.; Szeghalmi, A.; Kley, E.; Tünnermann, A. Materials Pushing the Application Limits of Wire Grid Polarizers Further into the Deep Ultraviolet Spectral Range. Adv. Opt. Mater. 2016, 4, 1780–1786. [Google Scholar]
- Kischkat, J.; Peters, S.; Gruska, B.; Semtsiv, M.; Chashnikova, M.; Klinkmüller, M.; Fedosenko, O.; Machulik, S.; Aleksandrova, A.; Monastyrskyi, G.; et al. Mid-Infrared Optical Properties of Thin Films of Aluminum Oxide, Titanium Dioxide, Silicon Dioxide, Aluminum Nitride, and Silicon Nitride. Appl. Opt. 2012, 51, 6789. [Google Scholar] [PubMed]
- Grobnic, D.; Mihailov, S.J.; Smelser, C.W.; Ding, H. Sapphire Fiber Bragg Grating Sensor Made Using Femtosecond Laser Radiation for Ultrahigh Temperature Applications. IEEE Photonics Technol. Lett. 2004, 16, 2505. [Google Scholar]
- Müller, M.S.; El-Khozondar, H.J.; Buck, T.C.; Koch, A.W. Analytical Solution of Four-Mode Coupling in Shear Strain Loaded Fiber Bragg Grating Sensors. Opt. Lett. 2009, 34, 2622. [Google Scholar]

| Edge Filter | Reference | Demodulation Range | Demodulation Rate | Linearity |
|---|---|---|---|---|
| Subwavelength Gratings | This Work | 40 nm | Real time | Medium high |
| WDM | [10] | 10 nm | High speed | Medium high |
| AWG | [11] | 2 nm | High speed | High |
| [12] | 0.3 nm | High speed | High | |
| F-P | [13] | 6 nm | 5 Khz | Low |
| Matched FBG | [14] | 0.06 nm | 500 Khz | Medium |
| LPFG | [15] | 8 nm | NA | High |
| CFBG | [16] | 0.4 nm | NA | High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, J.; Tang, P.; Chen, K.; Xue, J.; Meng, Z.; Zhou, J. Design of Real-Time Demodulation for FBG Sensing Signals Based on All-Dielectric Subwavelength Gratings Edge Filters. Nanomaterials 2025, 15, 536. https://doi.org/10.3390/nano15070536
Lin J, Tang P, Chen K, Xue J, Meng Z, Zhou J. Design of Real-Time Demodulation for FBG Sensing Signals Based on All-Dielectric Subwavelength Gratings Edge Filters. Nanomaterials. 2025; 15(7):536. https://doi.org/10.3390/nano15070536
Chicago/Turabian StyleLin, Jingliang, Ping Tang, Kaihao Chen, Jiancai Xue, Ziming Meng, and Jinyun Zhou. 2025. "Design of Real-Time Demodulation for FBG Sensing Signals Based on All-Dielectric Subwavelength Gratings Edge Filters" Nanomaterials 15, no. 7: 536. https://doi.org/10.3390/nano15070536
APA StyleLin, J., Tang, P., Chen, K., Xue, J., Meng, Z., & Zhou, J. (2025). Design of Real-Time Demodulation for FBG Sensing Signals Based on All-Dielectric Subwavelength Gratings Edge Filters. Nanomaterials, 15(7), 536. https://doi.org/10.3390/nano15070536






