The Interfacial Structure and Bonding Properties of the Al(111)/CrB2(0001) Interface: Insights for Advanced Al-Based Composites
Abstract
1. Introduction
2. Calculation Methods and Models
2.1. Methods
2.2. Models
3. Results and Discussion
3.1. Surface Properties
3.2. Interface Properties
3.3. Doping Interface Properties
4. Conclusions
- The Cr-terminated configuration of the Al(111)/CrB2(0001) interface displays enhanced stability relative to alternative terminations, characterized by increased adhesive energy and reduced segregation enthalpy. Among various atomic arrangements, the hollow-site geometry presents the most favorable interfacial characteristics.
- The adhesive energy of the Cr-terminated HCP-stacked Al(111)/CrB2(0001) interface exceeds that of the α-Al/Al boundary. This observation validates the potential of CrB2 particles as efficient substrates for α-Al grain nucleation, considering both structural and energetic aspects. The interface demonstrates pronounced covalent interactions, specifically involving Al-2p and Cr-3d orbital hybridization.
- Alloying elements substantially modify Al(111)/CrB2(0001) interface behavior: (a) Fe, Mn, and Mg increase adhesive energy, facilitating nucleation within the aluminum matrix. (b) Cu, Zn, and Si reduce adhesive energy, possibly limiting CrB2 nucleation in aluminum. (c) The relative effectiveness of dopants, based on their influence on interfacial binding, follows the sequence Fe > Mn > Mg > Si > Zn > Cu. It is worth noting that the current findings are based on specific dopant configurations within the unit cell framework, where the substitution of one Al atom represents a high local dopant concentration. Further studies with larger supercells are recommended to validate trends under diluted conditions.
- These results offer significant contributions to the development and refinement of Al-CrB2 composite materials, providing strategic directions for modifying interface characteristics through controlled alloying to improve material functionality across diverse applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, X.R.; Gao, M.Q.; Huan, M.; Li, Y.; Guan, R.G. Microstructure and strength-conductivity synergy of Al-Mg-Si-Cu alloy sheets prepared via vacuum melting and thermo-mechanical treatment. J. Alloys Compd. 2025, 1010, 177184. [Google Scholar] [CrossRef]
- Li, W.H.; Bai, P.C.; Cui, X.M.; Zhao, X.P.; Liang, S.B.; An, J.L.; Tian, Y.J. In-situ TEM study on the precipitation behavior of an Al-Mn-Mg-Sc-Zr alloy formed by SLM. Mater. Charact. 2024, 218, 114578. [Google Scholar]
- Li, Y.; Ma, Z.P.; Hao, H.N.; Zhu, Y.K. First-principles analysis of the stability and electronic structure at the Al/Al4SiC4 interface. J. Mater. Heat Treat. 2024, 6, 155–164. [Google Scholar]
- Xiong, C. Surface Electrospark Deposition of ZrB2-CrB2 Composite Coating for Spot Welding Electrodes. Master’s Thesis, Hubei University of Technology, Wuhan, China, 2018. [Google Scholar]
- Zhang, S.S.; Li, X.W.; Wang, L.; Zhang, D.; Yang, P.L.; Li, Z.Y.; Wang, A.Y. The Influence of Deposition Temperature on the Structure and Properties of CrB2 Coatings. Chin. J. Surf. Eng. 2016, 29, 69–76. [Google Scholar]
- Zhang, S.C.; Wang, Z.Y.; Guo, P.; Ke, P.L.; Odén, M.; Wang, A.Y. Temperature induced superhard CrB2 coatings with preferred (001) orientation deposited by DC magnetron sputtering technique. Surf. Coat. Technol. 2017, 322, 134–140. [Google Scholar] [CrossRef]
- Wang, Y.W.; Sun, X.W.; Wang, L.; Yang, Y.; Ren, X.X.; Ma, Y.D.; Cui, Y.H.; Sun, W.W.; Wang, X.Y.; Dong, Y.C. Microstructure and properties of CrB2-Cr3C2 composite coatings prepared by plasma spraying. Surf. Coat. Technol. 2021, 425, 127693. [Google Scholar]
- Choi, H.S.; Park, B.; Lee, J.J. CrB2 coatings deposited by inductively coupled plasma assisted DC magnetron sputtering. Surf. Coat. Technol. 2007, 202, 982–986. [Google Scholar] [CrossRef]
- Audronis, M.; Rosli, Z.M.; Leyland, A.; Kelly, P.J.; Matthews, A. Tribological behaviour of pulsed magnetron sputtered CrB2 coatings examined by reciprocating sliding wear testing against aluminium alloy and steel. Surf. Coat. Technol. 2008, 202, 1470–1478. [Google Scholar] [CrossRef]
- Morgiel, J.; Poliarus, O.; Pomorska, M.; Maj, Ł.; Szlezynger, M. Thermal stability of plasma-sprayed NiAl/CrB2 composite coatings investigated through in-situ TEM heating experiment. Mater. Charact. 2020, 159, 110068. [Google Scholar] [CrossRef]
- Zhuo, Z.M. Research on the Micro-Scale Interface Structure of Niobium-Based Heterocore with Aluminum Melt. Ph.D. Thesis, North University of China, Taiyuan, China, 2020. [Google Scholar]
- Saengdeejing, A.; Sahara, R.; Toda, Y. Al–Ni–Ti thermodynamic database from first-principles calculations. Calphad 2024, 84, 102658. [Google Scholar]
- Pang, X.Z.; Yang, J.B.; Li, A.; Pang, M.J.; Xiao, Y.; Nong, H.; Qin, H.Q.; Liu, C.Y. Understanding the atomic and electronic structure of the NbC(111)/Cu(111) interface via first principles calculation. Mater. Today Commun. 2023, 36, 106653. [Google Scholar] [CrossRef]
- Song, Y.L.; Wang, G.C.; Ni, J.J.; Song, B.; Guo, S.; Li, X.X.; Cheng, C. First-principles study on the structural, mechanical and thermodynamic properties of Cu-Cr-Zr alloy. Phys. B Condens. Matter 2024, 685, 416029. [Google Scholar]
- Yang, Z.C.; Cheng, L.X.; Chen, S.Z.; Zhang, Y. Active element Ti improves the Sn-based alloy filler/graphite soldering interface: A combined first-principles and experimental study. Mater. Sci. Semicond. Process. 2024, 177, 108390. [Google Scholar]
- Zou, X.; Liu, T.Y.; Liu, W.H.; Li, Y.M.; Zhao, Y.P. First principles calculations on stability, electronic structure and fracture failure of Cu-doped Al(100)/Mg2Si(111) interface. Mater. Chem. Phys. 2024, 315, 128978. [Google Scholar]
- Han, F.; Li, C.; Wang, Y.; Pai, Z.; Meng, Y.; Cao, M.; Liu, Y.; He, P.; Ma, X.; Xue, L.; et al. Comparative study on corrosion property of 2219 aluminum alloy sheet and additively manufactured 2319 aluminum alloy. J. Mater. Res. Technol. 2024, 30, 3178–3185. [Google Scholar]
- Wu, X.; Guan, Z.P.; Yang, H.Y.; Dong, B.X.; Zhang, L.C.; Meng, J.; Luo, C.J.; Wang, C.G.; Cao, K.; Qiao, J.; et al. Sub-rapid solidification microstructure characteristics and control mechanisms of twin-roll cast aluminum alloys: A review. J. Mater. Res. Technol. 2024, 32, 874–914. [Google Scholar]
- Wang, Z.X.; Zhan, L.L.; Yun, X. Experimental study of local buckling behaviour of 7A04-T6 high strength aluminium alloy H-section stub columns in fire. Eng. Struct. 2024, 317, 118631. [Google Scholar]
- You, X.; Xing, Z.; Jiang, S.; Zhu, Y.; Lin, Y.; Qiu, H.; Nie, R.; Yang, J.; Hui, D.; Chen, W.; et al. A review of research on aluminum alloy materials in structural engineering. Dev. Built Environ. 2024, 17, 100319. [Google Scholar]
- Yin, J.B.; Lu, X.F. Theoretical study of electronic structure and optical properties of tin doped CuS counter electrode for dye-sensitized solar cells. Sol. Energy 2018, 171, 871–875. [Google Scholar]
- Nazmul, H.; Mehedi, H.M.; Alamgir, K.; Harunur, R.M. Theoretical study of the structural, electronic, mechanical, and optical of transition metal (mn, co, and ni) doped FrGeI3 perovskites. Results Mater. 2023, 20, 100457. [Google Scholar]
- Dong, D.; Kuang, X.Y.; Guo, J.J.; Zheng, B.X. Density functional theory study of AunMn (n = 1–8) clusters. J. Phys. Chem. Solids 2010, 71, 770–775. [Google Scholar]
- Ganeshan, S.; Hector, L.G.; Liu, Z.-K. First-principles calculations of impurity diffusion coefficients in dilute Mg alloys using the 8-frequency model. Acta Mater. 2011, 59, 3214–3228. [Google Scholar]
- Ivashchenko, V.I.; Onoprienko, A.A.; Skrynskyy, P.L.; Kozak, A.O.; Vedel, D.V.; Mazur, P.V.; Sinelnichenko, A.K.; Buranych, V.V.; Pogrebnjak, A.D. Structure and properties of (TiZrHfNbTa)B2 films and first-principles models for high entropy diborides. Thin Solid Film. 2024, 803, 140478. [Google Scholar]
- Zhu, H.; Wang, Q.; Yang, C.; Wang, Y.; Xia, C.; Zhao, D.; Zhang, H.; Wang, M.; Chen, Z.; Wang, H. Improving TiB2 dispersion in Al-Si composites by interfacial projection: High-throughput first-principles calculations and experimental verification. Mater. Des. 2024, 244, 113184. [Google Scholar]
- Zhang, X.Q.; Yue, Y.L.; Xu, D.; Qin, J.Q.; Zhang, X.Y.; Liu, R.P. Effect of solutes segregation in a binary TiAl alloy: A first-principles calculation method. Mater. Today Commun. 2024, 39, 109252. [Google Scholar]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717–2744. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar]
- Fischer, T.H.; Almlöf, J. General methods for geometry and wave function optimization. J. Phys. Chem. 1996, 96, 9768–9774. [Google Scholar]
- Ji, L.G.; Liu, H.L.; Huang, C.Z.; Tang, Y.Q.; Huang, J.; Qiu, Y.H. Effect of Al and Si content on properties of Ti(1-x-y)AlxSiyN coating materials: First-principles calculation. Mater. Today Commun. 2024, 40, 109460. [Google Scholar]
- Liu, X.; Jiang, X.; Wang, T.; Zhang, Z.; Liu, Z. Lattice thermal conductivity of two-dimensional CrB4 and MoB4 monolayers against Slack’s guideline. Results Phys. 2023, 51, 106696. [Google Scholar]
- Wang, J.H.; Hong, W.; Liu, T.Y.; Lu, X.; Li, H.F. The electronic and optical properties of Al interstitial defects in KH2PO4 crystal: First principles study. Comput. Mater. Sci. 2024, 244, 113157. [Google Scholar] [CrossRef]
- Gao, D.L.; Yi, D.; Xia, J.; Yang, Y.G.; Wang, X. First-principles screening of Cu-based single-atom alloys for highly efficient electrocatalytic nitrogen reduction. Mol. Catal. 2024, 555, 113879. [Google Scholar] [CrossRef]
- Sun, M.Y.; Mao, H.; Xu, D.J.; Zhou, G.X.; Li, J.B.; Gong, H.R.; Liang, C.P. First-principles calculation of various phase transition in Al–Sc system. J. Mater. Res. Technol. 2023, 26, 3803–3812. [Google Scholar]
- Weng, J.H. Preparation and Property Study of Superhard and Corrosion-Resistant CrB2 Coating. Master’s Thesis, Shanghai University, Shanghai, China, 2019. [Google Scholar]
- Bramfitt, B.L. The effect of carbide and nitride additions on the heterogeneous nucleation behavior of liquid iron. Metall. Mater. Trans. B 1970, 1, 1987–1995. [Google Scholar] [CrossRef]
- Qin, N. The First Principles Study of the Stability for Transition Metal Diborides (0001)Surfaces. Master’s Thesis, Tianjin Normal University, Tianjin, China, 2011. [Google Scholar]
- Sun, Y. First-Principles Calculation of Phase Stability and Physical Properties of Transition Metal Borides. Master’s Thesis, Inner Mongolia University of Technology, Baotou, China, 2016. [Google Scholar]
- Zhang, S.S. Preparation and Study of Structure and Properties of Chromium Diboride Coating; North University of China: Taiyuan, China, 2016. [Google Scholar]
- Besson, R.; Macaluso, S.; Thuinet, L. Critical issues on coherent interface energy calculations revisited: The case of Al/TiB2. Surf. Interfaces 2022, 33, 102272. [Google Scholar]
- Zhang, S.; He, D.; Huang, P.; Wang, F. Moiré pattern at graphene/Al(111) interface: Experiment and simulation. Mater. Des. 2021, 201, 109509. [Google Scholar] [CrossRef]
- Xin, T.; Bai, L.J.; Chen, G.T.; Zhang, G.J.; Zhao, B. Fe/Cu doped black ceramic coating on magnesium alloy by plasma electrolytic oxidation method based on first principles. Surf. Interfaces 2024, 48, 104289. [Google Scholar] [CrossRef]
- Zunger, A.; Malyi, O.I. Understanding doping of quantum materials. Chem. Rev. 2021, 121, 3031–3060. [Google Scholar] [CrossRef]
- Wang, M.J.; Sun, J.W.; Li, S.Y.; Meng, Y.C.; Zheng, H.Y.; Yin, Z.; Fu, Y.Z.; Zhang, Y.J. Heterogeneous nucleation mechanisms in Mg(0001)/ Al3BC(0001) interfaces: Insights for advanced Mg-based composites. Surf. Interfaces 2024, 46, 104040. [Google Scholar]
- Pei, X.; Yuan, M.N.; Han, F.Z.; Wei, Z.Y.; Ma, J.; Wang, H.L.; Shen, X.Q.; Zhou, X.S. Investigation on tensile properties and failure mechanism of Al(111)/Al3Ti(112) interface using the first-principles method. Vacuum 2022, 196, 110784. [Google Scholar] [CrossRef]
- Wang, M.J.; Han, H.M.; Zhang, G.W.; Xu, H.; Yin, Z.; Dong, Y.; Fu, Y.Z. Effect of solute elements (Ni, Sn, P) on the adhesion electronic properties of γ-Fe/Cu heterogeneous interface: A first-principles study. Results Phys. 2022, 38, 105659. [Google Scholar]
- Wang, M.; Wei, D.; Lai, Y.; Shou, H.; Liu, S.; Zheng, H.; Zhang, Y.; Yang, X.; Zhao, T.; Wang, R. Enhanced nucleation at Al(111)/Ti3AlC2(0001) interfaces: The role of doping in adhesion and interfacial stability. Vacuum 2024, 229, 113553. [Google Scholar]
- Dai, Y.C.; Liu, J.; Shi, Y. Effects of transition elements additions on interfacial properties of Al(111)/B4C (0001) interface based on first-principles study. J. Phys. Chem. Solids 2025, 196, 112360. [Google Scholar]
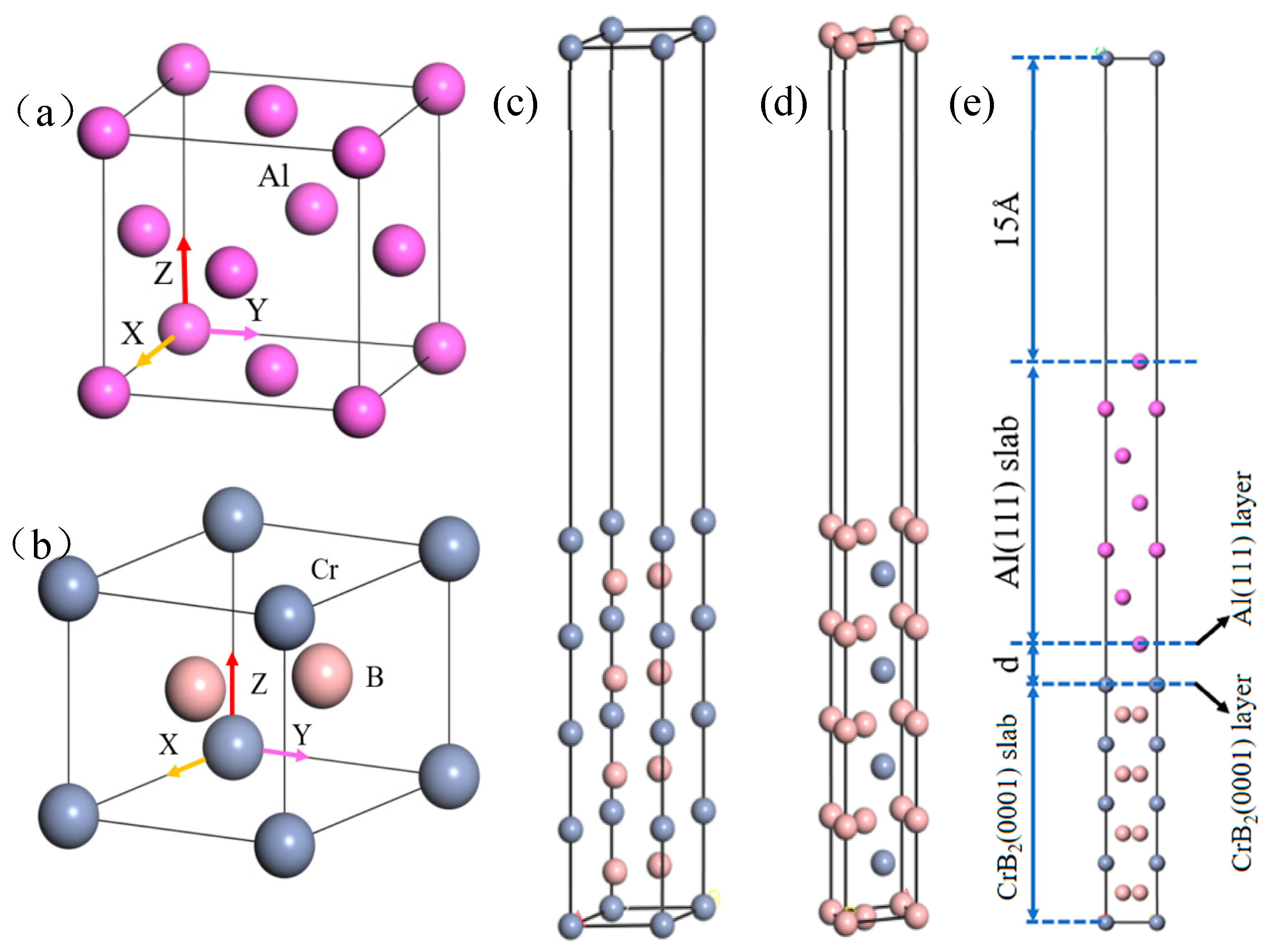
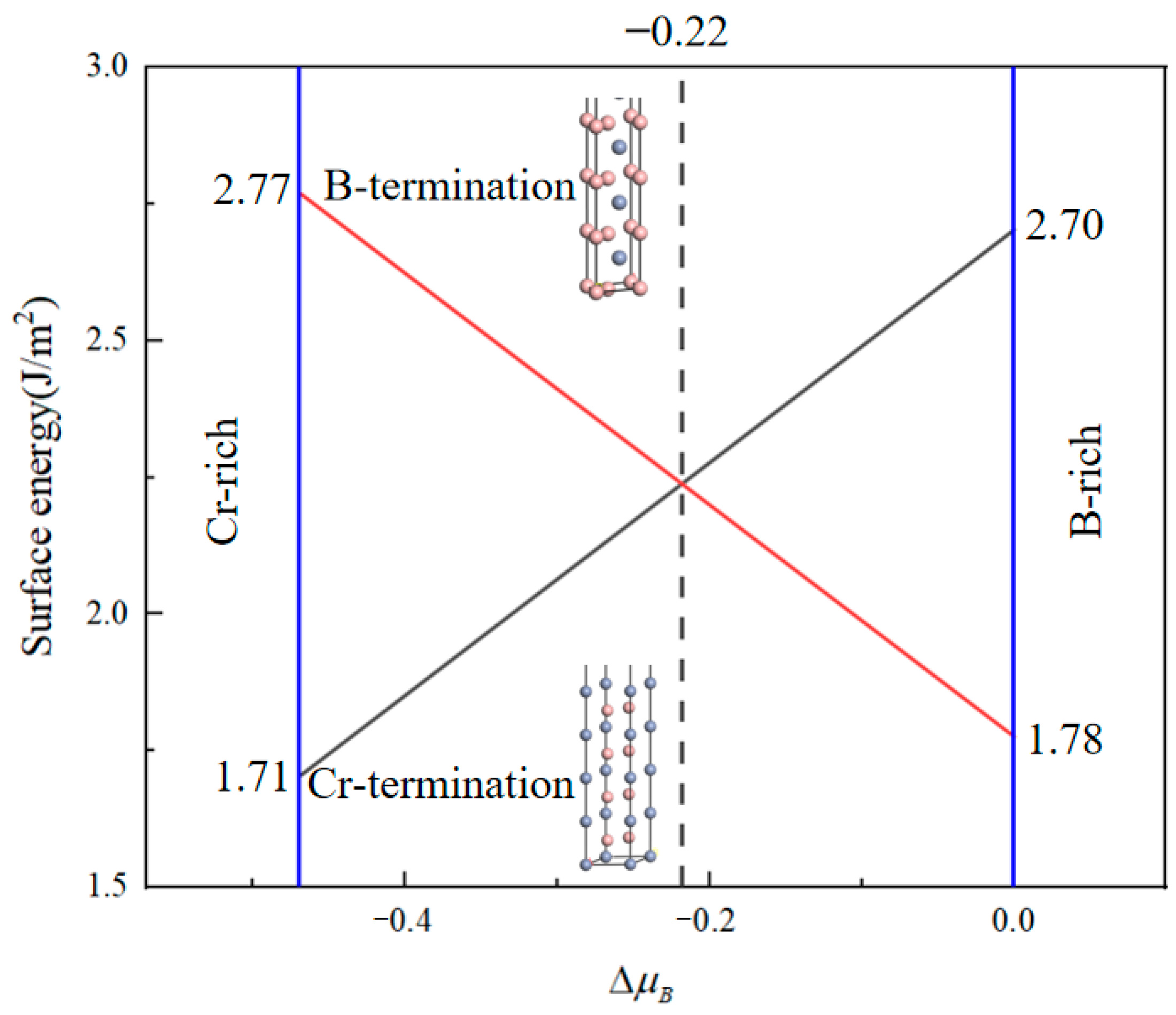

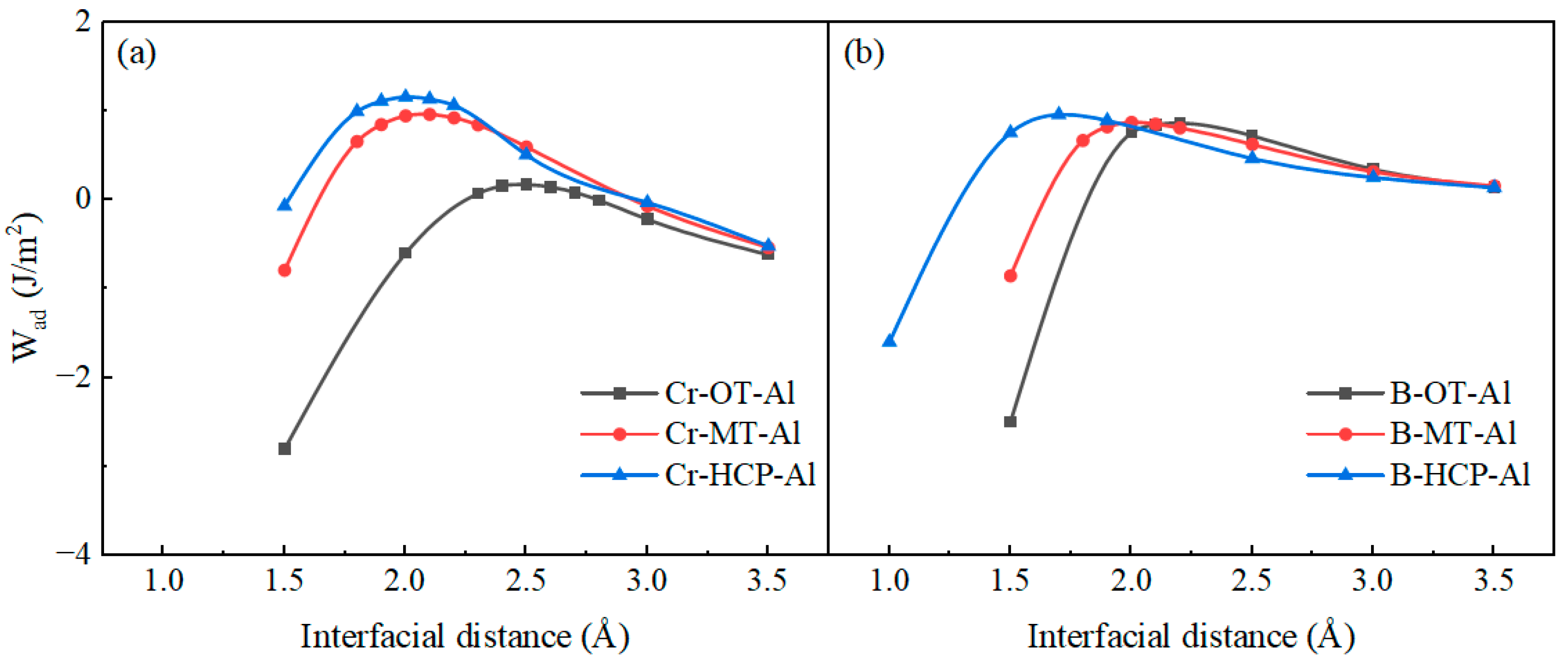
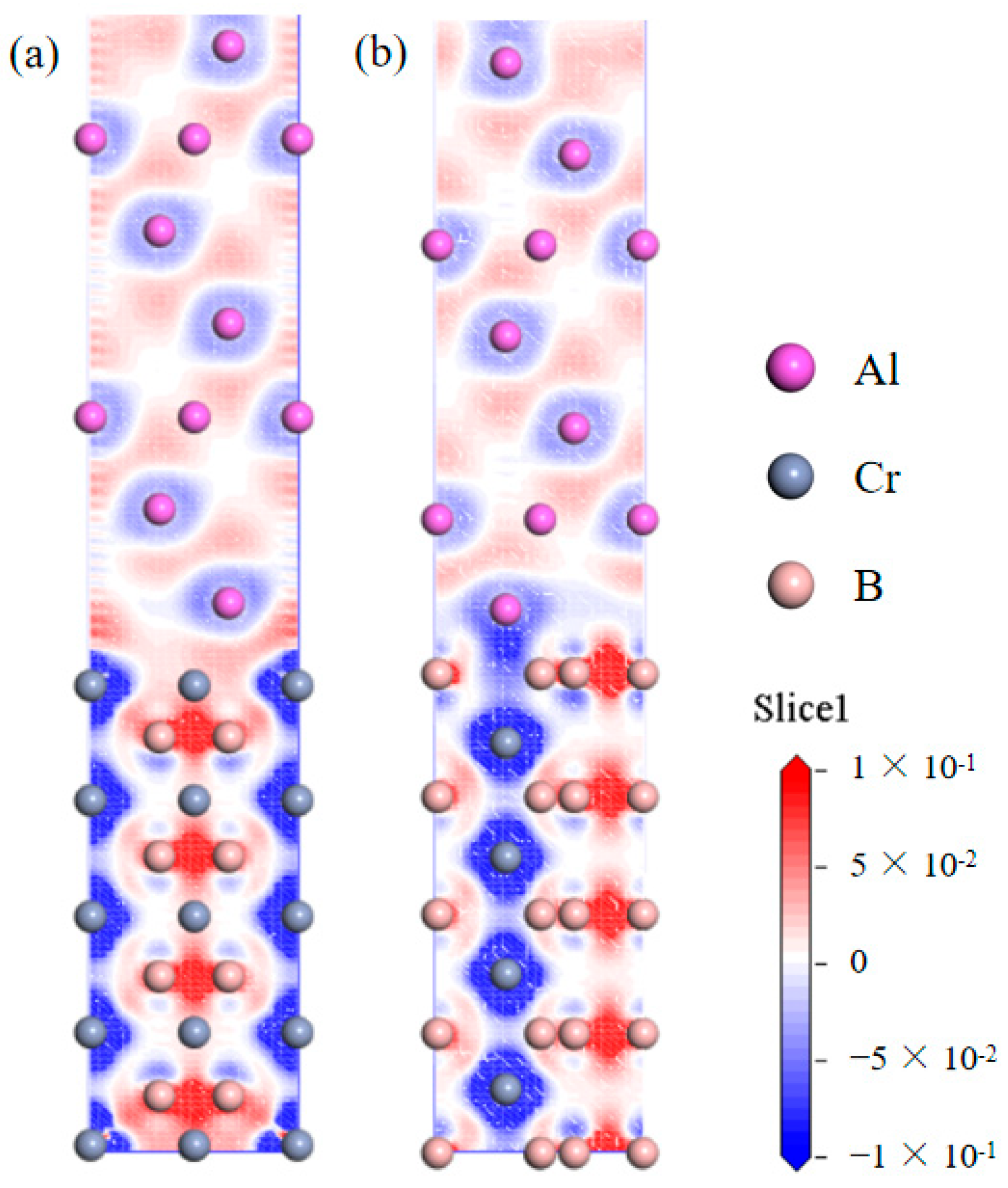
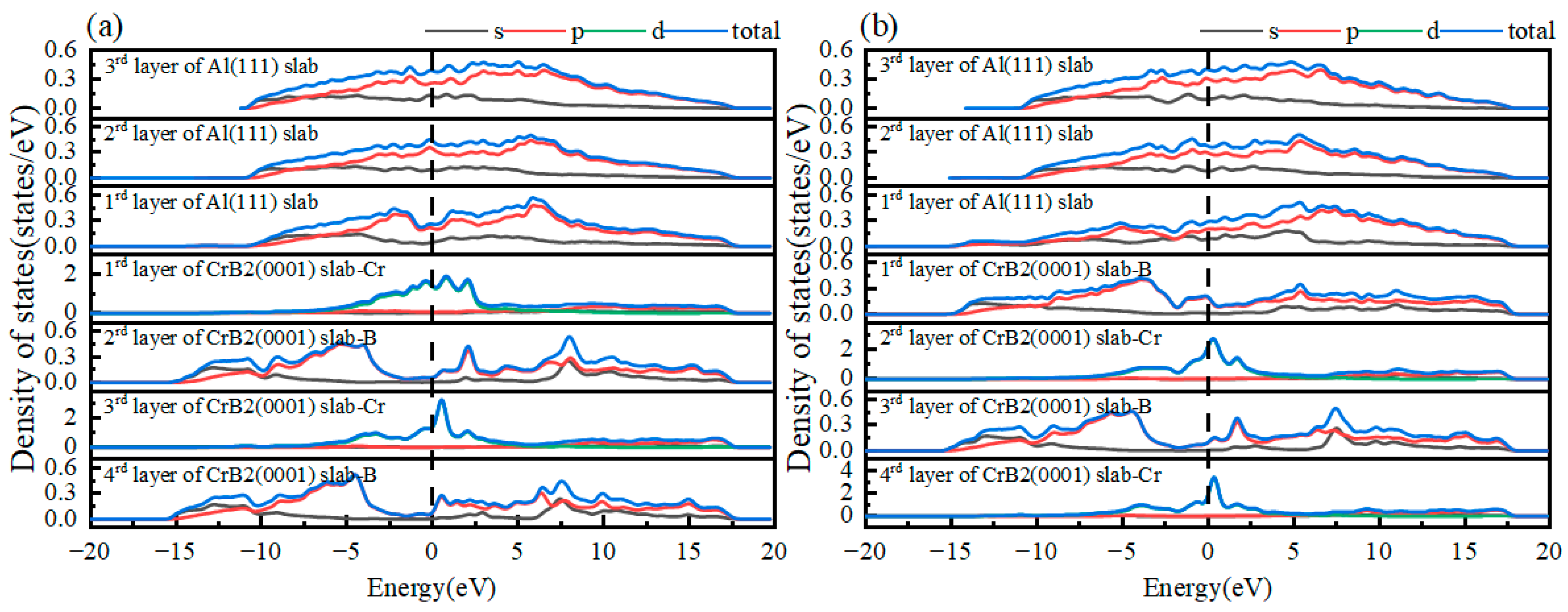
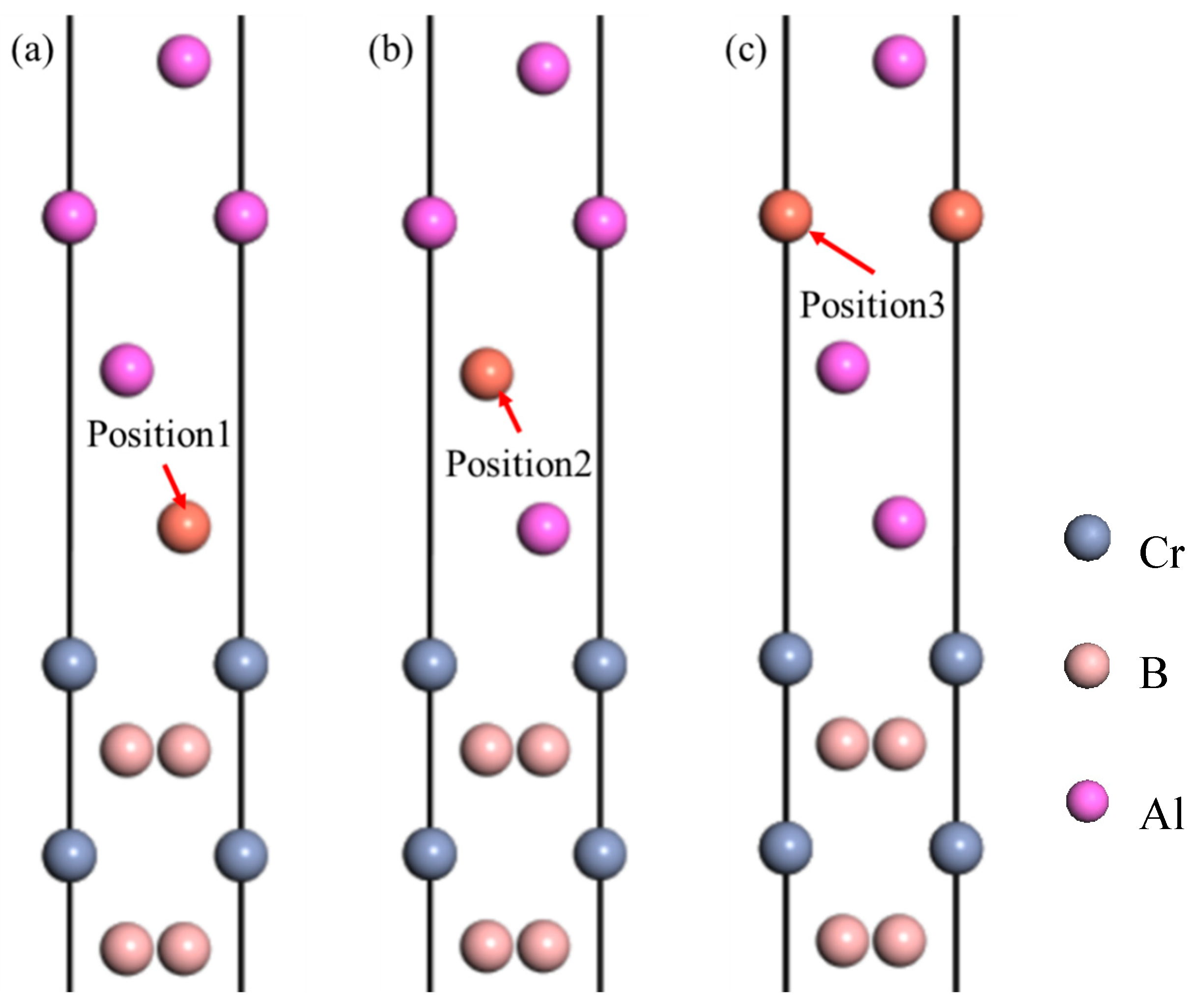
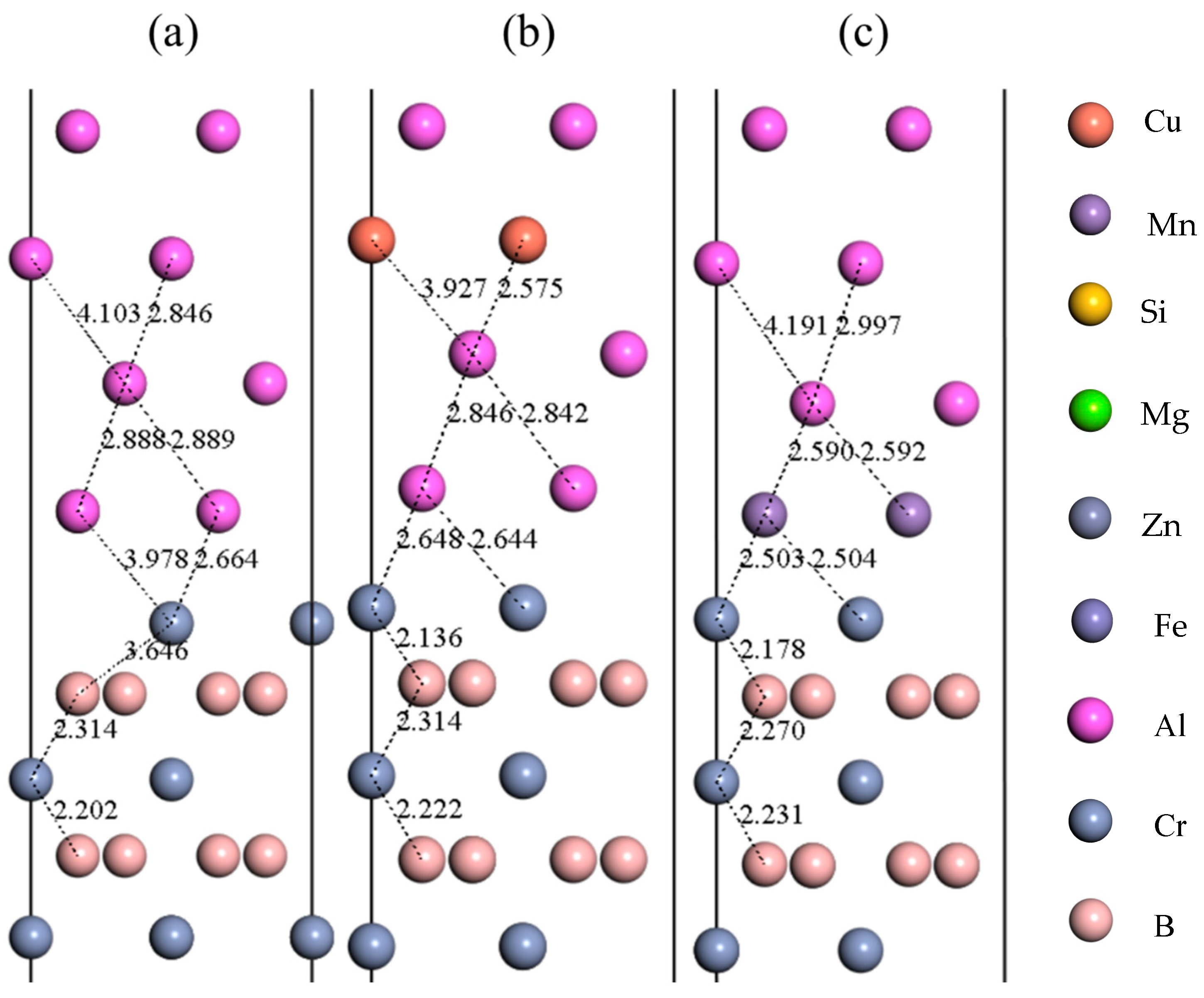


| Phase | K-Point Meshes | Cutoff Energy/eV | Atom Number in Cell |
|---|---|---|---|
| Bulk Al(111) | 10 × 10 × 10 | 500 | 4Al |
| Bulk CrB2(0001) | 12 × 12 × 12 | 500 | 2B 1Cr |
| CrB2(0001)-Cr slab | 16 × 16 × 1 | 500 | 8B 5Cr |
| CrB2(0001)-B slab | 16 × 16 × 1 | 500 | 10B 4Cr |
| Al(111)/CrB2(0001)-Cr interface | 18 × 18 × 1 | 500 | 8B 7Al 5Cr |
| Al(111)/CrB2(0001)-B interface | 18 × 18 × 1 | 500 | 10B 7Al 4Cr |
| Structures | Method | a = b | c | Volume (Å3) | ΔHf (eV) |
|---|---|---|---|---|---|
| CrB2 | GGA(PBE) [39] | 2.977 | 2.962 | 22.73 | −0.936 |
| Exp [40] | 2.969 | 3.066 | 23.41 | ||
| This work | 2.959 | 3.032 | 22.99 | −0.938 | |
| Al | GGA(PBE) [41] | 4.05 | 4.05 | 66.43 | |
| Exp [42] | 4.032 | 4.032 | 65.55 | ||
| This work | 4.049 | 4.049 | 66.38 | 0 |
| Termination | Interlayer | Slab Thickness (N) | |||
|---|---|---|---|---|---|
| 5 | 7 | 9 | 11 | ||
| Cr | Δ12 | −14.38% | −18.35% | −14.52% | −15.86% |
| Δ23 | 6.39% | 5.53% | 5.91% | 6.67% | |
| Δ34 | −4.51% | −4.06% | −3.67% | ||
| Δ45 | 0.16% | 1.83% | |||
| Δ56 | −0.15% | ||||
| B | Δ12 | 6.78% | 3.33% | 5.68% | 5.02% |
| Δ23 | −5.01% | −4.38% | −4.38% | −0.43% | |
| Δ34 | −0.65% | 0.50% | 2.59% | ||
| Δ45 | −0.13% | 0.98% | |||
| Δ56 | 0.12% | ||||
| Surface Energy (J/m2) | |||||
|---|---|---|---|---|---|
| Slab Thickness (N) | 5 | 7 | 9 | 11 | |
| Termination | Cr | 1.93 | 2.17 | 2.24 | 2.23 |
| B | 1.89 | 2.15 | 2.18 | 2.17 | |
| Termination | Stacking | Unrelaxed | Fully Relaxed | |||
|---|---|---|---|---|---|---|
| d0 (Å) | Wad (J/m2) | d0 (Å) | Wad (J/m2) | (J/m2) | ||
| Cr | OT | 2.5 | 0.17 | 2.41 | 0.56 | 2.55 |
| MT | 2.1 | 0.96 | 2.08 | 1.25 | 1.86 | |
| HCP | 2 | 1.15 | 2.05 | 1.75 | 1.31 | |
| B | OT | 2.2 | 0.86 | 2.13 | 1.37 | 1.74 |
| MT | 2 | 0.87 | 1.96 | 1.44 | 1.67 | |
| HCP | 1.7 | 0.96 | 1.58 | 1.56 | 1.55 | |
| Doping Element | Position | Energy (eV) | Wad (J/m2) | (J/m2) |
|---|---|---|---|---|
| Clean | −13,507.04 | 1.75 | 1.31 | |
| Cu | 1 | −15,076.33 | 1.26 | 2.48 |
| 2 | −15,076.86 | 1.55 | 1.90 | |
| 3 | −15,076.98 | 1.67 | 1.77 | |
| Mn | 1 | −14,020.16 | 1.98 | 1.25 |
| 2 | −14,020.20 | 1.20 | 2.45 | |
| 3 | −14,020.37 | 1.39 | 2.27 | |
| Si | 1 | −13,566.20 | 1.74 | 1.87 |
| 2 | −13,566.18 | 1.73 | 1.89 | |
| 3 | −13,566.09 | 1.68 | 1.99 | |
| Mg | 1 | −15,085.85 | 1.16 | 1.71 |
| 2 | −15,086.32 | 1.84 | 1.23 | |
| 3 | −15,086.38 | 1.90 | 1.17 | |
| Zn | 1 | −15,433.03 | 1.28 | 1.65 |
| 2 | −15,433.33 | 1.70 | 1.36 | |
| 3 | −15,433.34 | 1.73 | 1.34 | |
| Fe | 1 | −14,257.71 | 2.15 | 1.16 |
| 2 | −14,257.94 | 1.44 | 2.15 | |
| 3 | −14,258.07 | 1.54 | 1.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Wang, M.; Wang, B.; Chen, Z. The Interfacial Structure and Bonding Properties of the Al(111)/CrB2(0001) Interface: Insights for Advanced Al-Based Composites. Nanomaterials 2025, 15, 529. https://doi.org/10.3390/nano15070529
Sun J, Wang M, Wang B, Chen Z. The Interfacial Structure and Bonding Properties of the Al(111)/CrB2(0001) Interface: Insights for Advanced Al-Based Composites. Nanomaterials. 2025; 15(7):529. https://doi.org/10.3390/nano15070529
Chicago/Turabian StyleSun, Jingwen, Mingjie Wang, Ben Wang, and Zhongxian Chen. 2025. "The Interfacial Structure and Bonding Properties of the Al(111)/CrB2(0001) Interface: Insights for Advanced Al-Based Composites" Nanomaterials 15, no. 7: 529. https://doi.org/10.3390/nano15070529
APA StyleSun, J., Wang, M., Wang, B., & Chen, Z. (2025). The Interfacial Structure and Bonding Properties of the Al(111)/CrB2(0001) Interface: Insights for Advanced Al-Based Composites. Nanomaterials, 15(7), 529. https://doi.org/10.3390/nano15070529






