CPDDA: A Python Package for Discrete Dipole Approximation Accelerated by CuPy
Abstract
1. Introduction
2. Fundamentals of DDA
3. Implementation and Validation of CPDDA
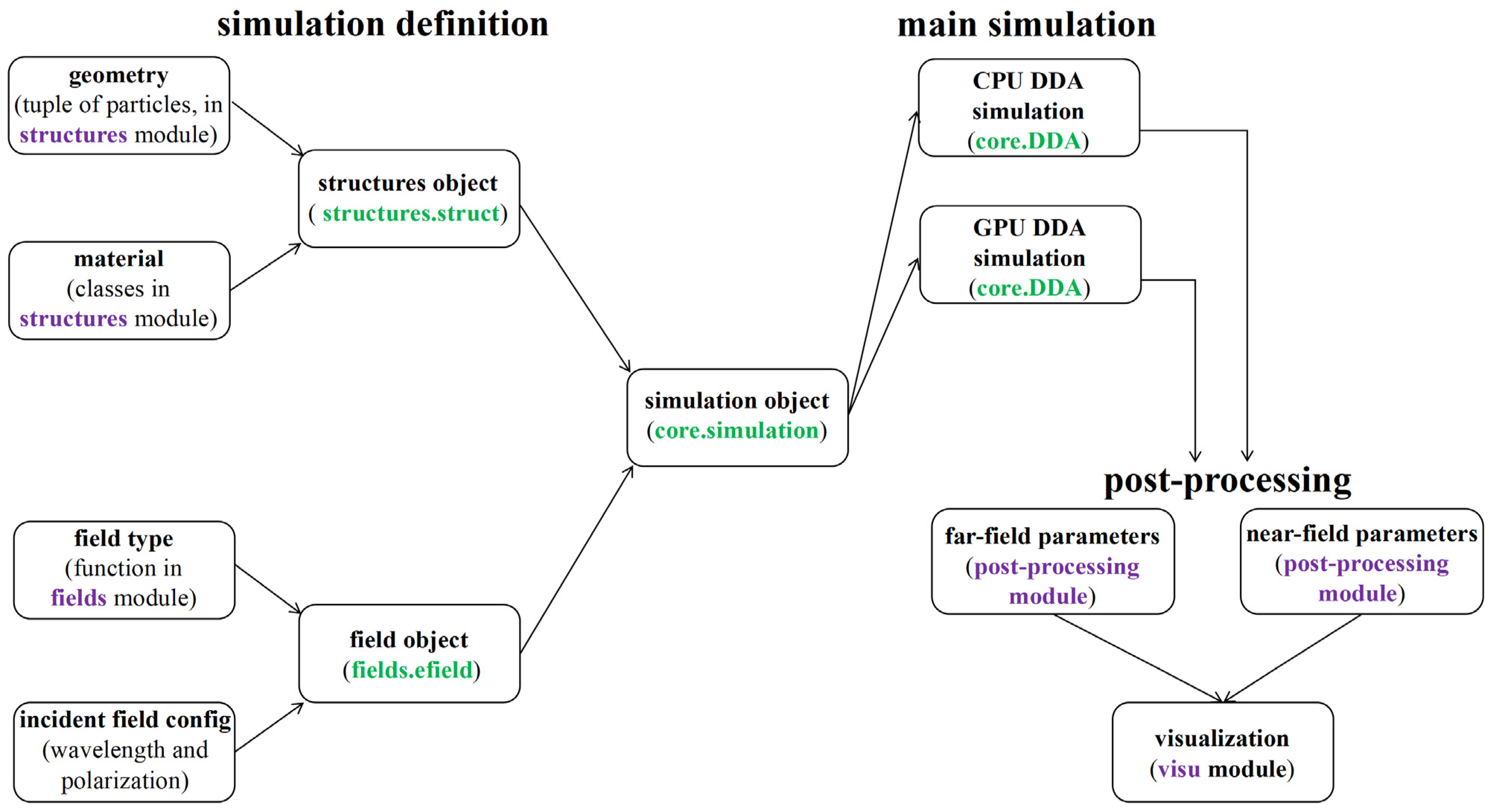
3.1. Implementation of CPDDA
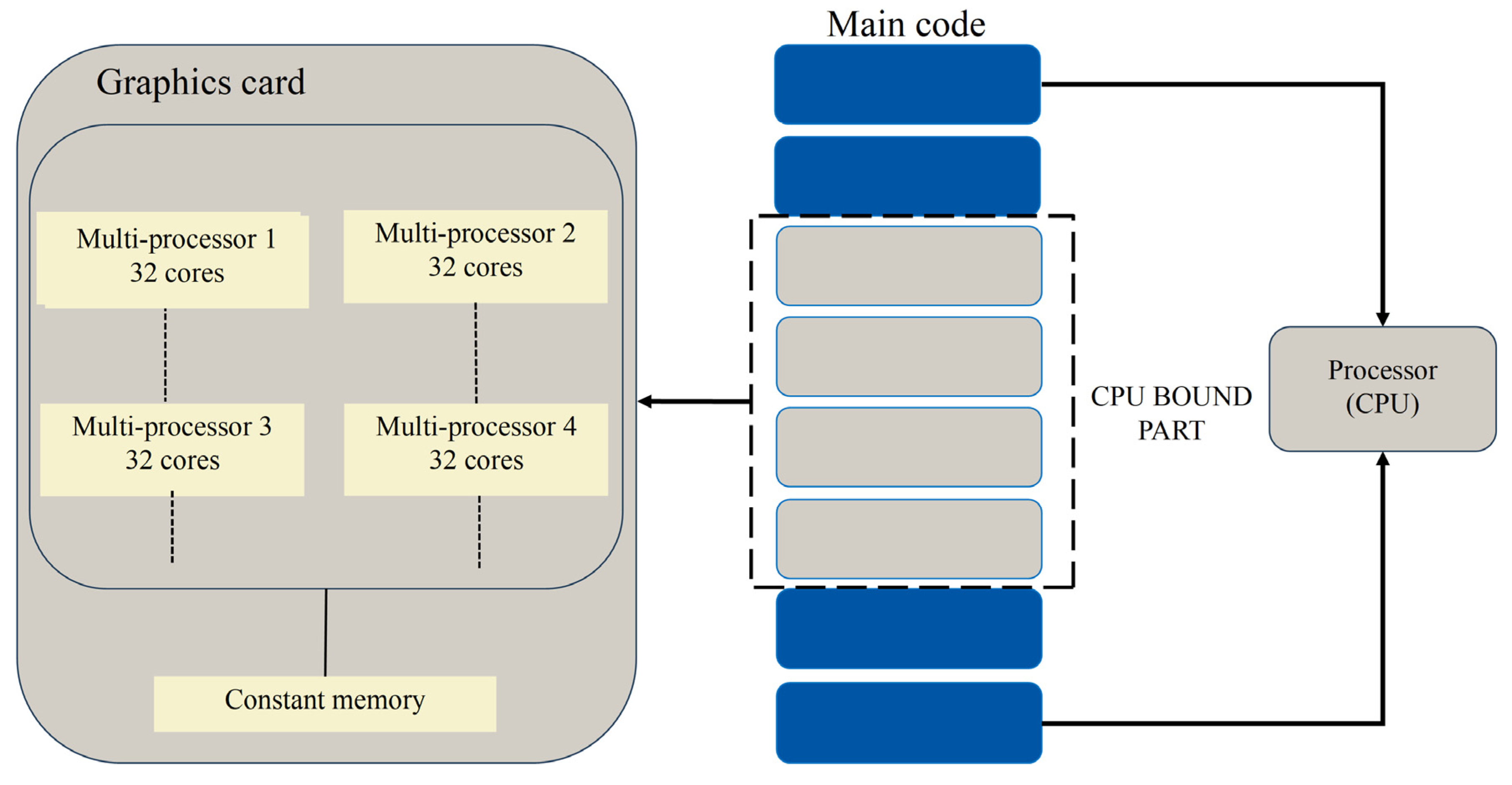
3.2. GPU Mode of CPDDA
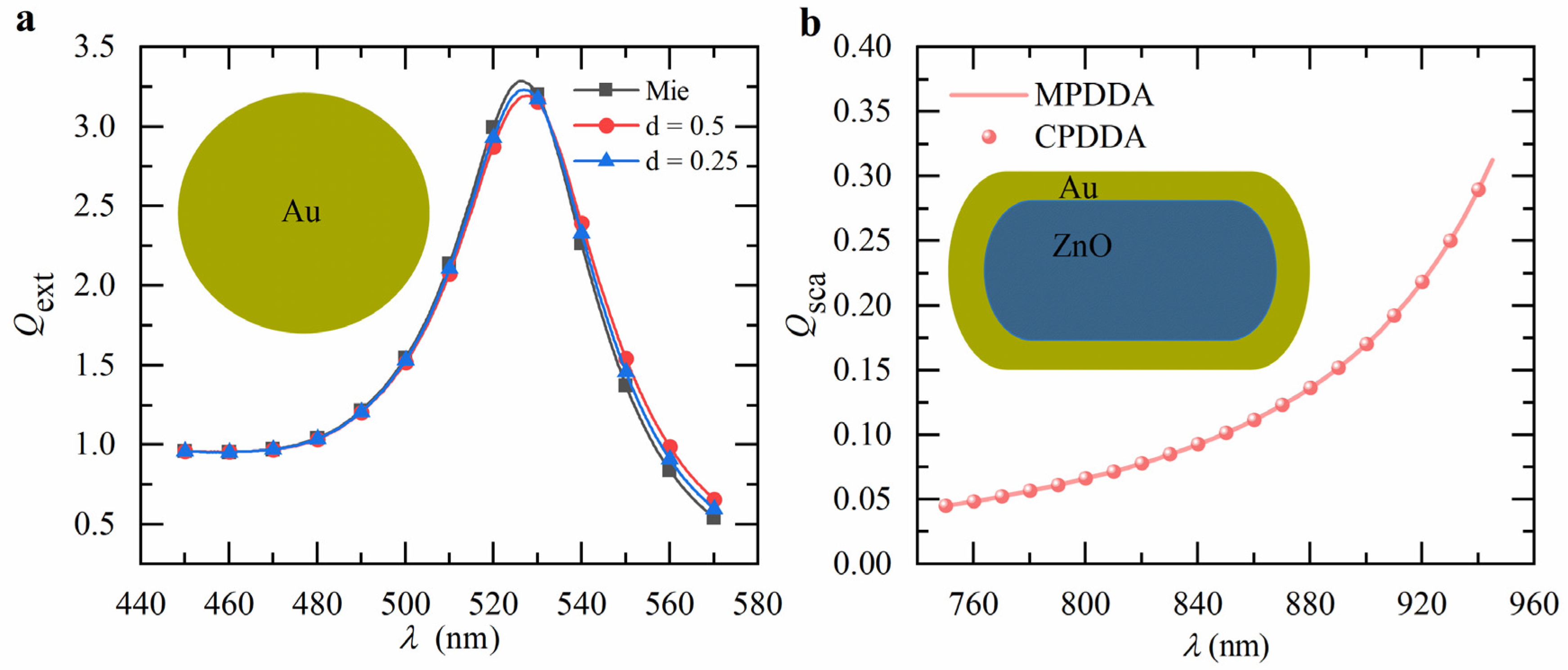
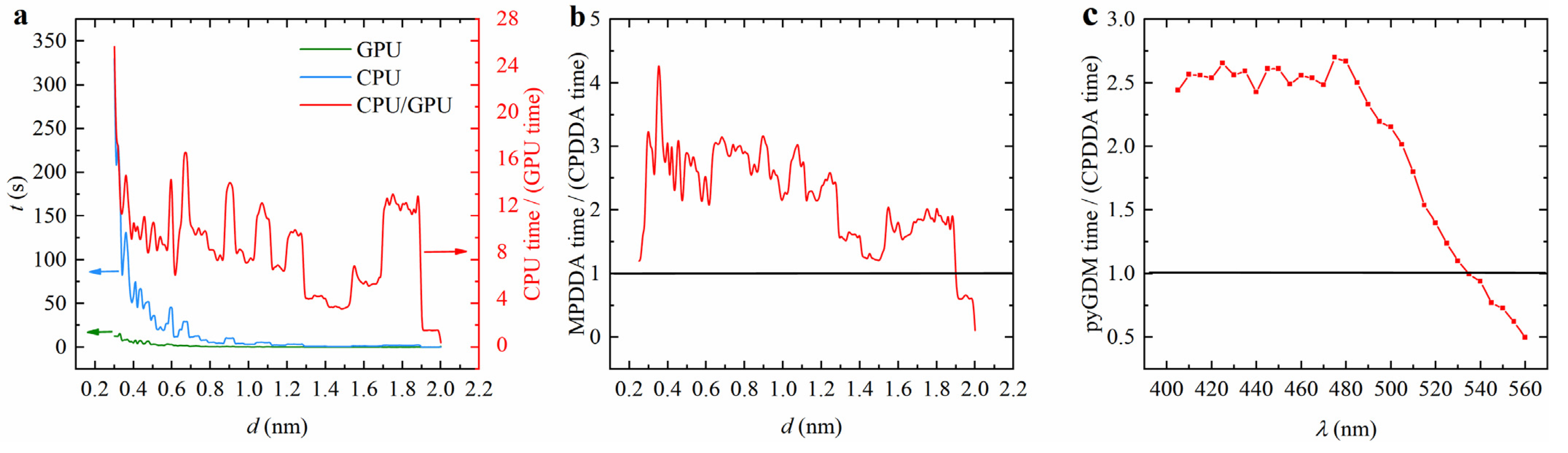
3.3. Numerical Validation of CPDDA
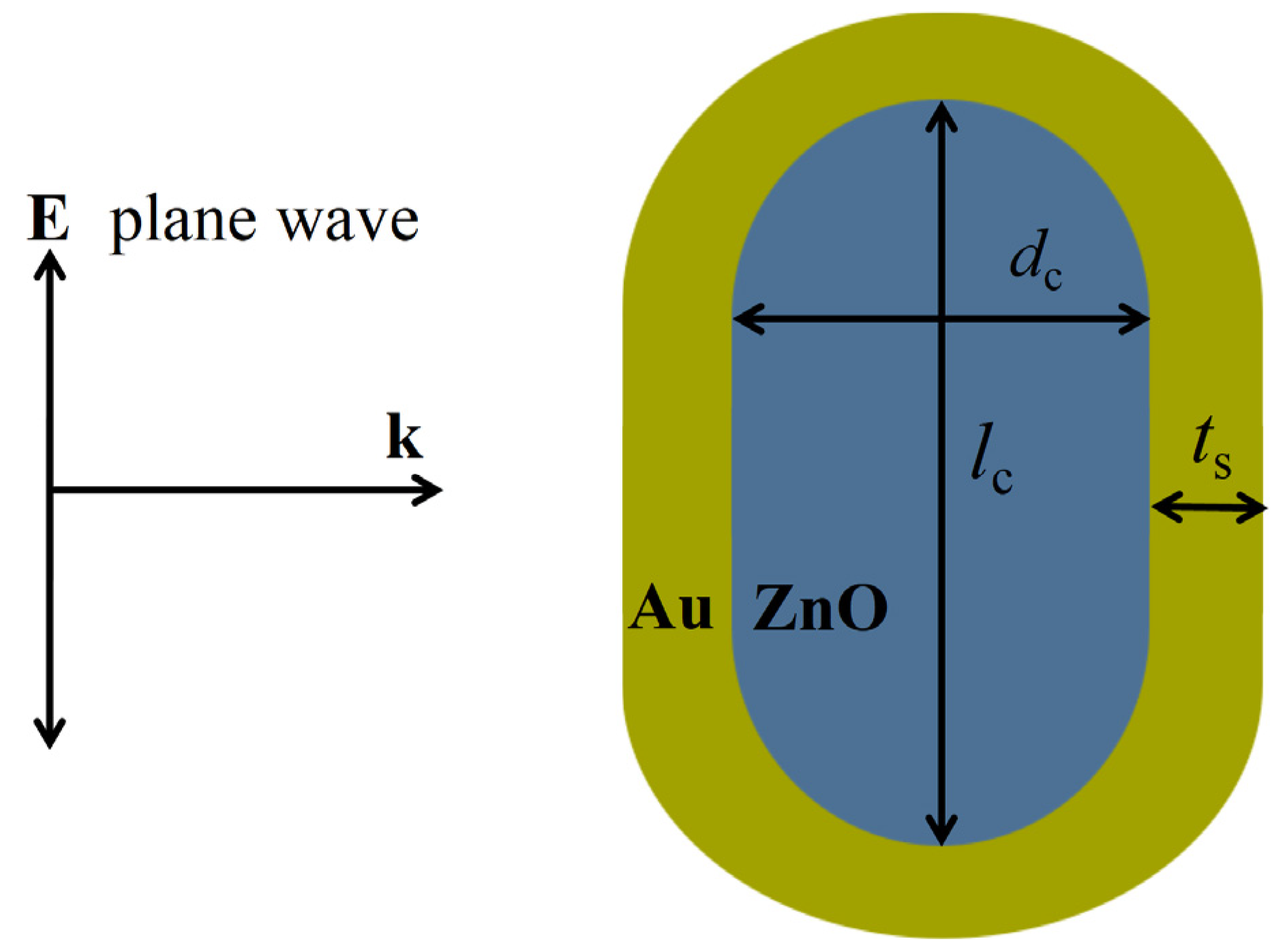
4. Optical Properties of ZnO@Au Nanorods
4.1. Effect of Aspect Ratio
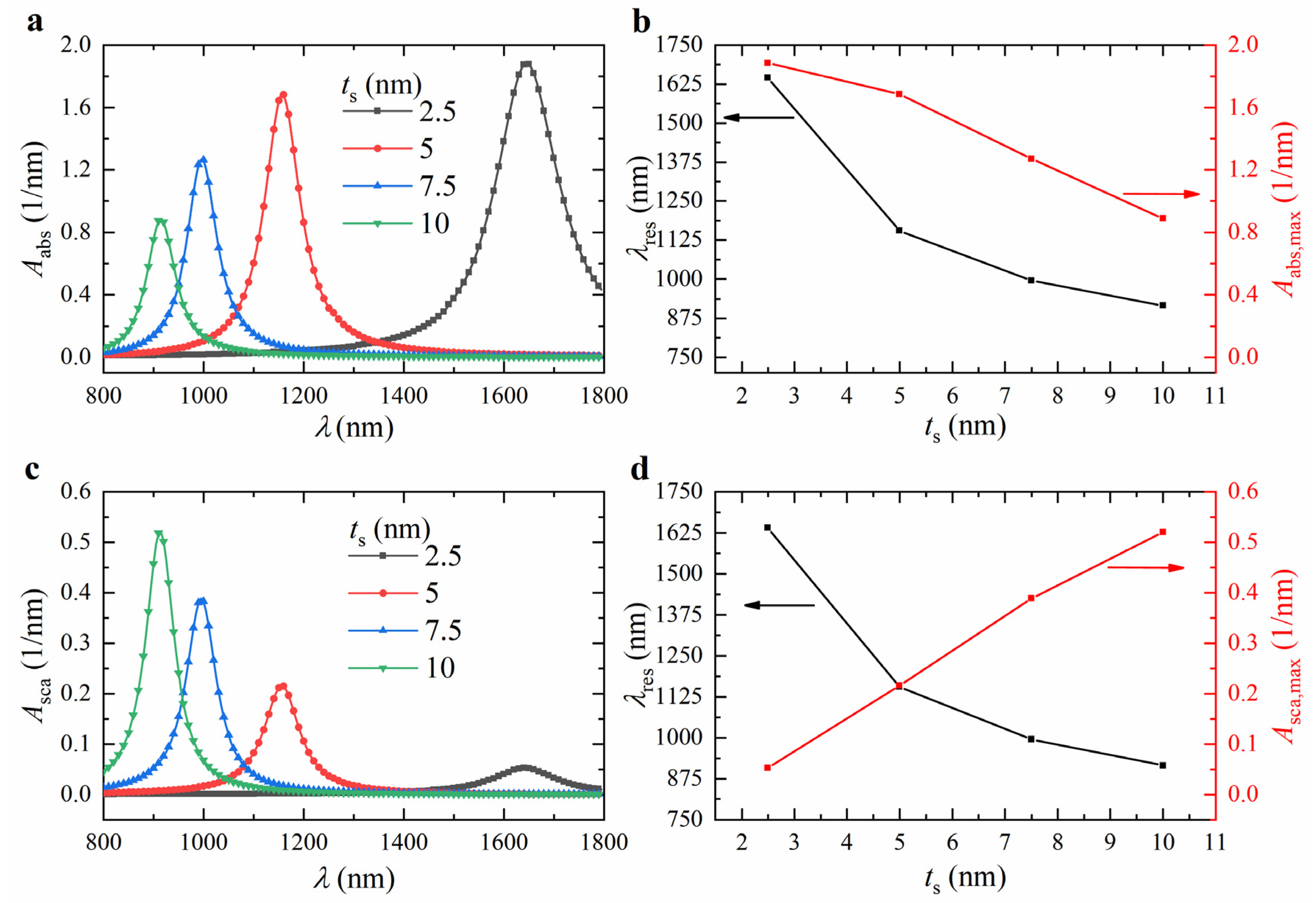
4.2. Effect of Shell Thickness
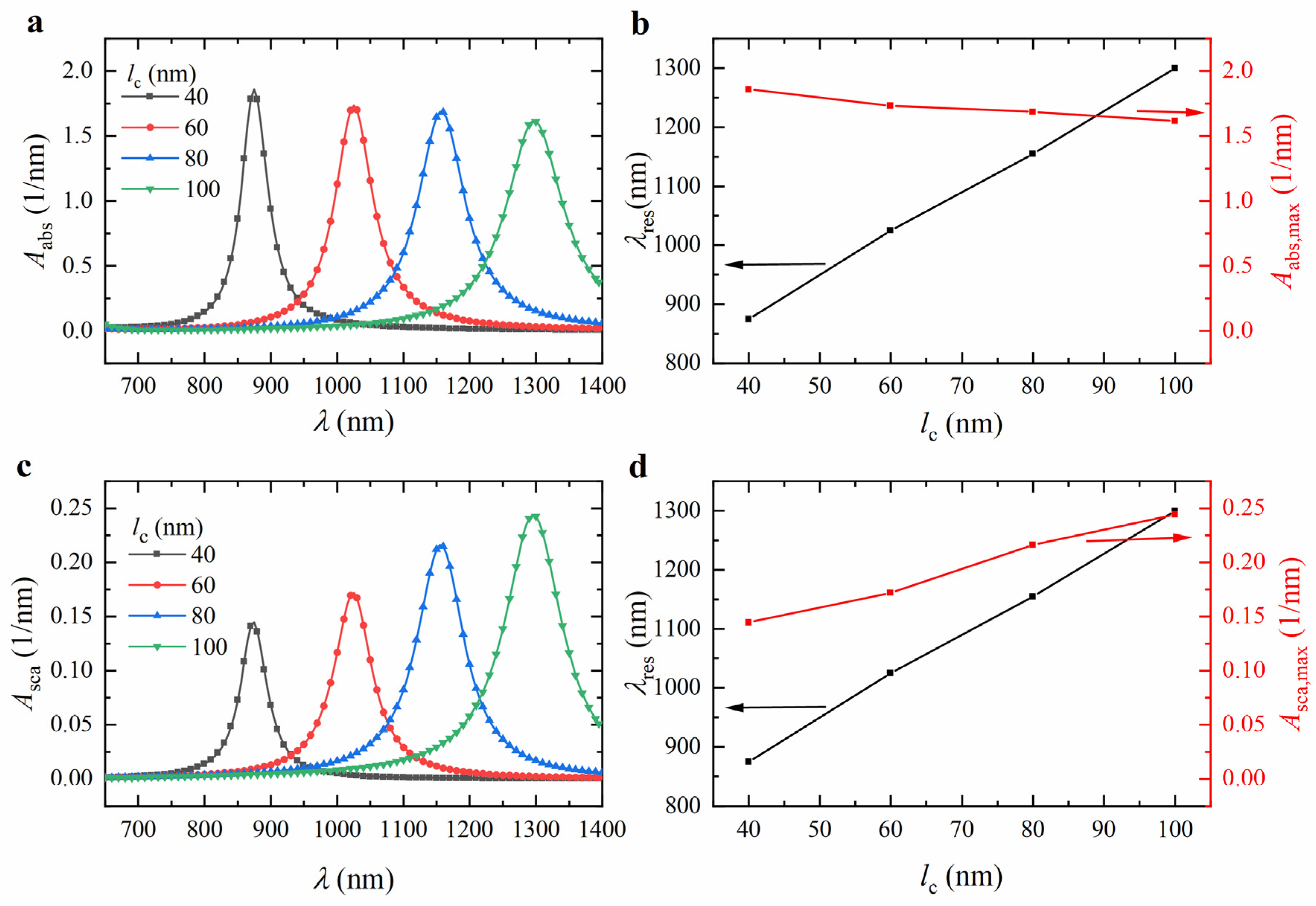
4.3. Effect of Core Length
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. A CPDDA Code Example for Setting the Simulation Object
| import numpy as np from CPDDA import materials from CPDDA import structures From CPDDA import fields from CPDDA import core from CPDDA import post_processing d = 2 r_eff = 20 wavelength = np.arange(450, 570, 5, dtype=np.float32) material1=materials.FromDatabase(shelf_name="main",book_name="Au", page_name="Johnson.yml",wl=wavelength, nb=1.33) material = [material1] geometry = structures.sphere(r_eff, d) occupied = structures.INDEX_in("spherical", geometry) struct = structures.struct(d, material, occupied, geometry) print(struct) field_generator = fields.plan_wave() K_kwargs = dict(K0=np.array([1, 0, 0])) E_kwargs = dict(E0=np.array([0, 0, 1])) efield = fields.efield(field_generator, wavelength, K_kwargs, E_kwargs) print(efield) sim = core.simulation(struct, efield) |
References
- Kumar, A.; Kim, S.; Nam, J.-M. Plasmonically Engineered Nanoprobes for Biomedical Applications. J. Am. Chem. Soc. 2016, 138, 14509–14525. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Yue, W.; Gao, P.; Gong, T.; Wang, C.; Luo, X. Surface-enhanced Raman spectroscopy (SERS) for the characterization of atmospheric aerosols: Current status and challenges. TrAC Trends Anal. Chem. 2024, 170, 117426. [Google Scholar] [CrossRef]
- Khurana, K.; Jaggi, N. Localized Surface Plasmonic Properties of Au and Ag Nanoparticles for Sensors: A Review. Plasmonics 2021, 16, 981–999. [Google Scholar] [CrossRef]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed.; Artech House: Boston, MA, USA, 2005. [Google Scholar]
- Jin, J.-M. The Finite Element Method in Electromagnetics, 3rd ed.; IEEE Press: Piscataway, NJ, USA, 2014. [Google Scholar]
- Liu, Y.J.; Mukherjee, S.; Nishimura, N.; Schanz, M.; Ye, W.; Sutradhar, A.; Pan, E.; Dumont, N.A.; Frangi, A.; Saez, A. Recent Advances and Emerging Applications of the Boundary Element Method. Appl. Mech. Rev. 2011, 64, 30802. [Google Scholar] [CrossRef]
- Doicu, A.; Mishchenko, M.I. An overview of the null-field method. I: Formulation and basic results. Phys. Open 2020, 5, 100020. [Google Scholar] [CrossRef]
- Doicu, A.; Mishchenko, M.I. An overview of the null-field method. II: Convergence and numerical stability. Phys. Open 2020, 3, 100019. [Google Scholar] [CrossRef]
- Chaumet, P.C. The Discrete Dipole Approximation: A Review. Mathematics 2022, 10, 3049. [Google Scholar] [CrossRef]
- Amirjani, A.; Sadrnezhaad, S.K. Computational electromagnetics in plasmonic nanostructures. J. Mater. Chem. C 2021, 9, 9791–9819. [Google Scholar] [CrossRef]
- Purcell, E.M.; Pennypacker, C.R. Scattering and Absorption of Light by Nonspherical Dielectric Grains. Astrophys. J. 1973, 186, 705–714. [Google Scholar] [CrossRef]
- Donald, J.M.; Golden, A.; Jennings, S.G. Opendda: A Novel High-Performance Computational Framework for the Discrete Dipole Approximation. Int. J. High Perform. Comput. Appl. 2009, 23, 42–61. [Google Scholar] [CrossRef]
- Horiuchi, I.; Aihara, K.; Suzuki, T.; Ishiwata, E. Global GPBiCGstab(L) method for solving linear matrix equations. Numer. Algorithms 2023, 93, 295–319. [Google Scholar] [CrossRef]
- Draine, B.T.; Flatau, P.J. Discrete-Dipole Approximation For Scattering Calculations. J. Opt. Soc. Am. A 1994, 11, 1491–1499. [Google Scholar] [CrossRef]
- Yurkin, M.A.; Hoekstra, A.G. The discrete-dipole-approximation code ADDA: Capabilities and known limitations. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 2234–2247. [Google Scholar] [CrossRef]
- Loke, V.L.Y.; Pinar Mengüç, M.; Nieminen, T.A. Discrete-dipole approximation with surface interaction: Computational toolbox for MATLAB. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 1711–1725. [Google Scholar] [CrossRef]
- Shabaninezhad, M.; Awan, M.G.; Ramakrishna, G. MATLAB package for discrete dipole approximation by graphics processing unit: Fast Fourier Transform and Biconjugate Gradient. J. Quant. Spectrosc. Radiat. Transf. 2021, 262, 107501. [Google Scholar] [CrossRef]
- Chaumet, P.C.; Sentenac, D.; Maire, G.; Rasedujjaman, M.; Zhang, T.; Sentenac, A. IFDDA, an easy-to-use code for simulating the field scattered by 3D inhomogeneous objects in a stratified medium: Tutorial. J. Opt. Soc. Am. A 2021, 38, 1841–1852. [Google Scholar] [CrossRef]
- Chaumet, P.C. A comparative study of efficient iterative solvers for the discrete dipole approximation. J. Quant. Spectrosc. Radiat. Transf. 2023, 312, 108816. [Google Scholar] [CrossRef]
- Van Der Walt, S.; Colbert, S.C.; Varoquaux, G. The NumPy Array: A Structure for Efficient Numerical Computation. Comput. Sci. Eng. 2011, 13, 22–30. [Google Scholar] [CrossRef]
- Wiecha, P.R. pyGDM—A python toolkit for full-field electro-dynamical simulations and evolutionary optimization of nanostructures. Comput. Phys. Commun. 2018, 233, 167–192. [Google Scholar] [CrossRef]
- Wiecha, P.R.; Majorel, C.; Arbouet, A.; Patoux, A.; Brûlé, Y.; Francs, G.C.D.; Girard, C. “pyGDM”—New functionalities and major improvements to the python toolkit for nano-optics full-field simulations. Comput. Phys. Commun. 2022, 270, 108142. [Google Scholar] [CrossRef]
- Egel, A.; Czajkowski, K.M.; Theobald, D.; Ladutenko, K.; Kuznetsov, A.S.; Pattelli, L. SMUTHI: A python package for the simulation of light scattering by multiple particles near or between planar interfaces. J. Quant. Spectrosc. Radiat. Transf. 2021, 273, 107846. [Google Scholar] [CrossRef]
- Zubko, E.; Kochergin, A.; Videen, G. Convergence of the DDA for ensembles of objects of irregular shape. J. Quant. Spectrosc. Radiat. Transf. 2024, 314, 108854. [Google Scholar] [CrossRef]
- Zhu, Z.; Wakin, M.B. On the Asymptotic Equivalence of Circulant and Toeplitz Matrices. IEEE Trans. Inf. Theory 2017, 63, 2975–2992. [Google Scholar] [CrossRef]
- Behnel, S.; Bradshaw, R.; Citro, C.; Dalcin, L.; Sverre Seljebotn, D.; Smith, K. Cython: The best of both worlds. Comput. Sci. Eng. 2011, 13, 31–39. [Google Scholar] [CrossRef]
- Smith, K.W. Cython: A Guide for Python Programmers, 1st ed.; O’Reilly Media: Tokyo, Japan, 2015. [Google Scholar]
- Ma, D.; Tuersun, P.; Cheng, L.; Zheng, Y.; Abulaiti, R. PyMieLab_V1.0: A software for calculating the light scattering and absorption of spherical particles. Heliyon 2022, 8, e11469. [Google Scholar] [CrossRef]
- Zhou, M.; Diao, K.; Zhang, J.; Wu, W. Controllable synthesis of plasmonic ZnO/Au core/shell nanocable arrays on ITO glass. Phys. E Low-Dimens. Syst. Nanostructures 2014, 56, 59–63. [Google Scholar] [CrossRef]
- Zamiri, R.; Zakaria, A.; Jorfi, R.; Zamiri, G.; Mojdehi, M.S.; Ahangar, H.A.; Zak, A.K. Laser assisted fabrication of ZnO/Ag and ZnO/Au core/shell nanocomposites. Appl. Phys. A 2013, 111, 487–493. [Google Scholar] [CrossRef]
- Senthilkumar, N.; Ganapathy, M.; Arulraj, A.; Meena, M.; Vimalan, M.; Potheher, I.V. Two step synthesis of ZnO/Ag and ZnO/Au core/shell nanocomposites: Structural, optical and electrical property analysis. J. Alloys Compd. 2018, 750, 171–181. [Google Scholar] [CrossRef]
- Beatto, T.G.; Gomes, W.E.; Etchegaray, A.; Gupta, R.; Mendes, R.K. Dopamine levels determined in synthetic urine using an electrochemical tyrosinase biosensor based on ZnO@Au core–shell. RSC Adv. 2023, 13, 33424–33429. [Google Scholar] [CrossRef]
- Srivastava, V.; Gusain, D.; Sharma, Y.C. Synthesis, characterization and application of zinc oxide nanoparticles (n-ZnO). Ceram. Int. 2013, 39, 9803–9808. [Google Scholar] [CrossRef]
- Mendes, R.; Arruda, B.; de Souza, E.; Nogueira, A.; Teschke, O.; Bonugli, L.; Etchegaray, A. Determination of Chlorophenol in Environmental Samples Using a Voltammetric Biosensor Based on Hybrid Nanocomposite. J. Braz. Chem. Soc. 2016, 28, 1212–1219. [Google Scholar] [CrossRef]
- Ponnuvelu, D.V.; Pullithadathil, B.; Prasad, A.K.; Dhara, S.; Ashok, A.; Mohamed, K.; Tyagi, A.K.; Raj, B. Rapid synthesis and characterization of hybrid ZnO@Au core–shell nanorods for high performance, low temperature NO2 gas sensor applications. Appl. Surf. Sci. 2015, 355, 726–735. [Google Scholar] [CrossRef]
- Tran, V.T.; Tran, T.H.; Le, M.P.; Pham, N.H.; Nguyen, V.T.; Do, D.B.; Nguyen, X.T.; Trinh, B.N.Q.; Van Nguyen, T.T.; Pham, V.T.; et al. Highly efficient photo-induced surface enhanced Raman spectroscopy from ZnO/Au nanorods. Opt. Mater. 2022, 134, 113069. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Querry, M.R. Optical Constants. 1985. Available online: https://apps.dtic.mil/sti/citations/ADA158623 (accessed on 21 March 2025).
- Duck, F.A. Physical Properties of Tissue: A Comprehensive Reference Book; Academic Press: London, UK, 1990. [Google Scholar]
- Lee, K.-S.; El-Sayed, M.A. Dependence of the Enhanced Optical Scattering Efficiency Relative to That of Absorption for Gold Metal Nanorods on Aspect Ratio, Size, End-Cap Shape, and Medium Refractive Index. J. Phys. Chem. B 2005, 109, 20331–20338. [Google Scholar] [CrossRef]
- A Garcia, M. Surface plasmons in metallic nanoparticles: Fundamentals and applications. J. Phys. D Appl. Phys. 2012, 45, 389501. [Google Scholar] [CrossRef]

| Material Classification | Description |
|---|---|
| MAIN | simple inorganic materials |
| GLASS | glasses |
| ORGANIC | organic materials |
| OTHER | miscellaneous materials |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, D.; Tuersun, P.; Li, S.; Wang, M.; Jiang, L. CPDDA: A Python Package for Discrete Dipole Approximation Accelerated by CuPy. Nanomaterials 2025, 15, 500. https://doi.org/10.3390/nano15070500
Xu D, Tuersun P, Li S, Wang M, Jiang L. CPDDA: A Python Package for Discrete Dipole Approximation Accelerated by CuPy. Nanomaterials. 2025; 15(7):500. https://doi.org/10.3390/nano15070500
Chicago/Turabian StyleXu, Dibo, Paerhatijiang Tuersun, Shuyuan Li, Meng Wang, and Lan Jiang. 2025. "CPDDA: A Python Package for Discrete Dipole Approximation Accelerated by CuPy" Nanomaterials 15, no. 7: 500. https://doi.org/10.3390/nano15070500
APA StyleXu, D., Tuersun, P., Li, S., Wang, M., & Jiang, L. (2025). CPDDA: A Python Package for Discrete Dipole Approximation Accelerated by CuPy. Nanomaterials, 15(7), 500. https://doi.org/10.3390/nano15070500





