Atomic-Scale Interfacial Dynamics and Twin Formation in Cu/Al2Cu/Al Layered Composites During Cooling: Insights from Molecular Dynamics Simulations
Abstract
1. Introduction
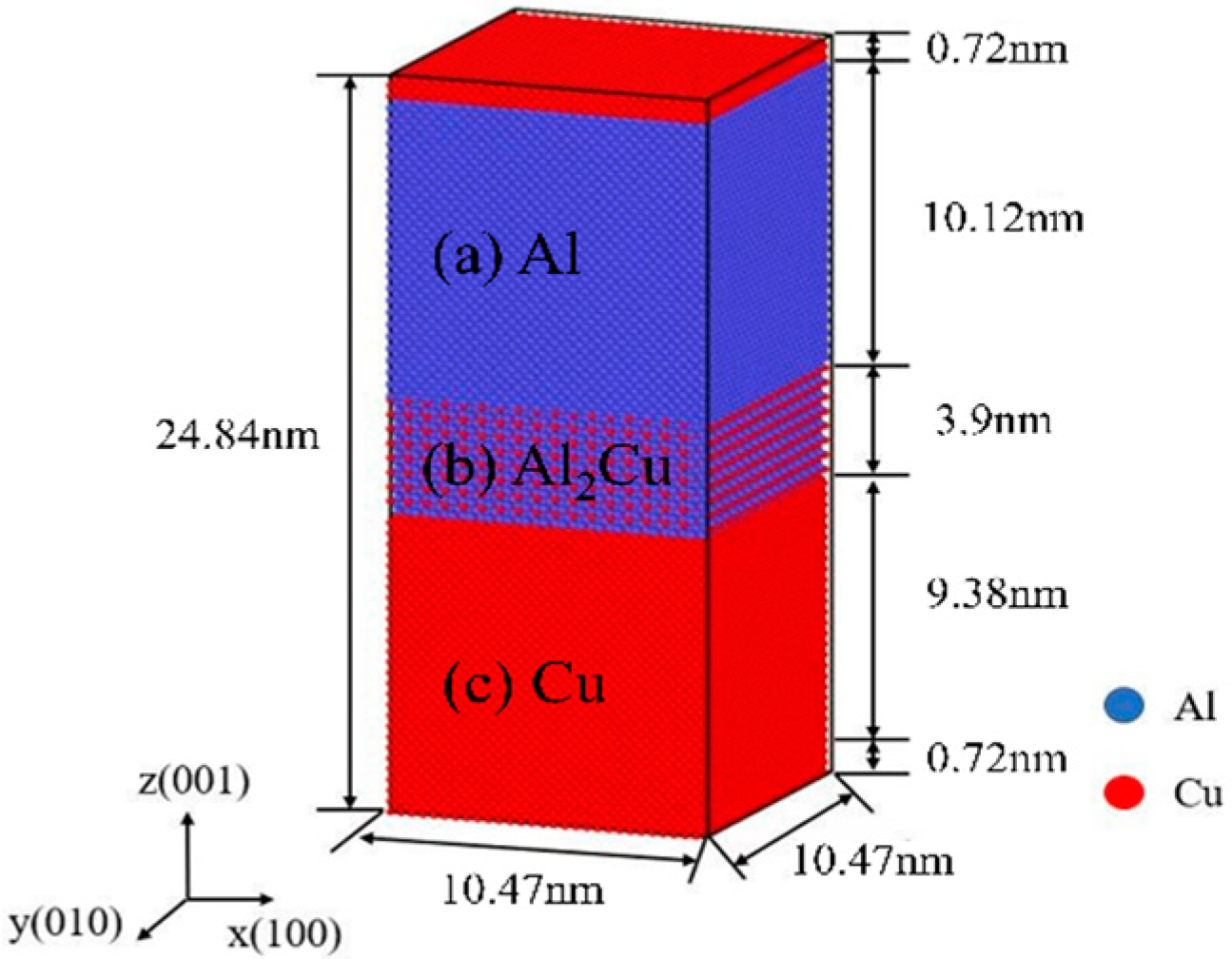
2. Models and Methods
3. Results and Discussion
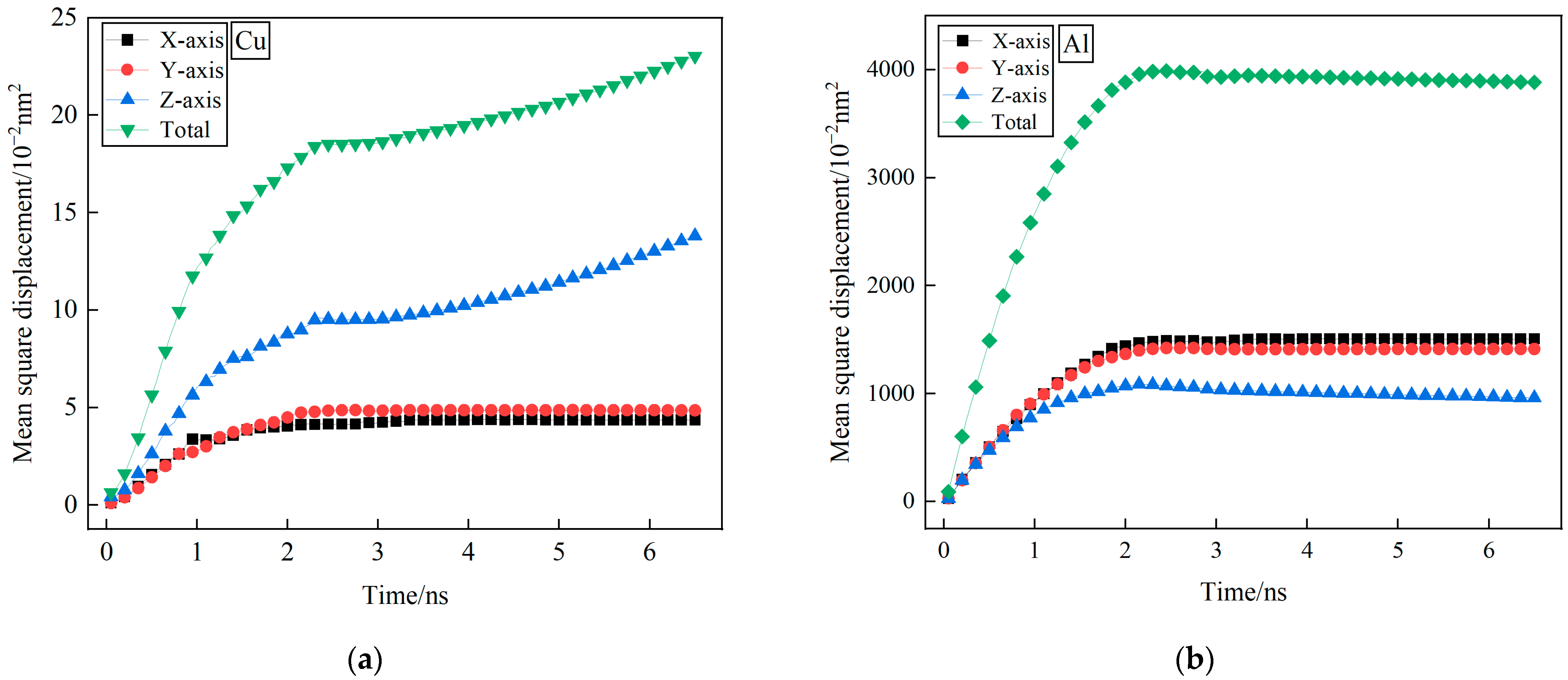
3.1. Mean Square Displacement Analysis
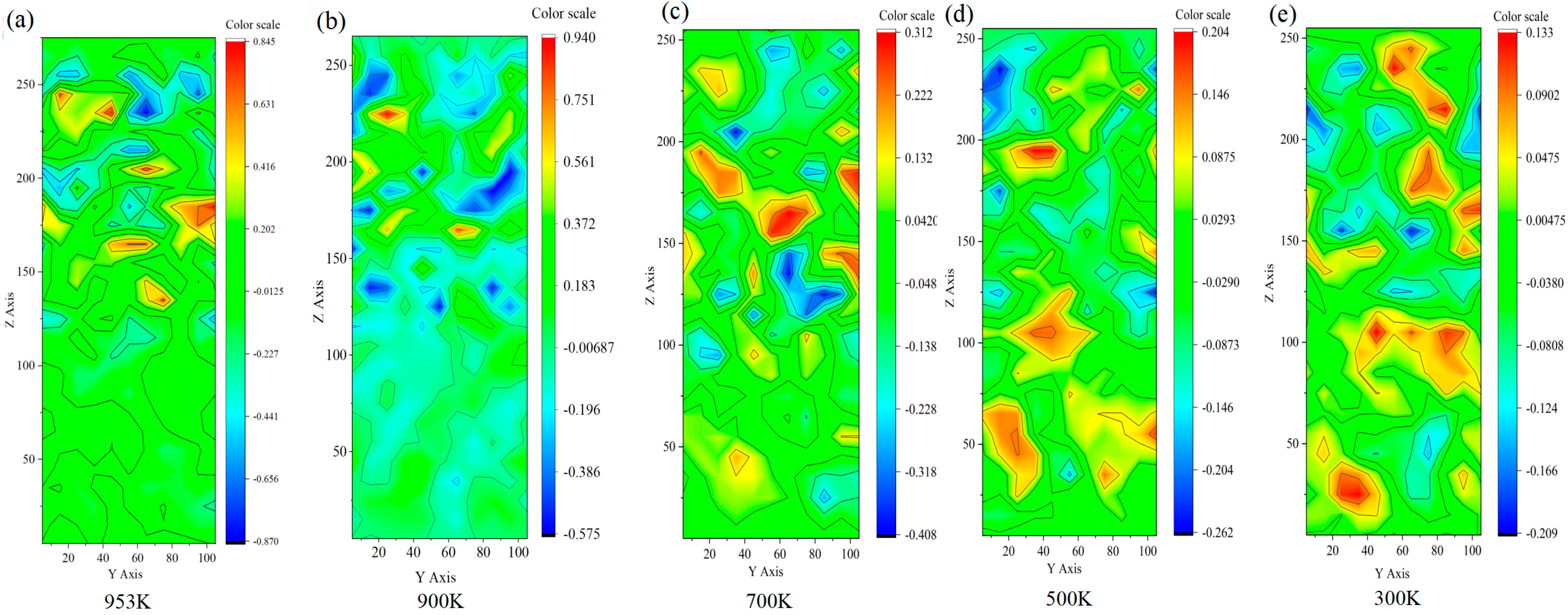
3.2. Velocity Contour Analysis
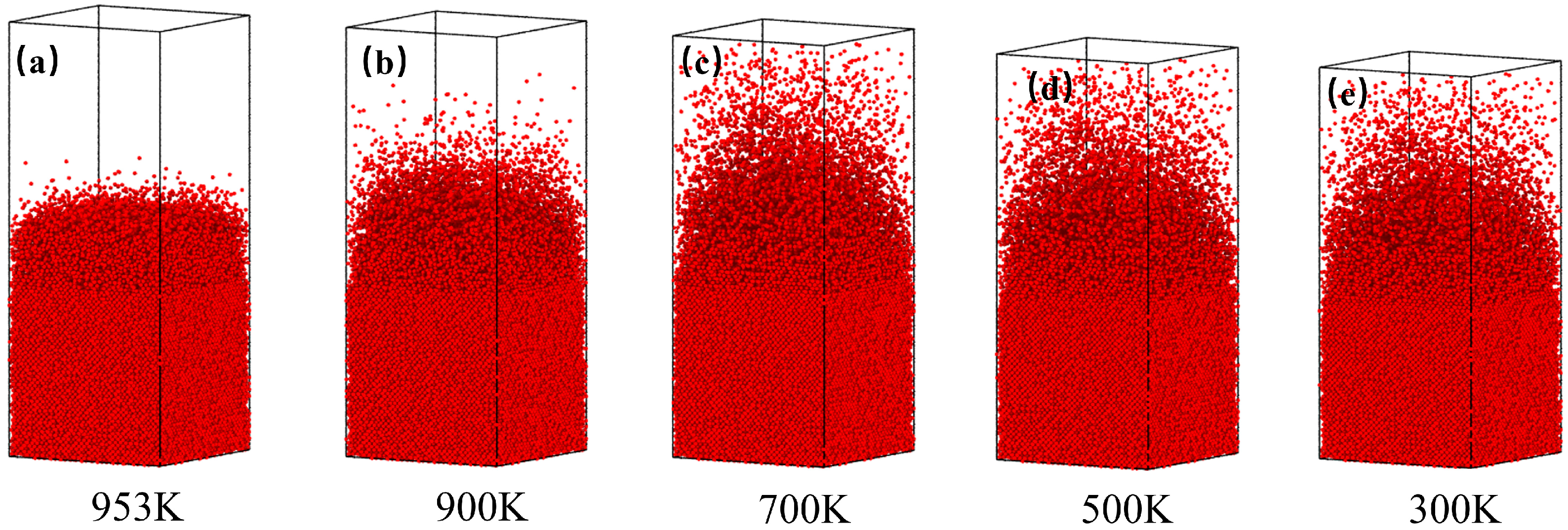
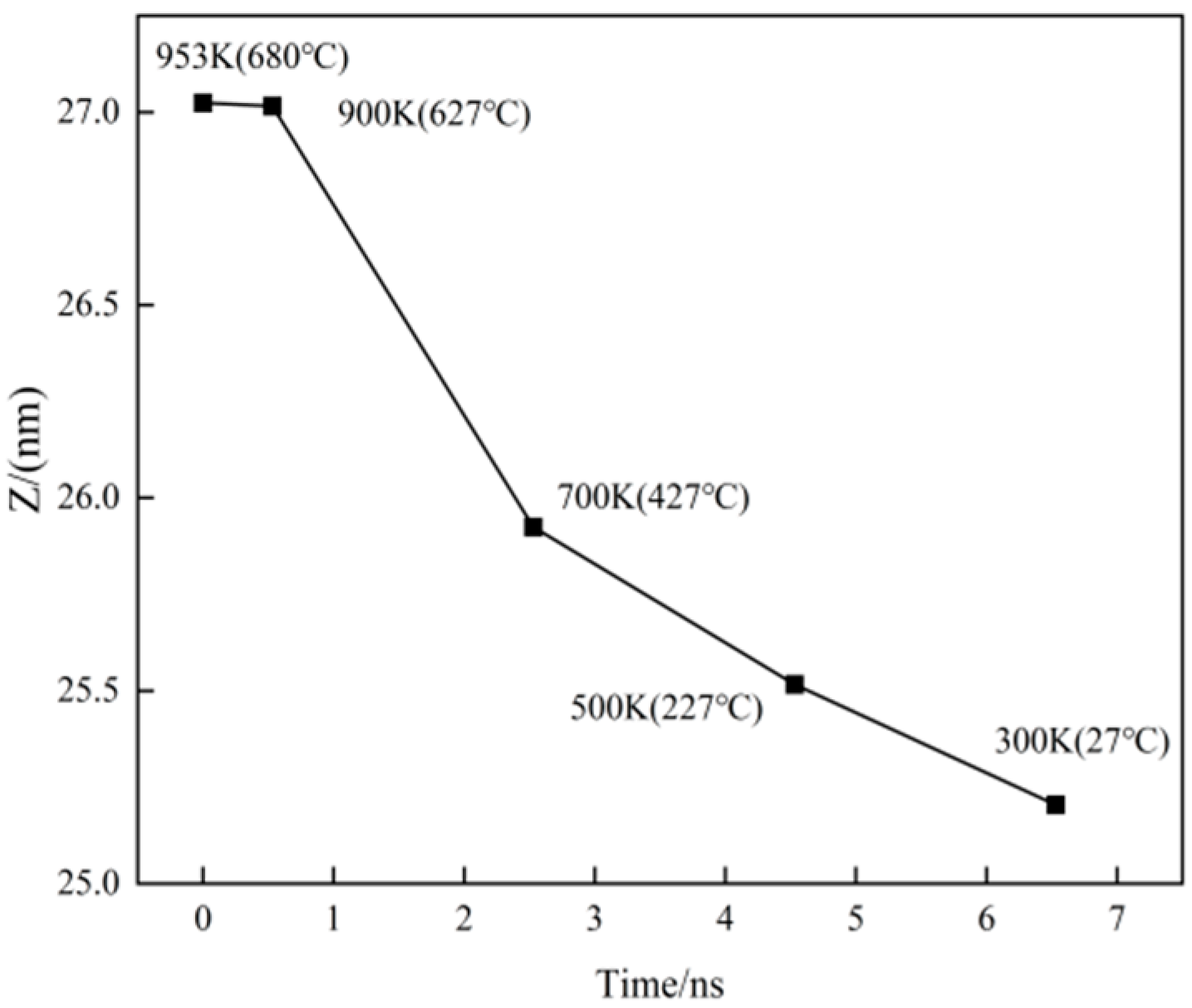
3.3. Distribution of Cu Atoms and Change in Model Volume During Cooling
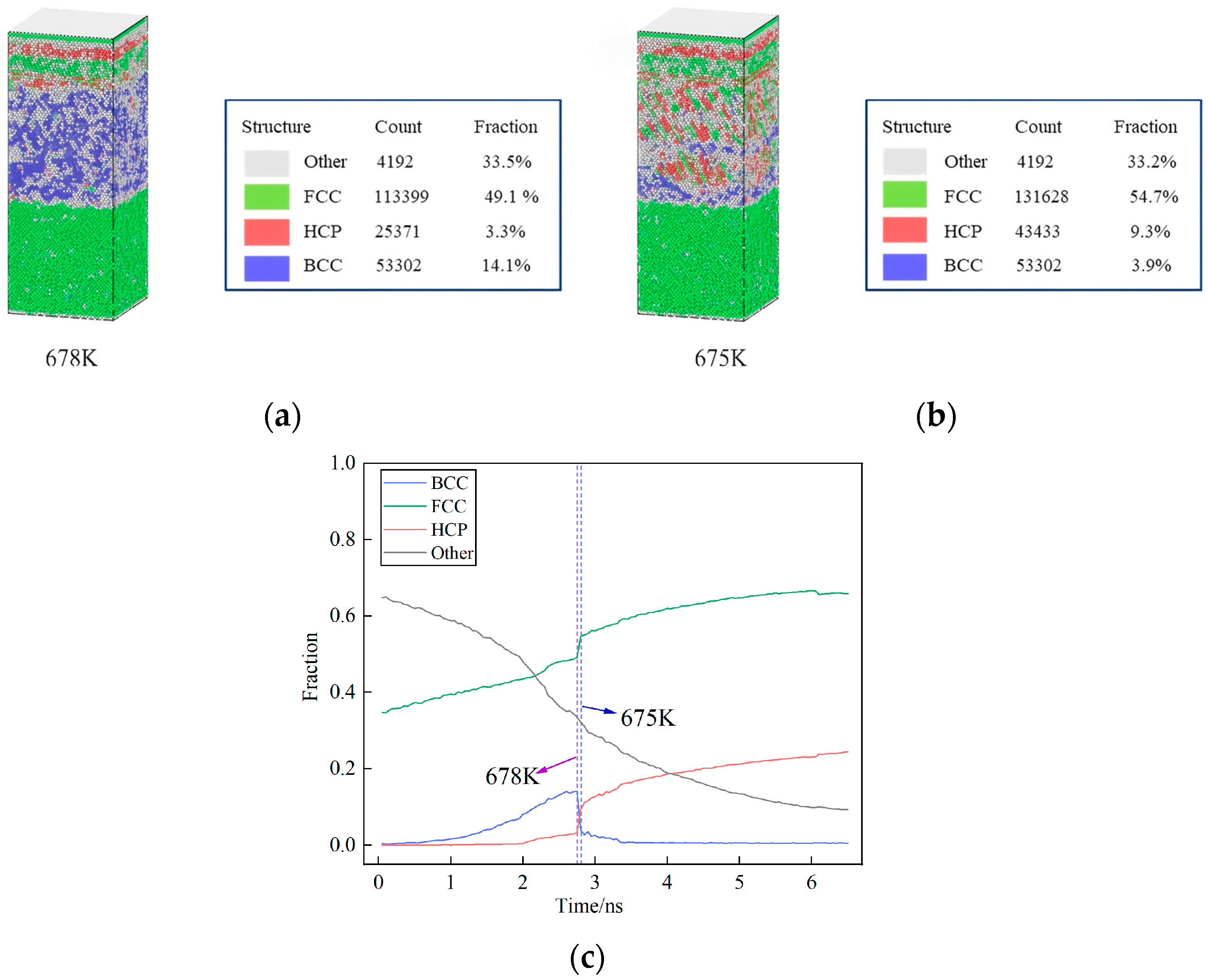
3.4. The Key Temperature of Crystal Transformation During Cooling
3.5. The Formation and Evolution of Dislocation Lines
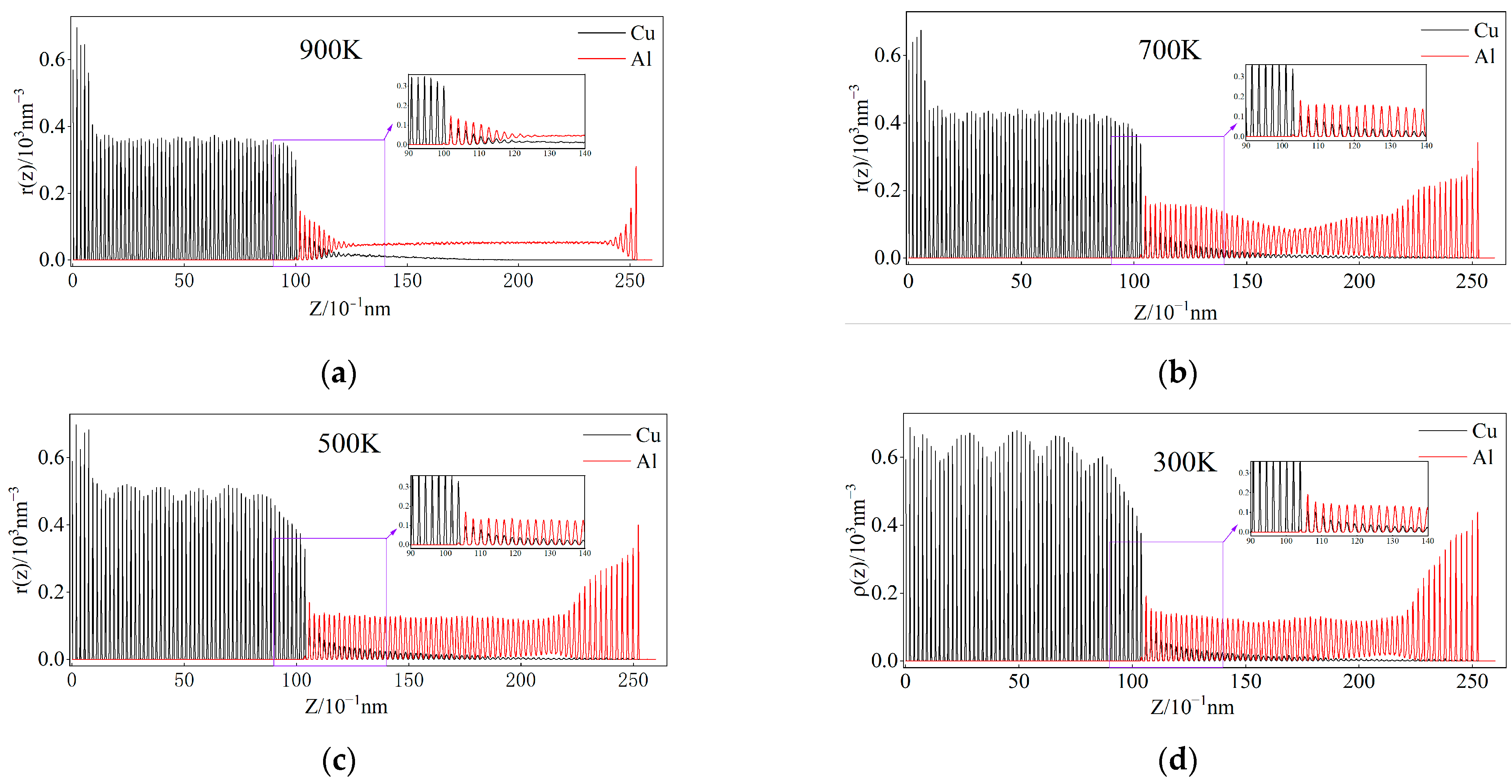
3.6. Atomic Number Density Analysis of Cu and Al During Cooling
4. Conclusion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Song, H.; Hao, W.; Mu, X.; Han, T.; Che, C.; Geng, G. Effect of Pulse Current-Assisted Rolling on the Interface Bonding Strength and Microstructure of Cu/Al Laminated Composite. Metals 2020, 10, 1555. [Google Scholar] [CrossRef]
- Yang, Y.-Y.; Chen, H.-S.; Zhou, J.; Nie, H.-H.; Xu, X.; Xi, S.-X.; Chang, Y.-L. Study on interface behavior and mechanical properties of Al/Cu laminated tubes fabricated by strong staggered spinning at room temperature. J. Mater. Res. Technol. 2023, 25, 7307–7324. [Google Scholar] [CrossRef]
- Fu, X.; Wang, R.; Zhu, Q.; Wang, P.; Zuo, Y. Effect of Annealing on the Interface and Mechanical Properties of Cu-Al-Cu Laminated Composite Prepared with Cold Rolling. Materials 2020, 13, 369. [Google Scholar] [CrossRef]
- Zhu, R.; Guo, S.; Huang, C.; Lei, Z.; Zhang, X.; Liu, J. Effects of Different Types of Interlayers on the Interfacial Reaction Mechanism at the Cu Side of Al/Cu Lap Joints Obtained by Laser Welding/Brazing. Materials 2021, 14, 7797. [Google Scholar] [CrossRef]
- Chang, Y.; Chen, H.; Zhou, J.; Liu, R.; Nie, H.; Wang, W. Comprehensive study of hot deformation behavior and fracture mechanism of Al/Cu laminated composite. J. Manuf. Process. 2023, 97, 48–61. [Google Scholar] [CrossRef]
- Wang, W.-J.; Wang, H.; Liu, X.-F.; Liu, Z.-C. Interface evolution and strengthening of two-step roll bonded copper/aluminum clad composites. Mater. Charact. 2023, 199, 112778. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, F.; Wang, R.; Liu, X. Preparation and properties of copper-aluminum composite strips and foils by horizontal continuous composite casting and rolling. J. Mech. Work. Technol. 2023, 322, 118168. [Google Scholar] [CrossRef]
- Liu, G.; Wang, Q.; Jiang, H. New Research Progress on Copper/Aluminum Bimetallic Composites. Cailiao Daobao 2020, 34, 7115–7122. [Google Scholar] [CrossRef]
- Wang, C.; Ma, L.-N.; Ma, X.-G.; Wang, T.; Jiang, Z.-Y.; Hasan, M.; Zhao, J.-W. Effect of annealing temperature on microstructure and tensile properties of copper/aluminum composite thin strip. Trans. Nonferrous Met. Soc. China 2023, 33, 701–713. [Google Scholar] [CrossRef]
- Chen, Y.; Xie, J.; Wang, A.; Mao, Z.; Gao, P.; Chang, Q. In-Situ Observation and Analysis of the Evolution of Copper Aluminum Composite Interface. Metals 2023, 13, 1558. [Google Scholar] [CrossRef]
- Liu, G.; Wang, Q.; Zhang, L.; Ye, B.; Jiang, H.; Ding, W. Effect of Cooling Rate on the Microstructure and Mechanical Properties of Cu/Al Bimetal Fabricated by Compound Casting. Met. Mater. Trans. A 2017, 49, 661–672. [Google Scholar] [CrossRef]
- Liu, G.; Wang, Q.; Zhang, L.; Ye, B.; Jiang, H.; Ding, W. Effects of Melt-to-Solid Volume Ratio and Pouring Temperature on Microstructures and Mechanical Properties of Cu/Al Bimetals in Compound Casting Process. Met. Mater. Trans. A 2018, 50, 401–414. [Google Scholar] [CrossRef]
- Mao, Z.; Xie, J.; Wang, A.; Wang, W.; Li, Y.; Ma, D. Interfacial microstructure and bonding strength of copper/aluminum clad sheets produced by horizontal twin-roll casting and annealing. Mater. Res. Express 2018, 6, 016505. [Google Scholar] [CrossRef]
- Wang, C.; Ma, X.; Ma, L.; Jiang, Z.; Hasan, M.; Islam, A.; Kasi, A.K.; Zhao, J. A study on the microstructural evolution of copper/aluminum composite strips fabricated by micro flexible rolling. Mater. Charact. 2023, 205, 113315. [Google Scholar] [CrossRef]
- Liu, X.; Fu, H.; He, X.; Fu, X.; Jiang, Y.; Xie, J. Numerical Simulation Analysis of Continuous Casting Cladding Forming for Cu-Al Composites. Acta Metall. Sin. 2018, 54, 470–484. [Google Scholar]
- Liu, H.; Ke, F.; Pan, H.; Zhou, M. Molecular dynamics simulation of the diffusion bonding and tensile behavior of a Cu-Al interface. Acta Phys. Sin. 2007, 56, 407–412. [Google Scholar] [CrossRef]
- Sahoo, S. Simulation study on rapid solidification of eutectic Al-Cu alloy: a molecular dynamics approach. Int. J. Comput. Mater. Sci. Surf. Eng. 2017, 7, 18. [Google Scholar] [CrossRef]
- Zhou, B.; Yang, L. Molecular dynamics simulation of effect of cooling rate on the microstructures and deformation behaviors in metallic glasses. Acta Phys. Sin. 2020, 69, 116101. [Google Scholar] [CrossRef]
- Li, J.; Chu, F.; Feng, Y. Effect of atomic diffusion on interfacial heat transfer and tensile property of copper/aluminum composites. Mater. Today Commun. 2023, 36, 106757. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, A.; Xie, J.; Guo, Y. Deformation mechanisms in Al/Al2Cu/Cu multilayer under compressive loading. J. Alloy. Compd. 2021, 885, 160921. [Google Scholar] [CrossRef]
- Celik, F.A. Pressure and cooling rate effect on polyhedron clusters in Cu–Al alloy by using molecular dynamics simulation. Phys. B Condens. Matter 2014, 450, 71–76. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Daw, M.S.; Baskes, M.I. Semiempirical, quantum mechanical calculation of hydrogen embrittlement in metals. Phys. Rev. Lett. 1983, 50, 1285. [Google Scholar] [CrossRef]
- Cai, J.; Ye, Y.Y. Simple analytical embedded-atom-potential model including a long-range force for fcc metals and their alloys. Phys. Rev. B 1996, 54, 8398. [Google Scholar] [CrossRef]
- Filipe, H.A.L.; Loura, L.M.S. Molecular Dynamics Simulations: Advances and Applications. Molecules 2022, 27, 2105. [Google Scholar] [CrossRef]
- Mao, A.; Zhang, J.; Yao, S.; Wang, A.; Wang, W.; Li, Y.; Qiao, C.; Xie, J.; Jia, Y. The diffusion behaviors at the Cu-Al solid-liquid interface: A molecular dynamics study. Results Phys. 2020, 16, 102998. [Google Scholar] [CrossRef]
- Fukuda, I. Coupled Nosé–Hoover lattice: A set of the Nosé–Hoover equations with different temperatures. Phys. Lett. A 2016, 380, 2465–2474. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, J.; Tang, S.; Wang, Z.; Wang, J. Atomistic Mechanism Underlying Nucleation in Al–Cu Alloys with Different Compositions and Cooling Rates. J. Phys. Chem. C 2021, 125, 3480–3494. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, X.; Ma, F.; Dong, S.; Yang, W.; Wu, M. Molecular dynamics simulation of the crystal structure evolution of titanium under different Tdamp values and heating/cooling rates. Chem. Phys. Lett. 2020, 763, 138187. [Google Scholar] [CrossRef]
- Chen, X.; Fan, W.; Jiang, W.; Lin, D.; Wang, Z.; Hui, X.; Wang, Y. Effects of Cooling Rate on the Solidification Process of Pure Metal Al: Molecular Dynamics Simulations Based on the MFPT Method. Metals 2022, 12, 1504. [Google Scholar] [CrossRef]
- Samanta, A.; Tuckerman, M.E.; Yu, T.-Q.; E, W. Microscopic mechanisms of equilibrium melting of a solid. Science 2014, 346, 729–732. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Zhang, F.; Yang, L.; Ye, Z.; Song, H.; Mendelev, M.I.; Wang, C.-Z.; Ho, K.-M. Effect of samarium doping on the nucleation of fcc-aluminum in undercooled liquids. Scr. Mater. 2018, 154, 202–206. [Google Scholar] [CrossRef]
- Pintore, M.; Starykov, O.; Mittler, T.; Volk, W.; Tonn, B. Experimental Investigations on the Influence of the Thermal Conditions During Composite Casting on the Microstructure of Cu-Al Bilayer Compounds. Int. J. Met. 2017, 12, 79–88. [Google Scholar] [CrossRef]
- Li, C.; Li, D.; Tao, X.; Chen, H.; Ouyang, Y. Molecular dynamics simulation of diffusion bonding of Al–Cu interface. Model. Simul. Mater. Sci. Eng. 2014, 22, 065013. [Google Scholar] [CrossRef]
- Xiong, J.; Peng, Y.; Zhang, H.; Li, J.; Zhang, F. Microstructure and mechanical properties of Al–Cu joints diffusion-bonded with Ni or Ag interlayer. Vacuum 2018, 147, 187–193. [Google Scholar] [CrossRef]
- Chen, S.Y.; Wu, Z.W.; Liu, K.X.; Li, X.J.; Luo, N.; Lu, G.X. Atomic diffusion behavior in Cu-Al explosive welding process. J. Appl. Phys. 2013, 113, 044901. [Google Scholar] [CrossRef]
- Wang, J.; Shin, S.; Nobakht, A.Y.; Shyam, A. Structural deformation and transformation of θ′-Al2Cu precipitate in Al matrix via interfacial diffusion. Comput. Mater. Sci. 2018, 156, 111–120. [Google Scholar] [CrossRef]
- Wang, A.; Bian, X.; Mao, Z.; Hou, Y.; Xie, J.; Liu, P.; Liu, Z. Effect of solid solution and vacancies on the mechanical properties of Cu(Al)/Al2Cu/(Cu)Al layered gradient heterostructures. Phys. B Condens. Matter 2024, 680, 415845. [Google Scholar] [CrossRef]
- Honeycutt, J.D.; Andersen, H.C. Molecular dynamics study of melting and freezing of small Lennard-Jones clusters. J. Phys. Chem. 1987, 91, 4950–4963. [Google Scholar] [CrossRef]
- Stukowski, A. Structure identification methods for atomistic simulations of crystalline materials. Model. Simul. Mater. Sci. Eng. 2012, 20, 045021. [Google Scholar] [CrossRef]
- Bian, X.; Wang, A.; Xie, J.; Liu, P.; Mao, Z.; Liu, Z. Effect of Al2Cu constituent layer thickness discrepancy on the tensile mechanical behavior of Cu/Al2Cu/Al layered composites: a molecular dynamics simulation. Nanotechnology 2023, 34, 445702. [Google Scholar] [CrossRef] [PubMed]
- Meguro, K.; O, M.; Kajihara, M. Growth behavior of compounds due to solid-state reactive diffusion between Cu and Al. J. Mater. Sci. 2012, 47, 4955–4964. [Google Scholar] [CrossRef]
- Lin, H.; Li, T.; Li, H. Molecular dynamics study on the heterogeneous nucleation of liquid Al–Cu alloys on different kinds of copper substrates. Phys. Chem. Chem. Phys. 2018, 20, 29856–29865. [Google Scholar] [CrossRef] [PubMed]



| Diffusion Coefficient of Cu (m2 s−1) | Diffusion Coefficient of Al (m2 s−1) | |||||
|---|---|---|---|---|---|---|
| Diffusion Coefficients | This Work (900 K) | R2 Value | Others’ Data | This Work (900 K) | R2 Value | Others’ Data |
| D | 3.16 × 10−9 | 0.996 | 4.83 × 10−10 (893 K) [34] 4.08 × 10−10 (813 K) [35] 1.32 × 10−10 (733 K) [36] | 6.81 × 10−9 | 0.997 | 6.24 × 10−9 (893 K) [34] 2.39 × 10−9 (813 K) [26] 8.18 × 10−15 (733 K) [35] |
| DX | 8.52 × 10−10 | 0.995 | -- | 2.35 × 10−9 | 0.995 | -- |
| DY | 7.56 × 10−10 | 0.995 | -- | 2.43 × 10−9 | 0.995 | -- |
| DZ | 1.55 × 10−9 | 0.997 | -- | 2.03 × 10−9 | 0.996 | -- |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Cui, Y.; Wang, W.; Xie, J.; Wang, A.; Zhang, F.; Mao, Z. Atomic-Scale Interfacial Dynamics and Twin Formation in Cu/Al2Cu/Al Layered Composites During Cooling: Insights from Molecular Dynamics Simulations. Nanomaterials 2025, 15, 437. https://doi.org/10.3390/nano15060437
Li S, Cui Y, Wang W, Xie J, Wang A, Zhang F, Mao Z. Atomic-Scale Interfacial Dynamics and Twin Formation in Cu/Al2Cu/Al Layered Composites During Cooling: Insights from Molecular Dynamics Simulations. Nanomaterials. 2025; 15(6):437. https://doi.org/10.3390/nano15060437
Chicago/Turabian StyleLi, Shuang, Yunfeng Cui, Wenyan Wang, Jingpei Xie, Aiqin Wang, Feiyang Zhang, and Zhiping Mao. 2025. "Atomic-Scale Interfacial Dynamics and Twin Formation in Cu/Al2Cu/Al Layered Composites During Cooling: Insights from Molecular Dynamics Simulations" Nanomaterials 15, no. 6: 437. https://doi.org/10.3390/nano15060437
APA StyleLi, S., Cui, Y., Wang, W., Xie, J., Wang, A., Zhang, F., & Mao, Z. (2025). Atomic-Scale Interfacial Dynamics and Twin Formation in Cu/Al2Cu/Al Layered Composites During Cooling: Insights from Molecular Dynamics Simulations. Nanomaterials, 15(6), 437. https://doi.org/10.3390/nano15060437






