A General Solution to the Continuum Rate Equation for Island-Size Distributions: Epitaxial Growth Kinetics and Scaling Analysis
Abstract
1. Introduction
2. General Considerations
3. General Solution for ISD in the Continuum Limit
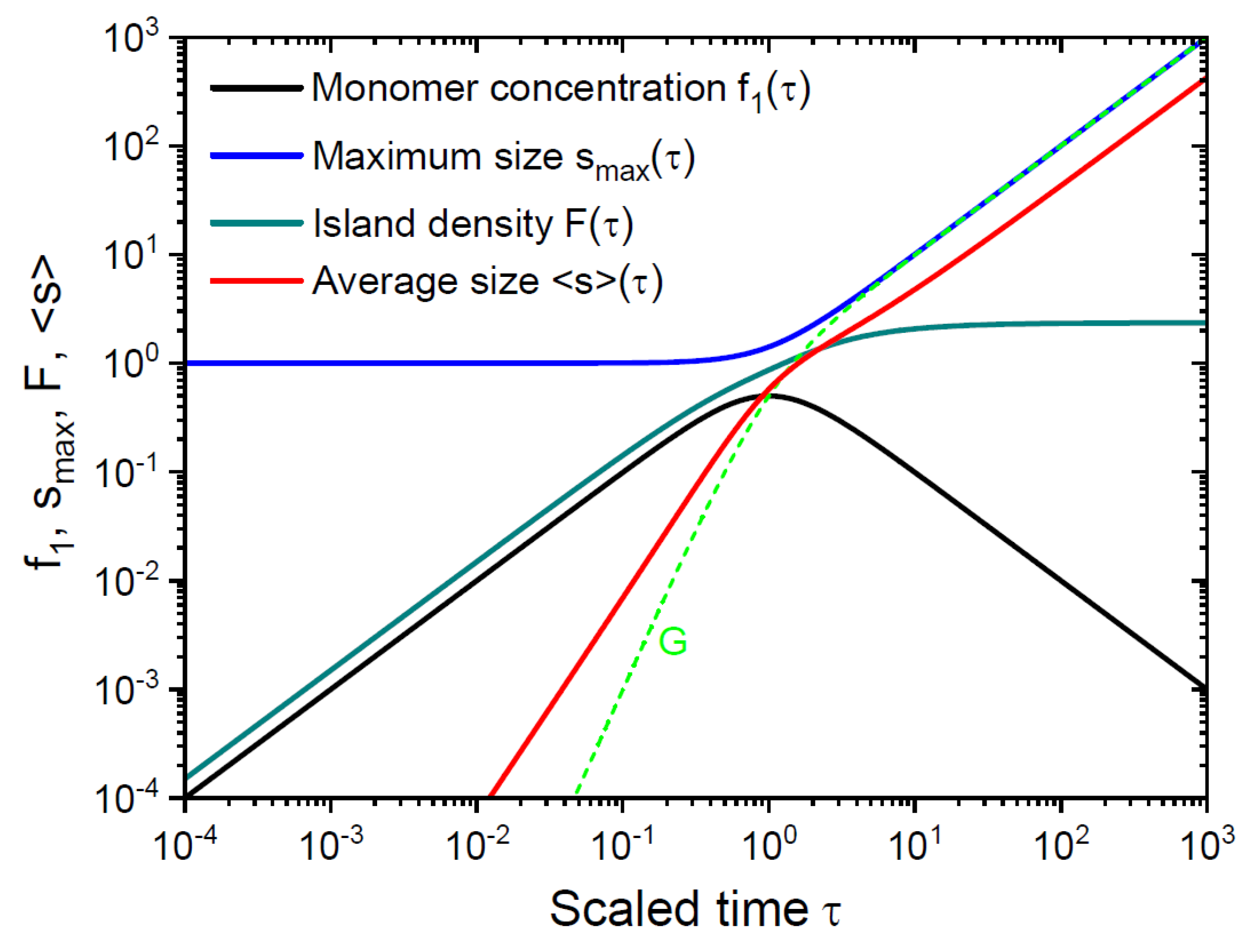
4. Family–Viscek Scaling
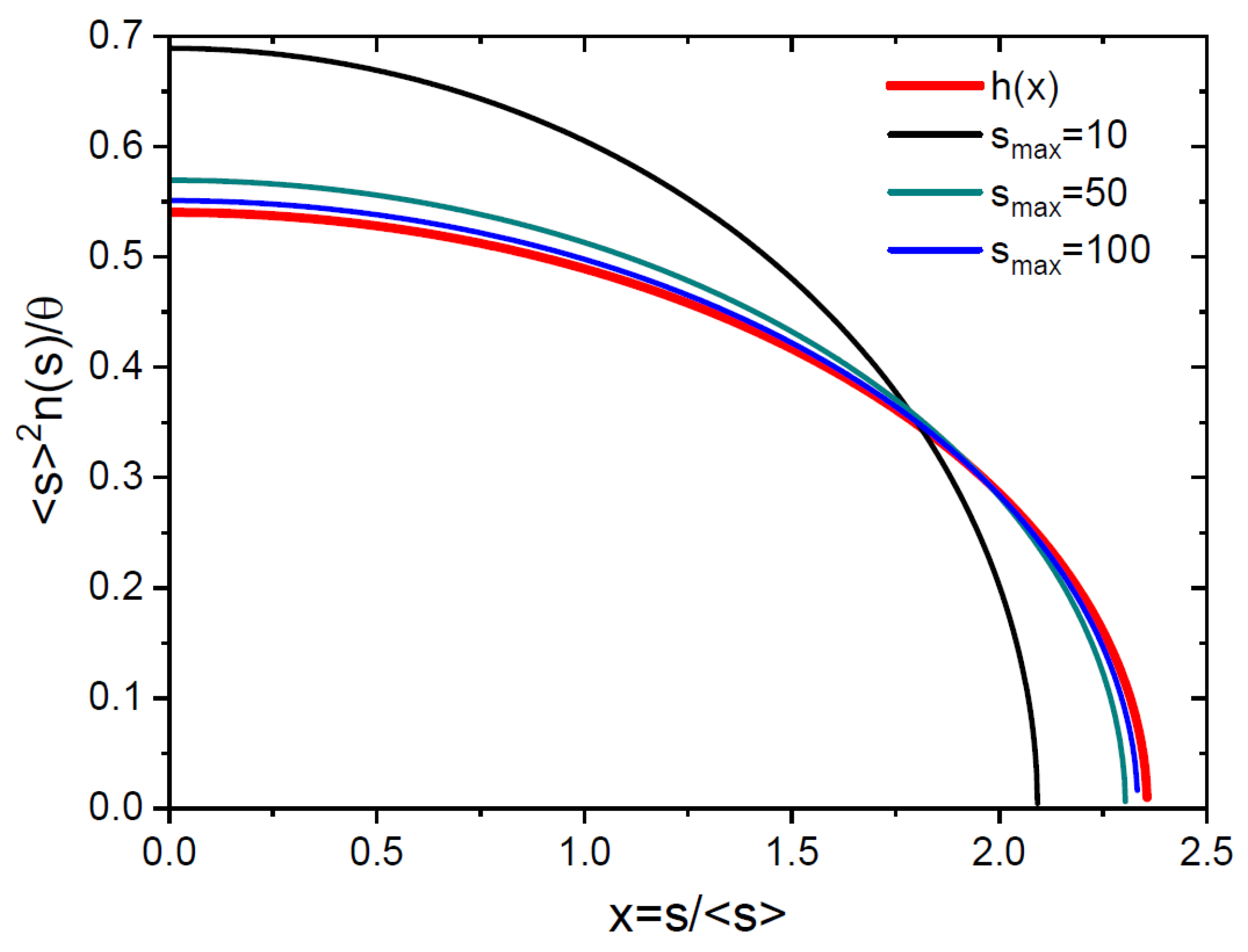
5. Exactly Solvable Model
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Venables, J.A. Rate equation approaches to thin film nucleation kinetics. Phil. Mag. 1973, 27, 697. [Google Scholar] [CrossRef]
- Brune, H. Microscopic view of epitaxial metal growth: Nucleation and aggregation. Surf. Sci. Rep. 1998, 31, 121. [Google Scholar] [CrossRef]
- Evans, J.W.; Thiel, P.A.; Bartelt, M.C. Morphological evolution during epitaxial thin film growth: Formation of 2D islands and 3D mounds. Surf. Sci. Rep. 2006, 61, 1. [Google Scholar] [CrossRef]
- Dieterich, W.; Einax, M.; Maass, P. Stochastic theories and scaling relations for early-stage surface growth. Eur. Phys. J. Spec. Top. 2008, 161, 151. [Google Scholar] [CrossRef]
- Einax, M.; Dieterich, W.; Maass, P. Colloquium: Cluster growth on surfaces: Densities, size distributions, and morphologies. Rev. Mod. Phys. 2013, 85, 921. [Google Scholar] [CrossRef]
- Kukushkin, S.A.; Osipov, A.V. New phase formation on solid surfaces and thin film condensation. Prog. Surf. Sci. 1996, 51, 1. [Google Scholar] [CrossRef]
- Kukushkin, S.A.; Osipov, A.V. Thin-film condensation processes. Phys. Usp. 2007, 41, 983. [Google Scholar] [CrossRef]
- Kuni, F.M.; Shchekin, A.K.; Grinin, A.P. Theory of heterogeneous nucleation for vapor undergoing a gradual metastable state formation. Phys. Usp. 2001, 44, 331. [Google Scholar] [CrossRef]
- McIntyre, P.C.; Fontcuberta i Morral, A. Semiconductor nanowires: To grow or not to grow? Mater. Today Nano 2020, 9, 100058. [Google Scholar] [CrossRef]
- Dubrovskii, V.G.; Berdnikov, Y.; Schmidtbauer, J.; Borg, M.; Storm, K.; Deppert, K.; Johansson, J. Length distributions of nanowires growing by surface diffusion. Cryst. Growth Des. 2016, 16, 2167. [Google Scholar] [CrossRef]
- Bikmeeva, K.R.; Bolshakov, A.D. Diffusion-induced ordered nanowire growth: Mask patterning insights. Nanomaterials 2024, 14, 1743. [Google Scholar] [CrossRef] [PubMed]
- Dubrovskii, V.G. Nucleation Theory and Growth of Nanostructures; Springer: Berlin/Heidelberg, Germany; New York, NY, USA; Dordrecht, The Netherlands; London, UK, 2014. [Google Scholar]
- Vicsek, T.; Family, F. Dynamic scaling for aggregation of clusters. Phys. Rev. Lett. 1984, 52, 1669. [Google Scholar] [CrossRef]
- Bartelt, M.C.; Evans, J.W. Scaling analysis of diffusion-mediated island growth in surface adsorption processes. Phys. Rev. B 1992, 46, 12675. [Google Scholar] [CrossRef] [PubMed]
- Ratsch, C.; Zangwill, A.; Šmilauer, P.; Vvedensky, D.D. Saturation and scaling of epitaxial island densities. Phys. Rev. Lett. 1994, 72, 3194. [Google Scholar] [CrossRef]
- Bartelt, M.C.; Evans, J.W. Exact island-size distributions for submonolayer deposition: Influence of correlations between island size and separation. Phys. Rev. B 1996, 54, R17359. [Google Scholar] [CrossRef]
- Bales, G.S.; Chrzan, D.C. Dynamics of irreversible island growth during submonolayer epitaxy. Phys. Rev. B 1994, 50, 6057. [Google Scholar] [CrossRef]
- Bales, G.S.; Zangwill, A. Self-consistent rate theory of submonolayer homoepitaxy with attachment/detachment kinetics. Phys. Rev. B 1997, 55, R1973. [Google Scholar] [CrossRef]
- Amar, J.G.; Family, F. Critical cluster size: Island morphology and size distribution in submonolayer epitaxial growth. Phys. Rev. Lett. 1995, 74, 2066. [Google Scholar] [CrossRef]
- Jensen, P.; Larralde, H.; Pimpinelli, A. Effect of monomer evaporation on a simple model of submonolayer growth. Phys. Rev. B 1997, 55, 2556. [Google Scholar] [CrossRef]
- Bartelt, M.C.; Stoldt, C.R.; Jenks, C.J.; Tiel, P.A.; Evans, J.W. Adatom capture by arrays of two-dimensional Ag islands on Ag(100). Phys. Rev. B 1999, 59, 3125. [Google Scholar] [CrossRef]
- Vvedensky, D.D. Scaling functions for island-size distributions. Phys. Rev. B 2000, 62, 15435. [Google Scholar] [CrossRef]
- Mulheran, P.A.; Robbie, D.A. Theory of the island and capture zone size distributions in thin film growth. Europhys. Lett. 2000, 49, 617. [Google Scholar] [CrossRef]
- Gibou, F.G.; Ratsch, C.; Gyure, M.F.; Chen, S.; Caflisch, R.E. Rate equations and capture numbers with implicit islands correlations. Phys. Rev. B 2001, 63, 115401. [Google Scholar] [CrossRef]
- Evans, J.W.; Bartelt, M.C. Nucleation, adatom capture, and island size distributions: Unified scaling analysis for submonolayer deposition. Phys. Rev. B 2001, 63, 235408. [Google Scholar] [CrossRef]
- Amar, J.G.; Popescu, M.N.; Family, F. Rate-equation approach to island capture zones and size distributions in epitaxial growth. Phys. Rev. Lett. 2001, 86, 3092. [Google Scholar] [CrossRef]
- Gibou, F.G.; Ratsch, C.; Caflisch, R.E. Capture numbers in rate equations and scaling laws for epitaxial growth. Phys. Rev. B 2003, 67, 155403. [Google Scholar] [CrossRef]
- Shi, F.; Shim, Y.; Amar, J.G. Island-size distribution and capture numbers in three-dimensional nucleation: Comparison with mean-field behavior. Phys. Rev. B 2005, 71, 245411. [Google Scholar] [CrossRef]
- Pimpinelli, A.; Einstein, T.L. Capture-zone scaling in island nucleation: Universal fluctuation behavior. Phys. Rev. Lett. 2007, 99, 226102. [Google Scholar] [CrossRef]
- Royston, J.; Amar, J.G. Island-size distribution and capture numbers in three-dimensional nucleation: Dependence on island morphology. Phys. Rev. E 2009, 80, 041602. [Google Scholar] [CrossRef]
- Korner, M.; Einax, M.; Maass, P. Island size distributions in submonolayer growth: Prediction by mean field theory with coverage dependent capture numbers. Phys. Rev. B 2010, 82, 201401. [Google Scholar] [CrossRef]
- Korner, M.; Einax, M.; Maass, P. Capture numbers and island size distributions in models of submonolayer surface growth. Phys. Rev. B 2012, 86, 085403. [Google Scholar] [CrossRef]
- Javorský, J.; Setvín, M.; Oštádal, I.; Sobotík, P.; Kotrla, M. Heterogeneous nucleation and adatom detachment at one-dimensional growth of In on Si(100)−2×1. Phys. Rev. B 2009, 79, 165424. [Google Scholar] [CrossRef]
- Oliveira, T.J.; Aarao Reis, F.D.A. Crossover in the scaling of island size and capture zone distributions. Phys. Rev. B 2012, 86, 115402. [Google Scholar] [CrossRef]
- Joshi, C.P.; Shim, Y.; Bigioni, T.P.; Amar, J.G. Critical island size, scaling, and ordering in colloidal nanoparticle self-assembly. Phys. Rev. E 2014, 90, 032406. [Google Scholar] [CrossRef] [PubMed]
- Dubrovskii, V.G.; Sibirev, N.V. Size distributions, scaling properties, and Bartelt-Evans singularities in irreversible growth with size-dependent capture coefficients. Phys. Rev. B 2014, 89, 054305. [Google Scholar] [CrossRef]
- Dubrovskii, V.G.; Berdnikov, Y.S. Natural scaling of size distributions in homogeneous and heterogeneous rate equations with size-linear capture rates. J. Chem. Phys. 2015, 142, 124110. [Google Scholar] [CrossRef]
- Dubrovskii, V.G.; Sibirev, N.V. Analytic scaling function for island-size distributions. Phys. Rev. E 2015, 91, 042408. [Google Scholar] [CrossRef]
- Petrov, P.P.; Miller, W.; Rehse, U.; Fornari, R. A new method for calculation of island-size distribution in submonolayer epitaxial growth. Appl. Math. Model. 2011, 35, 1331. [Google Scholar] [CrossRef]
- Einstein, T.L.; Pimpinelli, A.; González, D.L. Analyzing capture zone distributions (CZD) in growth: Theory and applications. J. Cryst. Growth 2014, 401, 67. [Google Scholar] [CrossRef][Green Version]
- González, D.L.; Camargo, M.; Sánchez, J.A. Island size distribution with hindered aggregation. Phys. Rev. E 2018, 97, 052802. [Google Scholar] [CrossRef]
- de Boer, J.P.; Ford, I.J.; Kantorovich, L.; Vvedensky, D.D. Phase-field method for epitaxial kinetics on surfaces. J. Chem. Phys. 2018, 149, 194107. [Google Scholar] [CrossRef] [PubMed]
- Álvarez-Cuartas, J.D.; González-Cabrera, D.L.; Camargo, M. Epitaxial growth in one dimension. J. Phys. Cond. Matter 2024, 36, 463001. [Google Scholar] [CrossRef]
- Álvarez-Cuartas, J.D.; Camargo, M.; González-Cabrera, D.L. Colloidal model for nucleation and aggregation in one dimension: Accessing the interaction parameters. Phys. Rev. E 2024, 109, 064604. [Google Scholar] [CrossRef] [PubMed]
- Fujimoto, K.; Hamazaki, R.; Kawaguchi, Y. Family-Vicsek scaling of roughness growth in a strongly interacting Bose gas. Phys. Rev. Lett. 2020, 124, 210604. [Google Scholar] [CrossRef]
- Dubrovskii, V.G. Analytic form of the size distribution in irreversible growth of nanoparticles. Phys. Rev. E 2019, 99, 012105. [Google Scholar] [CrossRef]
- Dubrovskii, V.G.; Sibirev, N.V.; Sokolovskii, A.S. Kinetic broadening of size distribution in terms of natural versus invariant variables. Phys. Rev. E 2021, 103, 012112. [Google Scholar] [CrossRef] [PubMed]
- Tomellini, M.; De Angelis, M. Fokker-Planck equation for the crystal-size probability density in progressive nucleation and growth with application to lognormal, Gaussian and gamma distributions. J. Cryst. Growth 2025, 650, 127970. [Google Scholar] [CrossRef]
- Kotrla, M.; Krug, J.; Smilauer, P. Submonolayer epitaxy with impurities: Kinetic Monte Carlo simulations and rate-equation analysis. Phys. Rev. B 2000, 62, 2889. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dubrovskii, V.G. A General Solution to the Continuum Rate Equation for Island-Size Distributions: Epitaxial Growth Kinetics and Scaling Analysis. Nanomaterials 2025, 15, 396. https://doi.org/10.3390/nano15050396
Dubrovskii VG. A General Solution to the Continuum Rate Equation for Island-Size Distributions: Epitaxial Growth Kinetics and Scaling Analysis. Nanomaterials. 2025; 15(5):396. https://doi.org/10.3390/nano15050396
Chicago/Turabian StyleDubrovskii, Vladimir G. 2025. "A General Solution to the Continuum Rate Equation for Island-Size Distributions: Epitaxial Growth Kinetics and Scaling Analysis" Nanomaterials 15, no. 5: 396. https://doi.org/10.3390/nano15050396
APA StyleDubrovskii, V. G. (2025). A General Solution to the Continuum Rate Equation for Island-Size Distributions: Epitaxial Growth Kinetics and Scaling Analysis. Nanomaterials, 15(5), 396. https://doi.org/10.3390/nano15050396



