Inverse Design of Multi-Port Power Splitter with Arbitrary Ratio Based on Shape Optimization
Abstract
1. Introduction
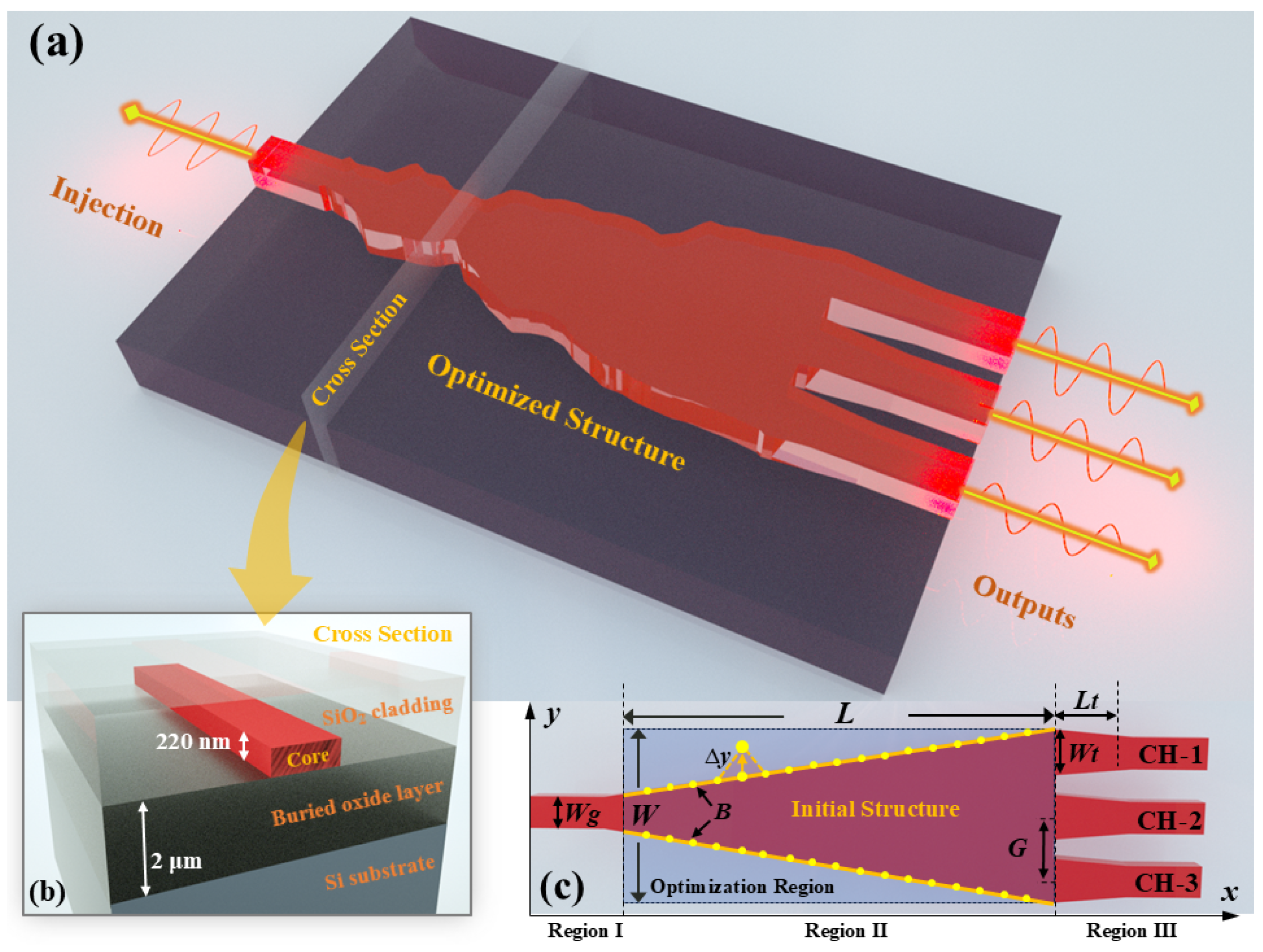
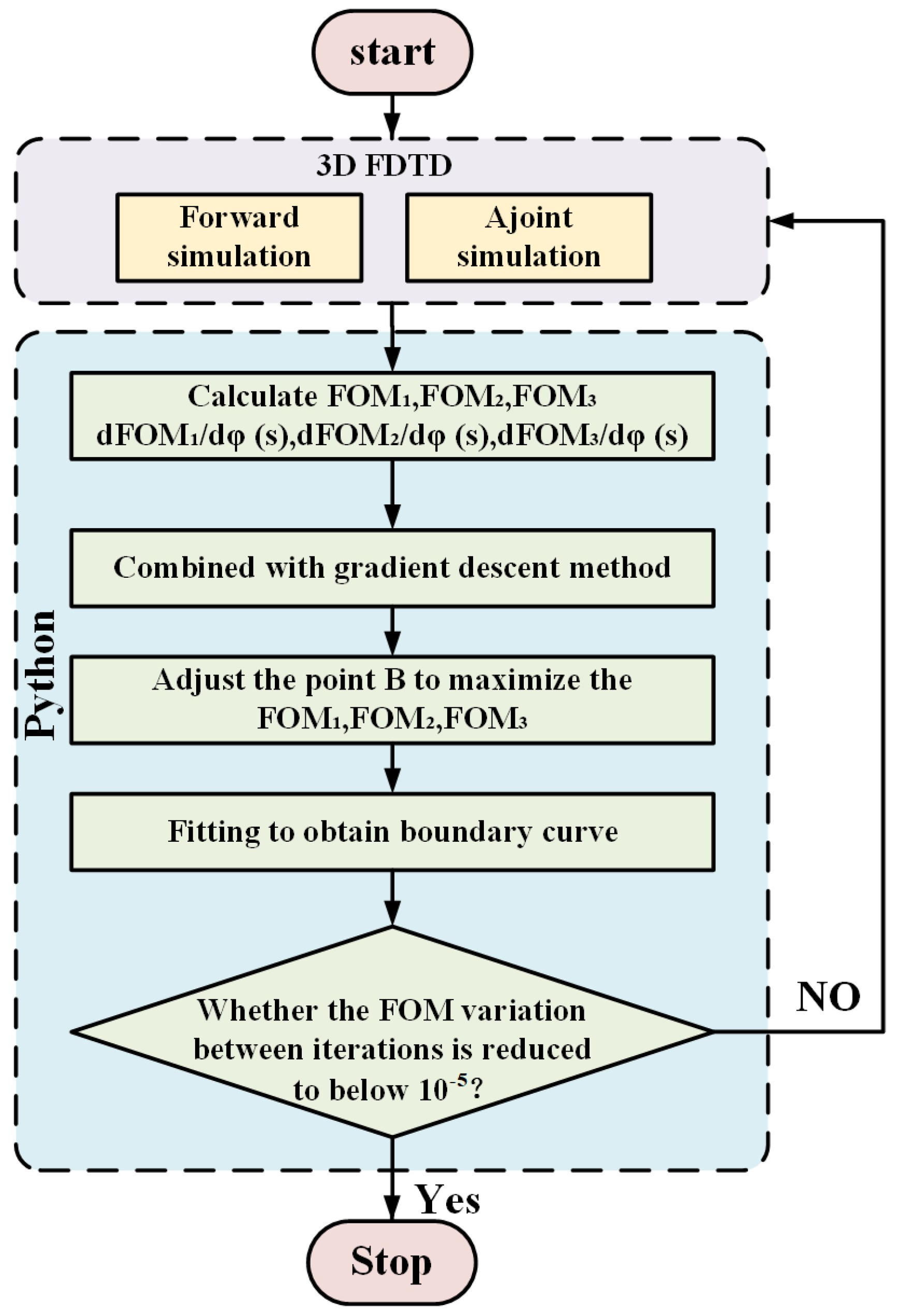
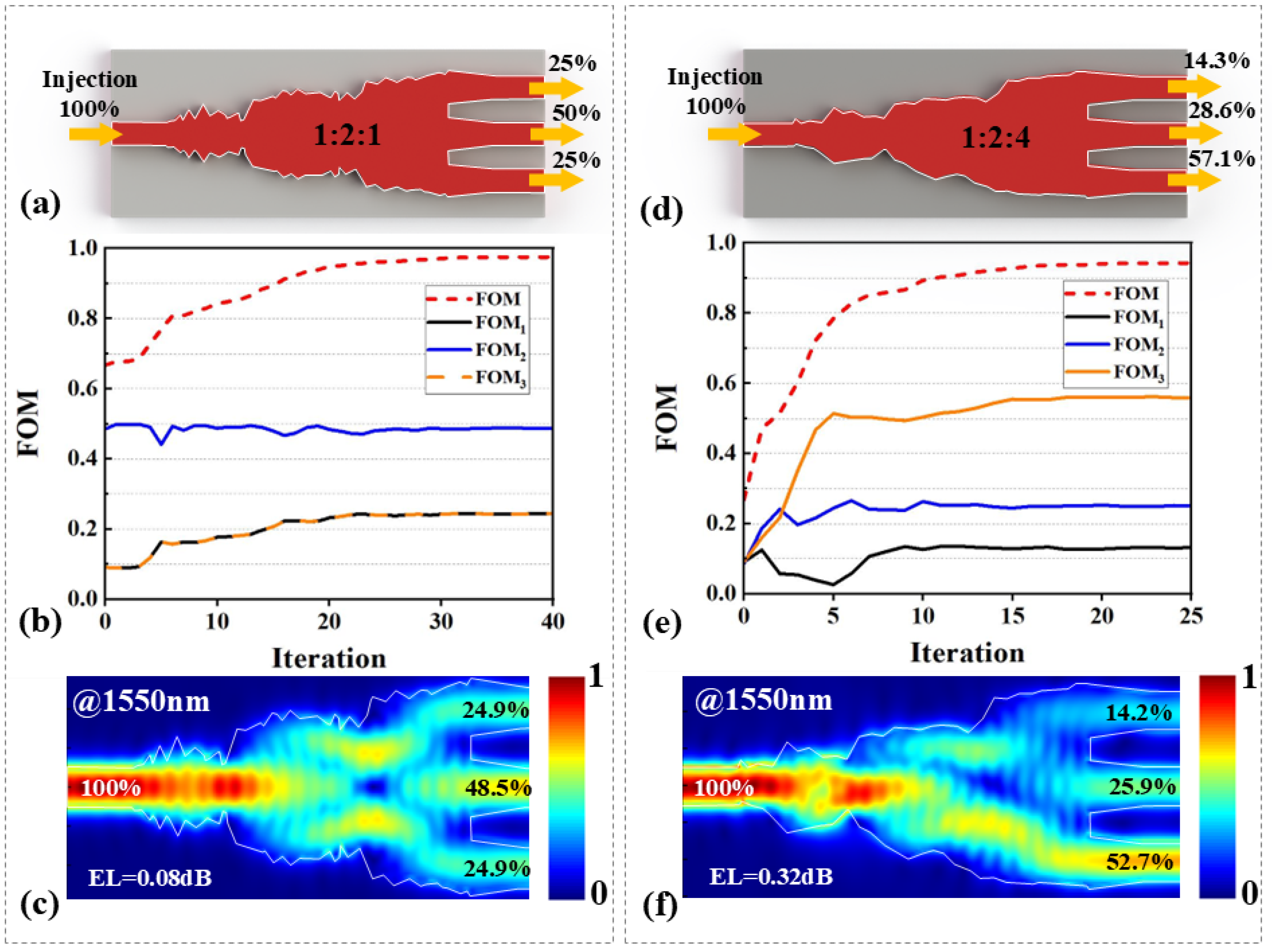
2. Design and Simulations
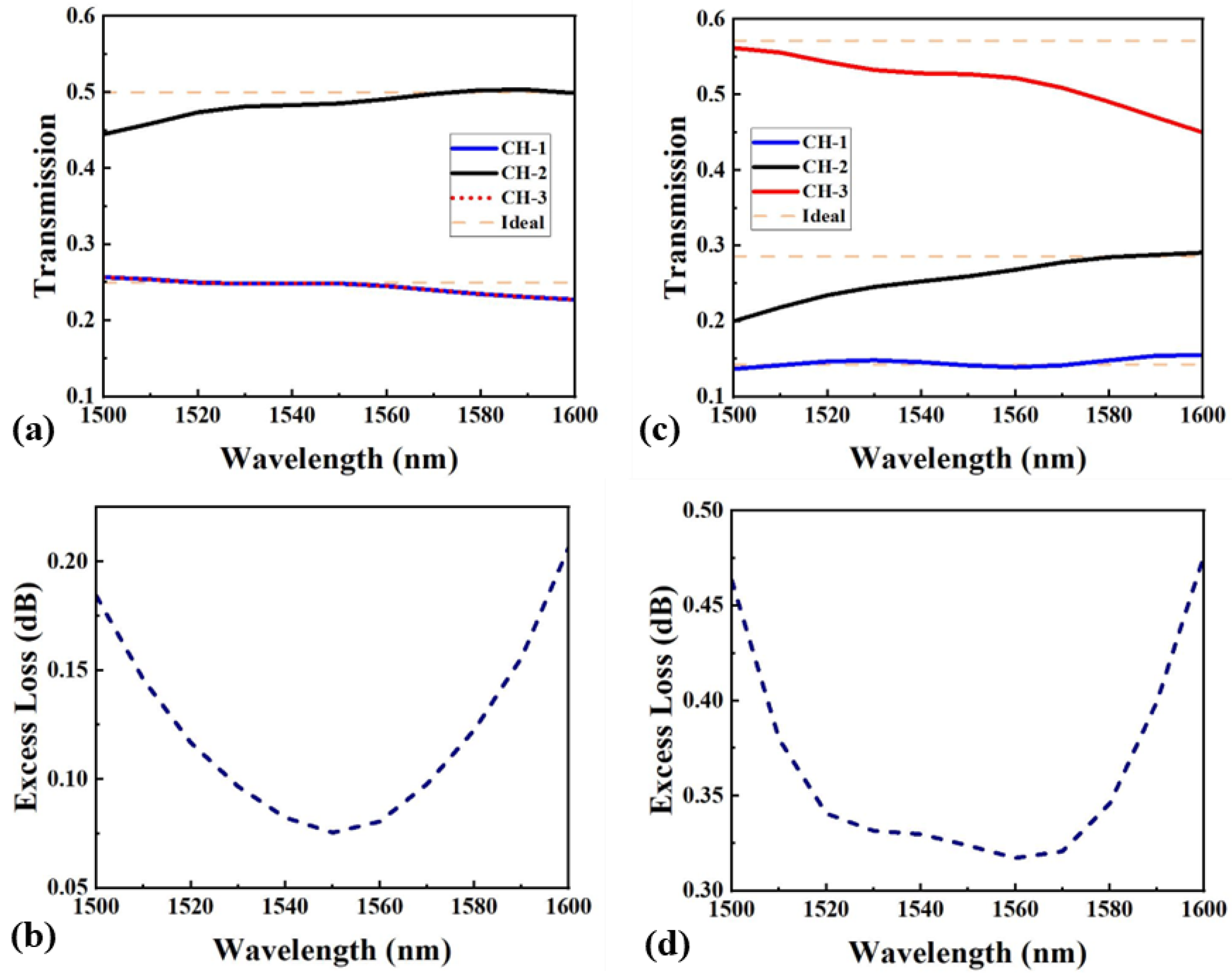
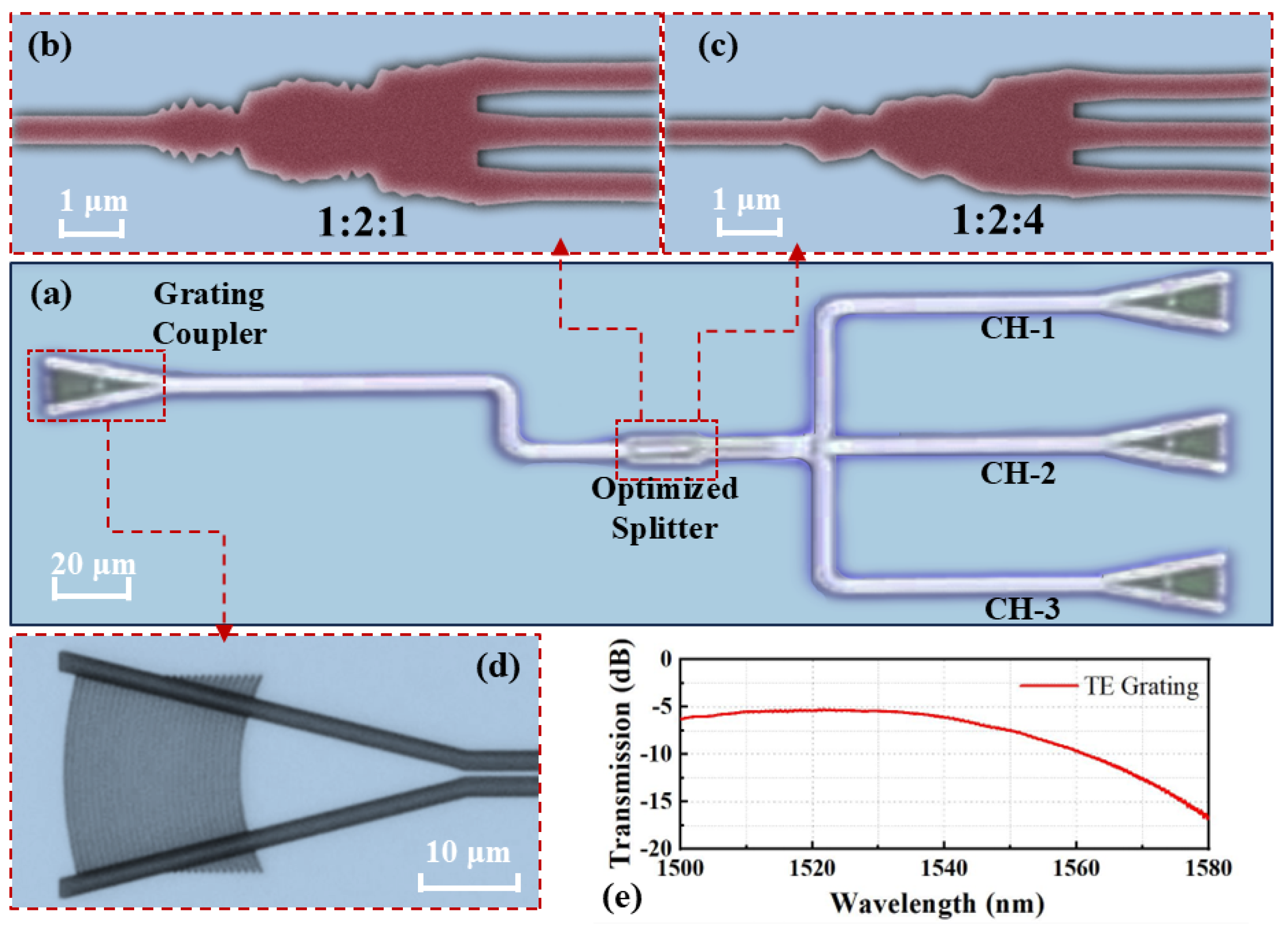
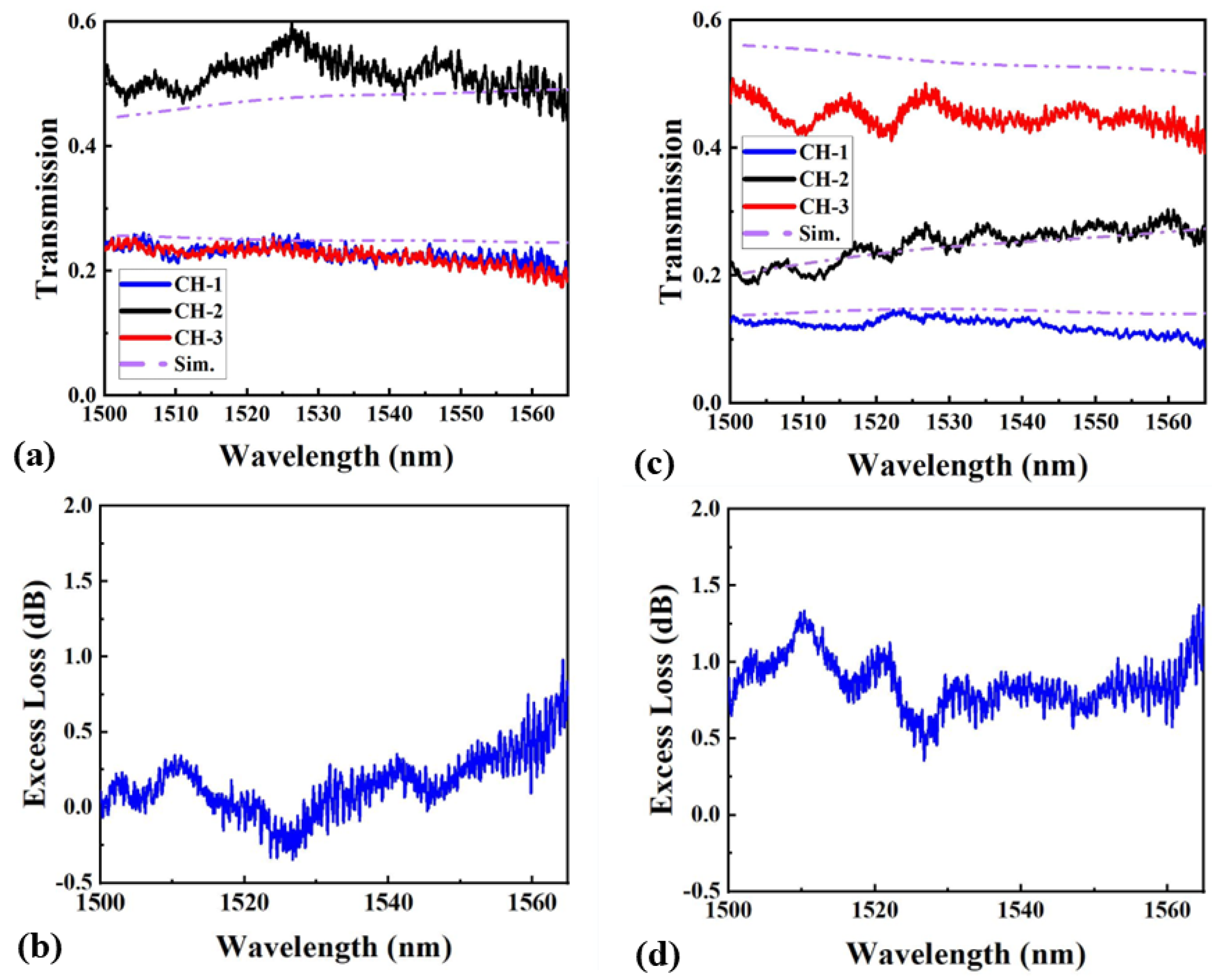
3. Fabrication and Measurement
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shacham, A.; Bergman, K.; Carloni, L.P. Photonic networks-on-chip for future generations of chip multiprocessors. IEEE Trans. Comput. 2008, 57, 1246–1260. [Google Scholar] [CrossRef]
- Sun, J.; Timurdogan, E.; Yaacobi, A.; Su, Z.; Hosseini, E.S.; Cole, D.B.; Watts, M.R. Large-scale silicon photonic circuits for optical phased arrays. IEEE J. Sel. Top. Quantum Electron. 2013, 20, 264–278. [Google Scholar] [CrossRef]
- Ummethala, S.; Kemal, J.N.; Alam, A.S.; Lauermann, M.; Kuzmin, A.; Kutuvantavida, Y.; Nandam, S.H.; Hahn, L.; Elder, D.L.; Dalton, L.R.; et al. Hybrid electro-optic modulator combining silicon photonic slot waveguides with high-k radio-frequency slotlines. Optica 2021, 8, 511–519. [Google Scholar] [CrossRef]
- Ghosh, S.; Rahman, B. Design of on-chip hybrid plasmonic Mach-Zehnder interferometer for temperature and concentration detection of chemical solution. Sens. Actuators B Chem. 2019, 279, 490–502. [Google Scholar] [CrossRef]
- Zhao, S.; Han, S.; Zhu, M.; Chen, J.; Shi, Y. Ultra-broadband dual-polarization and arbitrary ratio power splitters based on Bezier curve optimized multimode interference. Opt. Lett. 2023, 48, 1331–1334. [Google Scholar] [CrossRef]
- Tian, Y.; Huang, Z.; Qiu, J.; Zhang, X.; Wu, J. On-chip OSNR monitoring system based on power-balanced Mach-Zehnder interferometers. Opt. Laser Technol. 2021, 141, 107157. [Google Scholar] [CrossRef]
- Tian, Y.; Kang, Z.; He, J.; Zheng, Z.; Qiu, J.; Wu, J.; Zhang, X. Cascaded all-optical quantization employing step-size MMI and shape-optimized power splitter. Opt. Laser Technol. 2023, 158, 108820. [Google Scholar] [CrossRef]
- Franz, Y.; Guasoni, M. Compact 1 × N power splitters with arbitrary power ratio for integrated multimode photonics. J. Opt. 2021, 23, 095802. [Google Scholar] [CrossRef]
- Wang, L.L.; An, J.M.; Zhang, J.S.; Wu, Y.D.; Li, J.G.; Yin, X.J.; Wang, H.J.; Wang, Y.; Zhong, F.; Zha, Q.; et al. Design and fabrication of a low-loss and asymmetric 1 × 5 arbitrary optical power splitter. Appl. Opt. 2016, 55, 8601–8605. [Google Scholar] [CrossRef]
- Zhang, M.; Malureanu, R.; Krüger, A.C.; Kristensen, M. 1x3 beam splitter for TE polarization based on self-imaging phenomena in photonic crystal waveguides. Opt. Express 2010, 18, 14944–14949. [Google Scholar] [CrossRef]
- Shang, K.; Pathak, S.; Liu, G.; Feng, S.; Li, S.; Lai, W.; Yoo, S. Silicon nitride tri-layer vertical Y-junction and 3D couplers with arbitrary splitting ratio for photonic integrated circuits. Opt. Express 2017, 25, 10474–10483. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Liu, Y.; Guan, H.; Han, W.; Li, Z. Ultra-compact low-loss 1 × 4 optical power splitter with splitting ratio of 1:2:4:8 based on two-stage cascaded MMI couplers. Opt. Lett. 2019, 44, 5622–5625. [Google Scholar] [CrossRef] [PubMed]
- Deng, Z.; Dang, Z.; Chen, T.; Ding, Z.; Zhang, Z. 3-Port beam splitter of arbitrary power ratio enabled by deep learning on a multimode waveguide. Opt. Laser Technol. 2024, 169, 109950. [Google Scholar] [CrossRef]
- Liao, J.; Tian, Y.; Yangd, Z.; Xu, H.; Dai, T.; Zhang, X.; Kang, Z. Broadband and Compact Silicon Multimode Waveguide Bends Based on Hybrid Shape Optimization. J. Light. Technol. 2024, 42, 4882–4891. [Google Scholar] [CrossRef]
- Xu, K.; Liu, L.; Wen, X.; Sun, W.; Zhang, N.; Yi, N.; Sun, S.; Xiao, S.; Song, Q. Integrated photonic power divider with arbitrary power ratios. Opt. Lett. 2017, 42, 855–858. [Google Scholar] [CrossRef]
- Ma, H.; Huang, J.; Zhang, K.; Yang, J. Inverse-designed arbitrary-input and ultra-compact 1 × N power splitters based on high symmetric structure. Sci. Rep. 2020, 10, 11757. [Google Scholar] [CrossRef]
- Ma, H.; Huang, J.; Zhang, K.; Yang, J. Arbitrary-direction, multichannel and ultra-compact power splitters by inverse design method. Opt. Commun. 2020, 462, 125329. [Google Scholar] [CrossRef]
- Xu, Y.; Ma, H.; Xie, T.; Yang, J.; Zhang, Z. Ultra-compact power splitters with low loss in arbitrary direction based on inverse design method. Photonics 2021, 8, 516. [Google Scholar] [CrossRef]
- Yuan, H.; Wu, J.; Zhang, J.; Pu, X.; Zhang, Z.; Yu, Y.; Yang, J. Non-volatile programmable ultra-small photonic arbitrary power splitters. Nanomaterials 2022, 12, 669. [Google Scholar] [CrossRef]
- Shi, P.; Ke, H.; Li, P.; Ma, F.; Shi, W. 1 × 5 broadband photonic crystal power splitter designed by the Powell algorithm. Appl. Opt. 2023, 62, 1303–1312. [Google Scholar] [CrossRef]
- Lebbe, N.; Glière, A.; Hassan, K.; Dapogny, C.; Oudet, E. Shape optimization for the design of passive mid-infrared photonic components. Opt. Quantum Electron. 2019, 51, 1–14. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J.Y.; Yoon, J.; Yoon, H.; Park, H.H.; Kurt, H. Experimental demonstration of inverse-designed silicon integrated photonic power splitters. Nanophotonics 2022, 11, 4581–4590. [Google Scholar] [CrossRef] [PubMed]
- Piggott, A.Y.; Ma, E.Y.; Su, L.; Ahn, G.H.; Sapra, N.V.; Vercruysse, D.; Netherton, A.M.; Khope, A.S.; Bowers, J.E.; Vuckovic, J. Inverse-designed photonics for semiconductor foundries. ACS Photonics 2020, 7, 569–575. [Google Scholar] [CrossRef]
- Lalau-Keraly, C.M.; Bhargava, S.; Miller, O.D.; Yablonovitch, E. Adjoint shape optimization applied to electromagnetic design. Opt. Express 2013, 21, 21693–21701. [Google Scholar] [CrossRef]
- Miller, O.D. Photonic Design: From Fundamental Solar Cell Physics to Computational Inverse Design; University of California: Berkeley, CA, USA, 2012. [Google Scholar]

| Method | Ports | Footprint (µm2) | MFS (nm) | SRs | EL (dB) | Bandwidth (nm) | ||
|---|---|---|---|---|---|---|---|---|
| Sim. | Exp. | Sim. | Exp. | |||||
| DBS [15] | 1 × 3 | 3.6 × 3.6 | 120 | 1:2:1 | <1 | <1 | 30 | 30 |
| DBS [16] | 1 × 3 | 4 × 4 | 70 | 1:1:1 | <1.9 | - | 100 | - |
| SO [23] | 1 × 3 | 3.8 × 2.5 | 100 | 1:1:1 | <0.4 | <0.4 | 150 | 150 |
| DBS [18] | 1 × 3 | 2.4 × 2.4 | 90 | 1:1:1 | <0.63 | - | 30 | - |
| SO [22] | 1 × 4 | 6 × 7.2 | 150 | 1:1:1:1 | - | <1.08 | - | 15 |
| PA [20] | 1 × 5 | 41.5 × 41.5 | 40 | 1:1:1:1:1 | <0.21 | - | 40 | - |
| 2:3:1:3:2 | <0.23 | - | 40 | - | ||||
| 1:2:1:4:1 | <0.18 | - | 40 | - | ||||
| This Work | 1×3 | 2.7×6 | 180 | 1:2:1 | <0.2 | <0.7 | 100 | 65 |
| 1:2:4 | <0.47 | <1.3 | 100 | 65 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Kang, Z.; Xu, H.; Zhong, G.; Zhang, R.; Fu, C.; Tian, Y. Inverse Design of Multi-Port Power Splitter with Arbitrary Ratio Based on Shape Optimization. Nanomaterials 2025, 15, 393. https://doi.org/10.3390/nano15050393
Liu Y, Kang Z, Xu H, Zhong G, Zhang R, Fu C, Tian Y. Inverse Design of Multi-Port Power Splitter with Arbitrary Ratio Based on Shape Optimization. Nanomaterials. 2025; 15(5):393. https://doi.org/10.3390/nano15050393
Chicago/Turabian StyleLiu, Yang, Zhe Kang, Haoda Xu, Guangbiao Zhong, Ruitao Zhang, Chaoying Fu, and Ye Tian. 2025. "Inverse Design of Multi-Port Power Splitter with Arbitrary Ratio Based on Shape Optimization" Nanomaterials 15, no. 5: 393. https://doi.org/10.3390/nano15050393
APA StyleLiu, Y., Kang, Z., Xu, H., Zhong, G., Zhang, R., Fu, C., & Tian, Y. (2025). Inverse Design of Multi-Port Power Splitter with Arbitrary Ratio Based on Shape Optimization. Nanomaterials, 15(5), 393. https://doi.org/10.3390/nano15050393






