Impact of the Nano-Precipitation Size Distribution on the Mechanical Behavior of Nickel-Based Alloys by Experiment and Simulation
Abstract
1. Introduction
2. Experiment
2.1. Material Preparation
2.2. End Quenching Test
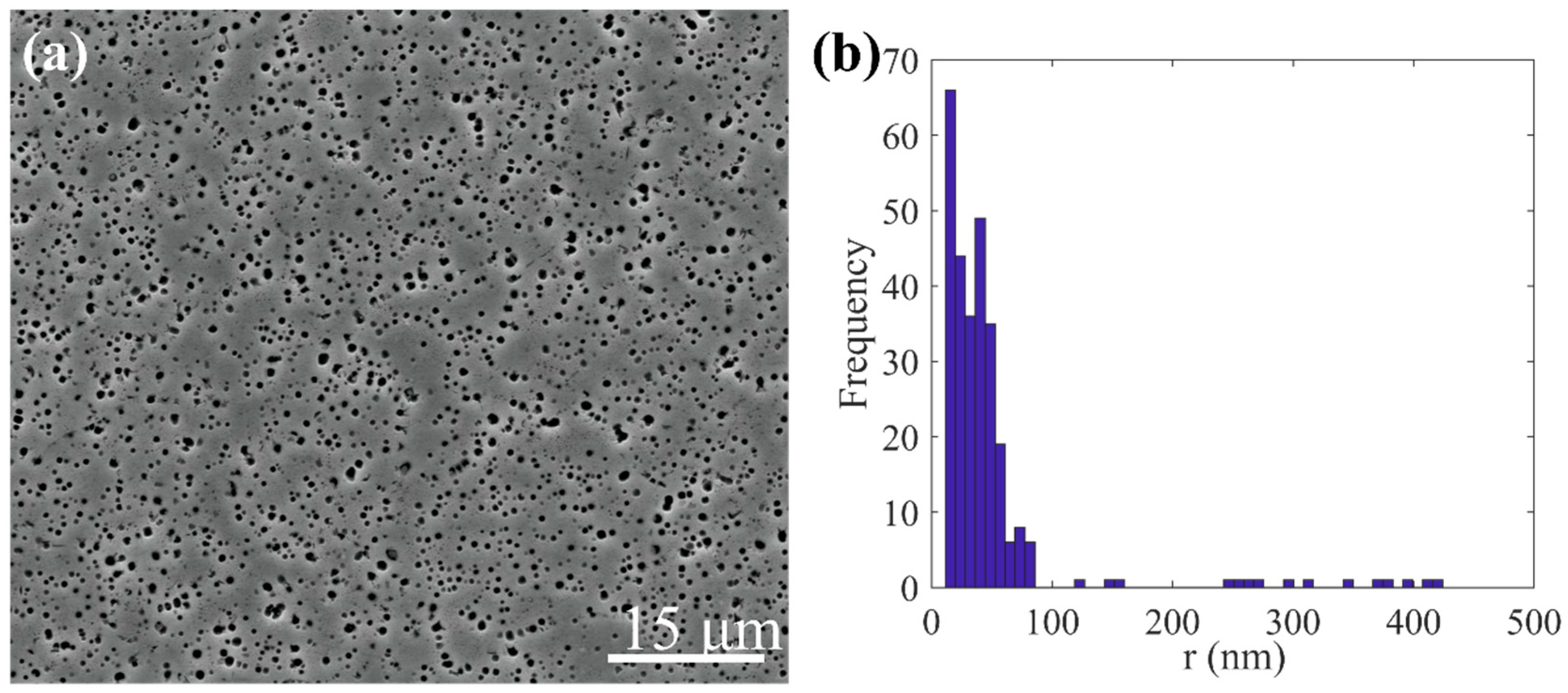
2.3. Microstructure Characterization
3. Methods
3.1. Dislocation Dynamics Simulation

| Parameter | Symbol | Value |
|---|---|---|
| Magnitude of the Burgers vector | b | 0.248 nm [31] |
| Dislocation core size | r0 | 1 b |
| Shear modulus | μ | 80 GPa [31] |
| Poisson’s ratio | v | 0.31 |
| Drag coefficient | B | 2.5 × 10−4 (Pa·s) [32] |
| Anti-phase boundary energy | 0.27 J/m2 [33] | |
| Precipitation mean size | d | 161.4 nm [34] |
| Volume fraction | fv | 0.245 [34] |
3.2. Machine Learning Method
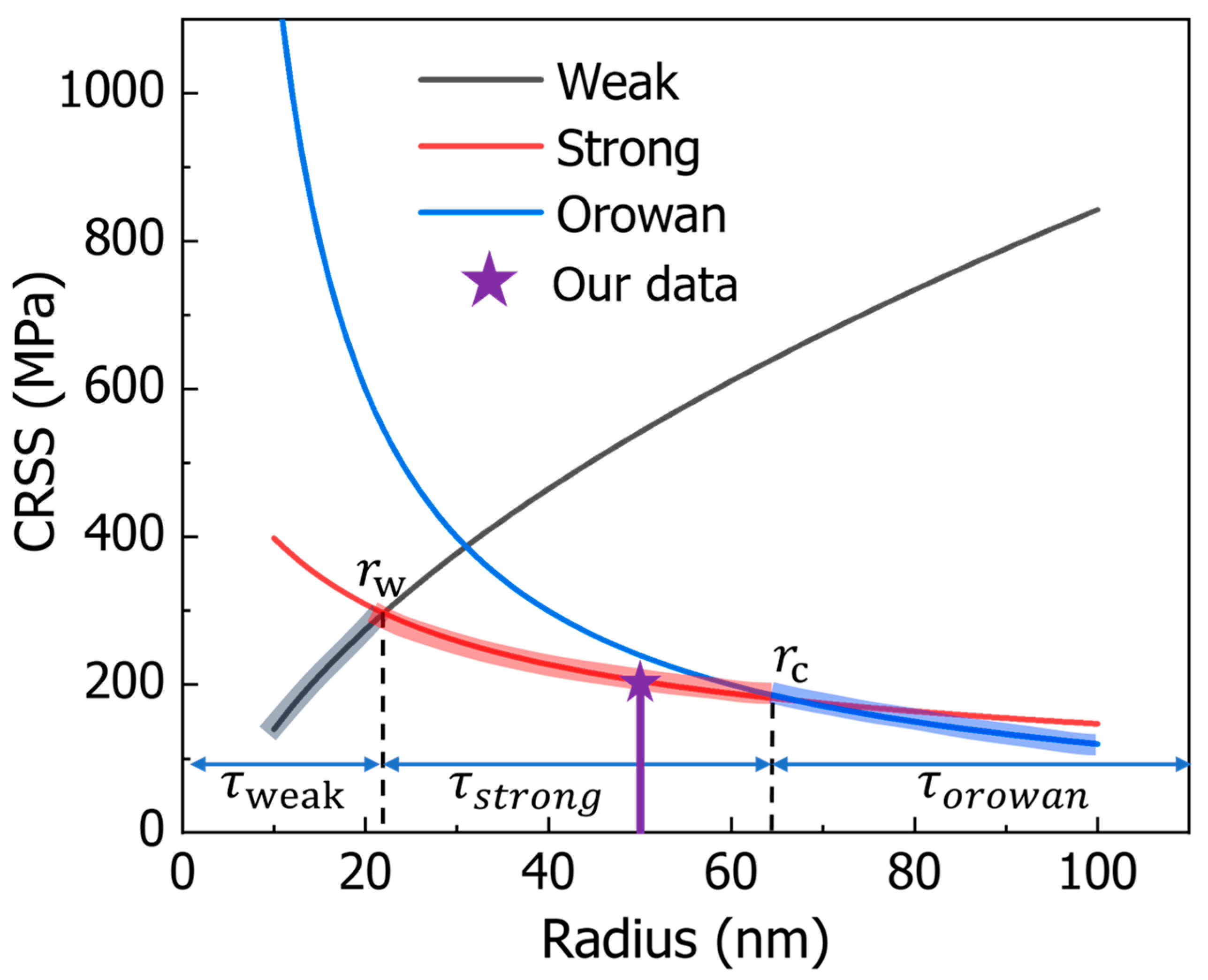
3.3. Classical Precipitation-Strengthening Model
4. Results and Discussion
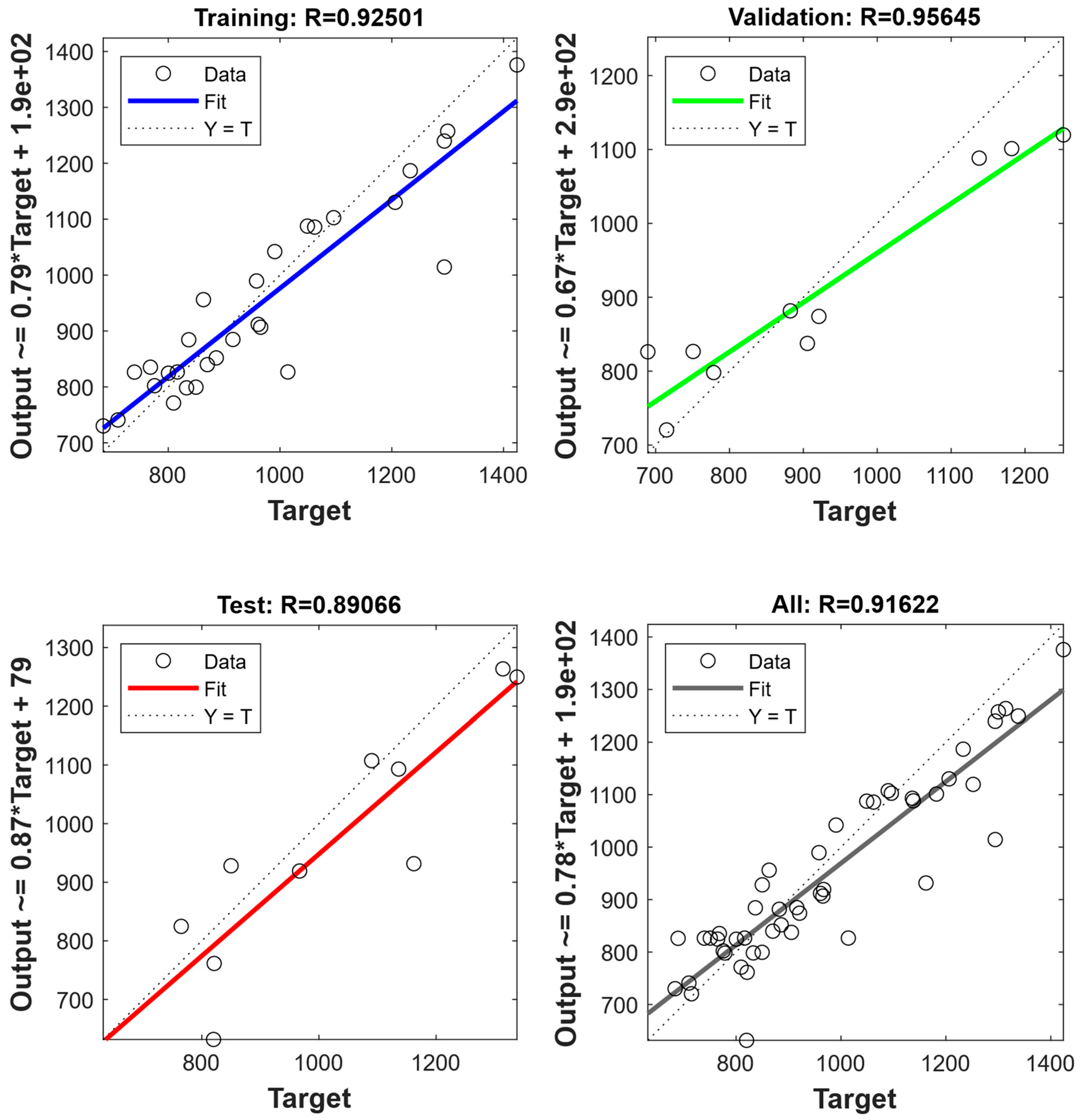
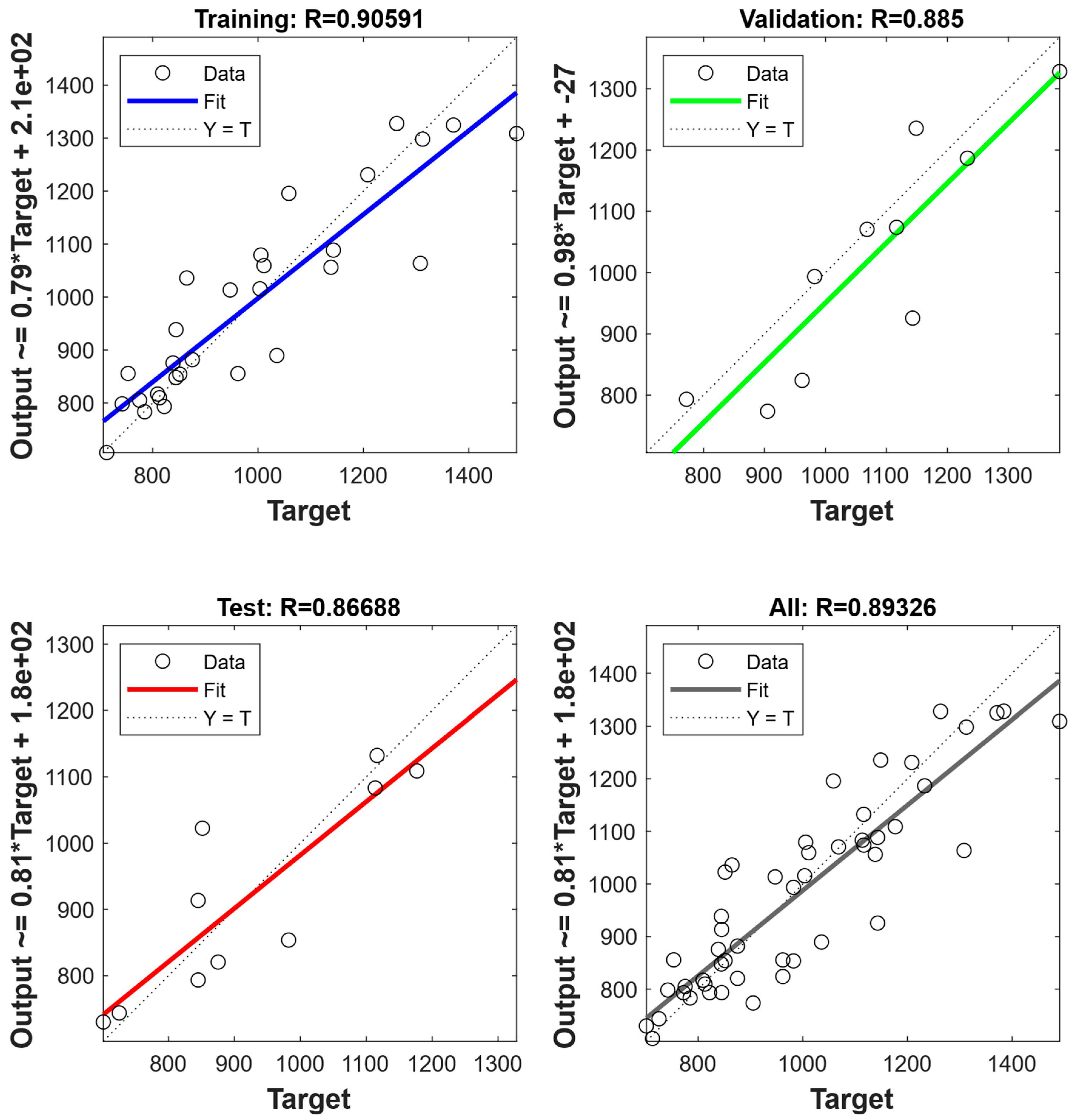
4.1. Machine Learning Prediction
4.2. Dislocation Evolution
4.3. Average Size Effect
4.4. Size Dispersion Effect
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
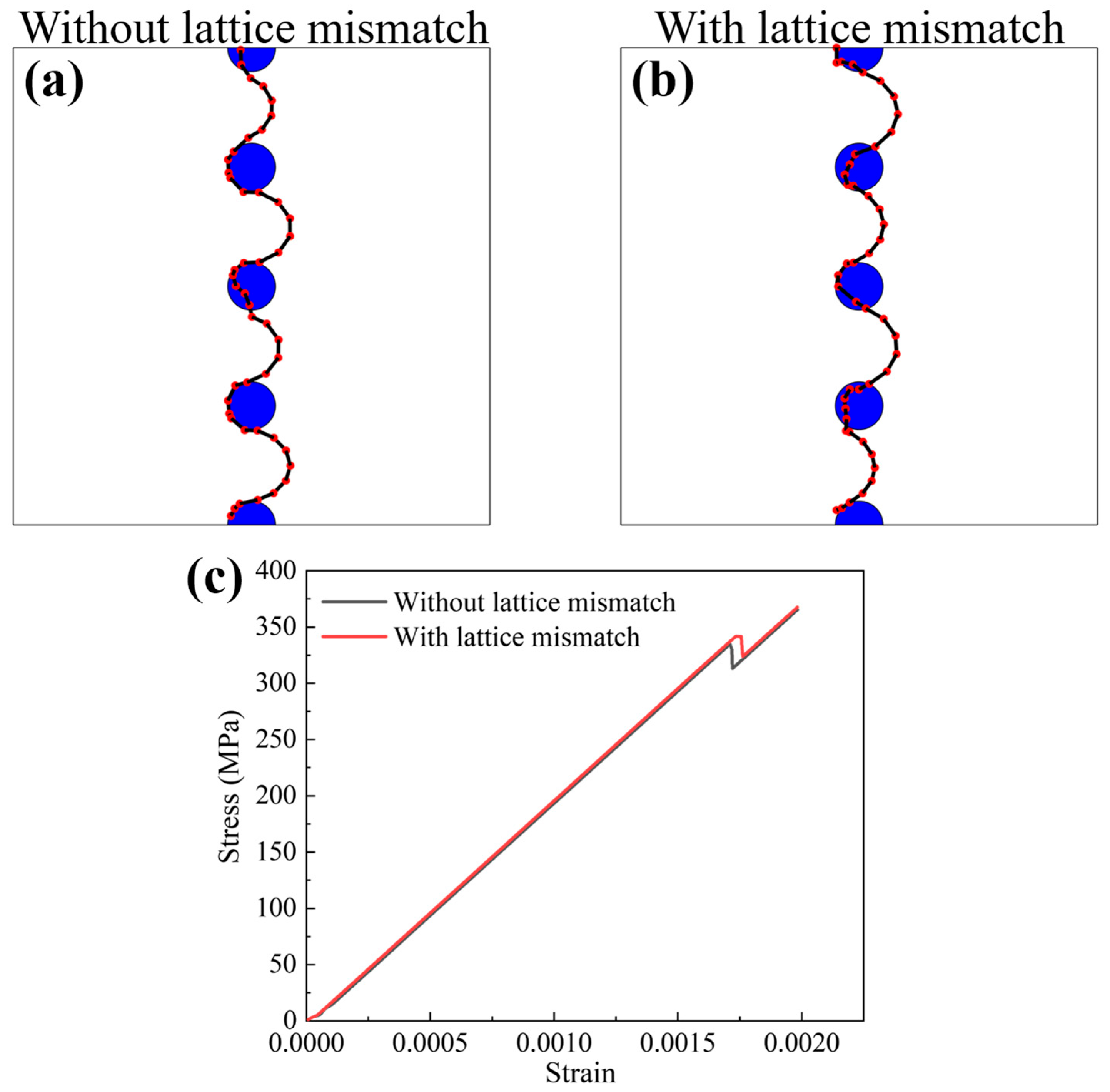
Appendix A. The Influence of Lattice Mismatch
Appendix B. The Dataset Used for Machine Learning
| Average Size of Precipitates (nm) | Distribution of Precipitates | Flow Stress (MPa) | Yield Strength (MPa) |
|---|---|---|---|
| 30 | 10 | 1384.1 | 1294 |
| 50 | 10 | 1113.6 | 1136 |
| 70 | 10 | 1005.4 | 990.6 |
| 90 | 10 | 851.47 | 849.9 |
| 110 | 10 | 798.19 | 778.6 |
| 130 | 10 | 813.06 | 816.2 |
| 150 | 10 | 1035.7 | 1014 |
| 30 | 20 | 1263.3 | 1338 |
| 50 | 20 | 1068.2 | 1049 |
| 70 | 20 | 1308.1 | 1294 |
| 90 | 20 | 982.19 | 960.9 |
| 110 | 20 | 778.95 | 775.5 |
| 130 | 20 | 772.05 | 768.1 |
| 150 | 20 | 753.28 | 750.8 |
| 30 | 40 | 1370.9 | 1314 |
| 50 | 40 | 1138.4 | 1138 |
| 70 | 40 | 864.66 | 863 |
| 90 | 40 | 844.28 | 836.7 |
| 110 | 40 | 893.69 | 870 |
| 130 | 40 | 905.07 | 905.5 |
| 150 | 40 | 742.04 | 739.5 |
| 30 | 80 | 1312.4 | 1300 |
| 50 | 80 | 1116.6 | 1090 |
| 70 | 80 | 947.07 | 921 |
| 90 | 80 | 961.78 | 965.4 |
| 110 | 80 | 915.17 | 886 |
| 130 | 80 | 784.68 | 800.4 |
| 150 | 80 | 701.08 | 689.5 |
| 30 | 160 | 1232.8 | 1182 |
| 50 | 160 | 1058.5 | 1206 |
| 70 | 160 | 1116.4 | 1062 |
| 90 | 160 | 875.26 | 882.4 |
| 110 | 160 | 900.56 | 915.7 |
| 130 | 160 | 775.23 | 764.8 |
| 150 | 160 | 809.3 | 809.5 |
| 30 | 240 | 1176.7 | 1096 |
| 50 | 240 | 1490.8 | 1424 |
| 70 | 240 | 1148.8 | 1233 |
| 90 | 240 | 1143 | 1162 |
| 110 | 240 | 826.28 | 821.1 |
| 130 | 240 | 712.78 | 710 |
| 150 | 240 | 822 | 820 |
| 30 | 320 | 1011.2 | 958 |
| 50 | 320 | 1208.2 | 1252 |
| 70 | 320 | 1003.6 | 966.9 |
| 90 | 320 | 844.94 | 849.6 |
| 110 | 320 | 685.5 | 683.7 |
| 130 | 320 | 725.23 | 714.9 |
| 150 | 320 | 838.54 | 832.8 |
References
- Lindström, T.; Ewest, D.; Simonsson, K.; Eriksson, R.; Lundgren, J.-E.; Leidermark, D. Constitutive Model of an Additively Manufactured Ductile Nickel-Based Superalloy Undergoing Cyclic Plasticity. Int. J. Plast. 2020, 132, 102752. [Google Scholar] [CrossRef]
- León-Cázares, F.D.; Monni, F.; Jackson, T.; Galindo-Nava, E.I.; Rae, C.M.F. Stress Response and Microstructural Evolution of Nickel-Based Superalloys during Low Cycle Fatigue: Physics-Based Modelling of Cyclic Hardening and Softening. Int. J. Plast. 2020, 128, 102682. [Google Scholar] [CrossRef]
- Obasi, G.C.; Zhang, Z.; Sampath, D.; Morana, R.; Akid, R.; Preuss, M. Effect of Microstructure and Alloy Chemistry on Hydrogen Embrittlement of Precipitation-Hardened Ni-Based Alloys. Metall. Mater. Trans. A 2018, 49, 1167–1181. [Google Scholar] [CrossRef]
- Barat, K.; Ghosh, A.; Doharey, A.; Mukherjee, S.; Karmakar, A. Crystallographic Evaluation of Low Cycle Fatigue Crack Growth in a Polycrystalline Ni Based Superalloy. Int. J. Plast. 2022, 149, 103174. [Google Scholar] [CrossRef]
- Sun, W.; Zhu, Y.; Marceau, R.; Wang, L.; Zhang, Q.; Gao, X.; Hutchinson, C. Precipitation Strengthening of Aluminum Alloys by Room-Temperature Cyclic Plasticity. Science 2019, 363, 972–975. [Google Scholar] [CrossRef]
- Xu, S.S.; Zhao, Y.; Chen, D.; Sun, L.W.; Chen, L.; Tong, X.; Liu, C.T.; Zhang, Z.W. Nanoscale Precipitation and Its Influence on Strengthening Mechanisms in an Ultra-High Strength Low-Carbon Steel. Int. J. Plast. 2019, 113, 99–110. [Google Scholar] [CrossRef]
- Chen, H.; Chen, Z.; Ji, G.; Zhong, S.; Wang, H.; Borbély, A.; Ke, Y.; Bréchet, Y. The Influence of Shearable and Nonshearable Precipitations on the Portevin-Le Chatelier Behavior in Precipitation Hardening AlMgScZr Alloys. Int. J. Plast. 2021, 147, 103120. [Google Scholar] [CrossRef]
- Long, B.Z.; Zhang, Y.; Guo, C.H.; Cui, Y.; Sun, L.X.; Chen, D.; Jiang, F.C.; Zhao, T.; Zhao, G.; Zhang, Z.W. Enhanced Dynamic Mechanical Properties and Resistance to the Formation of Adiabatic Shear Band by Cu-Rich Nano-Precipitations in High-Strength Steels. Int. J. Plast. 2021, 138, 102924. [Google Scholar] [CrossRef]
- Fang, Q.; Huang, Z.; Li, L.; Huang, Z.; Liu, B.; Liu, Y.; Li, J.; Liaw, P.K. Modeling the Competition between Solid Solution and Precipitation Strengthening of Alloys in a 3D Space. Int. J. Plast. 2022, 149, 103152. [Google Scholar] [CrossRef]
- Li, J.; Chen, H.; Fang, Q.; Jiang, C.; Liu, Y.; Liaw, P.K. Unraveling the Dislocation–Precipitation Interactions in High-Entropy Alloys. Int. J. Plast. 2020, 133, 102819. [Google Scholar] [CrossRef]
- Santos-Guemes, R.; Capolungo, L.; Segurado, J.; LLorca, J. Dislocation Dynamics Prediction of the Strength of Al-Cu Alloys Containing Shearable θ’’ Precipitations. J. Mech. Phys. Solids 2021, 151, 104375. [Google Scholar] [CrossRef]
- Goodfellow, A.J.; Galindo-Nava, E.I.; Christofidou, K.A.; Jones, N.G.; Martin, T.; Bagot, P.A.J.; Boyer, C.D.; Hardy, M.C.; Stone, H.J. Gamma Prime Precipitation Evolution during Aging of a Model Nickel-Based Superalloy. Metall. Mater. Trans. A 2018, 49, 718–728. [Google Scholar] [CrossRef]
- Fang, Q.; Li, L.; Li, J.; Wu, H.; Huang, Z.; Liu, B.; Liu, Y.; Liaw, P.K. A Statistical Theory of Probability-Dependent Precipitation Strengthening in Metals and Alloys. J. Mech. Phys. Solids 2019, 122, 177–189. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, Y.; Li, C.; Xia, X.; Wu, J.; Li, H. Coarsening Behavior of Γ′ Precipitations in the γ’+ γ Area of a Ni3Al-Based Alloy. J. Alloys Compd. 2019, 771, 526–533. [Google Scholar] [CrossRef]
- Cui, W.; Cui, Y.; Liu, W. A Statistical Model of Irradiation Hardening Induced by Non-Periodic Irradiation Defects. Scripta Mater. 2021, 201, 113959. [Google Scholar] [CrossRef]
- Pollock, T.M. Alloy Design for Aircraft Engines. Nat. Mater. 2016, 15, 809–815. [Google Scholar] [CrossRef]
- Bulatov, V.V.; Hsiung, L.L.; Tang, M.; Arsenlis, A.; Bartelt, M.C.; Cai, W.; Florando, J.N.; Hiratani, M.; Rhee, M.; Hommes, G.; et al. Dislocation Multi-Junctions and Strain Hardening. Nature 2006, 440, 1174–1178. [Google Scholar] [CrossRef]
- Krasnikov, V.S.; Mayer, A.E.; Pogorelko, V.V. Prediction of the Shear Strength of Aluminum with θ Phase Inclusions Based on Precipitation Statistics, Dislocation and Molecular Dynamics. Int. J. Plast. 2020, 128, 102672. [Google Scholar] [CrossRef]
- Song, H.; Dimiduk, D.; Papanikolaou, S. Universality Class of Nanocrystal Plasticity: Localization and Self-Organization in Discrete Dislocation Dynamics. Phys. Rev. Lett. 2019, 122, 178001. [Google Scholar] [CrossRef]
- Chatterjee, S.; Li, Y.; Po, G. A Discrete Dislocation Dynamics Study of Precipitation Bypass Mechanisms in Nickel-Based Superalloys. Int. J. Plast. 2021, 145, 103062. [Google Scholar] [CrossRef]
- Gao, S.; Hou, J.; Yang, F.; Guo, Y.; Zhou, L. Effect of Ta on Microstructural Evolution and Mechanical Properties of a Solid-Solution Strengthening Cast Ni-Based Alloy during Long-Term Thermal Exposure at 700 °C. J. Alloys Compd. 2017, 729, 903–913. [Google Scholar] [CrossRef]
- Kumar, S.; Sharma, J.K. Stable phase CdS nanoparticles for optoelectronics: A study on surface morphology, structural and optical characterization. Mater. Sci. 2016, 34, 368–373. [Google Scholar] [CrossRef]
- Lehtinen, A.; Laurson, L.; Granberg, F.; Nordlund, K.; Alava, M.J. Effects of Precipitations and Dislocation Loops on the Yield Stress of Irradiated Iron. Sci. Rep. 2018, 8, 6914. [Google Scholar] [CrossRef]
- Santos-Guemes, R.; Bellon, B.; Esteban-Manzanares, G.; Segurado, J.; Capolungo, L.; LLorca, J. Multiscale Modelling of Precipitation Hardening in Al-Cu Alloys: Dislocation Dynamics Simulations and Experimental Validation. Acta Mater. 2020, 188, 475–485. [Google Scholar] [CrossRef]
- Collins, D.M.; Stone, H.J. A Modelling Approach to Yield Strength Optimisation in a Nickel-Base Superalloy. Int. J. Plast. 2014, 54, 96–112. [Google Scholar] [CrossRef]
- Nan, C.W.; Clarke, D.R. The Influence of Particle Size and Particle Fracture on the Elastic/Plastic Deformation of Metal Matrix Composites. Acta Mater. 1996, 44, 3801–3811. [Google Scholar] [CrossRef]
- Ardell, A.J. Precipitation Hardening. Metall. Trans. A 1985, 16, 2131–2165. [Google Scholar] [CrossRef]
- Reed, R.C. The Superalloys: Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2008; ISBN 1-139-45863-9. [Google Scholar]
- Mohles, V. Simulations of Dislocation Glide in Overaged Precipitation-Hardened Crystals. Philos. Mag. A 2001, 81, 971–990. [Google Scholar] [CrossRef]
- Wang, X.; Xiong, W. Uncertainty Quantification and Composition Optimization for Alloy Additive Manufacturing through a CALPHAD-Based ICME Framework. Npj Comput. Mater. 2020, 6, 188. [Google Scholar] [CrossRef]
- Galindo-Nava, E.I.; Connor, L.D.; Rae, C.M.F. On the Prediction of the Yield Stress of Unimodal and Multimodal Γ′ Nickel-Base Superalloys. Acta Mater. 2015, 98, 377–390. [Google Scholar] [CrossRef]
- Rao, S.I.; Woodward, C.; Akdim, B.; Antillon, E.; Parthasarathy, T.A.; El-Awady, J.A.; Dimiduk, D.M. Large-Scale Dislocation Dynamics Simulations of Strain Hardening of Ni Microcrystals under Tensile Loading. Acta Mater. 2019, 164, 171–183. [Google Scholar] [CrossRef]
- Raynor, D.; Silcock, J.M. Strengthening Mechanisms in Γ′ Precipitating Alloys. Met. Sci. J. 1970, 4, 121–130. [Google Scholar] [CrossRef]
- Wu, H.; Li, J.; Liu, F.; Huang, L.; Zeng, X.; Fang, Q.; Huang, Z.; Jiang, L. A High-Throughput Methodology Search for the Optimum Cooling Rate in an Advanced Polycrystalline Nickel Base Superalloy. Mater. Design. 2017, 128, 176–181. [Google Scholar] [CrossRef]
- Li, J.; Xie, B.; Fang, Q.; Liu, B.; Liu, Y.; Liaw, P.K. High-Throughput Simulation Combined Machine Learning Search for Optimum Elemental Composition in Medium Entropy Alloy. J. Mater. Sci. Technol. 2021, 68, 70–75. [Google Scholar] [CrossRef]
- Li, J.; Xie, B.; He, Q.; Liu, B.; Zeng, X.; Liaw, P.K.; Fang, Q.; Yang, Y.; Liu, Y. Chemical-Element-Distribution-Mediated Deformation Partitioning and Its Control Mechanical Behavior in High-Entropy Alloys. J. Mater. Sci. Technol. 2022, 120, 99–107. [Google Scholar] [CrossRef]
- Kumari, N.; Bhatt, A.K.; Dwivedi, R.K.; Belwal, R. Accuracy testing of data classification using tensor flow a python framework in ANN designing. In Proceedings of the 2018 International Conference on System Modeling & Advancement in Research Trends, Moradabad, India, 23–24 November 2018; pp. 40–48. [Google Scholar]
- Xie, B.; Fang, Q.; Li, J. Investigation of Nanomachining-Induced Plastic Behavior Using Machine Learning-Assisted High-Throughput Molecular Dynamics Simulations. Int. J. Adv. Manuf. Technol. 2022, 119, 8057–8068. [Google Scholar] [CrossRef]
- Reppich, B. Some new aspects concerning particle hardening mechanisms in γ’ precipitating Ni-base alloys—I. Theoretical Concept. Acta Metall 1982, 30, 87–94. [Google Scholar] [CrossRef]
- Li, J.; Xie, B.; Li, L.; Liu, B.; Liu, Y.; Shaysultanov, D.; Fang, Q.; Stepanov, N.; Liaw, P.K. Performance-Oriented Multistage Design for Multi-Principal Element Alloys with Low Cost yet High Efficiency. Mater. Horiz. 2022, 9, 1518–1525. [Google Scholar] [CrossRef]
- Hart, G.L.; Mueller, T.; Toher, C.; Curtarolo, S. Machine Learning for Alloys. Nat. Rev. Mater. 2021, 6, 730–755. [Google Scholar] [CrossRef]
- Aagesen, L.K.; Miao, J.; Allison, J.E.; Aubry, S.; Arsenlis, A. Prediction of Precipitation Strengthening in the Commercial Mg Alloy AZ91 Using Dislocation Dynamics. Metall. Mater. Trans. A 2018, 49, 1908–1915. [Google Scholar] [CrossRef]
- Gilbert, M.R.; Schuck, P.; Sadigh, B.; Marian, J. Free Energy Generalization of the Peierls Potential in Iron. Phys. Rev. Lett. 2013, 111, 095502. [Google Scholar] [CrossRef] [PubMed]
- Szajewski, B.A.; Pavia, F.; Curtin, W.A. Robust Atomistic Calculation of Dislocation Line Tension. Modell. Simul. Mater. Sci. Eng. 2015, 23, 085008. [Google Scholar] [CrossRef]
- Chen, Y.; Fang, Q.; Luo, S.; Liu, F.; Liu, B.; Liu, Y.; Huang, Z.; Liaw, P.K.; Li, J. Unraveling a Novel Precipitation Enrichment Dependent Strengthening Behaviour in Nickel-Based Superalloy. Int. J. Plast. 2022, 155, 103333. [Google Scholar] [CrossRef]


 ) at different strains in (a). The blue ball
) at different strains in (a). The blue ball  is the precipitation. The orange arrows (
is the precipitation. The orange arrows ( ) represent the free motion path of dislocation.
) represent the free motion path of dislocation.
 ) at different strains in (a). The blue ball
) at different strains in (a). The blue ball  is the precipitation. The orange arrows (
is the precipitation. The orange arrows ( ) represent the free motion path of dislocation.
) represent the free motion path of dislocation.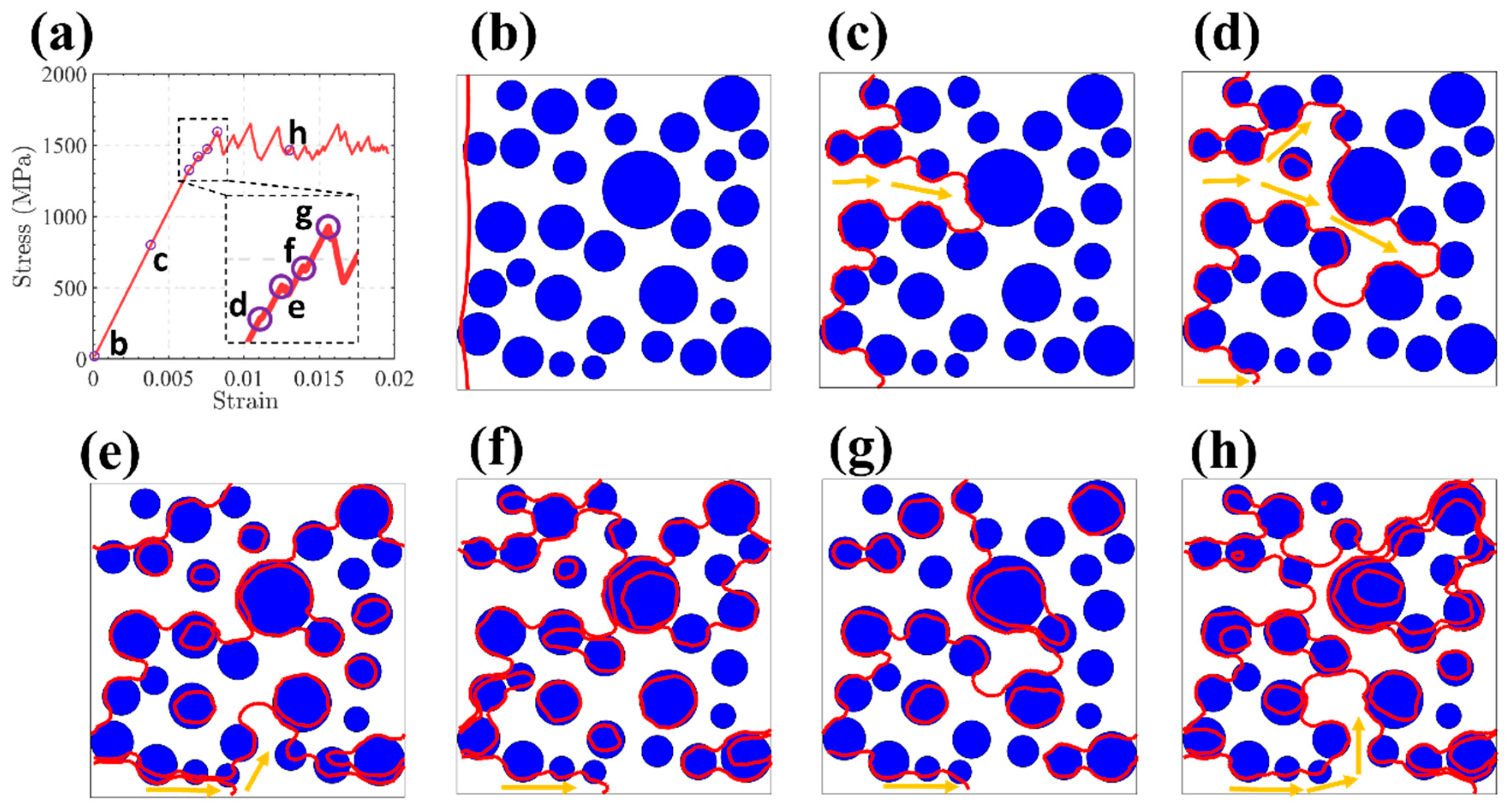
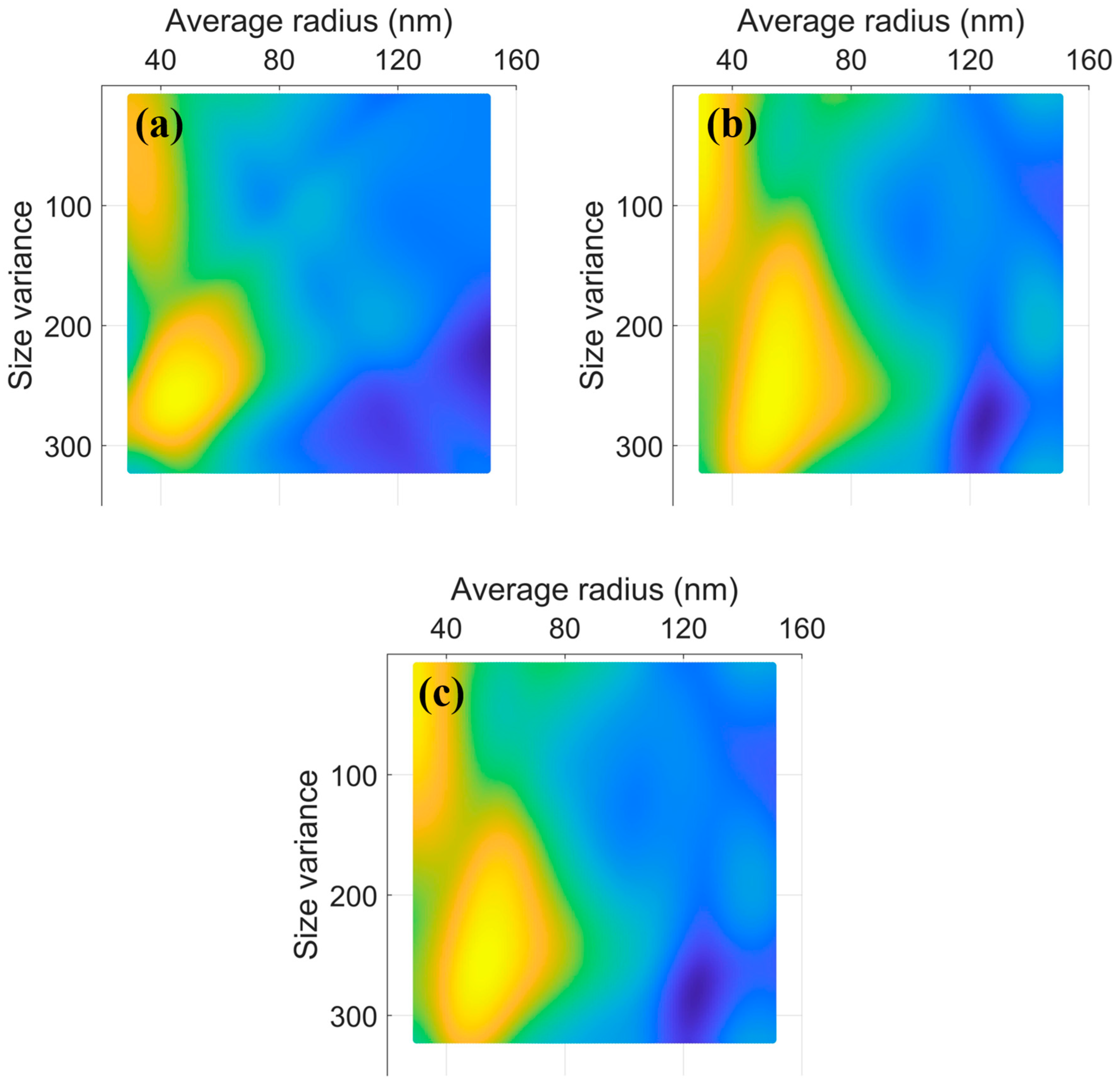
 ) at various average precipitation sizes under the same size variance. These configurations represent dislocation lines spanning vertically across the simulation domain once the applied stress attains the CRSS threshold. The blue ball
) at various average precipitation sizes under the same size variance. These configurations represent dislocation lines spanning vertically across the simulation domain once the applied stress attains the CRSS threshold. The blue ball  is the precipitation.
is the precipitation.
 ) at various average precipitation sizes under the same size variance. These configurations represent dislocation lines spanning vertically across the simulation domain once the applied stress attains the CRSS threshold. The blue ball
) at various average precipitation sizes under the same size variance. These configurations represent dislocation lines spanning vertically across the simulation domain once the applied stress attains the CRSS threshold. The blue ball  is the precipitation.
is the precipitation.
 ), formed under CRSS conditions across varying degrees of precipitation size variance, all within the context of a consistent 50 nm average radius. The blue ball
), formed under CRSS conditions across varying degrees of precipitation size variance, all within the context of a consistent 50 nm average radius. The blue ball  is the precipitation.
is the precipitation.
 ), formed under CRSS conditions across varying degrees of precipitation size variance, all within the context of a consistent 50 nm average radius. The blue ball
), formed under CRSS conditions across varying degrees of precipitation size variance, all within the context of a consistent 50 nm average radius. The blue ball  is the precipitation.
is the precipitation.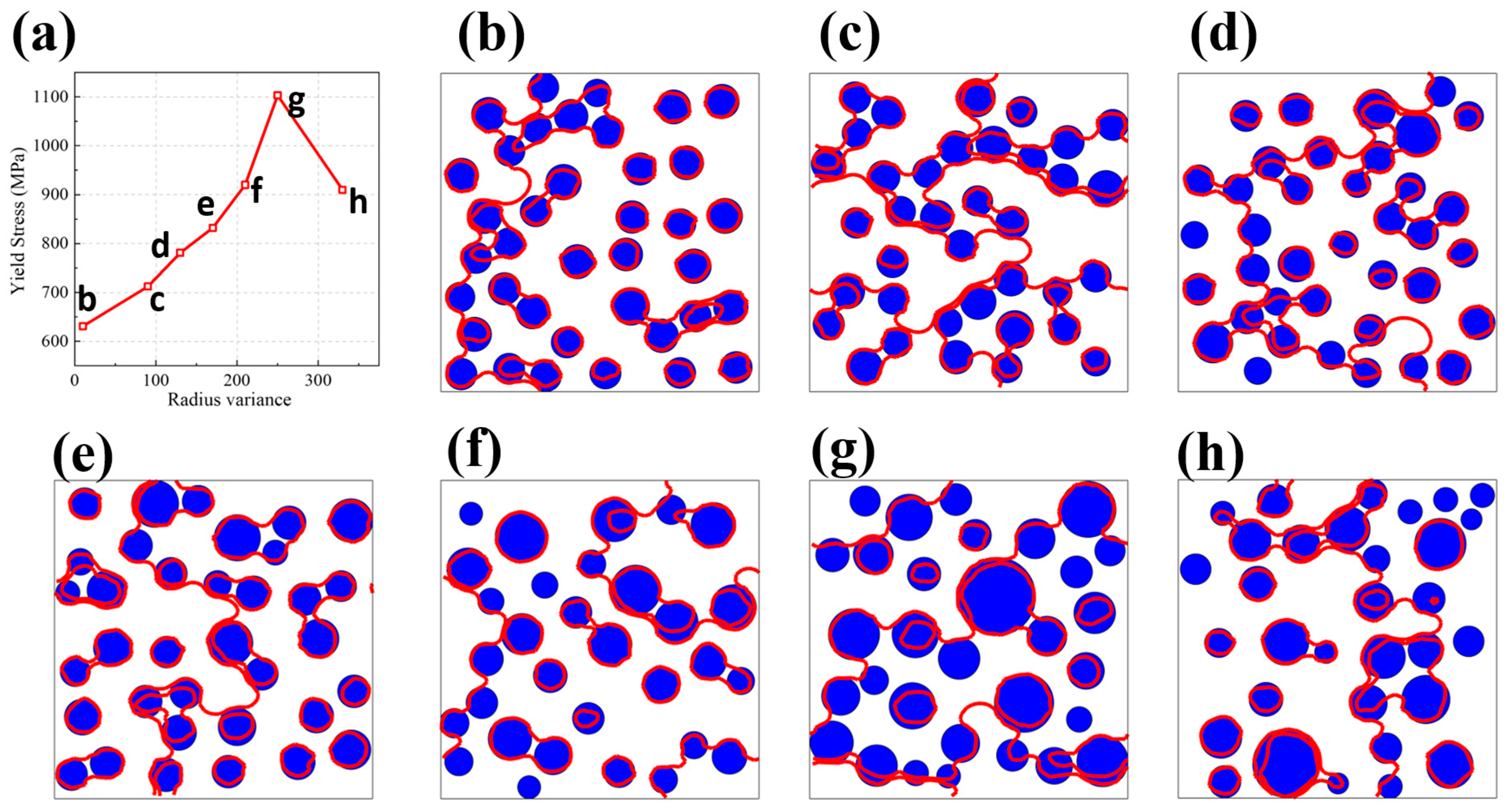
| Parameter | Input/Output | Descriptions |
|---|---|---|
| Average size of precipitates | Input features | Average size of the precipitated phases in DDD simulations. |
| Distribution of precipitates | Input features | Variance of the radii of the discrete precipitated phases. |
| Flow stresses | Output features | Average stress after the first drop point of the stress–strain curve. |
| Yield strength | Output features | The first drop point of the stress–strain curve. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, Y.; Liu, Y.; Teng, S.; Yuan, R.; Song, Y.; Sun, S.; Cai, S.; Li, Z.; Liu, B.; Gao, D.; et al. Impact of the Nano-Precipitation Size Distribution on the Mechanical Behavior of Nickel-Based Alloys by Experiment and Simulation. Nanomaterials 2025, 15, 1759. https://doi.org/10.3390/nano15231759
Wen Y, Liu Y, Teng S, Yuan R, Song Y, Sun S, Cai S, Li Z, Liu B, Gao D, et al. Impact of the Nano-Precipitation Size Distribution on the Mechanical Behavior of Nickel-Based Alloys by Experiment and Simulation. Nanomaterials. 2025; 15(23):1759. https://doi.org/10.3390/nano15231759
Chicago/Turabian StyleWen, Yuebing, Yunlong Liu, Shuhua Teng, Ruixue Yuan, Yuwei Song, Shiyuan Sun, Song Cai, Zhou Li, Bowen Liu, Dan Gao, and et al. 2025. "Impact of the Nano-Precipitation Size Distribution on the Mechanical Behavior of Nickel-Based Alloys by Experiment and Simulation" Nanomaterials 15, no. 23: 1759. https://doi.org/10.3390/nano15231759
APA StyleWen, Y., Liu, Y., Teng, S., Yuan, R., Song, Y., Sun, S., Cai, S., Li, Z., Liu, B., Gao, D., & Chen, Y. (2025). Impact of the Nano-Precipitation Size Distribution on the Mechanical Behavior of Nickel-Based Alloys by Experiment and Simulation. Nanomaterials, 15(23), 1759. https://doi.org/10.3390/nano15231759






