Abstract
The Ostwald ripening process in 3D and 2D systems has been studied in great detail over decades. In the application to surface nanoislands and nanodroplets, it is usually assumed that the capture coefficients of adatoms by supercritical nanoparticles of size scale as , where the growth index is smaller than unity. Here, we study theoretically the Ostwald ripening of 3D and 2D nanoparticles whose capture coefficients scale linearly with . This case includes submonolayer surface islands that compete for the flux of highly diffusive adatoms upon termination of the material influx. We obtain analytical solutions for the size distributions using the Lifshitz–Slezov scaled variables. The distributions over size and radius are monotonically decreasing, and satisfy the normalization condition for different values of the Lifshitz–Slezov constant . The obtained size distributions satisfy the Family–Vicsek scaling hypothesis, although the material influx is switched off. The model is validated by fitting the monotonically decreasing size distributions of Au nanoparticles that serve as catalysts for the vapor–liquid–solid growth of III-V nanowires on silicon substrates.
1. Introduction
The Ostwald ripening (OR) occurs in a late asymptotic stage of first-order phase transitions, where larger nuclei grow at the expense of smaller ones [1,2,3]. The OR process is usually considered at a time-independent total number of monomers (“mass” ) in a system [1,2,3,4,5,6,7,8,9,10,11,12,13], although it may also occur under weak material inputs [5,14]. When the critical size (number of monomers in the critical nucleus) enters the pre-existing size spectrum, subcritical nuclei with dissolve and increase supersaturation of a depleted mother phase, thus accelerating growth of supercritical nuclei with . This is described by the term in the first-order kinetic equation for the SD, with or 2 as the dimension of 3D or 2D nuclei [1,2,5,12]. The form of this kinetic equation and the physical meaning suggest that the appropriately scaled SD depends only on the scaled size . Lifshitz and Slezov [1,2] obtained the universal scaled SD in the specific case of diffusive decomposition of supersaturated solid solutions () at , where the regular growth rate of nuclei (at scales as . Later on, the Lifshitz–Slezov (LS) method was successfully used for modeling the OR process in 2D and 3D systems for the power-law capture coefficients with different growth indices [1,2,3,4,5,6,7,8,9,10,11,12,13,14], including the data of in situ monitoring by transmission electron microscopy (TEM) [4,7]. The classical LS spectra at are unimodal and tend to zero at and at the “blocking” point [1,2,5,6,8,9,10,11,12]. The shape of the LS spectra critically depends on the numerical value of a constant (the LS constant) that arises due to separation of variables in the kinetic equation for the SD. The scaled SDs at any are consistent with the normalization condition only for . The mass becomes discontinuous for . In their first paper [1], Lifshits and Slezov presented the arguments for the well-defined choice of . These arguments are definitely valid in the case of infinite initial spectra without a maximum nucleus. Later on, it was shown that other may be relevant in a more complex situation of finite spectra having a maximum nucleus size [9,12]. Therefore, the LS solutions generally yield a family of solutions for the SD, where the correct choice of the LS constant depends on the prehistory of the system in the preceding earlier growth steps.
According to the LS theory, the scaled SDs in the OR stage acquire universal shapes. This is strongly reminiscent of the Family–Viscek (FV) scaling [15], which is observed in the SDs of surface islands in the pre-coalescence stage of their growth [16,17,18,19,20,21,22,23] and has far-reaching implications in areas far beyond epitaxial growth [24,25,26,27,28]. One may also recall the similarity considerations that lead to the universal SDs of coagulating aerosols described by the Smoluchowsky equation [29,30] and even more complex models with simultaneous coagulation and condensation [31], or similarity solutions of the Becker–Döring equations for reversible growth [32,33,34,35]. The universality of the scaled SDs is important from a fundamental viewpoint and for understanding and modeling particular systems [4,5,6,13,14,25,36,37,38,39,40]. The case of size-linear growth rates or capture coefficients is relevant for large enough 2D surface islands [19,21,22,23,24], vertical nanowires [25], other 1D structures [14], and aerosols [31], which often yield exact solutions for the universal SDs [24,29,31,32,34,40]. In the limit of infinitely large ratios of the adatom diffusion coefficient over the deposition rate, the asymptotically linear size dependence of the capture coefficients of epitaxial islands arises due to subtle correlations between island sizes and separation [19,20,21,22,23]. For surface islands, the capture coefficient is roughly proportional to the mean capture zone area . Larger islands typically exhibit larger , which lead to faster growth of these inlands. In the agglomeration regime, is proportional to , which gives [19,23]. In the vapor–liquid–solid growth of semiconductor nanowires, the size linearity of vertical growth rate is explained by surface diffusion of adatoms along the entire length of nanowire sidewalls. In this regime of the diffusion-induced nanowire growth, the capture rate is given by , with as a constant that describes direct impingement of the vapor flux onto the droplet surface [25]. All these growth regimes are distinctly different from the power-law with . However, the size-linear model has not been considered in the theory of OR to our knowledge. Our goal in this paper is to obtain the analytic SDs for 3D and 2D nanoparticles with size-linear capture coefficients in the OR stage upon termination of the material influx. We will show that these SDs are monotonically decreasing in the entire range of possible LS constants from zero to , in contrast to the previously obtained unimodal LS functions at [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. It will also be demonstrated that these SDs satisfy a modified FV scaling hypothesis with the same sum rule for the island size, despite the fact that the nanoparticle density decreases in the OR stage. The model will be used to describe the SDs of Au nanodroplets on patterned SiOx/Si (111) substrates that are used as catalysts for the vapor–liquid–solid growth of semiconductor nanowires [25,41,42,43,44].
2. Model
We consider the SD over size , which equals the number of monomers in the nucleus, with as a dimensionless time. In a closed system, upon termination of a monomer input, supersaturation tends to zero. Due to a steep exponential dependence of the Zeldovich nucleation rate on supersaturation, no new particles nucleate in the asymptotic OR stage [1,2]. The nanoparticle density , the constant mass , and the average size are given by
Obviously, the average size can increase only due to a decreasing density, which is a typical feature of the OR process at . The first-order kinetic equation for the SD is written as [14]:
Here,
is the condensation rate, which contains a time-dependent supersaturation and is proportional to a size-dependent capture coefficient . In the theory of OR, it is usually assumed that [1,2,5,6,9,10,11,12,13,14], where the growth index depends on the dimensionality of the nucleus and the mother phase, and the mechanism of material transport into the nucleus [14]. Below, we consider the size-linear capture coefficient
which is relevant for a wide range of systems as discussed above.
The term in Equation (2) describes the evaporation of monomers from nuclei. The free energy of forming the nucleus with size in thermal units of is given by [14]
The second term describes the energetically favorable decrease in chemical potential due to condensation. The first term describes the energetically unfavorable process of forming a nucleus surface. The parameter equals the appropriately normalized surface energy : , with as the interatomic spacing in a condensed phase. It contains a large ratio of the characteristic surface energy over thermal energy and hence is much larger than unity. The surface area scales as for 2D and for 3D nucleus, hence for and for . The nucleus formation energy given by Equation (5) reaches its maximum at the critical size
The critical islands are in unstable equilibrium with a supersaturated mother phase; subcritical islands with tend to dissolve, while supercritical islands with tend to grow. From Equations (5) and (6), the derivative of the formation energy with respect to size equals for and . Using this in Equation (2), we obtain:
Regular growth continues as long as , corresponding to . The asymptotic OR stage occurs at , corresponding to the full depletion of a mother phase with monomers available for further growth. At , the critical size tends to infinity according to Equation (6). Therefore, one can use
This reduces Equation (2) to
which is the starting point for the theory of OR [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. In our case, the size-linear capture coefficient is given by Equation (4).
3. The Lifshitz–Slezov Method
Following the LS method [1], we search for the SD in the form
Such SD satisfies the normalization provided that the function is integrable from zero to infinity (or from zero to a locking point where becomes zero [1,2]). Substituting this SD into Equation (9) with and using Equation (8) to express the unknown supersaturation through the critical size, we arrive at a separable equation, whose form depends on the nucleus dimensionality . At , we obtain
Upon separation of variables, this is equivalent to
and
Here, is the LS integration constant, which is the same in Equations (12) and (13). From Equation (12), the critical size scales as :
Equation (12) for the scaled SD can be put in the form
This can be analytically integrated at any :
with as the normalization amplitude that will be found later. This function describes infinite LS spectra at and finite spectra at that tend to zero at the blocking point . Both infinite and finite spectra satisfy the required normalization of constant mass at . From Equation (16), it is clear that decreases faster than at a large when , corresponding to finite in Equation (1). At , equals zero at [1]. At , the distribution becomes non-physical, because it leads to discontinuous mass. At , Equation (16) is reduced to
Repeating the same calculations in 2D space, we obtain
Showing that the critical size of 2D islands scales as . The equation for the LS scaling function is given by
and has the solution
This function describes infinite LS spectra at and finite spectra at that tend to zero at the blocking point . The total mass remains finite at and becomes infinite at .
4. Density and Average Size
The time-dependent nanoparticle density is obtained from the corresponding Equation (1). From Equation (10) for the scaled SD, it is clear that the density is inversely proportional to the critical size. The integration of given by Equation (16) in the case of 3D case and Equation (20) in case of 2D is easily performed and yields the same result
for any . Calculation of the average size is more easily performed using the normalized SD
From the corresponding Equation (1), it is clear that the average size is proportional to :
The integral depends on the nucleus dimensionality. From Equations (10), (16) and (21), for 3D nuclei, we have
The integral in Equation (23) is calculated using
Here, the infinite upper integration limit that corresponds to is changed to unity for . Hence, the normalization is the same for infinite and finite spectra . Using Equation (25), we find:
Hence, the average size is smaller than critical for any . For example, at . From the normalization condition and Equations (21) and (26), we find the normalization amplitude in the form
From Equation (10), (20) and (21), for 2D nuclei we have
The integral in Equation (23) is calculated using
As above, infinite and finite upper integration limits correspond to and , respectively. This gives another relationship between the average and critical sizes in 2D space:
As in the previous case, the average size is smaller than critical for any . For example, at . The normalization amplitude of the SD is obtained from the condition , Equations (21) and (30), and equals
It is easy to check that
in all cases, as it should be in the OR process at .
5. Size Distributions in Different Variables
Using the obtained normalization amplitudes given by Equation (27) for 3D nuclei and (31) for 2D nuclei, the size distributions over the natural size (which equals the number of monomers in the nucleus) in the LS variables are obtained in the form
The scaled SD of 3D nuclei is given by
For 2D nuclei, the scaled SD has the form
These SDs are relevant at , that is, smaller than 4 for 3D nuclei and smaller than 3 for 2D nuclei. In both cases, the scaled SDs are monotonically decreasing, and discontinuous at ( at and at ). As discussed above, the scaled SDs are infinite at and finite at , with the maximum scaled size . The scaled SDs satisfy the required sum rule
for any . At , the infinite limit of integration is changed to . Figure 1 shows the infinite scaled SDs at and , and finite scaled SD at with a blocking point at , obtained from Equation (34) at and (35) at .
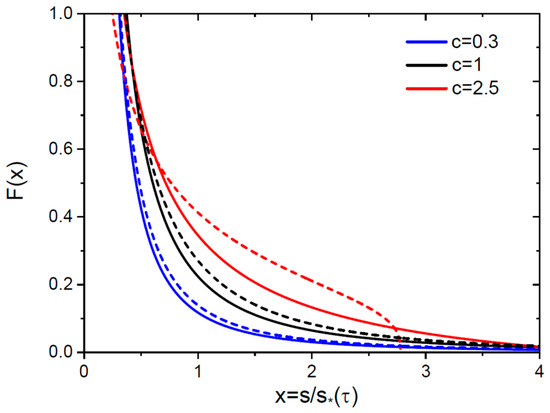
Figure 1.
Scaled SDs versus scaled size at three different for 3D (solid lines) and 2D (dashed lines, same colors for each ) nuclei.
Let us now consider the radius distributions of nuclei, studied in the original works of Lifshitz and Slezov at [1,2]. According to the general rule [14], the radius distribution should preserve the normalization:
The radius and the critical radius or, more generally, the linear sizes of a nanoparticle of any shape are related to the corresponding sizes and according to
where is an interatomic spacing. Using Equations (37) and (38) at in Equations (33) and (34), the distribution over radius of 3D nuclei is obtained in the form
From Equation (14), the critical radius of 3D nuclei increases linearly with time:
For 2D nuclei, the radius distribution is obtained from Equations (37) and (38) at and Equations (33) and (35). The result is given by
From Equation (18), the critical radius of 2D nuclei also scales linearly with time:
A common feature of the obtained radius distributions is that the discontinuities in the scaled distributions at are circumvented due to for 3D nuclei and for 2D nuclei. Consequently, the scaled functions tend to a constant at and monotonically decrease with , as shown in Figure 2 for the same parameters as above.
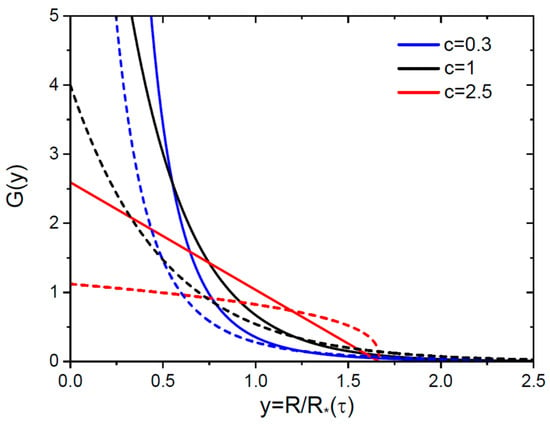
Figure 2.
Scaled radius distributions versus scaled radius at three different for 3D (solid lines) and 2D (dashed lines, same colors for each ) nuclei.
As mentioned above, the scaled LS distributions at [1,2,5,9,10,12] are unimodal. They vanish at and at the blocking point, and reach a maximum around [1]. Our results for the size-linear capture coefficients at are different, because the scaled SDs over size and radius are monotonically decreasing. This property of the linear model for correlates with the earlier results of Refs. [31,32,34], where the monotonically decreasing scaled SDs at were obtained in different growth stages without OR, including the simplest exponential scaling function . The monotonically decreasing scaled SDs at , with discontinuity at for physically mean that small subcritical nuclei remain most representative in the ensemble of nanoparticles. We note, however, that our solution yields unimodal SD over the so-called invariant size for which the regular growth rate becomes size-independent [12,14]. This invariant size is commonly used in nucleation and growth theory because the time-invariant SD of nanoparticles in the regular growth stage significantly simplifies mathematical computations and analysis of experimental data [14]. At , the invariant size is given by
because . Using for the “invariant” SD such that , we obtain:
Using Equation (33) for , the distribution over the invariant size of 3D nuclei becomes
where is the critical invariant size.
From Equation (34), we obtain the scaled invariant SD of 3D nuclei:
Equation (35) yields the scaled invariant SD of 2D islands in the form
These scale as at for any and . These scaling functions are shown in Figure 3 for the same as above. The distributions at resemble the classical LS shapes [1,2,5,6,7,8,9,10,11,12,13,14], because they are unimodal and tend to zero at and at the blocking point . The infinite SDs at and are unimodal, but different from the usual LS shapes with the blocking points.
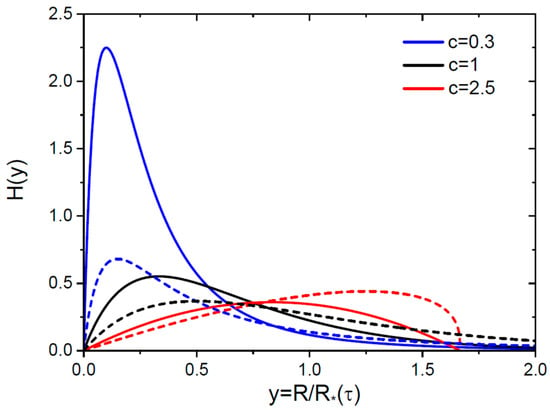
Figure 3.
Scaled invariant distributions versus scaled radius at three different shown in the legend for 3D (solid lines) and 2D (dashed lines, same colors for each ) nuclei.
The FV scaling considered widely in the theory of 2D surface growth is formulated as follows [15,16,17,18,19,20,21,22,23,24]. In the limit of infinitely large ratios of the adatom diffusion coefficient over the deposition rate , the island SD over is expected to have the form for all but very short times. Here, is the surface coverage, is the average size and is a universal function of the scaled size . This type of scaling was studied based on the rate equations for irreversible growth (with the critical size one) under a time-independent deposition rate [18,19,22,23,24]. In this case, both island density and average size increase with time. Due to , any FV scaling function should satisfy the two sum rules for the island density and size. Due to subtle correlations between the island size and separation, the capture coefficients are much more complex than linear, but become asymptotically linear at large [19,21,22,23]. The simplified linear model yields, however, a monotonically decreasing FV scaling function that satisfies both sum rules [24]. The OR process considered here is very different from irreversible growth, and occurs upon the flux termination. The mass equals the surface coverage for 2D islands, but it stays constant rather than increases linearly with time. At , the average size increases only due to the decrease in the island density that occurs due to dissolution of smaller islands into monomers. However, our analysis shows that the FV scaling hypothesis holds in the OR stage.
Indeed, using Equation (26) or (30) for the average size of 3D or 2D islands, the LS representation of the scaled SD given by Equation (33) can equivalently be presented in the FV form:
The FV scaling function for 3D islands is obtained from Equation (34) for , re-written in terms of :
In 2D space, Equation (35) for yields the FV scaling function of the form
These scaling functions satisfy the sum rule for the average island size
for any and . The time dependencies of the average size are given by Equation (14) for 3D islands and (18) for 2D islands, while the density is related to the average size by Equation (32) in both cases. The FV scaling functions, shown in Figure 4 for the same parameters as above, are not very different from the LS scaling functions in Figure 1. This is not surprising, because they are obtained by the simple transformation of variables from to .
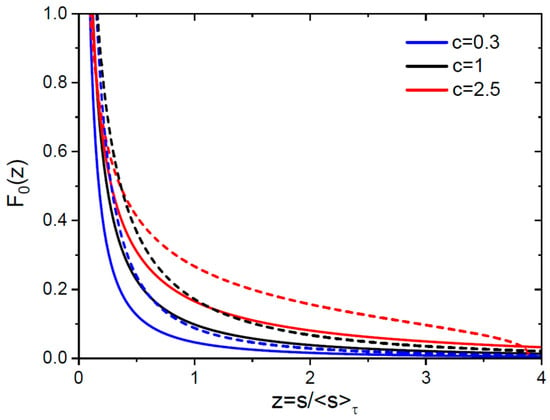
Figure 4.
Scaled SDs versus scaled size at three different for 3D (solid lines) and 2D (dashed lines, same colors for each ) islands.
6. Theory and Experiment
From the early days of nanowire physics and technology [41], Au has been used as catalyst for the vapor–liquid–solid growth of vertical nanowires of elemental [41] and III-V [25,42,43] semiconductors. To fabricate size-uniform nanowires in regular arrays, Au nanodroplets are positioned in the lithographically defined openings in an oxide or nitride mask on a substrate, often Si(111) [44,45]. It is important therefore to understand and control the radius distribution of Au droplets on SiOx/Si(111) prior to the nanowire growth [44,45]. In Ref. [45] the Au droplet dynamics on SiOx/Si(111) was monitored in situ using environmental TEM. Au was deposited onto the substrate at a low temperature, and then the temperature was increased up to ~ 800 °C to facilitate surface diffusion, formation of Au droplets, and filling the openings in the oxide layer. It was found that the droplet dynamics on the SiOx/Si(111) surface consist of distinctly different steps involving different processes. The 3D droplets are immovable at the beginning and participate in the OR process. In this step, the total volume of Au droplets is kept constant; smaller droplets disappear and larger droplets grow in size. The droplet density gradually decreases, and their average radius increases linearly with time. These features are typical for the classical OR process at a constant mass. In the next step, Au droplets start to move and coagulate. This process is complicated by the presence of an additional influx of Au adatoms from the surrounding substrate area. Finally, large droplets migrate to the openings, dissolve at a certain distance from the boundaries, Au adatoms migrate to the pinholes, and the droplets reappear in the openings.
Figure 5 shows the scaled radius distributions of Au nanodroplets in the LS variables. The scaled distributions are obtained from the radius histograms of Ref. [45] at different annealing times from 90 s to 160 s, corresponding to the OR of immovable Au droplets at a constant mass. The migration of droplets and their binary coagulation cannot be described within the current model. This sets the upper limit for the annealing time of 160 s where these processes start. The histograms were obtained from the same sample size of 20 µm × 20 µm. We can clearly see the monotonically decreasing shape of the scaled SDs despite the scattered data, at least for large enough droplets observed in TEM. These SDs are well-fitted by Equation (39) for the LS radius distribution at , as demonstrated by the curves at and in the figure. We saw earlier that the values of around unity yield close-to-exponential LS curves. Therefore, the fitting values of are chosen to match the exponential SDs in the regular growth stage before the OR [14] and the in the coagulation stage after the OR [30]. The unknown critical radii are calculated from the measured average radii using Equation (26). We may thus conclude that the capture rates of these 3D droplets are approximately linear in , because other LS spectra at any yield the unimodal SDs that are not observed experimentally. We suspect that the linear behavior of at large is related to the high diffusivity of Au adatoms on the oxide surface, similarly to Refs. [19,23]. The microscopic analysis of the dependence in this system requires additional studies and will be presented elsewhere.
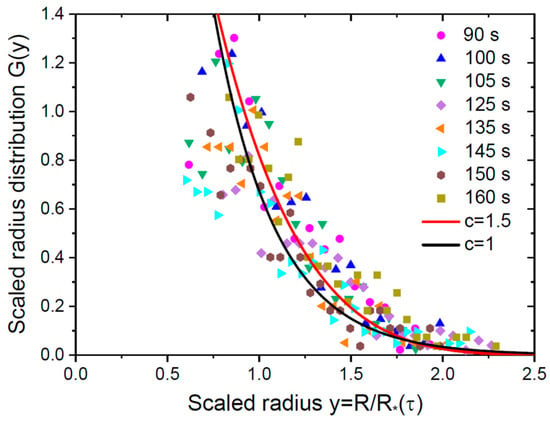
Figure 5.
Scaled radius distributions of Au nanodroplets versus the scaled radius at different times shown in legend, obtained from the data of Ref. [45] (symbols). Lines show the fits by Equation (39) at and .
7. Conclusions
In summary, we have obtained the analytic LS spectra in the OR stage of 3D and 2D nanoparticles with size-linear capture coefficients . It has been shown that the scaled SDs over are monotonically decreasing and discontinuous at . The sum rule for the constant total mass is satisfied for any value of the LS constant between zero and , with for 3D and for 2D particles. The scaled SDs are infinite at and finite at , with the blocking point at . The scaled LS SDs over the radius (or linear size of anisotropic crystal islands) are monotonically decreasing, but tend to a constant at . The unimodal SDs that vanish at are observed only for the invariant size variable for which the regular growth rate is size-independent. It has been demonstrated that the LS spectra can equivalently be presented in the FV scaling form. Therefore, the FV scaling hypothesis works well also in the OR stage, although it was originally proposed for epitaxial islands growing under a constant deposition flux with the critical size one. The obtained results should be useful for modeling and analysis of the monotonically decreasing SDs in the OR stage, as demonstrated by the example of Au nanodroplets on SiOx/Si(111) substrates. The 2D surface islands in different material systems and morphologies require a separate study. It will be interesting to consider a more complex growth scenario for the OR of 2D islands, where the scaled capture coefficient have the form with the asymptotic linear increase at large [19,23]. This case corresponds to a wide range of practically important epitaxial systems with very high ratios of the adatom diffusion coefficient over the deposition rate. Scaling of the capture coefficient and the decomposition rate of subcritical nuclei with the average size should lead to a scaling solution for the SD, but its form is expected to be very different from the classical LS shapes. The physical choice of the LS constant should depend on the shape of the initial SD that is determined in an early growth stage preceding the OR process. We plan to study these questions in a future paper.
Author Contributions
Conceptualization, V.G.D.; Formal analysis, V.G.D.; Data curation, E.D.L.; Writing—review & editing, V.G.D. and E.D.L.; Supervision, V.G.D. All authors have read and agreed to the published version of the manuscript.
Funding
VGD gratefully acknowledges St. Petersburg State University for a research project No. 129360164.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Lifshitz, I.M.; Slezov, V.V. Kinetics of diffusive decomposition of supersaturated solid solutions. Sov. Phys. JETP 1959, 8, 331. [Google Scholar]
- Lifshitz, I.M.; Slezov, V.V. The kinetics of precipitation from supersaturated solid solutions. J. Phys. Chem. Solids 1961, 19, 35. [Google Scholar] [CrossRef]
- Galvani, N.; Pitois, O.; Cohen-Addad, S. Coarsening of bubble assemblies: From dry foams to dilute bubbly liquids. J. Col. Interface Sci. 2025, 696, 137661. [Google Scholar] [CrossRef]
- Geng, L.; Liu, Q.; Chen, J.; Jia, P.; Ye, H.; Yan, J.; Zhang, L.; Tang, Y.; Huang, J. In situ observation of electrochemical Ostwald ripening during sodium deposition. Nano Res. 2022, 15, 2650. [Google Scholar] [CrossRef]
- Kukushkin, S.A.; Osipov, A.V. Thin-film condensation processes. Phys. Usp. 2007, 41, 983. [Google Scholar] [CrossRef]
- Voorhees, P.W. The theory of Ostwald ripening. J. Stat. Phys. 1985, 38, 231. [Google Scholar] [CrossRef]
- Simonsen, S.B.; Chorkendorff, I.; Dahl, S.; Skoglundh, M.; Sehested, J.; Helveg, S. Ostwald ripening in a Pt/SiO2 model catalyst studied by in situ TEM. J. Catal. 2011, 281, 147. [Google Scholar] [CrossRef]
- Koroleva, M.Y.; Yurtov, E.V. Ostwald ripening in macro- and nanoemulsions. Russ. Chem. Rev. 2021, 90, 293. [Google Scholar] [CrossRef]
- Giron, B.; Meerson, B.; Sasorov, P.V. Weak selection and stability of localized distributions in Ostwald ripening. Phys. Rev. E 1998, 58, 4213. [Google Scholar] [CrossRef]
- Behrens, M.A.; Franzén, A.; Carlert, S.; Skantze, U.; Lindfors, L.; Olsson, U. On the Ostwald ripening of crystalline and amorphous nanoparticles. Soft Matter 2025, 21, 2349. [Google Scholar] [CrossRef]
- Streets, A.M.; Quake, S.R. Ostwald ripening of clusters during protein crystallization. Phys. Rev. Lett. 2010, 104, 178102. [Google Scholar] [CrossRef]
- Dubrovskii, V.G.; Kazansky, M.A.; Nazarenko, M.V.; Adzhemyan, L.T. Numerical analysis of Ostwald ripening in two-dimensional systems. J. Chem. Phys. 2011, 134, 094507. [Google Scholar] [CrossRef]
- Slezov, V.V. Kinetics of First-Order Phase Transitions; Wiley: Berlin, Germany, 2009. [Google Scholar]
- Dubrovskii, V.G. Nucleation Theory and Growth of Nanostructures; Springer: Heidelberg, Germany, 2014. [Google Scholar]
- Vicsek, T.; Family, F. Dynamic scaling for aggregation of clusters. Phys. Rev. Lett. 1984, 52, 1669. [Google Scholar] [CrossRef]
- Evans, J.W.; Thiel, P.A.; Bartelt, M.C. Morphological evolution during epitaxial thin film growth: Formation of 2D islands and 3D mounds. Surf. Sci. Rep. 2006, 61, 1–128. [Google Scholar] [CrossRef]
- Einax, M.; Dieterich, W.; Maass, P. Colloquium: Cluster growth on surfaces: Densities, size distributions, and morphologies. Rev. Mod. Phys. 2013, 85, 921. [Google Scholar] [CrossRef]
- Bartelt, M.C.; Evans, J.W. Scaling analysis of diffusion-mediated island growth in surface adsorption processes. Phys. Rev. B 1992, 46, 12675. [Google Scholar] [CrossRef]
- Bartelt, M.C.; Evans, J.W. Exact island-size distributions for submonolayer deposition: Influence of correlations between island size and separation. Phys. Rev. B 1996, 54, R17359. [Google Scholar] [CrossRef] [PubMed]
- Bales, G.S.; Chrzan, D.C. Dynamics of irreversible island growth during submonolayer epitaxy. Phys. Rev. B 1994, 50, 6057. [Google Scholar] [CrossRef] [PubMed]
- Gibou, F.G.; Ratsch, C.; Caflisch, R.E. Capture numbers in rate equations and scaling laws for epitaxial growth. Phys. Rev. B 2003, 67, 155403. [Google Scholar] [CrossRef]
- Vvedensky, D.D. Scaling functions for island-size distributions. Phys. Rev. B 2000, 62, 15435. [Google Scholar] [CrossRef]
- Korner, M.; Einax, M.; Maass, P. Capture numbers and island size distributions in models of submonolayer surface growth. Phys. Rev. B 2012, 86, 085403. [Google Scholar] [CrossRef]
- Dubrovskii, V.G. A general solution to the continuum rate equation for island-size distributions: Epitaxial growth kinetics and scaling analysis. Nanomaterials 2025, 15, 396. [Google Scholar] [CrossRef]
- Dubrovskii, V.G.; Berdnikov, Y.; Schmidtbauer, J.; Borg, M.; Storm, K.; Deppert, K.; Johansson, J. Length distributions of nanowires growing by surface diffusion. Cryst. Growth Des. 2016, 16, 2167. [Google Scholar] [CrossRef]
- Fujimoto, K.; Hamazaki, R.; Kawaguchi, Y. Family-Vicsek scaling of roughness growth in a strongly interacting Bose gas. Phys. Rev. Lett. 2020, 124, 210604. [Google Scholar] [CrossRef]
- Bhakuni, D.S.; Lev, Y.B. Dynamic scaling relation in quantum many-body systems. Phys. Rev. B 2024, 110, 014203. [Google Scholar] [CrossRef]
- Aditya, S.; Roy, N. Family-Vicsek dynamical scaling and Kardar-Parisi-Zhang-like superdiffusive growth of surface roughness in a driven one-dimensional quasiperiodic model. Phys. Rev. B 2024, 109, 035164. [Google Scholar] [CrossRef]
- Friedlander, S.K. Similarity considerations for the particle size spectrum of a coagulating, sedimenting aerosol. J. Meteorol. 1960, 17, 479. [Google Scholar] [CrossRef]
- Piskunov, V.N.; Golubev, A.I.; Goncharov, E.A.; Ismailova, N.A. Kinetic modeling of composite particles coagulation. J. Aerosol Sci. 1997, 28, 1215. [Google Scholar] [CrossRef]
- Aloyan, A.E.; Egorov, V.D.; Marchuk, G.I.; Piskunov, V.N. Aerosol formation mathematical modelling with consideration for condensation kinetics. Rus. J. Num. Anal. Math. Model. 1992, 7, 457. [Google Scholar]
- Brilliantov, N.V.; Krapivsky, P.L. Non-scaling and source-induced scaling behaviour in aggregation models of movable monomers and immovable clusters. J. Phys. A Math. Gen. 1991, 24, 4787. [Google Scholar] [CrossRef]
- Wattis, J.A.D. Similarity solutions of a Becker-Döring system with time-dependent monomer input. J. Phys. A Math. Gen. 2004, 37, 7823. [Google Scholar] [CrossRef]
- Dubrovskii, V.G. Analytical solutions of the Becker–Doring equations with size-linear rate constants: Transition from limited to infinite growth regime. J. Phys. A Math. Theor. 2025, 58, 29500. [Google Scholar] [CrossRef]
- King, J.R.; Wattis, J.A.D. Asymptotic solutions of the Becker–Döring equations with size-dependent rate constants. J. Phys. A Math. Gen. 2002, 35, 1357. [Google Scholar] [CrossRef]
- Petrov, P.P.; Miller, W.; Rehse, U.; Fornari, R. A new method for calculation of island-size distribution in submonolayer epitaxial growth. Appl. Math. Model. 2011, 35, 1331. [Google Scholar] [CrossRef]
- González, D.L.; Camargo, M.; Sánchez, J.A. Island size distribution with hindered aggregation. Phys. Rev. E 2018, 97, 052802. [Google Scholar] [CrossRef] [PubMed]
- Álvarez-Cuartas, J.D.; González-Cabrera, D.L.; Camargo, M. Epitaxial growth in one dimension. J. Phys Cond. Matter 2024, 36, 463001. [Google Scholar] [CrossRef]
- Dubrovskii, V.G. Family-Vicsek scaling in classical nucleation theory. Phys. Rev. E 2025, 111, 064114. [Google Scholar] [CrossRef]
- Tomellini, M.; De Angelis, M. Fokker-Planck equation for the crystal-size probability density in progressive nucleation and growth with application to lognormal, Gaussian and gamma distributions. J. Cryst. Growth 2025, 650, 127970. [Google Scholar] [CrossRef]
- Wagner, R.S.; Ellis, W.C. Vapor-liquid-solid mechanism of single crystal growth. Appl. Phys. Lett. 1964, 4, 89. [Google Scholar] [CrossRef]
- Dalacu, D.; Kam, A.; Austing, D.G.; Wu, X.; Lapointe, J.; Aers, G.C.; Poole, P.J. Selective-area vapour–liquid–solid growth of InP nanowires. Nanotechnology 2009, 20, 395602. [Google Scholar] [CrossRef]
- Kelrich, A.; Calahorra, Y.; Greenberg, Y.; Gavrilov, A.; Cohen, S.; Ritter, D. Shadowing and mask opening effects during selective-area vapor-liquid-solid growth of InP nanowires by metalorganic molecular beam epitaxy. Nanotechnology 2013, 24, 475302. [Google Scholar] [CrossRef] [PubMed]
- Hijazi, H.; Leroy, F.; Monier, G.; Grégoire, G.; Gil, E.; Trassoudaine, A.; Dubrovskii, V.G.; Castelluci, D.; Goktas, N.I.; LaPierre, R.R.; et al. Dynamics of Au droplet formation on SiO2/Si(111) surface. J. Phys. Chem. C 2020, 124, 11946. [Google Scholar] [CrossRef]
- Panciera, F.; Dubrovskii, V.G.; Reznik, R.R.; Cirlin, G.E.; Harmand, J.C. In situ monitoring and modeling of the Au droplet dynaimcs on patterned SiOx/Si(111) substrate. ACS Nano 2025, submitted.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).