On the Energy Contributions Driving Pyridine Adsorption on Silver and Gold Nanoparticles
Abstract
1. Introduction
2. Methods
2.1. Kohn–Sham Fragment Localized Molecular Orbitals
2.2. Kohn–Sham Fragment Energy Decomposition Analysis
- Calculation of A and B DFT energies ( and ) in the gas phase using the full AO basis. The Self-Consistent Field (SCF) converged density matrix of the two fragments is defined as and .
- From the isolated fragment densities, the interaction frozen energy terms can be calculated by [69]where . , , and represent the electrostatic, HF exchange, and correlation energy contributions to the frozen interaction energy.
- To obtain a physically sound description, the antisymmetry of the total wavefunction must be enforced. A convenient route is to orthonormalize the dimer MOs (i.e., ) using a Löwdin procedure [103]. From the orthonormalized MOs, the density matrix and density function related to the antisymmetrized (ASN) wavefunction can be calculated. These define the physically admissible single-determinant representation of the frozen fragment MOs. The associated energy is then evaluated by inserting and into Equation (1).
- By antisymmetrizing the system, we obtain a delocalized wavefunction. Therefore, a partial charge transfer between the two fragments occurs. We can then perform a KS-FLMO procedure to construct the density matrices () and energies () of the moieties in the electronic structure of the ASN dimer. This allows us to decompose the ASN energy into the electrostatic, HF exchange, correlation, and electronic preparation energies as [69]We can now calculate the energy change due to the antisymmetrization of the total wavefunction, , which can be further decomposed into electrostatic, HF exchange, and correlation contributions:where contains the energy variations due to electrostatic, HF exchange, and electronic preparation. By combining Equation (8) with Equation (7a), we can define the electrostatic (), exchange (), and repulsion () quantities that are commonly exploited in other EDA techniques:
- To obtain the energetic contributions due to orbital relaxation, the total system DFT energy E is minimized (see Equation (1)).
- The Self-Consistent Field (SCF)-converged density of the total system fully accounts for charge transfer between the two subsystems and the orbital relaxation. The obtained MOs are localized by an additional KS-FLMO procedure, to obtain the fragment density matrices () and energies () in the relaxed electronic structure of the dimer.
- By using the definition of (see Equation (4d), readjusted in a GKS framework; see Equation (1b)), the total interaction energy (Equation (5)) can be finally decomposed as [69]where accounts for the dispersion interaction in additive schemes (such as Grimme’s D3 or D4 [81,82,83,84,85,86]) and is calculated from the dispersion energies of the A and B monomers (, ), and the dimer (). We remark that, in case an NLC functional is exploited, this term is accounted for by the correlation energy contribution. In both cases, it is worth highlighting that KS-FEDA total interaction energies correspond to the interaction energies computed using the underlying density functional [69]. In general, interaction energies computed using KS-FEDA display energy deviations with respect to CCSD(T) well below the chemical accuracy (1 kcal/mol) for common intermolecular datasets (A24 [104], S22 [105], and IHB15 [106]).By combining Equations (9) and (10), we can decompose the total interaction energy (see Equation (5)) as follows:where accounts for the interaction energy due to the orbital relaxation, and readsBy explicating all the terms in Equation (11) (using Equations (8) and (12)), we obtain the total 12-term KS-FEDA [69]:This energy decomposition allows for investigating the physical origin of the and energy terms, and, remarkably, underscores how the interaction energy terms evolve as the densities of the monomers evolve as the adduct is electronically formed. Furthermore, Equation (11) can also be rewritten by including the total correlation energy (see Equation (10d)), resulting in a six-term KS-FEDA:where and can also be combined, similarly to most EDA schemes, such as KM-EDA and SAPT. In particular, SAPT decomposes the total interaction energy into electrostatic, exchange (also accounting for repulsive effects), polarization (or induction), and dispersion. We have recently shown that KS-FEDA energy terms directly correlate with SAPT ones, by the following correspondence [69]To summarize, the KS-FEDA protocol comprises (i) two monomer SCF optimizations in the full AO basis, (ii) two KS-FLMO localization cycles, and (iii) one SCF on the dimer.
3. Results
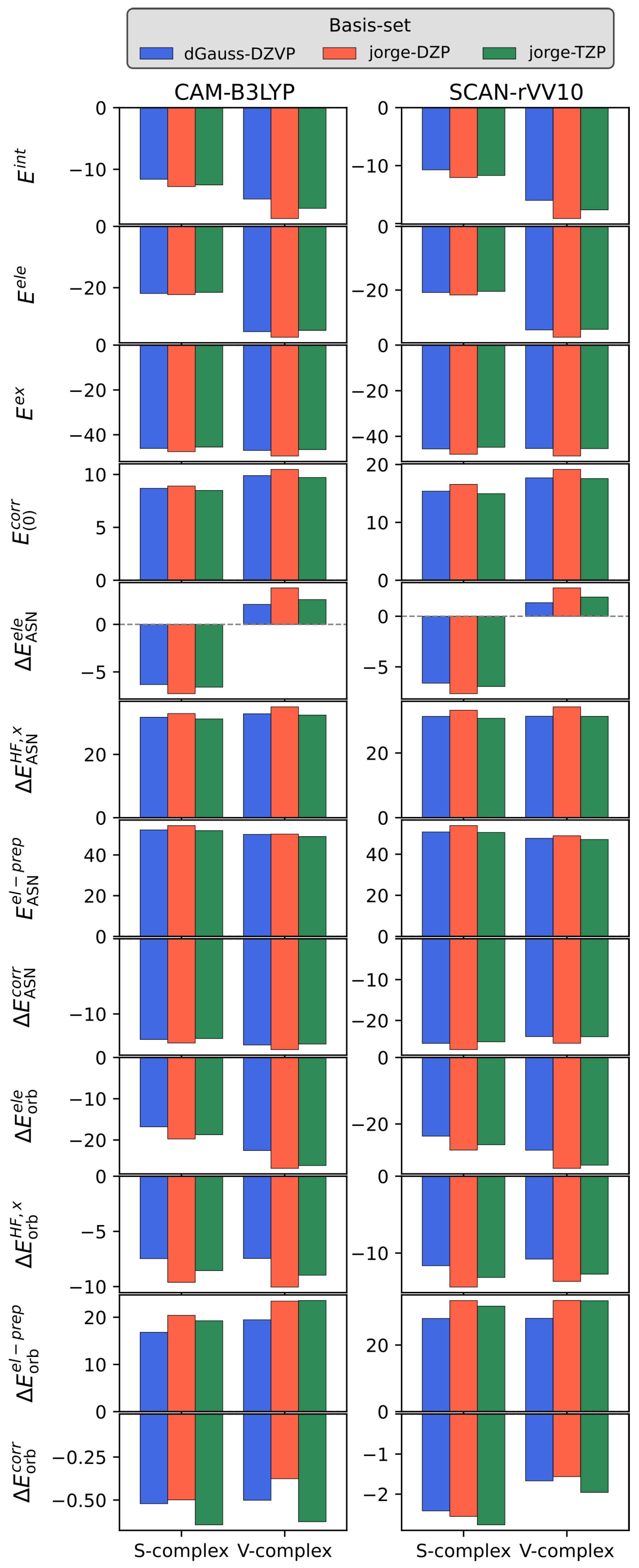
3.1. Basis Set Dependence
3.2. KS-FEDA on Py-Ag and Py-Au
4. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, J.; Yang, H.B.; Zhou, D.; Liu, B. Adsorption energy in oxygen electrocatalysis. Chem. Rev. 2022, 122, 17028–17072. [Google Scholar] [CrossRef]
- Schimka, L.; Harl, J.; Stroppa, A.; Grüneis, A.; Marsman, M.; Mittendorfer, F.; Kresse, G. Accurate surface and adsorption energies from many-body perturbation theory. Nat. Mater. 2010, 9, 741–744. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Chen, Y.; Li, B.; Liu, S.P.; Liu, X.; Jiang, Q. Determining the adsorption energies of small molecules with the intrinsic properties of adsorbates and substrates. Nat. Commun. 2020, 11, 1196. [Google Scholar] [CrossRef] [PubMed]
- Xie, C.; Yan, D.; Chen, W.; Zou, Y.; Chen, R.; Zang, S.; Wang, Y.; Yao, X.; Wang, S. Insight into the design of defect electrocatalysts: From electronic structure to adsorption energy. Mater. Today 2019, 31, 47–68. [Google Scholar] [CrossRef]
- Montemore, M.M.; Medlin, J.W. Scaling relations between adsorption energies for computational screening and design of catalysts. Catal. Sci. Technol. 2014, 4, 3748–3761. [Google Scholar] [CrossRef]
- Ding, X.; Li, Z.; Yang, J.; Hou, J.; Zhu, Q. Adsorption energies of molecular oxygen on Au clusters. J. Chem. Phys. 2004, 120, 9594–9600. [Google Scholar] [CrossRef]
- Sardar, R.; Funston, A.M.; Mulvaney, P.; Murray, R.W. Gold nanoparticles: Past, present, and future. Langmuir 2009, 25, 13840–13851. [Google Scholar] [CrossRef] [PubMed]
- Dreaden, E.C.; Alkilany, A.M.; Huang, X.; Murphy, C.J.; El-Sayed, M.A. The golden age: Gold nanoparticles for biomedicine. Chem. Soc. Rev. 2012, 41, 2740–2779. [Google Scholar] [CrossRef]
- Amendola, V.; Pilot, R.; Frasconi, M.; Maragò, O.M.; Iatì, M.A. Surface plasmon resonance in gold nanoparticles: A review. J. Phys. Condens. Matter 2017, 29, 203002. [Google Scholar] [CrossRef]
- Link, S.; El-Sayed, M.A. Size and temperature dependence of the plasmon absorption of colloidal gold nanoparticles. J. Phys. Chem. B 1999, 103, 4212–4217. [Google Scholar] [CrossRef]
- Mock, J.J.; Barbic, M.; Smith, D.R.; Schultz, D.; Schultz, S. Shape effects in plasmon resonance of individual colloidal silver nanoparticles. J. Chem. Phys. 2002, 116, 6755–6759. [Google Scholar] [CrossRef]
- Sabela, M.; Balme, S.; Bechelany, M.; Janot, J.M.; Bisetty, K. A review of gold and silver nanoparticle-based colorimetric sensing assays. Adv. Eng. Mater. 2017, 19, 1700270. [Google Scholar] [CrossRef]
- McFarland, A.D.; Van Duyne, R.P. Single silver nanoparticles as real-time optical sensors with zeptomole sensitivity. Nano Lett. 2003, 3, 1057–1062. [Google Scholar] [CrossRef]
- Lee, K.S.; El-Sayed, M.A. Gold and silver nanoparticles in sensing and imaging: Sensitivity of plasmon response to size, shape, and metal composition. J. Phys. Chem. B 2006, 110, 19220–19225. [Google Scholar] [CrossRef] [PubMed]
- Nicoli, L.; Sodomaco, S.; Lafiosca, P.; Giovannini, T.; Cappelli, C. Atomistic Multiscale Modeling of Colloidal Plasmonic Nanoparticles. ACS Phys. Chem. Au 2024, 4, 669–678. [Google Scholar] [CrossRef] [PubMed]
- Kamat, P.V.; Hartland, G.V. Plasmons for energy conversion. ACS Energy Lett. 2018, 3, 1467–1469. [Google Scholar] [CrossRef]
- Cushing, S.K.; Wu, N. Progress and perspectives of plasmon-enhanced solar energy conversion. J. Phys. Chem. Lett. 2016, 7, 666–675. [Google Scholar] [CrossRef]
- Lafiosca, P.; Nicoli, L.; Pipolo, S.; Corni, S.; Giovannini, T.; Cappelli, C. Real-time formulation of atomistic electromagnetic models for plasmonics. J. Phys. Chem. C 2024, 128, 17513–17525. [Google Scholar] [CrossRef]
- Cortés, E.; Besteiro, L.V.; Alabastri, A.; Baldi, A.; Tagliabue, G.; Demetriadou, A.; Narang, P. Challenges in plasmonic catalysis. ACS Nano 2020, 14, 16202–16219. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, C.; Zheng, H.; Xu, H. Plasmon-driven catalysis on molecules and nanomaterials. Acc. Chem. Res. 2019, 52, 2506–2515. [Google Scholar] [CrossRef]
- Camargo, P.H.; Cortés, E. Plasmonic Catalysis: From Fundamentals to Applications; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Liebsch, A. Surface-plasmon dispersion and size dependence of Mie resonance: Silver versus simple metals. Phys. Rev. B 1993, 48, 11317. [Google Scholar] [CrossRef]
- Giovannini, T.; Bonatti, L.; Lafiosca, P.; Nicoli, L.; Castagnola, M.; Illobre, P.G.; Corni, S.; Cappelli, C. Do we really need quantum mechanics to describe plasmonic properties of metal nanostructures? ACS Photonics 2022, 9, 3025–3034. [Google Scholar] [CrossRef]
- Kelly, K.L.; Coronado, E.; Zhao, L.L.; Schatz, G.C. The optical properties of metal nanoparticles: The influence of size, shape, and dielectric environment. J. Phys. Chem. B 2003, 107, 668–677. [Google Scholar] [CrossRef]
- Baumberg, J.J. Picocavities: A primer. Nano Lett. 2022, 22, 5859–5865. [Google Scholar] [CrossRef]
- Giovannini, T.; Nicoli, L.; Corni, S.; Cappelli, C. The Electric Field Morphology of Plasmonic Picocavities. Nano Lett. 2025, 25, 10802–10808. [Google Scholar] [CrossRef] [PubMed]
- Noguez, C. Surface plasmons on metal nanoparticles: The influence of shape and physical environment. J. Phys. Chem. C 2007, 111, 3806–3819. [Google Scholar] [CrossRef]
- Nicoli, L.; Lafiosca, P.; Grobas Illobre, P.; Bonatti, L.; Giovannini, T.; Cappelli, C. Fully atomistic modeling of plasmonic bimetallic nanoparticles: Nanoalloys and core-shell systems. Front. Photonics 2023, 4, 1199598. [Google Scholar] [CrossRef]
- Lafiosca, P.; Giovannini, T.; Benzi, M.; Cappelli, C. Going beyond the limits of classical atomistic modeling of plasmonic nanostructures. J. Phys. Chem. C 2021, 125, 23848–23863. [Google Scholar] [CrossRef]
- Albella, P.; Garcia-Cueto, B.; González, F.; Moreno, F.; Wu, P.C.; Kim, T.H.; Brown, A.; Yang, Y.; Everitt, H.O.; Videen, G. Shape matters: Plasmonic nanoparticle shape enhances interaction with dielectric substrate. Nano Lett. 2011, 11, 3531–3537. [Google Scholar] [CrossRef]
- Esteban, R.; Aguirregabiria, G.; Borisov, A.G.; Wang, Y.M.; Nordlander, P.; Bryant, G.W.; Aizpurua, J. The morphology of narrow gaps modifies the plasmonic response. ACS Photonics 2015, 2, 295–305. [Google Scholar] [CrossRef]
- Rindzevicius, T.; Alaverdyan, Y.; Sepulveda, B.; Pakizeh, T.; Käll, M.; Hillenbrand, R.; Aizpurua, J.; García de Abajo, F.J. Nanohole plasmons in optically thin gold films. J. Phys. Chem. C 2007, 111, 1207–1212. [Google Scholar] [CrossRef]
- Moskovits, M. Surface-enhanced spectroscopy. Rev. Mod. Phys. 1985, 57, 783. [Google Scholar] [CrossRef]
- Aroca, R.F.; Ross, D.J.; Domingo, C. Surface-enhanced infrared spectroscopy. Appl. Spectrosc. 2004, 58, 324A–338A. [Google Scholar] [CrossRef]
- Han, X.X.; Rodriguez, R.S.; Haynes, C.L.; Ozaki, Y.; Zhao, B. Surface-enhanced Raman spectroscopy. Nat. Rev. Methods Prim. 2021, 1, 87. [Google Scholar] [CrossRef]
- Fort, E.; Grésillon, S. Surface enhanced fluorescence. J. Phys. D 2007, 41, 013001. [Google Scholar] [CrossRef]
- Liebermann, T.; Knoll, W. Surface-plasmon field-enhanced fluorescence spectroscopy. Colloids Surfaces A Physicochem. Eng. Asp. 2000, 171, 115–130. [Google Scholar] [CrossRef]
- Illobre, P.G.; Lafiosca, P.; Guidone, T.; Mazza, F.; Giovannini, T.; Cappelli, C. Multiscale modeling of surface enhanced fluorescence. Nanoscale Adv. 2024, 6, 3410–3425. [Google Scholar] [CrossRef]
- Schlücker, S. Surface-enhanced Raman spectroscopy: Concepts and chemical applications. Angew. Chem. Int. Ed. 2014, 53, 4756–4795. [Google Scholar] [CrossRef]
- Jensen, L.; Aikens, C.M.; Schatz, G.C. Electronic structure methods for studying surface-enhanced Raman scattering. Chem. Soc. Rev. 2008, 37, 1061–1073. [Google Scholar] [CrossRef]
- Fleischmann, M.; Hendra, P.J.; McQuillan, A.J. Raman spectra of pyridine adsorbed at a silver electrode. Chem. Phys. Lett. 1974, 26, 163–166. [Google Scholar] [CrossRef]
- Van Duyne, R.; Jeanmaire, D. Surface Raman spectroelectochemistry: Part1. heterocyclic, aromatic, and aliphatic Amines adsorbed on the anodized silver electrode. J. Electroanal. Chem. 1977, 84, 1–20. [Google Scholar]
- Albrecht, M.G.; Creighton, J.A. Anomalously intense Raman spectra of pyridine at a silver electrode. J. Am. Chem. Soc. 1977, 99, 5215–5217. [Google Scholar] [CrossRef]
- Morton, S.M.; Jensen, L. Understanding the molecule- surface chemical coupling in SERS. J. Am. Chem. Soc. 2009, 131, 4090–4098. [Google Scholar] [CrossRef]
- Langer, J.; Jimenez de Aberasturi, D.; Aizpurua, J.; Alvarez-Puebla, R.A.; Auguié, B.; Baumberg, J.J.; Bazan, G.C.; Bell, S.E.J.; Boisen, A.; Brolo, A.G.; et al. Present and Future of Surface-Enhanced Raman Scattering. ACS Nano 2020, 14, 28–117. [Google Scholar] [CrossRef]
- Lafiosca, P.; Nicoli, L.; Bonatti, L.; Giovannini, T.; Corni, S.; Cappelli, C. QM/Classical Modeling of Surface Enhanced Raman Scattering Based on Atomistic Electromagnetic Models. J. Chem. Theory Comput. 2023, 19, 3616–3633. [Google Scholar] [CrossRef]
- Kitaura, K.; Morokuma, K. A new energy decomposition scheme for molecular interactions within the Hartree-Fock approximation. Int. J. Quantum Chem. 1976, 10, 325–340. [Google Scholar] [CrossRef]
- Schneider, W.B.; Bistoni, G.; Sparta, M.; Saitow, M.; Riplinger, C.; Auer, A.A.; Neese, F. Decomposition of intermolecular interaction energies within the local pair natural orbital coupled cluster framework. J. Chem. Theory Comput. 2016, 12, 4778–4792. [Google Scholar] [CrossRef]
- Altun, A.; Saitow, M.; Neese, F.; Bistoni, G. Local energy decomposition of open-shell molecular systems in the domain-based local pair natural orbital coupled cluster framework. J. Chem. Theory Comput. 2019, 15, 1616–1632. [Google Scholar] [CrossRef] [PubMed]
- Bistoni, G. Finding chemical concepts in the Hilbert space: Coupled cluster analyses of noncovalent interactions. WIREs Comput. Mol. Sci. 2020, 10, e1442. [Google Scholar] [CrossRef]
- Altun, A.; Izsák, R.; Bistoni, G. Local energy decomposition of coupled-cluster interaction energies: Interpretation, benchmarks, and comparison with symmetry-adapted perturbation theory. Int. J. Quantum Chem. 2021, 121, e26339. [Google Scholar] [CrossRef]
- Szalewicz, K. Symmetry-adapted perturbation theory of intermolecular forces. WIRES Comput. Mol. Sci. 2012, 2, 254–272. [Google Scholar] [CrossRef]
- Hohenstein, E.G.; Sherrill, C.D. Wavefunction methods for noncovalent interactions. WIRES Comput. Mol. Sci. 2012, 2, 304–326. [Google Scholar] [CrossRef]
- Parker, T.M.; Burns, L.A.; Parrish, R.M.; Ryno, A.G.; Sherrill, C.D. Levels of symmetry adapted perturbation theory (SAPT). I. Efficiency and performance for interaction energies. J. Chem. Phys. 2014, 140, 094106. [Google Scholar] [CrossRef]
- Su, P.; Li, H. Energy decomposition analysis of covalent bonds and intermolecular interactions. J. Chem.Phys. 2009, 131, 014102. [Google Scholar] [CrossRef] [PubMed]
- Su, P.; Jiang, Z.; Chen, Z.; Wu, W. Energy decomposition scheme based on the generalized Kohn–Sham scheme. J. Phys. Chem. A 2014, 118, 2531–2542. [Google Scholar] [CrossRef] [PubMed]
- Su, P.; Liu, H.; Wu, W. Free energy decomposition analysis of bonding and nonbonding interactions in solution. J. Chem. Phys. 2012, 137, 034111. [Google Scholar] [CrossRef]
- Su, P.; Tang, Z.; Wu, W. Generalized Kohn-Sham energy decomposition analysis and its applications. WIREs Comput. Mol. Sci. 2020, 10, e1460. [Google Scholar] [CrossRef]
- Khaliullin, R.Z.; Cobar, E.A.; Lochan, R.C.; Bell, A.T.; Head-Gordon, M. Unravelling the origin of intermolecular interactions using absolutely localized molecular orbitals. J. Phys. Chem. A 2007, 111, 8753–8765. [Google Scholar] [CrossRef]
- Khaliullin, R.Z.; Bell, A.T.; Head-Gordon, M. Analysis of charge transfer effects in molecular complexes based on absolutely localized molecular orbitals. J. Chem. Phys. 2008, 128, 184112. [Google Scholar] [CrossRef]
- Mao, Y.; Horn, P.R.; Head-Gordon, M. Energy decomposition analysis in an adiabatic picture. Phys. Chem. Chem. Phys. 2017, 19, 5944–5958. [Google Scholar] [CrossRef]
- Mao, Y.; Loipersberger, M.; Horn, P.R.; Das, A.; Demerdash, O.; Levine, D.S.; Prasad Veccham, S.; Head-Gordon, T.; Head-Gordon, M. From intermolecular interaction energies and observable shifts to component contributions and back again: A tale of variational energy decomposition analysis. Annu. Rev. Phys. Chem. 2021, 72, 641–666. [Google Scholar] [CrossRef]
- Mitoraj, M.P.; Michalak, A.; Ziegler, T. A combined charge and energy decomposition scheme for bond analysis. J. Chem. Theory Comput. 2009, 5, 962–975. [Google Scholar] [CrossRef]
- Shen, H.; Head-Gordon, M. Occupied-Virtual Orbitals for Chemical Valence with Applications to Charge Transfer in Energy Decomposition Analysis. J. Phys. Chem. A 2024, 128, 5202–5211. [Google Scholar] [CrossRef]
- Mao, Y.; Loipersberger, M.; Kron, K.J.; Derrick, J.S.; Chang, C.J.; Sharada, S.M.; Head-Gordon, M. Consistent inclusion of continuum solvation in energy decomposition analysis: Theory and application to molecular CO2 reduction catalysts. Chem. Sci. 2021, 12, 1398–1414. [Google Scholar] [CrossRef]
- Pecher, L.; Tonner, R. Deriving bonding concepts for molecules, surfaces, and solids with energy decomposition analysis for extended systems. WIREs Computat. Mol. Sci. 2019, 9, e1401. [Google Scholar] [CrossRef]
- Staub, R.; Iannuzzi, M.; Khaliullin, R.Z.; Steinmann, S.N. Energy decomposition analysis for metal surface–Adsorbate interactions by block localized wave functions. J. Chem. Theory Comput. 2018, 15, 265–275. [Google Scholar] [CrossRef] [PubMed]
- Clabaut, P.; Staub, R.; Galiana, J.; Antonetti, E.; Steinmann, S.N. Water adlayers on noble metal surfaces: Insights from energy decomposition analysis. J. Chem. Phys. 2020, 153, 054703. [Google Scholar] [CrossRef] [PubMed]
- Giovannini, T. Kohn–Sham fragment energy decomposition analysis. J. Chem. Phys. 2024, 161, 104110. [Google Scholar] [CrossRef]
- Giovannini, T.; Koch, H. Energy-based molecular orbital localization in a specific spatial region. J. Chem. Theory Comput. 2021, 17, 139–150. [Google Scholar] [CrossRef] [PubMed]
- Giovannini, T.; Koch, H. Fragment localized molecular orbitals. J. Chem. Theory Comput. 2022, 18, 4806–4813. [Google Scholar] [CrossRef]
- Goletto, L.; Gómez, S.; Andersen, J.H.; Koch, H.; Giovannini, T. Linear response properties of solvated systems: A computational study. Phys. Chem. Chem. Phys. 2022, 24, 27866–27878. [Google Scholar] [CrossRef]
- Goletto, L.; Giovannini, T.; Folkestad, S.D.; Koch, H. Combining multilevel Hartree–Fock and multilevel coupled cluster approaches with molecular mechanics: A study of electronic excitations in solutions. Phys. Chem. Chem. Phys. 2021, 23, 4413–4425. [Google Scholar] [CrossRef]
- Klimeš, J.; Michaelides, A. Perspective: Advances and challenges in treating van der Waals dispersion forces in density functional theory. J. Chem. Phys. 2012, 137, 120901. [Google Scholar] [CrossRef]
- Johnson, E.R.; Mackie, I.D.; DiLabio, G.A. Dispersion interactions in density-functional theory. J. Phys. Org. Chem. 2009, 22, 1127–1135. [Google Scholar] [CrossRef]
- Tkatchenko, A.; Romaner, L.; Hofmann, O.T.; Zojer, E.; Ambrosch-Draxl, C.; Scheffler, M. Van der Waals interactions between organic adsorbates and at organic/inorganic interfaces. MRS Bull. 2010, 35, 435–442. [Google Scholar] [CrossRef]
- Hermann, J.; DiStasio, R.A.; Tkatchenko, A. First-Principles Models for van der Waals Interactions in Molecules and Materials: Concepts, Theory, and Applications. Chem. Rev. 2017, 117, 4714–4758. [Google Scholar] [CrossRef]
- Andersson, Y.; Hult, E.; Rydberg, H.; Apell, P.; Lundqvist, B.I.; Langreth, D.C. Van der Waals interactions in density functional theory. In Electronic Density Functional Theory; Springer: Berlin/Heidelberg, Germany, 1998; pp. 243–260. [Google Scholar]
- Vydrov, O.A.; Van Voorhis, T. Dispersion interactions from a local polarizability model. Phys. Rev. A 2010, 81, 062708. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Van Voorhis, T. Nonlocal van der Waals density functional made simple. Phys. Rev. Lett. 2009, 103, 063004. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Grimme, S. Density functional theory with London dispersion corrections. WIRES Comput. Mol. Sci. 2011, 1, 211–228. [Google Scholar] [CrossRef]
- Ehrlich, S.; Moellmann, J.; Reckien, W.; Bredow, T.; Grimme, S. System-Dependent Dispersion Coefficients for the DFT-D3 Treatment of Adsorption Processes on Ionic Surfaces. ChemPhysChem 2011, 12, 3414–3420. [Google Scholar] [CrossRef]
- Caldeweyher, E.; Bannwarth, C.; Grimme, S. Extension of the D3 dispersion coefficient model. J. Chem. Phys. 2017, 147, 034112. [Google Scholar] [CrossRef]
- Caldeweyher, E.; Ehlert, S.; Hansen, A.; Neugebauer, H.; Spicher, S.; Bannwarth, C.; Grimme, S. A generally applicable atomic-charge dependent London dispersion correction. J. Chem. Phys. 2019, 150, 154122. [Google Scholar] [CrossRef]
- Caldeweyher, E.; Mewes, J.M.; Ehlert, S.; Grimme, S. Extension and evaluation of the D4 London-dispersion model for periodic systems. Phys. Chem. Chem. Phys. 2020, 22, 8499–8512. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.L.; Schatz, G.C. Pyridine- Ag20 cluster: A model system for studying surface-enhanced Raman scattering. J. Am. Chem. Soc. 2006, 128, 2911–2919. [Google Scholar] [CrossRef]
- Jensen, L.; Zhao, L.L.; Schatz, G.C. Size-dependence of the enhanced Raman scattering of pyridine adsorbed on Ag n (n = 2–8, 20) Clusters. J. Phys. Chem. C 2007, 111, 4756–4764. [Google Scholar] [CrossRef]
- Aikens, C.M.; Schatz, G.C. TDDFT studies of absorption and SERS spectra of pyridine interacting with Au20. J. Phys. Chem. A 2006, 110, 13317–13324. [Google Scholar] [CrossRef]
- Aikens, C.M. Modelling small gold and silver nanoparticles with electronic structure methods. Mol. Simul. 2012, 38, 607–614. [Google Scholar] [CrossRef]
- Seidl, A.; Görling, A.; Vogl, P.; Majewski, J.A.; Levy, M. Generalized Kohn-Sham schemes and the band-gap problem. Phys. Rev. B 1996, 53, 3764. [Google Scholar] [CrossRef] [PubMed]
- Baer, R.; Livshits, E.; Salzner, U. Tuned range-separated hybrids in density functional theory. Annu. Rev. Phys. Chem. 2010, 61, 85–109. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Rohrdanz, M.A.; Martins, K.M.; Herbert, J.M. A long-range-corrected density functional that performs well for both ground-state properties and time-dependent density functional theory excitation energies, including charge-transfer excited states. J. Chem. Phys. 2009, 130, 054112. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Van Voorhis, T. Nonlocal van der Waals density functional: The simpler the better. J. Chem. Phys. 2010, 133, 244103. [Google Scholar] [CrossRef]
- Goerigk, L.; Grimme, S. Double-hybrid density functionals. WIREs Comput. Mol. Sci. 2014, 4, 576–600. [Google Scholar] [CrossRef]
- Peng, H.; Yang, Z.H.; Perdew, J.P.; Sun, J. Versatile van der Waals density functional based on a meta-generalized gradient approximation. Phys. Rev. X 2016, 6, 041005. [Google Scholar] [CrossRef]
- Marrazzini, G.; Giovannini, T.; Scavino, M.; Egidi, F.; Cappelli, C.; Koch, H. Multilevel density functional theory. J. Chem. Theory Comput. 2021, 17, 791–803. [Google Scholar] [CrossRef]
- Giovannini, T.; Marrazzini, G.; Scavino, M.; Koch, H.; Cappelli, C. Integrated multiscale multilevel approach to open shell molecular systems. J. Chem. Theory Comput. 2023, 19, 1446–1456. [Google Scholar] [CrossRef]
- Helgaker, T.; Jorgensen, P.; Olsen, J. Molecular Electronic-Structure Theory; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Boys, S.F.; Bernardi, F.d. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Löwdin, P.O. On the nonorthogonality problem. In Advances in Quantum Chemistry; Elsevier: Amsterdam, The Netherlands, 1970; Volume 5, pp. 185–199. [Google Scholar]
- Rezac, J.; Hobza, P. Describing noncovalent interactions beyond the common approximations: How accurate is the “gold standard,” CCSD (T) at the complete basis set limit? J. Chem. Theory Comput. 2013, 9, 2151–2155. [Google Scholar] [CrossRef]
- Jurečka, P.; Šponer, J.; Černỳ, J.; Hobza, P. Benchmark database of accurate (MP2 and CCSD (T) complete basis set limit) interaction energies of small model complexes, DNA base pairs, and amino acid pairs. Phys. Chem. Chem. Phys. 2006, 8, 1985–1993. [Google Scholar] [CrossRef]
- Rezac, J.; Hobza, P. Advanced corrections of hydrogen bonding and dispersion for semiempirical quantum mechanical methods. J. Chem. Theory Comput. 2012, 8, 141–151. [Google Scholar] [CrossRef]
- Wang, J.; Wang, G.; Zhao, J. Structures and electronic properties of Cu20, Ag20, and Au20 clusters with density functional method. Chem. Phys. Lett. 2003, 380, 716–720. [Google Scholar] [CrossRef]
- Fernández, E.M.; Soler, J.M.; Garzón, I.L.; Balbás, L.C. Trends in the structure and bonding of noble metal clusters. Phys. Rev. B 2004, 70, 165403. [Google Scholar] [CrossRef]
- Li, J.; Li, X.; Zhai, H.J.; Wang, L.S. Au20: A tetrahedral cluster. Science 2003, 299, 864–867. [Google Scholar] [CrossRef] [PubMed]
- Folkestad, S.D.; Kjønstad, E.F.; Myhre, R.H.; Andersen, J.H.; Balbi, A.; Coriani, S.; Giovannini, T.; Goletto, L.; Haugland, T.S.; Hutcheson, A.; et al. eT 1.0: An open source electronic structure program with emphasis on coupled cluster and multilevel methods. J. Chem. Phys. 2020, 152, 184103. [Google Scholar] [CrossRef] [PubMed]
- Godbout, N.; Salahub, D.R.; Andzelm, J.; Wimmer, E. Optimization of Gaussian-type basis sets for local spin density functional calculations. Part I. Boron through neon, optimization technique and validation. Can. J. Chem. 1992, 70, 560–571. [Google Scholar] [CrossRef]
- Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. New basis set exchange: An open, up-to-date resource for the molecular sciences community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef]
- Barros, C.; De Oliveira, P.; Jorge, F.; Canal Neto, A.; Campos, M. Gaussian basis set of double zeta quality for atoms Rb through Xe: Application in non-relativistic and relativistic calculations of atomic and molecular properties. Mol. Phys. 2010, 108, 1965–1972. [Google Scholar] [CrossRef]
- Parrish, R.M.; Burns, L.A.; Smith, D.G.A.; Simmonett, A.C.; DePrince, A.E.; Hohenstein, E.G.; Bozkaya, U.; Sokolov, A.Y.; Di Remigio, R.; Richard, R.M.; et al. Psi4 1.1: An Open-Source Electronic Structure Program Emphasizing Automation, Advanced Libraries, and Interoperability. J. Chem. Theory Comput. 2017, 13, 3185–3197. [Google Scholar] [CrossRef]
- Smith, D.G.A.; Burns, L.A.; Simmonett, A.C.; Parrish, R.M.; Schieber, M.C.; Galvelis, R.; Kraus, P.; Kruse, H.; Di Remigio, R.; Alenaizan, A.; et al. PSI4 1.4: Open-source software for high-throughput quantum chemistry. J. Chem. Phys. 2020, 152, 184108. [Google Scholar] [CrossRef]
- Ziegler, T.; Rauk, A. On the calculation of bonding energies by the Hartree Fock Slater method. Theor. Chim. Acta 1977, 46, 1–10. [Google Scholar] [CrossRef]
- Ziegler, T.; Rauk, A. A theoretical study of the ethylene-metal bond in complexes between copper (1+), silver (1+), gold (1+), platinum (0) or platinum (2+) and ethylene, based on the Hartree-Fock-Slater transition-state method. Inorg. Chem. 1979, 18, 1558–1565. [Google Scholar] [CrossRef]
- Ziegler, T.; Rauk, A. Carbon monoxide, carbon monosulfide, molecular nitrogen, phosphorus trifluoride, and methyl isocyanide as. sigma. donors and. pi. acceptors. A theoretical study by the Hartree-Fock-Slater transition-state method. Inorg. Chem. 1979, 18, 1755–1759. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822. [Google Scholar] [CrossRef]
- Urbieta, M.; Barbry, M.; Zhang, Y.; Koval, P.; Sánchez-Portal, D.; Zabala, N.; Aizpurua, J. Atomic-Scale Lightning Rod Effect in Plasmonic Picocavities: A Classical View to a Quantum Effect. ACS Nano 2018, 12, 585–595. [Google Scholar] [CrossRef] [PubMed]
- Abraham, S.; Dutta, A.; Joseph, J.P.; Rajapakse, B.M.; Baev, A.; Zeng, H.; Velarde, L.; Prasad, P.N.; Swihart, M.T. Simultaneous Incorporation of Magnetic and Plasmonic Nanocrystals in a Chiral Conducting Polymer Yields Unprecedented Magneto-Optic Response. Small 2025, 21, 2409752. [Google Scholar] [CrossRef]
- Garcia-Leis, A.; Garcia-Ramos, J.V.; Sanchez-Cortes, S. Silver nanostars with high SERS performance. J. Phys. Chem. C 2013, 117, 7791–7795. [Google Scholar] [CrossRef]
- Sati, A.; Ranade, T.N.; Mali, S.N.; Ahmad Yasin, H.K.; Pratap, A. Silver nanoparticles (AgNPs): Comprehensive insights into bio/synthesis, key influencing factors, multifaceted applications, and toxicity—A 2024 update. ACS Omega 2025, 10, 7549–7582. [Google Scholar] [CrossRef]
- Kleinman, S.L.; Frontiera, R.R.; Henry, A.I.; Dieringer, J.A.; Van Duyne, R.P. Creating, characterizing, and controlling chemistry with SERS hot spots. Phys. Chem. Chem. Phys. 2013, 15, 21–36. [Google Scholar] [CrossRef]
- Shiohara, A.; Wang, Y.; Liz-Marzán, L.M. Recent approaches toward creation of hot spots for SERS detection. In Colloidal Synthesis of Plasmonic Nanometals; Jenny Stanford Publishing: Singapore, 2020; pp. 563–622. [Google Scholar]
- Pilot, R.; Signorini, R.; Durante, C.; Orian, L.; Bhamidipati, M.; Fabris, L. A review on surface-enhanced Raman scattering. Biosensors 2019, 9, 57. [Google Scholar] [CrossRef]
- Kang, Y.; João, S.M.; Lin, R.; Liu, K.; Zhu, L.; Fu, J.; Cheong, W.C.; Lee, S.; Frank, K.; Nickel, B.; et al. Effect of crystal facets in plasmonic catalysis. Nat. Commun. 2024, 15, 3923. [Google Scholar] [CrossRef]
- Ramachandran, S.; João, S.M.; Jin, H.; Lischner, J. Hot carriers from intra-and interband transitions in gold-silver alloy nanoparticles. Commun. Chem. 2024, 7, 169. [Google Scholar] [CrossRef] [PubMed]
- Simão, J.M.; Bassano, O.; Lischner, J. Aspect ratio controls hot-carrier generation in gold nanobricks. J. Phys. Chem. C 2025, 129, 4886–4892. [Google Scholar] [CrossRef] [PubMed]
- Dall’Osto, G.; Marsili, M.; Vanzan, M.; Toffoli, D.; Stener, M.; Corni, S.; Coccia, E. Peeking into the femtosecond hot-carrier dynamics reveals unexpected mechanisms in plasmonic photocatalysis. J. Am. Chem. Soc. 2024, 146, 2208–2218. [Google Scholar] [CrossRef]
- Giovannini, T.; Scavino, M.; Koch, H. Time-Dependent Multilevel Density Functional Theory. J. Chem. Theory Comput. 2024, 20, 3601–3612. [Google Scholar] [CrossRef]
- Giovannini, T.; Egidi, F.; Cappelli, C. Molecular spectroscopy of aqueous solutions: A theoretical perspective. Chem. Soc. Rev. 2020, 49, 5664–5677. [Google Scholar] [CrossRef] [PubMed]
- Giovannini, T.; Cappelli, C. Continuum vs. atomistic approaches to computational spectroscopy of solvated systems. Chem. Commun. 2023, 59, 5644–5660. [Google Scholar] [CrossRef]
- Di Remigio, R.; Giovannini, T.; Ambrosetti, M.; Cappelli, C.; Frediani, L. Fully polarizable QM/fluctuating charge approach to two-photon absorption of aqueous solutions. J. Chem. Theory Comput. 2019, 15, 4056–4068. [Google Scholar] [CrossRef]
- Ambrosetti, M.; Skoko, S.; Giovannini, T.; Cappelli, C. Quantum mechanics/fluctuating charge protocol to compute solvatochromic shifts. J. Chem. Theory Comput. 2021, 17, 7146–7156. [Google Scholar] [CrossRef]
- Huang, L.; Roux, B. Automated force field parameterization for nonpolarizable and polarizable atomic models based on ab initio target data. J. Chem. Theory Comput. 2013, 9, 3543–3556. [Google Scholar] [CrossRef] [PubMed]
- McDaniel, J.G.; Schmidt, J. Next-generation force fields from symmetry-adapted perturbation theory. Annu. Rev. Phys. Chem. 2016, 67, 467–488. [Google Scholar] [CrossRef] [PubMed]
- Sodomaco, S.; Gómez, S.; Giovannini, T.; Cappelli, C. Computational Insights into the Adsorption of Ligands on Gold Nanosurfaces. J. Phys. Chem. A 2023, 127, 10282–10294. [Google Scholar] [CrossRef]
- Iori, F.; Di Felice, R.; Molinari, E.; Corni, S. GolP: An atomistic force-field to describe the interaction of proteins with Au (111) surfaces in water. J. Comput. Chem. 2009, 30, 1465–1476. [Google Scholar] [CrossRef]
- Wright, L.B.; Rodger, P.M.; Corni, S.; Walsh, T.R. GolP-CHARMM: First-principles based force fields for the interaction of proteins with Au (111) and Au (100). J. Chem. Theory Comput. 2013, 9, 1616–1630. [Google Scholar] [CrossRef] [PubMed]
- Heinz, H.; Farmer, B.L.; Pandey, R.B.; Slocik, J.M.; Patnaik, S.S.; Pachter, R.; Naik, R.R. Nature of molecular interactions of peptides with gold, palladium, and Pd- Au bimetal surfaces in aqueous solution. J. Am. Chem. Soc. 2009, 131, 9704–9714. [Google Scholar] [CrossRef]
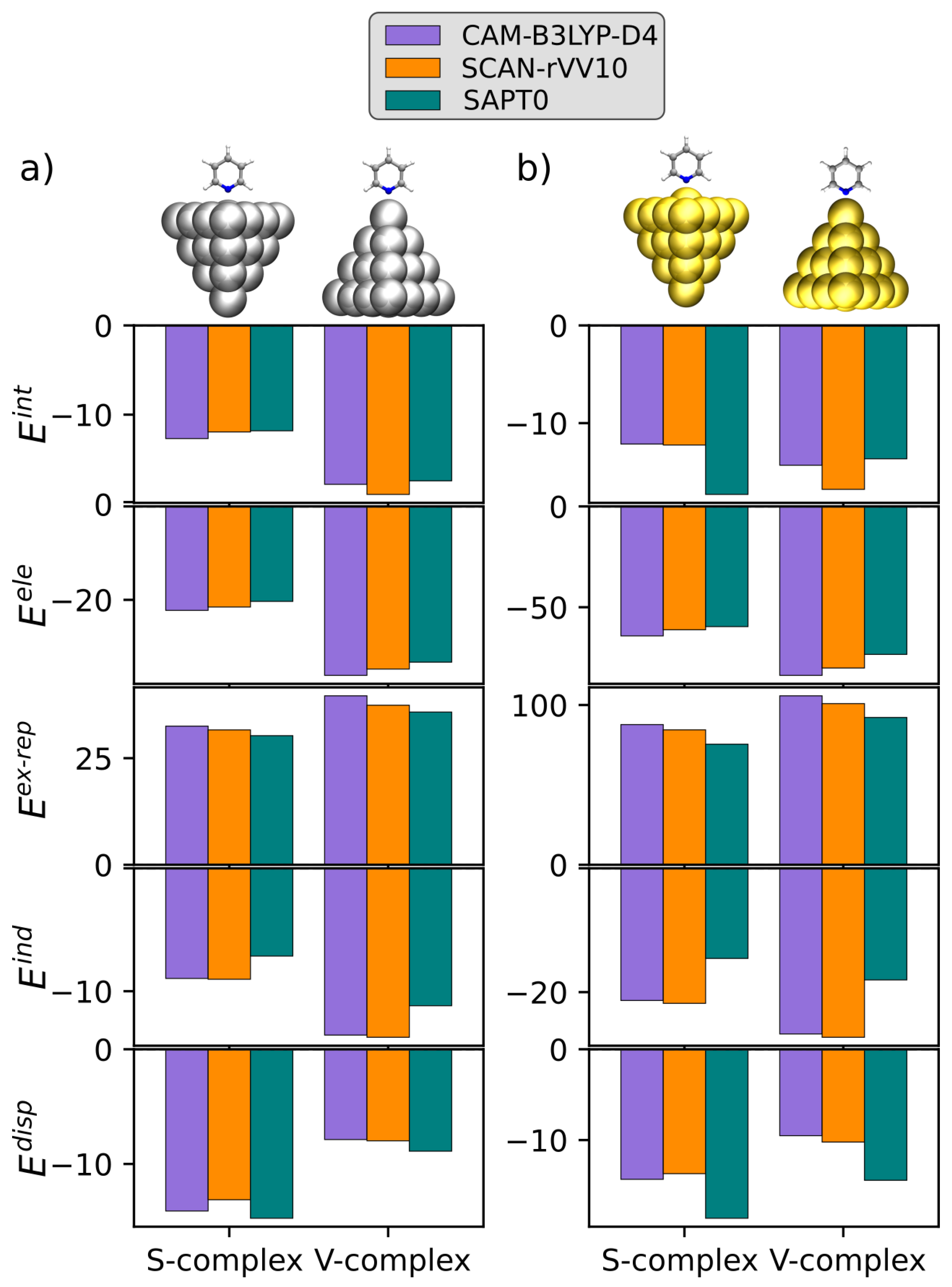
| S-Complex | V-Complex | |||||||
|---|---|---|---|---|---|---|---|---|
| CAM-B3LYP-D4 | SCAN-rVV10 | SAPT0 | BP86 [87] | CAM-B3LYP-D4 | SCAN-rVV10 | SAPT0 | BP86 [87] | |
| −22.26 | −21.54 | −20.33 | −23.37 | −36.17 | −34.82 | −33.34 | −35.81 | |
| 32.51 | 31.63 | 30.28 | 30.64 | 39.62 | 37.42 | 35.82 | 38.15 | |
| −8.96 | −9.03 | −7.14 | −9.26 | −13.57 | −13.75 | −11.18 | −11.53 | |
| −14.10 | −13.12 | −14.74 | – | −7.87 | −7.98 | −8.89 | – | |
| −12.81 | −12.06 | −11.93 | −1.99 | −17.99 | −19.13 | −17.59 | −9.19 | |
| S-Complex | V-Complex | ||||||
|---|---|---|---|---|---|---|---|
| CAM-B3LYP-D4 | SCAN-rVV10 | SAPT0 | CAM-B3LYP-D4 | SCAN-rVV10 | SAPT0 | ||
| Py-Ag | 49% | 49% | 48% | 63% | 62% | 62% | |
| 20% | 21% | 17% | 24% | 24% | 21% | ||
| 31% | 30% | 35% | 14% | 14% | 17% | ||
| Py-Au | 64% | 63% | 64% | 70% | 68% | 69% | |
| 21% | 23% | 16% | 22% | 23% | 17% | ||
| 14% | 14% | 20% | 8% | 9% | 14% | ||
| S-Complex | V-Complex | |||||||
|---|---|---|---|---|---|---|---|---|
| CAM-B3LYP-D4 | SCAN-rVV10 | SAPT0 | BP86 [89] | CAM-B3LYP-D4 | SCAN-rVV10 | SAPT0 | BP86 [89] | |
| −64.21 | −61.17 | −59.61 | – | −83.79 | −80.14 | −73.39 | – | |
| 87.74 | 84.45 | 75.47 | – | 105.75 | 100.87 | 92.19 | – | |
| −21.35 | −21.82 | −14.55 | – | −26.76 | −27.30 | −18.03 | – | |
| −14.33 | −13.70 | −18.61 | – | −9.52 | −10.22 | −14.43 | – | |
| −12.14 | −12.24 | −17.30 | −5.54 | −14.31 | −16.78 | −13.65 | −17.13 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giovannini, T. On the Energy Contributions Driving Pyridine Adsorption on Silver and Gold Nanoparticles. Nanomaterials 2025, 15, 1720. https://doi.org/10.3390/nano15221720
Giovannini T. On the Energy Contributions Driving Pyridine Adsorption on Silver and Gold Nanoparticles. Nanomaterials. 2025; 15(22):1720. https://doi.org/10.3390/nano15221720
Chicago/Turabian StyleGiovannini, Tommaso. 2025. "On the Energy Contributions Driving Pyridine Adsorption on Silver and Gold Nanoparticles" Nanomaterials 15, no. 22: 1720. https://doi.org/10.3390/nano15221720
APA StyleGiovannini, T. (2025). On the Energy Contributions Driving Pyridine Adsorption on Silver and Gold Nanoparticles. Nanomaterials, 15(22), 1720. https://doi.org/10.3390/nano15221720






