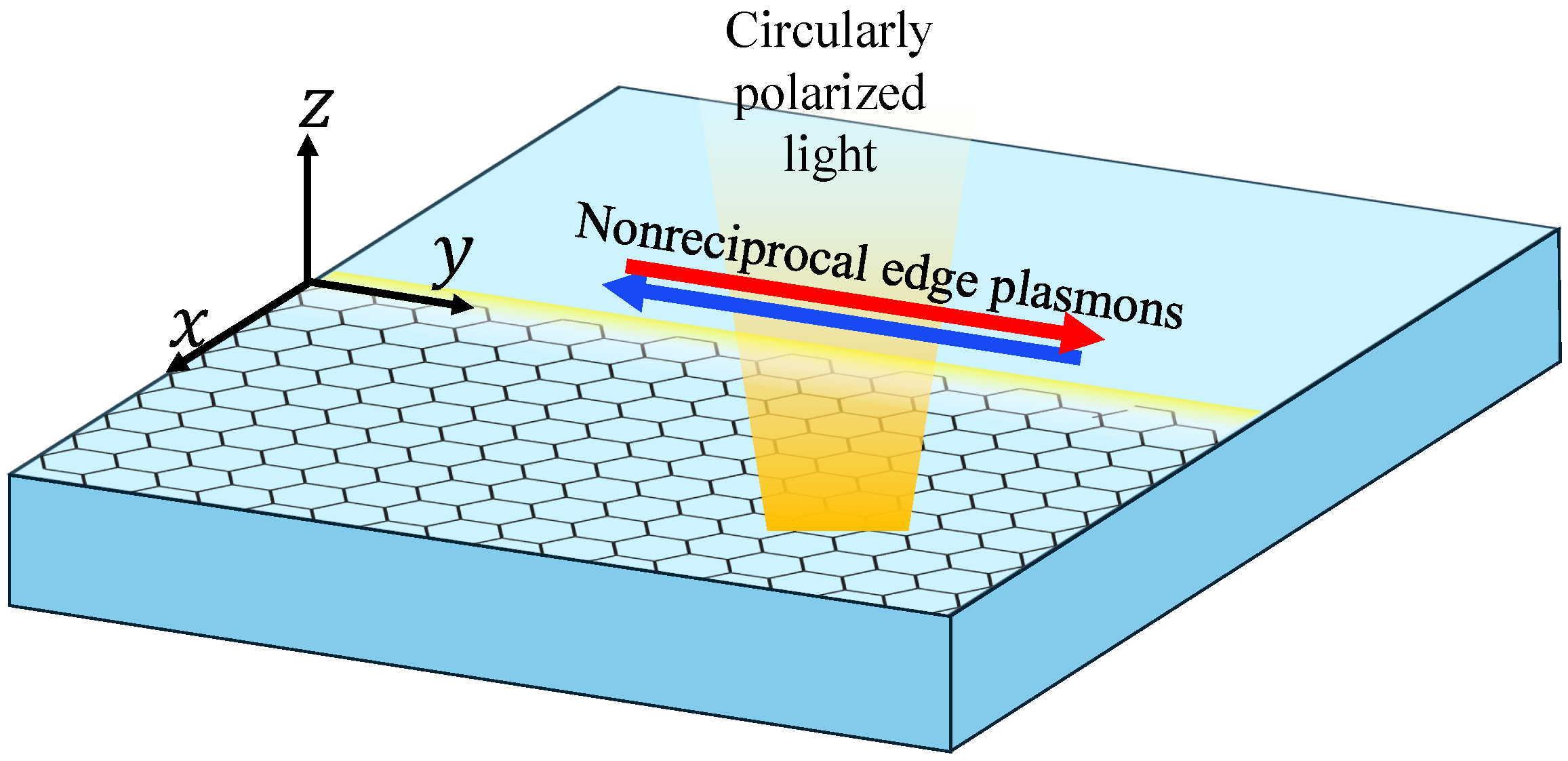
Magnet-Free Nonreciprocal Edge Plasmons in Optically Pumped Bilayer Graphene
Abstract
1. Introduction
2. Theoretical Framework
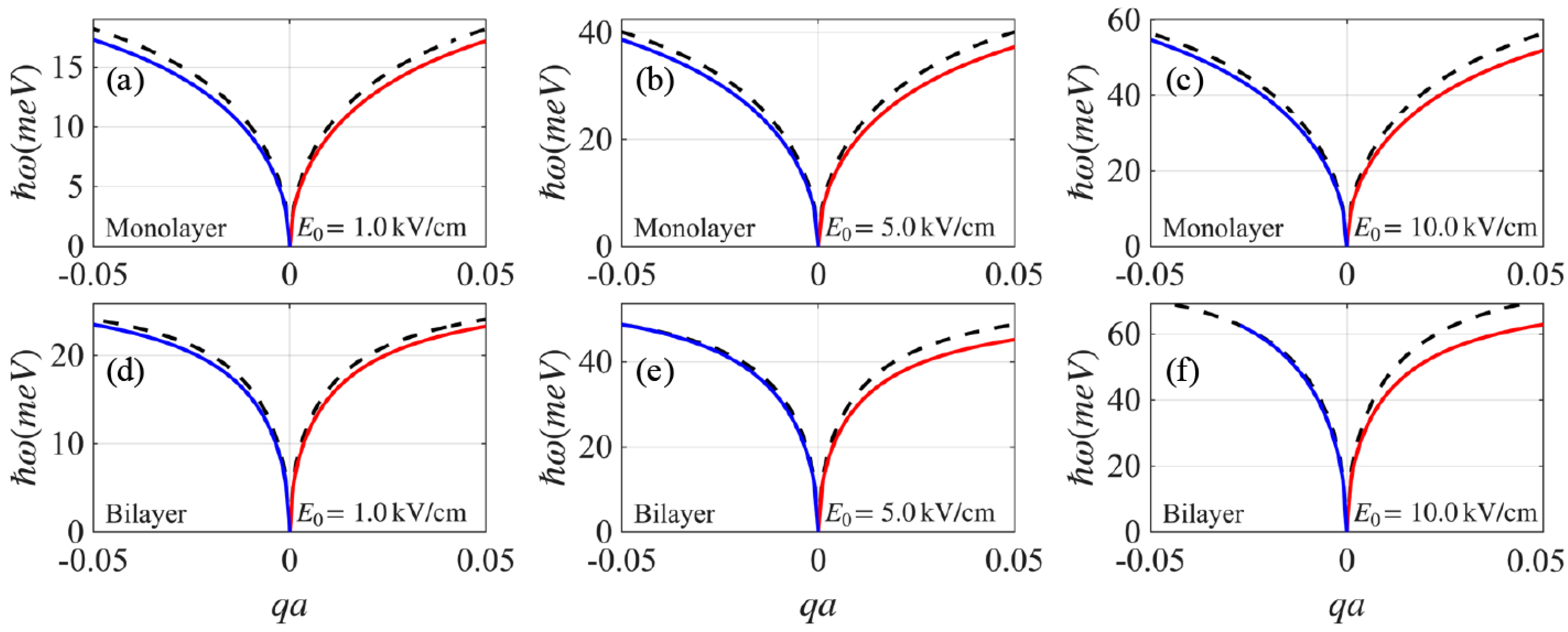
2.1. Edge Plasmons
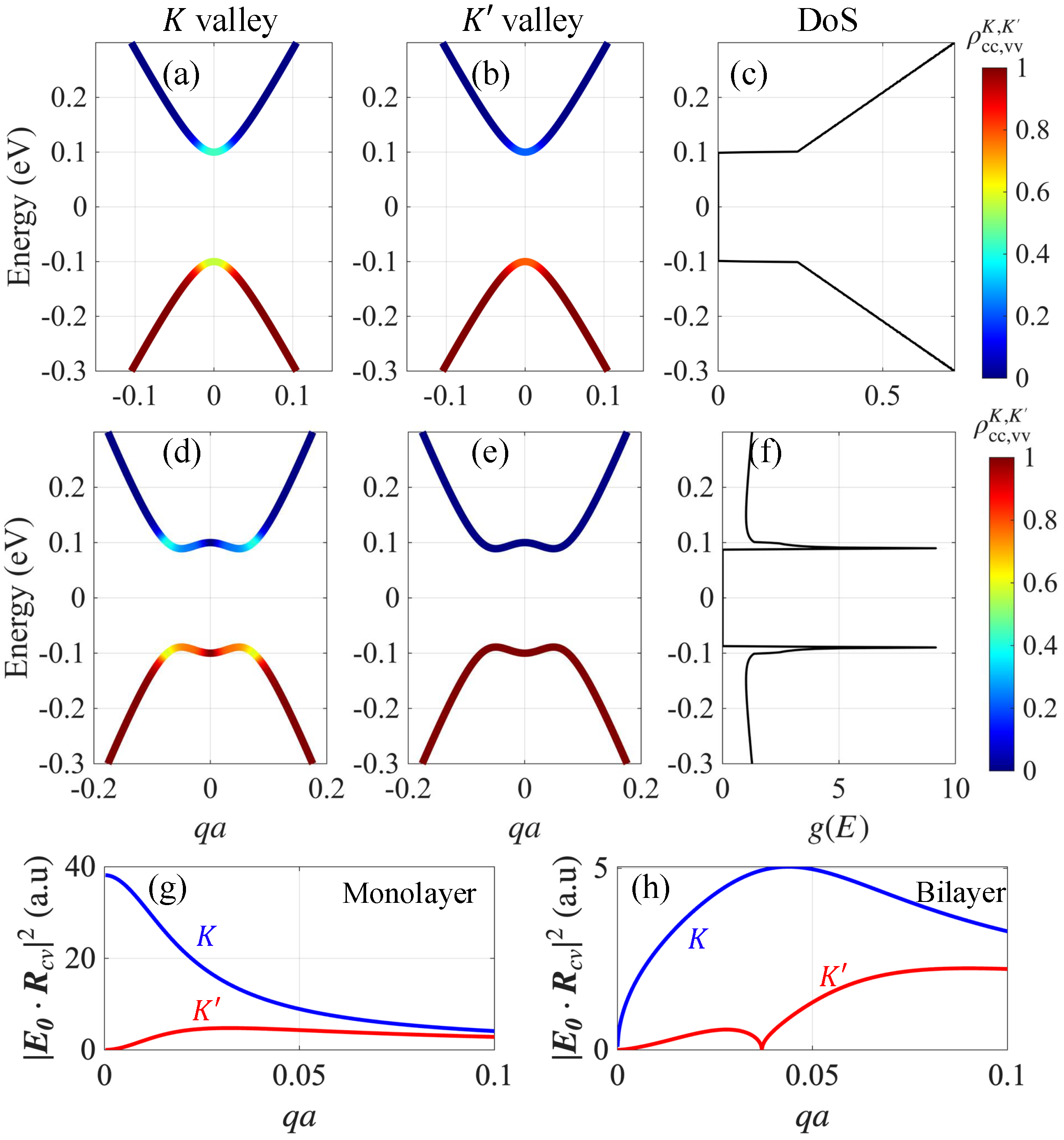
2.2. Graphene Model
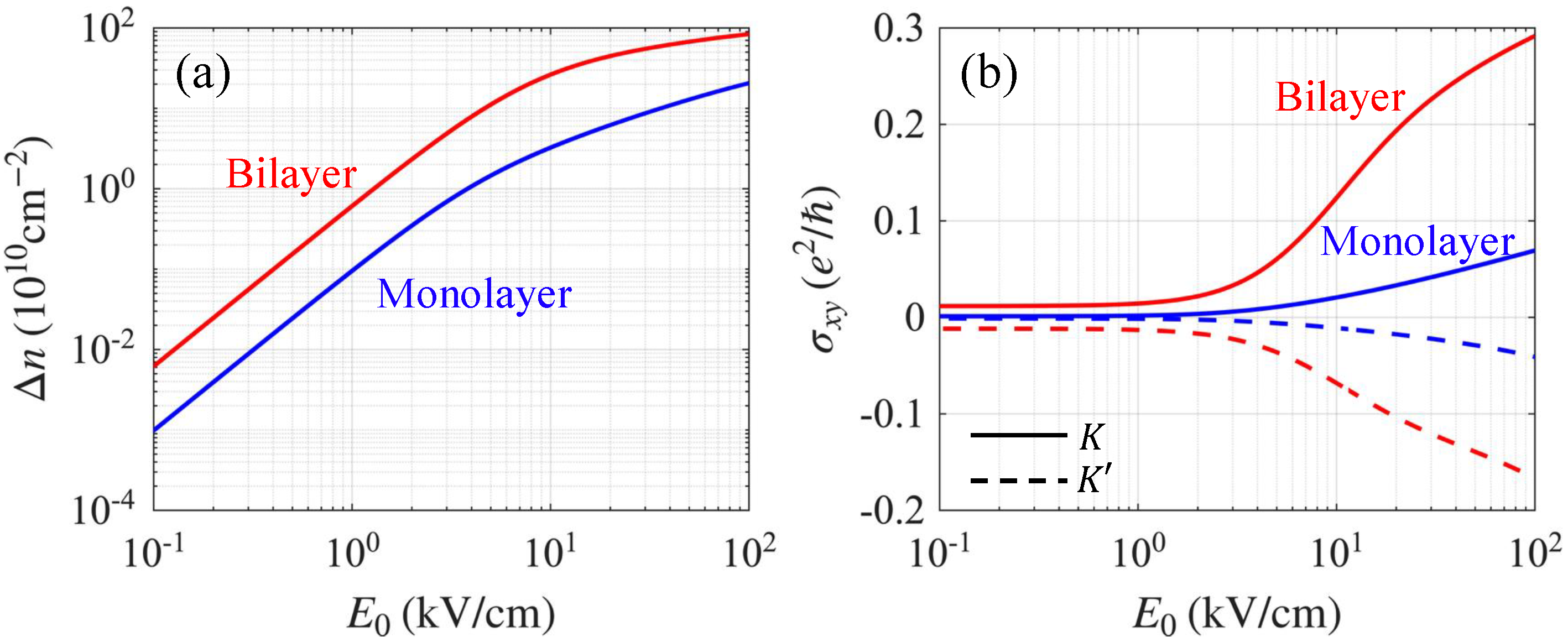
2.3. Steady-State Charge Distribution and Optical Conductivity
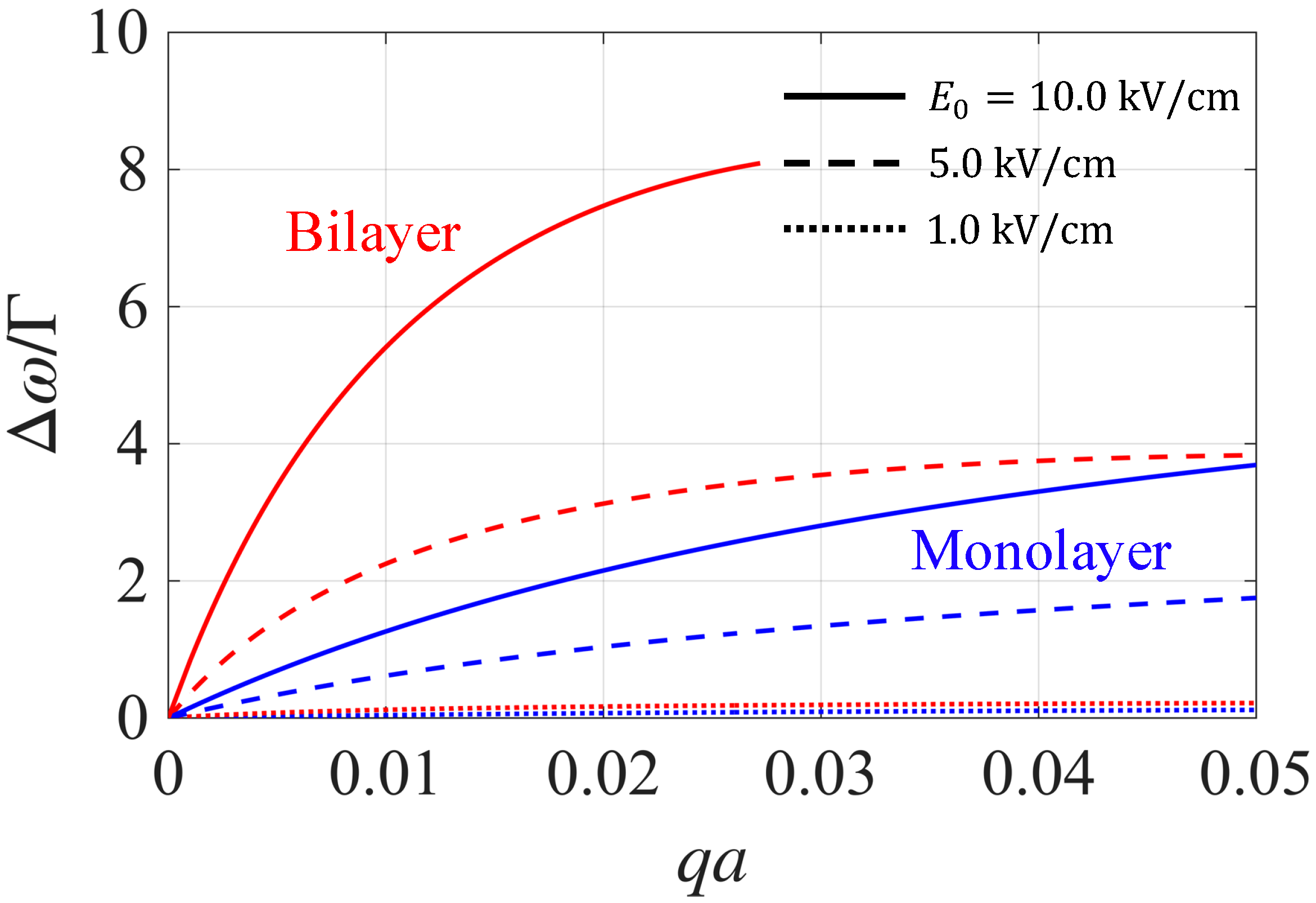
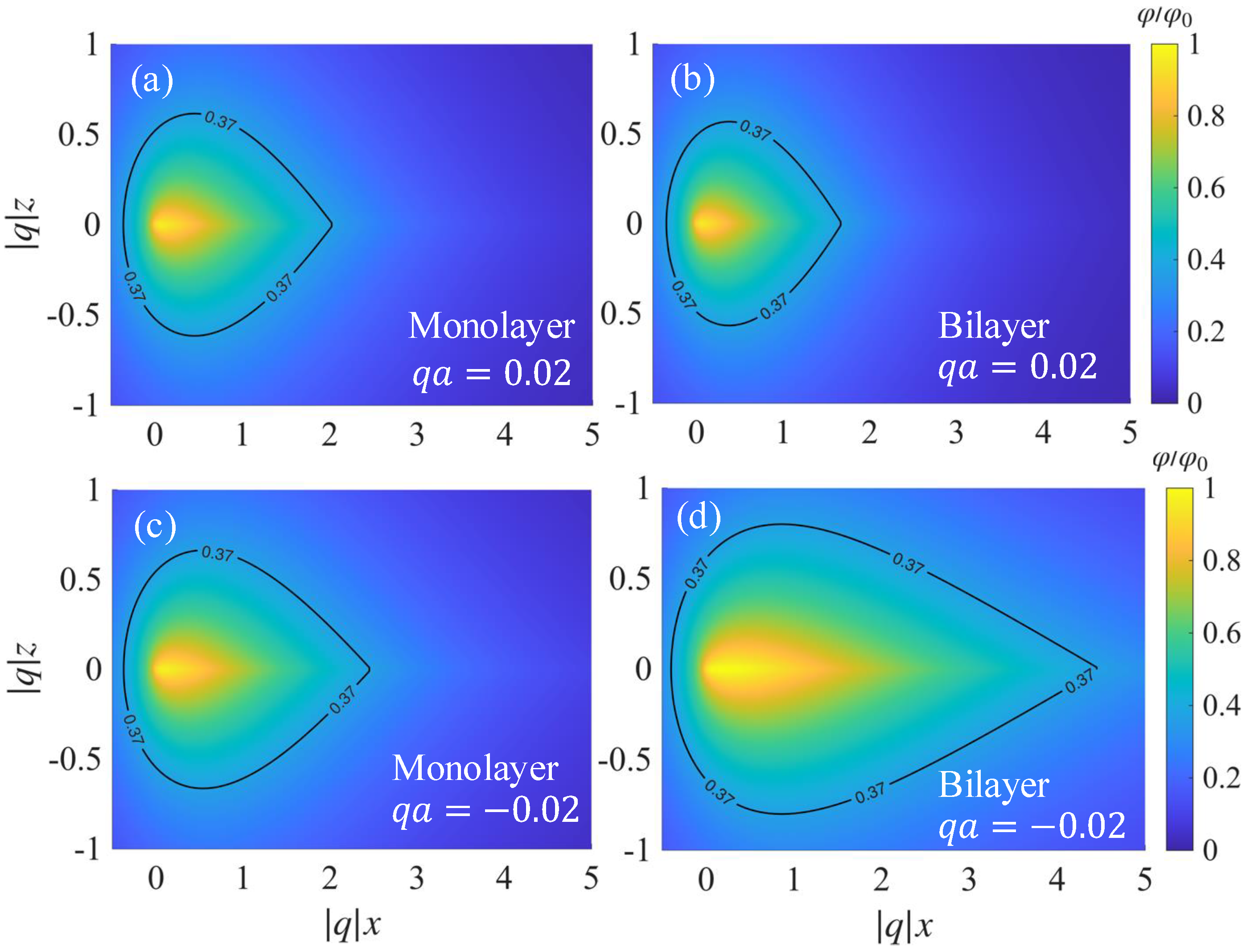
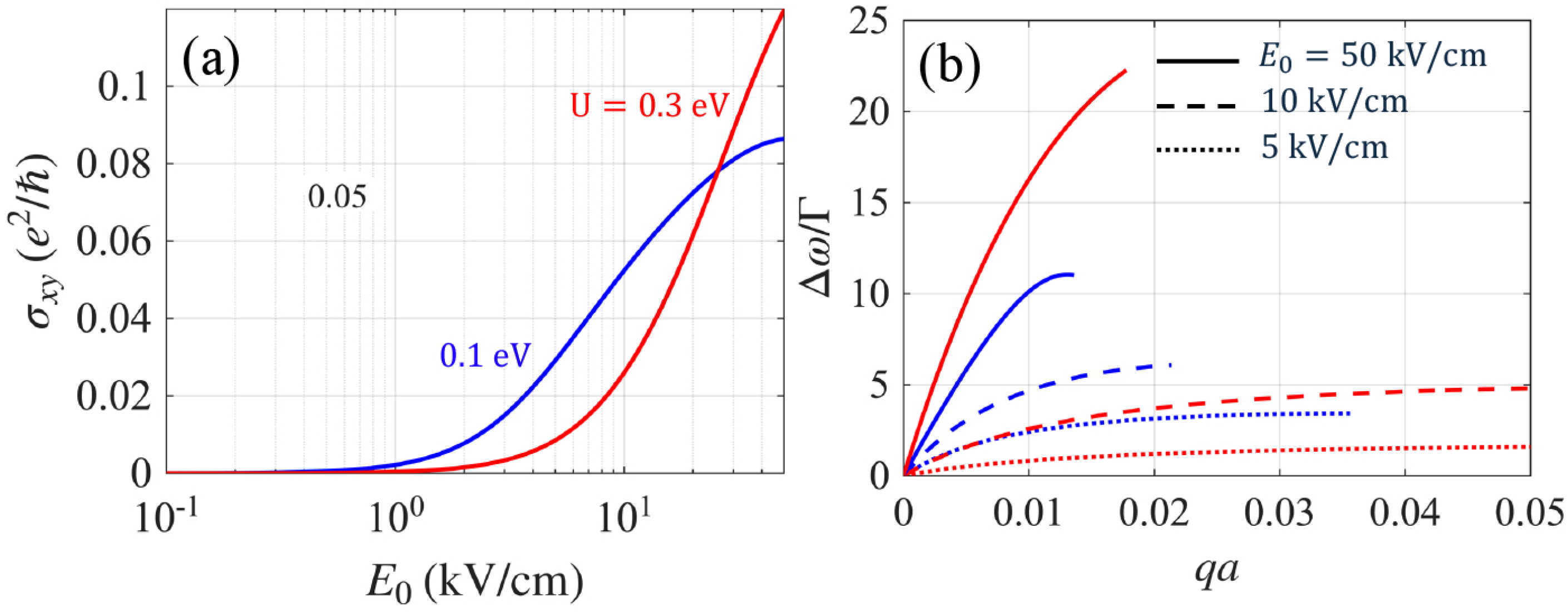
3. Results and Discussion
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 824–830. [Google Scholar] [CrossRef]
- Ozbay, E. Plasmonics: Merging Photonics and Electronics at Nanoscale Dimensions. Science 2006, 311, 189–193. [Google Scholar] [CrossRef]
- Gramotnev, D.K.; Bozhevolnyi, S.I. Plasmonics beyond the diffraction limit. Nat. Photonics 2010, 4, 83–91. [Google Scholar] [CrossRef]
- Schuller, J.A.; Barnard, E.S.; Cai, W.; Jun, Y.C.; White, J.S.; Brongersma, M.L. Plasmonics for extreme light concentration and manipulation. Nat. Mater. 2010, 9, 193–204. [Google Scholar] [CrossRef]
- Brongersma, M.L.; Shalaev, V.M. Applied Physics: The case for plasmonics. Science 2010, 328, 440–441. [Google Scholar] [CrossRef] [PubMed]
- Sounas, D.L.; Alù, A. Non-reciprocal photonics based on time modulation. Nat. Photonics 2017, 11, 774–783. [Google Scholar] [CrossRef]
- Caloz, C.; Alù, A.; Tretyakov, S.A.; Sounas, D.; Achouri, K.; Deck-Léger, Z.L. Electromagnetic Nonreciprocity. Phys. Rev. Appl. 2018, 10, 047001. [Google Scholar] [CrossRef]
- Jalas, D.; Petrov, A.; Eich, M.; Freude, W.; Fan, S.; Yu, Z.; Baets, R.; Popović, M.; Melloni, A.; Joannopoulos, J.D.; et al. What is—and what is not—an optical isolator. Nat. Photonics 2013, 7, 579–582. [Google Scholar] [CrossRef]
- Potton, R.J. Reciprocity in optics. Rep. Prog. Phys. 2004, 67, 717–754. [Google Scholar] [CrossRef]
- Brillouin, L. Wave Propagation and Group Velocity; Academic Press: New York, NY, USA, 1960. [Google Scholar]
- Shastri, K.; Monticone, F. Nonlocal flat optics. Nat. Photonics 2023, 17, 36–47. [Google Scholar] [CrossRef]
- Fetter, A.L. Edge Magnetoplasmons in a Two-Dimensional Electron Fluid Confined to a Half-Plane. Phys. Rev. B 1985, 33, 3717–3723. [Google Scholar] [CrossRef]
- Mast, D.B.; Dahm, A.J.; Fetter, A.L. Observation of Bulk and Edge Magnetoplasmons in a Two-Dimensional Electron Fluid. Phys. Rev. Lett. 1985, 54, 1706–1709. [Google Scholar] [CrossRef]
- Volkov, V.A.; Mikhailov, S.A. Edge Magnetoplasmons: Low Frequency Weakly Damped Excitations in Inhomogeneous Two-Dimensional Electron Systems. JETP 1988, 67, 1639–1653. [Google Scholar]
- Wang, W.; Kinaret, J.M.; Apell, S.P. Excitation of Edge Magnetoplasmons in Semi-Infinite Graphene Sheets: Temperature Effects. Phys. Rev. B 2012, 85, 235444. [Google Scholar] [CrossRef]
- Jin, D.; Lu, L.; Wang, Z.; Fang, C.; Joannopoulos, J.D.; Soljačić, M.; Fu, L.; Fang, N.X. Topological magnetoplasmon. Nat. Commun. 2016, 7, 13486. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Nemilentsau, A.; Fung, K.H.; Hanson, G.; Fang, N.X.; Low, T. Chiral Plasmon in Gapped Dirac Systems. Phys. Rev. B 2016, 93, 041413. [Google Scholar] [CrossRef]
- Song, J.C.W.; Rudner, M.S. Chiral Plasmons without Magnetic Field. Proc. Natl. Acad. Sci. USA 2016, 113, 4658–4663. [Google Scholar] [CrossRef] [PubMed]
- Tian, H.; Liu, J.; Siddharth, A.; Wang, R.N.; Blésin, T.; He, J.; Kippenberg, T.J.; Bhave, S.A. Magnetic-Free Silicon Nitride Integrated Optical Isolator. Nat. Photonics 2021, 15, 828–836. [Google Scholar] [CrossRef]
- Zhang, S.; Zhan, Y.; Gong, S.; Niu, Y. Noiseless single-photon isolator at room temperature. Commun. Phys. 2023, 6, 33. [Google Scholar] [CrossRef]
- Lapointe, J.; Coia, C.; Dupont, A.; Vallée, R. Passive broadband Faraday isolator for hybrid integration to photonic circuits without lens and external magnet. Nat. Photonics 2025, 19, 248–257. [Google Scholar] [CrossRef]
- Mak, K.F.; Lui, C.H.; Shan, J.; Heinz, T.F. Observation of an Electric-Field-Induced Band Gap in Bilayer Graphene by Infrared Spectroscopy. Phys. Rev. Lett. 2009, 102, 256405. [Google Scholar] [CrossRef]
- Kuzmenko, A.B.; van Heumen, E.; Carbone, F.; van der Marel, D. Determination of the Gate-Tunable Band Gap and Tight-Binding Parameters in Bilayer Graphene Using Infrared Spectroscopy. Phys. Rev. B 2009, 80, 165406. [Google Scholar] [CrossRef]
- Ohta, T.; Bostwick, A.; Seyller, T.; Horn, K.; Rotenberg, E. Controlling the Electronic Structure of Bilayer Graphene. Science 2006, 313, 951–954. [Google Scholar] [CrossRef]
- Oostinga, J.B.; Heersche, H.B.; Liu, X.; Morpurgo, A.F.; Vandersypen, L.M.K. Gate-Induced Insulating State in Bilayer Graphene Devices. Nat. Mater. 2008, 7, 151–157. [Google Scholar] [CrossRef]
- Taychatanapat, T.; Jarillo-Herrero, P. Electronic Transport in Dual-Gated Bilayer Graphene at Large Displacement Fields. Phys. Rev. Lett. 2010, 105, 166601. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Tang, T.T.; Girit, C.; Hao, Z.; Martin, M.C.; Zettl, A.; Crommie, M.F.; Shen, Y.R.; Wang, F. Direct Observation of a Widely Tunable Bandgap in Bilayer Graphene. Nature 2009, 459, 820–823. [Google Scholar] [CrossRef]
- Kisil, A.V.; Abrahams, I.D.; Mishuris, G.; Rogosin, S.V. The Wiener–Hopf Technique, Its Generalizations and Applications: Constructive and Approximate Methods. Proc. R. Soc. A 2021, 477, 20210533. [Google Scholar] [CrossRef] [PubMed]
- Lawrie, J.B.; Abrahams, I.D. A Brief Historical Perspective of the Wiener–Hopf Technique. J. Eng. Math. 2007, 59, 351–358. [Google Scholar] [CrossRef]
- Margetis, D.; Stauber, T. Theory of Plasmonic Edge States in Chiral Bilayer Systems. Phys. Rev. B 2021, 104, 115422. [Google Scholar] [CrossRef]
- Margetis, D.; Maier, M.; Luskin, M. On the Wiener–Hopf Method for Surface Plasmons: Diffraction from Semiinfinite Metamaterial Sheet. Stud. Appl. Math. 2017, 139, 599–625. [Google Scholar] [CrossRef]
- Nikulin, E.; Bandurin, D.; Svintsov, D. Edge Diffraction, Plasmon Launching, and Universal Absorption Enhancement in Two-Dimensional Junctions. Phys. Rev. B 2021, 103, 085306. [Google Scholar] [CrossRef]
- Principi, A.; Katsnelson, M.I.; Vignale, G. Edge Plasmons in Two-Component Electron Liquids in the Presence of Pseudomagnetic Fields. Phys. Rev. Lett. 2016, 117, 196803. [Google Scholar] [CrossRef]
- Sokolik, A.A.; Lozovik, Y.E. Drift Velocity of Edge Magnetoplasmons Due to Magnetic Edge Channels. Phys. Rev. B 2024, 109, 165430. [Google Scholar] [CrossRef]
- Sokolik, A.A.; Kotov, O.V.; Lozovik, Y.E. Plasmonic Modes at Inclined Edges of Anisotropic Two-Dimensional Materials. Phys. Rev. B 2021, 103, 155402. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The Electronic Properties of Graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- McCann, E.; Koshino, M. The Electronic Properties of Bilayer Graphene. Rep. Prog. Phys. 2013, 76, 056503. [Google Scholar] [CrossRef]
- Yao, W.; Xiao, D.; Niu, Q. Valley-dependent optoelectronics from inversion symmetry breaking. Phys. Rev. B 2008, 77, 235406. [Google Scholar] [CrossRef]
- Li, P.; Appelbaum, I. Excitons without effective mass: Biased bilayer graphene. Phys. Rev. B 2019, 99, 035429. [Google Scholar] [CrossRef]
- Kubo, R. Statistical-Mechanical Theory of Irreversible Processes. I. General Theory and Simple Applications to Magnetic and Conduction Problems. J. Phys. Soc. Jpn. 1957, 12, 570–586. [Google Scholar] [CrossRef]
- Mahan, G.D. Many-Particle Physics, 3rd ed.; Kluwer Academic/Plenum Publishers: New York, NY, USA, 2000. [Google Scholar] [CrossRef]
- Giuliani, G.; Vignale, G. Quantum Theory of the Electron Liquid; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar] [CrossRef]
- Broers, L.; Mathey, L. Observing Light-Induced Floquet Band Gaps in the Longitudinal Conductivity of Graphene. Commun. Phys. 2021, 4, 248. [Google Scholar] [CrossRef]
- Bukov, M.; D’Alessio, L.; Polkovnikov, A. Universal High-Frequency Behavior of Periodically Driven Systems: From Dynamical Stabilization to Floquet Engineering. Adv. Phys. 2015, 64, 139–226. [Google Scholar] [CrossRef]
- Cayssol, J.; Dóra, B.; Simon, F.; Moessner, R. Floquet Topological Insulators. Phys. Status Solidi (RRL) Rapid Res. Lett. 2013, 7, 101–108. [Google Scholar] [CrossRef]
- Goldman, N.; Dalibard, J. Periodically Driven Quantum Systems: Effective Hamiltonians and Engineered Gauge Fields. Phys. Rev. X 2014, 4, 031027. [Google Scholar] [CrossRef]
- McIver, J.W.; Schulte, B.; Stein, F.U.; Matsuyama, T.; Jotzu, G.; Meier, G.; Cavalleri, A. Light-Induced Anomalous Hall Effect in Graphene. Nat. Phys. 2020, 16, 38–41. [Google Scholar] [CrossRef]
- Merboldt, M.; Schüler, M.; Schmitt, D.; Bange, J.P.; Bennecke, W.; Gadge, K.; Pierz, K.; Schumacher, H.W.; Momeni, D.; Steil, D.; et al. Observation of Floquet States in Graphene. Nat. Phys. 2025, 21, 1093–1099. [Google Scholar] [CrossRef]
- Oka, T.; Aoki, H. Photovoltaic Hall Effect in Graphene. Phys. Rev. B 2009, 79, 081406. [Google Scholar] [CrossRef]
- Sentef, M.A.; Claassen, M.; Kemper, A.F.; Moritz, B.; Oka, T.; Freericks, J.K.; Devereaux, T.P. Theory of Pump-Probe Photoemission in Graphene: Ultrafast Tuning of Floquet Bands and Local Pseudospin Textures. Nat. Commun. 2015, 6, 7047. [Google Scholar] [CrossRef]
- Usaj, G.; Pérez-Piskunow, P.M.; Torres, L.E.F.F.; Balseiro, C.A. Irradiated Graphene as a Tunable Floquet Topological Insulator. Phys. Rev. B 2014, 90, 115423. [Google Scholar] [CrossRef]
- Li, Z.Q.; Henriksen, E.A.; Jiang, Z.; Hao, Z.; Martin, M.C.; Kim, P.; Stormer, H.L.; Basov, D.N. Dirac charge dynamics in graphene by infrared spectroscopy. Nat. Phys. 2008, 4, 532–535. [Google Scholar] [CrossRef]
- Horng, J.; Chen, C.F.; Geng, B.; Girit, C.; Zhang, Y.; Hao, Z.; Bechtel, H.A.; Martin, M.; Zettl, A.; Crommie, M.F.; et al. Drude conductivity of Dirac fermions in graphene. Phys. Rev. B 2011, 83, 165113. [Google Scholar] [CrossRef]
- Yu, K.; Jeon, J.; Kim, J.; Oh, C.W.; Yoon, Y.; Kim, B.J.; Cho, J.H.; Choi, E.J. Infrared study of carrier scattering mechanism in ion-gated graphene. Appl. Phys. Lett. 2019, 114, 083503. [Google Scholar] [CrossRef]
- Gao, F.; Gao, Z.; Shi, X.; Yang, Z.; Lin, X.; Xu, H.; Joannopoulos, J.D.; Soljačić, M.; Chen, H.; Lu, L.; et al. Probing Topological Protection Using a Designer Surface Plasmon Structure. Nat. Commun. 2016, 7, 11619. [Google Scholar] [CrossRef]
- Gangaraj, S.A.H.; Nemilentsau, A.; Hanson, G.W. The Effects of Three-Dimensional Defects on One-Way Surface Plasmon Propagation for Photonic Topological Insulators Comprised of Continuum Media. Sci. Rep. 2016, 6, 30055. [Google Scholar] [CrossRef]
- Mukherjee, S.; Savchuk, V.; Allen, J.W.; Allen, M.S.; Shvets, G. Co-Existing Topological and Volkov-Pankratov Plasmonic Edge States in Magnetized Graphene. Opt. Mater. Express 2025, 15, 501–512. [Google Scholar] [CrossRef]
- Teuber, A.; Caniglia, G.; Kranz, C.; Mizaikoff, B. Graphene-enhanced quantum cascade laser infrared spectroscopy using diamond thin-film waveguides. Analyst 2023, 148, 5144–5151. [Google Scholar] [CrossRef]
- Jung, S.; Kirch, J.; Kim, J.H.; Mawst, L.J.; Botez, D.; Belkin, M.A. Quantum cascade lasers transfer-printed on silicon-on-sapphire. Appl. Phys. Lett. 2017, 111, 211102. [Google Scholar] [CrossRef]
- Lepage, M.; Chobé, M.; Messaoudene, S.; Barbiero, J.; Mathieu, V.; Jany, C.; Hartmann, J.; Lartigue, O.; Bourlon, B.; Seassal, C.; et al. Hybrid Si/III-V quantum cascade lasers integrated on a phase-matched mid-infrared silicon photonic platform. Opt. Express 2025, 33, 37614–37628. [Google Scholar] [CrossRef] [PubMed]
- Fei, T.; Zhai, S.; Zhang, J.; Lu, Q.; Zhuo, N.; Liu, J.; Wang, L.; Liu, S.; Jia, Z.; Li, K.; et al. 3 W Continuous-Wave Room Temperature Quantum Cascade Laser Grown by Metal-Organic Chemical Vapor Deposition. Photonics 2023, 10, 47. [Google Scholar] [CrossRef]
- Hou, C.; Zhao, Y.; Zhang, J.; Zhai, S.; Zhuo, N.; Liu, J.; Wang, L.; Liu, S.; Liu, F.; Wang, Z. Room temperature continuous wave operation of quantum cascade laser at λ∼9.4 μm. J. Semicond. 2018, 39, 034001. [Google Scholar] [CrossRef]
- Freitag, M.; Steiner, M.; Martin, Y.; Perebeinos, V.; Chen, Z.; Tsang, J.C.; Avouris, P. Energy Dissipation in Graphene Field-Effect Transistors. Nano Lett. 2009, 9, 1883–1888. [Google Scholar] [CrossRef] [PubMed]
- Pogna, E.A.A.; Jia, X.; Principi, A.; Block, A.; Banszerus, L.; Zhang, J.; Liu, X.; Sohier, T.; Forti, S.; Soundarapandian, K.; et al. Hot-Carrier Cooling in High-Quality Graphene Is Intrinsically Limited by Optical Phonons. ACS Nano 2021, 15, 11285–11295. [Google Scholar] [CrossRef] [PubMed]
- Tabert, C.J.; Nicol, E.J. Dynamical conductivity of AA-stacked bilayer graphene. Phys. Rev. B 2012, 86, 075439. [Google Scholar] [CrossRef]
- Xiao, D.; Chang, M.C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2010, 82, 1959–2007. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahn, S. Magnet-Free Nonreciprocal Edge Plasmons in Optically Pumped Bilayer Graphene. Nanomaterials 2025, 15, 1622. https://doi.org/10.3390/nano15211622
Ahn S. Magnet-Free Nonreciprocal Edge Plasmons in Optically Pumped Bilayer Graphene. Nanomaterials. 2025; 15(21):1622. https://doi.org/10.3390/nano15211622
Chicago/Turabian StyleAhn, Seongjin. 2025. "Magnet-Free Nonreciprocal Edge Plasmons in Optically Pumped Bilayer Graphene" Nanomaterials 15, no. 21: 1622. https://doi.org/10.3390/nano15211622
APA StyleAhn, S. (2025). Magnet-Free Nonreciprocal Edge Plasmons in Optically Pumped Bilayer Graphene. Nanomaterials, 15(21), 1622. https://doi.org/10.3390/nano15211622




