3.1. Realization of Two-Dimensional Annular Microstructure
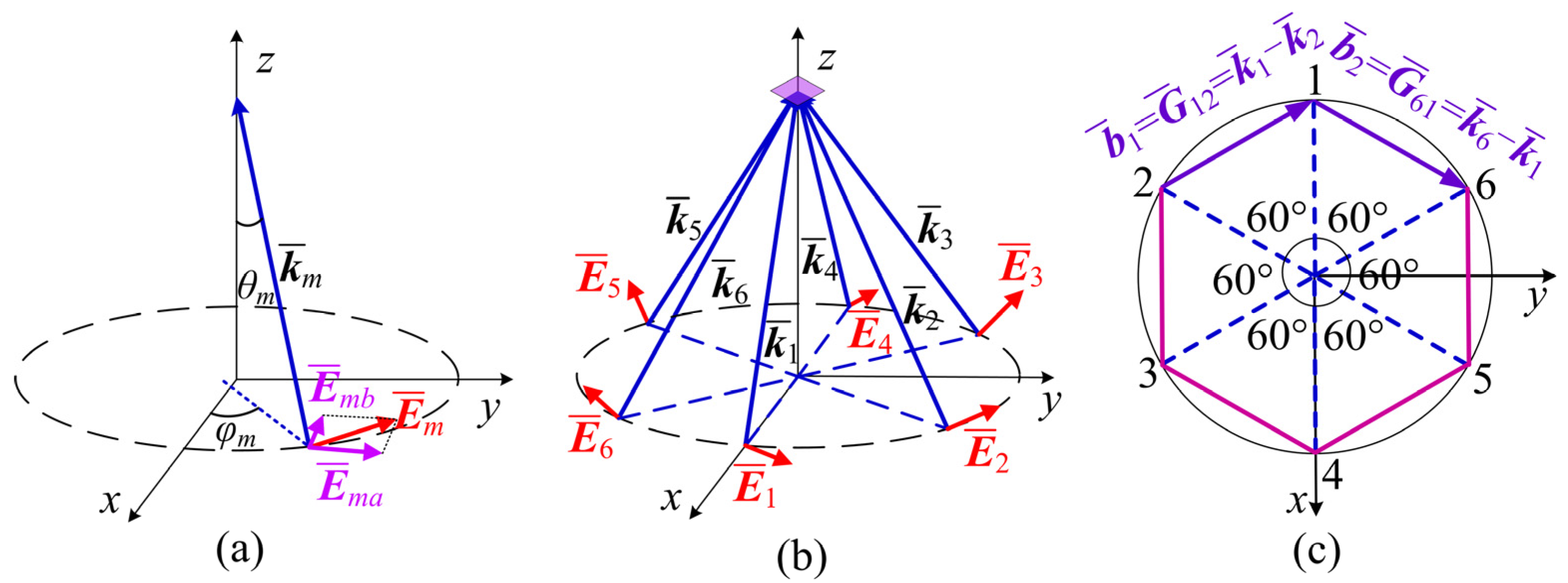
In the following text, we will discuss how to generate a two-dimensional annular microstructure, which is important for further generating a split-ring metamaterial. The beam configuration is shown in
Figure 1b. There are six coherent light beams symmetrically distributed around the
z-axis, intersecting at a zone on the
z-axis. Their projections in the
xoy plane are shown in
Figure 1c. For convenience, the propagating direction of
km is described by the polar angle
θm (defined as the angle between the
mth beam and the
z-axis) and the azimuth angle
φm (defined as the angle between its projection in the
xoy plane and the
x-axis). In terms of polarization decomposition, the direction of the long axis
is defined as the intersection of the plane perpendicular to the wave vector
km and the
xoy plane, while the direction of the short axis
can be obtained by cross multiplication of
. Such six coherent light beams can interfere with each other to produce a microstructure with a special unitcell. The clarity of the interference pattern is an important indicator which is described by interference contrast
V [
24]:
where
Imax and
Imin are the maximum and minimum values of the interference light intensities, respectively. When
Imin = 0,
V is equal to 1, and the interference strips are the clearest, which is called complete coherence; when
Imax =
Imin,
V is equal to zero and the light intensity appears completely bright or completely dark with no interference stripes, which is called completely incoherent; when 0 <
Imin <
Imax and thus 0 <
V < 1, the interference stripes can be observed but not the clearest, which is called partially coherent. The higher the contrast
V, the more advantageous it is for conducting interference experiments.
In order to obtain an intuitive understanding of the formation of microstructures, we use the Matlab tool to write and debug a program based on Formulas (1)–(4) to simulate the interference behaviors of multi-beam holographic interferometry. The main steps of our program are described as follows: (i) According to the lattice type to be fabricated, we set all necessary parameters of beam configuration, including the number of coherent light beams (N), the wave vector direction of km (m = 1, …, N) described by the polar angle θm and the azimuth angle φm, the polarization components Ema and Emb for each beam, and their initial phases. (ii) Next, we use the Matlab tool, which contains rich functions and matrix operations to write and debug an effective program to calculate the spatial intensity distribution of the interference of N coherent beams. After the calculation area and grid size are given, together with all the parameters given in step (i), the intensity of I(x, y, z) at each grid point is calculated. The contrast V is also given with Formula (4). (iii) Finally, we plot out the figures to show the intensity distributions under various conditions of polarization combinations and power ratios of the N coherent beams. We have proved that our program works well by comparing the simulation results carried out by our program and those in the reported literature under the same beam parameters.
Without loss of generality, in the following calculations, we assume that the six beams have the same intensities, and their initial phases are zero. For the convenience of characterizing the polarization of each beam, the polarization degree parameter is defined as γm = Emb/Ema (m = 1, 2,…, 6), which is the ratio of Emb and Ema components of the mth beam. Several special polarizations are explained as follows: when γm = 0 (meaning Emb = 0), it represents a linearly polarized light vibrating along ; when γm = 1 (meaning Emb = Ema), it represents a circularly polarized light; when γm >> 1, e.g., γm = 106 (i.e., Emb >> Ema), it can be regarded as a linearly polarized light vibrating along the direction . In other cases, the light beams are elliptical polarized light beams.
The actual fabrication procedure for split-ring metamaterials is briefly described as follows: firstly, a template with an array of split rings is obtained on a photoresist using the proposed multi-beam holography method here together with a series of operations such as post-drying and development, then, a metal material (e.g., gold) is evaporated onto the template, and after lifting off the template, the actual split-ring metamaterial is obtained. The current work focuses on the first step to generating metamaterial templates, which is crucial for the actual fabrication of metamaterials. The split-ring array can be recorded with a positive photoresist (e.g., diazonaphthoquinone (DNQ)-based photoresist) under an appropriate intensity threshold.
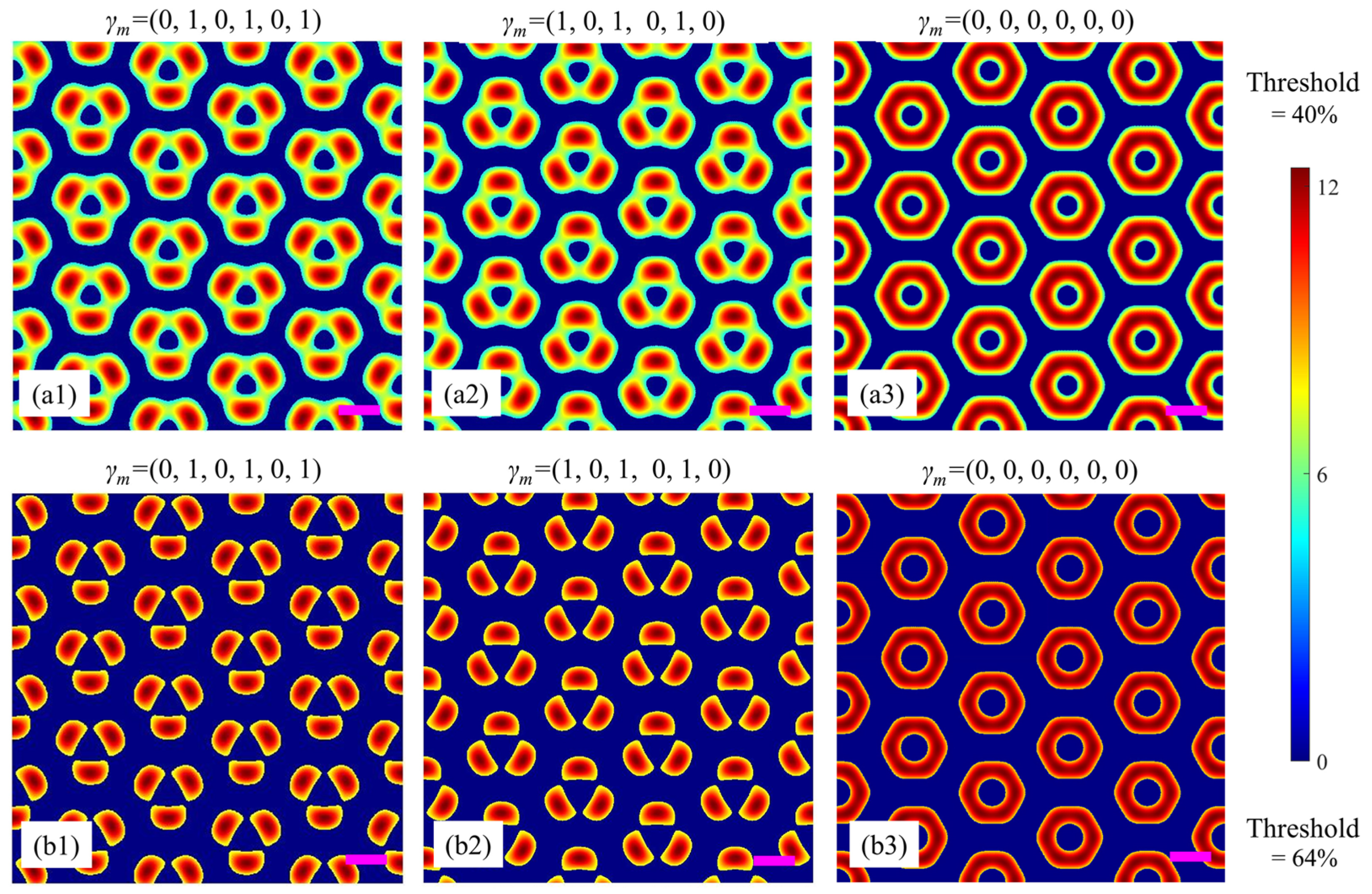
Figure 2(a1) is a simulation example based on the beam configuration in
Figure 1 and the corresponding parameters in
Table 1. Among them, beams 1, 3, and 5 are linearly polarized along
, while beams 2, 4, and 6 are circularly polarized lights. In other words, the polarization degrees (
γm =
Emb/
Ema) of the six beams are (0, 1, 0, 1, 0, 1). For these parameters, the interference result is a microstructure composed of three sets of nested simple triangular lattices. The unitcell of such a microstructure contains three ‘atoms’ distributed in an equilateral triangle. Similarly, when the polarizations of beams 1, 3, 5, and 2, 4, 6 are exchanged, i.e., the polarization degrees (
γm =
Emb/
Ema) of the six beams become (1, 0, 1, 0, 1, 0), another similar microstructure but with its unitcell rotated 180° is formed, as shown in
Figure 2(a2). Furthermore, when all of the six beams are linearly polarized with their polarization degrees to be (0, 0, 0, 0, 0, 0), they interfere with each other to form an interesting microstructure with an annular unitcell, as shown in
Figure 2(a3). The lattice constant (i.e., the distance between the centers of the two nearest annular unitcells) is calculated to be 2.3
λ ≈ 1 μm. For comparison, the interference wavelength
λ = 445 nm is denoted by the purple scale bars in all the simulation figures in the following discussions.
It should be noted that in practical holographic experiments, the relative intensity threshold is also an important parameter to influence the unitcell. By combining with the characteristics of the photoresist, the “threshold” can be easily controlled through the exposure time to achieve a desired metamaterial template in practical fabrication. For comparison,
Figure 2(a1–a3) are obtained under a relative intensity threshold of 40%, while
Figure 2(b1–b3) are the simulation results under a higher relative intensity threshold of 64%. Obviously, it is convenient to adjust the threshold and polarization combination of the coherent light beams to achieve different microstructures with desired unitcells.
3.2. Realization of Split-Ring Metamaterial
From the above simulation example of annular microstructures, one can find that the polarization combination plays an important role in the formation of special shapes of unitcells in multi-beam holographic interferometry. Here, we proceed to study the evolution of the unitcell under different polarization combinations to generate a split-ring metamaterial. Considering different types of polarization (such as linear, elliptical, or circular polarization) and various polarization degrees, there are a number of polarization combinations for the six coherent beams, which makes it difficult to analyze all cases of polarization combinations. Inspired by
Figure 2, we find that circular polarization is a key point in producing an annular microstructure. Therefore, for simplicity, we only consider combinations of circular and linear polarizations for the six beams to analyze the optimal polarization combination to produce a split-ring metamaterial.
Figure 3 shows the simulation results of different polarization combinations, i.e., one, two, three, four, five, or six beams are circularly polarized (
γm = 1), while the left beams are kept as linearly polarized (
γm = 0). All simulation results are obtained under a relative intensity threshold of 64%.
For the case of only one circularly polarized beam among the six beams, we only need to consider one typical polarization combination of
γm = (1, 0, 0, 0, 0, 0) due to the six-fold rotational symmetry of the beam configuration shown in
Figure 1b.
Figure 3a shows that when beam 1 is changed from linear to circular polarization, the intensity distribution of the unitcell deviates from the perfect annular shape in
Figure 2(b3) for
γm = (0, 0, 0, 0, 0, 0), leading to a small gap at the bottom of the unitcell and a contrast of
V = 0.975. This is because the circularly polarized beam has a less effective component contributing to the interference with other linear beams. It is worth noting that this type of unitcell has a similar shape to the split-ring metamaterial, which means that multi-beam holographic interferometry combined with beam polarization control can be used to fabricate split-ring metamaterial template as discussed in
Section 3.1, and then the practical metamaterial can be produced by reversely filling with metal material with evaporation and subsequent lifting off operation, providing an effective approach for the fabrication of metamaterials.
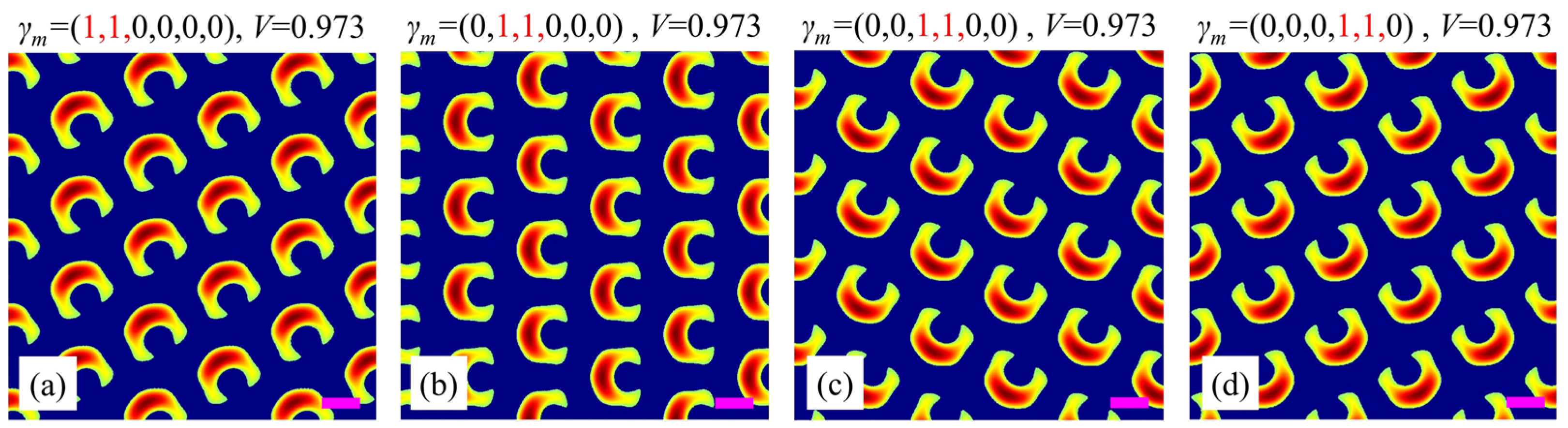
When the number of circularly polarized beams increases to two, there exist three sub-cases due the six-fold rotational symmetry of the beam configuration, i.e., adjacent case [
γm = (1, 1, 0, 0, 0, 0)], separated case [
γm = (1, 0, 1, 0, 0, 0)], and opposite case [
γm = 1, 0, 0, 1, 0, 0)]. The simulation results are shown in
Figure 3(b1–b3). It is seen that the shapes of the unitcells are very different from each other. For the adjacent case in
Figure 3(b1), the unitcell is also a split ring (
V = 0.973) but with a much better intensity distribution than that shown in
Figure 3a. The gap of the split ring is along the bottom-right direction. For the separated case in
Figure 3(b2), the unitcell consists of two connected ‘atoms’ and a separated long-shaped ‘atom’ (
V = 0.928), while for the opposite case in
Figure 3(b3), the unitcell is still annular but with lower intensity on its left and right parts (
V = 0.923). These differences can be understood by the symmetry of the polarization combinations of the six beams. A circularly polarized beam has only a half-effective component to interfere with the other beams. When the circularly polarized beams are located at different positions, various intensity distributions appear for different polarization combinations.
Similarly, when the number of circularly polarized beams increases to three or four, there also exist three sub-cases, respectively. As for the case of three circularly polarized beams, their polarization combinations are
γm = (1, 1, 1, 0, 0, 0), (1, 1, 0, 1, 0, 0), and (1, 0, 1, 0, 1, 0). The simulation results are shown in
Figure 3(c1–c3). Their unitcells are crescent-shaped (
V = 0.983), small gap split ring (
V = 0.958), and three-separate-spot (
V = 0.866), respectively. As for the case of the four circularly polarized beams, their polarization combinations are
γm = (1, 1, 1, 1, 0, 0), (1, 1, 1, 0, 1, 0), and (1, 1, 0, 1, 1, 0), respectively. The results in
Figure 3(d1–d3) indicate that their unitcells are all annular but with different degrees of distortion, and their contrasts are
V = 0.916, 0.966, and 1, respectively.
When the number of circularly polarized beams further increases to five or six, there exists only one set of polarization combination, respectively, i.e.,
γm = (1, 1, 1, 1, 1, 0) or (1, 1, 1, 1, 1, 1). For the case of (1, 1, 1, 1, 1, 0), the unitcell is annular but with a weak intensity at its upper-right part (
V = 0.922), as shown in
Figure 3e. While for the case of (1, 1, 1, 1, 1, 1), since the polarizations and the propagation directions of all beams are six-fold symmetrical with respect to the
z-axis, the unitcell becomes a perfect annular shape again but with a relative lower contrast of
V = 0.916, as shown in
Figure 3f, when compared with the annular unitcell (
V = 1) shown in
Figure 2(b3) for
γm = (0, 0, 0, 0, 0, 0).
Based on the above analyses, one can find that the optimal polarization combination to create a split-ring metamaterial is the adjacent case of γm = (1, 1, 0, 0, 0, 0). Therefore, in the following text, we will start from this set of configuration parameters to further discuss the influence of other important factors on the unitcell.
3.3. Influence of Polarization Position, Polarization Degree, and Power Ratio
Firstly, we investigate the influence of the position of the adjacent circularly polarized beams on the split-ring metamaterial. As shown in
Figure 4, when
γm = (1, 1, 0, 0, 0, 0), the gap of the split ring points along the bottom-right direction with an angle of −60° with respect to the horizontal direction. When
γm = (0, 1, 1, 0, 0, 0), the gap of the split ring rotates at an angle of 60° counterclockwise, pointing along the right direction. Similarly, when
γm = (0, 0, 1, 1, 0, 0) and (0, 0, 0, 1, 1, 0), the gap of the split ring continues to rotate 60° counterclockwise, as shown in
Figure 4c,d. These results imply that one can achieve a split-ring metamaterial with a specific gap direction by simply changing the positions of the adjacent circularly polarized beams, which is convenient and beneficial for the practical fabrication of split-ring metamaterials.
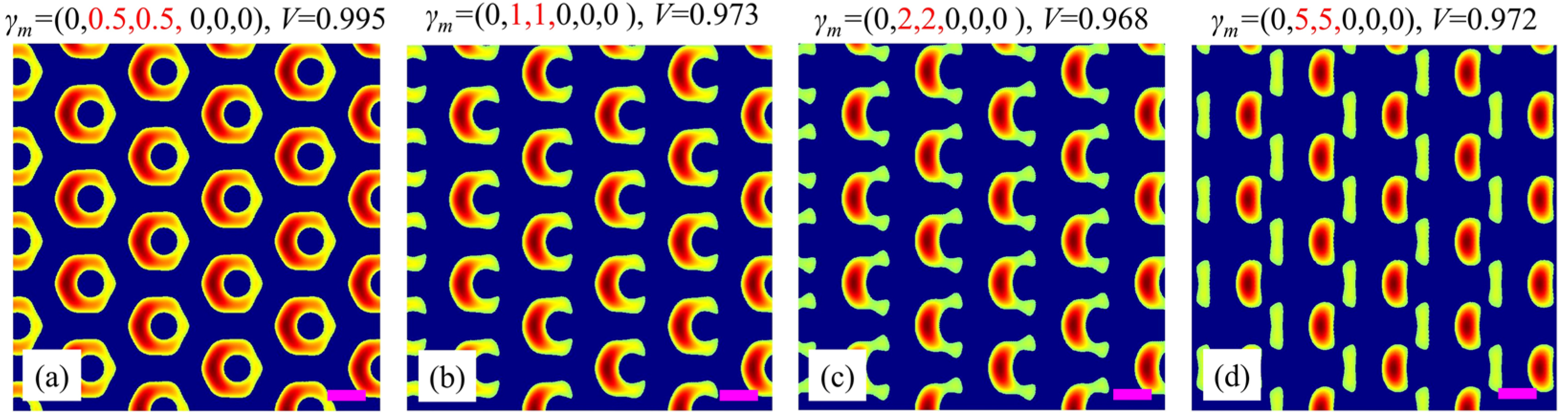
Next, we discuss the influence of the polarization degree of the adjacent beams on the split-ring metamaterial. Without loss of generality, the polarization of beams 2 and 3 are changed simultaneously, while all the left beams are kept unchanged as linear polarized beams.
Figure 5a–d present the simulation results as the polarization degree increases. When
γm is changed from (0, 0.5, 0.5, 0, 0, 0) to (0, 1, 1, 0, 0, 0) (i.e., beams 2 and 3 vary from elliptical to circular polarization simultaneously), the unitcell changes from a slightly asymmetrical annular shape to a split-ring shape, as shown in
Figure 5a,b. When the polarization degrees of beams 2 and 3 further increase to 2 (i.e., to be elliptical polarization but with its major axis along
), it is still a split-ring unitcell but with its two arms being much weaker, as shown in
Figure 5c. Moreover, when their polarization degrees further increase to 5 (i.e., to be elliptical polarization with higher eccentricity), the unitcell degenerates from a split ring to a complex one consisting of a strong short-shaped ‘atom’ and a weak long-shaped ‘atom’, as shown in
Figure 5d. These results demonstrate the sensitive dependence of the unitcell on the polarization degree. This property makes it possible to accurately adjust the arm shape of the split-ring unitcell within a certain range by simply changing the polarization degree of the adjacent beams.
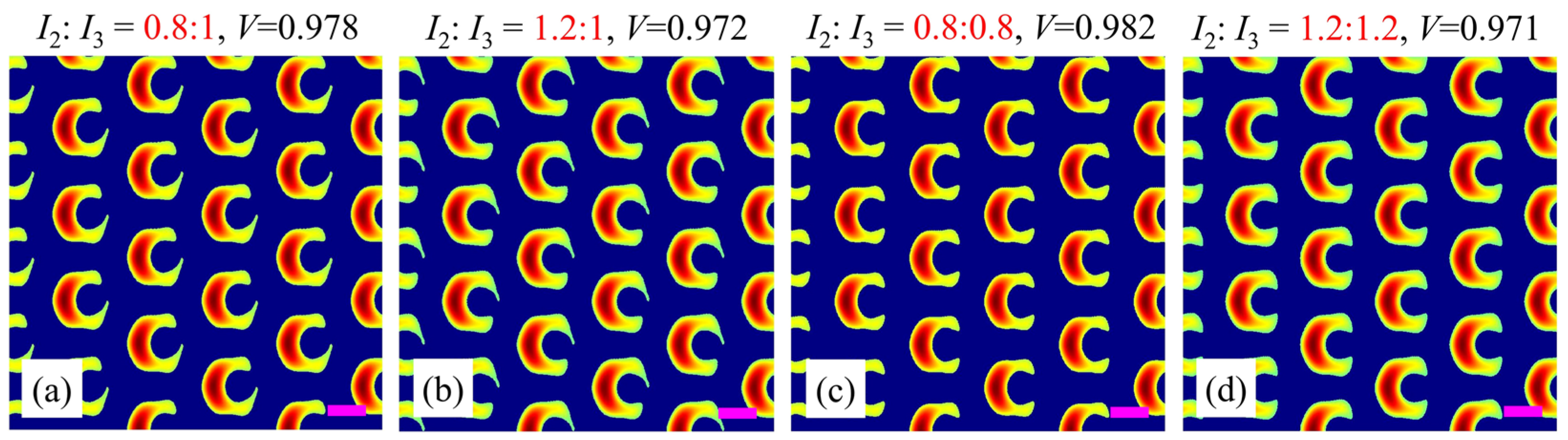
Finally, we study the influence of the power ratio of circularly polarized beams 2 and 3 (
I2:
I3) on the split-ring metamaterial. For convenience, the powers of the other beams are kept unchanged as
I1:
I4:
I5:
I6 = 1:1:1:1. The simulation results are shown in
Figure 6. For
I2:
I3 = 0.8:1, the lower arm of the split-ring unitcell is longer than the upper one, which is a reversal of the case of
I2:
I3 = 1.2:1, as shown in
Figure 6a,b. Furthermore, when both powers of beams 2 and 3 vary simultaneously, i.e., the power ratio of
I2:
I3 increases from 0.8:0.8 to 1.2:1.2, both arms become thicker and thicker simultaneously. In addition, it is noted that the values of contrast
V for all these cases stay at a stable level around 0.975. Undoubtedly, these results provide an efficient way to control each arm or both arms of the split-ring metamaterial by changing the power ratio of beams 2 and 3 independently or simultaneously. As a result, based on the aforementioned discussions, one can obtain the optimal beam configuration to generate a high-quality split-ring metamaterial (
V > 0.97) in the adjacent case with
γm = (0, 1, 1, 0, 0, 0), which generates the eventually produced split-ring metamaterial template as shown in
Figure 5b. Its lattice constant is calculated to be 2.3
λ ≈ 1 μm, and such a structure typically operates at near-infrared spectrum. Of course, the parameters can be further adjusted to generate other desired microstructures.