Multi-Scale Modeling of Doped Magnesium Hydride Nanomaterials for Hydrogen Storage Applications
Abstract
1. Introduction
- Novel coupled atomistic and dynamic thermal modeling framework: This study pioneers the direct, integrated application of atomistic (DFT) and system-level (dynamic thermal) models specifically for the analysis and optimization of hydrogen storage materials. Unlike previous studies that might use these methods in isolation or in a less integrated fashion, our framework establishes a seamless connection to bridge the disparate length and timescales.
- Direct correlation of atomic-scale doping with macroscopic system performance: A central innovative aspect is the explicit linkage established between the fundamental effects of specific dopants (Ti, Zr, V) on MgH2 at the atomic scale (e.g., changes in reaction barriers and enthalpies from DFT) and their direct impact on observable, macroscopic system-level outcomes (e.g., overall hydrogenation time, energy consumption, and thermal management). This provides a mechanistic understanding that was previously lacking.
- Comprehensive quantification of system behavior under realistic conditions: Beyond just material properties, our framework allows for the comprehensive quantification of crucial system performance indicators such as hydrogenation/dehydrogenation time, total energy consumption, and detailed thermal behavior under dynamic operating conditions. This moves beyond theoretical predictions to practical system-level performance assessment.
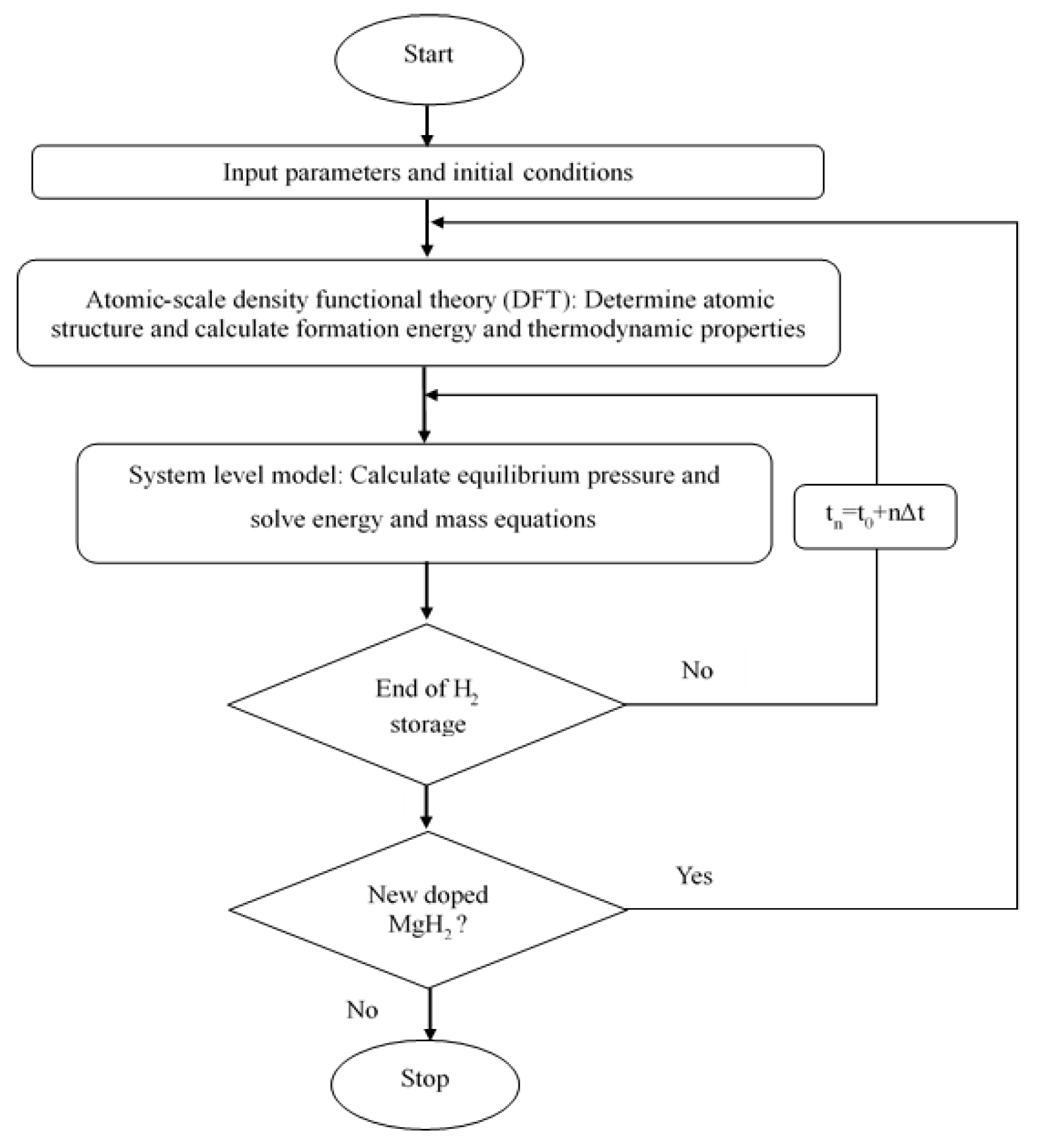
2. Multi-Scale Modeling Method
2.1. Microscopic Scale: DFT Modeling of Doped MgH2
2.1.1. Computational Theory
2.1.2. Formation Energy and Atomic Structure
2.2. Macroscopic Scale: Lumped Modeling for Hydrogen Storage Performance
2.2.1. Energy and Mass Balances
- The hydrogen reactor has a uniform temperature and pressure.
- The hydrogen is considered as an ideal gas.
- The hydrogen reactor properties are independent of the temperature.
- The hydrogen storage tank is well insulted and exchanges heat only with the thermal management system.
- Energy balance:
- Mass balance
- Reaction kinetic
2.2.2. Key Performance Indicators
- Hydrogenation Time (thyd)
- Maximum Reactor Temperature (Tmax)
- Required heating/cooling thermal energy (Qth)
2.2.3. Model Validation
3. Results and Discussion
3.1. Microscopic Investigation: DFT Results
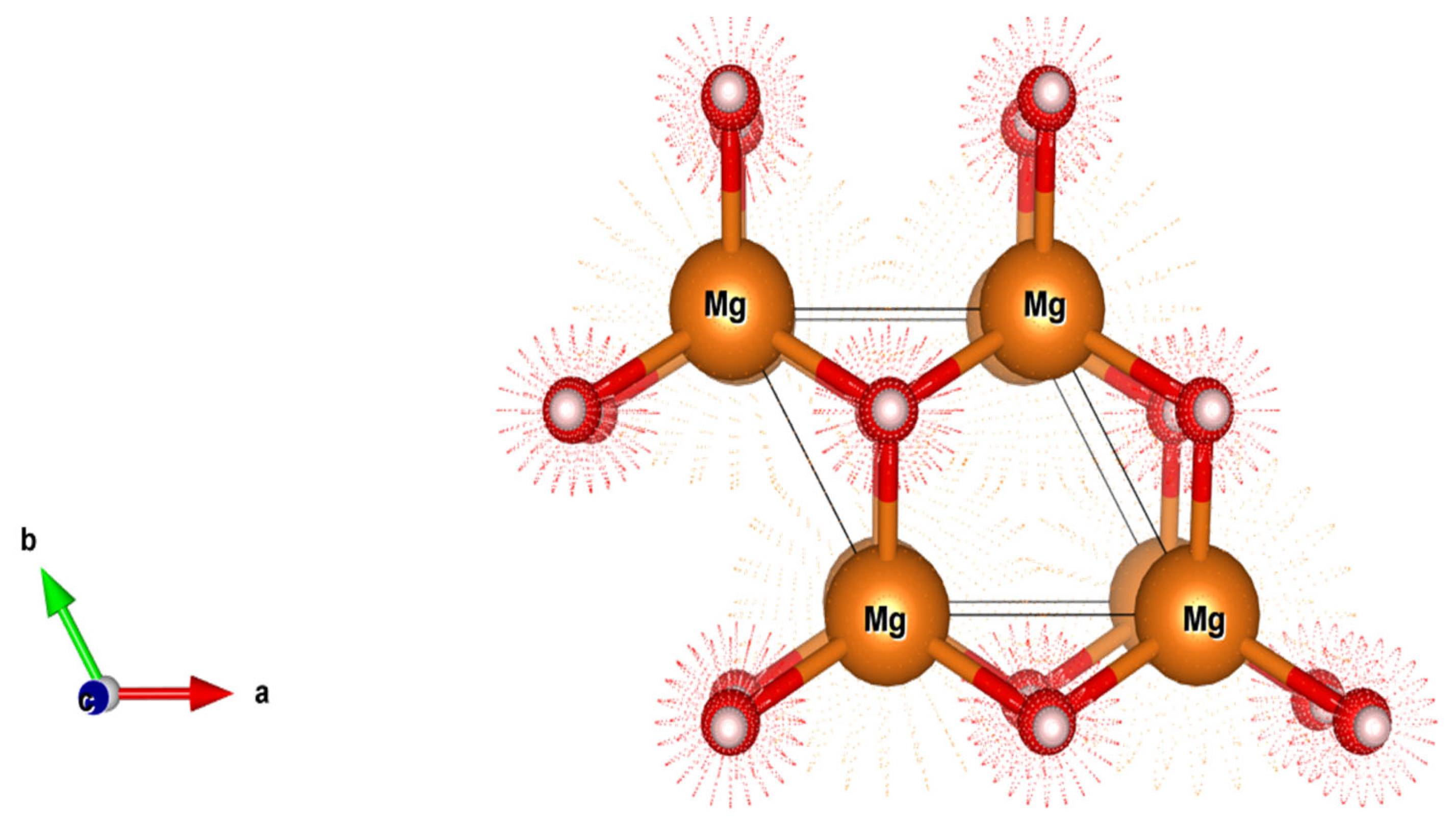
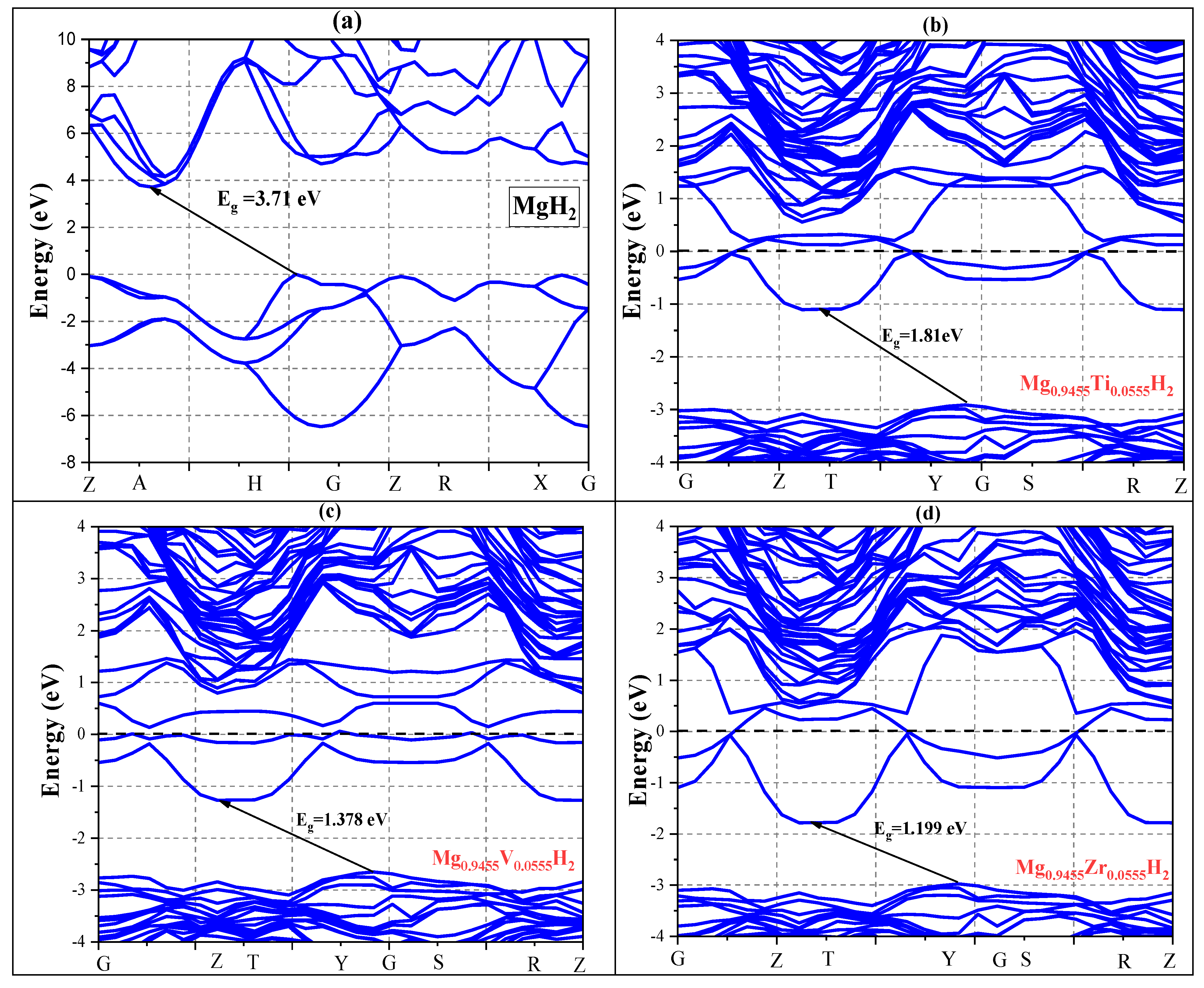
3.1.1. Electronic and Structural Parameters
- Two ‘apical’ hydrogen atoms are located above and below the magnesium, with an Mg-H distance of approximately 1.94 Å.
- Four ‘equatorial’ hydrogen atoms are located around the magnesium, forming a square, with a slightly larger Mg-H distance of about 2.03 Å.
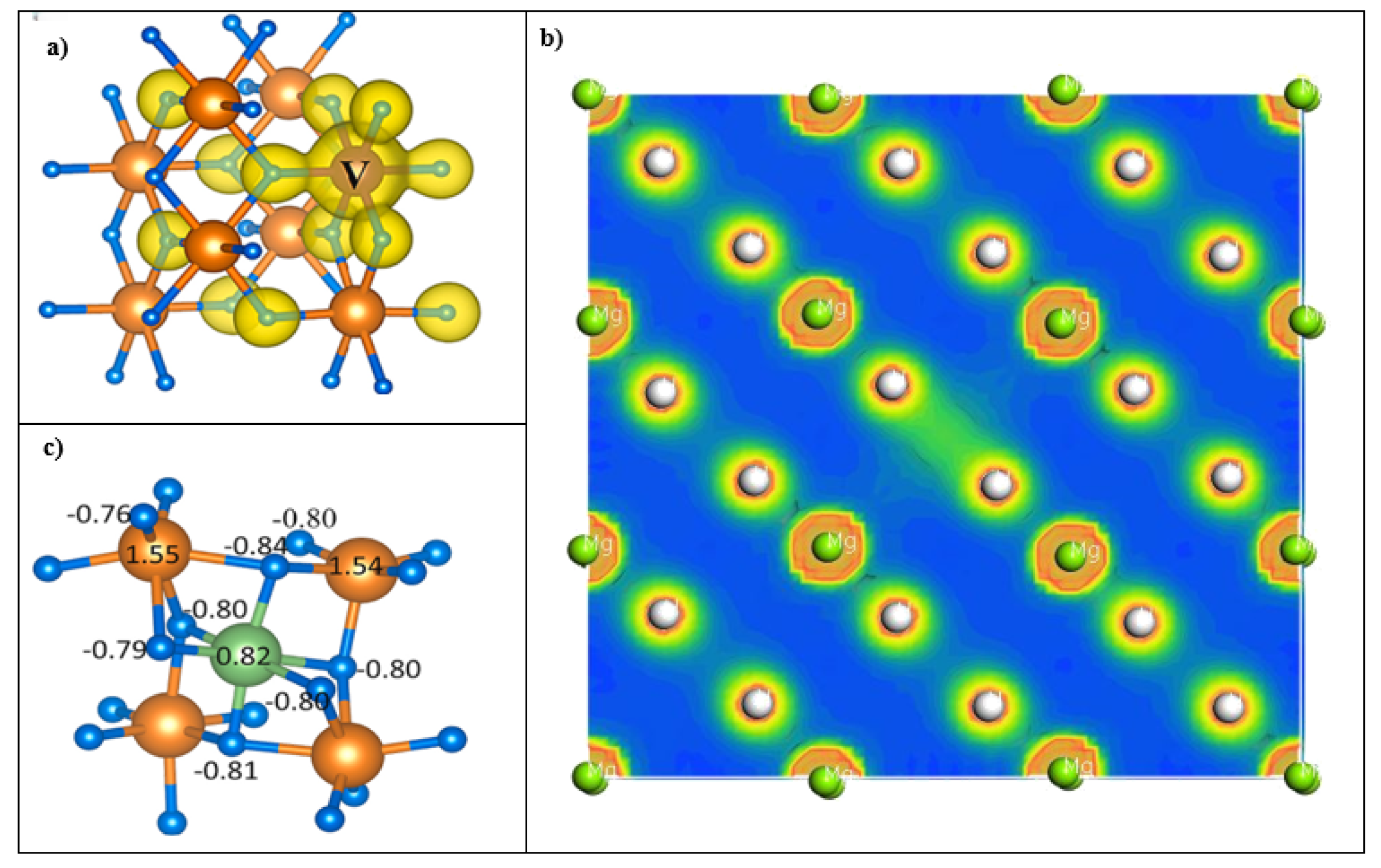
3.1.2. Charge Density Distribution
3.1.3. Thermodynamic Properties
- (a)
- Hydrogen desorption energy
- (b) Formation enthalpy
- (c) Desorption temperature of the pure and doped MgH2
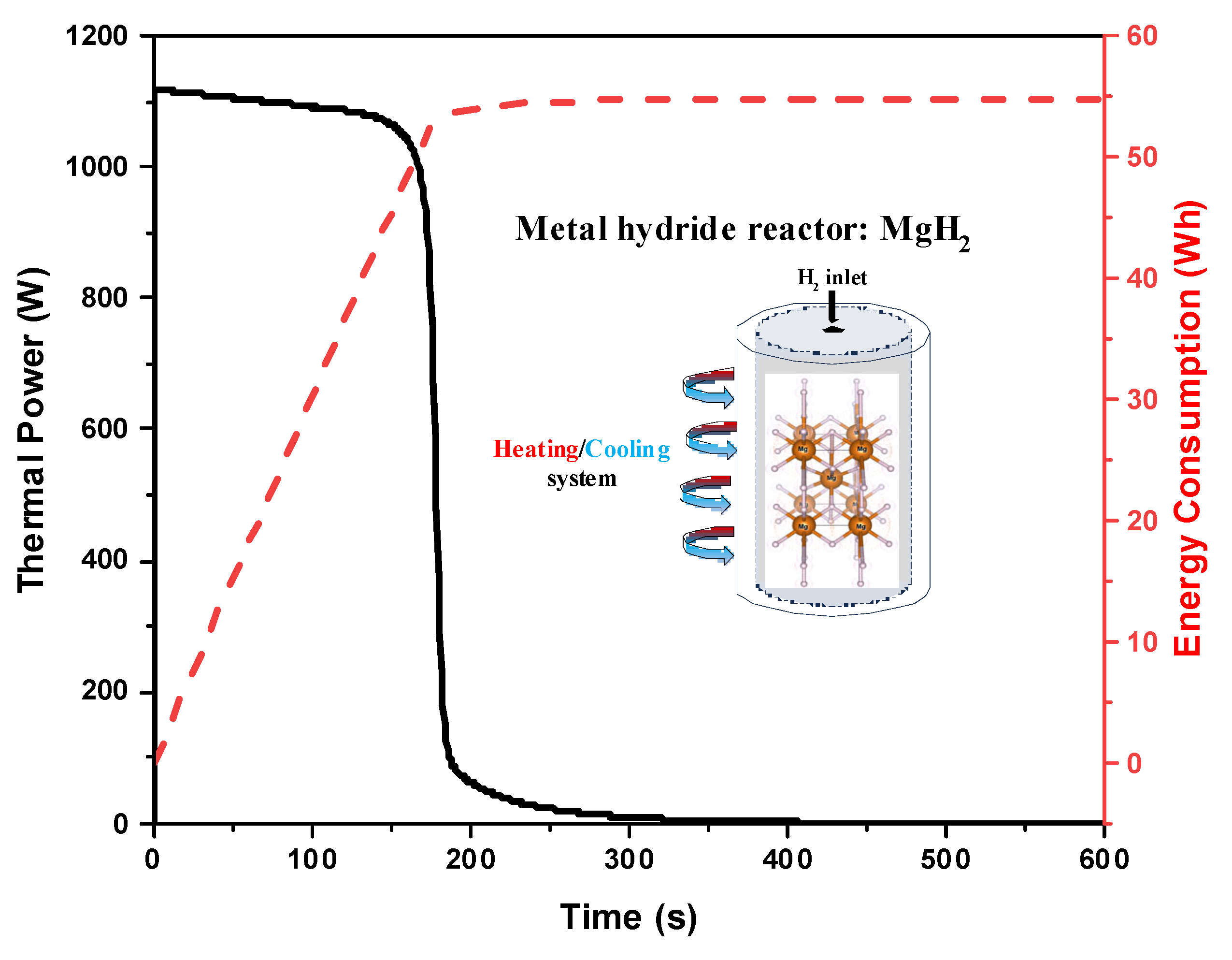
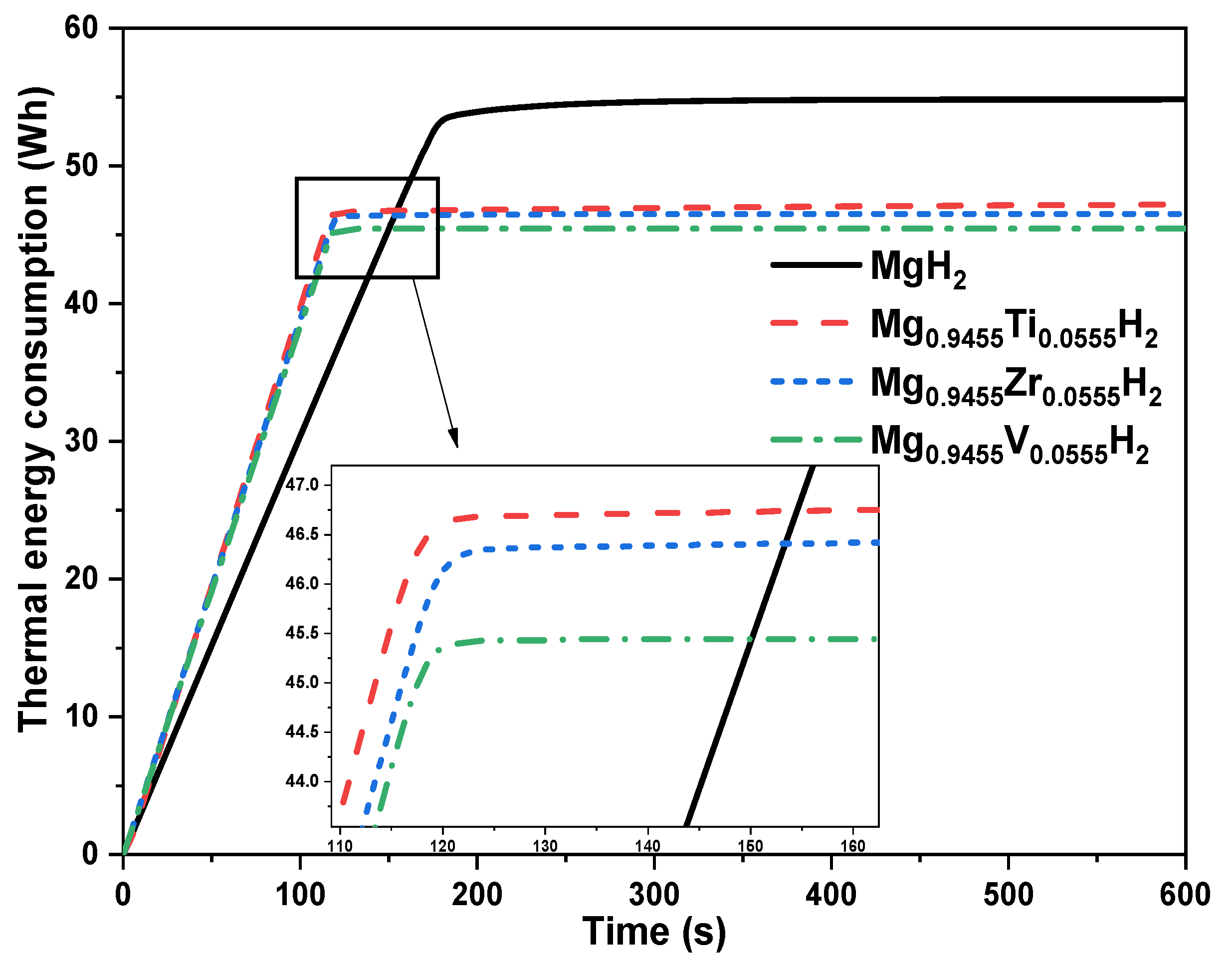
3.2. Macroscopic Investigation: System-Scale Modeling Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alobaid, A.; Kamil, M.; Khalil, K.A. Metal hydrides for solid hydrogen storage: Experimental insights, suitability evaluation, and innovative technical considerations for stationary and mobile applications. Int. J. Hydrogen Energy 2025, 128, 432–456. [Google Scholar] [CrossRef]
- Lebrouhi, B.E.; Djoupo, J.J.; Lamrani, B.; Benabdelaziz, K.; Kousksou, T. Global hydrogen development—A technological and geopolitical overview. Int. J. Hydrogen Energy 2022, 47, 7016–7048. [Google Scholar] [CrossRef]
- Hong, H.; Guo, H.; Cui, Z.; Ball, A.; Nie, B. Structure modification of magnesium hydride for solid hydrogen storage. Int. J. Hydrogen Energy 2024, 78, 793–804. [Google Scholar] [CrossRef]
- Lamrani, B.; Alqahtani, R.T.; Ajbar, A.; Kousksou, T. Resistance-capacitance dynamic model for hydrogen storage in metal hydrides with phase change material as thermal management system. Energy Convers. Manag. X 2025, 26, 101007. [Google Scholar] [CrossRef]
- Zavaliy, I.; Berezovets, V.; Denys, R.; Kononiuk, O.; Yartys, V. Hydrogen absorption-desorption properties and hydrolysis performance of MgH2-Zr3V3O0.6Hx and MgH2-Zr3V3O0.6Hx-C composites. J. Energy Storage 2023, 65, 107245. [Google Scholar] [CrossRef]
- Xiao, H.; Qian, F.; Zhang, X.; Hu, H.; Tang, R.; Hu, C.; Zhou, W.; He, X.; Pu, Z.; Ma, C.; et al. Effect of Ce0.6Zr0.4O2 nanocrystals on boosting hydrogen storage performance of MgH2. Chem. Eng. J. 2024, 494, 153203. [Google Scholar] [CrossRef]
- Li, Z.; Lu, Y.; Wang, J.; Chen, Y.; Li, Q.; Pan, F. Improved hydrogen storage kinetics of MgH2 using TiFe0.92Mn0.04Co0.04 with in-situ generated α-Fe as catalyst. Mater. Rep. Energy 2024, 4, 100247. [Google Scholar] [CrossRef]
- Han, B.; Wang, J.; Tan, J.; Ouyang, Y.; Du, Y.; Sun, L. First-principles study on the dehydrogenation thermodynamics and kinetics of Ti, Zr, V and Nb doped MgH2. J. Energy Storage 2024, 83, 110612. [Google Scholar] [CrossRef]
- Lobo, R.; Alvarez, N.; Shanov, V. Hydrogen nanometrology in advanced carbon nanomaterial electrodes. Nanomaterials 2021, 11, 1079. [Google Scholar] [CrossRef]
- Firlej, L.; Kuchta, B.; Walczak, K.; Journet, C. Hydrogen storage in pure and boron-substituted nanoporous carbons—Numerical and experimental perspective. Nanomaterials 2021, 11, 2173. [Google Scholar] [CrossRef]
- Elman, R.R.; Kurdyumov, N.; Laptev, R.S.; Kudiiarov, V.N. The influence of single-walled carbon nanotubes additives on the structure and hydrogenation behavior of magnesium hydride. J. Energy Storage 2025, 119, 116408. [Google Scholar] [CrossRef]
- Gaztañaga, F.; Luna, C.R.; Sandoval, M.; Macchi, C.; Jasen, P. Geometric, Electronic, and Magnetic Properties of MgH2: Influence of Charged Defects. J. Phys. Chem. C 2016, 120, 22844–22851. [Google Scholar] [CrossRef]
- Germán, E.; Luna, C.; Marchetti, J.; Jasen, P.; Macchi, C.; Juan, A. A DFT study of dopant (Zr, Nb) and vacancies on the dehydrogenation on MgH2 (001) surface. Int. J. Hydrogen Energy 2014, 39, 1732–1739. [Google Scholar] [CrossRef]
- Luna, C.R.; Germán, E.; Macchi, C.; Juan, A.; Somoza, A. On the perfect MgH2(–Nb,–Zr) systems and the influence of vacancy-like defects on their structural properties. A self-consistent first principle calculations study of the electron and positron parameters. J. Alloys Compd. 2013, 556, 188–197. [Google Scholar] [CrossRef]
- Reddad, K.; Labrim, H.; Zejli, D.; El Bouayadi, R. Enhancing hydrogen desorption in MgH2: A DFT study on the effects of copper and zinc doping. Int. J. Hydrogen Energy 2024, 87, 1474–1479. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Ii, C.J.P.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Kristallogr./Cryst. Mater. 2005, 220, 567–570. Available online: https://www.degruyterbrill.com/document/doi/10.1524/zkri.220.5.567.65075/html?srsltid=AfmBOooHXrwmvmka3msvr3p_C7MFl36ZznDvyCXeP6n38UUk3wT6GFir (accessed on 10 July 2025). [CrossRef]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717–2744. [Google Scholar] [CrossRef]
- Perdew, J.P. Generalized gradient approximations for exchange and correlation: A look backward and forward. Phys. B Condens. Matter 1991, 172, 1–6. [Google Scholar] [CrossRef]
- Bende, D.; Wagner, F.R.; Sichevych, O.; Grin, Y. Chemical Bonding Analysis as a Guide for the Preparation of New Compounds: The Case of VIrGe and HfPtGe. Angew. Chem. 2017, 129, 1333–1338. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillonin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Lebrouhi, B.E.; Lamrani, B.; Ouassaid, M.; Abd-Lefdil, M.; Maaroufi, M.; Kousksou, T. Low-cost numerical lumped modelling of lithium-ion battery pack with phase change material and liquid cooling thermal management system. J. Energy Storage 2022, 54, 105293. [Google Scholar] [CrossRef]
- Talagañis, B.A.; Meyer, G.O.; Aguirre, P.A. Modeling and simulation of absorption-desorption cyclic processes for hydrogen storage-compression using metal hydrides. Int. J. Hydrogen Energy 2011, 36, 13621–13631. [Google Scholar] [CrossRef]
- Bhouri, M.; Bürger, I. Numerical investigation of H2 absorption in an adiabatic high-temperature metal hydride reactor based on thermochemical heat storage: MgH2 and Mg(OH)2 as reference materials. Int. J. Hydrogen Energy 2017, 42, 16632–16644. [Google Scholar] [CrossRef]
- Jain, I.P.; Lal, C.; Jain, A. Hydrogen storage in Mg: A most promising material. Int. J. Hydrogen Energy 2010, 35, 5133–5144. [Google Scholar] [CrossRef]
- Klopčič, N.; Grimmer, I.; Winkler, F.; Sartory, M.; Trattner, A. A review on metal hydride materials for hydrogen storage. J. Energy Storage 2023, 72, 108456. [Google Scholar] [CrossRef]
- Hassan, I.A.; Mohammed, R.H.; Ramadan, H.S.; Saleh, M.A.; Cuevas, F.; Hissel, D. Performance evaluation of a novel concentric metal hydride reactor assisted with phase change material. Appl. Therm. Eng. 2023, 224, 120065. [Google Scholar] [CrossRef]
- Laurencelle, F.; Goyette, J. Simulation of heat transfer in a metal hydride reactor with aluminium foam. Int. J. Hydrogen Energy 2007, 32, 2957–2964. [Google Scholar] [CrossRef]
- Van De Walle, C.G.; Neugebauer, J. First-principles calculations for defects and impurities: Applications to III-nitrides. J. Appl. Phys. 2004, 95, 3851–3879. [Google Scholar] [CrossRef]
- Sprunger, P.T.; Plummer, E.W. An experimental study of the interaction of hydrogen with the Mg(000 1) surface. Chem. Phys. Lett. 1991, 187, 559–564. [Google Scholar] [CrossRef]
- Bouhadda, Y.; Rabehi, A.; Bezzari, S.T.-C. First-principle calculation of MgH2 and LiH for hydrogen storage. J. Renew. Energ. 2007, 10, 545–550. [Google Scholar] [CrossRef]
- Wu, G.; Zhang, J.; Li, Q.; Wu, Y.; Chou, K.; Bao, X. Dehydrogenation kinetics of magnesium hydride investigated by DFT and experiment. Comput. Mater. Sci. 2010, 49, S144–S149. [Google Scholar] [CrossRef]
- Fernández, J.F.; Sánchez, C.R. Simultaneous TDS-DSC measurements in magnesium hydride. J. Alloys Compd. 2003, 356, 348–352. [Google Scholar] [CrossRef]
- Park, M.S.; Janotti, A.; Van de Walle, C.G. Formation and migration of charged native point defects in MgH2: First-principles calculations. Phys. Rev. B 2009, 80, 64102. [Google Scholar] [CrossRef]
- Bogdanovic, B.; Bohmhammel, K.; Christ, B.; Reiser, A.; Schlichte, K.; Vehlen, R.; Wolf, U. Thermodynamic investigation of the magnesium-hydrogen system. J. Alloys Compd. 1999, 282, 84–92. [Google Scholar] [CrossRef]
- Bahou, S.; Labrim, H.; Ez-Zahraouy, H. Role of vacancies and transition metals on the thermodynamic properties of MgH2: Ab-initio study. Int. J. Hydrogen Energy 2023, 48, 8179–8188. [Google Scholar] [CrossRef]
- Pozzo, M.; Alfè, D. Structural properties and enthalpy of formation of magnesium hydride from quantum Monte Carlo calculations. Phys. Rev. B Condens. Matter. Mater. Phys. 2008, 77, 104103. [Google Scholar] [CrossRef]









| Structures | ΔH (kJ/(mol H2)) | Td (K) | Activation Energy (kJ/mol) |
|---|---|---|---|
| MgH2 | −63.961 | 489.37 | 109.21 |
| Mg0.9455Ti0.0555H2 | −51.212 | 391.82 | 78.24 |
| Mg0.9455V0.0555H2 | −50.117 | 383.45 | 69.11 |
| Mg0.9455Zr0.0555H2 | −51.192 | 391.67 | 75.49 |
| Material | Hydrogenation Time (min) | Reduction in Time (%) | Thermal Energy Consumption (Wh) | Energy Reduction (%) | Specific Thermal Energy Removal (Wh/g H2) |
|---|---|---|---|---|---|
| Pure MgH2 | 3.5 | — | 55.0 | — | 34.9 |
| Ti-doped MgH2 | 2.76 | 21% | 47.0 | 14.5% | 29.8 |
| Zr-doped MgH2 | 2.10 | 40% | 46.5 | 15.5% | 29.5 |
| V-doped MgH2 | 2.03 | 42% | 45.5 | 17.3% | 28.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chrafih, Y.; Alqahtani, R.T.; Ajbar, A.; Lamrani, B. Multi-Scale Modeling of Doped Magnesium Hydride Nanomaterials for Hydrogen Storage Applications. Nanomaterials 2025, 15, 1470. https://doi.org/10.3390/nano15191470
Chrafih Y, Alqahtani RT, Ajbar A, Lamrani B. Multi-Scale Modeling of Doped Magnesium Hydride Nanomaterials for Hydrogen Storage Applications. Nanomaterials. 2025; 15(19):1470. https://doi.org/10.3390/nano15191470
Chicago/Turabian StyleChrafih, Younes, Rubayyi T. Alqahtani, Abdelhamid Ajbar, and Bilal Lamrani. 2025. "Multi-Scale Modeling of Doped Magnesium Hydride Nanomaterials for Hydrogen Storage Applications" Nanomaterials 15, no. 19: 1470. https://doi.org/10.3390/nano15191470
APA StyleChrafih, Y., Alqahtani, R. T., Ajbar, A., & Lamrani, B. (2025). Multi-Scale Modeling of Doped Magnesium Hydride Nanomaterials for Hydrogen Storage Applications. Nanomaterials, 15(19), 1470. https://doi.org/10.3390/nano15191470







