Excitonic States in GaAs/AlxGa1−xAs Quantum Wells: Direct Coulomb Interaction Modeling via Finite Element Electrostatics and Parametric Analysis Under Impurity and Field Effects
Abstract
1. Introduction
2. Theoretical Background
2.1. Effective Mass Approximation and Confinement Model with Impurity Interaction
2.2. Schrödinger Equation in Cylindrical Coordinates with External Fields
3. Methodology
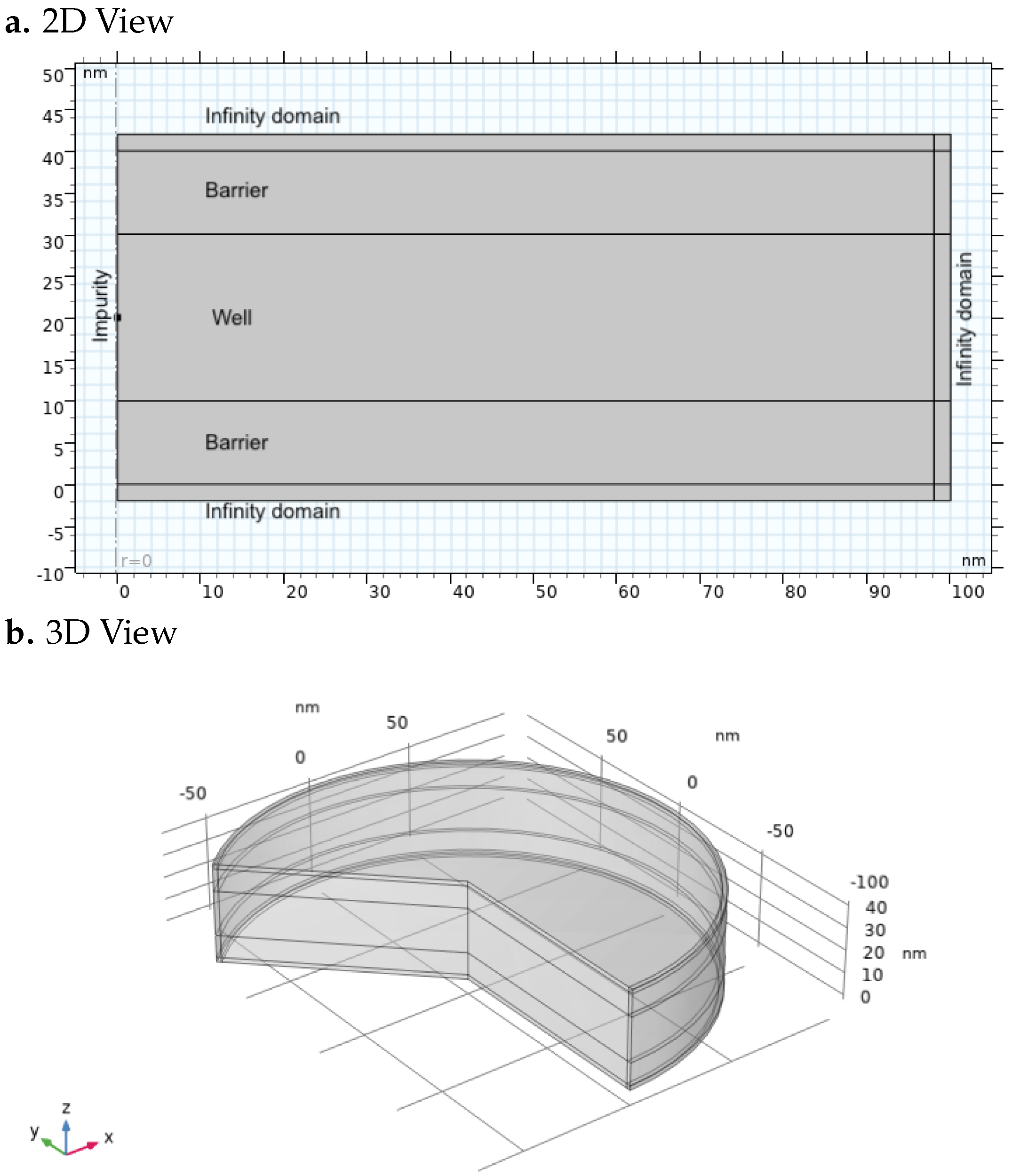
3.1. Geometry of Interest
3.2. Coulomb Interaction and Exciton Formation
3.3. Coulomb Interaction Using FEM in COMSOL
4. Results
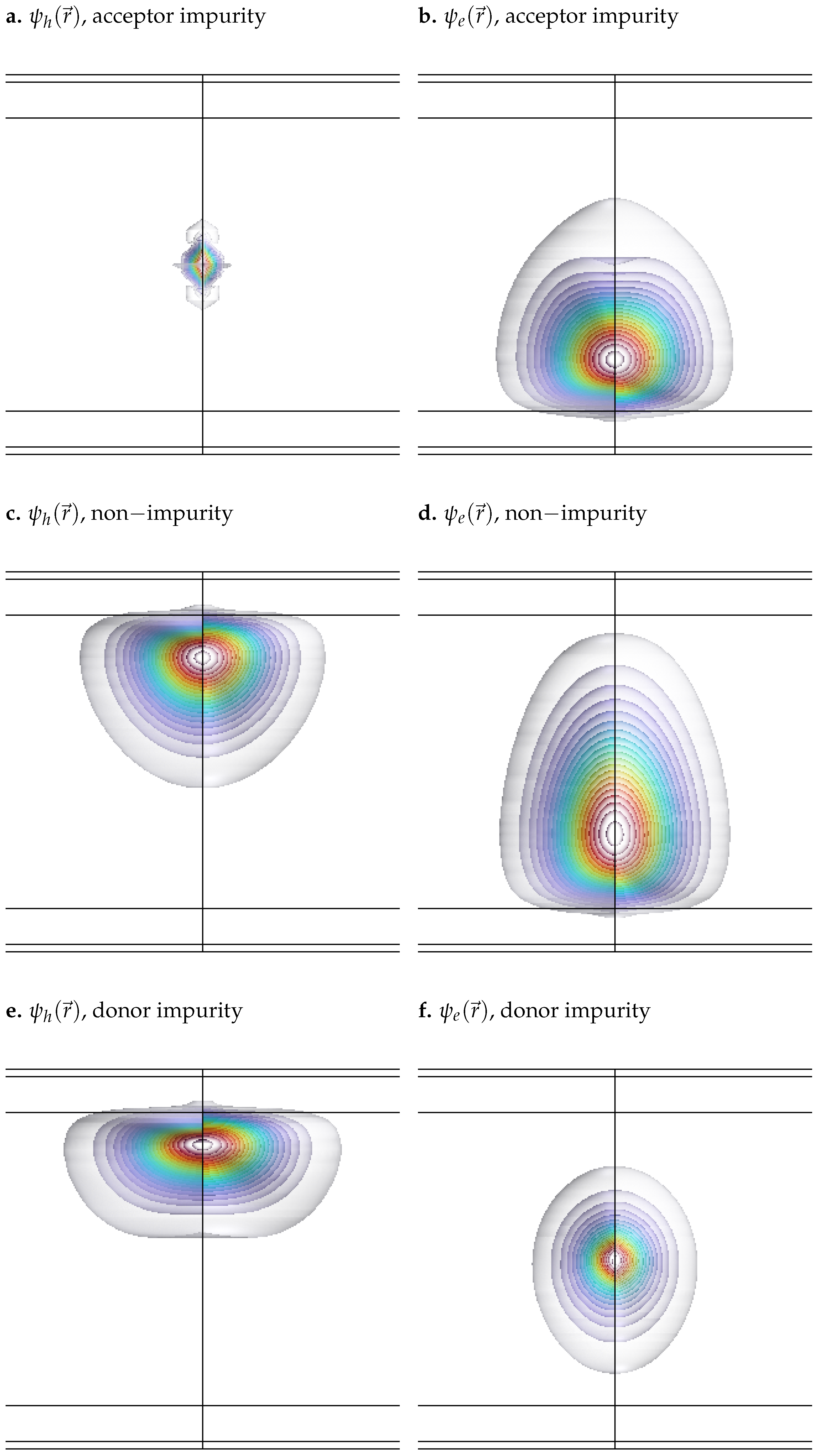
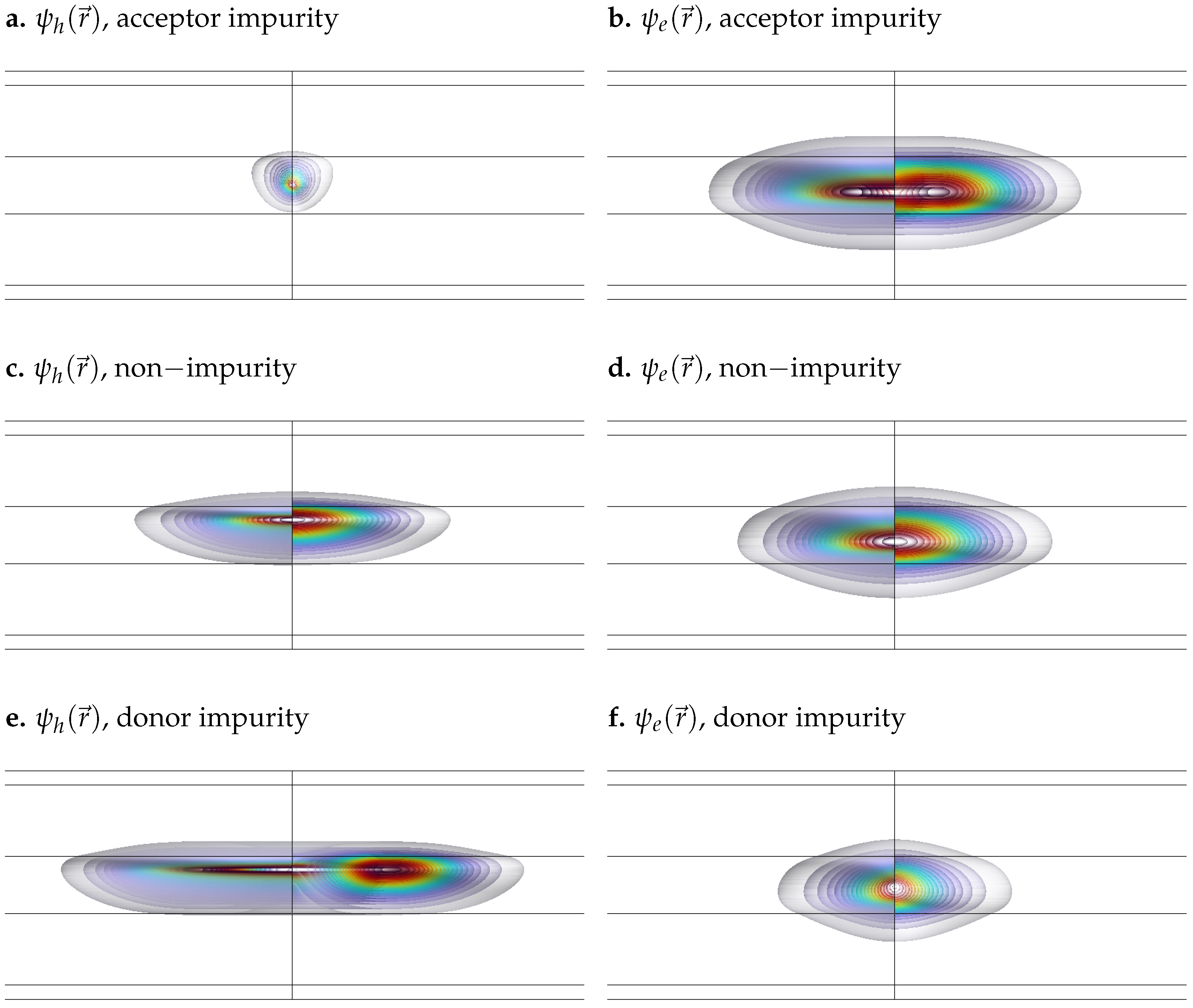
4.1. Solution of the Schrödinger Equation for the Electron and the Hole
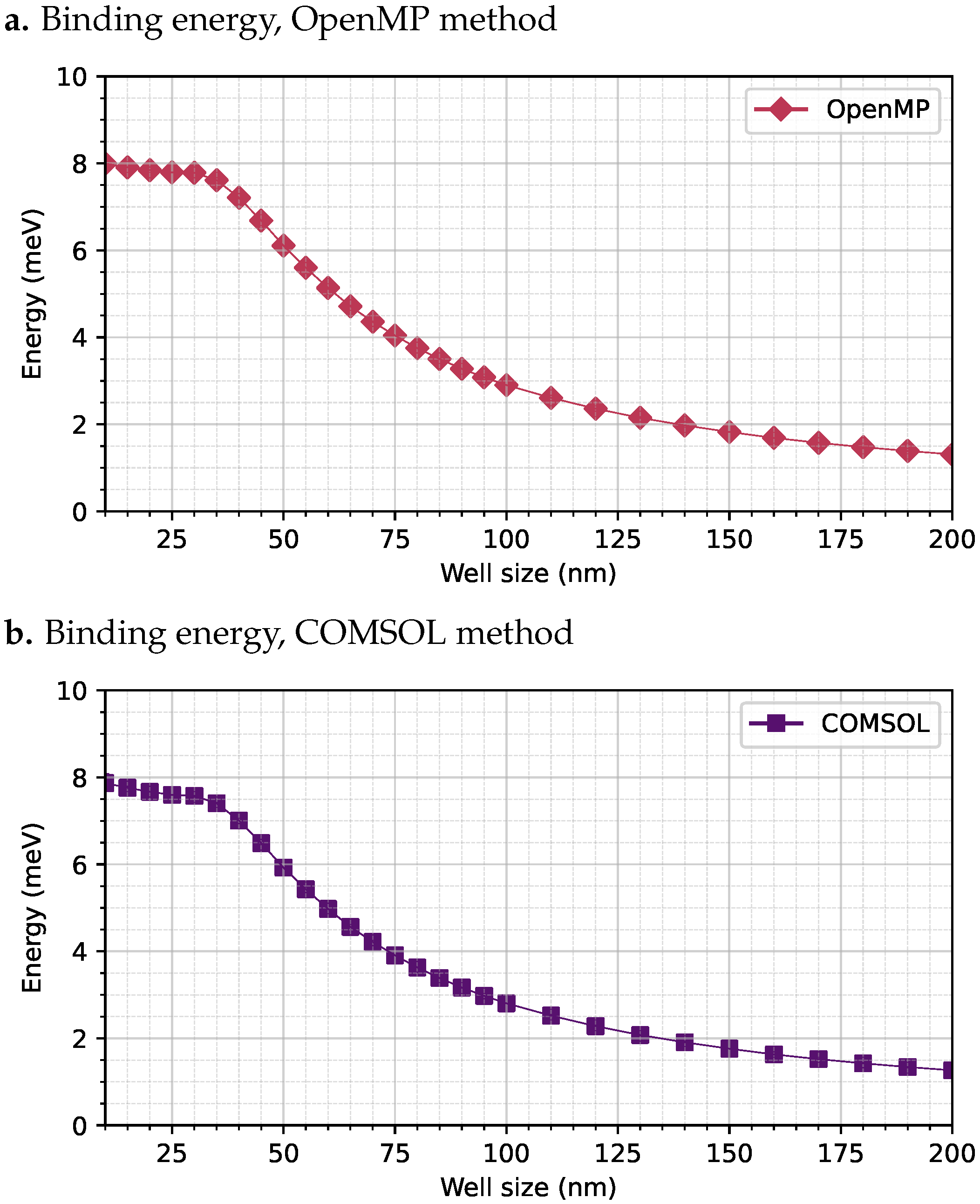
4.2. Validation of the Binding Energy Calculation Using C/OpenMP and COMSOL
4.3. Exciton Binding Energy in the GaAs Quantum Well
4.4. Scalar Electric Potential Field Generated by the Hole
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bastard, G.; Mendez, E.E.; Chang, L.L.; Esaki, L. Exciton binding energy in quantum wells. Phys. Rev. B 1982, 26, 1974–1979. [Google Scholar] [CrossRef]
- Greene, R.L.; Bajaj, K.K.; Phelps, D.E. Energy levels of wannier excitons in gaas-ga1−xalxas quantum-well structures. Phys. Rev. B 1984, 29, 1807–1812. [Google Scholar] [CrossRef]
- Riva, C.; Peeters, F.M.; Varga, K. Excitons and charged excitons in semiconductor quantum wells. Phys. Rev. B 2000, 61, 13873–13881. [Google Scholar] [CrossRef]
- Fan, B.; Zhao, X.; Zhang, J.; Sun, Y.; Yang, H.; Guo, L.J.; Zhou, S. Monolithically integrating iii-nitride quantum structure for full-spectrum white led via bandgap engineering heteroepitaxial growth. Laser Photonics Rev. 2023, 17, 2200455. [Google Scholar] [CrossRef]
- Zhou, S.; Wan, Z.; Lei, Y.; Tang, B.; Tao, G.; Du, P.; Zhao, X. Ingan quantum well with gradually varying indium content for high-efficiency gan-based green light-emitting diodes. Opt. Lett. 2022, 47, 1291. [Google Scholar] [CrossRef]
- Hasanirokh, K.; Tuzemen, E.A.L.A.; Sayrac, M.; Sayrac, H.; Ungan, F. Investigation of nonlinear optical properties in gaas/gaalas quantum well with modified lennard-jones potential: Role of static electromagnetic fields, intense laser radiation and structure parameters. Photonics Nanostructures-Fundam. Appl. 2025, 65, 101403, Erratum in Photonics Nanostructures-Fundam. Appl. 2025, 101419. [Google Scholar] [CrossRef]
- González-Reyes, R.; Correa, J.; Mora-Ramos, M.; Rodríguez-Magdaleno, K.; Nava-Maldonado, F.; Martínez-Orozco, J. Optoelectronic properties of a van der waals heterostructure black-phosphorene/mos 2 considering p-atoms vacancy defects. Phys. B Condens. Matter 2024, 694, 416455. [Google Scholar] [CrossRef]
- Jaouane, M.; Arraoui, R.; Ed-Dahmouny, A.; Fakkahi, A.; Azmi, H.; El-Bakkari, K.; Althib, H.; Ghazi, H.E.; Sali, A.; Ungan, F. Optical and electronic properties of confined exciton in a dot-in-rod structure. Mater. Sci. Semicond. Process. 2025, 194, 109559. [Google Scholar] [CrossRef]
- Ed-Dahmouny, A.; Sali, A.; Es-Sbai, N.; Arraoui, R.; Jaouane, M.; Fakkahi, A.; El-Bakkari, K.; Duque, C.A. Combined effects of hydrostatic pressure and electric field on the donor binding energy, polarizability, and photoionization cross-section in double gaas/ga1−xalxas quantum dots. Eur. Phys. J. B 2022, 95, 136. [Google Scholar] [CrossRef]
- Zhong, X.; Ni, X.; Sidhik, S.; Li, H.; Mohite, A.D.; Brédas, J.; Kahn, A. Direct Characterization of Type-I Band Alignment in 2D Ruddlesden–Popper Perovskites. Adv. Energy Mater. 2022, 12, 2202333. [Google Scholar] [CrossRef]
- Maldonado-Villa, B.; Rodríguez-Magdaleno, K.; Nava-Maldonado, F.; Duque, C.; Ungan, F.; Martínez-Orozco, J. Intra and interband optical absorption coefficient for asymmetric double algaas/gaas quantum well under hydrostatic pressure and electric field effects. Phys. Lett. A 2024, 523, 129780. [Google Scholar] [CrossRef]
- Tuzemen, A.T.; Dakhlaoui, H.; Mora-Ramos, M.; Al, E.; Ungan, F. Nonlinear optical properties of gaas/algaas asymmetric triple quantum wells designed for quantum cascade lasers: Effect of externally applied electric and magnetic fields. Phys. B Condens. Matter 2024, 690, 416223. [Google Scholar] [CrossRef]
- Belov, P.A.; Khramtsov, E.S. The binding energy of excitons in narrow quantum wells. J. Phys. Conf. Ser. 2017, 816, 012018. [Google Scholar] [CrossRef]
- Gerlach, B.; Wüsthoff, J.; Dzero, M.O.; Smondyrev, M.A. Exciton binding energy in a quantum well. Phys. Rev. B 1998, 58, 10568–10577. [Google Scholar] [CrossRef]
- Gil-Corrales, J.; Dagua-Conda, C.; Mora-Ramos, M.; Morales, A.; Duque, C. Shape and size effects on electronic thermodynamics in nanoscopic quantum dots. Phys. E Low-Dimens. Syst. Nanostructures 2025, 170, 116228. [Google Scholar] [CrossRef]
- Davlatov, A.; Gulyamov, G.; Nabiyev, A.; Feddi, E.; Feddi, K.; Abdukarimov, A.; Botirjonov, A. Unraveling the effects of non-parabolicity on electron energy levels in InP/InAs/InP heterostructures. Phys. Scr. 2024, 99, 075933. [Google Scholar] [CrossRef]
- Christol, P.; Lefebvre, P.; Mathieu, H. Fractional-dimensional calculation of exciton binding energies in semiconductor quantum wells and quantum-well wires. J. Appl. Phys. 1993, 74, 5626–5637. [Google Scholar] [CrossRef]
- de Dios-Leyva, M.; Bruno-Alfonso, A.; Matos-Abiague, A.; Oliveira, L.E. Fractional-dimensional space and applications in quantum-confined semiconducting heterostructures. J. Appl. Phys. 1997, 82, 3155–3157. [Google Scholar] [CrossRef]
- Heyn, C.; Radu, A.; Vinasco, J.; Laroze, D.; Restrepo, R.; Tulupenko, V.; Hieu, N.N.; Phuc, H.V.; Mora-Ramos, M.; Ojeda, J.; et al. Exciton states in conical quantum dots under applied electric and magnetic fields. Opt. Laser Technol. 2021, 139, 106953. [Google Scholar] [CrossRef]
- Hbibi, M.; Chouef, S.; Boussetta, R.; Moussaouy, A.E.; Mommadi, O.; Duque, C. Optical absorption and photovoltaic performance in inn/ingan multilayer quantum dots: Effects of confinement, in-fraction, and built-in electric field. Sol. Energy 2025, 298, 113620. [Google Scholar] [CrossRef]
- Filinov, A.V.; Riva, C.; Peeters, F.M.; Lozovik, Y.E.; Bonitz, M. Influence of well-width fluctuations on the binding energy of excitons, charged excitons, and biexcitons in gaas-based quantum wells. Phys. Rev. B 2004, 70, 035323. [Google Scholar] [CrossRef]
- Leavitt, R.P.; Little, J.W. Simple method for calculating exciton binding energies in quantum-confined semiconductor structures. Phys. Rev. B 1990, 42, 11774–11783. [Google Scholar] [CrossRef]
- Bouhlal, A.; Azar, M.E.; Naciri, A.E.; Feddi, E.; Jellal, A. Electron trapping via magnetic and laser fields in gapped graphene quantum dots. Phys. E Low-Dimens. Syst. Nanostructures 2025, 172, 116273. [Google Scholar] [CrossRef]
- Heckötter, J.; Aßmann, M.; Bayer, M. Rydberg excitons and quantum sensing. MRS Bull. 2024, 49, 948–957. [Google Scholar] [CrossRef]
- Belov, P.; Arkhipov, R. Formation of the stopped polarization pulse in a rectangular quantum well. Micro Nanostructures 2023, 180, 207607. [Google Scholar] [CrossRef]
- Belamkadem, L.; Mommadi, O.; Vinasco, J.; Laroze, D.; Moussaouy, A.E.; Chnafi, M.; Duque, C. Electronic properties and hydrogenic impurity binding energy of a new variant quantum dot. Phys. E Low-Dimens. Syst. Nanostructures 2021, 129, 114642. [Google Scholar] [CrossRef]
- Chuu, D.-S.; Won, W.-L.; Pei, J.-H. Longitudinal-optical-phonon effects on the exciton binding energy in a semiconductor quantum well. Phys. Rev. B 1994, 49, 14554–14563. [Google Scholar] [CrossRef]
- Yücel, M.B.; Sari, H.; Duque, C.M.; Duque, C.A.; Kasapoglu, E. Theoretical Study of the Exciton Binding Energy and Exciton Absorption in Different Hyperbolic-Type Quantum Wells under Applied Electric, Magnetic, and Intense Laser Fields. Int. J. Mol. Sci. 2022, 23, 11429. [Google Scholar] [CrossRef]
- Huang, J.; Hoang, T.; Mikkelsen, M. Probing the origin of excitonic states in monolayer wse2. Sci. Rep. 2016, 6, 22414. [Google Scholar] [CrossRef] [PubMed]
- Blancon, J.-C.; Stier, A.V.; Tsai, H.; Nie, W.; Stoumpos, C.C.; Traoré, B.; Pedesseau, L.; Kepenekian, M.; Katsutani, F.; Noe, G.T.; et al. Scaling law for excitons in 2D perovskite quantum wells. Nat. Commun. 2018, 9, 2254. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, J.; Parveen, S.; Sellin, P.J.; Giri, P.K. Recent Advances and Opportunities in Low-Dimensional Layered Perovskites for Emergent Applications beyond Photovoltaics. Adv. Mater. Technol. 2023, 8, 2300400. [Google Scholar] [CrossRef]
- Barseghyan, M.; Hakimyfard, A.; López, S.; Duque, C.; Kirakosyan, A. Simultaneous effects of hydrostatic pressure and temperature on donor binding energy and photoionization cross section in pöschl–teller quantum well. Phys. E Low-Dimens. Syst. Nanostructures 2010, 42, 1618–1622. [Google Scholar] [CrossRef]
- Ortakaya, S.; Hammouda, K.; Zeiri, N.; Duque, C.A. Excitonic phenomena in the multilayer qds: Perturbative approach. Phys. Lett. A 2025, 544, 130474. [Google Scholar] [CrossRef]
- Wang, F.; Wang, Y.; Liu, Y.-H.; Morrison, P.J.; Loomis, R.A.; Buhro, W.E. Two-Dimensional Semiconductor Nanocrystals: Properties, Templated Formation, and Magic-Size Nanocluster Intermediates. Accounts Chem. Res. 2015, 48, 13–21. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Marie, X.; Gerber, I.; Amand, T.; Lagarde, D.; Bouet, L.; Vidal, M.; Balocchi, A.; Urbaszek, B. Giant Enhancement of the Optical Second-Harmonic Emission of WSe2 Monolayers by Laser Excitation at Exciton Resonances. Phys. Rev. Lett. 2015, 114, 097403. [Google Scholar] [CrossRef] [PubMed]
- Turner, D.B.; Nelson, K.A.; Cundiff, S.T. Persistent exciton-type many-body interactions in gaas quantum wells measured using two-dimensional optical spectroscopy. Phys. Rev. B 2012, 85, 201303(R). [Google Scholar] [CrossRef]
- Bauer, G.E.W.; Ando, T. Theory of magnetoexcitons in quantum wells. Phys. Rev. B 1988, 37, 3130(R). [Google Scholar] [CrossRef]
- Jakubczyk, T.; Delmonte, V.; Koperski, M.; Nogajewski, K.; Faugeras, C.; Langbein, W.; Potemski, M.; Kasprzak, J. Radiatively Limited Dephasing and Exciton Dynamics in MoSe 2 Monolayers Revealed with Four-Wave Mixing Microscopy. Nano Lett. 2016, 16, 5333–5339. [Google Scholar] [CrossRef] [PubMed]
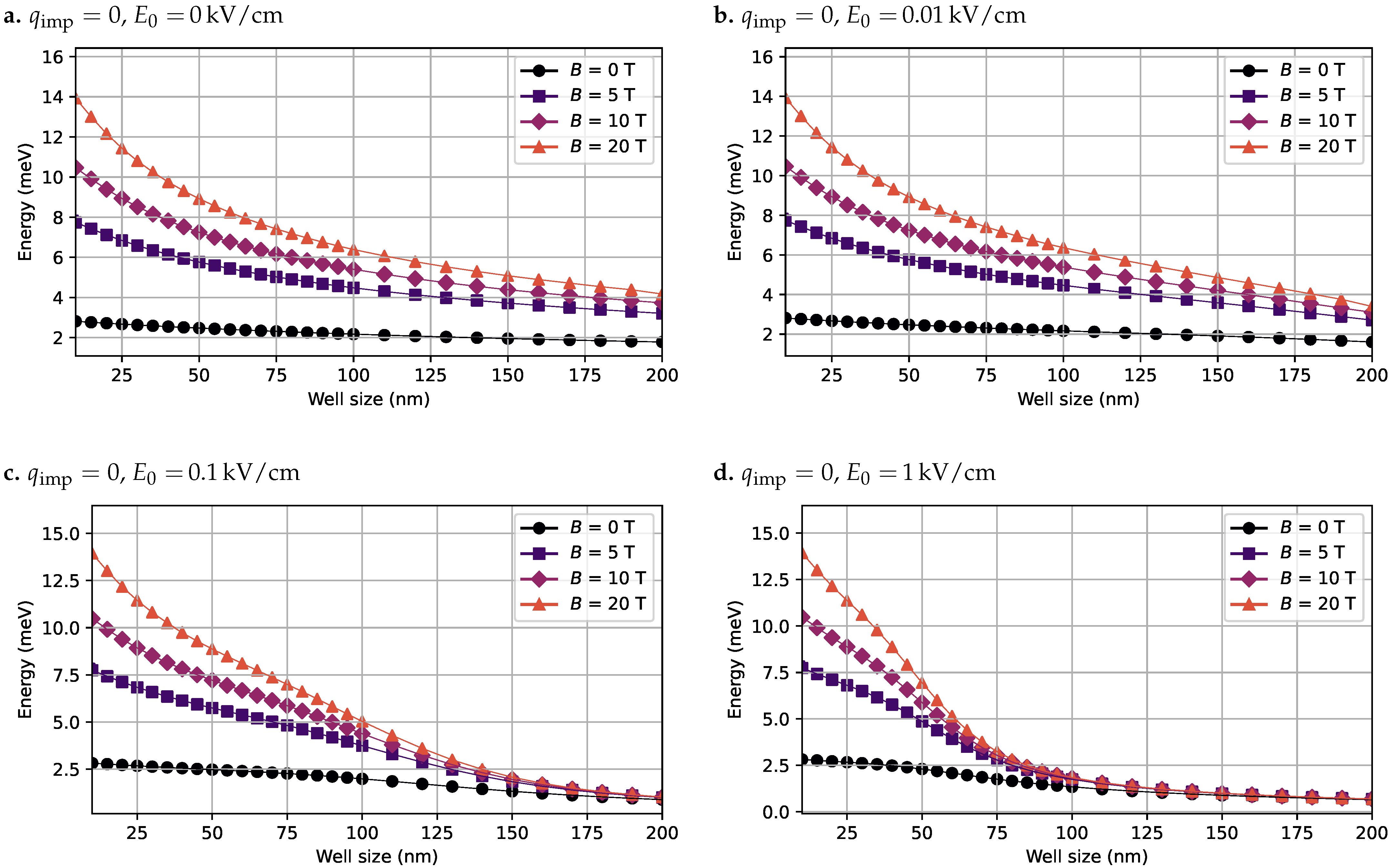


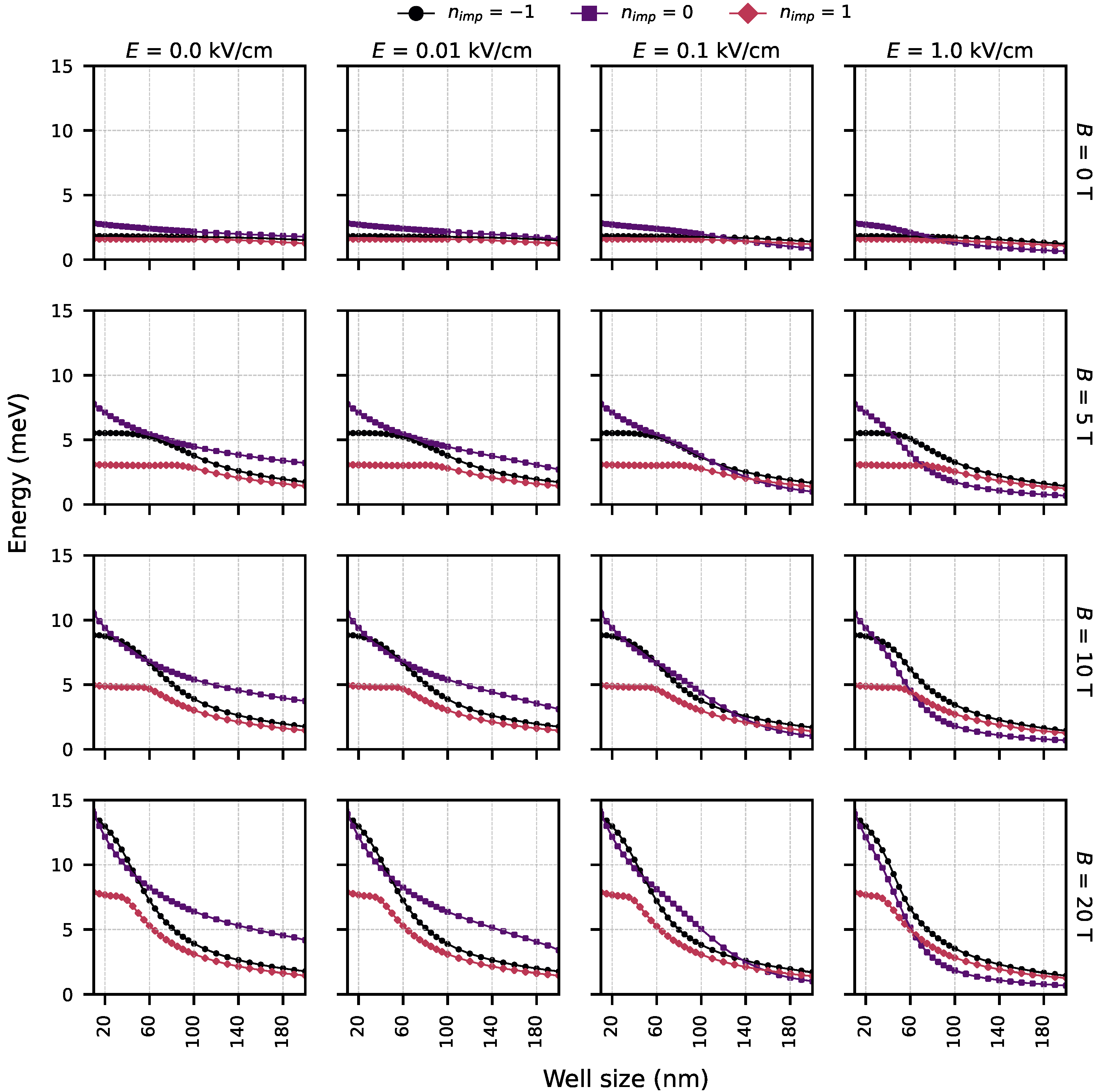
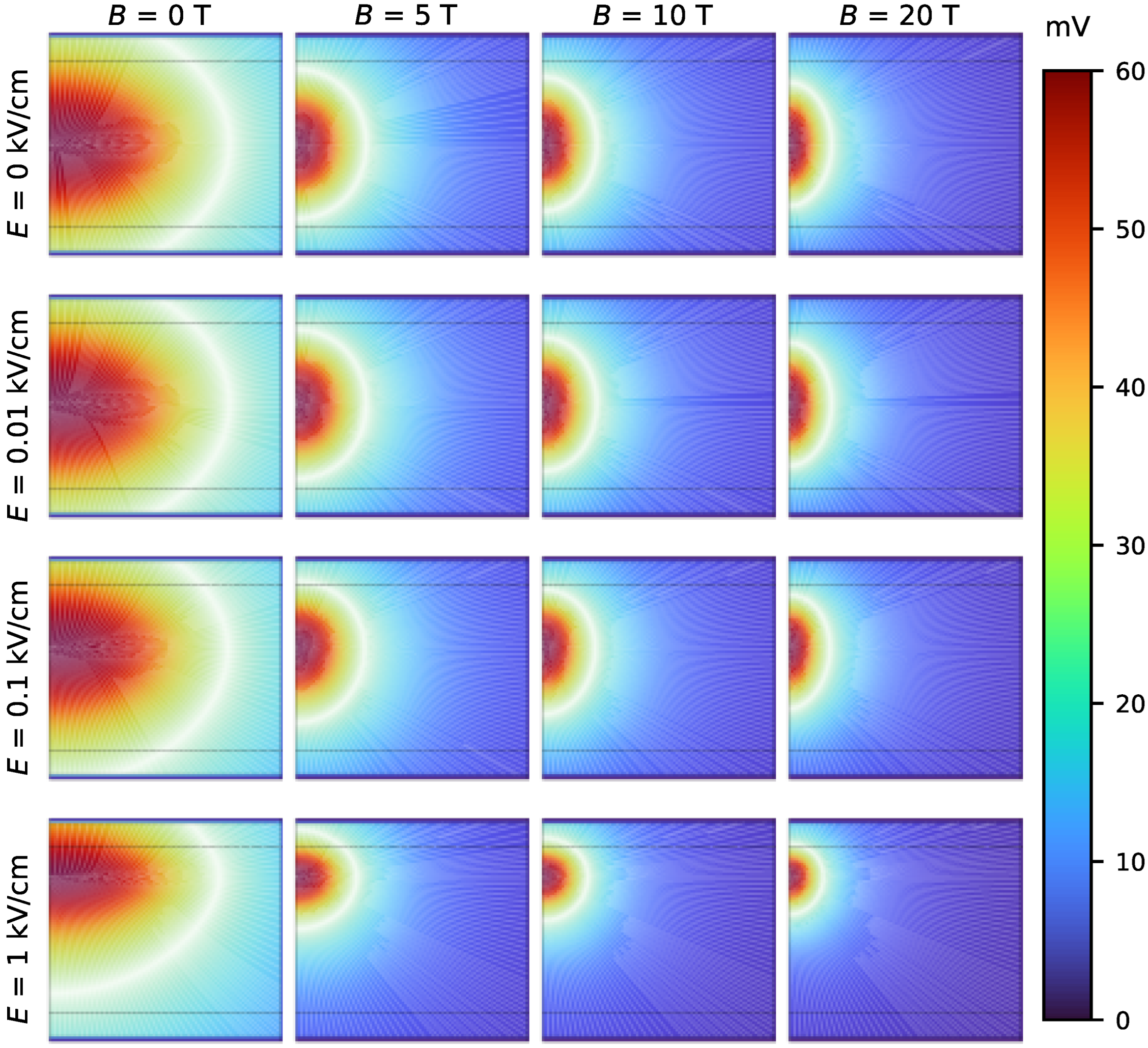
| Index | ||
|---|---|---|
| 0 | ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
| Parameter | C/OpenMP | COMSOL FEM |
|---|---|---|
| Number of CPU cores | 8 | 8 |
| Number of mesh nodes | 11,269 | 15,151 |
| Mesh quality (skewness) | 100% | 100% |
| Total number of integrals | 37 | 37 |
| Average time per integral | ||
| Total execution time | ||
| Relative error in J | Reference | <1% |
| Spatial resolution | 1 nm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castaño, F.A.; Laroze, D.; Duque, C.A. Excitonic States in GaAs/AlxGa1−xAs Quantum Wells: Direct Coulomb Interaction Modeling via Finite Element Electrostatics and Parametric Analysis Under Impurity and Field Effects. Nanomaterials 2025, 15, 1345. https://doi.org/10.3390/nano15171345
Castaño FA, Laroze D, Duque CA. Excitonic States in GaAs/AlxGa1−xAs Quantum Wells: Direct Coulomb Interaction Modeling via Finite Element Electrostatics and Parametric Analysis Under Impurity and Field Effects. Nanomaterials. 2025; 15(17):1345. https://doi.org/10.3390/nano15171345
Chicago/Turabian StyleCastaño, Fabian Andres, David Laroze, and Carlos Alberto Duque. 2025. "Excitonic States in GaAs/AlxGa1−xAs Quantum Wells: Direct Coulomb Interaction Modeling via Finite Element Electrostatics and Parametric Analysis Under Impurity and Field Effects" Nanomaterials 15, no. 17: 1345. https://doi.org/10.3390/nano15171345
APA StyleCastaño, F. A., Laroze, D., & Duque, C. A. (2025). Excitonic States in GaAs/AlxGa1−xAs Quantum Wells: Direct Coulomb Interaction Modeling via Finite Element Electrostatics and Parametric Analysis Under Impurity and Field Effects. Nanomaterials, 15(17), 1345. https://doi.org/10.3390/nano15171345






