Influence of Carbon Quantum Dots on the Orientational Order and Rotational Viscosity of 8CB
Abstract
1. Introduction
2. Materials and Techniques
2.1. Materials
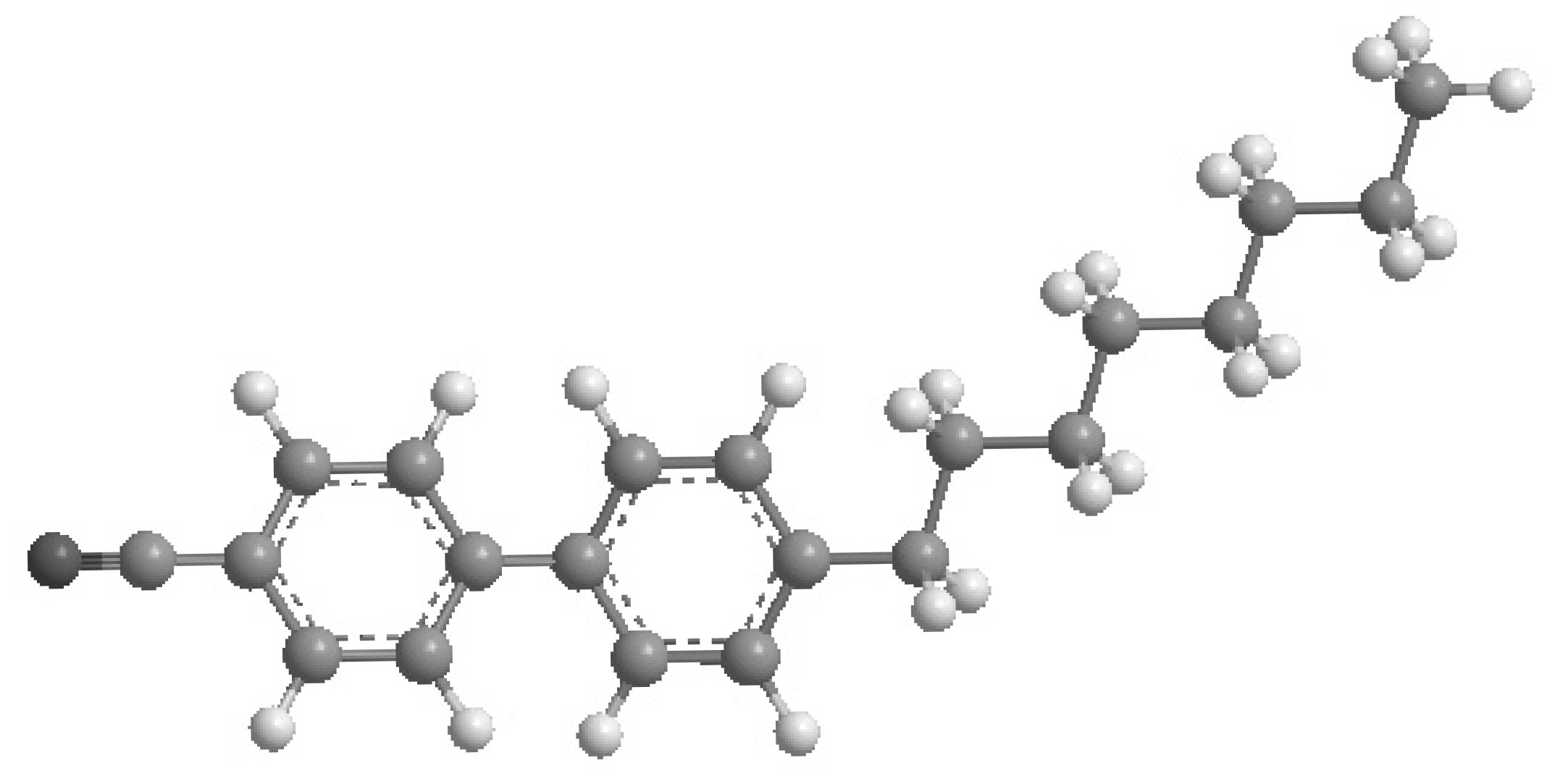
2.1.1. Liquid Crystal
2.1.2. Carbon Nanoparticles
2.1.3. Nanocomposites
2.2. Techniques
2.2.1. Experimental Setup
2.2.2. Procedure
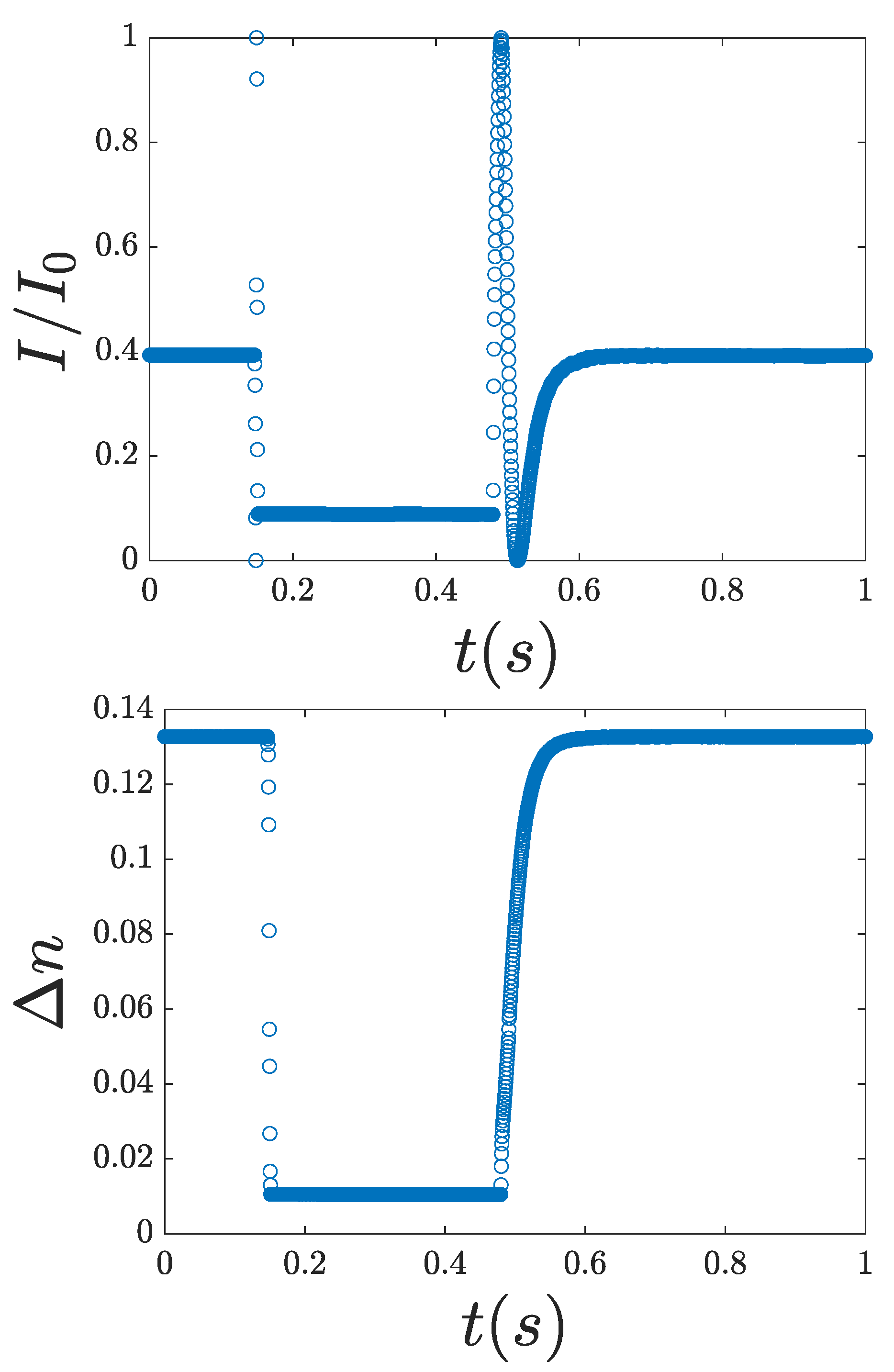
2.2.3. Dynamics
2.2.4. Data Acquisition and Analysis
3. Experimental Results
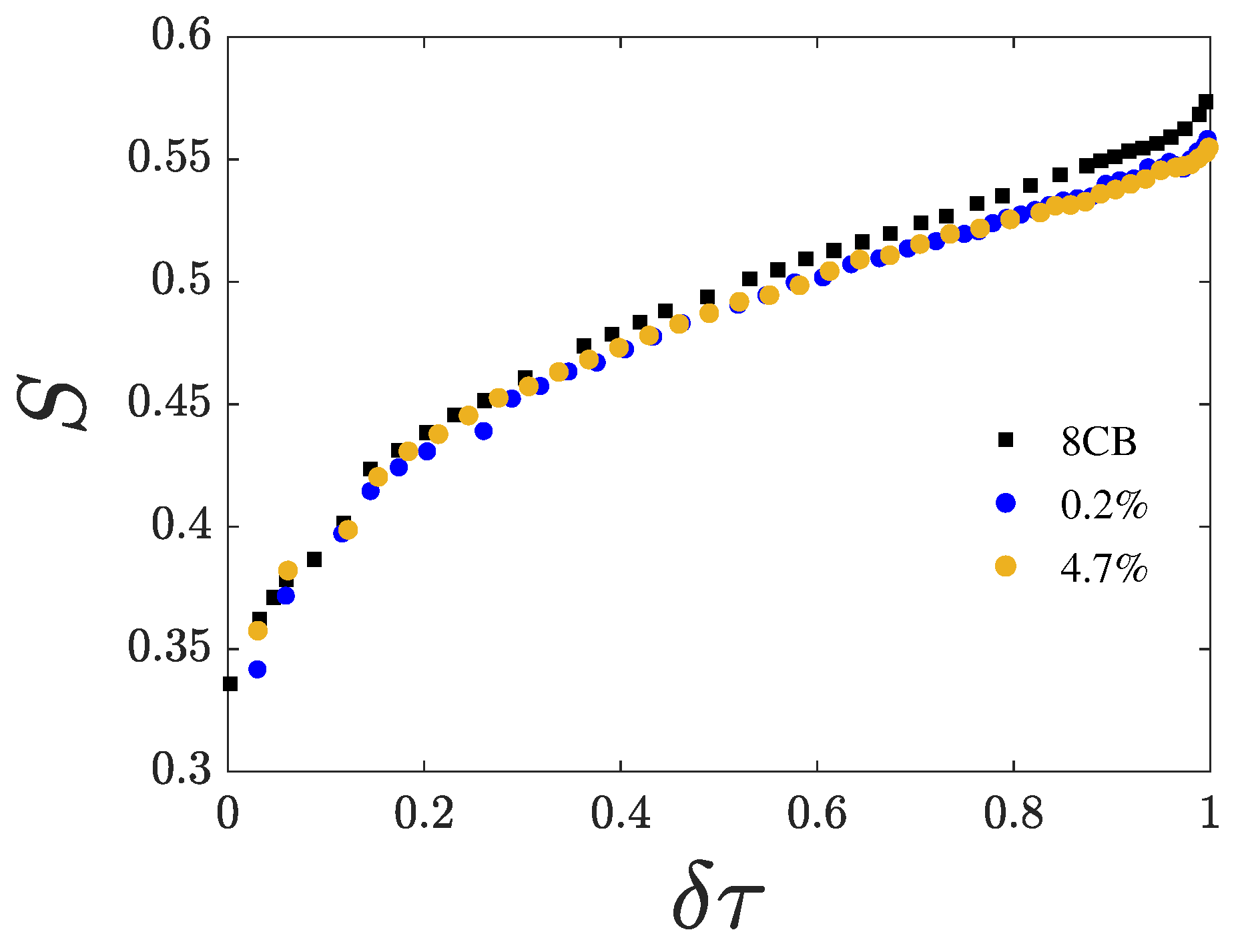
3.1. Microstructure, Phase Transitions, and Birefringence
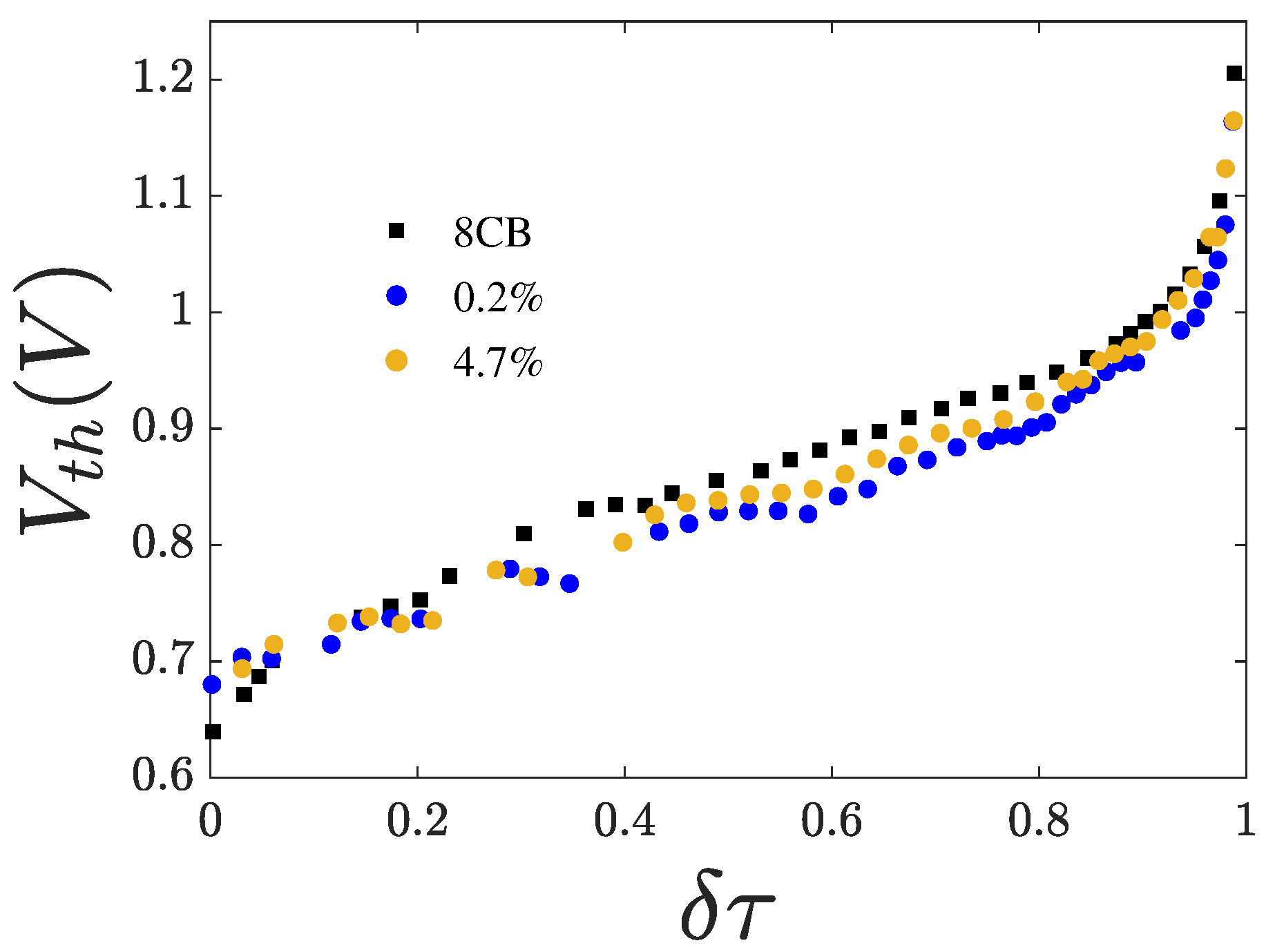
3.2. Threshold Voltage
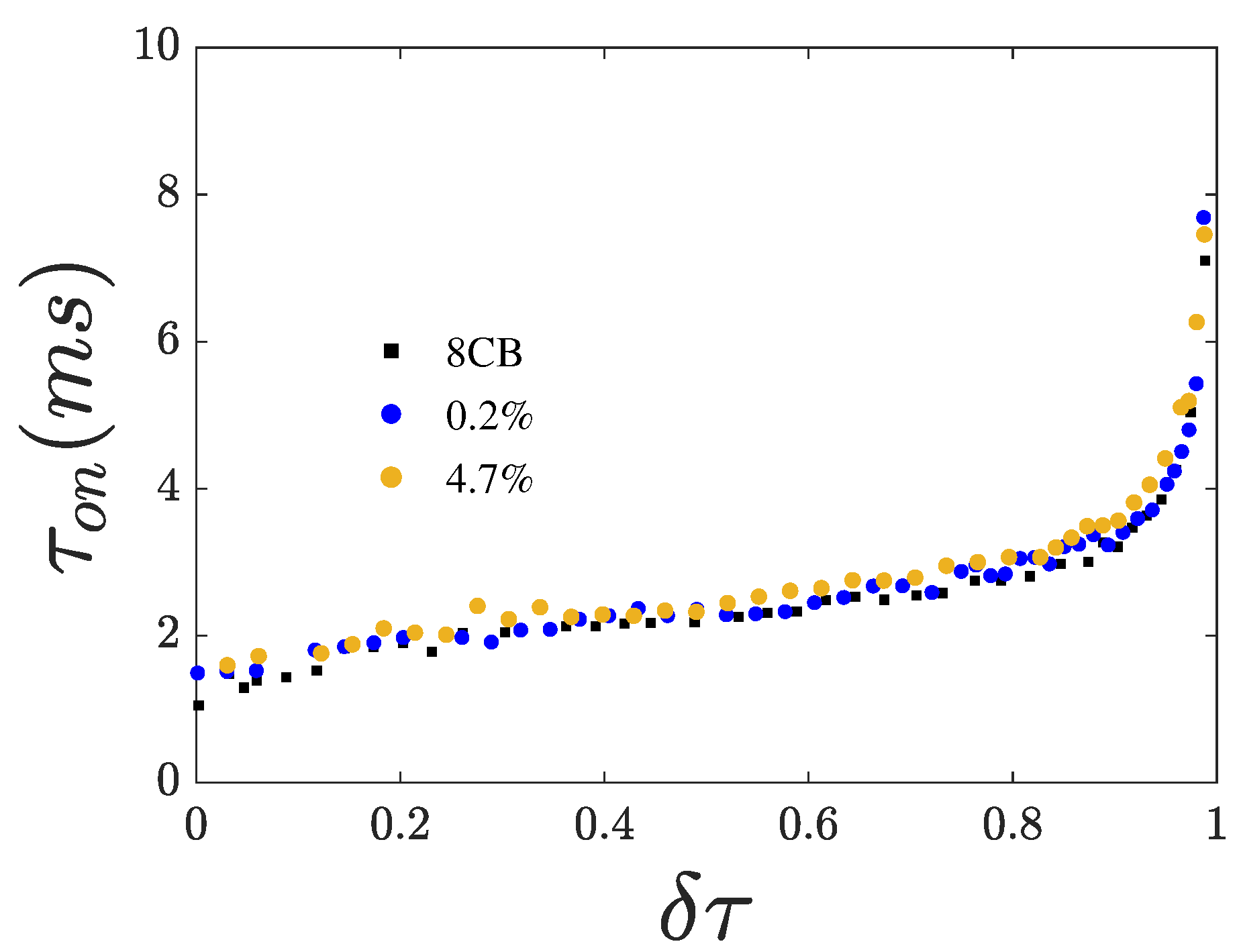
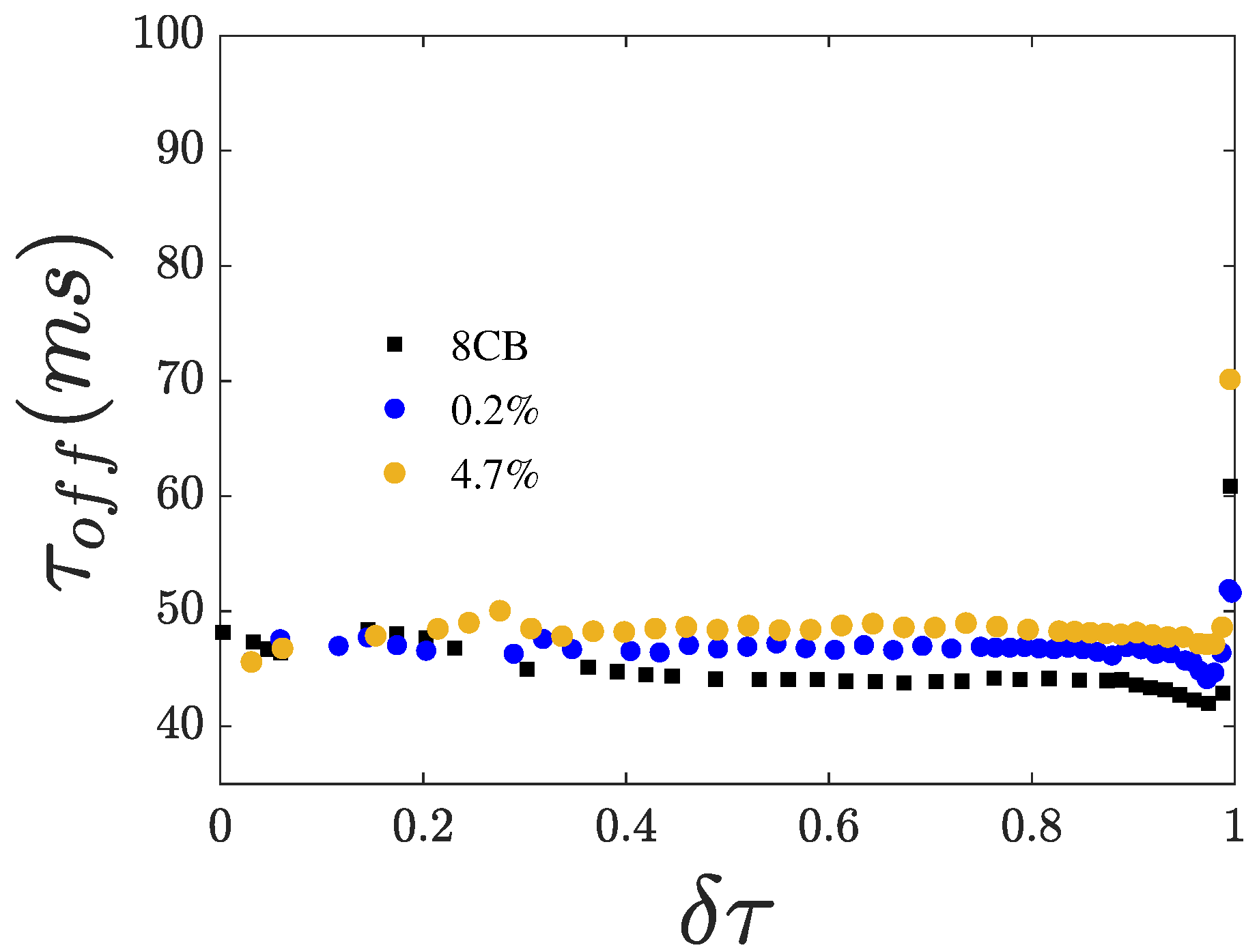
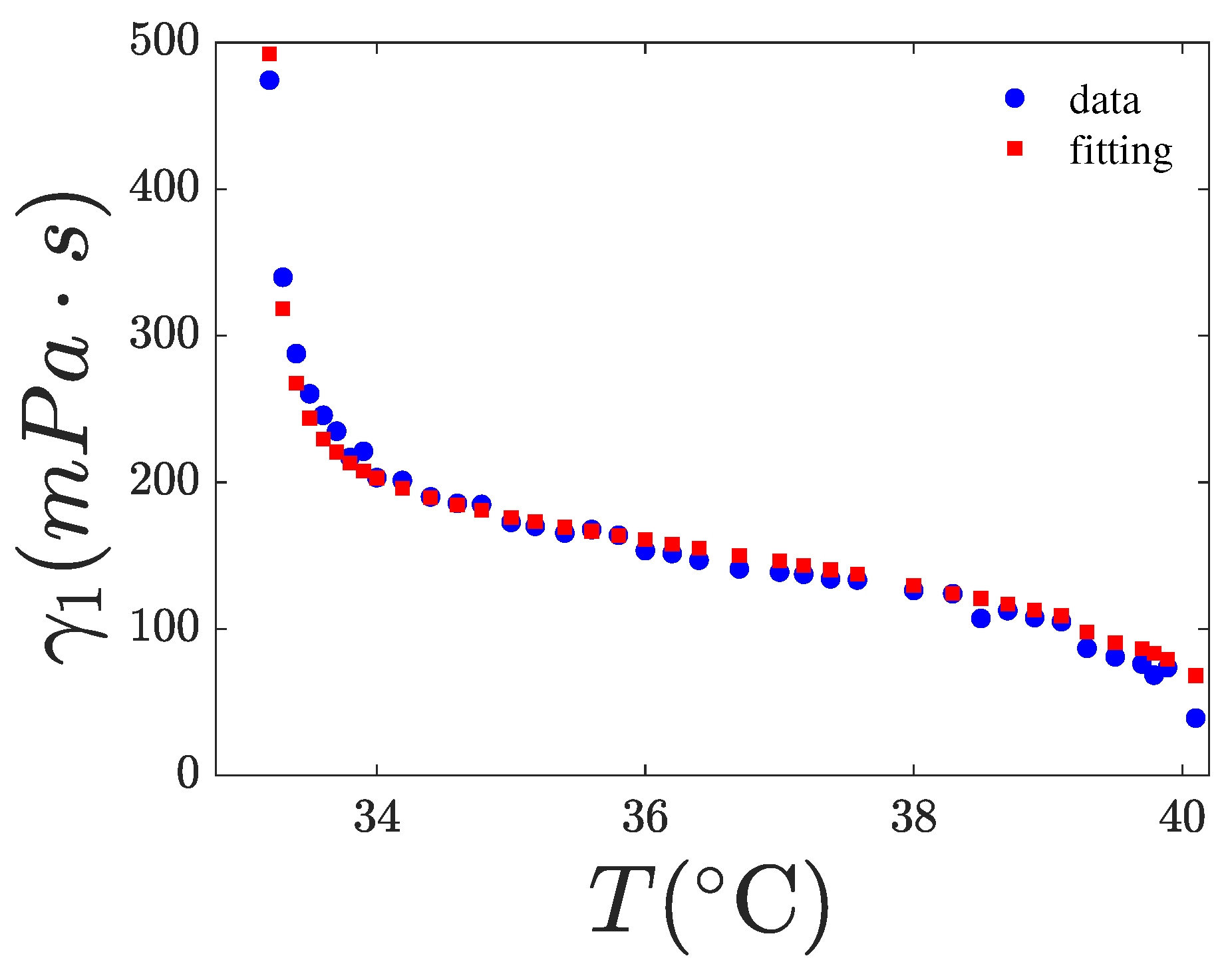
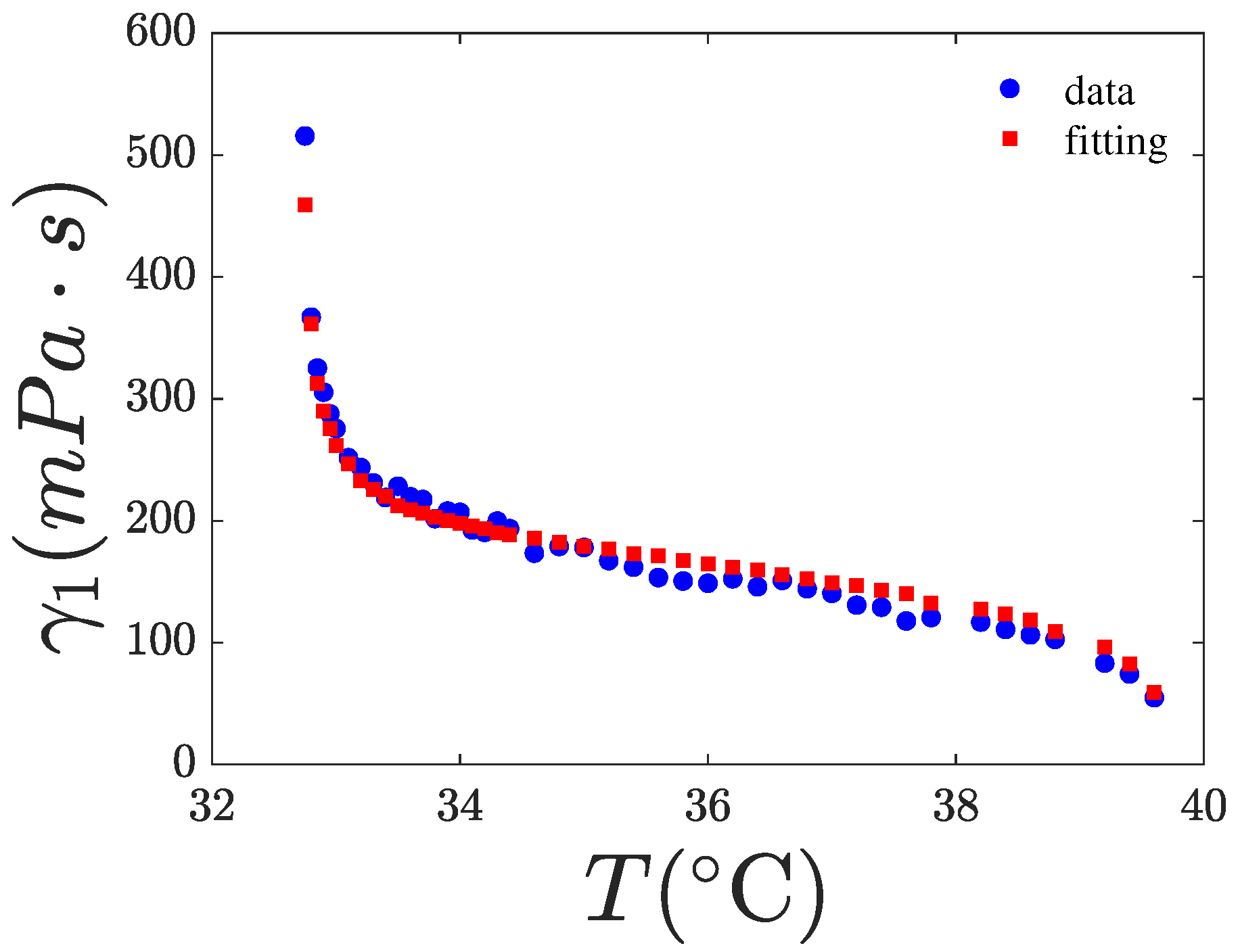
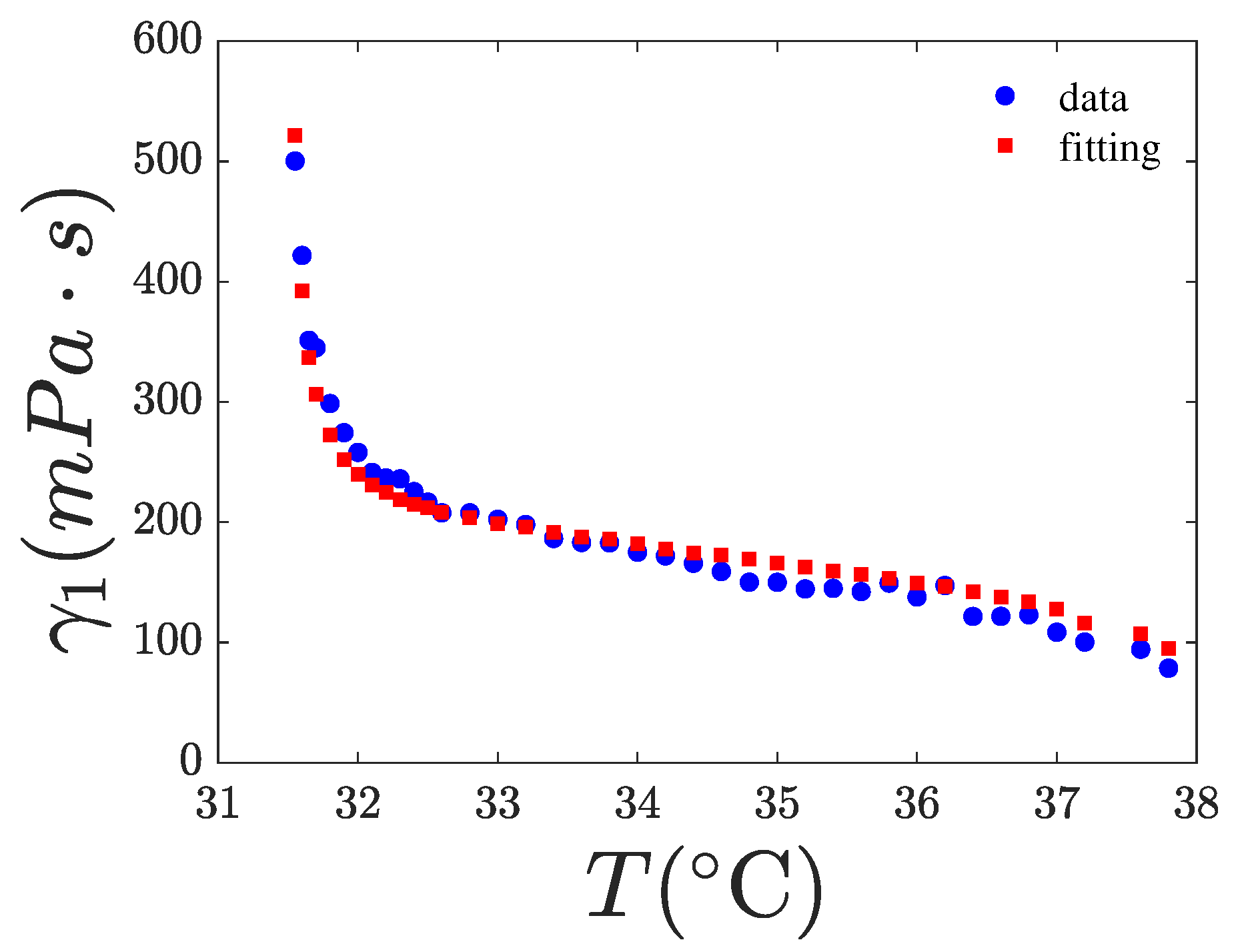
3.3. Switching Times
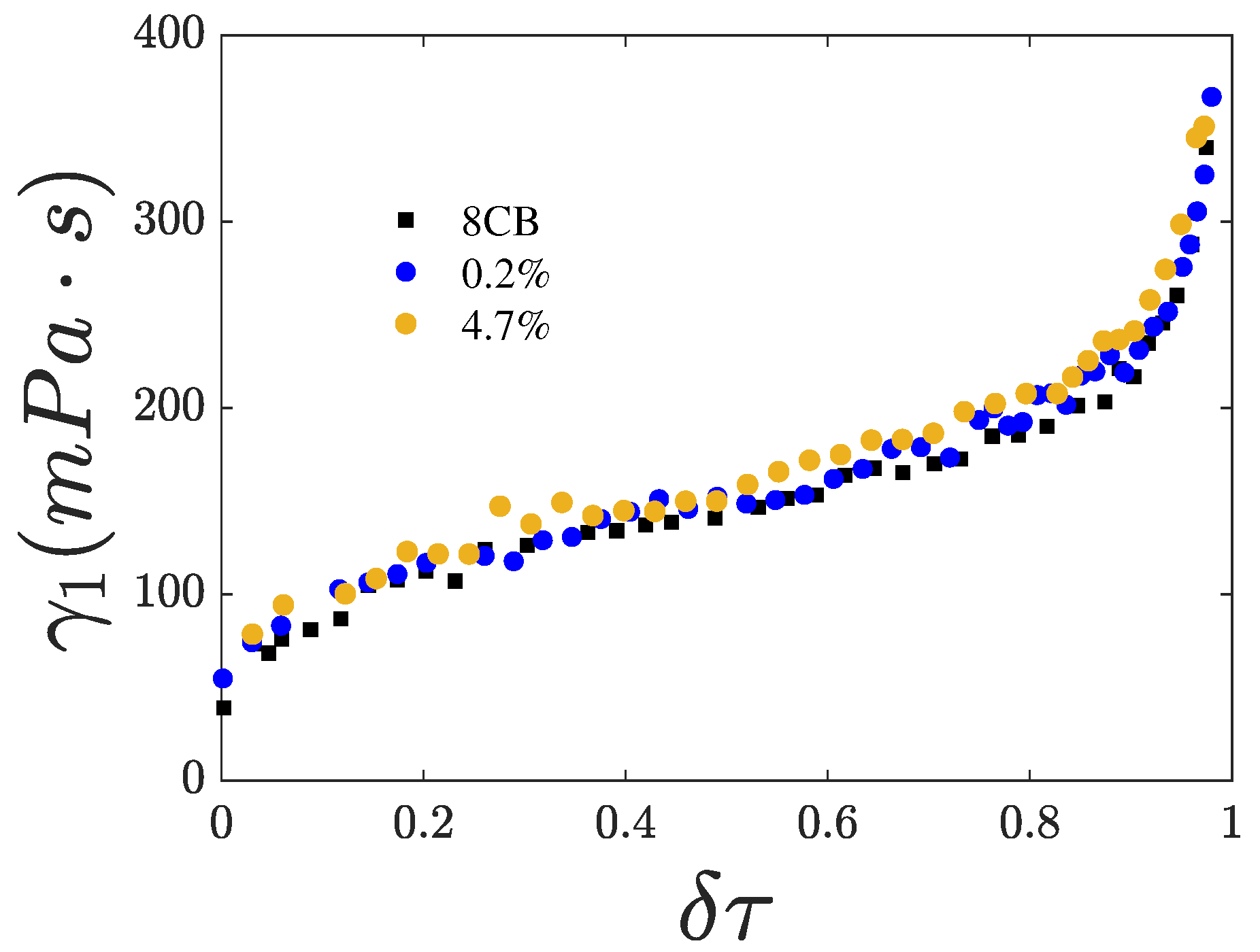
4. Analysis
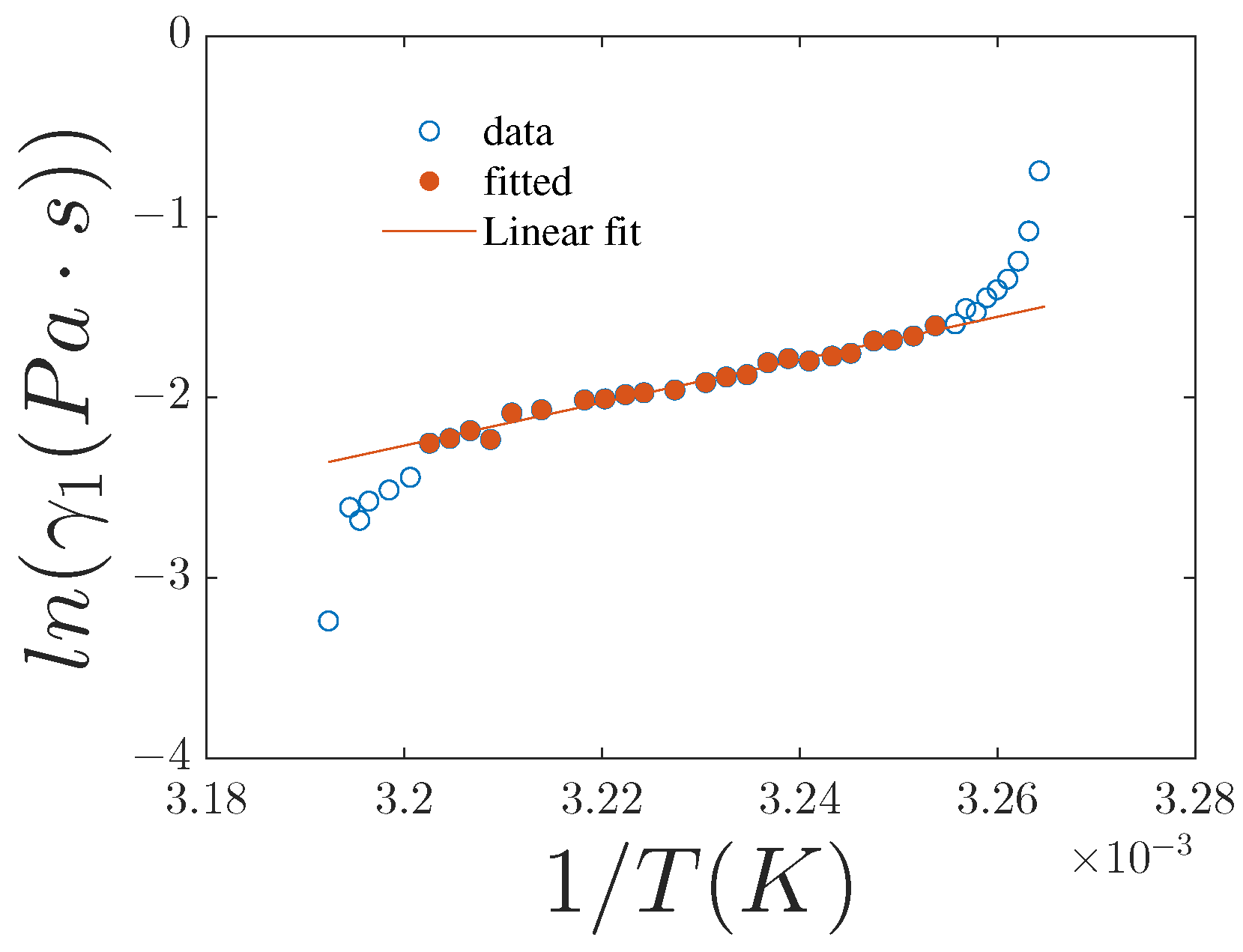
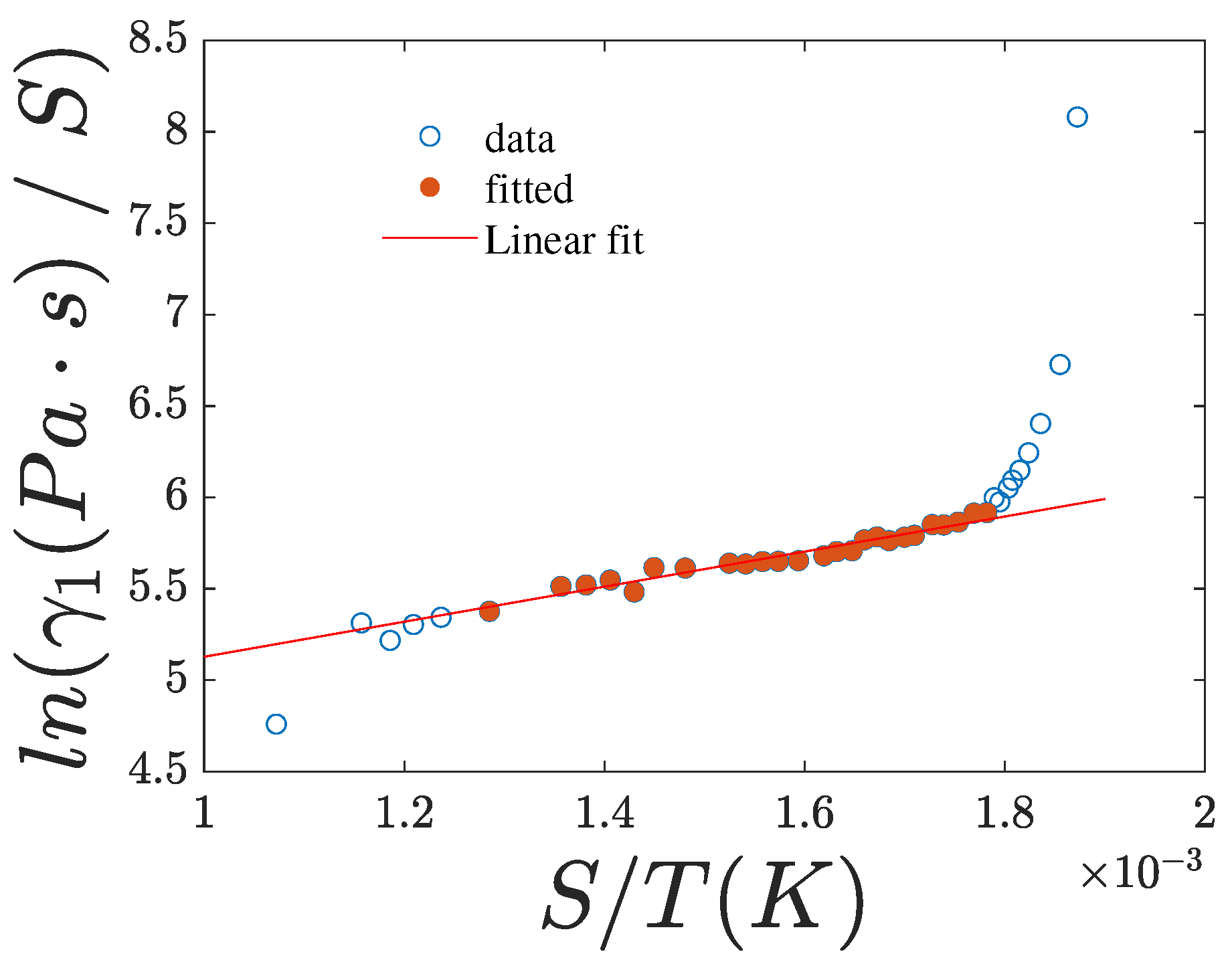
4.1. Activation Energy
4.2. Fitting of
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- De Gennes, P.G.; Prost, J. The Physics of Liquid Crystals; Clarendon Press: Oxford, UK, 1993; ISBN 0198517858. [Google Scholar]
- Kleman, M.; Lavrentovich, O.D. Soft Matter Physics: An Introduction; Springer: New York, NY, USA, 2003; ISBN 1441929274. [Google Scholar]
- Ericksen, J.L. Conservation Laws for Liquid Crystals. Trans. Soc. Rheol. 1961, 5, 22–34. [Google Scholar] [CrossRef]
- Leslie, F.M. Some Constitutive Equations for Liquid Crystals. Arch. Ration. Mech. Anal. 1968, 28, 265–283. [Google Scholar] [CrossRef]
- Forster, D.; Lubensky, T.C.; Martin, P.C.; Swift, J.; Pershan, P.S. Hydrodynamics of Liquid Crystals. Phys. Rev. Lett. 1971, 26, 1016–1019. [Google Scholar] [CrossRef]
- Martin, P.C.; Parodi, O.; Pershan, P.S. Unified Hydrodynamic Theory for Crystals, Liquid Crystals, and Normal Fluids. Phys. Rev. A 1972, 6, 2401–2420. [Google Scholar] [CrossRef]
- Jakeman, E.; Raynes, E.P. Electro-optic Response Times in Liquid Crystals. Phys. Lett. A 1972, 30, 69–70. [Google Scholar] [CrossRef]
- Diogo, A.C.; Martins, A.F. Thermal Behaviour of the Twist Viscosity in a Series of Homologous Nematic Liquid Crystals. Mol. Cryst. Liq. Cryst. 1981, 66, 133–146. [Google Scholar] [CrossRef]
- Belyaev, V.V. The Viscosity of Nematic Liquid Crystals. Russ. Chem. Rev. 1989, 58, 917–947. [Google Scholar] [CrossRef]
- Osipov, M.A.; Terentjev, E.M. Rotational Diffusion and Rheological Properties of Liquid Crystals. Z. Naturforsch. A 1989, 44, 785–792. [Google Scholar] [CrossRef]
- Kuzuu, N.; Doi, M. Constitutive Equation for Nematic Liquid Crystals under Weak Velocity Gradient Derived from a Molecular Kinetic Equation. J. Phys. Soc. Jpn. 1983, 52, 3486–3494. [Google Scholar] [CrossRef]
- Baalss, D.; Hess, S. Nonequilibrium Molecular-Dynamics Studies on the Anisotropic Viscosity of Perfectly Aligned Nematic Liquid Crystals. Phys. Rev. Lett. 1986, 57, 86–89. [Google Scholar] [CrossRef]
- Simões, M.; Correia da Silva, J.L. Geometrical Content of Leslie Coefficients. Phys. Rev. E 2011, 83, 051702. [Google Scholar] [CrossRef]
- Zakharov, A.V.; Komolki, A.V.; Maliniak, A. Rotational Viscosity in a Nematic Liquid Crystal: A Theoretical Treatment and Molecular Dynamics Simulation. Phys. Rev. E 1999, 59, 6802–6807. [Google Scholar] [CrossRef]
- Kuwajima, S.; Manabe, A. Computing the Rotational Viscosity of Nematic Liquid Crystals by an Atomistic Molecular Dynamics Simulation. Chem. Phys. Lett. 2000, 332, 105–109. [Google Scholar] [CrossRef]
- Cheung, D.L.; Clark, S.J.; Wilson, M.R. Calculation of the Rotational Viscosity of a Nematic Liquid Crystal. Chem. Phys. Lett. 2002, 356, 140–146. [Google Scholar] [CrossRef]
- Wu, S.T.; Wu, C.S. Rotational Viscosity of Nematic Liquid Crystals: A Critical Examination of Existing Models. Liq. Cryst. 1990, 8, 171–182. [Google Scholar] [CrossRef]
- Simões, M.; Domiciano, S.M. Agreements and Disagreements Between Theories and Experiments in Nematoviscosity. Phys. Rev. E 2003, 68, 011705. [Google Scholar] [CrossRef] [PubMed]
- Chrzanowska, A. Nematic Liquid Crystal Viscosity: Inadequacies of Microscopic Theories. Phys. Rev. E 2000, 62, 1431–1434. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.T.; Wu, C.S. Experimental Confirmation of the Osipov–Terentjev Theory on the Viscosity of Nematic Liquid Crystals. Phys. Rev. A 1990, 42, 2219–2228. [Google Scholar] [CrossRef] [PubMed]
- Scheffer, T.J.; Nehring, J. Accurate Determination of the Tilt Bias Angle of Liquid Crystals. J. Appl. Phys. 1977, 48, 1783–1792. [Google Scholar] [CrossRef]
- Wu, S.T. Phase Retardation Dependent Optical Response Time of Parallel Aligned Liquid Crystals. J. Appl. Phys. 1986, 60, 1836–1838. [Google Scholar] [CrossRef]
- Dark, M.L.; Moore, M.H.; Shenoy, D.K.; Shashidhar, R. Rotational Viscosity and Molecular Structure of Nematic Liquid Crystals. Liq. Cryst. 2006, 33, 67–73. [Google Scholar] [CrossRef]
- Kumar, M.P.; Sai, D.V.; Dhara, S. Effect of Sm-A Short-Range Order on the Activation Energies of Translational and Rotational Viscosities of Nematic Liquid Crystals with Highly Polar Molecules. Phys. Rev. E 2018, 98, 062701. [Google Scholar] [CrossRef]
- Zvetkov, V.; Sosnovsky, A. Diamagnetic Anisotropy of Crystalline Liquids. Acta Physicochim. URSS 1943, 18, 358–369. [Google Scholar]
- Gasparoux, H.; Prost, J. Détermination directe de l’anisotropie magnétique de cristaux liquides nématiques. J. Phys. 1971, 32, 953–962. [Google Scholar] [CrossRef]
- Kneppe, H.; Schneider, F.; Sharma, N.K. Rotational Viscosity γ1 of Nematic Liquid Crystals. J. Chem. Phys. 1982, 77, 3203–3208. [Google Scholar] [CrossRef]
- Oswald, P. Measurement with a Rotating Magnetic Field of the Surface Viscosity of a Nematic Liquid Crystal. EPL 2012, 100, 26001. [Google Scholar] [CrossRef]
- Imai, M.; Naito, H.; Okuda, M.; Sugimura, A. Determination of rotational viscosity of nematic liquid crystals from transient current: Numerical analysis and experiment. Jpn. J. Appl. Phys. 1994, 33, 3482. [Google Scholar] [CrossRef]
- Siedler, L.T.S.; Hyde, A.J.; Pethrick, R.A.; Leslie, F.M. Zvetkow Twist Viscosity Measurements of Some Nematic Liquid Crystals. Mol. Cryst. Liq. Cryst. 1983, 90, 255–270. [Google Scholar] [CrossRef]
- Thoen, J.; Marynissen, H.; Van Dael, W. Temperature Dependence of the Enthalpy and the Heat Capacity of the Liquid-Crystal Octylcyanobiphenyl (8CB). Phys. Rev. A 1982, 26, 2886–2905. [Google Scholar] [CrossRef]
- Oswald, P.; Colombier, J. On the Measurement of the Bend Elastic Constant in Nematic Liquid Crystals Close to the Nematic-to-SmA and the Nematic-to-NTB Phase Transitions. Liq. Cryst. 2021, 48, 1608–1632. [Google Scholar] [CrossRef]
- Rasna, M.V.; Cmok, L.; Evans, D.R.; Mertelj, A.; Dhara, S. Phase Transitions, Optical, Dielectric and Viscoelastic Properties of Colloidal Suspensions of BaTiO3 Nanoparticles and Cyanobiphenyl Liquid Crystals. Liq. Cryst. 2015, 42, 1059–1067. [Google Scholar] [CrossRef]
- Ratna, B.R.; Shashidhar, R. Dielectric Properties of 4′-n-Alkyl-4-Cyanobiphenyls in Their Nematic Phases. Pramana 1976, 6, 278–283. [Google Scholar] [CrossRef]
- Kaminari, A.; Nikoli, E.; Athanasopoulos, A.; Sakellis, E.; Sideratou, Z.; Tsiourvas, D. Engineering Mitochondriotropic Carbon Dots for Targeting Cancer Cells. Pharmaceuticals 2021, 14, 932. [Google Scholar] [CrossRef]
- Atata, S.; Lelidis, I. Exploring Quantum Dots Size Impact at Phase Diagram and Electrooptical Properties in 8CB Liquid Crystal Soft-Nanocomposites. Nanomaterials 2023, 13, 2980. [Google Scholar] [CrossRef] [PubMed]
- Kyrou, C.; Kralj, S.; Panagopoulou, M.; Raptis, Y.; Nounesis, G.; Lelidis, I. Impact of Spherical Nanoparticles on Nematic Order Parameters. Phys. Rev. E 2018, 97, 042701. [Google Scholar] [CrossRef]
- Brochard, F. Backflow Effects in Nematic Liquid Crystals. Mol. Cryst. Liq. Cryst. 1973, 23, 51–58. [Google Scholar] [CrossRef]
- DasGupta, S.; Chattopadyay, P.; Roy, S.K. Effect of a Rigid Nonpolar Solute on the Splay, Bend Elastic Constants, and on Rotational Viscosity Coefficient of 4,4′-n-Octyl-Cyanobiphenyl. Phys. Rev. E 2001, 63, 041703. [Google Scholar] [CrossRef]
- Oswald, P.; Scalliet, C. Measurements of the Dielectric and Viscoelastic Constants in Mixtures of 4,4′-n-Octyl-Cyanobiphenyl and Biphenyl. Phys. Rev. E 2014, 89, 032504. [Google Scholar] [CrossRef]
- Sai, D.V.; Sathyanarayana, P.; Sastry, V.S.S.; Kula, P.; Dabrowski, R.; Dhara, S. Birefringence, Permittivity, Elasticity and Rotational Viscosity of Ambient Temperature, High Birefringent Nematic Liquid Crystal Mixtures. Liq. Cryst. 2014, 41, 591–596. [Google Scholar] [CrossRef]
- Chakraborty, S.; Das, M.K.; Weissflog, W. Measurement of Visco-Elastic Properties in a Binary System of Hockey Stick-Shaped and Calamitic Mesogens. Eur. Phys. J. E 2019, 42, 138. [Google Scholar] [CrossRef] [PubMed]
- Sathyanarayana, P.; Sadashiva, B.K.; Dhara, S. Splay-Bend Elasticity and Rotational Viscosity of Liquid Crystal Mixtures of Rod-Like and Bent-Core Molecules. Soft Matter 2011, 7, 8556–8560. [Google Scholar] [CrossRef]
- Cordoyiannis, G.; Lavrič, M.; Tzitzios, V.; Trček, M.; Lelidis, I.; Nounesis, G.; Kralj, S.; Thoen, J.; Kutnjak, Z. Experimental Advances in Nanoparticle-Driven Stabilization of Liquid-Crystalline Blue Phases and Twist-Grain Boundary Phases. Nanomaterials 2021, 11, 2968. [Google Scholar] [CrossRef] [PubMed]
- Rzoska, S.J.; Starzonek, S.; Łoś, J.; Drozd-Rzoska, A.; Kralj, S. Dynamics and Pretransitional Effects in C60 Fullerene Nanoparticles and Liquid Crystalline Dodecylcyanobiphenyl (12CB) Hybrid System. Nanomaterials 2020, 10, 2343. [Google Scholar] [CrossRef] [PubMed]
- Kyrou, C.; Ambrozic, M.; Tsiourvas, D.; Kralj, S.; Atata, S.; Lelidis, I. Effect of Quantum Dots on the Phase Behavior and Order of 8CB Liquid Crystal. J. Mol. Liq. 2023, 387, 122568. [Google Scholar] [CrossRef]
- Rani, A.; Sinha, A. Enhanced Dielectric, Electrical and Electro-Optical Properties: Towards Understanding the Interaction in Mesophases of 8OCB Liquid Crystal Dispersed with CdSe/ZnS Quantum Dots. J. Mol. Liq. 2024, 398, 124201. [Google Scholar] [CrossRef]
- Atata, S.B.; Basina, G.; Tzitzios, V.; Lelidis, I. Influence of Chalcopyrite Nanoplatelets on Nematic Phases of Bend-Shaped Dimeric Molecules: Phase Diagram, Birefringence, and Reorientation Transition. J. Mol. Liq. 2024, 412, 125842. [Google Scholar] [CrossRef]
- Garbovskiy, Y.; Glushchenko, A. Ferroelectric Nanoparticles in Liquid Crystals: Recent Progress and Current Challenges. Nanomaterials 2017, 7, 361. [Google Scholar] [CrossRef]



| Characteristic | Value |
|---|---|
| Shape | Square |
| Function | Sinusoidal |
| Frequency | 1 KHz |
| Voltage | 0–5 V |
| Duration of pulse | 0.333 s |
| Step of acquisition | 0.4 ms |
| Duration of acquisition | 1 s |
| 8CB | 0.2% w/w | 4.7% w/w | |
|---|---|---|---|
| 0.155 ± 0.005 | 0.1604 ± 0.0006 | 0.1628 ± 0.0007 | |
| 40.17 | 39.85 | 38.74 | |
| 40.12 | 39.61 | 38.0 | |
| 33.12 | 32.66 | 31.47 | |
| Nematic Range | 7.00 | 6.95 | 6.53 |
| Fit Function | 8CB | 0.2% w/w | 4.7% w/w | |||
|---|---|---|---|---|---|---|
| (eV) | (eV) | (eV) | ||||
| ln() vs. | 0.67 ± 0.07 | 0.944 | 0.70 ± 0.09 | 0.917 | 0.76 ± 0.10 | 0.909 |
| ln() vs. | 0.083 ± 0.008 | 0.947 | 0.092 ± 0.015 | 0.879 | 0.107 ± 0.017 | 0.877 |
| ln() vs. | 0.25 ± 0.07 | 0.721 | 0.31 ± 0.10 | 0.637 | 0.41 ± 0.11 | 0.707 |
| ln() vs. | 0.030 ± 0.009 | 0.679 | 0.040 ± 0.015 | 0.561 | 0.056 ± 0.018 | 0.652 |
| ln() vs. | 0.135 ± 0.008 | 0.981 | 0.144 ± 0.014 | 0.95 | 0.157 ± 0.017 | 0.943 |
| ln() vs. | 0.145 ± 0.008 | 0.982 | 0.155 ± 0.014 | 0.956 | 0.166 ± 0.017 | 0.949 |
| ln() vs. | 1.03 ± 0.06 | 0.982 | 1.12 ± 0.07 | 0.975 | 1.11 ± 0.09 | 0.965 |
| Parameters | 8CB | 0.2% w/w | 4.7% w/w |
|---|---|---|---|
| Range (°C) | 33.2–40.1 | 32.7–39.6 | 31.6–37.8 |
| Tf (°C) | 33.07 | 32.61 | 31.43 |
| g (mPa·s) | 601 ± 16 | 601 | 601 |
| (°C) | 0.375 ± 0.021 | 0.375 | 0.375 |
| 2 ± 0.02 | 1.86 ± 0.03 | 1.80 ± 0.04 | |
| 0.983 | 0.985 | 0.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schinas, A.; Atata, S.B.; Tsiourvas, D.; Lelidis, I. Influence of Carbon Quantum Dots on the Orientational Order and Rotational Viscosity of 8CB. Nanomaterials 2025, 15, 1278. https://doi.org/10.3390/nano15161278
Schinas A, Atata SB, Tsiourvas D, Lelidis I. Influence of Carbon Quantum Dots on the Orientational Order and Rotational Viscosity of 8CB. Nanomaterials. 2025; 15(16):1278. https://doi.org/10.3390/nano15161278
Chicago/Turabian StyleSchinas, Alfredos, Stefanos Basim Atata, Dimitris Tsiourvas, and Ioannis Lelidis. 2025. "Influence of Carbon Quantum Dots on the Orientational Order and Rotational Viscosity of 8CB" Nanomaterials 15, no. 16: 1278. https://doi.org/10.3390/nano15161278
APA StyleSchinas, A., Atata, S. B., Tsiourvas, D., & Lelidis, I. (2025). Influence of Carbon Quantum Dots on the Orientational Order and Rotational Viscosity of 8CB. Nanomaterials, 15(16), 1278. https://doi.org/10.3390/nano15161278







